1 Introduction

In recent years scientific machine learning has been on the rise many problems have been solved using scientific machine learning. The algorithms of these methods are solely based on the mathematical structure of optimisation. Daily new methods are coming up that work with different techniques of optimisation [1, 2]. Neural networks are the base for scientific machine learning. They are a graph structure in which, when given a set of inputs and outputs, the structure learns the behaviour between these inputs and outputs then it can predict the output for any given input. After recent work in this field, an algorithm called automatic differentiation has come up in which the computer can differentiate any functions at any point quickly [3]. This method is not numerical, so even for complex structures, the algorithm can find its derivatives with really low errors. Then with the help of automatic differentiation, the problem of differential equations was looked at using the neural networks. These methods were referred to as physics-informed neural networks (PINNs) as the neural network train using the physical properties of the equations like in [4,5,6,7,8,9,10,11]. It was seen that using PINNs, a few of the classical problems in the field of numerical methods for differential equations were solved. One of them was the problem of dimensionality. Also, it was seen that using automatic differentiation to solve differential equations was faster than traditional numerical techniques. PINNs have been made even faster, such as conservative physics-informed neural networks (cPINN), where the neural networks constructed are such that they are deep in complex sub-domains and shallow in relatively simple and smooth sub-domains [12]. In other methods like XPINNs, where domain decomposition results in several sub-problems on subdomains, the individual networks can solve each sub-problem parallelly to accelerate convergence and improve generalization empirically [13,14,15]. Furthermore, [16,17,18] recently presented a detailed error analysis for PINNs.

The use of PINNs in modelling has shown promising results in a variety of fields. PINNs are advantageous as they need less data to predict solutions. They are practically useful when experimental data is scarce or expensive to obtain. For finding microstructure properties of polycrystalline Nickel so that we can infer the spatial variation of compliance coefficients of the material using ultrasound data, we find that traditional methods face problems as the wavefield data acquired experimentally or numerically are often sparse and high-dimensional in nature; the PINNs method provides a promising approach for solving inverse problems, where free parameters can be inferred, or missing physics can be recovered using noisy, sparse, and multi-fidelity scattered data sets [19]. Inverse water wave problems refer to the problem of obtaining the ocean floor deviation from the surface wave elevation. These problems are ill-posed since the direct problem that maps ocean floor deformations to sur- face water waves is not one-to-one, and thus small changes in the boundary conditions can cause significant differences in the outputs. PINNs can be used to generate solutions to such ill-posed problems using only data on the free surface elevation and depth of the water [20]. The use of shock waves in supersonic compressible flow is essential in many engineering applications, such as in the design of high-speed aircraft and spacecraft. The shock wave causes the solutions to become locally discontinuous and challenging to approximate using traditional numerical methods. However, PINNs can tackle such problems since they can approximate local discontinuities and extract relevant features from the data even in the presence of discontinuities [21]. High-speed aerodynamic flow can be modelled by the Euler equations, which follow the conservation of mass, momentum, and energy for compressible flow in the inviscid limit. Solutions of these conservation laws often develop discontinuities in some finite time, even though the initial conditions may be smooth. Still, PINNs can get a relatively stable solution without any regularization [22]. Black Scholes equation is a famous equation predicting options value in financial trading, these equations involve many variables and are difficult to solve numerically using standard mesh based numerical methods PINNs are good numerical techniques to tackle such problems [23]. PINNS have also been used in solving some families of fractional differential equations which are hard to solve using standard methods [24]. Overall, the use of PINNs in modelling has shown great potential in a wide range of fields. As the field continues to develop, PINNs will likely become an increasingly important tool for scientists and engineers seeking to understand better and predict the behaviour of complex systems.

In Sect. 2, we work with a fully connected neural network which not only tries to solve the differential equation but also tries to predict the gradient of the differential equation called gradient-enhanced physics-informed neural networks (GPINNs) [25]. We look at the neural tangent kernel (NTK) technique, which is a famous technique used to understand the behaviour of a neural network for the GPINN [26,27,28,29]. We look at the popular optimisation technique of stochastic gradient descent and try to understand the behaviour of the neural network when it uses this optimisation technique. We come across the problem of frequency bias, also called the F-Principle and try to work our way around the problem [30,31,32,33,34,35,36]. In Sect. 3, we provide some numerical results for different kinds of two point boundary value problems using techniques discussed in Sect. 2.

2 The GPINN-NTK Method

In this section, we discuss how the weights associated with individual terms of the loss function affect network training. For this, we will consider a single hidden layer feed-forward neural network. Theoretically, we will demonstrate that for a sufficiently large number of neurons in the hidden layer, the neural network solution approaches the exact solution as training time increases. Consider the nonlinear boundary value problem

$$\begin{aligned} \begin{aligned} u_{x x} =f(x,u,u_{x}),\quad x \in (a,b),\quad u(a)=g_{1}, \quad u(b)=g_{2}. \end{aligned} \end{aligned}$$
(1)

We construct a neural network that automatically satisfies the boundary condition. There are further methods for creating these neural networks, such as creating a differential equation solution and multiplying it with an approximate distance function to the boundary that perfectly meets the boundary constraints [37]. The method also uses generalized barycentric coordinates to construct the distance function. Here we construct the distance function using linear Lagrange interpolation. The function N outputs the value

$$\begin{aligned} N(x) = \frac{1}{b-a}\left[ (x-a) g_{2} - (x-b) g_{1}\right] + (x-a)(x-b)\mathcal {N}(x), \end{aligned}$$
(2)

where \(\mathcal {N}\) is a feedforward neural network with initialised parameters that will be trained also it can be seen that at \(x=a\) and \(x=b\), the network N depends only on the Lagrange interpolant and hence satisfies the boundary conditions exactly. Further, the loss function \(L(\Theta )\) is taken in such a way that the neural network N(x) satisfies Eq. (1).

$$\begin{aligned} L(\Theta )=w_{r} {L}_r(\Theta )+w_{s} {L}_s(\Theta ), \end{aligned}$$
(3)

where \(w_{r}\) and \(w_{s}\) are the associated weights and

$$\begin{aligned} {L}_r(\Theta )&= \frac{1}{2} \sum _{i=1}^{N_r}\vert N_{x x}\left( {x}_r^i, \Theta \right) - f\left( {x}_r^i,N\left( {x}_r^i, \Theta \right) ,N_{x}\left( {x}_r^i, \Theta \right) \right) \vert ^2 \nonumber \\&=\frac{1}{2} \sum _{i=1}^{N_r}\vert \mathcal {L} N\left( {x}_r^i, \Theta \right) \vert ^2, \end{aligned}$$
(4)
$$\begin{aligned} {L}_s(\Theta )&=\frac{1}{2} \sum _{i=1}^{N_r}\vert N_{x x x}\left( {x}_r^i, \Theta \right) - f_{x}-\frac{df}{dN}N_{x}-\frac{df}{dN_{x}}N_{xx}\vert ^2 \nonumber \\&=\frac{1}{2} \sum _{i=1}^{N_r}\vert \mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) \vert ^2. \end{aligned}$$
(5)

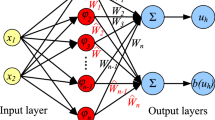
Here, the loss term \({L}_{s}(\Theta )\) is the \({l}_{2}\)-error of the neural network trying to fit the gradient of the differential equation. For the differential operator \(\mathcal {L}\) and the spatial derivative operator \(\mathcal {L}_x\). The term \({L}_{s}(\Theta )\) helps the network better understand the properties of the equation, mainly their derivatives. The graphical representation of the proposed network can be found in Fig. 1.

We use the NTK method for our constructed GPINN which satisfies the boundary condition automatically. The theory of NTK for PINNs has already been developed in [26], where the convergence of PINNs has been shown theoretically considering the boundary condition in their loss term. Here the theory of NTK has been developed for a network which does not contain the boundary term but contains a gradient loss term. Also, the network constructed here depends on the distance function created using Lagrange interpolation.

2.1 The Network Architecture

Consider a neural network having a single hidden layer with N nodes. Assuming weight parameters in the network be \(\mathcal {W} = \{{W}_{0},{W}_{1}\}\) where both \({W}_{0}\) and \({W}_{1}\) are \(N\times 1\) matrices. The bias parameters are \(\mathcal {B} = \{b_{0},b_{1}\}\), \(b_{0}\) and \(b_{1}\) are \(N\times 1\) and \(1\times 1\) matrix respectively. Define \(\Theta \) as the collection of all weights and biases. The network’s activation function is selected to be the hyperbolic tangent function, which is provided by

$$\begin{aligned} \sigma (x)={\left( e^x-e^{-x}\right) }/{\left( e^{-x}+e^x\right) }, \quad x \in \mathbb {R}. \end{aligned}$$
(6)

Then, for an input vector X, the network results the output

$$\begin{aligned} \mathcal {N}(X) = \frac{1}{\sqrt{N}} \sum _{k=1}^N {W}_{1k} \sigma \left( {W}_{0k} X+{b}_{0k}\right) +{b}_{1}, \end{aligned}$$
(7)

where k is the index of the k th row of the matrices \(W_0,W_1\) and \(b_0\).

Fig. 1
figure 1

Model of the network with gradient descent

Full size image

2.2 Training of the Network

The gradient descent optimization approach is used to train the neural network. The algorithm for which is provided by

$$\begin{aligned} W_{jk}^{t+1} = W_{jk}^{t}+\eta \left( -\frac{\partial {L}^t}{\partial W_{jk}^{t}}\right) ,\quad \quad \forall k = {1,2,3,...,N}, \end{aligned}$$
(8)

where \(j=0,1\) and \(\eta \) is the learning rate for the algorithm. For infinitesimally small values of \(\eta \), and a large number of neurons, the above discrete equation shows continuous behaviour, and the algorithm can be seen as

$$\begin{aligned} \frac{d W_{jk}}{d t} = -\nabla {L}(W_{jk}), \end{aligned}$$
(9)

where the discrete iteration steps become a continuous domain of time and each \(W_{jk}\) is a continuous function over time t. In general, for all weights and biases, we can write this relation as

$$\begin{aligned} \frac{d \Theta }{d t} = -\nabla {L}(\Theta ), \end{aligned}$$
(10)

The gradient descent shows a learning bias known as the F-principle. The network shows a bias toward the loss term having lower frequencies, and it trains the term with lower frequencies first and then the terms with higher frequencies. Let

$$\begin{aligned} \mathcal {L}u(t)&=\mathcal {L}\left( \varvec{x}_r, \Theta (t)\right) =\left\{ \mathcal {L}\left( x_r^i, \Theta (t)\right) \right\} _{i=1}^{N r}, \end{aligned}$$
(11)
$$\begin{aligned} \mathcal {L}_x u(t)&=\mathcal {L}_x u\left( \varvec{x}_r, \Theta (t)\right) =\left\{ \mathcal {L}_x u\left( x_r^i, \Theta (t)\right) \right\} _{i=1}^{N r}. \end{aligned}$$
(12)

Consider the loss function

$$\begin{aligned} {L}(\Theta )=\frac{1}{2} \sum _{i=1}^{N_r}\vert \mathcal {L} N\left( {x}_r^i, \Theta \right) \vert ^2+\frac{1}{2} \sum _{i=1}^{N_r} \vert \mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) \vert ^2. \end{aligned}$$
(13)

Then, according to the definition, we obtain

$$\begin{aligned} \nabla L(\Theta ) = \frac{dL}{d\Theta }&= \sum _{i=1}^{N_r}\vert \mathcal {L} N\left( {x}_r^i, \Theta \right) \vert \frac{d\mathcal {L} N\left( {x}_r^i, \Theta \right) }{d\Theta } \nonumber \\&\quad +\sum _{i=1}^{N_r}\vert \mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) \vert \frac{d\mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) }{d\Theta }. \end{aligned}$$
(14)

Now, for \(0 \le j \le N_b\), consider

$$\begin{aligned} \frac{d \mathcal {L} N\left( {x}_r^j, \Theta \right) }{d t}=\frac{d \mathcal {L} N\left( {x}_r^j, \Theta \right) ^{\top }}{d \Theta } \cdot \frac{d \Theta }{d t}. \end{aligned}$$
(15)

Substituting the value of \(\frac{d \Theta }{d t}\), we find

$$\begin{aligned} \frac{d \mathcal {L} N\left( {x}_r^j, \Theta \right) }{d t}&= - \frac{d \mathcal {L} N\left( {x}_r^j, \Theta \right) ^{\top }}{d \Theta } \cdot \ \Biggl [ \sum _{i=1}^{N_r} \vert \mathcal {L} N\left( {x}_r^i, \Theta \right) \vert .\frac{d\mathcal {L} N\left( {x}_r^i, \Theta \right) }{d\Theta } \nonumber \\&\quad + \sum _{i=1}^{N_r} \vert \mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) \vert .\frac{d\mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) }{d\Theta }\Biggr ], \end{aligned}$$
(16)

and

$$\begin{aligned} \frac{d \mathcal {L} N \left( x_r^j, \Theta \right) }{d \Theta }^{\top }=&\left[ \begin{array}{c} \frac{d \mathcal {L} N \left( x_r^{1}, \Theta \right) }{d \Theta } \\ \frac{d \mathcal {L} N\left( x_r^2, \Theta \right) }{d \Theta } \\ \vdots \\ \frac{d \mathcal {L} N \left( x_r^{N_r}, \Theta \right) }{d \Theta } \end{array}\right] . \end{aligned}$$
(17)

Therefore, the matrix multiplication

$$\begin{aligned} \frac{d \mathcal {L} N\left( x_r^j, \Theta \right) }{d \Theta }^{\top }\sum _{i=1}^{N_r} \vert \mathcal {L} N\left( {x}_r^i, \Theta \right) \vert .\frac{d\mathcal {L} N\left( {x}_r^i, \Theta \right) }{d\Theta } \end{aligned}$$

yields

$$\begin{aligned} \left[ \begin{array}{c} \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \\ \vdots \\ \frac{d \mathcal {L} N \left( x_r^{N r}, \Theta \right) }{d \Theta } \end{array}\right]&\cdot \left[ \begin{array}{l} \vert \mathcal {L} N\left( x_r^{1}, \Theta \right) \vert \frac{d\mathcal {L} N\left( x_r^{1}, \Theta \right) }{d\Theta } +\\ \quad \ldots +\vert \mathcal {L} N\left( x_r^{Nr}, \Theta \right) \vert \frac{d \mathcal {L} N\left( x_r^{Nr}\right. )}{d \Theta } \end{array}\right] \nonumber \\&= \left[ \begin{array}{l} \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \vert \mathcal {L} N\left( x_r^{1}, \Theta \right) \vert +\ldots \\ \quad \quad \quad \quad \quad +\frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \vert \mathcal {L} N\left( x_r^{Nr}, \Theta \right) \vert \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \vert \mathcal {L} N\left( x_r^{1}, \Theta \right) \vert +\ldots \\ \quad \quad \quad \quad \quad +\frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \vert \mathcal {L} N\left( x_r^{Nr}, \Theta \right) \vert \\ \end{array}\right] , \end{aligned}$$
(18)

which is equivalent to

$$\begin{aligned} {\left[ \begin{array}{lll} \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } &{} \ldots \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \\ &{} \vdots \\ \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{1}, \Theta \right) }{d \Theta } &{} \ldots \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \frac{d \mathcal {L} N\left( x_r^{Nr}, \Theta \right) }{d \Theta } \end{array}\right] } \cdot \left[ \begin{array}{c} \vert \mathcal {L} N\left( x_r^1 ,\Theta \right) \vert \\ \vert \mathcal {L} N\left( x_r^2 ,\Theta \right) \vert \\ \vdots \\ \vert \mathcal {L} N\left( x_r^{Nr}, \Theta \right) \vert \end{array}\right] . \end{aligned}$$
(19)

We know that \(\Theta \) are weights and biases, therefore, one obtains

$$\begin{aligned} \frac{d \mathcal {L} N\left( x_r^i, \Theta \right) }{d \Theta }=\frac{d \mathcal {L} N\left( x_r^i, w_{11}\right) }{d w_{11}}+\frac{d \mathcal {L} N\left( x_{r}^i, w_{12}\right) }{d w_{12}}+\cdots \cdot + \frac{d \mathcal {L} N\left( x_r^i, b_1\right) }{d b_1}. \end{aligned}$$
(20)

As a result, \(\forall \theta \in \Theta \), we can write

$$\begin{aligned} \frac{d \mathcal {L} N\left( x_r^i ,\Theta \right) }{d \Theta }=\sum _{\theta \in \Theta } \frac{d \mathcal {L} N\left( x_r^i, \Theta \right) }{ d \theta } . \end{aligned}$$
(21)

As a result, now we define a matrix \(\varvec{k}_{rr}\), with dimension \( Nr \times Nr\), whose (i, j)th element is defined as the inner product representation

$$\begin{aligned} ({k}_{rr})_{ij}&=\sum _{\theta \in \Theta } \frac{d \mathcal {L} N\left( x_r^j, \Theta \right) }{d \theta } \frac{d \mathcal {L} N\left( x_r^i, \Theta \right) }{d \theta }\nonumber \\&=\left\langle \frac{d \mathcal {L} N\left( x_b^j, \Theta \right) }{d \Theta }, \frac{d \mathcal {L} N\left( x_b^i, \Theta \right) }{d \Theta }\right\rangle . \end{aligned}$$
(22)

Similarly, the matrix multiplication

$$\begin{aligned} \frac{d \mathcal {L} N \left( x_r^j, \Theta \right) }{d \Theta }^{\top }\sum _{i=1}^{N_r} \vert \mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) \vert .\frac{d\mathcal {L}_{x} N\left( {x}_r^i, \Theta \right) }{d\Theta } \end{aligned}$$

yields

$$\begin{aligned} \varvec{k}_{rt}\cdot \left[ \begin{array}{c} \vert \mathcal {L}_{x} N\left( x_r^1 ,\Theta \right) \vert \\ \vert \mathcal {L}_{x} N\left( x_r^2 ,\Theta \right) \vert \\ \vdots \\ \vert \mathcal {L}_{x} N\left( x_r^{Nr}, \Theta \right) \vert \end{array}\right] , \end{aligned}$$
(23)

where

$$\begin{aligned} ({k}_{rt})_{i j}=\left\langle \frac{d \mathcal {L} N\left( x_r^j, \Theta \right) }{d \Theta }, \frac{d \mathcal {L}_{x} N\left( x_r^i, \Theta \right) }{d \Theta }\right\rangle . \end{aligned}$$
(24)

Therefore, for an input vector of collocation points \(\varvec{x}_r\), we have

$$\begin{aligned} \frac{d \mathcal {L} N\left( \varvec{x}_r, \Theta \right) }{d t}=-\left[ \begin{array}{ll} \varvec{k}_{rr}&\varvec{k}_{rt} \end{array}\right] \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta \right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta \right) \vert \end{array}\right] , \end{aligned}$$
(25)

where the dimensions of the matrices are

$$\begin{aligned} {\left[ \varvec{k}_{rr}\right] =N_r \times N_r,\quad \left[ \varvec{k}_{rt}\right] =N_r \times N_r}, \quad {\left[ \begin{array}{l} \vert \mathcal {L} N(\varvec{x}_r, \Theta )\vert \\ \vert {\mathcal {L}_{x} N}(\varvec{x}_r, \Theta )\vert \end{array}\right] =N_r+N_r}. \end{aligned}$$

Similarly, we can show that

$$\begin{aligned} \frac{d \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta \right) }{d t}=-\left[ \begin{array}{ll} \varvec{k}_{tr}&\varvec{k}_{tt} \end{array}\right] \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta \right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta \right) \vert \end{array}\right] , \end{aligned}$$
(26)

where \(\varvec{k}_{tr}=\varvec{k}_{rt}^{\top }\), and

$$\begin{aligned} ({k}_{tt})_{ij}&=\sum _{\theta \in \Theta } \frac{d \mathcal {L}_{x} N\left( x_r^j, \Theta \right) }{d \theta } \frac{d \mathcal {L}_{x} N\left( x_r^i, \Theta \right) }{d \theta } \nonumber \\&=\left\langle \frac{d \mathcal {L}_{x} N\left( x_r^j, \Theta \right) }{d \Theta }, \frac{d \mathcal {L}_{x} N\left( x_r^i, \Theta \right) }{d \Theta }\right\rangle . \end{aligned}$$
(27)

The above algebraic simplification provides us with a complete system, given by

$$\begin{aligned} \left[ \begin{array}{l} \frac{d \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) }{d t} \\ \frac{d \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (t)\right) }{d x} \end{array}\right] = - \left[ \begin{array}{ll} \varvec{k}_{rr} &{} \varvec{k}_{rt} \\ \varvec{k}_{tr} &{} \varvec{k}_{tt} \end{array}\right] \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta \right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta \right) \vert \end{array}\right] . \end{aligned}$$
(28)

The matrix

$$\begin{aligned} \varvec{k}=\left[ \begin{array}{ll} \varvec{k}_{rr} &{} \varvec{k}_{rt} \\ \varvec{k}_{tr} &{} \varvec{k}_{tt} \end{array}\right] , \end{aligned}$$

is called the neural tangent kernel. It follows that

$$\begin{aligned} \frac{d\mathcal {L}N}{d\Theta } = \frac{dN_{x x}}{d\Theta }-\frac{df}{dN_{x}}\frac{dN_{x}}{d\Theta }- \frac{df}{dN}\frac{dN}{d\Theta }, \end{aligned}$$
(29)

and

$$\begin{aligned} \frac{d\mathcal {L}_{x}N}{d\Theta } = \frac{dN_{xxx}}{d\Theta }-\frac{df}{dN_{x}}\frac{dN_{xx}}{d\Theta }- \left( \frac{df}{dN}+\frac{d^2f}{dN^2_{x}}N_{xx}\right) \frac{dN_{x}}{d\Theta }-\frac{d^2f}{dN^2}N_{x}\frac{dN}{d\Theta }. \end{aligned}$$
(30)

From Eq. (2), using the structure of \(\mathcal {N}(x)\), we have the output of N(x). Differentiating N(x) in the spatial domain, we find

$$\begin{aligned} N_{x}&={(g_{2}-g_{1})}/{(b-a)} +(2x-b-a)\mathcal {N}+ (x-b)(x-a)\mathcal {N}_x, \end{aligned}$$
(31)
$$\begin{aligned} N_{xx}&=2\mathcal {N} +2(2x-b-a)\mathcal {N}_x+ (x-b)(x-a)\mathcal {N}_{xx},\end{aligned}$$
(32)
$$\begin{aligned} N_{xxx}&=6\mathcal {N}_x +3(2x-b-a)\mathcal {N}_{xx}+ (x-b)(x-a)\mathcal {N}_{xxx}. \end{aligned}$$
(33)

Upon using the structure of \(\mathcal {N}(x)\), we have

(34)
(35)
(36)
(37)

Here \(\dot{\sigma }\), \(\ddot{\sigma }\) and denote the first, second and third derivative of the hyperbolic tangent activation function. This is possible to do since the hyperbolic tangent function is a \(C^{\infty }\) function. Here it can be seen that the derivatives \(\frac{dN_{xx}}{d\Theta }\) and \(\frac{dN_{xxx}}{d\Theta }\) depend only on the network \(\mathcal {N}\) and its spatial derivative.

2.3 Initialisation of Parameters

The behaviour of the neural network relies heavily on the initial values of the hyperparameters. The number of layers defines the depth of a network; deeper networks can capture more complex relationships in the data. However, striking a balance is essential as deeper networks might also suffer from vanishing or exploding gradients, making them harder to train. The width of a network is defined by the number of neurons in the hidden layer. Wider networks help better approximate the solution of the physical equation, especially for problems with high-dimensional input or complex dynamics. Still, they may also increase overfitting and require more computational resources. Learning rate is the rate by which weights and bias hyperparameters are updated. A higher learning rate can lead to fast convergence but may result in overshooting and instability. On the other hand, a very low learning rate can cause slow convergence and might get stuck in local minima. Weights and bias hyperparameters are responsible for the output of the neural network. Since we need to optimize the loss function, the network would converge to the solution faster if we choose the biases and weights close to the minima. The learning rate is another crucial factor of the gradient descent optimization technique. If the initial parameters are not close to the minimum, the initial loss would be higher, and the value of \({\delta \mathcal {L}^t}/{\delta W_{jk}^{t}}\) may blow up. Hence, we need a small learning rate to control the change in the weight and bias so that it does not diverge. Controlling the relation between initial weights and the learning rate makes neural network training more successful.

It is always advised to take small initial parameters and a small learning rate and train the network over a bigger data set for a longer number of iterations so that the network converges. As for a small learning rate, more information and more training iterations are required. We need the initial loss term to be small so that the Jacobian \({\delta \mathcal {L}^t}/{\delta W_{jk}^{t}}\) does not blow up. Consider the mean square error (MSE) loss term

$$\begin{aligned} {L}(\Theta )=\frac{w_r}{2} \sum _{i=1}^{N_r}\vert \mathcal {L}N\left( {x}_r^i, {\Theta }\right) \vert ^2+\frac{w_s}{2} \sum _{i=1}^{N_r}\vert \mathcal {L}_{x}N\left( {x}_r^i, {\Theta }\right) \vert ^2, \end{aligned}$$
(38)

where \(w_{r}\) and \(w_{s}\) are the weights associated with the loss term in the differential equation and their gradient. To have a good initial loss which will be easy to minimize, we need to choose appropriate values of these weights. Which will be the main aim of the algorithm.

3 Convergence of Neural Network Through Neural Tangent Kernels

If we assume the initial parameter \(\Theta \) to be a Gaussian process N(0, 1) (see [26]), then it can be shown that

$$\begin{aligned} N_{xx}(x,\Theta ) \xrightarrow {D}\mathcal {G}_{p}(0,\Sigma _{xx}(x,x^{\prime })), \end{aligned}$$
(39)

and

$$\begin{aligned} N_{xxx}(x,\Theta ) \xrightarrow {D} \mathcal {G}_{p}(0,\Sigma _{xxx}(x,x^{\prime })), \end{aligned}$$
(40)

where

$$\begin{aligned} \Sigma _{xx}(x,x^{\prime }) = \underset{u,v\in N(0,1)}{E}[u^4 \ddot{\sigma }(wx+v) \ddot{\sigma }(ux^{\prime }+v) ], \end{aligned}$$

and

In other words if the initial parameters are taken from the normal distribution then the resulting output of the network, and its derivatives also follow a Gaussian process. We will demonstrate that as the number of neurons in the single hidden layer are sufficiently large then, the initial tangent kernel approaches a deterministic value.

Firstly, let us consider the derivatives of the output of the network and the spatial derivative of the output of the network with respect to the parameters of the network. For \(t=0,1\), we have

$$\begin{aligned} \frac{\partial N_{x}\left( x ,\Theta \right) }{\partial W_{tk}}&= (2x-a-b)\frac{\partial \mathcal {N}\left( x ,\Theta \right) }{\partial W_{tk}}+(x-a)(x-b)\frac{\partial \mathcal {N}_{x}\left( x, \Theta \right) }{\partial W_{tk}}, \end{aligned}$$
(41)
$$\begin{aligned} \frac{\partial N_{x}\left( x ,\Theta \right) }{\partial b_{tk}}&=(2x-a-b)\frac{\partial \mathcal {N}\left( x ,\Theta \right) }{\partial b_{tk}}+(x-a)(x-b)\frac{\partial \mathcal {N}_{x}\left( x, \Theta \right) }{\partial b_{tk}} , \end{aligned}$$
(42)
$$\begin{aligned} \frac{\partial N_{xx}\left( x ,\Theta \right) }{\partial W_{tk}}&=2\frac{\partial \mathcal {N}\left( x , \Theta \right) }{\partial W_{tk}} + 2(2x-a-b)\frac{\partial \mathcal {N}_{x}\left( x ,\Theta \right) }{\partial W_{tk}} \nonumber \\&\quad +(x-a)(x-b)\frac{\partial \mathcal {N}_{xx}\left( x, \Theta \right) }{\partial W_{tk}}, \end{aligned}$$
(43)
$$\begin{aligned} \frac{\partial N_{xx}\left( x, \Theta \right) }{\partial b_{tk}}&=2\frac{\partial \mathcal {N}\left( x , \Theta \right) }{\partial b_{tk}} + 2(2x-a-b)\frac{\partial \mathcal {N}_{x}\left( x ,\Theta \right) }{\partial b_{tk}} \nonumber \\&\quad +(x-a)(x-b)\frac{\partial \mathcal {N}_{xx}\left( x, \Theta \right) }{\partial b_{tk}}, \end{aligned}$$
(44)
$$\begin{aligned} \frac{\partial N_{xxx}\left( x ,\Theta \right) }{\partial W_{tk}}&=6\frac{\partial \mathcal {N}_{x}\left( x , \Theta \right) }{\partial W_{tk}} + 3(2x-a-b)\frac{\partial \mathcal {N}_{xx}\left( x ,\Theta \right) }{\partial W_{tk}} \nonumber \\&\quad +(x-a)(x-b)\frac{\partial \mathcal {N}_{xxx}\left( x, \Theta \right) }{\partial W_{tk}}, \end{aligned}$$
(45)
$$\begin{aligned} \frac{\partial N_{xxx}\left( x, \Theta \right) }{\partial b_{tk}}&=6\frac{\partial \mathcal {N}_{x}\left( x , \Theta \right) }{\partial b_{tk}} + 3(2x-a-b)\frac{\partial \mathcal {N}_{xx}\left( x ,\Theta \right) }{\partial b_{tk}} \nonumber \\&\quad +(x-a)(x-b)\frac{\partial N^{\prime \prime \prime }_{1}\left( x, \Theta \right) }{\partial b_{tk}}. \end{aligned}$$
(46)

where \(\mathcal {N}_{x}\), \(\mathcal {N}_{xx}\) and \(\mathcal {N}_{xxx}\) are defined in Eqs. (35)–(37). The derivatives of the output \(\mathcal {N}\) of the network and the derivatives of the spatial derivatives \(\mathcal {N}_{x}\), \(\mathcal {N}_{xx}\) and \(\mathcal {N}_{xxx}\) of the network with respect to the parameters of the network are given in Appendix A. After that, we may update the weights and biases in the gradient descent iterative method using the above-provided derivatives for the backpropagation technique.

We assume the weights and biases parameters to be bounded by some constant to achieve bounded numerical data from the network and their derivatives with respect to the parameters. Moreover, the bounded derivatives yield a deterministic value in each iteration from the tangent kernel and render a convergent algorithm.

Theorem 3.1

For a fully connected single-layer neural network having N neurons, if there exists a constant \(C>0\) such that \(\sup _{t \in [0, T]}\Vert \Theta (t)\Vert _{\infty } \le C\), and \(D^{2}f \in C^{\infty }([a,b])\). Then, the following holds

$$\begin{aligned} \sup _{t \in [0, T]}\left\| \frac{\partial \mathcal {L}N}{\partial {W}_{(t)}}\right\| _{\infty }&=\mathcal {O}\left( \frac{1}{\sqrt{N}}\right) , \quad \quad \sup _{t \in [0, T]}\left\| \frac{\partial \mathcal {L}_{x}N}{\partial {W}_{(t)}}\right\| _{\infty }=\mathcal {O}\left( \frac{1}{\sqrt{N}}\right) , \end{aligned}$$
(47)
$$\begin{aligned} \sup _{t \in [0, T]}\left\| \frac{\partial \mathcal {L}N}{\partial {b}_{(0)}}\right\| _{\infty }&=\mathcal {O}\left( \frac{1}{\sqrt{N}}\right) , \quad \quad \sup _{t \in [0, T]}\left\| \frac{\partial \mathcal {L}_{x}N}{\partial {b}_{(0)}}\right\| _{\infty }=\mathcal {O}\left( \frac{1}{\sqrt{N}}\right) , \end{aligned}$$
(48)

for \(N \xrightarrow {} \infty \), \(t=0,1\). Here, D denotes the partial differentiation with respect to arguments.

Proof

Combining the Eqs. (31)–(37), it can be seen that the derivatives of \(N_{xx}\) and \(N_{xxx}\) with respect to the parameter depend only on some finite algebraic relations between the weights \(W_0,W_1\) biases \(b_0\) and the hyperbolic tangent activation function and its derivatives. The initial assumption of the theorem was \(\sup _{t \in [0, T]}\Vert {\Theta }(t)\Vert _{\infty } \le C\). This implies, \( \sup _{t \in [0, T]}\Vert {W}_{t}(t)\Vert _{\infty } \le C, \sup _{t \in [0, T]}\Vert {b}_{0}(t)\Vert _{\infty } \le C \). Moreover, by the definition of the hyperbolic tangent function, we have \(\Vert \sigma ^{k}(x)\Vert _{\infty } \le 1\), for its \(k^{th}\) derivative \(k=0,1,...\) and \(x \in [a,b]\). By the second assumption of the theorem, we have that \(\Vert \frac{df}{du}\Vert _{\infty } \le M\), \(\Vert \frac{d^2f}{du^2}\Vert _{\infty } \le M\) and \(\Vert \frac{df}{du_{x}}\Vert _{\infty } \le M\), \(\Vert \frac{d^2f}{du_{x}^2}\Vert _{\infty } \le M\). Taking (41)–(46), substituting the bounds of (47) and (48) and using them for Eqs. (34)–(37) we have that

$$\begin{aligned}&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}\left( x , \Theta \right) }{\partial W_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C\cdot b,&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{x}\left( x , \Theta \right) }{\partial W_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^{2} \cdot b, \nonumber \\&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xx}\left( x , \Theta \right) }{\partial W_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^3 \cdot b,&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xxx}\left( x , \Theta \right) }{\partial W_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^4 \cdot b, \nonumber \\&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}\left( x , \Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}},&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{x}\left( x , \Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C, \nonumber \\&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xx}\left( x , \Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}}C^2,&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xxx}\left( x , \Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^3, \nonumber \\&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}\left( x , \Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C,&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{x}\left( x , \Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^2, \nonumber \\&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xx}\left( x , \Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}}C^3,&\sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {N}_{xxx}\left( x , \Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{1}{\sqrt{N}} C^4. \end{aligned}$$
(49)

Now substituting the values of the spatial derivatives of the equation in Eqs. (31)–(33) we find

$$\begin{aligned} \sup _{t \in [0, T]}\Vert \frac{\partial N_{x}\left( x ,\Theta \right) }{\partial W_{0k}}\Vert _{\infty }&\le \frac{3C^2b^3}{\sqrt{N}}\nonumber , \sup _{t \in [0, T]}\Vert \frac{\partial N_{x}\left( x ,\Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{3Cb^2}{\sqrt{N}} \nonumber ,\\&\quad \sup _{t \in [0, T]}\Vert \frac{\partial N_{x}\left( x ,\Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{3C^2b^2}{\sqrt{N}}. \end{aligned}$$
(50)
$$\begin{aligned} \sup _{t \in [0, T]}\Vert \frac{\partial N_{xx}\left( x ,\Theta \right) }{\partial W_{0k}}\Vert _{\infty }&\le \frac{7C^3b^3}{\sqrt{N}}\nonumber , \sup _{t \in [0, T]}\Vert \frac{\partial N_{xx}\left( x ,\Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{7C^2b^2}{\sqrt{N}} \nonumber ,\\&\quad \sup _{t \in [0, T]}\Vert \frac{\partial N_{xx}\left( x ,\Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{7C^3b^2}{\sqrt{N}}. \end{aligned}$$
(51)
$$\begin{aligned} \sup _{t \in [0, T]}\Vert \frac{\partial N_{xxx}\left( x ,\Theta \right) }{\partial W_{0k}}\Vert _{\infty }&\le \frac{13C^4b^3}{\sqrt{N}},\sup _{t \in [0, T]}\Vert \frac{\partial N_{xxx}\left( x ,\Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{13C^3b^2}{\sqrt{N}} \nonumber ,\\&\quad \sup _{t \in [0, T]}\Vert \frac{\partial N_{xxx}\left( x ,\Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{13C^4b^2}{\sqrt{N}}. \end{aligned}$$
(52)

Further substituting the values of (50), (51) and (52), in (29) and (30), we have

$$\begin{aligned} \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L} N\left( x ,\Theta \right) }{\partial W_{0k}}\Vert _{\infty }&\le \frac{10MC^3b^3}{\sqrt{N}}, \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L} N\left( x ,\Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{10MC^2b^2}{\sqrt{N}} \nonumber ,\\&\quad \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L} N\left( x ,\Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{10MC^3b^2}{\sqrt{N}}. \end{aligned}$$
(53)
$$\begin{aligned} \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L}_{x} N\left( x ,\Theta \right) }{\partial W_{0k}}\Vert _{\infty }&\le \frac{27MC^3b^3}{\sqrt{N}}, \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L}_{x} N\left( x ,\Theta \right) }{\partial W_{1k}}\Vert _{\infty } \le \frac{27MC^2b^2}{\sqrt{N}} \nonumber ,\\&\quad \sup _{t \in [0, T]}\Vert \frac{\partial \mathcal {L}_{x} N\left( x ,\Theta \right) }{\partial b_{0k}}\Vert _{\infty } \le \frac{27MC^3b^2}{\sqrt{N}}. \end{aligned}$$
(54)

This completes the proof. \(\square \)

Consequently, by employing the definition of the neural tangent kernel from Eq. (28) and Theorem 3.1   it can be shown that

$$\begin{aligned} \varvec{k}_{rr} = \mathcal {O}\left( \frac{1}{N}\right) ,\quad \varvec{k}_{rt} = \mathcal {O}\left( \frac{1}{N}\right) ,\quad \varvec{k}_{tr} = \mathcal {O}\left( \frac{1}{N}\right) ,\quad \varvec{k}_{tt} = \mathcal {O}\left( \frac{1}{N}\right) . \end{aligned}$$
(55)

Therefore, the kernel tangents approaches zero as the number of nodes in the hidden layer tends to infinity. This also shows that the NTK is bounded and has a definite value. In Wang et al. [26] it can be seen that the change in the NTK is negligible over the training process. Meaning that the NTK behaves similarly to the initial NTK. Denote the initial NTK as \(\varvec{k}(0) = \varvec{k}^*\) then we have that \(\varvec{k}(t) \approx \varvec{k}^*\), \(\forall t \in [0,T]\).

Now, consider the first row of the matrix Eq. (28) where we denote the parameters \(\Theta \) as a function of time as they evolve over time by the gradient descent algorithm.

$$\begin{aligned} \frac{d \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) }{d t} = - \left[ \varvec{k}(t) \right] \cdot \vert \mathcal {L} N\left( x_r, \Theta (t)\right) \vert . \end{aligned}$$

Replacing \(\varvec{k}(t)\) with its approximate value

$$\begin{aligned} \frac{d \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) }{d t} = -\varvec{k}^*\cdot \vert \mathcal {L} N\left( \varvec{x}_r, \Theta (t)\right) \vert . \end{aligned}$$
(56)

Let \(\mathcal {L} N\left( \varvec{x}_r, \Theta (t)\right) =y(t)\), then solving the differential equation

$$\begin{aligned}&\frac{d y(t)}{d t}=-\varvec{k}^* \cdot \left[ y(t)\right] , \end{aligned}$$
(57)

we obtain,

$$\begin{aligned} y(t)= ce^{-\varvec{k}^{*}t}, \end{aligned}$$
(58)

where \(c=\mathcal {L} N(0)\). Replacing the value of c in (58), we obtain

$$\begin{aligned} \mathcal {L} N\left( \varvec{x}_r, \Theta (t)\right) = e^{-\varvec{k}^{*}t}\mathcal {L} N(\varvec{x}_r, \Theta (0)). \end{aligned}$$
(59)

Similarly, it can be shown that

$$\begin{aligned} \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (t)\right) = e^{-\varvec{k}^{*}t}\mathcal {L}_{x} N(\varvec{x}_r, \Theta (0)), \end{aligned}$$
(60)

so we have

$$\begin{aligned} \left[ \begin{array}{l} \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) \\ \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (t)\right) \end{array}\right] = e^{-\varvec{k}^{*}t}\cdot \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta (0)\right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (0)\right) \vert \end{array}\right] . \end{aligned}$$
(61)

If the kernel matrix \(\varvec{k}^*\) was invertible, then values of \(\mathcal {L} N\) and \(\mathcal {L}_{x} N\) can be found in Eqs. (59) and (60) using kernel regression for some created test data at points \(x_{\text {test}}\). But in numerical results, the matrix \(\varvec{k}^*\) is close to a singular matrix and hence finding its inverse is difficult. This is called kernel regression.

3.1 Frequency Bias

Consider the matrix \(\varvec{k}_{rr}\) given in Eq. (22) it can be written as the multiplication of two matrices

$$\begin{aligned} \varvec{J}_1=\left[ \begin{array}{c} \frac{d \mathcal {L} N}{d \Theta }\left( x_r^{1}, \Theta \right) \\ \frac{d \mathcal {L} N}{d \Theta }\left( x_r^2, \Theta \right) \\ \vdots \\ \frac{d \mathcal {L} N}{d \Theta }\left( x_r^{N_r}, \Theta \right) \end{array}\right] . \end{aligned}$$
(62)

Then, we have that

$$\begin{aligned}{}[\varvec{k}_{rr}]_{ij} = \varvec{J}_1 \cdot \varvec{J}_1^{\top }. \end{aligned}$$
(63)

Similarly for

$$\begin{aligned} \varvec{J}_2=\left[ \begin{array}{c} \frac{d \mathcal {L}_{x} N}{d \Theta }\left( x_r^{1}, \Theta \right) \\ \frac{d \mathcal {L}_{x} N}{d \Theta }\left( x_r^2, \Theta \right) \\ \vdots \\ \frac{d \mathcal {L}_{x} N}{d \Theta }\left( x_r^{N_r}, \Theta \right) \end{array}\right] , \end{aligned}$$
(64)

we have obtained

$$\begin{aligned}{}[\varvec{k}_{tt}]_{ij} = \varvec{J}_2 \cdot \varvec{J}_2^{\top }. \end{aligned}$$

It is also true that for \(\varvec{J} = [\varvec{J}_1 \quad \varvec{J}_2],\)

$$\begin{aligned} \varvec{k}= \varvec{J}\cdot \varvec{J}^{\top }. \end{aligned}$$
(65)

Remark 1

For a matrix \(\varvec{A}\) having full rank it is true that \(\varvec{A}\varvec{A}^{\top }\) is always positive semi definite.

From the given remark we have that the matrices \(\varvec{k}_{rr}\), \(\varvec{k}_{tt}\) and \(\varvec{k}\) are all positive semi definite. Matrix \(\varvec{k*}\) has real positive eigenvalues means that matrix \(\varvec{k*}\) can be decomposed into the multiplication of two orthogonal matrices and one diagonal matrix. Consequently the spectral decomposition of the neural tangent kernel gives us

$$\begin{aligned} e^ {-\varvec{k}^{*}t} = {Q}^T e^{-\Lambda t} {Q}, \end{aligned}$$
(66)

where Q is a orthogonal matrix \(Q^{-1} = Q^{\top }\), and \(\Lambda \) is a diagonal matrix having positive eigenvalues \(\lambda _i\) corresponding to the neural tangent matrix \(\varvec{k}^*\). Further, replacing (66) in (61), we get

$$\begin{aligned} \left[ \begin{array}{l} \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) \\ \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (t)\right) \end{array}\right] = -{Q}^T e^{-\Lambda t} {Q}\cdot \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta (0)\right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (0)\right) \vert \end{array}\right] , \end{aligned}$$
(67)

and

$$\begin{aligned} {Q} \left[ \begin{array}{l} \mathcal {L} N\left( \varvec{x}_{r}, \Theta (t)\right) \\ \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (t)\right) \end{array}\right] = - e^{-\Lambda t} {Q}\cdot \left[ \begin{array}{l} \vert \mathcal {L} N\left( \varvec{x}_r, \Theta (0)\right) \vert \\ \vert \mathcal {L}_{x} N\left( \varvec{x}_r, \Theta (0)\right) \vert \end{array}\right] . \end{aligned}$$
(68)

As \(t \xrightarrow {} \infty \), it can be seen that the right side approaches 0, indicating that \(\mathcal {L} N (x_r)\xrightarrow {} 0\).

The convergence of \(\mathcal {L} N\) at the point \(x_i\) depends on the respective eigenvalue \(\lambda _i\). Moreover, it exhibits a faster rate of convergence for the large eigenvalues associated with the neural tangent kernel matrix. The eigenvalues with larger magnitudes correspond to eigenvectors having lower frequencies. The neural network first learns the part of the loss function with lower frequencies and then learns the part with higher frequencies since the convergence rate is faster for smaller frequencies. This is known as the frequency bias performed by the neural network. In order to solve this issue, it is necessary to ensure that the loss function does not contain a part with higher and lower frequencies.

In general, it is observed that the greater magnitude eigenvalues of the NTK matrix correspond to the portion of the loss function that deals with the derivative of the differential equation. The weights \(w_r\) and \(w_s\) multiplied by each part of the loss function are the parameters that can be altered to make the eigenvalues of both parts of the loss function equal. Increase the weight \(w_r\) or reduce the weight \(w_s\) to ensure that the eigenvalues of both terms remain identical, the neural network does not exhibit frequency bias, and the network is trained simultaneously for both parts of the loss function. We define the algorithm which will be used in the numerical simulations.

Algorithm 1
figure a

The GPINN method

Full size image

4 Numerical Simulations

We will solve a few differential equations where our loss term to be optimized is given by Eqs. (4) and (5). We take a network with a single hidden layer to compare the results between different values of weights for loss terms. By doing so, we reduce computational time. We take 1000 neurons in the hidden layer so that the network can understand the complex dynamics of the differential equation. We use Xavier initialization as it helps set the initial weights so that the gradients in the network remain well-behaved during training. This helps prevent vanishing and exploding gradient problems, which can hinder the convergence of deep neural networks. Experimental results show that taking the learning rate as \(10^{-3}\) suits optimizing the loss function created. The activation function for the hidden layer is an important hyperparameter as it converts the linear network into a non-linear model. One can refer to the detailed description of the activation and adaptive activation functions in [38,39,40,41]. Here a scalable hyperparameter a is used in the activation function to optimize the network’s performance, resulting in better learning capabilities and a vastly improved convergence rate, especially at the early stages of training. A change in the parameter results in a change in the slope of the activation function. In these examples, we use the Swish activation function, which is a scalable sigmoidal function given by

$$\begin{aligned} \sigma (x) = \frac{x}{1+e^{-ax}} . \end{aligned}$$
(69)

Experiments show that parameter value \(a=1\) gives the best results. We first train the network using LBFGS optimizer and then use ADAM optimization for 20000 iterations.

The results are calculated for different values of the weights \(w_s\) and \(w_r\). All the problems have been solved on Python 3.0 using Tensorflow and Deepxde library see [42]. The relative error in \(l_2\) norm is calculated for 1000 points in the domain and the \(l_{\infty }\) error representing the maximum error value are computed with 1000 points in the domain. For all the examples, we take the parameters as shown in Table 1. Results have been shown for different residual points for all examples.

Table 1 Hyperparmeter values
Full size table

Example 4.1

[43] Consider the convection-diffusion concentration equation given by

$$\begin{aligned} u_{xx}-bu_{x}-a^2u=0,\quad a,b \in \mathbb {R}, \quad \quad 0<x<1, \end{aligned}$$
(70)

with the boundary data \(u(0)=0\) and \(u(1)=1\). The analytical solution to the problem is given by

$$\begin{aligned} u(x) = \frac{\sinh \left( \theta x\right) }{\sinh \left( \theta \right) }e^{b(x-1)/2}, \quad \quad \quad \theta = \frac{\sqrt{4a^2+b^2}}{2}. \end{aligned}$$

Table 2 shows the \(l_2-\)errors and relative \(l_{\infty }-\)errors at different weights and different nodes 10, 20 and 40 respectively, for \(a=6\) and \(b=20\).

Table 2 Solution error for Example 4.1
Full size table

Example 4.2

[44] Consider the finite deflection of elastic string equation given by

$$\begin{aligned} u_{xx}+ (u_{x})^2+1=0, \quad \quad 0<x<1, \end{aligned}$$
(71)

with the boundary data \(u(0)=0\) and \(u(1)=0\). The analytical solution is given by

$$\begin{aligned} u(x) = \log \left( \frac{\cos \left( \frac{1}{2}-x\right) }{\cos \left( \frac{1}{2}\right) }\right) . \end{aligned}$$

Table 3 shows the relative \(l_2-\)errors and \(l_{\infty }-\)errors at different weights and different nodes 10, 20 and 40 respectively.

Table 3 Solution error for Example 4.2
Full size table

Example 4.3

Consider the Bessel differential equation given by

$$\begin{aligned} x^2 u_{xx}+ x u_{x} + (x^2 -\tau ^2) u=0,\quad \quad -1<x<1, \end{aligned}$$
(72)

The analytical solution to the problem is given by the BesselJ(x) function. Table 4 shows the relative \(l_2-\)errors and \(l_{\infty }-\)errors at different weights and different nodes 10, 20 and 40 respectively, for \(\tau =8\).

Table 4 Solution error for Example 4.3
Full size table

Example 4.4

Consider a nonlinear Burger’s equation given by

$$\begin{aligned} u_{xx}- R_{e}(u -\alpha ) u_{x} =0, \quad \quad 0<x<1, \end{aligned}$$
(73)

with the boundary data \(u(0)=0\) and \(u(1)=0\).The analytical solution to the problem is given by

$$\begin{aligned} u(x)= \alpha \left[ 1- \tanh \left( \frac{R_{e}\alpha x}{2} \right) \right] , \end{aligned}$$

where \(R_e\) is the Reynolds number [45]. Table 5 shows the relative \(l_2-\)errors and \(l_{\infty }-\)errors at different weights and different nodes 10, 20 and 40 respectively, for \(R_e=100\) and \(\alpha =0.1\).

Table 5 Solution error for Example 4.4
Full size table

Example 4.5

Consider a boundary value problem given by

$$\begin{aligned} u_{xx} =2u_{x}-u-3, \quad \quad 0<x<1, \end{aligned}$$
(74)

with the boundary data \(u(0)=-3\), \(u(1)=-2.2642421\). The analytical solution to the problem is given by \(u(x)= 2xe^{x-2} -3\). A comparison report is given in Table 6 for the exact and numerical solutions values at various grid points and \(w_r = 100\) and \(w_s=0.001\). The proposed GPINN technique exhibits superiority over the existing biologically inspired differential evolution algorithm [46].

Table 6 Comparison between differential evolution method and our method for example 4.5
Full size table

Example 4.6

[47] Consider the Poisson’s equation given by

$$\begin{aligned} u_{xx} + u_{yy} =(x^{2}+y^{2})e^{xy}, \quad \quad 0<x<2,0<y<1, \end{aligned}$$
(75)

with the boundary data \(u(0,y)=1\), \(u(x,0)=1\), \(u(x,1)=e^{x}\) and \(u(2,y)=e^{2y}\). The analytical solution to the problem is given by \(u(x,y)= e^{xy}\). Table 7 shows the relative \(l_2-\)errors and \(l_{\infty }-\)errors at different weights and different nodes 10, 20 and 40 respectively.

Table 7 Solution error for Example 4.6
Full size table
Fig. 2
figure 2

Exact and approximate solution plot at different values of weights for Example 4.1

Full size image
Fig. 3
figure 3

Log log plot for error vs number of grid points

Full size image

5 Conclusion

Understanding why neural networks with some specific structure work better in a few places of the solution domain and not so well in other places is important for training the network well. Here we construct a network that automatically meets the boundary data, which reduces the cost of training the network on the boundary and gives the exact value at the boundary. We then introduce a loss term where the network tries to fit the derivative of the differential equation; this helps the network in problems where the derivative is steep (see Burger’s equation). Adding the loss component raises the back-propagated derivatives of the neural network with respect to its parameters, which causes the weights to change with each iteration rapidly. We look at this problem through the lens of NTK and then see that this problem can be solved just by adjusting the weights of each loss term. Results show that increasing the weight of the loss term containing the residual of the differential equation and decreasing the weight of the loss term containing the residual of the gradient of the differential equation helps in better solutions. The proposed method can be deployed on different network architectures as each of them might have another problem with training and can be seen easily with the help of NTK.