Boundedness and Convergence of Mini-batch Gradient Method with Cyclic Dropconnect and Penalty

Abstract

Dropout is perhaps the most popular regularization method for deep learning. Due to the stochastic nature of the Dropout mechanism, the convergence analysis of Dropout learning is challenging and the existing convergence results are mainly of probability nature. In this paper, we investigate the deterministic convergence of the mini-batch gradient learning method with Dropconnect and penalty. By drawing and presenting a set of samples of the mask matrix of Dropconnect regularization into the learning process in a cyclic manner, we establish an upper bound of the norm of the weight vector sequence and prove that the gradient of the cost function, the cost function itself, and the weight vector sequence deterministically converge to zero, a constant, and a fixed point respectively. Considering Dropout is mathematically a specific realization of Dropconnect, the established theoretical results in this paper are also valid for Dropout learning. Illustrative simulations on the MNIST dataset are provided to verify the theoretical analysis.

1 Introduction

Thanks to the availability of big data and advanced computation resources, in recent years deep neural networks (DNNs) have gained popularity in a wide range of real applications [1,2,3,4]. The hierarchy structure endows DNNs with powerful capability in extracting higher-level features, but also makes DNNs prone to overfitting [5]. Dropout is almost the most widely used regularization technique to tackle the overfitting problem for DNNs [6]. By randomly dropping a certain proportion of hidden units during the training process, Dropout implicitly performs network ensemble and thus improves the generalization performance. As a generalization of Dropout, DropConnect randomly forces a portion of the weights of the network to zero and obtains the state-of-the-art results at that time [7]. To cater to the diverse network structures of DNNs, many variants of Dropout have been proposed, such as Standout [8], Maxout [9], RNNdrop [10], and Dropout for RNNs [11]. Besides extensively reported empirical evidence, many insightful theoretical investigations have also been carried out concerning the approximation capability [12], generalization bound [7], and working mechanism [13].

As a classical training strategy for neural networks, the gradient method is also prevalent in training DNNs. The gradient method can be executed in three modes: batch learning [14, 15], online learning [16], and mini-batch learning [17]. Batch learning updates the network weights based on the whole training data set, while online learning updates the weights immediately after a sample is presented to the network. As a result, batch learning requires a large memory cost for DNNs and online learning usually requires a large number of iterations to converge. As an intermediate mode, mini-batch learning updates the network weights each time based on a chunk of data, thus can efficiently balance the tradeoff between the memory cost and the learning speed.

Convergence is a prerequisite for gradient-based learning algorithms to be used in real applications [18]. Batch gradient learning corresponds to the standard gradient descent algorithm and its deterministic convergence nature can be easily obtained from traditional optimization theory. However, online learning and mini-batch learning are basically of stochastic nature and accordingly their convergence was usually established in the sense of probability [16]. It is interesting to find that when the training samples are presented to networks in a certain fixed sequence, the deterministic convergence for online learning [19] and mini-batch learning [17] can also be guaranteed. Moreover, the deterministic convergence results for some other variants of gradient method, such as gradient method with momentum [20], chaos injection-based gradient method [21], and complex gradient method [17, 22], have also been established.

Due to the uncertainty brought to the network structure and the learning process, the convergence analysis of Dropout learning is challenging work. By utilizing the stochastic approximation theory, a probability convergence result for the stochastic gradient learning algorithm with Dropout was established in [23]. Moreover, a convergence theorem for SpikeProp with Dropout is given in [24]. However, the deterministic convergence for mini-batch gradient learning with dropout is still unknown in the literature. To this end, in this paper, we consider establishing the deterministic convergence of the mini-batch gradient method with cyclic Dropconnect and penalty (MBGMCDP). The main contribution of this paper is listed as follows.

• (i) In [7, 23, 24], the boundedness of the network weights is implicitly or explicitly required. In this paper, by including a penalty term in the cost function, we prove that the network weights are bounded during the learning process. Thus this condition is not extra required in our convergence analysis. From the viewpoint of real application, the combination of the dropout and the weight decay is also helpful to enhance the generalization performance.

• (ii) By presenting the samples of the mask matrix of Dropconnect into the network in a cyclic way, we prove the deterministic convergence, covering both the weak convergence and strong convergence, of the mini-batch gradient learning method with Dropconnect and penalty. Considering Dropout can be mathematically viewed as a specific realization of Dropconnect by setting the mask matrix in a certain form, our convergence results can also be applied to Dropout learning.

• (iii) The theoretical findings and the efficiency of MBGMCDP are validated by simulations of MNIST problems.

The remainder of this paper is structured as follows. The MBGMCDP algorithm is formally described in Sect. 2. The main theoretical results are provided in Sect. 3. Section 4 provides the simulation results to validate our theoretical findings and the efficiency of MBGMCDP. Finally, we summarize our work in Sect. 5. The proof of the theorems in Sect. 3 is shown in the appendix. In this paper, we use $|| \cdot ||$ to denote the Euclidean norm.

2 Mini-batch Gradient Method with Cyclic Dropconnect and Penalty

Given a set of training samples $\left\{ {\xi ^{j},O^{j}} \right\} _{j = 0}^{J - 1}$, where $\xi ^{j}$ is the jth input vector, and $O^{j}$ is the corresponding objective output of the network, the training of neural networks is mathematically equivalent to solving the following optimization problem

$$\begin{aligned} {{{\textbf {w}}}^{*}}=\mathop {\textrm{argmin}}\limits _{{\textbf {w}}}\sum \limits _{j = 0}^{J-1}{e({\textbf {w}},\xi ^{j})}, \end{aligned}$$

(1)

where ${\textbf {w}}$ is the network weight vector, $e({\textbf {w}},\xi ^{j})$ is a function to measure the discrepancy between the desired output $O^{j}$ and the corresponding actual output of the network with respect to the jth input $\xi ^{j}$. In real applications, such a function can be the square error function or the cross-entropy loss function.

In order to prevent the neural network from overfitting, Dropconnect introduces dynamic sparsity in the network weight vector by randomly dropping some weights during the training stage. To implement the Dropconnect learning, we define a modified cost function as follows

$$\begin{aligned} E({\textbf {w}})=\mathbb {E}(\sum \limits _{j = 0}^{J-1}e({\textbf {m}}\star {\textbf {w}},\xi ^{j})+\lambda \Vert {\textbf {m}}\star {\textbf {w}}\Vert ^{2}), \end{aligned}$$

(2)

where ${\textbf {m}}$ is a binary mask vector whose elements are randomly drawn to be 0 or 1 according to a certain probability distribution, $\mathbb {E}$ denotes the mathematical expectation operation with respect to the random vector ${\textbf {m}}$, "$\star$" denotes the Hadamard product operation, and $\lambda$ is a penalty coefficient.

In order to balance the tradeoff between memory overheads and computational efficiency, the mini-batch learning allows the network weights to be updated once a block of training samples are available. Suppose that the training samples are presented cyclically in a fixed order of b blocks: $B_{0},B_{1},\ldots ,B_{b-1}$, where $B_{0} = \left\{ {\xi ^{j},O^{j}} \right\} _{j = 0}^{j_{1}},B_{1} = \left\{ {\xi ^{j},O^{j}} \right\} _{j = j_{1} + 1}^{j_{2}},\ldots ,$ and $B_{b-1} = \left\{ {\xi ^{j},O^{j}} \right\} _{j = j_{b - 1} + 1}^{J-1}$. Accordingly, suppose ${\textbf {m}}^0$,${\textbf {m}}^1$,$\ldots$, and ${\textbf {m}}^{b-1}$ are b samples of the mask vector, then we have a practical realization of the cost function (2)

$$\begin{aligned} E({\textbf {w}})=\sum \limits _{k = 0}^{b-1} E_k({\textbf {w}}), \end{aligned}$$

(3)

where

$$\begin{aligned} E_k({\textbf {w}})=\sum \limits _{j = j_{k}+1}^{j_{k + 1}}e({\textbf {m}}^k\star {\textbf {w}},\xi ^{j})+\lambda \Vert {\textbf {m}}^k\star {\textbf {w}}\Vert ^2 \end{aligned}$$

(4)

is an instant error defined based on a block of samples $B_{k}$.

Starting from an arbitrary initial value ${\textbf {w}}^{0}$, the mini-batch gradient method with cyclic Dropconnect and penalty updates the weights iteratively by

$$\begin{aligned} {\textbf {w}}^{nb + k + 1}= & {} {\textbf {w}}^{nb + k}- \eta _{n}\nabla _{{\textbf {w}}} E_k({\textbf {w}}^{nb+k})\nonumber \\= & {} {\textbf {w}}^{nb + k}\nonumber \\{} & {} - \eta _{n}\left( {\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}}} + 2\lambda \left( {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k} \right) \right) , \end{aligned}$$

(5)

where n denotes the cycle (epoch) number, k denotes the block number and $\eta _{n}$ is the step size for the nth cycle. Write $m=nb+k$, then a weight vector sequence $\{{\textbf {w}}^m\}$ can be generated using (5).

3 Main Results

We will establish the main theoretical results for MBGMCDP in this section.

Let $\Phi = \left\{ {\textbf {w}}:\nabla _{{\textbf {w}}}E({\textbf {w}}) = 0 \right\}$ be the stationary point set of the cost function $E({\textbf {w}})$, and $\Phi _{s} \in R$ be the projection of $\Phi$ onto the sth coordinate axis.

The following assumptions will be used in our theoretical analysis.

• (A1) The function $e\left( {{\textbf {w}},\xi } \right)$ is twice continuously differentiable with respect to ${\textbf {w}}$. Moreover, $e\left( {{\textbf {w}},\xi } \right)$, $\frac{\partial e\left( {{\textbf {w}},\xi } \right) }{\partial {\textbf {w}}}$, and $\frac{\partial ^{2}e\left( {{\textbf {w}},\xi } \right) }{\partial {\textbf {w}}^{2}}$ are uniformly bounded.

• (A2) There exists an $\alpha \in (0,1)$, such that $\left\| {{\textbf {m}}\star {\textbf {w}}} \right\| \ge \alpha \left\| {\textbf {w}} \right\|$.

• (A3) $\eta _{n} > 0,{\sum \limits _{n = 0}^{\infty }\eta _{n}} = \infty ,{\sum \limits _{n = 0}^{\infty }\eta _{n}^{2}} < \infty$.

• (A4) $\Phi _{s}$ does not contain any interior points for any s.

Theorem 1

Suppose that $\left\{ {\textbf {w}}^{m} \right\}$ is the weight sequence generated by (5) from an arbitrary initial value ${\textbf {w}}^{0}$. Then $\left\{ {\textbf {w}}^{m} \right\}$ is uniformly bounded under Assumptions $(A1)-(A3)$ and condition $0< 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n} < 1$.

Theorem 2

Suppose that $E({\textbf {w}})$ is the cost function defined by (3), that $\left\{ {\textbf {w}}^{m} \right\}$ is the weight sequence generated by (5) from an arbitrary initial value ${\textbf {w}}^{0}$, and the Assumptions $(A1)-(A3)$ are valid. Then

• (a) There exists a constant $E^{*}$ such that

  $$\begin{aligned} {\lim \limits _{n\rightarrow \infty }{E({\textbf {w}}^{nb})}} = E^{*}; \end{aligned}$$

  (6)

• (b) There holds that

  $$\begin{aligned} {\lim \limits _{n\rightarrow \infty }\left\| {\nabla _{{\textbf {w}}}E({\textbf {w}}^{nb})} \right\| } = 0. \end{aligned}$$

  (7)

• (c) Furthermore, if Assumption (A4) is valid, then there exists a point ${\textbf {w}}^{*} \in \Phi$ such that

  $$\begin{aligned} {\lim \limits _{m\rightarrow \infty }{} {\textbf {w}}^{nb}} = {\textbf {w}}^{*}. \end{aligned}$$

  (8)

Remark 1

Assumption (A1) can be satisfied by typical square error function or cross-entropy loss function for neural networks with activation functions such as softmax function and sigmoid functions. Assumption (A2) is listed only for the sake of mathematical deduction and is certainly satisfied in real applications. Assumption (A3) is a typical condition of the step size for the convergence analysis of gradient learning method. Assumption (A4) is used to establish the strong convergence of the MBGMCDP algorithm. Equations (6) and (7) mean the weak convergence, while (8) means the strong convergence.

Remark 2

The additional condition for the step size $\eta _{n}$ and the penalty parameter $\lambda$ required in Theorem 1 is not restrictive. In real applications, $\eta _{n}$ and $\lambda$ are usually small enough to satisfy $0< 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n} < 1$.

4 Experiments

In this section, the theoretical findings and the efficiency of MBGMCDP will be validated through simulations on MNIST and CIFAR-10 datasets, which are two benchmark classification problems.

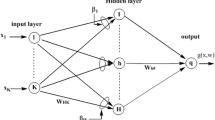
MNIST dataset is composed of 60,000 gray-scale images of handwritten digits (0–9), each of which is made up of $28\times 28$ pixels. We randomly selected 5000 images for training and 1000 images for testing. The network used was a four-layer fully connected network of structure 784-128-32-10. The activation function was set as the sigmoid function, the batch size was set to 200, the step size $\eta _{n} = \frac{1}{(n + 1)^{0.51}}$, and the penalty coefficient $\lambda = 0.001$. The simulation results illustrated were obtained by averaging over 50 independent trials.

Figures 1, 2, and 3 illustrate the learning curves of MBGMCDP. It can be observed from Fig. 1 and Fig. 2 that the gradient tends to zero and the cost function tends to a constant as the epoch increases. This validates our theoretical findings in Theorem 2. Figure 3 reveals that there are oscillations for the instant cost curves with respect to the number of iterations during the Dropconnect learning, while the oscillations vanish for the loss curves for the whole network with respect to the number of epochs as shown in Fig. 2. It can be observed from Fig. 4 that, if the training set is shuffled at each epoch, the oscillations occur again for the loss curves of the whole network with respect to the number of epochs. Tables 1 and 2 illustrate the testing results for $\lambda =0$ and $\lambda =0.001$, respectively, where the drop rate varies as 0, 0.1, 0.2 and 0.5. It can be observed from the two tables that, the testing accuracy obtained here is close to the state-of-the-art results [25], and both the Dropconnect and the penalty contribute to enhancing the generalization capability of the network. However, if the drop rate is too large, the trained network may be underfitting, which also degrades the performance.

Fig. 1

Learning curves of the norm of gradient with respect the number of epochs

Fig. 2

Learning curves of the training cost with respect the number of epochs

Fig. 3

Learning curves of the instant cost with respect the number of iterations

Fig. 4

Learning curves of the training cost with respect the number of epochs for MBGMCDP with shuffled training data

The CIFAR-10 dataset is composed of 60,000 $32\times 32$ colour images in 10 classes, with 6000 images per class. We randomly selected 50,000 images for training and 10,000 images for testing. The network used was a pretrained Alexnet network with three linear layers of structure 9126-4096-10 to be retrained. The batch size was set to 64. The testing loss and testing accuracy are listed in Table 3, from which the contribution of the dropout method with different drop rate can also be observed.

Table 1 Testing loss and testing accuracy of MBGMCDP with $\lambda = 0$ for MNIST dataset

Table 2 Testing loss and testing accuracy of MBGMCDP with $\lambda = 0.001$ for MNIST dataset

Table 3 Testing loss and testing accuracy of MBGMCDP with $\lambda = 0.001$ for CIFAR-10 dataset

5 Conclusion

In this paper, we investigated the mini-batch gradient method with Dropconnect and the penalty for the regularization learning of deep neural networks. By presenting a set of samples of the mask matrix of Dropconnect to the learning process in a cyclic manner and adding a penalty term to the cost function, the boundedness of the weight sequence and the deterministic convergence of the MBGMCDP, including both the weak convergence and strong convergence, were theoretically established. Illustrative simulation on the MNIST dataset verified the theoretical findings and justified that both the Dropconnect and the penalty contributed to the generalization performance promotion. However, in this paper, we only consider the case that the training samples are presented cyclically and the activation functions are twice continuously differentiable. In the future, we will extend our work to a more general case where the training samples are shuffled in each epoch and the ReLU activation function is used.

Appendix

1.1 Proof of Theorem 1

In the following we will show that there exists a constant $C_{1}$ such that for any nonnegative integer n and k

$$\begin{aligned} \left\| {\textbf {w}}^{nb + k} \right\| \le C_{1}. \end{aligned}$$

(9)

According to Assumption (A3), we know that ${\lim \limits _{n\rightarrow \infty }\eta _{n}} = 0$ and $\eta _n<1$ for sufficiently large n. By $0< 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n} < 1$, we have

$$\begin{aligned} 0< 1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n} < 1. \end{aligned}$$

(10)

Equation (5) can be rewritten as:

$$\begin{aligned} {\textbf {w}}^{nb + k +1} =&\left( {{\textbf {1}} - 2\lambda \eta _{n}{} {\textbf {m}}^{k}} \right) \star {\textbf {w}}^{nb + k} - \eta _{n}\left( {\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}}} \right) , \end{aligned}$$

(11)

where 1 represents a vector of all-ones.

According to Assumption (A1), there exists a constant $C_{2} > 0$, such that for all $n \in N$ and $k=0,\ldots ,b-1$, there holds that

$$\begin{aligned} \left\| {\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}}} \right\| \le C_{2}. \end{aligned}$$

(12)

Using Assumption (A3), Equs. (10)–(12), and the triangle inequality, we have that

$$\begin{aligned} \left\| {\textbf {w}}^{nb + k +1} \right\| \\&= \left\| {\left( {{\textbf {1}} - 2\lambda \eta _{n}{} {\textbf {m}}^{k}} \right) \star {\textbf {w}}^{nb + k} - \eta _{n}\left( {\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}}} \right) } \right\| \\&\le \left\| {\left( {{\textbf {1}} - 2\lambda \eta _{n}{} {\textbf {m}}^{k}} \right) \star {\textbf {w}}^{nb + k}} \right\| + \eta _{n}C_{2} \\&= \left( {\left( {1 - 2\lambda \eta _{n}} \right) ^{2}\left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}} \right\| ^{2} + \left\| {\left( {{\textbf {1}} - {\textbf {m}}^{k}} \right) \star {\textbf {w}}^{nb + k}} \right\| ^{2}} \right) ^{\frac{1}{2}} + \eta _{n}C_{2} \\&= \left( {\left\| {\textbf {w}}^{nb + k} \right\| ^{2} + \left( {- 4\lambda \eta _{n} + 4\lambda ^{2}\eta _{n}^{2}} \right) \left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}} \right\| ^{2}} \right) ^{\frac{1}{2}} + \eta _{n}C_{2} \\&\le \left( {\left\| {\textbf {w}}^{nb + k} \right\| ^{2} + \left( {- 4\lambda \eta _{n} + 4\lambda ^{2}\eta _{n}^{2}} \right) \alpha ^{2}\left\| {\textbf {w}}^{nb + k} \right\| ^{2}} \right) ^{\frac{1}{2}} + \eta _{n}C_{2} \\&= \left( {1 - 4\lambda \alpha ^{2}\eta _{n} + 4\lambda ^{2}\alpha ^{2}\eta _{n}^{2}} \right) ^{\frac{1}{2}}\left\| {\textbf {w}}^{nb + k} \right\| + \eta _{n}C_{2} \\&\le \left( {1 - 2\lambda \alpha ^{2}\eta _{n} + 2\lambda ^{2}\alpha ^{2}\eta _{n}^{2}} \right) \left\| {\textbf {w}}^{nb + k} \right\| + \eta _{n}C_{2} \\&\le \left( {1 - 2\lambda \alpha ^{2}\eta _{n} + 2\lambda ^{2}\alpha ^{2}\eta _{n}} \right) \left\| {\textbf {w}}^{nb + k} \right\| + \eta _{n}C_{2} \\&= \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \left\| {\textbf {w}}^{nb + k} \right\| + \eta _{n}C_{2} \\&= \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \left\| {\textbf {w}}^{m} \right\| + \eta _{n}C_{2}. \end{aligned}$$

Now, we proceed to show (9) is always true by considering the following two cases.

Case (i): For any m (or $nb+k)$, there always holds that

$$\begin{aligned} \left\| {\textbf {w}}^{m} \right\| < \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) }. \end{aligned}$$

(13)

In this case, we can simply set $C_{1} = \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) }$ to validate (9).

Case (ii): There exists an integer $N(N \ge 0)$ such that

$$\begin{aligned} \left\| {\textbf {w}}^{N} \right\| \ge \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) }. \end{aligned}$$

(14)

In this case, we shall prove by induction on m to show that

$$\begin{aligned} \left\| {\textbf {w}}^{m} \right\| \le \left\| {\textbf {w}}^{N} \right\| + C_{2},\forall m = N,N + 1,\ldots . \end{aligned}$$

(15)

Equation (15) evidently holds for $m = N$. Then we suppose that (15) holds for an integer $m(m \ge N)$, and we try to show that (15) also holds for $m+1$.

1. If $\left\| {\textbf {w}}^{m} \right\| < \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) }$, by (10), (13), and (14) we have

$$\begin{aligned} \left\| {\textbf {w}}^{m+1} \right\|&\le \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \left\| {\textbf {w}}^{m} \right\| + \eta _{n}C_{2} \nonumber \\&\le \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) } + \eta _{n}C_{2} \nonumber \\&= \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) } \nonumber \\&\le \left\| {\textbf {w}}^{N} \right\| \nonumber \\&\le \left\| {\textbf {w}}^{N} \right\| + C_{2}. \end{aligned}$$

(16)

2. On the other hand, if $\left\| {\textbf {w}}^{m} \right\| \ge \frac{C_{2}}{2\lambda \alpha ^{2}\left( {1 - \lambda } \right) }$, a combination of (10), (13), and (14) produces

$$\begin{aligned} \left\| {\textbf {w}}^{m+1} \right\|&\le \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \left\| {\textbf {w}}^{m} \right\| + \eta _{n}C_{2} \nonumber \\&\le \left( {1 - 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}} \right) \left\| {\textbf {w}}^{m} \right\| + 2\lambda \alpha ^{2}\left( {1 - \lambda } \right) \eta _{n}\left\| {\textbf {w}}^{m} \right\| \nonumber \\&= \left\| {\textbf {w}}^{m} \right\| \nonumber \\&\le \left\| {\textbf {w}}^{N} \right\| + C_{2}. \end{aligned}$$

(17)

Now we have shown by induction that (15) always holds for Case (ii). Hence, (9) is valid in this case by setting

$$\begin{aligned} C_{1} = {\max \left\{ {\left\| {\textbf {w}}^{0} \right\| ,\left\| {\textbf {w}}^{1} \right\| ,\ldots ,\left\| {\textbf {w}}^{N - 1} \right\| ,\left\| {\textbf {w}}^{N} \right\| + C_{2}} \right\} }. \end{aligned}$$

(18)

Thus, (9) is true for both Cases (i) and (ii), and this completes the proof of Theorem 1. $\square$

1.2 Proof of Theorem 2

Lemma 1

([26]) Suppose that the step size ${\eta _n}$ satisfies the Assumption (A3) and the sequence $\{a_n\}(n \in N)$ satisfies ${a_n} \ge 0$, $\sum \limits _{n = 0}^\infty {{\eta _n}a_n^\beta } < \infty$ and $\left| {{a_{n + 1}} - {a_n}} \right| \le \mu {\eta _n}$ for some positive constants $\beta$ and $\mu$. Then we have

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } {a_n} = 0. \end{aligned}$$

(19)

Lemma 2

([27]) Let $\{Y_n\}$, $\{W_n\}$, $\{Z_n\}$ be three sequences, where ${W_n}$ is nonnegative and $\{Y_n\}$ is bounded for all n. Assume that ${Y_{n + 1}} \le {Y_n} - {W_n} + {Z_n}$ and $\sum \limits _{n = 0}^\infty {{Z_n}}$ is convergent. Then either ${Y_n} \rightarrow - \infty$ or else ${Y_n}$ converges to a finite value and $\sum \limits _{n = 0}^\infty {{W_n}} < \infty$.

Lemma 3

([27]) Let $G:\phi \in {R^m} \rightarrow R(m \ge 1)$ be continuous for a bounded closed region $\phi$, and ${\phi _0} = \{ {\textbf {x}} \in \phi :G({\textbf {x}}) = 0\}$. Suppose the projection of ${\phi _0}$ on each coordinate axis does not contain any interior points. If the sequence $\{ {{\textbf {x}}^q}\}$ satisfies

• (a) $\mathop {\lim }\limits _{q \rightarrow \infty } G({{\textbf {x}}^q}) = 0$,

• (b) $\mathop {\lim }\limits _{q \rightarrow \infty } \left\| {{{\textbf {x}}^{q + 1}} - {{\textbf {x}}^q}} \right\| = 0$,

then there exists a unique ${{\textbf {x}}^ * } \in {\phi _0}$ such that $\mathop {\lim }\limits _{q \rightarrow \infty } {{\textbf {x}}^q} = {{\textbf {x}}^ * }$.

Lemma 4

Suppose that the sequence $\left\{ {\textbf {w}}^{nb+k} \right\}$ is generated by (5) and that conditions (A1) and (A2) are satisfied, then there holds that

$$\begin{aligned} E({\textbf {w}}^{(n+1)b}) \le E({\textbf {w}}^{nb}) - \eta _{n}\left\| {\nabla _{{\textbf {w}}}E({\textbf {w}}^{nb})} \right\| ^{2} + C_{3}\eta _{n}^{2},n = 0,1,\ldots , \end{aligned}$$

(20)

where the constant ${C_3} > 0$ is independent of n and ${\eta _n}$.

Proof

According to Equation (3), we have

$$\begin{aligned}&E({\textbf {w}}^{(n+1)b}) - E({\textbf {w}}^{nb})\nonumber \\&= {\sum \limits _{k = 0}^{b - 1}{\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left( e({{\textbf {m}}^{k}}\star {{\textbf {w}}^{(n+1)b}},\xi ^{j}) - e({{\textbf {m}}^{k}}\star {{\textbf {w}}^{nb}},\xi ^{j}) \right) }} \nonumber \\&\quad + \lambda {\sum \limits _{k = 0}^{b - 1}\left( {{\left\| {{\textbf {m}}^{k}} \star {{\textbf {w}}^{(n+1)b}}\right\| }^2} - {{\left\| {{\textbf {m}}^{k}} \star {{\textbf {w}}^{nb}}\right\| }^2} \right) } \nonumber \\&= \left( {\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k}}\star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}}}\right) }\right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) \nonumber \\&\quad + \delta _{1} + \lambda {\sum \limits _{k = 0}^{b - 1}\left( {\left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b}} \right\| ^{2} - \left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right\| ^{2}} \right) }, \end{aligned}$$

(21)

where

$$\begin{aligned} \delta _{1} = \frac{1}{2}{\sum \limits _{k = 0}^{b - 1}{\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}{\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) ^{T}\left( \left. \frac{\partial ^{2}e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial ^{2}{} {\textbf {u}}} \right| _{{\textbf {u}} = \pi _{n,b,k}} \right) \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }}}. \end{aligned}$$

(22)

The first term of (21) can be rewritten as follows

$$\begin{aligned}&\left( {\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k}}\star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}}}\right) }\right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) \nonumber \\ =&\left( {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) - 2\lambda {\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) }} \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) \nonumber \\ =&\left( {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) - 2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^T\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }} \nonumber \\ =&- \eta _{n}\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| ^{2} + \delta _{2} - 2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^T\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }}, \end{aligned}$$

(23)

where

$$\begin{aligned} \delta _{2} =&- \eta _{n}\left( {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right) ^{T}\sum \limits _{k = 0}^{b - 1}(\nabla _{{\textbf {w}}} E_k({\textbf {w}}^{nb+k})-\nabla _{{\textbf {w}}} E_k({\textbf {w}}^{nb}))\nonumber \\&=- \eta _{n}\left( {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right) ^{T} \nonumber \\&\times \left( {\sum \limits _{k = 0}^{b - 1}{{\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left( {\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}} - \left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}}} \right) }}} \right) \nonumber \\&- 2\lambda \eta _{n}\left( {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right) ^{T}{\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{nb + k} - {\textbf {w}}^{nb}} \right) } \right) }. \end{aligned}$$

(24)

Using Assumption (A1) and Theorem 1, we know that there exists a constant ${C_4}$ such that

$$\begin{aligned} \left\| {{\textbf {w}}^{nb + s} - {\textbf {w}}^{nb}} \right\|&= \left\| {- \eta _{n}{\sum \limits _{k = 0}^{s - 1}{{\textbf {m}}^{k} \star \Big ( {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}}}}}} +2\lambda {\textbf {w}}^{nb + k} \Big )\right\| \nonumber \\&\le C_{4}\eta _{n}. \end{aligned}$$

(25)

Similarly, there exists a constant $C_5$ such that

$$\begin{aligned} \left\| \delta _{1} \right\|&= \left\| {\frac{1}{2}{\sum \limits _{k = 0}^{b - 1}{\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}{\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) ^{T}\left( \left. \frac{\partial ^{2}e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial ^{2}{} {\textbf {u}}} \right| _{{\textbf {u}} = \pi _{n,b,k}} \right) \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }}}} \right\| \nonumber \\&\le C_{5}\eta _{n}^{2}. \end{aligned}$$

(26)

Using Assumption (A1) and the mean value theorem, we can deduce that there exists a constant L such that

$$\begin{aligned} \left\| {\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb + k}} - \left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}} }\right\| \le L\Vert {\textbf {w}}^{nb + k} - {\textbf {w}}^{nb}\Vert . \end{aligned}$$

(27)

In this way, based on Eqs. (24) and (25), we know that there exists a constant $C_6$ such that

$$\begin{aligned} \left\| \delta _{2} \right\|&\le \eta _{n}L\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| \left( {{\sum \limits _{k = 0}^{b - 1}{\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}}}\left\| {{\textbf {w}}^{nb + k} - {\textbf {w}}^{nb}} \right\| } \right) \nonumber \\&\quad + 2\lambda \eta _{n}\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| \left( {\sum \limits _{k = 0}^{b - 1}\left\| {{\textbf {w}}^{nb + k} - {\textbf {w}}^{nb}} \right\| } \right) \nonumber \\&\le C_{6}\eta _{n}^{2}. \end{aligned}$$

(28)

Using (25), the third term of (21) can be reformulated and estimated as

$$\begin{aligned}&\lambda {\sum \limits _{k = 0}^{b - 1}\left( {\left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b}} \right\| ^{2} - \left\| {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right\| ^{2}} \right) } \nonumber \\ =&\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b} + {\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^T\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b} - {\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) }} \nonumber \\ =&\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{{({n + 1})}b} + {\textbf {w}}^{nb}} \right) } \right) ^{T}\left( {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) } \right) }} \nonumber \\ =&\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star \left( {2{\textbf {w}}^{nb} + \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) } \right) } \right) ^{T}\left( {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) } \right) }} \nonumber \\ =&2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }} + \lambda {\sum \limits _{k = 0}^{b - 1}\left\| {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) } \right\| ^{2}} \nonumber \\ \le&2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }} + C_{7}\eta _{n}^{2}, \end{aligned}$$

(29)

where ${C_7}$ is a positive constant. Now, combining (21)–(29), we can obtain that

$$\begin{aligned}&E\left( {\textbf {w}}^{{({n + 1})}b} \right) - E\left( {\textbf {w}}^{nb} \right) \nonumber \\&\le - \eta _{n}\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| ^{2} - 2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }} \nonumber \\&\quad + C_{5}\eta _{n}^{2} + C_{6}\eta _{n}^{2} + 2\lambda {\sum \limits _{k = 0}^{b - 1}{\left( {{\textbf {m}}^{k} \star {\textbf {w}}^{nb}} \right) ^{T}\left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) }} + C_{7}\eta _{n}^{2} \nonumber \\&= - \eta _{n}\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| ^{2} + \left( C_{5} + C_{6} + C_{7} \right) \eta _{n}^{2}. \end{aligned}$$

(30)

This completes the proof by simply setting $C_{3} = C_{5} + C_{6} + C_{7}$. $\square$

Proof of (6) and (7). Applying Lemma 2 to (20), we can conclude that

$$\begin{aligned} {\sum \limits _{n = 0}^{\infty }{{\eta _{n}}{\left\| {\nabla _{{\textbf {w}}}E\left( {\textbf {w}}^{nb} \right) } \right\| ^{2}}}} < \infty \end{aligned}$$

(31)

and $E\left( {\textbf {w}}^{nb} \right) \rightarrow - \infty$ or converges to a constant $E^{*}$ as $n\rightarrow + \infty$. Since $E\left( {\textbf {w}}^{nb} \right) > 0$, then we have

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } E \left( {{{\textbf {w}}^{nb}}} \right) = {E ^*}. \end{aligned}$$

Combining (27) and (25), we have

$$\begin{aligned}&\left\| {\frac{\partial E\left( {\textbf {w}}^{(n + 1)b} \right) }{\partial {\textbf {w}}} - \frac{\partial E\left( {\textbf {w}}^{nb} \right) }{\partial {\textbf {w}}}} \right\| \nonumber \\&= \left\| {\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k} \star {\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left( {\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b}} - \left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}}} \right) }} \right) } \right\| \nonumber \\&+ \left\| {2\lambda {\sum \limits _{k = 0}^{b - 1}\left( {{\textbf {m}}^{k} \star \left( {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right) } \right) }} \right\| \nonumber \\&\le {\sum \limits _{k = 0}^{b - 1}{\sum \limits _{j = j_{k} + 1}^{j_{k + 1}}\left\| {\left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{{({n + 1})}b}} - \left. \frac{\partial e\left( {{\textbf {u}},\xi ^{j}} \right) }{\partial {\textbf {u}}} \right| _{{\textbf {u}} = {\textbf {m}}^{k} \star {\textbf {w}}^{nb}}} \right\| }} \nonumber \\&+ 2\lambda {\sum \limits _{k = 0}^{b - 1}\left\| {{\textbf {w}}^{{({n + 1})}b} - {\textbf {w}}^{nb}} \right\| } \nonumber \\&\le D\eta _{n}. \end{aligned}$$

(32)

where D is a positive constant. Then we have

$$\begin{aligned} \left| {\left\| \frac{\partial E\left( {\textbf {w}}^{{({n + 1})}b} \right) }{\partial {\textbf {w}}} \right\| - \left\| \frac{\partial E\left( {\textbf {w}}^{nb} \right) }{\partial {\textbf {w}}} \right\| } \right| \le \left\| {\frac{\partial E\left( {\textbf {w}}^{{({n + 1})}b} \right) }{\partial {\textbf {w}}} - \frac{\partial E\left( {\textbf {w}}^{nb} \right) }{\partial {\textbf {w}}}} \right\| \le D\eta _{n}. \end{aligned}$$

(33)

A combination of (31), (33) and lemma 1 immediately gives

$$\begin{aligned} {\lim \limits _{n\rightarrow \infty }\left\| {\nabla _{{\textbf {w}}} E\left( {\textbf {w}}^{nb} \right) } \right\| } = 0. \end{aligned}$$

$\square$

Proof of (8). According to Equ. (5) and Assumptions (A1) and (A3), we have

$$\begin{aligned} \lim \limits _{m\rightarrow \infty }\left\| {{\textbf {w}}^{(n + 1)b} - {\textbf {w}}^{nb}} \right\| \nonumber \\ =&{\lim \limits _{n\rightarrow \infty }\left\| \sum \limits _{k=0}^{b-1}({{\textbf {w}}^{nb + k + 1} - {\textbf {w}}^{nb + k}}) \right\| }\nonumber \\ \le&\lim \limits _{n\rightarrow \infty } \eta _n{\sum \limits _{k=0}^{b-1}\left\| {\nabla _{{\textbf {w}}} E_k\left( {\textbf {w}}^{nb + k} \right) } \right\| }\nonumber \\ =&0. \end{aligned}$$

(34)

Therefore, based on (6), (34), and Assumption (A4), we can conclude from Lemma 3 that there exists a unique ${\textbf {w}}^{*} \in \Phi$ such that

$$\begin{aligned}{\lim \limits _{m\rightarrow \infty }{} {\textbf {w}}^{nb}} = {\textbf {w}}^{*}. \end{aligned}$$

$\square$