1 Introduction

Fractional-order calculus, which naturally extends classical integer-order calculus, offers a precise approach to modeling the dynamic behavior of complex systems and achieving more accurate solutions to mathematical problems [1, 2]. Furthermore, by incorporating nonlocal and history-dependent properties [1], fractional-order systems prove to be effective in modeling various processes with memory and heredity. Examples include electrical circuits models [3], infectivity SIR model [4], quantum mechanics [5], logistic models [6], economic systems [7], financial models [8]. In the neural areas, Boroomand and Menhaj [9] have advanced the concept of fractional-order neural networks within neural domains, wherein the conventional capacitor in integer-order neural networks is replaced by the concept of fractance. The infusion of fractional calculus principles into neural network modeling stands poised to yield a substantial enhancement. This stems from the intrinsic capacity of fractional calculus to delineate the memory and hereditary attributes of the network. Furthermore, in the context of engineering applications and real-world systems, the presence of measurement inaccuracies, environmental noise, and parameter fluctuations frequently results in parameter variability within defined ranges. This inherent variability can, in turn, engender divergence or instability [10]. Thus, it is both germane and meaningful to introduce parametric uncertainty to fractional systems, thereby elucidating the more authentic dynamical characteristics inherent to fractional-order neural networks. Consequently, fractional-order neural networks have garnered growing attention and seen numerous noteworthy publications that have made substantial contributions to this field [10,11,12,13,14].

Dissipativity, originally introduced by Willems in 1972 [15], presents a broader problem scope compared to Lyapunov stability, \(H_{\infty }\) performance, and passivity analysis. Its essence lies in the existence of a nonnegative energy function, ensuring that the energy dissipation within the system is consistently lower than the rate of externally supplied energy. The central objective within the context of the finite-time dissipative control problem for dynamical systems is the formulation of a suitable control strategy that guarantees not only the finite-time boundedness of the closed-loop system but also the fulfillment of the dissipativity performance criteria. Building upon this fundamental concept, the challenge of finite-time dissipative control has been investigated across a variety of dynamic systems. Saravanan et al. [16] conducted an analysis of the finite-time non-fragile dissipativity in the context of time-delayed neural networks by constructing appropriate Lyapunov–Krasovskii functionals, employing Jensen’s inequality and Wirtinger-based integral inequalities. Li and Ma [17] developed a state feedback controller to ensure the singular stochastic finite-time admissibility and the singular stochastic dissipative finite-time admissibility of the underlying closed-loop singular Markovian jump systems, expressed in the form of strict linear matrix inequalities. Chen et al. [18] investigated the dissipative control for stochastic delay Markovian switched systems within a fixed finite time interval. In [19], the problem of finite-time dissipative control was addressed for discrete-time stochastic delayed systems with Markovian switching and interval parameters. Introducing a novel concept of finite-time stochastic exponential dissipativity, Song et al. [20] examined the finite-time dissipative control problem for a specific class of discrete stochastic systems in the context of wireless communication networks, which entail both randomly occurring uncertainties and stochastic fading measurements. It is worth noting that all of the aforementioned findings primarily pertain to systems with integer-order dynamics [16,17,18,19,20]. In the realm of fractional-order systems, the existing literature is relatively sparse [21,22,23]. Hong and colleagues [21] devised an output feedback controller to tackle finite-time dissipative control in a category of nonlinear fractional-order systems. Their approach leveraged fundamental mathematical transformations, fractional calculus properties, and linear matrix inequality techniques. In another context, the problem of achieving finite-time dissipative control for semi-Markovian jump systems with time-varying delays and generally uncertain transition rates was explored in [22], using linear matrix inequality techniques. Phuong and collaborators [23] introduced an effective analytical methodology that incorporates mathematical transformations and fractional calculus to resolve dissipative control problems within one-sided Lipschitz singular Caputo fractional-order systems affected by nonlinear perturbations. Their work culminated in the design of a state feedback controller, ensuring the closed-loop is regular, impulse-free, and finite-time bounded with a dissipativity performance index. Note that the controllers in [16,17,18,19,20,21,22,23] are designed based on time-triggered schemes.

Over the past twenty years, there has been a significant focus on the adoption of event-triggered strategies to tackle control-related challenges [24,25,26]. Event-triggered control has proven effective in substantially reducing data transmission, communication costs, and the computational burden while still maintaining a satisfactory level of control performance, as noted in reference [27]. In contrast to conventional time-triggered control, event-triggered control employs an aperiodic control strategy, whereby sampling only occurs when a predetermined mathematical inequality is breached, as highlighted in reference [28]. As a result, not every system state is transmitted to the controller design [29]. Thanks to these advantages, recent research has extended the exploration of finite-time event-triggered control to various types of systems [30,31,32,33,34,35,36,37]. Syed Ali et al. [33] proposed an event-triggered scheme to address the challenge of achieving finite-time \(H_{\infty }\) boundedness for uncertain Markov jump neural networks with distributed time-varying delays based on utilizing the Lyapunov–Krasovskii function approach, the reciprocal convex combinational technique, Jensen’s inequality, and the free weight matrix method. Additionally, the issue of event-triggered \(H_{\infty }\) filter design for networked systems experiencing stochastic deception attacks, focusing on finite-time boundedness, was explored in reference [34]. In this context, Zhou et al. [35] tackled the problem of distributed event-triggered finite-time \(H_{\infty }\) filtering for switched systems on sensor networks, considering scenarios involving two-channel network attacks and asynchronous modes. The authors, through their work, established sufficient conditions by employing the multiple Lyapunov functional method and the average dwell time switching mechanism, ensuring that the filtering error system, under both synchronous and asynchronous modes, remains finite-time bounded and meets the \(H_{\infty }\) performance index. A distributed event-triggered control strategy was developed in [36] to handle the problem of finite-time guaranteed-cost \(H_{\infty }\) consensus for nonlinear multi-agent systems subject to disturbances and uncertain parameters. Furthermore, the challenge of event-triggered annular finite-time \(H_{\infty }\) filtering was addressed in stochastic network systems in reference [37]. Nonetheless, the findings documented in [30,31,32,33,34,35,36,37] are exclusively applicable to systems with integer orders. There is a paucity of research focusing on event-triggered control in the realm of fractional-order systems. Unlike their integer-order counterparts, which can leverage exact solutions of differential equations to determine the minimum inter-execution time, fractional-order systems cannot employ this same method due to the complexity inherent in their solution forms. Consequently, this paper’s primary challenges and obstacles revolve around establishing a novel theoretical framework for fractional-order systems to prevent the occurrence of the Zeno phenomenon.

Motivated by the above discussion, in this paper, we consider the problem of event-triggered finite-time dissipative control for fractional-order neural networks subject to uncertainties. This paper’s primary contributions can be summarized as follows: (i) Due to the memory and heritability characteristics of fractional calculus operators, particularly in the context of the Caputo fractional-order definition with distinct initial times (noted as \(t_0 \ne \tau _0\)), a specific relationship emerges: \(_{t_0}\texttt{I}_{t}^\alpha \,_{\tau _0}^{C}\texttt{D}_t^{\alpha }\upsilon (t) \not = \upsilon (t) - \upsilon (\tau _0)\). As a result, certain findings in previous studies (e.g., [38]) may lead to the occurrence of Zeno behavior. Utilizing inequality techniques, a positive lower bound on the inter-execution intervals is estimated to exclude the Zeno behavior for FONNs; (ii) For the first time, we have explored the event-triggered finite-time dissipative control problem for FONNs with uncertainties; (iii) A numerical example with simulation results is given to demonstrate the effectiveness of the theoretical results.

2 Problem formulation and preliminaries

Definition 1

( [1]) Let \(J=[t_0, b] \, (-\infty< t_0< b < +\infty )\) be a finite interval of \(\mathbb {R}\). The Riemann-Liouville fractional integrals of order \(\alpha \) of the function \(\texttt{g}(.) \) is defined by

$$\begin{aligned} _{t_0}\texttt{I}_t^{\alpha }\texttt{g}(t) = \frac{1}{\varGamma (\alpha )}\int _{{t_0}}^{t}(t-s)^{\alpha - 1}\texttt{g}(s)ds, \, t \in {J}, \alpha > 0, \end{aligned}$$
(1)

where \(\varGamma (s) = \int _{0}^{\infty }\tau ^{s-1}e^{-\tau }d\tau \) is the gamma function. When \(\alpha = n \in \mathbb {N}\), the definition (1) coincides with the n-th integrals of the form

$$\begin{aligned} _{t_0}\texttt{I}_t^{n}\texttt{g}(t) = \frac{1}{(n-1)!}\int _{t_0}^{t}(t-s)^{n-1}\texttt{g}(s)ds. \end{aligned}$$

Definition 2

( [1]) The Riemann-Liouville fractional derivatives of order \(\alpha > 0\) of the function \(\texttt{g}(.) \) is presented by

$$\begin{aligned} _{t_0}\texttt{D}_t^{\alpha }\texttt{g}(t) = \frac{1}{\varGamma (n-\alpha )}\frac{d^n}{dt^n}\left( \int _{t_0}^{t}(t-s)^{n-\alpha -1}\texttt{g}(s)ds\right) , \, t > t_0, \end{aligned}$$

where \(n = [\alpha ] + 1\), \([\alpha ]\) means the integer part of \(\alpha \). In particular, when \(\alpha = n \in \mathbb {N}\), then \( _{t_0}\texttt{D}_t^{0}\texttt{g}(t) = \texttt{g}(t), \, _{t_0}\texttt{D}_t^{n}\texttt{g}(t) = \texttt{g}^{(n)}(t),\) where \(\texttt{g}^{(n)}(t)\) is the usual derivative of \(\texttt{g}(t)\) of order n. If \(0< \alpha < 1\), then

$$\begin{aligned} _{t_0}\texttt{D}_t^{\alpha }\texttt{g}(t) = \frac{1}{\varGamma (1-\alpha )}\frac{d}{dt}\left( \int _{t_0}^{t}(t-s)^{-\alpha }\texttt{g}(s)ds\right) , \, t > {t_0}. \end{aligned}$$

Definition 3

( [1]) The Caputo fractional derivatives of order \(\alpha > 0\) of the function \(\texttt{g}(.) \) is presented by

$$\begin{aligned} _{{t_0}}^{C}\texttt{D}_{t}^{\alpha }\texttt{g}(t) = \, _{t_0}\texttt{D}_t^{\alpha }\left( \texttt{g}(t) - \sum _{k=0}^{n-1}\frac{\texttt{g}^{(k)}({t_0)}}{k!}(t-{t_0})^k \right) , { t \ge t_0 \ge 0}, \end{aligned}$$

where \(n = [\alpha ]+1\) for \(\alpha \not \in \mathbb {N}, n = \alpha \) for \(\alpha \in \mathbb {N}\). In particular, when \(0< \alpha < 1\), then

$$\begin{aligned} _{{t_0}}^{C}\texttt{D}_{t}^{\alpha }\texttt{g}(t) = \, _{{t_0}}\texttt{D}_t^{\alpha }\left( \texttt{g}(t) - \texttt{g}({t_0})\right) , { t \ge t_0 \ge 0}. \end{aligned}$$

We revisit certain attributes associated with fractional-order calculus.

Property 1 ( [1]): If \({ \upsilon (.)} \in AC([0, +\infty ), \mathbb {R})\) and \(0 < \alpha \le 1\), then

$$\begin{aligned} _{{t_0}}\texttt{I}_{t}^\alpha \left( \,_{{t_0}}^{C}\texttt{D}_t^{\alpha }\upsilon (t)\right) = \upsilon (t) - \upsilon ({t_0}), \, t {\ge t_{0} \ge 0}. \end{aligned}$$

Property 2 ( [1]): If \({\upsilon (.)} \in AC^{n}([0, +\infty ), \mathbb {R})\), then

$$\begin{aligned} _{{t_0}}\texttt{I}_{t}^{\alpha _1}(\,_{{t_0}}\texttt{I}_{t}^{\alpha _2}v(t)) = \, _{{t_0}}\texttt{I}_{t}^{\alpha _2}(\,_{{t_0}}\texttt{I}_{t}^{\alpha _1}{\upsilon (t)}) =\, _{{t_0}}\texttt{I}_{t}^{\alpha _1+\alpha _2}({\upsilon (t)}), \forall t {\ge t_{0} \ge 0}, \alpha _1, \alpha _2 > 0. \end{aligned}$$

Let us consider the following fractional-order neural networks with uncertainties

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = -\left[ A+\varDelta A(t)\right] x(t) + \left[ D+\varDelta D(t)\right] g(x(t)) + \left[ W+\varDelta W(t)\right] \omega (t)\\ &{} \qquad \qquad \qquad + \left[ B+\varDelta B(t)\right] u(t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^n, \end{array}\right. } \end{aligned}$$
(2)

where \(\alpha \in (0, 1)\) is the fractional order of the system. The state vector is denoted as \(x(t) = { \left( x_1(t), \ldots , x_n(t)\right) ^T} \in {\mathbb {R}}^{n}\), the control input vector as \(u(t) \in {\mathbb {R}}^m\), the disturbance vector as \(\omega (t) \in \mathbb {R}^q\), the output vector as \(z(t) \in \mathbb {R}^{p}\), and the initial condition is given by \(x_0\). \(g(x(t)) = (g_1(x_1(t)), \ldots , g_n(x_n(t)))^{ T} \in \mathbb {R}^n\) denotes the activation function. \(A = {{\,\textrm{diag}\,}}\{a_1, a_2, \ldots , a_n\} \in {\mathbb {R}}^{n \times n}\) is a positive diagonal matrix, \(D \in {\mathbb {R}}^{n \times n}\) represents the interconnection weight matrix, while \(W \in \mathbb {R}^{n \times q}\), \(B \in {\mathbb {R}}^{n \times m}\), \(M \in {\mathbb {R}}^{p \times n}\), and \(N \in \mathbb {R}^{p \times q}\) are known constant matrices.

We need the following assumptions for further study.

Assumption 1

[12, 39] The unknown matrices \(\varDelta A(t), \varDelta D(t), \varDelta W(t), \varDelta B(t)\) satisfy the following condition

$$\begin{aligned} \varDelta A(t) = E_aF_a(t)H_a, \, \varDelta D(t) = E_dF_d(t)H_d, \, \varDelta W(t) = E_wF_w(t)H_w, \, \varDelta B(t) = E_bF_b(t)H_b, \end{aligned}$$

where \(E_a, E_d, E_w, E_b, H_a, H_d, H_w, H_b\) are identified as constant real matrices with appropriate dimensions, and \(F_a(t), F_d(t), F_w(t), F_b(t)\) are unfamiliar time-varying matrices that fulfill the subsequent condition for all time instances \(t \ge 0\)

$$\begin{aligned} I \ge F_a^T(t)F_a(t), I \ge F_d^T(t)F_d(t), I \ge F_w^T(t)F_w(t), I \ge F_b^T(t)F_b(t), \, \forall t \ge 0. \end{aligned}$$

Assumption 2

[12] The activation functions \(g_i(\cdot )\) exhibit continuity, along with the property that \(g_i(0) = 0\) for \(i = 1, 2, \ldots , n\). Additionally, these functions satisfy the Lipschitz condition across the real numbers domain, with a non-negative Lipschitz constant denoted as \(l_i \ge 0\):

$$\begin{aligned} |g_i(\theta _1) - g_i(\theta _2)| \le l_i|\theta _1 - \theta _2|, \, \forall \theta _1, \theta _2 \in \mathbb {R}. \end{aligned}$$

In particular, when \(\theta _2 = 0\), the subsequent inequality holds:

$$\begin{aligned} |g_i(\theta _1)| \le l_i |\theta _1|, \, \forall l_i \in \mathbb {R}^{+}. \end{aligned}$$

Assumption 3

[40] The disturbance input vector, denoted as \(\omega (t) \in {\mathbb {R}}^q\), is constrained by the following condition:

$$\begin{aligned} \exists d > 0: \omega ^T(t)\omega (t) \le d, \, \forall t \ge 0. \end{aligned}$$

The nominal unforced systems of system (2) can be written as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = -\left[ A+\varDelta A(t)\right] x(t) + \left[ D+\varDelta D(t)\right] g(x(t)) + \left[ W+\varDelta W(t)\right] \omega (t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^n. \end{array}\right. } \end{aligned}$$
(3)

In the absence of output vector vector, the system (3) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = -\left[ A+\varDelta A(t)\right] x(t) + \left[ D+\varDelta D(t)\right] g(x(t)) + \left[ W+\varDelta W(t)\right] \omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^n. \end{array}\right. } \end{aligned}$$
(4)

Definition 4

[40] Given positive scalars \(c_1, c_2, d, T_f\) and a positive definite matrix R. The system (4) is said to be robustly finite-time boundedness with respect to (w.r.t) \((c_1, c_2, R, T_f, d)\) if \(x^T(0)Rx(0) \le c_1 \Rightarrow x^T(t)Rx(t) \le c_2, \forall t \in [0, T_f]\).

Definition 5

[21, 41] Given positive scalars \(c_1, c_2, d, T_f\), and a positive definite matrix R, the system described by equation (2) is said to be robustly finite-time (S, T, U)-dissipative with respect to \((c_1, c_2, R, T_f, d)\) under the following conditions:

(i) The system represented by equation (4) is robustly finite-time bounded concerning \((c_1, c_2, R, T_f, d)\).

(ii) Under the assumption of zero initial conditions, there exists a positive constant \(\gamma > 0\) satisfying the subsequent inequality

$$\begin{aligned} { \int _{0}^{t}\left( 2z^T(s)S\omega (s) + z^T(s)Tz(s) + \omega ^T(s)U\omega (s)\right) ds \ge \gamma \int _{0}^{t}\omega ^T(s)\omega (s)ds, \forall t \in [0, T_f], } \end{aligned}$$

for all non-zero functions \(\omega (\cdot ) \in L_2([0, +\infty ), {\mathbb {R}}^q)\) that fulfill Assumption 3, \(S \in {\mathbb {R}}^{p \times q}\) is a predefined real matrix, \(T \in {\mathbb {R}}^{p \times p}\), and \(U \in {\mathbb {R}}^{q \times q}\) are given real symmetric matrices.

In this paper, we propose an event-triggered state feedback controller as follows

$$\begin{aligned} u(t) = Kx(t_k), \, t \in [t_k, t_{k+1}), \end{aligned}$$
(5)

where the feedback gain matrix K is determined later and the triggering sequece \(\{t_k\}_{k \in \mathbb {N}}\) is defined as below:

$$\begin{aligned} t_0 = 0, \, t_{k+1} = \inf \{t>t_k: \Vert e(t)\Vert > \eta \Vert x(t)\Vert \}, \end{aligned}$$
(6)

where e(t) is defined as the difference between the current state x(t) and the most recent sampled state \(x(t_k)\) (\(e(t) = x(t) - x(t_k)\)). Here, \(x(t_k)\) corresponds to the state measurement obtained at the latest sampling instant, and x(t) signifies the state at the current time. Additionally, \(\eta \) represents a predetermined threshold constant. It is pertinent to emphasize that when an event is activated, the error term e(t) is reset to zero, subsequently resuming its accumulation until it elicits a fresh measurement update. Consequently, during these event-triggered occurrences, it remains valid that \(e(t_k) = 0\).

Substituting (5) into (2), we obtain the event-triggered closed-loop system

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = \left[ -A-\varDelta A(t) + BK + \varDelta B(t)K\right] x(t) - \left[ BK+\varDelta B(t)K\right] e(t)\\ &{} \qquad \qquad \qquad + \left[ D+\varDelta D(t)\right] g(x(t)) + \left[ W+\varDelta W(t)\right] \omega (t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^n. \end{array}\right. } \end{aligned}$$
(7)

The primary aim of this paper is to develop an event-triggered feedback controller that establishes robust finite-time (S, T, U)-dissipativity for the closed-loop system described by (7).

Lemma 1

[42] Let \(g:[t_0, + \infty )\rightarrow \mathbb {R}\) be a continuously differentiable function, and let’s assume that it satisfies the inequality:

$$\begin{aligned} _{t_0}^{C}\texttt{D}_{t}^{\alpha }g(t) \le \beta g(t) + \texttt{m}, \end{aligned}$$

where \(\beta \) and \(\texttt{m}\) are positive constants, \(\alpha \in (0,1)\). Then

$$\begin{aligned} g(t) \le -\frac{\texttt{m}}{\beta } + \left( g(t_0) + \frac{\texttt{m}}{\beta }\right) \exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t-t_0)^{\alpha }\right) . \end{aligned}$$

The following lemma ensures that for dynamic event-triggered mechanism (ETM) (6), the Zeno behavior does not happen.

Lemma 2

The distance between two arbitrary triggering instants \(t_k\) and \(t_{k+1}\) of the dynamic ETM (6) is positive, which indicates that the inter-event interval has a positive lower bound, and then the sequence of event-triggering instants \(\{t_k\}\) has no Zeno behavior.

Proof

For \(t \in [t_k, t_{k+1})\), it follows \(e(t) = x(t) - x(t_k)\) that \(_{0}^{C}\texttt{D}_{t}^{\alpha }e(t) =\, _{0}^{C}\texttt{D}_{t}^{\alpha }x(t) - \, _{0}^{C}\texttt{D}_{t}^{\alpha }x(t_k) = \,_{0}^{C}\texttt{D}_{t}^{\alpha }x(t)\). Thus, we obtain

$$\begin{aligned} \begin{aligned} _{t_k}^{C}\texttt{D}_{t}^{\alpha }\Vert e(t)\Vert&= \, _{0}^{C}\texttt{D}_{t}^{\alpha }\Vert e(t)\Vert - \,_{0}^{C}\texttt{D}_{t_k}^{\alpha }\Vert e(t)\Vert \\&\le \Vert \,_{0}^{C}\texttt{D}_{t}^{\alpha }x(t) \Vert - \,_{0}^{C}\texttt{D}_{t_k}^{\alpha }\Vert e(t)\Vert \\&\le \left( \Vert A + \varDelta A(t)\Vert +\Vert BK\Vert +\Vert \varDelta B(t)K\Vert \right) \Vert x(t)\Vert + \left( \Vert BK+ \varDelta B(t)K\Vert \right) \Vert e(t)\Vert \\&\qquad + \Vert D+\varDelta D(t)\Vert \Vert g(x(t))\Vert + \left( \Vert W + \varDelta W(t)\Vert \right) \Vert \omega (t)\Vert - \,_{0}^{C}\texttt{D}_{t_k}^{\alpha }\Vert e(t)\Vert \\&\le \left( \Vert A + \varDelta A(t)\Vert +\Vert BK\Vert +\Vert \varDelta B(t)K\Vert \right) \Vert x(t)\Vert + \left( \Vert BK+ \varDelta B(t)K\Vert \right) \Vert e(t)\Vert \\&\qquad + \Vert D+\varDelta D(t)\Vert \Vert g(x(t))\Vert + \left( \Vert W + \varDelta W(t)\Vert \right) \Vert \omega (t)\Vert \\&\qquad + \bigg | \frac{1}{\varGamma (1-\alpha )}\int _{0}^{t_k}\frac{\Vert e(s)\Vert '}{(t_k-s)^{\alpha }}ds \bigg |. \end{aligned} \end{aligned}$$
(8)

Using Assumptions 1, 2, and 3 combined with the fact that \(x(t) = e(t) + x(t_k)\), we get the following estimate

$$\begin{aligned} _{t_k}^{C}\texttt{D}_t^{\alpha }\Vert e(t)\Vert \le \beta \Vert e(t)\Vert + \texttt{m}, \end{aligned}$$
(9)

where

$$\begin{aligned}&l = \max \limits _{i = 1, 2, \ldots , n}\{l_i\},\\&\beta = \Vert A\Vert +\Vert E_a\Vert \Vert H_a\Vert + 2\Vert B\Vert \Vert K\Vert +2\Vert E_b\Vert \Vert H_b\Vert \Vert K\Vert +l\left( \Vert D\Vert +\Vert E_d\Vert \Vert H_d\Vert \right) ,\\&\texttt{m} = \left[ \Vert A\Vert +\Vert E_a\Vert \Vert H_a\Vert + \Vert B\Vert \Vert K\Vert +\Vert E_b\Vert \Vert H_b\Vert \Vert K\Vert +l\left( \Vert D\Vert +\Vert E_d\Vert \Vert H_d\Vert \right) \right] \Vert x(t_k)\Vert \\&\qquad \qquad \qquad + \left( \Vert W\Vert +\Vert E_w\Vert \Vert H_w\Vert \right) \sqrt{d} + \bigg | \frac{1}{\varGamma (1-\alpha )}\int _{0}^{t_k}\frac{\Vert e(s)\Vert '}{(t_k-s)^{\alpha }}ds \bigg |. \end{aligned}$$

By utilizing Lemma 1, we get the following estimate

$$\begin{aligned} \Vert e(t)\Vert \le - \frac{\texttt{m}}{\beta } + \left( \Vert e(t_k)\Vert + \frac{\texttt{m}}{\beta }\right) \exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t-t_k)^{\alpha }\right) . \end{aligned}$$
(10)

Since \(\Vert e(t_k)\Vert = \Vert x(t_k) - x(t_k)\Vert = 0\), (10) becomes

$$\begin{aligned} \Vert e(t)\Vert \le - \frac{\texttt{m}}{\beta } + \frac{\texttt{m}}{\beta }\exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t-t_k)^{\alpha }\right) . \end{aligned}$$
(11)

By taking the limit \(t \longrightarrow t_{k+1}^{-}\) on both sides of (11), we derive

$$\begin{aligned} \Vert e(t_{k+1}^{-})\Vert \le - \frac{\texttt{m}}{\beta } + \frac{\texttt{m}}{\beta }\exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t_{k+1}-t_k)^{\alpha }\right) . \end{aligned}$$
(12)

Considering (12) alongside the event-triggered condition in (6), we deduce that

$$\begin{aligned} \eta \Vert x(t_k)\Vert < \Vert e(t_{k+1}^{-})\Vert \le - \frac{\texttt{m}}{\beta } + \frac{\texttt{m}}{\beta }\exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t_{k+1}-t_k)^{\alpha }\right) . \end{aligned}$$
(13)

The inequality (13) is equivalent to the following inequality

$$\begin{aligned} \exp \left( \frac{\beta }{\varGamma (\alpha +1)}(t_{k+1}-t_k)^{\alpha }\right) > \frac{\texttt{m}+\beta \eta \Vert x(t_k)\Vert }{{\texttt{m}}}. \end{aligned}$$
(14)

Inequality (14) implies that

$$\begin{aligned} t_{k+1}-t_{k}> \left[ \frac{\varGamma (\alpha +1)}{\beta }\ln \left( 1+\frac{\beta \eta \Vert x(t_k)\Vert }{\texttt{m}}\right) \right] ^{\frac{1}{\alpha }} > 0. \end{aligned}$$
(15)

This concludes the proof. \(\square \)

Lemma 3

[43] For any \(x, y \in {\mathbb {R}}^n\) and a symmetric positive definite matrix \(P \in {\mathbb {R}}^{n \times n}\), we have

$$\begin{aligned} \pm 2x^Ty\leqslant x^TPx +y^TP^{-1} y. \end{aligned}$$

3 Main results

In this section, we present an event-triggered feedback controller (5) such that the closed-loop system (7) is robustly finite-time (S, T, U)-dissipative.

Theorem 1

Assume assumption 1, 2 and 3 are satisfied. Given positive scalars \(c_1, c_2, T_f, d\) and a matrix \(R > 0\). If there exist positive scalars \(\eta , \gamma , \epsilon _1, \epsilon _2\), and matrices \(P \in \mathbb {R}^{n \times n}, { P > 0}, Y \in \mathbb {R}^{m \times { n}}\) such that the following inequalities hold

$$\begin{aligned}&U - \gamma I > 0, \end{aligned}$$
(16a)
$$\begin{aligned}&\varXi = \begin{bmatrix} \varXi _{11} &{} -BY &{} D &{} W &{} PH_a^T &{} Y^TH_b^T &{} \eta ^2 P &{} PL^T&{}0\\ * &{} I-2P &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{} Y^TH_b^T \\ * &{} * &{} \varXi _{33} &{} -M^TS -M^TTN &{} 0 &{}0 &{} 0 &{}0 &{} 0\\ * &{} * &{} * &{} \varXi _{44} &{} 0 &{} 0 &{}0 &{} 0 &{}0 \\ * &{} * &{} * &{} * &{} -\epsilon _1I &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} * &{} * &{} -\epsilon _2I &{} 0 &{}0 &{} 0\\ * &{} * &{} * &{} * &{} * &{} * &{} -\eta ^2 I &{} 0 &{} 0\\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} -I &{} 0\\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} -I \end{bmatrix} < 0, \end{aligned}$$
(16b)
$$\begin{aligned}&\lambda _2 c_1 + \frac{\lambda _{\max }(U - \gamma I)d}{\varGamma (\alpha +1)}T_f^{\alpha } < \lambda _1 c_2, \end{aligned}$$
(16c)

where

$$\begin{aligned}&L = {{\,\textrm{diag}\,}}\{l_1, \ldots , { l_n}\}, \, {\hat{P}} = R^{-\frac{1}{2}}P^{-1}R^{-\frac{1}{2}}, \, \lambda _1 = \lambda _{\min }({\hat{P}}), \, \lambda _2 = \lambda _{\max }({\hat{P}}), \\&\varXi _{11} = -AP+BY+Y^TB^T-PA^T + \epsilon _1 E_aE_a^T + (1+\epsilon _2) E_bE_b^T + E_dE_d^T+E_wE_w^T, \\&\varXi _{33} = H_d^TH_d - I -M^TTM, \\&\varXi _{44} = H_w^TH_w+\gamma I - U -N^TTN-N^TS - S^TN, \end{aligned}$$

then under the triggered condition (6), the system (7) is robustly finite-time (S, T, U)-dissipative w.r.t. \((c_1, c_2, R, T_f, d)\). Concurrently, the state feedback controller gain matrix K can be computed as \(K = YP^{-1}\).

Proof

As P is a symmetric positive definite matrix, \(P^{-1}\) is also a symmetric positive definite matrix. We will now construct a Lyapunov function for the fractional-order closed-loop system (7):

$$\begin{aligned} V(t) = x^T(t)P^{-1}x(t). \end{aligned}$$

Taking the fractional-order derivative of V(t) along the trajectory (7) and using Assumption 1, we obtain:

$$\begin{aligned} \begin{aligned} _{0}^{C}\texttt{D}_t^{\alpha }V(t)&\le 2x^T(t)P^{-1}\, _{0}^{C}\texttt{D}_t^{\alpha }x(t) \\&= x^T(t)\left[ -P^{-1}A - A^TP^{-1} + P^{-1}BK + K^TB^TP^{-1}\right] x(t) \\&\qquad - 2x^T(t)P^{-1}E_aF_a(t)H_ax(t)\\&\qquad + 2x^T(t)P^{-1}E_bF_b(t)H_bKx(t) -2x^T(t)P^{-1}BKe(t) \\&\qquad - 2x^T(t)P^{-1}E_bF_b(t)H_bKe(t) + 2x^T(t)P^{-1}Dg(x(t))\\&\qquad + 2x^T(t)P^{-1}E_dF_d(t)H_dg(x(t)) + 2x^T(t)P^{-1}W\omega (t)\\&\qquad + 2x^T(t)P^{-1}E_wF_w(t)H_w\omega (t). \end{aligned} \end{aligned}$$
(17)

Using Lemma 3, we can derive the following estimates:

$$\begin{aligned}{} & {} -2x^T(t)P^{-1}E_aF_a(t)H_ax(t) \le \epsilon _1x^T(t)P^{-1}E_aE_a^TP^{-1}x(t) + \epsilon _{1}^{-1}x^T(t)H_a^TH_ax(t), \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned}{} & {} 2x^T(t)P^{-1}E_bF_b(t)H_bKx(t) \le \epsilon _2 x^T(t)P^{-1}E_bE_b^TP^{-1}x(t) + \epsilon _2^{-1}x^T(t)K^TH_b^TH_bKx(t), \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned}{} & {} - 2x^T(t)P^{-1}E_bF_b(t)H_bKe(t) \le x^T(t)P^{-1}E_bE_b^TP^{-1}x(t) + e^{T}(t)K^TH_b^TH_bKe(t),\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned}{} & {} 2x^T(t)P^{-1}E_dF_d(t)H_dg(x(t)) \le x^T(t)P^{-1}E_dE_d^TP^{-1}x(t) + g^T(x(t))H_d^TH_dg(x(t)), \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned}{} & {} 2x^T(t)P^{-1}E_wF_w(t)H_w\omega (t) \le x^T(t)P^{-1}E_wE_w^TP^{-1}x(t) + \omega ^T(t)H_w^TH_w\omega (t).\nonumber \\ \end{aligned}$$
(22)

From the triggering condition (6), we can deduce:

$$\begin{aligned} \eta ^2 x^T(t)x(t) - e^T(t)e(t) \ge 0, \forall t \in [t_k, t_{k+1}). \end{aligned}$$
(23)

Utilizing Assumption 2, we have:

$$\begin{aligned} x^T(t)L^TLx(t) - g^T(x(t))g(x(t)) \ge 0, \end{aligned}$$
(24)

where \(L = {{\,\textrm{diag}\,}}\{l_1, \ldots , l_n\}\).

Substituting inequalities (18)–(24) into (17), we obtain the following estimate:

$$\begin{aligned}{} & {} _{0}^{C}\texttt{D}_t^{\alpha }V(t) \le x^T(t)\bigg [ -P^{-1}A + P^{-1}BK - A^{T}P^{-1} + K^TB^TP^{-1}\nonumber \\{} & {} \qquad + \epsilon _1P^{-1}E_aE_a^TP^{-1} + \epsilon _1^{-1}H_a^TH_a + (1 + \epsilon _2)P^{-1}E_bE_b^TP^{-1} \nonumber \\{} & {} \qquad + \epsilon _2^{-1}K^TH_b^TH_bK + P^{-1}E_dE_d^TP^{-1} + P^{-1}E_wE_w^TP^{-1} + \eta ^2I + L^TL \bigg ]x(t) \nonumber \\{} & {} \qquad + e^T(t)\left[ K^TH_b^TH_bK - I\right] e(t) + g^T(x(t))\left[ H_d^TH_d - I\right] g(x(t)) + \omega ^T(t)H_w^TH_w\omega (t)\nonumber \\{} & {} \qquad - 2x^T(t)P^{-1}BKe(t) + 2x^T(t)P^{-1}Dg(x(t)) + 2x^T(t)P^{-1}W\omega (t). \end{aligned}$$
(25)

By performing some simple computations, we have:

$$\begin{aligned} J(t)&= -2z^T(t)S\omega (t) - z^T(t)Tz(t) - \omega ^T(t)(U-\gamma I)\omega (t)\\&= -g^T(x(t))\left[ M^TTM\right] g(x(t)) + \omega ^T(t)\left[ \gamma I - U -N^TTN - N^TS - S^TN\right] \omega (t)\\&\qquad + 2g^T(x(t))\left[ -M^TS - M^TTN\right] \omega (t). \end{aligned}$$

Therefore, we obtain the estimate:

$$\begin{aligned}&_{0}^{C}\texttt{D}_t^{\alpha }V(t) + J(t)\nonumber \\&\le x^T(t)\bigg [ -P^{-1}A + P^{-1}BK - A^{T}P^{-1} + K^TB^TP^{-1}\nonumber \\&\qquad + \epsilon _1P^{-1}E_aE_a^TP^{-1} + \epsilon _1^{-1}H_a^TH_a + (1 + \epsilon _2)P^{-1}E_bE_b^TP^{-1} \nonumber \\&\qquad + \epsilon _2^{-1}K^TH_b^TH_bK + P^{-1}E_dE_d^TP^{-1} + P^{-1}E_wE_w^TP^{-1} + \eta ^2I + L^TL \bigg ]x(t)\nonumber \\&\qquad + e^T(t)\left[ K^TH_b^TH_bK - I\right] e(t) + g^T(x(t))\left[ H_d^TH_d - I - M^TTM\right] g(x(t))\nonumber \\&\qquad + \omega ^T(t)\left[ H_w^TH_w+\gamma I - U - N^TTN - N^TS - S^TN\right] \omega (t)- 2x^T(t)P^{-1}BKe(t) \nonumber \\&\qquad + 2x^T(t)P^{-1}Dg(x(t))+ 2x^T(t)P^{-1}W\omega (t) + 2g^T(x(t))\left[ -M^TS - M^TTN\right] \omega (t)\nonumber \\&= \xi ^T(t)\varOmega \xi (t), \end{aligned}$$
(26)

where

$$\begin{aligned}&\xi ^T(t) = \begin{bmatrix} x^T(t)&e^T(t)&g^T(x(t))&\omega ^T(t) \end{bmatrix}, \\&\varOmega = \begin{bmatrix} \varOmega _{11} &{} -P^{-1}BK &{} P^{-1}D &{} P^{-1}W \\ * &{} \varOmega _{22} &{} 0 &{} 0 \\ * &{} * &{} \varOmega _{33} &{} -M^TS - M^TTN\\ * &{} * &{} * &{} \varOmega _{44} \end{bmatrix}, \end{aligned}$$

in which

$$\begin{aligned}&\varOmega _{11} = -P^{-1}A + P^{-1}BK - A^{T}P^{-1} + K^TB^TP^{-1} + \epsilon _1P^{-1}E_aE_a^TP^{-1} + \epsilon _1^{-1}H_a^TH_a\\&\qquad \qquad + (1 + \epsilon _2)P^{-1}E_bE_b^TP^{-1} \\&\qquad \qquad + \epsilon _2^{-1}K^TH_b^TH_bK + P^{-1}E_dE_d^TP^{-1} + P^{-1}E_wE_w^TP^{-1} + \eta ^2I + L^TL, \\&\varOmega _{22} = K^TH_b^TH_bK - I,\, \varOmega _{33} = H_d^TH_d - I - M^TTM,\\&\varOmega _{44} = H_w^TH_w+\gamma I - U - N^TTN - N^TS - S^TN. \end{aligned}$$

Setting \(K = YP^{-1}\). Pre- and post-multiply both sides \(\varOmega \) by \({\mathcal {P}} = {{\,\textrm{diag}\,}}\{P, P, I, I\}\), we have condition \(\varOmega < 0\) is equivalent to the following condition

$$\begin{aligned} {\hat{\varOmega }} = {\mathcal {P}}\varOmega {\mathcal {P}} = \begin{bmatrix} {\hat{\varOmega }}_{11} &{} -BY &{} D &{} W \\ * &{} {\hat{\varOmega }}_{22} &{} 0 &{} 0\\ * &{} * &{} \varOmega _{33} &{} -M^TS - M^TTN\\ * &{} * &{} * &{} \varOmega _{44} \end{bmatrix} < 0, \end{aligned}$$
(27)

where

$$\begin{aligned}&{\hat{\varOmega }}_{11} = -AP + BY - PA^T + Y^TB^T + \epsilon _1E_aE_a^T + \epsilon _1^{-1}PH_a^TH_aP + (1+\epsilon _2)E_bE_b^T \\&\qquad \qquad + \epsilon _2^{-1}Y^TH_b^TH_bY + E_dE_d^T + E_wE_w^T + \eta ^2PP + PL^TLP,\\&{\hat{\varOmega }}_{22} = Y^TH_b^TH_bY - P^{2}. \end{aligned}$$

Since \(-P^2 \le I - 2P\), condition (27) is also equivalent to the following condition

$$\begin{aligned} \begin{bmatrix} {\hat{\varOmega }}_{11} &{} -BY &{} D &{} W \\ * &{} Y^TH_b^TH_bY + I-2P &{} 0 &{} 0\\ * &{} * &{} \varOmega _{33} &{} -M^TS - M^TTN\\ * &{} * &{} * &{} \varOmega _{44} \end{bmatrix} < 0. \end{aligned}$$
(28)

Using the Schur complement Lemma, the condition \({\hat{\varOmega }} < 0\) is equivalent to the condition (16b). Therefore, we have

$$\begin{aligned} _{0}^{C}\texttt{D}_t^{\alpha }V(t) + J(t) \le 0, \, \forall t \ge 0. \end{aligned}$$
(29)

Claim 1: We show that system (7) without the output vector z(t) is robustly finite-time bounded w.r.t. \((c_1, c_2, R, T_f, d)\). Indeed, when \(z(t) \equiv 0\), \(J(t) = -\omega ^T(t)\left( U - \gamma I\right) \omega (t)\). From (16a) and (29), we have

$$\begin{aligned} _{0}^{C}\texttt{D}_t^{\alpha }V(t) \le \omega ^T(t)\left( U - \gamma I\right) \omega (t) \le \lambda _{\max }(U-\gamma I)\Vert \omega (t)\Vert ^2. \end{aligned}$$
(30)

By performing integration with a fractional order \(\alpha \) over both sides of Eq. (30) within the interval from 0 to t (where \(0 \le t \le T_f\)), and making use of Assumption 3, the following result is derived:

$$\begin{aligned} \begin{aligned} x^T(t)P^{-1}x(t) - x^T(0)P^{-1}x(0)&\le \frac{\lambda _{\max }(U-\gamma I)}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha - 1}\Vert \omega (s)\Vert ^2ds. \end{aligned} \end{aligned}$$
(31)

Inequality (31) implies that

$$\begin{aligned} \begin{aligned} x^T(t)P^{-1}x(t)&\le x^T(0)P^{-1}x(0) + \frac{\lambda _{\max }(U-\gamma I)d}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}ds\\&\le x^T(0)P^{-1}x(0) + \frac{\lambda _{\max }(U-\gamma I)d}{\varGamma (\alpha +1)}T_f^{\alpha }. \end{aligned} \end{aligned}$$
(32)

Using sevaral simple computations, we have

$$\begin{aligned} \begin{aligned} x^T(t)P^{-1}x(t)&= x^T(t)R^{\frac{1}{2}}{\hat{P}}R^{\frac{1}{2}}x(t)\\&\ge \lambda _{\min }({\hat{P}})x^T(t)Rx(t) = \lambda _1 x^T(t)Rx(t), \end{aligned} \end{aligned}$$
(33)
$$\begin{aligned} \begin{aligned} x^T(0)P^{-1}x(0)&= x^T(0)R^{\frac{1}{2}}{\hat{P}}R^{\frac{1}{2}}x(0)\\&\le \lambda _{\max }({\hat{P}})x^T(0)Rx(0) = \lambda _2x^T(0)Rx(0) \le \lambda _2c_1. \end{aligned} \end{aligned}$$
(34)

Combining conditions (32), (33) and (34), we get

$$\begin{aligned} \lambda _1 x^T(t)Rx(t) \le V(t) = x^T(t)P^{-1}x(t) \le \lambda _2c_1 + \frac{\lambda _{\max }(U-\gamma I)d}{\varGamma (\alpha +1)}T_f^{\alpha }. \end{aligned}$$
(35)

Condition (16c) implies that \(x^T(t)Rx(t) < c_2\). Thus, the system (7) without the output vector z(t) is robustly finite-time bounded w.r.t. \((c_1, c_2, R, T_f, d)\).

Claim 2: We establish the robust finite-time (S, T, U)-dissipativity of system (7) with respect to \((c_1, c_2, R, T_f, d)\). Integrating (29) over the time interval from 0 to t, where \((0 \le t \le T_f)\), we obtain:

$$\begin{aligned} _{0}\texttt{I}_{{t}}^{1}\left( \,_{0}^{C}\texttt{D}_t^{\alpha }V(t)\right) + \int _{0}^{{t}}J({s})d{s} \le 0, \forall {t} \in [0, T_f]. \end{aligned}$$
(36)

By employing Property 1 and Property 2, we can express:

$$\begin{aligned} \begin{aligned} _{0}\texttt{I}_{{t}}^{1}\left( \,_{0}^{C}\texttt{D}_t^{\alpha }V(t)\right)&= \, _{0}\texttt{I}_{{t}}^{1-\alpha }\, _{0}\texttt{I}_{{t}}^{\alpha }\left( \,\,_{0}^{C}\texttt{D}_t^{\alpha }V(t)\right) \\&= \, _{0}\texttt{I}_{{t}}^{1-\alpha }\left( \,_{0}\texttt{I}_{{t}}^{\alpha }\,_{0}^{C}\texttt{D}_t^{\alpha }V(t)\right) \\&= \, _{0}\texttt{I}_{{t}}^{1-\alpha }\left( V(t) - V(0)\right) \\&= \, _{0}\texttt{I}_{{t}}^{1-\alpha }V(t) - \, _{0}\texttt{I}_{{t}}^{1-\alpha }V(0). \end{aligned} \end{aligned}$$
(37)

Under zero initial condition, we have \(_{0}\texttt{I}_{{t}}^{1-\alpha }V(0) = 0\) and

$$\begin{aligned} _{0}\texttt{I}_{{t}}^{1-\alpha }V(t) = \frac{1}{\varGamma (1-\alpha )}\int _{0}^{{t}}({t}-s)^{-\alpha }x^T(s)P^{-1}x(s)ds \ge 0. \end{aligned}$$

Hence

$$\begin{aligned} _{0}\texttt{I}_{{t}}^{1}\left( \,_{0}^{C}\texttt{D}_t^{\alpha }V(t)\right) \ge 0, \forall {t} \in [0, T_f]. \end{aligned}$$
(38)

Combining (37) and (38), we deduce:

$$\begin{aligned} \int _{0}^{{t}}J({s})d{s} \le 0, \forall {t} \in [0, T_f]. \end{aligned}$$

Consequently, we arrive at the following inequality:

$$\begin{aligned} \int _{0}^{{t}}\left( 2z^T({s})S\omega ({s}) + z^T({s})Tz({s}) + \omega ^T({s})U\omega ({s})\right) d{s}\ge \gamma \int _{0}^{{t}}\omega ^T({s})\omega ({s})d{s}, \forall {t} \in [0, T_f]. \end{aligned}$$

This concludes the proof. \(\square \)

Remark 1

In contrast to the architectural principles underpinning finite-time dissipative controllers as expounded upon in references [21,22,23], where the requisite condition stipulates the continuous monitoring and acquisition of state information for the considered dynamical systems, the event-triggered controller (designated as (5)) relies upon the selective acquisition and updating of state information denoted as x(t) exclusively during discrete triggering instances characterized by the sequence \(\{t_k\}_{k \in \mathbb {N}}\) with the initial point set at \(t_0 = 0\). This dichotomy underscores the superior resource-efficiency, particularly in the context of constrained communication and energy resources, exhibited by the event-triggered control paradigm (5) in comparison to the established finite-time dissipative control frameworks presented in [21,22,23].

Remark 2

Compared with the event-triggered finite-time dissipative control in [30,31,32,33,34,35,36,37], the difficulty facing the design of the event-triggered controller (5) is that we have to design an event-triggered mechanism such that the Zeno behavior does not happen. Based on inequality techniques, to exclude the Zeno behavior, a positive lower bound on the inter-execution intervals is firstly estimated in this paper. Then, based on the event-triggering strategies approach, the problem of finite-time dissipative control for fractional-order neural networks was investigated for the first time.

In the absence of uncertainties, the system (2) is reduced to the Hopfield fractional order which has been considered in the literature by many authors:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = -Ax(t) + Dg(x(t)) + W\omega (t) + Bu(t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^n. \end{array}\right. } \end{aligned}$$
(39)

Based on Theorem 1, Corolloary 1 can be easily obtained.

Corollary 1

Assume assumptions 2 and 3 are satisfied. Given positive scalars \(c_1, c_2, T_f, d\), and a matrix \(R > 0\). If there exist positive scalars \(\eta , \gamma \), and matrices \(P \in \mathbb {R}^{n \times n}, \, { P > 0},Y \in \mathbb {R}^{m \times { n}}\) such that the following inequalities hold

$$\begin{aligned}&U - \gamma I > 0, \end{aligned}$$
(40a)
$$\begin{aligned}&\begin{bmatrix} {\hat{\varXi }}_{11} &{} -BY &{} D &{} W &{} \eta ^2P &{} PL^T\\ * &{} I - 2P &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} -I - M^TTM &{} { {\hat{\varXi }}_{34}} &{} 0 &{} 0\\ * &{} * &{} * &{} {\hat{\varXi }}_{44} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -\eta ^2 I &{} 0\\ * &{} * &{} * &{} * &{} * &{} -I \end{bmatrix} < 0, \end{aligned}$$
(40b)
$$\begin{aligned}&\lambda _2 c_1 + \frac{\lambda _{\max }(U - \gamma I)d}{\varGamma (\alpha +1)}T_f^{\alpha } < \lambda _1 c_2, \end{aligned}$$
(40c)

where

$$\begin{aligned}&L = {{\,\textrm{diag}\,}}\{l_1, \ldots , l_n\}, \, {\hat{P}} = R^{-\frac{1}{2}}P^{-1}R^{-\frac{1}{2}}, \, \lambda _1 = \lambda _{\min }({\hat{P}}), \, \lambda _2 = \lambda _{\max }({\hat{P}}), \\&{\hat{\varXi }}_{11} = -AP+BY+Y^TB^T-PA^T, \, { {\hat{\varXi }}_{34} = -M^TS - M^TTN}, \, {\hat{\varXi }}_{44} \\&= \gamma I - U -N^TTN-N^TS - S^TN, \end{aligned}$$

then under the triggered condition (6), the system (39) is robustly finite-time (S, T, U)-dissipative w.r.t. \((c_1, c_2, R, T_f, d)\). Concurrently, the state feedback controller gain matrix K can be computed as \(K = YP^{-1}\).

Remark 3

When a parameter \(\eta > 0\) is given, the conditions outlined in (16b) of Theorem 1 and (40b) of Corollary 1 are reconfigured into LMIs. Consequently, the conditions (16a) and (16b) specified in Theorem 1, along with the conditions (40a) and (40b) detailed in Corollary 1, are transformed into conditions rooted in the framework of LMIs. Subsequently, we proceed to scrutinize the validity of inequalities (16c) presented in Theorem 1 and (40c) featured in Corollary 1. The MATLAB LMI Control toolbox exhibits the capability to systematically address LMIs of arbitrary dimensions, theoretically speaking. However, in practical applications, the expansion of LMI sizes during the process of verifying their feasibility results in elevated computational complexity and greater time consumption. This phenomenon could be construed as a limitation of the proposed methodology. Conversely, these challenges can be effectively mitigated when high-powered processors are employed.

4 A numerical example

Let us consider the following fractional-order neural networks with uncertainties

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{\alpha }x(t) = -\left[ A+E_aF_a(t)H_a\right] x(t) + \left[ D+E_dF_d(t)H_d\right] g(x(t)) \\ &{} \qquad \qquad \qquad + \left[ W+E_wF_w(t)H_w\right] \omega (t) + \left[ B+E_bF_b(t)H_b\right] u(t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^2, \end{array}\right. } \end{aligned}$$
(41)

where \(\alpha = 0.3, x(t) = (x_1(t), x_2(t))^T \in \mathbb {R}^2, \omega (t) = 0.01 \sin t { \in \mathbb {R}}, u(t) \in \mathbb {R}^2, { z(t) \in \mathbb {R}}\), and

$$\begin{aligned}&A = \begin{bmatrix} 0.5 &{} 0 \\ 0 &{} 0.5 \end{bmatrix}, \, E_a = \begin{bmatrix} 0.05 \\ 0.06 \end{bmatrix}, \, H_a = \begin{bmatrix} 0.01&0.01 \end{bmatrix}, \, F_a(t) = \sin t, \\&D = \begin{bmatrix} 2 &{} 1 \\ 0 &{} 2 \end{bmatrix}, \, E_d = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix}, \, H_d = \begin{bmatrix} 0.6&0.5 \end{bmatrix}, \, F_d(t) = \cos t,\\&W = \begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix}, \, E_w = \begin{bmatrix} 0.05 \\ 0.08 \end{bmatrix}, \, H_w = \begin{bmatrix} 0.01 \end{bmatrix}, \, { F_w(t) = \cos t}, \\&B = \begin{bmatrix} 3&{}0 \\ 0&{}3 \end{bmatrix}, \, E_b = \begin{bmatrix} 0.03 \\ 0.02 \end{bmatrix}, \, H_b = \begin{bmatrix} 0.01&0.02 \end{bmatrix},\\&M = \begin{bmatrix} 1&1 \end{bmatrix}, \, N = \begin{bmatrix} 1 \end{bmatrix}. \end{aligned}$$

It is not hard to verify that the disturbance \(\omega (t)\) satisfying the Assumption 3 with \(d = 0.0001\). The activation function is chosen as \(g(x(t)) = 0.5\left( \tanh x_1(t), \tanh x_2(t)\right) \in \mathbb {R}^2\). We have the activation function g(x(t)) satisfies Assumption 2 with \(L = {{\,\textrm{diag}\,}}\{0.5, 0.5\}\). The closed-loop system with an event-triggered state feedback controller of the form (5) of system (41) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} _{0}^{C}\texttt{D}_t^{0.3}x(t) = \left[ -A-E_aF_a(t)H_a + BK +E_bF_b(t)H_bK\right] x(t) - \left[ BK+E_bF_b(t)H_bK\right] e(t)\\ &{} \qquad \qquad \qquad + \left[ D+E_dF_d(t)H_d\right] g(x(t)) + \left[ W+E_wF_w(t)H_w\right] \omega (t),\, t \ge 0,\\ &{} z(t) = Mg(x(t)) + N\omega (t),\, t \ge 0,\\ &{} x(0) = x_0 \in \mathbb {R}^2. \end{array}\right. } \end{aligned}$$
(42)

Given \(c_1 = 1, c_2 = 1.2, R = I, T_f = 10, S = \begin{bmatrix} -2 \end{bmatrix} { \in \mathbb {R}^{1 \times 1}}, T = \begin{bmatrix} 1 \end{bmatrix} { \in \mathbb {R}^{1 \times 1}}\), and \(U = \begin{bmatrix} 10 \end{bmatrix} { \in \mathbb {R}^{1 \times 1}}\). We now consider the problem of robustly finite-time dissipative control for the system (41) with the above parameters. By using LMI Control Toolbox in MATLAB, the conditions (16a), (16b), and (16c) in Theorem 1 are feasible with \(\eta = 0.5, \gamma = 0.4251, \epsilon _1 = 8.7470, \epsilon _2 = 48.3687\), and

$$\begin{aligned} P = \begin{bmatrix} 3.2606 &{} -0.2450 \\ -0.2450 &{} 3.1900 \end{bmatrix}, \, Y = \begin{bmatrix} -1.8355 &{} 0.1585\\ 0.1614 &{}-1.7878\end{bmatrix}. \end{aligned}$$

According to Theorem 1, the closed-loop system (42) is robustly (S, T, U)-dissipative w.r.t. (1, 1.2, I, 10, 0.0001) by the event-triggered state feedback controller

$$\begin{aligned} u(t) = YP^{-1}x(t_k) = \begin{bmatrix} -0.5624 &{} 0.0065\\ 0.0074&{}-0.5599 \end{bmatrix}x(t_k), \, t \in [t_k, t_{k+1}), \end{aligned}$$

where the triggering sequence \(\{t_k\}_{k \in \mathbb {N}}\) is determined as below

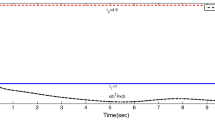
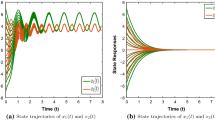
$$\begin{aligned} t_0 = 0, \, t_{k+1} = \inf \{t>t_k: \Vert x(t) - x(t_k)\Vert \ge 0.5 \Vert x(t)\Vert \}. \end{aligned}$$

Simulation results presented in Figs. 1, 2 and 3 with the initial condition \(x_0=(0.7, -0.7)^T \in \mathbb {R}^2\). Fig. 1 shows the history of \(\Vert x(t)\Vert ^2\) without event-triggered state feedback controller. Figure 2 shows the history of \(\Vert x(t)\Vert ^2\) with event-triggered state feedback controller. Figures 1 and 2 demonstrate that the open system is not robustly finite-time bounded and the closed-loop system under the event-triggered state feedback controller \(u(t) = Kx(t_k)\) is robustly finite-time (S, T, U)-dissipative. In order to assess the (S, T, U)-dissipativity performance within a specified finite-time interval, we introduce a dissipativity performance function denoted as \(\gamma (t)\), defined as follows: \(\gamma (t): = \frac{\int _{0}^{t}\left( 2z^T(s)S\omega (s) + z^T(s)Tz(s) + \omega ^T(s)U\omega (s)\right) ds}{\int _{0}^{t}\omega ^T(s)\omega (s)ds}, t \in [0, 10]\). The graphical representation in Fig. 3 illustrates that the dissipativity performance function \(\gamma (t)\) consistently exceeds a threshold value of \(\gamma = 0.4251\). This observation indicates that the condition (ii) as delineated in Definition 5 is consistently satisfied.

Fig. 1
figure 1

The history of \(x^T(t)Rx(t)\) without event-triggered state feedback controller

Full size image
Fig. 2
figure 2

The history of \(x^T(t)Rx(t)\) with event-triggered state feedback controller

Full size image
Fig. 3
figure 3

The response of function \(\gamma (t)\)

Full size image

5 Conclusion

We have considered the problem of event-triggered finite-time dissipative control for fractional-order neural networks in this paper. First, the Zeno behavior has been discussed and a positive lower bound on the interexecution intervals has also been estimated. Then, sufficient conditions are proposed for solving the problem that provides the designing of the event-triggered state feedback controllers and guaranteeing the concerned closed-loop system is finite-time bounded with a dissipative performance index. To validate the efficacy of our proposed methodology, we furnish a numerical illustration. As a prospective avenue of inquiry, we anticipate extending the findings presented herein to address the challenge of event-triggered finite-time dissipative control within fractional-order neural network systems with unknown time-varying delays.