1 Introduction

Neurons or nerve cells are connected through synapses in a specific way to form biological neural networks [1]. To simulate various biological processes of the human brain, artificial neural networks are constructed. These models find applications in diverse fields, including pattern recognition [2, 3], signal processing [4], financial forecasting [5] and biological engineering [6]. It is worth noting that all the above applications rely on the dynamic behaviours of neural networks. For instance, certain dynamic neurological diseases such as epilepsy and Parkinson are caused by bifurcation resulting from changes in regulatory parameters of the neuronal system. Thus, researching the dynamic behaviors of neural networks is crucial as it can provide theoretical guidance for practical applications.

The Hopfield neural network (HNN) plays a critical role in numerous neuronal systems, despite having a simple algebraic expression. It is capable of emulating complex dynamic behaviors [7]. In recent years, several modified HNN models have been proposed, including those that incorporate time delays, fractional orders, and increased numbers of neurons [8,9,10]. Notably, the two-neuron HNN network, as one of the most basic models, can serve as a prototype for constructing models that enhance our understanding of the dynamic behaviors of multi-neuron networks. Additionally, due to its structural characteristics, the two-neuron network has a low energy consumption level. Therefore, further research is necessary to better understand the dynamics of the two-neuron network

Time delays are prevalent in neural networks and their variations can significantly impact system stability. Actually, due to the spatial heterogeneity in the breadth of the space occupied by neural networks, synapses of individual neurons tend to vary in size and length, leading to voltage distribution along the synaptic path when electrical signals are conducted [11]. This distribution cannot be described in terms of conventional discrete delays, but rather requires distributed delays to reflect signal delays over an infinite or finite period of time. Compared with discrete delays, distributed delays are more pertinent in simulating neural network signal propagation. Recently, many researchers have been working on combining distributed delays with various neural networks and analysing their system dynamics, such as the impulsive reaction–diffusion neural network [12], the fuzzy memristive neural network [13] and the quaternion-valued neural network [14]. Yao et al. [15] proposed a class of neural network models containing leakage and distributed delays. They investigated Hopf bifurcation induced by leakage delay and presented conditions for its occurrence. Rahman et al. [16] constructed a ring neural network system containing discrete and one-way coupling distributed delays. By selecting the Dirac delta function and the gamma distribution as the distribution kernel, they gave stability conditions for the trivial steady state of the ring neural network in a specific parameter space. Xu et al. [17] introduced fractional order to the neural network containing mixed delays. The discrete delay was chosen as bifurcation parameters, and sufficient conditions were obtained to guarantee the stability behaviour and the appearance of Hopf bifurcation for the fractional-order delayed neural network. However, none of the above studies considered introducing diffusion into neural network systems with mixed delays. The models concerned cannot reflect the spatial-scale dynamical properties of neural networks. Furthermore, relevant control strategies have not been proposed to achieve control of the spatiotemporal dynamics of neural networks.

The inhomogeneous electromagnetic field density in neural networks can cause the diffusion phenomenon in electron trajectories as the electrons move through the field [12]. When the above factors are taken into account, introducing diffusion into the neural network can exhibit rich spatial dynamics behaviour, such as various Turing patterns, which is no doubt more consistent with reality. In recent years, some research on reaction–diffusion neural networks has been consistently advancing [18,19,20,21], based on the theory proposed by Turing [22]. Lin et al. [23] derived conditions for the generation of Turing instability and Hopf bifurcation for reaction–diffusion neural networks containing leakage delays. They also analysed the parametric stability domain of the Turing-Hopf bifurcation when two system parameters were altered. Chen et al. [24] introduced diffusion into a high-dimensional fractional-order delayed neural network with a ring-hub structure. Considering the time delay as the bifurcation parameter, they established the criterion on the local stability of the system and Hopf bifurcation. Dong et al. [25] studied coupled neural networks with diffusion and time delays. The period and direction of Hopf bifurcation were determined through the normal form theory of partial differential equations and the center manifold theorem. It should be noted that the majority of the above studies on Turing patterns only consider the diffusion in one dimension. As the spatial extent is one-dimensional, the reaction–diffusion neural network demonstrates less rich and complex dynamical behaviour than in two dimensions. Therefore, to comprehensively reflect the spatiotemporal characteristics of the neural network, we add two-dimensional diffusion to a two-neuron Hopfield neural network with discrete and distributed delays.

In the study of bifurcation control of dynamical systems, many control strategies [26,27,28,29], such as time-delayed feedback control, state feedback control and PD control, enable the control of Hopf bifurcation, namely delaying the occurrence of the Hopf bifurcation versus expanding the stability domain of the system parameters. Tiba et al. [30] proposed a set of control strategies, including washout filter control, polynomial control and adaptive control, for Hopf bifurcation in Chaotic Associative Memory (CAM). Guo et al. [31] applied a nonlinear state feedback control strategy to a hydro-turbine governing system to realise Hopf bifurcation control. They analysed the mechanism of the proposed controller by comparing it with the PID control strategy. Although the Hopf bifurcation control has been extensively investigated, the control of Turing patterns in reaction–diffusion systems is sparse and tends to limit in the one-dimensional diffusion systems [32,33,34]. Compared to bifurcation control, the design of control strategies for Turing modes can directly affect the spatial dynamics behaviour of the system. Inspired by the present research status, we adapt the state feedback control strategy to the reaction–diffusion neural network system to achieve the control over both Hopf bifurcation and Turing modes.

The main innovations of this paper are listed as follows.

  1. (1)

    By introducing the two-dimensional diffusion into the classical Hopfield neural network, a class of reaction–diffusion neural network system with discrete and distributed delays is proposed, allowing it to better reflect spatiotemporal properties.

  2. (2)

    Taking the discrete delay and the diffusion coefficient as Hopf and Turing bifurcation parameters, respectively, specific expressions for the bifurcation threshold points are given through the analysis of the characteristic equation.

  3. (3)

    Near the Turing bifurcation threshold point, the amplitude equations and the stability conditions for each Turing pattern are derived via the multi-scale perturbation method.

  4. (4)

    By employing the state feedback control strategy to the reaction–diffusion neural network, we find that such controller can effectively delay the occurrence of Hopf bifurcation and suppress the appearance of Turing instability. In addition, numerical simulations reveal the joint influence of system parameters and control parameters on the Turing bifurcation threshold point.

The paper is structured as follows. In Sect. 2, we propose a reaction–diffusion neural network with discrete and distributed delays. In Sect. 3, we verify the local stability, Hopf bifurcation induced by the discrete delay and Turing instability without the discrete delay according to the characteristic equation. In Sect. 4, the derivation of amplitude equations are explored by using weakly nonlinear analysis. Section 5 shows the numerical simulation results. In Sect. 6, we give the conclusion of this paper.

2 Model Description

Li et al. [35] proposed the following two-neuron system with discrete and distributed delays:

$$\begin{aligned} \begin{aligned} \dfrac{{d{p_1}(t)}}{{dt}} = - {p_1}(t) + {a_{11}}f\left( {\int _{ - \infty }^t {F(t - s){p_1}(s)ds} } \right) + {a_{12}}f({p_2}(t - \tau )),\\ \dfrac{{d{p_2}(t)}}{{dt}} = - {p_2}(t) + {a_{21}}f({p_1}(t - \tau )) + {a_{22}}f\left( {\int _{ - \infty }^t {F(t - s){p_2}(s)ds} } \right) . \end{aligned} \end{aligned}$$
(1)

Based on system (1), we introduce the two-dimensional diffusion and get a new system described by partial differential equations:

$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}} =&\, {d_1}\varDelta {p_1}(x,y,t) - {p_1}(x,y,t) \\&+ {a_{11}}f\left( {\int _{ - \infty }^t {F(t - s){p_1}(x,y,s)ds} } \right) + {a_{12}}f({p_2}(x,y,t - \tau )),\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}} =&\,{d_2}\varDelta {p_2}(x,y,t) - {p_2}(x,y,t) + {a_{21}}f({p_1}(x,y,t - \tau ))\\&+ {a_{22}}f\left( {\int _{ - \infty }^t {F(t - s){p_2}(x,y,s)ds} } \right) , \end{aligned} \end{aligned}$$
(2)

under the homogeneous Neumann boundary condition

$$\begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial n}} = \frac{{\partial {p_2}(x,y,t)}}{{\partial n}} = 0, \end{aligned}$$

with initial conditions

$$\begin{aligned} {p_1}(x,y,0) = {p_{10}}(x,y),{p_2}(x,y,0) = {p_{20}}(x,y), \end{aligned}$$

for \((x,y) \in \varOmega \).

Here, \({p_1}(x,y,t)\) and \({p_2}(x,y,t)\) represents the state variables of neurons at spatial position (x, y) and time t; \(\varOmega = (0,A) \times (0,A)\) is the square domain, where the positive constant A is bounded. \(d_1\) and \(d_2\) stand for the diffusion coefficients of the neurons \(p_1\) and \(p_2\). \(\varDelta = \frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}\) is Laplacian operator corresponding to the spatial variables x and y. n is the unit normal vector outward of the smooth boundary \(\partial \varOmega \). \(\tau \) denotes the discrete delay. \({a_{ij}}\) (\(i,j = 1,2\)) represents the connective intensity. \(F( \cdot )\) is the delayed kernel function satisfying \(\int _0^\infty {F(s)ds} = 1\). Considering the gamma distribution, then \(F( \cdot )\) can be written in the form of

$$\begin{aligned} F(s) = {\alpha ^{q + 1}}\frac{{{s^q}{e^{ - \alpha q}}}}{{q!}},~q = 0,1,2,\cdots , \end{aligned}$$

where \(\alpha > 0\) indicates the declining rate of the past memory. In this paper, we adopt the weak delay kernel with \(q = 0\), namely \(F(s) = \alpha {e^{ - \alpha s}}\).

Remark 1

Up to now, there have been relatively few researches on two-dimensional reaction–diffusion neural networks. Moreover, the studies on the spatiotemporal characteristics of reaction–diffusion neural networks with distributed delays has not been reported. In this paper, for the first time, we investigate the dynamic properties of a two-dimensional reaction–diffusion neural network with discrete and distributed delays, such as Hopf bifurcation and Turing patterns.

In addition, \(f( \cdot )\) denotes the activation function and meets the following hypothesis:

(H1) \(f(0) = 0\), \(f \in {C^3}\).

In order to realise the control of the spatiotemporal dynamic behaviours of system (2), the state feedback control strategy is taken as follows

$$\begin{aligned} U(x,y,t) = k\left( {u(x,y,t) - {u^*}} \right) , \end{aligned}$$

where k is the state feedback gain factor, u(x, y, t) indicates the controlled neuron state and \({u^*}\) is the equilibrium state. Applying the controller to the neuron \(p_1\), the controlled system can be written as

$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}} =&\,{d_1}\varDelta {p_1}(x,y,t) - {p_1}(x,y,t)\\&+ {a_{11}}f\left( {\int _{ - \infty }^t {F(t - s){p_1}(x,y,s)ds} } \right) \\&+ {a_{12}}f({p_2}(x,y,t - \tau )) + k\left( {{p_1}(x,y,t) - p_1^*} \right) ,\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}} =&\,{d_2}\varDelta {p_2}(x,y,t) - {p_2}(x,y,t)+ {a_{21}}f({p_1}(x,y,t - \tau ))\\&+{a_{22}}f\left( {\int _{ - \infty }^t {F(t - s){p_2}(x,y,s)ds} } \right) , \end{aligned} \end{aligned}$$
(3)

in which \(p_1^*\) represents the equilibrium state of \(p_1\) at the equilibrium point \(E(p_1^*,p_2^*)\).

Remark 2

In view of the strong symmetry of system (2), the relevant conclusions obtained from the controller imposed on the neuron \(p_1\) are applicable to the case imposed on the neuron \(p_2\) after conversion of the coefficients. Therefore, in this paper, only the case of system (3) is discussed.

Through the introduction of two virtual neurons

$$\begin{aligned} {p_3}(x,y,t) = \int _{ - \infty }^t {F(t - s){p_1}(x,y,s)ds} ,\\ {p_4}(x,y,t) = \int _{ - \infty }^t {F(t - s){p_2}(x,y,s)ds} , \end{aligned}$$

the original system (3) can be transformed into a neural network system which only involves the discrete delay as follows

$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}} =&\,{d_1}\varDelta {p_1}(x,y,t) - {p_1}(x,y,t)+{a_{11}}f\left( {{p_3}(x,y,t)} \right) \\&+ {a_{12}}f({p_2}(x,y,t - \tau ))+k( {{p_1}(x,y,t) - p_1^*} ),\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}} =&\,{d_2}\varDelta {p_2}(x,y,t) - {p_2}(x,y,t)+ {a_{21}}f({p_1}(x,y,t - \tau )) \\&+ {a_{22}}f\left( {{p_4}(x,y,t)} \right) ,\\ \dfrac{{\partial {p_3}(x,y,t)}}{{\partial t}} =&\, - \alpha {p_3}(x,y,t) + \alpha {p_1}(x,y,t),\\ \dfrac{{\partial {p_4}(x,y,t)}}{{\partial t}} =&\, - \alpha {p_4}(x,y,t) + \alpha {p_2}(x,y,t). \end{aligned} \end{aligned}$$
(4)

Remark 3

It should be pointed out that system (4) comprises four partial differential equations, two of which have diffusion terms, while the other two have none. This suggests that neurons \(p_3\) and \(p_4\) have no diffusion on the spatial scale and their states are tightly linked to those of \(p_1\) and \(p_2\).

In the following, we will further analyse Hopf bifurcation with the discrete delay \(\tau > 0\) and the occurrence of Turing instability without the discrete delay (i.e. \(\tau = 0\)) on the basis of system (4).

3 Analysis of Hopf Bifurcation and Turing Instability

From \((H_1)\), it is obvious that \({E^*}(p_1^*,p_2^*,p_3^*,p_4^*) = (0,0,0,0)\) is the equilibrium point of system (4). Taking \(p_1^* = 0\), the linearized equation of system (4) at the origin is

$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}}&= {d_1}\varDelta {p_1}(x,y,t) + (k - 1){p_1}(x,y,t) + {\alpha _{12}}{p_2}(x,y,t - \tau ) \\&\quad + {\alpha _{11}}{p_3}(x,y,t),\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}}&= {d_2}\varDelta {p_2}(x,y,t) + {\alpha _{21}}{p_1}(x,y,t - \tau )- {p_2}(x,y,t) \\&\quad + {\alpha _{22}}{p_4}(x,y,t),\\ \dfrac{{\partial {p_3}(x,y,t)}}{{\partial t}}&= \alpha {p_1}(x,y,t) - \alpha {p_3}(x,y,t),\\ \dfrac{{\partial {p_4}(x,y,t)}}{{\partial t}}&= \alpha {p_2}(x,y,t) - \alpha {p_4}(x,y,t), \end{aligned} \end{aligned}$$
(5)

where \({\alpha _{ij}} = {a_{ij}}f'(0)\) \((i = 1,2;j = 1,2)\).

By adding a small perturbation to the steady state \({E^*}\), we can obtain

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{p_1}}\\ {{p_2}}\\ {{p_3}}\\ {{p_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{c_1}}\\ {{c_2}}\\ {{c_3}}\\ {{c_4}} \end{array}} \right] {e^{(\lambda t + i({\kappa _x}x + {\kappa _y}y))}}, \end{aligned}$$
(6)

in which \({c_i}\) \((i = 1,2,3,4)\) is the coefficient, \(\lambda \) denotes the growth rate of the perturbation, \(\kappa = ({\kappa _x},{\kappa _y})\) denotes the wave number vector and \(\kappa \cdot \kappa = {\nu ^2}\). Substituting (6) into system (5), the characteristic equation with respect to system (5) is

$$\begin{aligned} {J^*} = \left| {\begin{array}{*{20}{c}} {k - 1 - {d_1}{\nu ^2} - \lambda }&{}{{\alpha _{12}}{e^{ - \lambda \tau }}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{21}}{e^{ - \lambda \tau }}}&{}{ - 1 - {d_2}{\nu ^2} - \lambda }&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha - \lambda }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha - \lambda } \end{array}} \right| = 0. \end{aligned}$$

Expanding \({J^*}\) in polynomial format, we get

$$\begin{aligned} \begin{aligned} {\lambda ^4} + {m_1}({\nu ^2}){\lambda ^3} + {m_2}({\nu ^2}){\lambda ^2} + {m_3}({\nu ^2})\lambda + {m_4}({\nu ^2})&\\ + ({n_1}{\lambda ^2}+ {n_2}\lambda + {n_3}){e^{ - 2\tau \lambda }}&= 0, \end{aligned} \end{aligned}$$
(7)

where

$$\begin{aligned} {m_1}({\nu ^2})&= ({d_1} + {d_2}){\nu ^2} + 2\alpha - k + 2, \\ {m_2}({\nu ^2})&= {d_1}{d_2}{\nu ^4} + \left( {(2\alpha + 1)({d_1} + {d_2}) - k{d_2}} \right) {\nu ^2} + {\alpha ^2} + (4 - {\alpha _{11}} - {\alpha _{22}})\alpha \\&\quad - (2\alpha + 1)k + 1,\\ {m_3}({\nu ^2})&= 2\alpha {d_1}{d_2}{\nu ^4} + \left( {({\alpha ^2} + \alpha )({d_1} + {d_2}) - \alpha {\alpha _{11}}{d_2} - \alpha {\alpha _{22}}{d_1} - 2k{d_2}} \right) {\nu ^2} \\&\quad + (2 - {\alpha _{11}} - {\alpha _{22}})({\alpha ^2} + \alpha ) + ({\alpha _{22}}\alpha - 2\alpha - {\alpha ^2})k,\\ {m_4}({\nu ^2})&= {\alpha ^2}\Big [ {d_1}{d_2}{\nu ^4} + \left( {(1 - {\alpha _{22}}){d_1} + (1 - {\alpha _{11}} - k){d_2}} \right) {\nu ^2} + {\alpha _{11}}{\alpha _{22}}- \alpha _{11} \\&\quad - \alpha _{22} + ({\alpha _{22}} - 1)k + 1 \Big ], \end{aligned}$$

and

$$\begin{aligned} {n_1} = - {\alpha _{12}}{\alpha _{21}}, ~{n_2} = - 2\alpha {\alpha _{12}}{\alpha _{21}}, ~{n_3} = - {\alpha ^2}{\alpha _{12}}{\alpha _{21}}. \end{aligned}$$

Remark 4

For nonlinear system dynamics, the linearisation is a more straightforward and concise method. Furthermore, we are interested in the dynamical behaviour of the system in the vicinity of the equilibrium point. Thus linearisation is sufficient to provide us with all details for analysing stability.

3.1 Hopf Bifurcation Analysis When \(\tau >0\)

Considering the discrete delay as the bifurcation parameter, we then discuss the conditions for the emergence of Hopf bifurcation and the value of the bifurcation threshold point in the following. Let \(\lambda = i\omega ~(\omega > 0)\) be a pure imaginary root of (7). Then the characteristic equation (7) becomes

$$\begin{aligned} \begin{aligned}&{m_4}({\nu ^2}) + i{m_3}({\nu ^2})\omega - {m_2}({\nu ^2}){\omega ^2} - i{m_1}({\nu ^2}){\omega ^3} + {\omega ^4}\\&\qquad + ( - {n_1}{\omega ^2} + i{n_2}\omega + {n_3})(\cos (2\tau \omega ) - i\sin (2\tau \omega )) = 0. \end{aligned} \end{aligned}$$
(8)

Separating real and imaginary parts, (8) turns into

$$\begin{aligned} \begin{aligned}&( - {n_1}{\omega ^2} + {n_3})\cos (2\tau \omega ) + {n_2}\omega \sin (2\tau \omega ) = - {\omega ^4} + {m_2}({\nu ^2}){\omega ^2}- {m_4}({\nu ^2}),\\&{n_2}\omega \cos (2\tau \omega ) - ( - {n_1}{\omega ^2} + {n_3})\sin (2\tau \omega ) = {m_1}({\nu ^2}){\omega ^3} - {m_3}({\nu ^2})\omega , \end{aligned} \end{aligned}$$
(9)

Add the squares of the two formulas of (9) to get

$$\begin{aligned} {\omega ^8} + {q_1}({\nu ^2}){\omega ^6} + {q_2}({\nu ^2}){\omega ^4} + {q_3}({\nu ^2}){\omega ^2} + {q_4}({\nu ^2}) = 0, \end{aligned}$$
(10)

in which

$$\begin{aligned}&{q_1}({\nu ^2}) = m_1^2({\nu ^2}) - 2{m_2}({\nu ^2}),\\&{q_2}({\nu ^2}) = m_2^2({\nu ^2}) - 2{m_1}({\nu ^2}){m_3}({\nu ^2}) + 2{m_4}({\nu ^2}) - n_1^2,\\&{q_3}({\nu ^2}) = m_3^2({\nu ^2}) - 2{m_2}({\nu ^2}){m_4}({\nu ^2}) - n_2^2 + 2{n_1}{n_3},\\&{q_4}({\nu ^2}) = m_4^2({\nu ^2}) - n_3^2. \end{aligned}$$

To ensure the existence of the positive solution \(\omega \) to (10), we give the following assumption:

(H2) \({\alpha ^2}{({\alpha _{22}} - 1)^2}{({\alpha _{11}} - 1 + k)^2} - 4\alpha _{12}^2\alpha _{21}^2 < 0\).

Lemma 1

If (H1) and (H2) holds, the equation (10) has at least one positive root.

Proof

When \(\nu = 0\), (10) becomes

$$\begin{aligned} {\omega ^8} + {q_{10}}{\omega ^6} + {q_{20}}{\omega ^4} + {q_{30}}{\omega ^2} + {q_{40}} = 0, \end{aligned}$$

where \({q_{i0}} = {q_i}(0)\), \(i = 1,2,3,4.\) Define

$$\begin{aligned} P({\omega ^2}) = {\omega ^8} + {q_{10}}{\omega ^6} + {q_{20}}{\omega ^4} + {q_{30}}{\omega ^2} + {q_{40}}. \end{aligned}$$
(11)

If (H2) holds, then it can been seen that \(P(0) = {\alpha ^2}[ {\alpha ^2}{{({\alpha _{22}} - 1)}^2}{{({\alpha _{11}} - 1 + k)}^2}\) \( - 4\alpha _{12}^2\alpha _{21}^2 ] < 0\) and \(\mathop {\lim }\limits _{\omega \rightarrow + \infty } P(\omega ) = + \infty \). Thus, (10) has at least one positive root. \(\square \)

Without loss of generality, we assume that the number of positive roots of (10) is \(m(1 \le m \le 8)\) when \(\nu = {\nu _0} \ge 0\). Therefore, for the j-th positive root \({\omega _j}(1 \le j \le m)\) of (10), we have

$$\begin{aligned} \cos (2{\omega _j}\tau ) = \frac{{{A_1}({\omega _j},{\nu _0})}}{{{A_2}({\omega _j},{\nu _0})}}, \end{aligned}$$

where

$$\begin{aligned} {A_1}(\omega ,\nu )&= ( - {\omega ^4} + {m_2}({\nu ^2}){\omega ^2} - {m_4}({\nu ^2}))( - {n_1}{\omega ^2} + {n_3}) \\&\quad + {n_2}\omega ({m_1}({\nu ^2}){\omega ^3} - {m_3}({\nu ^2})\omega ),\\ {A_2}(\omega ,\nu )&{( - {n_1}{\omega ^2} + {n_3})^2} + n_2^2{\omega ^2}. \end{aligned}$$

Hence

$$\begin{aligned} \tau _j^{(m,{\nu _0})} = \frac{1}{{2{\omega _j}}}\left( {\arccos \frac{{{A_1}({\omega _j},{\nu _0})}}{{{A_2}({\omega _j},{\nu _0})}} + 2l\pi } \right) ,~l = 0,1,2, \cdots . \end{aligned}$$

Define the Hopf bifurcation threshold point

$$\begin{aligned} {\tau _0} = \tau _{{j_0}}^{(0,{\nu _0})} = \min \{ \tau _j^{(0,{\nu _0})},1 \le j \le m\}, \end{aligned}$$

and \({\omega _0} = {\omega _{{j_0}}}\). Specially, when \(\nu = 0\), denote

$$\begin{aligned} {\tau _{00}} = \tau _{{j_{00}}}^{(0,0)} = \min \{ \tau _j^{(0,0)},1 \le j \le m\}. \end{aligned}$$
(12)

From [35], we can derive Lemma 2.

Lemma 2

Let \({\lambda _0}(\tau ) = \varsigma (\tau ) + i\omega (\tau )\) be the root of (7) at \(\tau = {\tau _{00}}\) satisfying \(\varsigma ({\tau _{00}}) = 0\) and \(\omega ({\tau _{00}}) = {\omega _{00}}\). Suppose \(P'(\omega _{00}^2) \ne 0\), where \(P({\omega ^2})\) is defined by (11), then \({\mathop {\textrm{Re}}\nolimits } \left( {\frac{{d\lambda }}{{d\tau }}} \right) \ne 0\) when \(\tau = {\tau _{00}}\).

Now the traversal condition is satisfied. Then we can draw the following theorem.

Theorem 1

Suppose that (H1), (H2) and \(P'(\omega _{00}^2) \ne 0\) hold. For system (4) without diffusion, we can derive the following conclusions:

  1. (i)

    The equilibrium point \({E^*}\) is locally asymptotically stable when \(\tau \in [0,{\tau _{00}})\) and unstable when \(\tau > {\tau _{00}}\);

  2. (ii)

    System (4) without diffusion undergoes a Hopf bifurcation at the equilibrium point \({E^*}\) when \(\tau = {\tau _{00}}\).

3.2 Turing Instability Analysis When \(\tau =0\)

Assuming that \(\tau =0\), system (4) is equivalent to

$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}}&= {d_1}\varDelta {p_1}(x,y,t) - {p_1}(x,y,t)+{a_{11}}f\left( {{p_3}(x,y,t)} \right) \\&\quad + {a_{12}}f({p_2}(x,y,t))+k( {{p_1}(x,y,t) - p_1^*} ),\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}}&= {d_2}\varDelta {p_2}(x,y,t) - {p_2}(x,y,t)+ {a_{21}}f({p_1}(x,y,t)) \\&\quad + {a_{22}}f\left( {{p_4}(x,y,t)} \right) ,\\ \dfrac{{\partial {p_3}(x,y,t)}}{{\partial t}}&= - \alpha {p_3}(x,y,t) + \alpha {p_1}(x,y,t),\\ \dfrac{{\partial {p_4}(x,y,t)}}{{\partial t}}&= - \alpha {p_4}(x,y,t) + \alpha {p_2}(x,y,t). \end{aligned} \end{aligned}$$
(13)

Therefore, the characteristic equation (7) turns into

$$\begin{aligned} {\lambda ^4} + {N_1}({\nu ^2}){\lambda ^3} + {N_2}({\nu ^2}){\lambda ^2} + {N_3}({\nu ^2})\lambda + {N_4}({\nu ^2}) = 0, \end{aligned}$$
(14)

in which

$$\begin{aligned}&{N_1}({\nu ^2}) = {m_1}({\nu ^2}),~~{N_2}({\nu ^2}) = {m_2}({\nu ^2}) + {n_1},\\&{N_3}({\nu ^2}) = {m_3}({\nu ^2}) + {n_2},~~{N_4}({\nu ^2}) = {m_4}({\nu ^2}) + {n_3}. \end{aligned}$$

Denote \({\lambda _i}(i = 1,2,3,4)\) as the root of the characteristic equation (14). According to Routh-Hurwitz criterion, we have \({\mathop {\textrm{Re}}\nolimits } ({\lambda _i}) < 0\) for \(i = 1,2,3,4\) when the conditions below are satisfied

$$\begin{aligned}&{N_1}({\nu ^2})> 0,\\&{N_4}({\nu ^2})> 0,\\&{N_1}({\nu ^2}){N_2}({\nu ^2}) - {N_3}({\nu ^2})> 0,\\&{N_3}({\nu ^2})({N_1}({\nu ^2}){N_2}({\nu ^2}) - {N_3}({\nu ^2})) - N_1^2({\nu ^2}){N_4}({\nu ^2}) > 0. \end{aligned}$$

When the real part of one of the roots of (14) is zero and all the other roots have negative real parts, Turing instability emerges. Hence, let

$$\begin{aligned} {\lambda _1} = 0,~~\mathrm{{ }}{\mathop {\textrm{Re}}\nolimits } ({\lambda _2})< 0,~~\mathrm{{ }}{\mathop {\textrm{Re}}\nolimits } ({\lambda _3})< 0,~~\mathrm{{ }}{\mathop {\textrm{Re}}\nolimits } ({\lambda _4}) < 0, \end{aligned}$$
(15)

when \(\nu = {\nu _T}\) (near the Turing bifurcation threshold). The relationship between the roots and coefficients of (14) gives

$$\begin{aligned} \begin{aligned}&{\lambda _1} + {\lambda _2} + {\lambda _3} + {\lambda _4} = - {N_1}({\nu ^2}),\\&{\lambda _1}{\lambda _2}{\lambda _3}{\lambda _4} = - {N_4}({\nu ^2}),\\&({\lambda _1} + {\lambda _2} + {\lambda _3})({\lambda _1} + {\lambda _3} + {\lambda _4})\\&\qquad \times ({\lambda _1} + {\lambda _2} + {\lambda _4})({\lambda _2} + {\lambda _3} + {\lambda _4}) = {N_3}({\nu ^2}) - {N_1}({\nu ^2}){N_2}({\nu ^2}),\\&({\lambda _1} + {\lambda _2})({\lambda _1} + {\lambda _3})({\lambda _1} + {\lambda _4})\\&\qquad \times ({\lambda _2} + {\lambda _3})({\lambda _2} + {\lambda _4})({\lambda _3} + {\lambda _4}) = {N_3}({\nu ^2})({N_1}({\nu ^2}){N_2}({\nu ^2})\\&\qquad - {N_3}({\nu ^2})) - {({N_1}({\nu ^2}))^2}{N_4}({\nu ^2}). \end{aligned} \end{aligned}$$
(16)

Combing (14) and (15), it is obvious that \({N_1}({\nu ^2}) > 0\), \({N_1}({\nu ^2}){N_2}({\nu ^2}) - {N_3}({\nu ^2}) > 0\), \({N_3}({\nu ^2})({N_1}({\nu ^2}){N_2}({\nu ^2}) - {N_3}({\nu ^2})) - N_1^2({\nu ^2}){N_4}({\nu ^2}) > 0\) and \({N_4}({\nu ^2}) = 0\) when \(\nu = \nu _{T}\). Thus, based on (14), one can obtain that the model stay stable if \({N_4}({\nu ^2}) > 0\) holds for all \(\nu > 0\) and Turing instability appears if \({N_4}({\nu ^2}) < 0\) holds for at least one \(\nu > 0\). Notice that

$$\begin{aligned} {N_4}({\nu ^2}) = {B_1}{\nu ^4} + {B_2}{\nu ^2} + {B_3}, \end{aligned}$$
(17)

where

$$\begin{aligned}&{B_1} = {\alpha ^2}{d_1}{d_2},\\&{B_2} = {\alpha ^2}(1 - {\alpha _{22}}){d_1} + {\alpha ^2}(1 - {\alpha _{11}} - k){d_2},\\&{B_3} = {\alpha ^2}({\alpha _{11}} - 1 + k)({\alpha _{22}} - 1) - {\alpha ^2}{\alpha _{12}}{\alpha _{21}}. \end{aligned}$$

To guarantee the existence of \({\nu _T}\), we make the following hypotheses.

(H3): \(\dfrac{{{B_2}}}{{{\alpha ^2}}} = (1 - {\alpha _{22}}){d_1} + (1 - {\alpha _{11}} - k){d_2} < 0\).

Therefore, if (H3) holds, then the Turing bifurcation occurs when

$$\begin{aligned} {\varDelta _{{N_4}}} = B_2^2 - 4{B_1}{B_3} = 0 \end{aligned}$$
(18)

and

$$\begin{aligned} \nu _T^2 = - \dfrac{{{B_2}}}{{2{B_1}}}. \end{aligned}$$
(19)

Take the diffusion coefficient \({d_2}\) as the Turing bifurcation parameter. (18) can be transformed into

$$\begin{aligned} {C_1}d_2^2 + {C_2}{d_2} + {C_3} = 0, \end{aligned}$$

where

$$\begin{aligned}&{C_1} = {(1 - {\alpha _{11}} - k)^2},\\&{C_2} = 2{d_1}(1 - {\alpha _{11}} - k)(1 - {\alpha _{22}}) - 4{d_1}\frac{{{B_3}}}{{{\alpha ^2}}},\\&{C_3} = {(1 - {\alpha _{22}})^2}d_1^2. \end{aligned}$$

Then, the Turing bifurcation threshold \(d_2^T\) can be written as

$$\begin{aligned} \begin{aligned}&d_2^{T(1)} = \frac{{ - {C_2} - \sqrt{C_2^2 - 4{C_1}{C_3}} }}{{2{C_1}}},\\&d_2^{T(2)} = \frac{{ - {C_2} + \sqrt{C_2^2 - 4{C_1}{C_3}} }}{{2{C_1}}}. \end{aligned} \end{aligned}$$
(20)
Fig. 1
figure 1

Curves of \({N_4}({\nu ^2})\) with respect to \({\nu ^{2}}\) for different values of \(d_2\)

Full size image
Fig. 2
figure 2

Curves of the maximum real part \(\max {\mathop {\textrm{Re}}\nolimits } (\lambda )\) of the eigenvalues with respect to \({\nu ^2}\) for different values of \(d_{2}\)

Full size image

Remark 5

The value of the discrete delay is taken to vary as the analysed target changes. When analysing Hopf bifurcation, we take the discrete delay as the bifurcation parameter, so its value is non-zero. When discussing the Turing instability, we are concerned with the effect of the diffusion coefficient on the occurrence of the Turing instability. Therefore, taking the value of discrete delay as zero can exclude its effect.

To verify the conditions for the generation of Turing bifurcation given in (18), and the Turing bifurcation threshold \(d_2^T\) given in (20), we choose \(f( \cdot ) = \tanh ( \cdot )\), \({a_{11}} = - 0.5\), \({a_{12}} = - 1.8\), \({a_{21}} = 1.3\), \({a_{22}} = 1.7\), \(\alpha = 1\), \(k = 0\) and \({d_1} = 10\). By (20), one can obtain that \(d_2^{T(1)} = 0.6897\) and \(d_2^{T(2)} = 31.5770\). Notice that \((1 - {\alpha _{22}}){d_1} + (1 - {\alpha _{11}} - k){d_2} = \mathrm{{40}}\mathrm{{.3655}} > 0\) when \({d_2} = 31.5770\), which means there is no critical wave \({\nu _T}\) corresponding to \(d_2^{T(2)}\). Thus, the solution \(d_2^{T(2)}\) is excluded. The values 0.58, 0.62, 0.74 and 0.80 are taken for \(d_2\) around the Turing bifurcation threshold \(d_2^T = d_2^{T(1)}\). Figure 1 illustrates that when \({d_2} = d_2^T = 0.6897\), the curve \({N_4}({\nu ^2})\) is tangent to the transverse axis at \({\nu ^2} = \nu _T^2 = 0.4325\). As \(d_2\) decreases, the range of \({\nu ^2}\) that causes \({N_4}({\nu ^2}) < 0\) gradually increases, and the Turing instability will occur when \({d_2} < d_2^T\). Figure 2 depicts the variation of the maximum real part \(\max {\mathop {\textrm{Re}}\nolimits } (\lambda )\) of the eigenvalues with \({\nu ^2}\). It can be seen that when \({d_2} > d_2^T = 0.6897\), the real part of \({\lambda _i}(i = 1,2,3,4)\) is all less than 0, which means that the equilibrium point \({E^*}\) of system (13) is stable. At this point, the Turing instability will not occur.

Although the conditions for the emergence of Turing instability and the Turing bifurcation threshold for \(d_2\) have been identified, we still do not know the transformation relations of the Turing patterns of system (13) after the emergence of Turing instability. In the following, still taking \(d_2\) as the Turing bifurcation parameter and using weak linear analysis, we derive the amplitude equations of system (13).

4 Weakly Nonlinear Analysis

When the Turing bifurcation arises, the dynamics of Turing patterns differ progressively. With the aid of the amplitude equation, the different manifestations of the pattern can be determined. This section applies weak linear analysis to derive equations for the evolution of key amplitudes near the Turing bifurcation threshold \(d_2^T\).

The Taylor expansions of system (13) at the equilibrium point \({E^*}\) gives

$$\begin{aligned} \dfrac{{\partial X}}{{\partial t}} = LX + S, \end{aligned}$$
(21)

where

$$\begin{aligned}&X = \left[ {\begin{array}{*{20}{c}} {{{\bar{p}}_1}}\\ {{{\bar{p}}_2}}\\ {{{\bar{p}}_3}}\\ {{{\bar{p}}_4}} \end{array}} \right] ,~~\mathrm{{ }}L = \left[ {\begin{array}{*{20}{c}} { - 1 + {d_1}\varDelta + k }&{}{{\alpha _{12}}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{21}}}&{}{ - 1 + {d_2}\varDelta }&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha } \end{array}} \right] ,\\&S = \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}p_3^2 + \frac{1}{3}{\gamma _{11}}p_3^3 + {\beta _{12}}p_2^2 + \frac{1}{3}{\gamma _{12}}p_2^3}\\ {{\beta _{21}}p_1^2 + \frac{1}{3}{\gamma _{21}}p_1^3 + {\beta _{22}}p_4^2 + \frac{1}{3}{\gamma _{22}}p_4^3}\\ 0\\ 0 \end{array}} \right] , \end{aligned}$$

and \({\beta _{ij}} = \frac{1}{2}{a_{ij}}f''(0)\), \({\gamma _{ij}} = \frac{1}{2}{a_{ij}}f'''(0)\), \(i = 1,2,j = 1,2\). Here, \({\bar{p}_i} = {p_i} - p_i^*\mathrm{{ }}~(i = 1,2,3,4)\) represents the perturbation near the equilibrium point \({E^*}\). To facilitate writing, \({\bar{p}_i}\) is still noted as \({p_i}\) \((i = 1,2,3,4)\) in the following.

The solution of system (13) near the Turing bifurcation threshold \(d_2^T\) can be written in the following form

$$\begin{aligned} X = \left[ {\begin{array}{*{20}{c}} {{p_1}}\\ {{p_2}}\\ {{p_3}}\\ {{p_4}} \end{array}} \right] = \sum \limits _{j = 1}^3 {({D_j}{e^{i{\nu _j}r}}} + {\bar{D}_j}{e^{ - i{\nu _j}r}}),\mathrm{{ }} \end{aligned}$$
(22)

where \({D_j}\) represents the amplitude vector corresponding to \({\nu _j}\) \((j = 1,2,3)\).

For system (13), we can perturb the Turing bifurcation parameter near \({d_2} = d_2^T\). According to the multiple scale perturbation method, it can be obtained that

$$\begin{aligned} \begin{aligned}&X = \left[ {\begin{array}{*{20}{c}} {{p_1}}\\ {{p_2}}\\ {{p_3}}\\ {{p_4}} \end{array}} \right] = \varepsilon \left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] + {\varepsilon ^2}\left[ {\begin{array}{*{20}{c}} {{p_{12}}}\\ {{p_{22}}}\\ {{p_{32}}}\\ {{p_{42}}} \end{array}} \right] + {\varepsilon ^3}\left[ {\begin{array}{*{20}{c}} {{p_{13}}}\\ {{p_{23}}}\\ {{p_{33}}}\\ {{p_{43}}} \end{array}} \right] + o({\varepsilon ^4}),\\&{d_2} = d_2^T + \varepsilon d_2^{(1)} + {\varepsilon ^2}d_2^{(2)} + {\varepsilon ^3}d_2^{(3)} + o({\varepsilon ^4}),\\&t = {t_0} + \varepsilon {t_1} + {\varepsilon ^2}{t_2} + {\varepsilon ^3}{t_3} + o({\varepsilon ^4}),\\&S = {\varepsilon ^2}{S_2} + {\varepsilon ^3}{S_3} + o({\varepsilon ^4}), \end{aligned} \end{aligned}$$
(23)

where

$$\begin{aligned}&{S_2} = \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}p_{31}^2 + {\beta _{12}}p_{21}^2}\\ {{\beta _{21}}p_{11}^2 + {\beta _{22}}p_{41}^2}\\ 0\\ 0 \end{array}} \right] ,\\&{S_3} = \left[ {\begin{array}{*{20}{c}} {2{\beta _{11}}{p_{31}}{p_{32}} + \frac{1}{3}{\gamma _{11}}p_{31}^3 + 2{\beta _{12}}{p_{21}}{p_{22}} + \frac{1}{3}{\gamma _{12}}p_{21}^3}\\ {2{\beta _{21}}{p_{11}}{p_{12}} + \frac{1}{3}{\gamma _{21}}p_{11}^3 + 2{\beta _{22}}{p_{41}}{p_{42}} + \frac{1}{3}{\gamma _{22}}p_{41}^3}\\ 0\\ 0 \end{array}} \right] . \end{aligned}$$

Furthermore, the linear operator L can be expanded to

$$\begin{aligned} L = {L_T} + \varepsilon ({d_2} - d_2^T)M, \end{aligned}$$
(24)

in which

$$\begin{aligned}&{L_T} = \left[ {\begin{array}{*{20}{c}} { - 1 + {d_1}\varDelta + k }&{}{{\alpha _{12}}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{21}}}&{}{ - 1 + d_2^T\varDelta }&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha } \end{array}} \right] ,\\&M = \left[ {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0\\ 0&{}\varDelta &{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \end{array}} \right] . \end{aligned}$$

Due to the slow variation of the amplitude vector \({D_j}\) (\(j = 1,2,3\)) with time t, combined with (21), we deduce that

$$\begin{aligned} \dfrac{{\partial {D_j}}}{{\partial t}} = \varepsilon \dfrac{{\partial {D_j}}}{{\partial {t_1}}} + {\varepsilon ^2}\dfrac{{\partial {D_j}}}{{\partial {t_2}}} + o({\varepsilon ^3}),~j = 1,2,3. \end{aligned}$$
(25)

Through substituting (23), (24) and (25) into system (21) and comparing the coefficients, the following three equations can be achieved, which correspond to three orders of the perturbation respectively

$$\begin{aligned}&\varepsilon :~{L_T}\left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] = 0; \end{aligned}$$
(26)
$$\begin{aligned}&{\varepsilon ^2}:\mathrm{{ }}{L_T}\left[ {\begin{array}{*{20}{c}} {{p_{12}}}\\ {{p_{22}}}\\ {{p_{32}}}\\ {{p_{42}}} \end{array}} \right] = \frac{\partial }{{\partial {t_1}}}\left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] - d_2^{(1)}M\left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] - {S_2} = \left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}}\\ {{F_4}} \end{array}} \right] ; \end{aligned}$$
(27)
$$\begin{aligned}&{\varepsilon ^3}:\mathrm{{ }}{L_T}\left[ {\begin{array}{*{20}{c}} {{p_{13}}}\\ {{p_{23}}}\\ {{p_{33}}}\\ {{p_{43}}} \end{array}} \right] = \frac{\partial }{{\partial {t_1}}}\left[ {\begin{array}{*{20}{c}} {{p_{12}}}\\ {{p_{22}}}\\ {{p_{32}}}\\ {{p_{42}}} \end{array}} \right] + \frac{\partial }{{\partial {t_2}}}\left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] - d_2^{(1)}M\left[ {\begin{array}{*{20}{c}} {{p_{12}}}\\ {{p_{22}}}\\ {{p_{32}}}\\ {{p_{42}}} \end{array}} \right] \nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~- d_2^{(2)}M\left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] - {S_3} = \left[ {\begin{array}{*{20}{c}} {{G_1}}\\ {{G_2}}\\ {{G_3}}\\ {{G_4}} \end{array}} \right] . \end{aligned}$$
(28)

Since \({L_T}\) is the linear operator of system (13) at the Turing bifurcation threshold, the solution of Eq. (25) is associated to a linear combination of eigenvectors of eigenvalue 0. Thus, the solution can be written as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{p_{11}}}\\ {{p_{21}}}\\ {{p_{31}}}\\ {{p_{41}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\varphi _1}}\\ {{\varphi _2}}\\ {{\varphi _3}}\\ 1 \end{array}} \right] \sum \limits _{j = 1}^3 {{W_j}{e^{i{\nu _j}r}} + c.c.} , \end{aligned}$$
(29)

where \({W_j}\) \((j = 1,2,3)\) is the amplitude of \({e^{i{\nu _j}r}}\) under first-order perturbation in the form determined by higher-order perturbation, and

$$\begin{aligned}&{\varphi _1} = {\varphi _3} = - \frac{{{\alpha _{12}}{\alpha _{22}}}}{{{\alpha _{12}}{\alpha _{21}} - (1 - {\alpha _{11}} - k + {d_1}\nu _T^2)(1 + d_2^T\nu _T^2)}},\\&{\varphi _2} = - \frac{{{\alpha _{22}}(1 - {\alpha _{11}} + {d_1}\nu _T^2)}}{{{\alpha _{12}}{\alpha _{21}} - (1 - {\alpha _{11}} - k + {d_1}\nu _T^2)(1 + d_2^T\nu _T^2)}}. \end{aligned}$$

According to Fredholm solubility condition, the vector function on the right side of (25–27) must be orthogonal to the null eigenvector of the adjoint operator \(L_T^*\). Denote the null eigenvector of \(L_T^*\) as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} 1\\ {{\phi _1}}\\ {{\phi _2}}\\ {{\phi _3}} \end{array}} \right] {e^{ - i{\nu _j}r}} + c.c., \end{aligned}$$

where

$$\begin{aligned}&{\phi _1} = \frac{{{\alpha _{12}}}}{{d_2^T\nu _T^2 + 1 - {\alpha _{22}}}},\\&{\phi _2} = {d_1}\nu _T^2 + 1 - k - \frac{{{\alpha _{12}}{\alpha _{21}}}}{{d_2^T\nu _T^2 + 1 - {\alpha _{22}}}},\\&{\phi _3} = \frac{{{\alpha _{12}}{\alpha _{22}}}}{{\alpha (d_2^T\nu _T^2 + 1 - {\alpha _{22}})}}. \end{aligned}$$

By the orthogonality condition, we derive

$$\begin{aligned} \left( {1,{\phi _1},{\phi _2},{\phi _3}} \right) \left[ {\begin{array}{*{20}{c}} {F_1^{(j)}}\\ {F_2^{(j)}}\\ {F_3^{(j)}}\\ {F_4^{(j)}} \end{array}} \right] = 0, \end{aligned}$$
(30)

in which \(F_1^{(j)}\), \(F_2^{(j)}\), \(F_3^{(j)}\) and \(F_4^{(j)}\) stand for the coefficients of \({e^{i{\nu _j}r}}\) in \({F_1}\), \({F_2}\), \({F_3}\) and \({F_4}\), respectively. Substituting (29) into (27) and comparing the coefficients of \({e^{i{\nu _1}r}}\), we get

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {F_1^{(1)}}\\ {F_2^{(1)}}\\ {F_3^{(1)}}\\ {F_4^{(1)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\varphi _1}}\\ {{\varphi _2}}\\ {{\varphi _3}}\\ 1 \end{array}} \right] \frac{{\partial {W_1}}}{{\partial {t_1}}} + \left[ {\begin{array}{*{20}{c}} 0\\ {d_2^{(1)}{\varphi _2}\nu _T^2}\\ 0\\ 0 \end{array}} \right] {W_1} - \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2}\\ {{\beta _{21}}\varphi _1^2 + {\beta _{22}}}\\ 0\\ 0 \end{array}} \right] {\bar{W}_2}{\bar{W}_3}, \end{aligned}$$

Applying the orthogonality condition, (30) yields

$$\begin{aligned} ({\varphi _1} + {\varphi _2}{\phi _1} + {\varphi _3}{\phi _2} + {\phi _3})\frac{{\partial {W_1}}}{{\partial {t_1}}}&= - {\phi _1}d_2^{(1)}\nu _T^2{W_1} \\&\quad + [{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2 + {\phi _1}({\beta _{21}}\varphi _1^2 + {\beta _{22}})]{\bar{W}_2}{\bar{W}_3}. \end{aligned}$$

Converting the coefficients, we also have

$$\begin{aligned} ({\varphi _1} + {\varphi _2}{\phi _1} + {\varphi _3}{\phi _2} + {\phi _3})\frac{{\partial {W_2}}}{{\partial {t_1}}}&= - {\phi _1}d_2^{(1)}\nu _T^2{W_2} \\&\quad + [{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2 + {\phi _1}({\beta _{21}}\varphi _1^2 + {\beta _{22}})]{\bar{W}_1}{\bar{W}_3},\\ ({\varphi _1} + {\varphi _2}{\phi _1} + {\varphi _3}{\phi _2} + {\phi _3})\frac{{\partial {W_3}}}{{\partial {t_1}}}&= - {\phi _1}d_2^{(1)}\nu _T^2{W_3} \\&\quad + [{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2 + {\phi _1}({\beta _{21}}\varphi _1^2 + {\beta _{22}})]{\bar{W}_1}{\bar{W}_2}, \end{aligned}$$

which correlate with coefficients of \({e^{i{\nu _2}r}}\) and \({e^{i{\nu _3}r}}\), respectively.

Solving (28) yields

$$\begin{aligned} \begin{aligned} \left[ {\begin{array}{*{20}{c}} {{p_{12}}}\\ {{p_{22}}}\\ {{p_{32}}}\\ {{p_{42}}} \end{array}} \right] =&\, \left[ {\begin{array}{*{20}{c}} {{\varpi _0}}\\ {{\xi _0}}\\ {{\psi _0}}\\ {{\zeta _0}} \end{array}} \right] + \sum \limits _{j = 1}^3 \left[ {\begin{array}{*{20}{c}} {{\varpi _j}}\\ {{\xi _j}}\\ {{\psi _j}}\\ {{\zeta _j}} \end{array}} \right] {e^{i{\nu _j}r}} + \sum \limits _{j = 1}^3 \left[ {\begin{array}{*{20}{c}} {{\varpi _{jj}}}\\ {{\xi _{jj}}}\\ {{\psi _{jj}}}\\ {{\zeta _{jj}}} \end{array}} \right] {e^{2i{\nu _j}r}} \\&+ \left[ {\begin{array}{*{20}{c}} {{\varpi _{12}}}\\ {{\xi _{12}}}\\ {{\psi _{12}}}\\ {{\zeta _{12}}} \end{array}} \right] {e^{i({\nu _1} - {\nu _2})r}} + \left[ {\begin{array}{*{20}{c}} {{\varpi _{23}}}\\ {{\xi _{23}}}\\ {{\psi _{23}}}\\ {{\zeta _{23}}} \end{array}} \right] {e^{i({\nu _2} - {\nu _3})r}} \\&+ \left[ {\begin{array}{*{20}{c}} {{\varpi _{31}}}\\ {{\xi _{31}}}\\ {{\psi _{31}}}\\ {{\zeta _{31}}} \end{array}} \right] {e^{i({\nu _3} - {\nu _1})r}} + c.c., \end{aligned} \end{aligned}$$
(31)

where

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\varpi _0}}\\ {{\xi _0}}\\ {{\psi _0}}\\ {{\zeta _0}} \end{array}} \right] =&\, - {\left[ {\begin{array}{*{20}{c}} { - 1}&{}{{\alpha _{12}}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{21}}}&{}{ - 1}&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha } \end{array}} \right] ^{ - 1}} \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2}\\ {{\beta _{21}}\varphi _1^2 + {\beta _{22}}}\\ 0\\ 0 \end{array}} \right] \\&\times ({\left| {{W_1}} \right| ^2} + {\left| {{W_2}} \right| ^2} + {\left| {{W_3}} \right| ^2}) \buildrel \varDelta \over = \left[ {\begin{array}{*{20}{c}} {{\ell _{01}}}\\ {{\ell _{02}}}\\ {{\ell _{03}}}\\ {{\ell _{04}}} \end{array}} \right] ({\left| {{W_1}} \right| ^2} + {\left| {{W_2}} \right| ^2} + {\left| {{W_3}} \right| ^2}),\\ \left[ {\begin{array}{*{20}{c}} {{\varpi _{jj}}}\\ {{\xi _{jj}}}\\ {{\psi _{jj}}}\\ {{\zeta _{jj}}} \end{array}} \right] =&\, - {\left[ {\begin{array}{*{20}{c}} { - 1 - 4{d_1}\nu _T^2}&{}{{\alpha _{12}}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{21}}}&{}{ - 1 - 4d_2^T\nu _T^2}&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha } \end{array}} \right] ^{ - 1}} \\&\times \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2}\\ {{\beta _{21}}\varphi _1^2 + {\beta _{22}}}\\ 0\\ 0 \end{array}} \right] W_j^2 \buildrel \varDelta \over = \left[ {\begin{array}{*{20}{c}} {{\ell _{11}}}\\ {{\ell _{12}}}\\ {{\ell _{13}}}\\ {{\ell _{14}}} \end{array}} \right] W_j^2,\mathrm{{ }}~~j = 1,2,3, \\ \left[ {\begin{array}{*{20}{c}} {{\varpi _{12}}}\\ {{\xi _{12}}}\\ {{\psi _{12}}}\\ {{\zeta _{12}}} \end{array}} \right] =&\,- {\left[ {\begin{array}{*{20}{c}} { - 1 - 3{d_1}\nu _T^2}&{}{{\alpha _{12}}}&{}{{\alpha _{11}}}&{}0\\ {{\alpha _{12}}}&{}{ - 1 - 3d_2^T\nu _T^2}&{}0&{}{{\alpha _{22}}}\\ \alpha &{}0&{}{ - \alpha }&{}0\\ 0&{}\alpha &{}0&{}{ - \alpha } \end{array}} \right] ^{ - 1}} \\&\times \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2}\\ {{\beta _{21}}\varphi _1^2 + {\beta _{22}}}\\ 0\\ 0 \end{array}} \right] {W_1}{{\bar{W}}_2} \buildrel \varDelta \over = \left[ {\begin{array}{*{20}{c}} {{\ell _{21}}}\\ {{\ell _{22}}}\\ {{\ell _{23}}}\\ {{\ell _{24}}} \end{array}} \right] {W_1}{{\bar{W}}_2}. \end{aligned}$$

Similarly, the coefficients of \({e^{i({\nu _2} - {\nu _3})r}}\) and \({e^{i({\nu _3} - {\nu _1})r}}\) in (31) can be accessed by transforming the suffixes.

Substituting (31) into (28) and comparing the coefficients of \({e^{i{\nu _1}r}}\), it can be obtained that

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {G_1^{(1)}}\\ {G_2^{(1)}}\\ {G_3^{(1)}}\\ {G_4^{(1)}} \end{array}} \right] =&\, \left[ {\begin{array}{*{20}{c}} {{\varphi _1}}\\ {{\varphi _2}}\\ {{\varphi _3}}\\ 1 \end{array}} \right] \left( {\frac{{\partial {W_1}}}{{\partial {t_1}}} + \frac{{\partial {Y_1}}}{{\partial {t_2}}}} \right) + \left[ {\begin{array}{*{20}{c}} 0\\ {{\varphi _2}d_2^{(2)}\nu _T^2}\\ 0\\ 0 \end{array}} \right] {W_1} + \left[ {\begin{array}{*{20}{c}} 0\\ {{\varphi _2}d_2^{(1)}\nu _T^2}\\ 0\\ 0 \end{array}} \right] {Y_1}\\&- \left[ {\begin{array}{*{20}{c}} {{U_1}}\\ {{V_1}}\\ 0\\ 0 \end{array}} \right] \left( {{{\bar{W}}_2}{{\bar{Y}}_3} + {{\bar{W}}_3}{{\bar{Y}}_2}} \right) - \left[ {\begin{array}{*{20}{c}} {{U_2}}\\ {{V_2}}\\ 0\\ 0 \end{array}} \right] {\left| {{W_1}} \right| ^2}{W_1} \\&- \left[ {\begin{array}{*{20}{c}} {{U_3}}\\ {{V_3}}\\ 0\\ 0 \end{array}} \right] \left( {{{\left| {{W_2}} \right| }^2} + {{\left| {{W_3}} \right| }^2}} \right) {W_1}, \end{aligned}$$

where

$$\begin{aligned}&{U_1} = {\beta _{11}}\varphi _3^2 + {\beta _{12}}\varphi _2^2,~~{V_1} = {\beta _{21}}\varphi _1^2 + {\beta _{22}},\\&{U_2} = 2{\beta _{11}}{\varphi _3}({\ell _{03}} + {\ell _{13}}) + {\gamma _{11}}\varphi _3^3 + 2{\beta _{12}}{\varphi _2}({\ell _{02}} + {\ell _{03}}) + {\gamma _{12}}\varphi _2^3,\\&{V_2} = 2{\beta _{21}}{\varphi _1}({\ell _{01}} + {\ell _{11}}) + {\gamma _{21}}\varphi _1^3 + 2{\beta _{22}}({\ell _{04}} + {\ell _{14}}) + {\gamma _{22}},\\&{U_3} = 2{\beta _{11}}{\varphi _3}({\ell _{03}} + {\ell _{23}}) + 2{\gamma _{11}}\varphi _3^3 + 2{\beta _{12}}{\varphi _2}({\ell _{02}} + {\ell _{22}}) + 2{\gamma _{12}}\varphi _2^3,\\&{V_3} = 2{\beta _{21}}{\varphi _1}({\ell _{01}} + {\ell _{21}}) + 2{\gamma _{21}}\varphi _1^3 + 2{\beta _{22}}({\ell _{04}} + {\ell _{24}}) + 2{\gamma _{22}}. \end{aligned}$$

The orthogonality condition gives

$$\begin{aligned} \left( {1,{\phi _1},{\phi _2},{\phi _3}} \right) \left[ {\begin{array}{*{20}{c}} {G_1^{(1)}}\\ {G_2^{(1)}}\\ {G_3^{(1)}}\\ {G_4^{(1)}} \end{array}} \right] = 0. \end{aligned}$$

Hence,

$$\begin{aligned} K\left( {\frac{{\partial {W_1}}}{{\partial {t_1}}} + \frac{{\partial {Y_1}}}{{\partial {t_2}}}} \right)&= - {\varphi _2}{\phi _1}\nu _T^2(d_2^{(2)}{W_1} + d_2^{(1)}{Y_1}) + ({U_1} + {\phi _1}{V_1})\left( {{{\bar{W}}_2}{{\bar{Y}}_3} + {{\bar{W}}_3}{{\bar{Y}}_2}} \right) \\&\quad + ({U_2} + {\phi _1}{V_2}){\left| {{W_1}} \right| ^2}{W_1} + ({U_3} + {\phi _1}{V_3})\left( {{{\left| {{W_2}} \right| }^2} + {{\left| {{W_3}} \right| }^2}} \right) {W_1}, \end{aligned}$$

where \( K={\varphi _1} + {\varphi _2}{\phi _1} + {\varphi _3}{\phi _2} + {\phi _3} \).

Changing the suffixes easily yields the other two equations, which are not listed here.

The amplitude \({D_j}\) (\(j=1,2,3\)) can be represented by

$$\begin{aligned} {D_j} = \varepsilon {W_i} + {\varepsilon ^2}{Y_j} + o({\varepsilon ^3}). \end{aligned}$$

Then the following amplitude equations can be obtained after integration:

$$\begin{aligned} \begin{aligned}&\tau _0^D\dfrac{{\partial {D_1}}}{{\partial t}} = \mu {D_1} + {g_0}{\bar{D}_2}{\bar{D}_3} - ({g_1}{\left| {{D_1}} \right| ^2} + {g_2}({\left| {{D_2}} \right| ^2} + {\left| {{D_3}} \right| ^2})){D_1}, \\&\tau _0^D\dfrac{{\partial {D_2}}}{{\partial t}} = \mu {D_2} + {g_0}{\bar{D}_3}{\bar{D}_1} - ({g_1}{\left| {{D_2}} \right| ^2} + {g_2}({\left| {{D_3}} \right| ^2} + {\left| {{D_1}} \right| ^2})){D_2}, \\&\tau _0^D\dfrac{{\partial {D_3}}}{{\partial t}} = \mu {D_1} + {g_0}{\bar{D}_1}{\bar{D}_2} - ({g_1}{\left| {{D_3}} \right| ^2} + {g_2}({\left| {{D_1}} \right| ^2} + {\left| {{D_2}} \right| ^2})){D_3}, \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned}&\tau _0^D = \dfrac{{{\varphi _1} + {\varphi _2}{\phi _1} + {\varphi _3}{\phi _2} + {\phi _3}}}{{{\varphi _2}{\phi _1}d_2^T\nu _T^2}},~~\mu = \dfrac{{d_2^T - {d_2}}}{{d_2^T}},~~{g_0} = \dfrac{{{U_1} + {\phi _1}{V_1}}}{{{\varphi _2}{\phi _1}d_2^T\nu _T^2}},\\&{g_1} = - \frac{{{U_2} + {\phi _1}{V_2}}}{{{\varphi _2}{\phi _1}d_2^T\nu _T^2}},~~{g_2} = - \frac{{{U_3} + {\phi _1}{V_3}}}{{{\varphi _2}{\phi _1}d_2^T\nu _T^2}}. \end{aligned}$$

Each amplitude \(D_j\) can be converted into a modulus \({\rho _j} = \left| {{D_j}} \right| \) and a corresponding phase angle \({\theta _j}\) (\( j=1,2,3 \)). Substituting \({D_j} = {\rho _j}{e^{i{\theta _j}}}\) (\( j=1,2,3 \)) into (32) and separating the real and imaginary parts results in the following differential equations for four real variables:

$$\begin{aligned} \begin{aligned}&\tau _0^D\dfrac{{\partial \theta }}{{\partial t}} = - {g_0}\dfrac{{\rho _1^2\rho _2^2 + \rho _2^2\rho _3^2 + \rho _3^2\rho _1^2}}{{{\rho _1}{\rho _2}{\rho _3}}}\sin \theta , \\&\tau _0^D\dfrac{{\partial {\rho _1}}}{{\partial t}} = \mu {\rho _1} + {g_0}{\rho _2}{\rho _3}\cos \theta - {g_1}\rho _1^3 - {g_2}(\rho _2^2 + \rho _3^2){\rho _1}, \\&\tau _0^D\dfrac{{\partial {\rho _2}}}{{\partial t}} = \mu {\rho _2} + {g_0}{\rho _3}{\rho _1}\cos \theta - {g_1}\rho _2^3 - {g_2}(\rho _3^2 + \rho _1^2){\rho _2}, \\&\tau _0^D\dfrac{{\partial {\rho _3}}}{{\partial t}} = \mu {\rho _3} + {g_0}{\rho _1}{\rho _2}\cos \theta - {g_1}\rho _3^3 - {g_2}(\rho _1^2 + \rho _2^2){\rho _3}, \end{aligned} \end{aligned}$$

where \(\theta = {\theta _1} + {\theta _2} + {\theta _3}\).

Fig. 3
figure 3

The phase diagram of the four neurons \({p_1},{p_2},{p_3}\) and \(p_4\) under the initial condition \((0.2,0.2, - 0.1, - 0.1)\) with \(k = 0\) and \(-\,0.05\)

Full size image
Fig. 4
figure 4

The evolution of the Turing patterns of neuron \(p_1\) at time 400, 1000, 3000 and 18,000

Full size image
Fig. 5
figure 5

The evolution of the Turing patterns of neuron \(p_2\) at time 400, 1000, 3000 and 18,000

Full size image
Fig. 6
figure 6

The homogeneous state of the neuron \(p_1\) with \(k=0.5\), in comparison to the Turing patterns of \(p_1\) with \(k=0\)

Full size image
Fig. 7
figure 7

The homogeneous state of the neuron \(p_2\) with \(k=0.5\), in comparison to the Turing patterns of \(p_2\) with \(k=0\)

Full size image
Fig. 8
figure 8

Surface diagram representing the relationship between \(d_2^T\) and \({a_{11}}\), k

Full size image
Fig. 9
figure 9

\(d_2^T\) versus the control parameter k with \({a_{11}} = - 0.5, - 0.8, - 1.2\) and \(-1.5\)

Full size image

According to the theory proposed by Turing, system (13) has four types of pattern solutions as follows

(1) Homogeneous solution \({\rho _1} = {\rho _2} = {\rho _3} = 0\).

If \(\mu < {\mu _2} = 0\), then the homogeneous solution is stable. Conversely, it is unstable when \(\mu > {\mu _2}\).

(2) Stripe pattern solution, described by

$$\begin{aligned} {\rho _1} = {\left( {\dfrac{\mu }{{{g_1}}}} \right) ^{\frac{1}{2}}} \ne 0,~~{\rho _2} = {\rho _3} = 0. \end{aligned}$$

The stripe pattern is stable when \(\mu > {\mu _3} = \frac{{g_0^2{g_1}}}{{{{({g_2} - {g_1})}^2}}}\) and unstable when \(\mu < {\mu _3}\).

(3) Spot pattern solution, described by

$$\begin{aligned} {\rho _1} = {\rho _2} = {\rho _3} = \dfrac{{\left| {{g_0}} \right| \pm {{\left( {g_0^2 + 4({g_1} + 2{g_2})\mu } \right) }^{\frac{1}{2}}}}}{{2({g_1} + 2{g_2})}}. \end{aligned}$$

Spot patterns exist when \(\mu > {\mu _1} = - \frac{{g_0^2}}{{4({g_1} + 2{g_2})}}\). If \(\mu < {\mu _4} = \frac{{2{g_1} + {g_2}}}{{{{({g_2} - {g_1})}^2}}}g_0^2\), then the solution

$$\begin{aligned} {\rho ^ + } = \frac{{\left| {{g_0}} \right| + {{\left( {g_0^2 + 4({g_1} + 2{g_2})\mu } \right) }^{\frac{1}{2}}}}}{{2({g_1} + 2{g_2})}} \end{aligned}$$

is stable. The solution

$$\begin{aligned} {\rho ^ - } = \frac{{\left| {{g_0}} \right| - {{\left( {g_0^2 + 4({g_1} + 2{g_2})\mu } \right) }^{\frac{1}{2}}}}}{{2({g_1} + 2{g_2})}} \end{aligned}$$

is always unstable.

(4) Mixed structure solution, described by

$$\begin{aligned} {\rho _1} = \frac{{\left| {{g_0}} \right| }}{{{g_1} - {g_2}}},~~{\rho _2} = {\rho _3} = {\left( {\frac{{\mu + {g_1}\rho _1^2}}{{{g_1} + {g_2}}}} \right) ^{\frac{1}{2}}}. \end{aligned}$$

The mixed structure solution is always unstable.

Therefore, we have induced the conditions for the emergence of different Turing modes by deriving the amplitude equations.

5 Numerical Simulation

In order to verify the validity of the main findings of this paper, we investigate the control effect of the state feedback controller on Hopf bifurcation and Turing instability through numerical simulations.

Firstly, for system (4) without diffusion, we select the parameter values as follows

$$\begin{aligned} \begin{aligned} \dfrac{{d{p_1}(t)}}{{dt}}&= - {p_1}(t) - 0.5\tanh ({p_3}(t)) - 1.8\tanh ({p_2}(t - \tau )) + k({p_1}(t) - p_1^*),\\ \dfrac{{d{p_2}(t)}}{{dt}}&= - {p_2}(t) + 1.3\tanh ({p_1}(t - \tau )) + 1.7\tanh ({p_4}(t)),\\ \dfrac{{d{p_3}(t)}}{{dt}}&= - {p_3}(t) + {p_1}(t),\\ \dfrac{{d{p_4}(t)}}{{dt}}&= - {p_4}(t) + {p_2}(t). \end{aligned} \end{aligned}$$
(33)

When the state feedback gain factor \(k = 0\) (i.e. without control), (12) gives that \({\tau _{00}} = 0.702 < \tau = 0.715\). The blue curve in Fig. 3 demonstrates that system (33) is unstable at the equilibrium point \({E^*}\) and the limit cycle appears. According to Theorem 1, system (33) undergoes a Hopf bifurcation when the discrete delay \(\tau \) crosses the Hopf bifurcation threshold \({\tau _{00}}\). Then, select the state feedback gain factor \(k = - 0.05\). By (12), we calculate \({\bar{\tau }_{00}} = \mathrm{{0}}\mathrm{{.748 > }}\tau \mathrm{{ = 0}}\mathrm{{.715}}\). As can be seen from the red curve in Fig. 3, system (33) is locally asymptotically stable at the equilibrium point \({E^*}\) and the limit cycle disappears. The comparison results show that the state feedback controller has a suppressive effect on the generation of Hopf bifurcations for system (33).

Remark 6

Currently, there are three mainstream neuron activation functions: piece-wise linear function, sigmoid function and Lipschitz function. The hyperbolic tangent function, which is a typical sigmoid function, has the properties of being monotonically increasing, continuously differentiable and bounded. In addition, the hyperbolic tangent function is consistent with the assumption (H1). Thus, the choice of the hyperbolic tangent function is reasonable.

Next, for system (13), we select the parameter values as follows

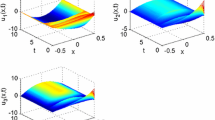
$$\begin{aligned} \begin{aligned} \dfrac{{\partial {p_1}(x,y,t)}}{{\partial t}}&= 10\varDelta {p_1}(x,y,t) - {p_1}(x,y,t) - 0.5\tanh ({p_3}(x,y,t))\\&\quad - 1.8\tanh ({p_2}(x,y,t)) + k{p_1}(x,y,t),\\ \dfrac{{\partial {p_2}(x,y,t)}}{{\partial t}}&= {d_2}\varDelta {p_2}(x,y,t) - {p_2}(x,y,t) + 1.3\tanh ({p_1}(x,y,t))\\&\quad + 1.7\tanh ({p_4}(x,y,t)),\\ \dfrac{{\partial {p_3}(x,y,t)}}{{\partial t}}&= - {p_3}(x,y,t) + {p_1}(x,y,t),\\ \dfrac{{\partial {p_4}(x,y,t)}}{{\partial t}}&= - {p_4}(x,y,t) + {p_2}(x,y,t). \end{aligned} \end{aligned}$$
(34)

We take \(k=0\) (i.e. without control). By (20), \(d_2^{T(1)} = 0.6897\) and \(d_2^{T(2)} = 31.5770\). \(d_2^{T(2)} = 31.5770\) is dropped due to the non-existence of the corresponding critical wave \({\nu _T}\). Thus, \(d_2^T = d_2^{T(1)} = 0.6897\). Selecting \({d_2} = 0.64 < d_2^T\), Turing instability will emerge according to the analysis in Sect. 3. Meanwhile, we have \(\tau _0^D = \mathrm{{8}}\mathrm{{.9365}}\), \({g_0} = 0\), \({g_1} = \mathrm{{4}}\mathrm{{.2351}}\), \({g_2} = \mathrm{{8}}\mathrm{{.4701}}\) and \(\mu = \mathrm{{0}}\mathrm{{.072 > }}{\mu _3} = {\mu _4} = 0\). Depending on the conditions for the Turing patterns switching given in Sect. 4, both stripe and spot patterns will appear, but only the stripe pattern can keep stable. Figures 4 and 5 show that stripe and spot patterns initially exist simultaneously, and as time passes, the spot patterns fade away and eventually only the stripe patterns occupy the entire space.

In order to test the inhibition effect of the state feedback controller on the appearance of Turing instability for system (34), we take \(d_2=0.64\) and \(k=0.5\). Similarly, it can be calculated that \(\bar{d}_2^T = \bar{d}_2^{T(1)}\mathrm{{ = 0}}\mathrm{{.6204 < }}{d_2} = 0.64\) (the other solution \(\bar{d}_2^{T(2)} = \mathrm{{78}}\mathrm{{.9796}}\) is discarded for the same reason as above). In addition, \(\tau _0^D = 9.7013\), \({g_0} = 0\), \({g_1} = 4.4226\), \({g_2} = 8.8451\) and \(\mu = -\,0.0316 < {\mu _2} = 0\). As can be observed in Figs. 6 and 7, after the introduction of the state feedback controller, Turing instability of system (34) vanishes and the neurons \(p_1\) and \(p_2\) end up behaving as the homogeneous state throughout the space.

Remark 7

System (33) is a ordinary differential system that disregards reaction diffusion, and we focus on the effect of the controller on the Hopf bifurcation threshold when the discrete delay is taken as the bifurcation parameter. System (34), on the other hand, considers reaction diffusion but ignores the discrete delay, and we concentrate on the control effect of the controller on the Turing bifurcation threshold.

Besides, we further explore the joint effect of the system parameters \({a_{11}}\) and the state feedback gain factor k on the Turing bifurcation threshold \(d_2^T\). Take \(f( \cdot ) = \tanh ( \cdot )\), and fix \({a_{12}} = - 1.8\), \({a_{21}} = 1.3\), \({a_{22}} = 1.7\), \(\alpha = 1\), \( d_1=10 \). Figures 8 and 9 portray the combined effect on the Turing bifurcation threshold \(d_2^T\) when \({a_{11}}\) and k are varied simultaneously. The simulation results reveal that as \({a_{11}}\) and k increase, the Turing bifurcation threshold \(d_2^T\) becomes smaller progressively, which implies that the Turing instability region is reduced and the stability of system (13) is improved.

Remark 8

Compared with the traditional state feedback control strategy [36, 37], we extend its control domain from ordinary differential equations to partial differential equations, and extend the control objective from Hopf bifurcation to Turing bifurcation. In fact, the state feedback control strategy is not only simple in design but also effective in control.

Remark 9

Notice that in (17), \(\alpha \) is the common factor of \(B_1\), \(B_2\) and \(B_3\). Therefore, the declining rate \(\alpha \) of the past memory in the distributed delay does not has no impact on the Turing bifurcation threshold. Actually, the main influence of the introduction of the distributed delay on system (2) is that the virtual neurons change the original topology and increase the dimensionality.

6 Conclusion

In this paper, we introduce the two-dimensional diffusion and the state feedback control strategy to a two-neuron Hopfield neural network system with mixed delays. By adding two virtual neurons, the original system is transformed into a neural network containing only the discrete delays. We analyse the conditions under which the Hopf bifurcation occurs when the discrete delay is adopted as the bifurcation parameter, and determine the Hopf bifurcation threshold. Then, letting the discrete delay be zero, the Turing instability generation condition and the value of the Turing bifurcation threshold \(d_2^T\) are given. Using the weak nonlinear analysis, we derive the amplitude equations and determine the selection of each Turing patterns. The results of numerical simulations reveal that the state feedback controller can achieve the control effects that delay the onset of Hopf bifurcation as well as suppress Turing pattern generation. In addition, the joint effect of the system parameter \({a_{11}}\) and control parameter k on the Turing bifurcation threshold is also given.

We can conclude that the state feedback controller designed in this paper can be implemented not only to control Hopf bifurcation thresholds in ordinary differential systems without reaction diffusion, but also to control the system Turing bifurcation threshold in partial differential systems with reaction diffusion. It can be seen that the state feedback control strategy possesses certain generalisability in Hopf bifurcation control and Turing bifurcation control. In addition, the controller features the advantages of simple design and good control effect.

The introduction of reaction diffusion into more complex neural networks and the analysis of their spatiotemporal dynamic behaviours are the worthy challenges for future studies. Furthermore, we will continue to explore the impact of more versatile control strategies on Turing patterns of neural networks, such as PD control and hybrid control.