Finite-Time Stability of Inertial Neural Networks with Delayed Impulses

Abstract

This paper studies the finite-time stability (FTS) of the inertial neural networks (INNs) with delayed impulses. Unlike previous related works, we consider the delayed impulses and propose a new impulsive control strategy. We extend the existing FTS results to the cases with delayed impulses. We also establish some global and local FTS criteria of INNs. Moreover, we estimate the settling-time in different cases and investigate the optimization strategy. We present three numerical examples to verify the validity of our theoretical results.

1 Introduction

In 1986, Babcock and Westervelt introduced the inertial term into their neural network model, which they named the Inertial Neural Networks (INNs) [1]. INNs have the information analysis and processing capabilities of traditional models, as well as various excellent dynamic characteristics such as strong robustness and fault tolerance [2]. Stability is an important dynamical property of INNs that has attracted much attention in recent years. Many effective stability criteria of INNs have been established [3,4,5,6,7].

Most studies on the stability of INNs are asymptotic, meaning the system can only reach the desired state as time approaches infinity [7, 8]. However, in many real-world engineering and biological systems, stability must be achieved in finite time [9, 10]. Recently, some interesting results about finite-time stability (FTS) of dynamical systems have been obtained [11,12,13,14]. In [11], the FTS problem under information transmission failure of partial nodes is studied, and in [12], the FTS of Markovian coupled neural networks is considered. However, there are still some relatively strict constraints in the practical use of FTS criteria. For example, in [13], FTS can only be achieved for a local range of initial values. In [14], the realization of FTS requires the parameters of the nonlinear terms sufficiently small, which may make the obtained criterion conservative. These restrictions motivate us to further study FTS theory and its applications.

In some real INNs, signal transmission may change abruptly at some discrete instants due to sudden noises or fluctuations, known as the impulsive effect of INNs. Generally, impulses can be divided into three categories: inactive impulses, destabilizing impulses [15, 16], and stabilizing impulses [17, 18]. Destabilizing impulses often destroy stability and can be seen as impulsive perturbation, while stabilizing impulses may promote stability and can be called impulsive control. Some relevant works about the asymptotic stability problem of INNs under impulse effects have been published [19,20,21,22]. A natural question arises: how do impulses affect the FTS of INNs? To the best of our knowledge, the problem of FTS of INNs under impulsive effects has not been studied. Considering the control effect of stabilizing impulses, we wonder whether the local finite-time stability (LFTS) of INNs can be extended to global finite-time stability (GFTS) under the effect of stabilizing impulses. Additionally, it is also important to estimate the settling-time for the FTS of INNs. In this paper, we also aim to estimate the settling-time and explore its relationship with the initial value and impulses.

Moreover, time delays are unavoidable in many real control systems, such as the vehicle active suspension system [23], communication security networks [24], etc [25, 26]. When impulsive signals are delayed in the transmission process, they are generally called delayed impulses [27]. In recent years, the potential effects of delayed impulses on enhancing or destabilizing network stability have been explored [26, 28]. However, few works have focused on the FTS of dynamical systems involving INNs with delayed impulses. In particular, although the GFTS and LFTS criteria under impulsive effects have been established, the impulsive delays were not taken into account in [29]. It is meaningful to study the FTS of INNs with delayed impulsive effects.

Motivated by the above discussions, this paper investigates the FTS of INNs with delayed impulses. The main contributions are as follows:

• (1) In contrast to the previous related work [29], the delayed impulses are considered and a new lemma about the FTS of the general nonlinear systems with delayed impulses is proposed.

• (2) A new hybrid control strategy is proposed and the GFTS criteria of INNs with delayed impulses are established, which improves upon [13].

• (3) The settling-time calculation is more accurate than [29], since more parameters are considered. It also considers the optimization problems to obtain the shorter settling-time for the same initial value.

The rest of the paper is organized as follows. Section 2 introduces some definitions, assumptions and lemmas for the next section. Section 3 studies the GFTS and LFTS of the INNs with delayed impulses. Section 4 provides three examples to demonstrate our results. Section 5 summarizes the paper.

Notations: See Table 1.

Table 1 Table of notations

2 Preliminaries and Model Description

2.1 Model Description

The inertial neural networks (INNs) can be described as follows:

$$\begin{aligned} \frac{d^{2}x_{i}(t)}{dt^{2}}=-c_{i}\frac{dx_{i}(t)}{dt}-d_{i}x_{i}(t)+\sum _{j=1}^{n}a_{ij}g_{j}(x_{j}(t))+H_{i}, \,\,\, i=1, \ldots , n, \end{aligned}$$

(1)

where $x_{i}(t)\in \mathbb {R}$ is the state of the i-th neuron, n is the number of neurons, $c_{i}$ and $d_{i}$ are positive constants, $H_{i}$ can be considered as the external input for i-th neuron, $a_{ij}$ are the connection strengths, and $g_{j}(\cdot )$ is the continuous activation function.

Let $p_{i}(t)=\frac{dx_{i}(t)}{dt}+r_{i}x_{i}(t)$, $i=1, \ldots , n$, $p(t)=(p_{1}(t), \ldots , p_{n}(t))^{\textsf{T}}$ and $x(t)=(x_{1}(t), \ldots , x_{n}(t))^{\textsf{T}}$. Then, we can transform (1) into

$$\begin{aligned} \left\{ \begin{array}{lcl} \frac{dx(t)}{dt}=p(t)-Rx(t)+I(t),\\ \frac{dp(t)}{dt}=-Cp(t)-Dx(t)+Ag(x(t))+H+J(t),\,\,\,\,\,\, t\ge t_{0},\\ \end{array} \right. \end{aligned}$$

(2)

where $R=\text {diag}\{r_{1},\ldots ,r_{n}\}$, $C=\text {diag}\{c_{1}-r_{1},\ldots ,c_{n}-r_{n}\}$, $D=\text {diag}\{d_{1}+r_{1}(r_{1}-c_{1}),\ldots ,d_{n}+r_{n}(r_{n}-c_{n})\}$, $A=(a_{ij})_{n\times n}$ and $H=(H_{1},\ldots ,H_{n})^{\textsf{T}}$. I(t) and J(t) donote the control inputs, which will be designed later.

Suppose $(\omega _0, \varsigma _0)^{\textsf{T}}$ is the equilibrium point of the INNs (2), i.e.,

$$\begin{aligned} \left\{ \begin{array}{lcl} \varsigma _0-R\omega _0=0,\\ -C\varsigma _0-D\omega _0+Ag(\omega _0)+H=0, \end{array} \right. \end{aligned}$$

(3)

where $\omega _0=(\omega _{01},\ldots ,\omega _{0n})^{\textsf{T}}$ and $\varsigma _0=(\varsigma _{01}, \ldots , \varsigma _{0n})^{\textsf{T}}$. Define the error variables as $w(t)=x(t)-\omega _0$ and $e(t)=p(t)-\varsigma _0$. By calculation, the following error system will be obtained:

$$\begin{aligned} \left\{ \begin{array}{lcl} \frac{dw(t)}{dt}=e(t)-Rw(t)+I(t),\\ \frac{de(t)}{dt}=-Ce(t)-Dw(t)+Af(w(t))+J(t),\,\,\,\,\,\, t\ge t_{0},\\ \end{array} \right. \end{aligned}$$

(4)

where $f(w(t))=g(x(t))-g(\omega _0)$.

2.2 Preliminaries

Before presenting the main theorems, we first provide some definitions, assumptions and lemmas as follows.

Definition 1

(Average Implusive Delay). [30] For impulsive delay sequence $\left\{ \tau _k\right\}$, assume that there exist positive numbers $\tau ^*$ and $\tilde{\tau }$ such that

$$\begin{aligned} \tilde{\tau }N(t,t_0)-\tau ^* \le \sum _{j=1}^{N(t,t_0)}{\tau _j} \le \tilde{\tau }N(t,t_0)+\tau ^*, \end{aligned}$$

(5)

where $N(t,t_0)$ denotes the number of impulses on the interval $[t_0, t)$. Then, we call $\tilde{\tau }$ the average impulsive delay of impulsive delay sequence $\left\{ \tau _k\right\}$.

Definition 2

[13] Given the initial values $(w(t_0), \, e(t_0))^{\textsf{T}}$, if there exists nonempty open sets $\mathscr {X}_1, \, \mathscr {X}_2 \subset \mathbb {R}^n$ such that $(w(t), \, e(t))^{\textsf{T}}$ converges to $\varvec{0}$ within a finite time T for any $(w(t_0), \, e(t_0))^{\textsf{T}} \in \mathscr {X}_1 \times \mathscr {X}_2$, i.e.,

$$\begin{aligned}&\lim \limits _{t \rightarrow T}||(w(t), \, e(t))^{\textsf{T}}||=0 \,\,\, \textrm{and}\\&||(w(t), \, e(t))^{\textsf{T}}||=0, \,\,\,\,\,\, \forall t \ge t_0+T, \end{aligned}$$

where $w(t)=(w_1(t),\ldots ,w_n(t))^{\textsf{T}}$ and $e(t)=(e_1(t),\ldots ,e_n(t))^{\textsf{T}}$ are the error variables of INNs (2) related to the equilibrium point $(\omega _0, \varsigma _0)^{\textsf{T}}$ as defined in (4). Then, the INNs (2) is said to realize local finite time stability (LFTS). Especially, if $\mathscr {X}_1=\mathscr {X}_2=\mathbb {R}^n$, the INNs (2) will be said to realize global finite time stability (GFTS).

We make the following assumptions in this paper.

Assumption 1

There exist the constants $\ell _{i}>0$ such that for any $y_{1}, y_{2}\in \mathbb {R}$, the activation function $g(\cdot )=(g_1(\cdot ),\ldots ,g_n(\cdot ))^{\textsf{T}}$ satisfies

$$\begin{aligned} |g_{i}(y_{1})-g_{i}(y_{2})|\le \ell _{i}|y_{1}-y_{2}|,\,\,\,\,\,\, i=1, \ldots , n, \end{aligned}$$

(6)

and $g_i(0)=0$. Denote $L={\text {diag}}\{\ell _{1}, \ldots , \ell _{n}\} \in \mathbb {R}^{n \times n}$.

Assumption 2

The impulsive instants $\{t_k\}_{k=1,\ldots ,n}$ satisfy

$$\begin{aligned} \underline{\tau } \le t_k-t_{k-1}-\tau _k \le \overline{\tau },\,\,\,\,\,\, k \in \mathbb {N^+}, \, \underline{\tau } \ge 0, \, \overline{\tau } \>0, \end{aligned}$$

(7)

where $t_0 \ge 0$ is the initial time and ${\tau _k}$ is the implusive delay. $\underline{\tau }$, $\overline{\tau }$ are called the impulsive-delay interval (IDI).

Remark 1

Assumption 2 outlines the relationship between ${t_k}$ and ${\tau _k}$. This assumption is logical, as impulsive control is a crucial component of our controllers, and dense impulses are essential for achieving finite-time stability in the systems. In fact, this assumption implies that $t_k-\tau _k \ge t_{k-1}$. It’s important to note that $\underline{\tau }$ can be equal to 0.

Lemma 1

[22] If $\upsilon _1,\upsilon _2, \ldots , \upsilon _n \ge 0$, then the following inequality holds:

$$\begin{aligned} \sum _{i=1}^{n}{{\upsilon _i}^\sigma } \ge \left( \sum _{i=1}^{n}{\upsilon _i}\right) ^\sigma , \end{aligned}$$

where $0 <\sigma \le 1$.

Lemma 2

[31] Suppose a nonnegative continuous function V(t) satisfies

$$\begin{aligned} \dot{V}(t) \le \alpha V(t)-\gamma V^\beta (t), \,\,\,\,\,\, t \ge t_0, \end{aligned}$$

(8)

where $\alpha \>0$, $\gamma \>0$, $\beta \in (0,1)$. If $V^{1-\beta }(t_0) \le \frac{\gamma }{\alpha }$, one has

$$\begin{aligned} V^{1-\beta }(t) \le e^{\alpha (1-\beta )(t-t_0)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+\frac{\gamma }{\alpha }, \,\,\,\,\,\, t_0 \le t \le T_0. \end{aligned}$$

In addition, it holds that $V(t)=0, t\ge t_0+T_0$, where

$$\begin{aligned} T_0=\frac{1}{\alpha (\beta -1)}ln\left( 1-\frac{\alpha }{\gamma }V^{1-\beta }(t_0)\right) . \end{aligned}$$

(9)

Lemma 2 suggests that, provided condition (8) is met, V(t) can decrease towords 0 if $V^{1-\beta }(t_0) \le \frac{\gamma }{\alpha }$. However, it is uncertain whether V(t) can reach 0 if $V^{1-\beta }(t_0) \>\frac{\gamma }{\alpha }$. This will be examined in the subsequent lemma.

Lemma 3

Soppose the nonnegative piecewise continuous function V(t) satisfies

$$\begin{aligned} \left\{ \begin{array}{lcl} \dot{V}(t) \le \alpha V(t)-\gamma V^\beta (t),\,\,\,\,\,\, t \ge t_0 , \, t \in [t_{k-1},t_k);\\ V(t_k) \le \eta ^ \frac{1}{1-\beta } V(t_k-\tau _k),\,\,\,\,\,\, k=1,2,\ldots , \end{array} \right. \end{aligned}$$

(10)

where $\alpha \ge 0$, $\gamma \ge 0$, $\beta \in (0,1)$ and $\eta \in (0,1)$ are constants. $\{t_k\}_{k=1,\ldots ,n}$ and $\{\tau _k\}_{k=1,\ldots ,n}$ are the sequences of impulses and impulsive delays respectively, which satisfied Assumption 2. Then, for any $\epsilon \in [0,1)$ and $0 \le V(t_0) \le \rho ^ \frac{1}{1-\beta }$, there exixts $k_0 \in \mathbb {N^+}$ such that

$$\begin{aligned} V(t_{k_0}) \leqslant \left( \epsilon \frac{\gamma }{\alpha }\right) ^ \frac{1}{1-\beta }, \end{aligned}$$

(11)

where

$$\begin{aligned} \rho =\left\{ \begin{array}{ll} +\infty , &{} {\delta ^* <1};\\ \left( \epsilon +\frac{1-\eta }{1-\delta }\right) \frac{\gamma }{\alpha }, &{} {\delta ^*=1};\\ \root -\log _{\delta ^*}\delta \of {[\frac{\ln \delta }{\ln {\frac{\delta }{\delta ^*}}}\frac{\gamma }{\alpha }\left( \epsilon +\frac{\delta -\eta }{1-\delta }\right) ]^{\log _{\delta ^*}{\frac{\delta ^*}{\delta }}}(\frac{1-\delta }{\eta -1}\frac{\ln {\delta ^*}}{\ln \delta }\frac{\alpha }{\gamma })}+\frac{\gamma }{\alpha }, &{} {\delta ^* \&{}gt;1}, \end{array} \right. \end{aligned}$$

$\delta =\eta e^{\alpha (1-\beta )\underline{\tau }}$ and $\delta ^*=\eta e^{\alpha (1-\beta )\overline{\tau }}$.

Proof

By applying Lemma 2, we can get

$$\begin{aligned} V^{1-\beta }(t) \leqslant e^{\alpha (1-\beta )(t-t_{k-1})}[V^{1-\beta }(t_{k-1})-\frac{\gamma }{\alpha }]+ \frac{\gamma }{\alpha },\,\,\,\,\,\, t \in [t_{k-1},t_k). \end{aligned}$$

While $t=t_k$, one has

$$\begin{aligned} V^{1-\beta }(t_k) = \eta V^{1-\beta }(t_k-\tau _k), \end{aligned}$$

that is

$$\begin{aligned} V^{1-\beta }(t_k) \leqslant \eta e^{\alpha (1-\beta )(t_k-\tau _k-t_{k-1})}[V^{1-\beta }(t_{k-1})-\frac{\gamma }{\alpha }]+ \eta \frac{\gamma }{\alpha }. \end{aligned}$$

By recurrence method, we can get

$$\begin{aligned} V^{1-\beta }(t_k) \leqslant&\eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]\nonumber \\&+\eta (\eta -1)e^{\alpha (1-\beta )(t_k-t_{k-1}-\tau _k)}\frac{\gamma }{\alpha }\nonumber \\&+\eta ^2(\eta -1)e^{\alpha (1-\beta )(t_k-t_{k-2}-(\tau _k+\tau _{k-1}))}\frac{\gamma }{\alpha }\nonumber \\&+\cdots \cdots \nonumber \\&+\eta ^{k-1}(\eta -1)e^{\alpha (1-\beta )(t_k-t_1-\sum _{i=2}^{k}\tau _i)}\frac{\gamma }{\alpha }+\eta \frac{\gamma }{\alpha }. \end{aligned}$$

(12)

Let

$$\begin{aligned} \delta _{j} =\eta ^{j} e^{\alpha (1-\beta )(t_k-t_{k-j}-\sum _{i=k-(j-1)}^{k}\tau _i)},\,\,\,\,\,\,j=1,\ldots ,k-1. \end{aligned}$$

(13)

It follows from Assumption 2 that

$$\begin{aligned} \delta _{j} =\eta ^{j} e^{\alpha (1-\beta )(t_k-t_{k-j}-\sum _{i=k-(j-1)}^{k}\tau _i)} \>\eta ^{j} e^{\alpha (1-\beta )j\underline{\tau }} ,\,\,\,\,\,\,j=1,\ldots ,k-1. \end{aligned}$$

(14)

Combined with (11), we have

$$\begin{aligned} V^{1-\beta }(t_k) \le&\eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]\nonumber \\&+ \sum _{j=1}^{k-1}{\eta ^{j} e^{\alpha (1-\beta )(t_k-t_{k-j}-\sum _{i=k-(j-1)}^{k}\tau _i)}} +\eta \frac{\gamma }{\alpha }\nonumber \\ \le&\eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]\nonumber \\&+ (\eta -1)\frac{\gamma }{\alpha }(\delta +\delta ^2+\delta ^3+\ldots +\delta ^{k-1})+\eta \frac{\gamma }{\alpha }\nonumber \\ \le&\eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]\nonumber \\&+ (\eta -1)\frac{\gamma }{\alpha }(1+\delta +\delta ^2+\delta ^3+\cdots +\delta ^{k-1})+\frac{\gamma }{\alpha } , \end{aligned}$$

(15)

where $\delta =\eta e^{\alpha (1-\beta )\underline{\tau }}$.

Notice that

$$\begin{aligned} k\underline{\tau }<t_k-t_0-\sum _{i=1}^{k}\tau _i <k\overline{\tau }, \end{aligned}$$

and

$$\begin{aligned} \delta ^k \le \eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)} \le {\delta ^*}^k, \end{aligned}$$

(16)

where $\delta =\eta e^{\alpha (1-\beta )\underline{\tau }}$ and $\delta ^*=\eta e^{\alpha (1-\beta )\overline{\tau }}$. Based on (16), we examine the following cases:

$Case \, I$: $\delta =1$. That is $\eta e^{\alpha (1-\beta )k \underline{\tau }}=1$, i.e., $\underline{\tau }=\frac{1}{\alpha (\beta -1)}\text {ln}\eta$. From (15), we have

$$\begin{aligned} V^{1-\beta }(t_k)&\le \eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }(1+1+\cdots +1)+\frac{\gamma }{\alpha }\nonumber \\&= \eta ^k e^{\alpha (1-\beta )(t_k-t_0-\sum _{i=1}^{k}\tau _i)}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }k+\frac{\gamma }{\alpha }. \end{aligned}$$

(17)

According to (17), if $V^{1-\beta }(t_0) <\frac{\gamma }{\alpha }$, one has

$$\begin{aligned} V^{1-\beta }(t_k)&\le \delta ^k[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+(\eta -1)\frac{\gamma }{\alpha }k+\frac{\gamma }{\alpha }\nonumber \\&= [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+(\eta -1)\frac{\gamma }{\alpha }k+\frac{\gamma }{\alpha }. \end{aligned}$$

(18)

Hence, $V^{1-\beta }(t_k) \le \epsilon \frac{\gamma }{\alpha }$ will hold if

$$\begin{aligned}{}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }k \le (\epsilon -1) \frac{\gamma }{\alpha } \end{aligned}$$

is satisfied. Noting $\eta \in (0,1)$, one implies that there must exist a $k_0$ such that $V(t_{k_0}) \leqslant \left( \epsilon \frac{\gamma }{\alpha }\right) ^ \frac{1}{1-\beta }$ holds, and $k_0$ can be choosen as the form

$$\begin{aligned} k_0=\bigg \lceil \frac{1}{\eta -1}\left( \epsilon -\frac{\alpha }{\gamma }V^{1-\beta }(t_0)\right) \bigg \rceil . \end{aligned}$$

(19)

In fact, according to (17), if $V^{1-\beta }(t_0) \ge \frac{\gamma }{\alpha }$, one has

$$\begin{aligned} V^{1-\beta }(t_k)&\le \delta ^{*k}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+(\eta -1)\frac{\gamma }{\alpha }k+\frac{\gamma }{\alpha }. \end{aligned}$$

(20)

We calculate

$$\begin{aligned} \delta ^{*k}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+(\eta -1)\frac{\gamma }{\alpha }k+\frac{\gamma }{\alpha }\le \epsilon \frac{\gamma }{\alpha } \end{aligned}$$

to obtain the sufficient conditions for $V^{1-\beta }(t_k) \le \epsilon \frac{\gamma }{\alpha }$. Then, we can get

$$\begin{aligned}&\delta ^{*k} [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }k \le (\epsilon -1) \frac{\gamma }{\alpha }. \end{aligned}$$

(21)

Due to $\delta ^*=\eta e^{\alpha (1-\beta )\overline{\tau }}\>1$, the left term $\delta ^{*k} [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]$ grows exponentially. Let

$$\begin{aligned} d(k)=\delta ^{*k} [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }k + (1-\epsilon ) \frac{\gamma }{\alpha }, \end{aligned}$$

and get the derivative

$$\begin{aligned} \dot{d}(k)={\delta ^*}^k \ln \delta ^*[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+(\eta -1)\frac{\gamma }{\alpha }. \end{aligned}$$

Let $\dot{d}(k)=0$, then we can get

$$\begin{aligned} k^0=\log _{\delta ^*}{\left( \frac{1-\eta }{\ln \delta ^*}\frac{1}{V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }}\frac{\gamma }{\alpha }\right) }. \end{aligned}$$

By simple calculation, we can know that $k^0$ is the minimum point of d(k) and

$$\begin{aligned} d(k^0)=\frac{1-\eta }{\ln \delta ^*}\frac{\gamma }{\alpha }+(1-\eta )\frac{\gamma }{\alpha }\log _{\delta ^*}\left( {\frac{1-\eta }{\ln \delta ^*}\frac{1}{V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }}\frac{\gamma }{\alpha }}\right) +(1-\epsilon )\frac{\gamma }{\alpha }. \end{aligned}$$

This means $d(k^0) \le 0$ for any $V^{1-\beta }(t_0) \le \frac{1}{\frac{\ln \delta ^*}{1-\eta }{\delta ^*}^(\frac{1}{\ln \delta ^*}+\frac{\epsilon -1}{\eta -1})}\frac{\gamma }{\alpha }+\frac{\gamma }{\alpha }$. Meanwhile,

$$\begin{aligned} k_0=\lceil k^0 \rceil = \bigg \lceil \log _{\delta ^*}{\left( \frac{1-\eta }{\ln \delta ^*}\frac{1}{V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }}\frac{\gamma }{\alpha }\right) } \bigg \rceil \end{aligned}$$

(22)

can realize $V(t_{k_0}) \leqslant (\epsilon \frac{\gamma }{\alpha }) ^ \frac{1}{1-\beta }$.

$Case \, II$: $\delta \ne 1$. If $V^{1-\beta }(t_0) <\frac{\gamma }{\alpha }$, one has

$$\begin{aligned} V^{1-\beta }(t_k)&\le \delta ^k[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }\frac{1-\delta ^k}{1-\delta }+\frac{\gamma }{\alpha }. \end{aligned}$$

(23)

Let

$$\begin{aligned} \delta ^k[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }\frac{1-\delta ^k}{1-\delta }+\frac{\gamma }{\alpha }\le \epsilon \frac{\gamma }{\alpha } \end{aligned}$$

to get the sufficient conditions, which indicate

$$\begin{aligned}&\delta ^k[V^{1-\beta }(t_0)-\frac{\delta -\eta }{\delta -1}\frac{\gamma }{\alpha }] -\frac{1-\eta }{1-\delta }\frac{\gamma }{\alpha }+\frac{\gamma }{\alpha } \le \epsilon \frac{\gamma }{\alpha }. \end{aligned}$$

$\delta <1$ implies $0<\eta<\delta <1$. Hence, it holds that $\frac{\delta -\eta }{\delta -1} <0$ and $-\frac{1-\eta }{1-\delta }\frac{\gamma }{\alpha }+\frac{\gamma }{\alpha } <0$. This implies there must exist a $k_0$ such that $V(t_{k_0}) \leqslant (\epsilon \frac{\gamma }{\alpha }) ^ \frac{1}{1-\beta }$. In addition, $k_0$ can be determined as the form

$$\begin{aligned} k_0= \bigg \lceil \log _\delta {\frac{\epsilon (\frac{\gamma }{\alpha })-(\frac{\delta -\eta }{\delta -1})(\frac{\gamma }{\alpha })}{V^{1-\beta }(t_0)-(\frac{\delta -\eta }{\delta -1})(\frac{\gamma }{\alpha })}} \bigg \rceil . \end{aligned}$$

(24)

Furthermore, $\delta \>1$ means that $\delta ^k[V^{1-\beta }(t_0)-\frac{\delta -\eta }{\delta -1}\frac{\gamma }{\alpha }]$ decreases exponentially. Hence, $k_0$ can be determined as the same form with (24).

If $V^{1-\beta }(t_0) \ge \frac{\gamma }{\alpha }$, one has

$$\begin{aligned} V^{1-\beta }(t_k)&\le \eta ^k e^{\alpha (1-\beta )k \overline{\tau }}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }\frac{1-\delta ^k}{1-\delta }+\frac{\gamma }{\alpha }\nonumber \\&= \delta ^{*k}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +(\eta -1)\frac{\gamma }{\alpha }\frac{1-\delta ^k}{1-\delta }+\frac{\gamma }{\alpha }. \end{aligned}$$

(25)

To get the $k_0$ exactly, we need to consider the following situations.

Firstly, if $\delta ^*=1$, according to (25), we have

$$\begin{aligned} V^{1-\beta }(t_k)&\le [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+\frac{1-\eta }{1-\delta }\delta ^k\frac{\gamma }{\alpha }+\frac{\eta -\delta }{1-\delta }\frac{\gamma }{\alpha }. \end{aligned}$$

Let

$$\begin{aligned}{}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+\frac{1-\eta }{1-\delta }\delta ^k\frac{\gamma }{\alpha }+\frac{\eta -\delta }{1-\delta }\frac{\gamma }{\alpha } \le \epsilon \frac{\gamma }{\alpha }. \end{aligned}$$

Notice that $\delta <\delta ^* =1$ and $\frac{1-\eta }{1-\delta }\delta ^k\frac{\gamma }{\alpha }$ is monotonically decreasing about k. Hence, there exists a $k_0$ as the form

$$\begin{aligned} k_0= \bigg \lceil \log _\delta \left( \epsilon \frac{1-\delta }{1-\eta }-\frac{1-\delta }{1-\eta }\frac{\alpha }{\gamma }V^{1-\beta }(t_0)+1\right) \bigg \rceil \end{aligned}$$

(26)

such that $V(t_{k_0}) \leqslant \left( \epsilon \frac{\gamma }{\alpha } \right) ^ \frac{1}{1-\beta }$ holds if $V^{1-\beta }(t_0) \le (\epsilon +\frac{1-\eta }{1-\delta })\frac{\gamma }{\alpha }$.

Secondly, if $\delta ^* <1$, according to (25), let

$$\begin{aligned} \delta ^{*k}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+\frac{1-\eta }{1-\delta }\delta ^{k}\frac{\gamma }{\alpha }+\frac{\eta -\delta }{1-\delta }\frac{\gamma }{\alpha } \le \epsilon \frac{\gamma }{\alpha }. \end{aligned}$$

(27)

It follows from $\delta<\delta ^* <1$ that $\frac{1-\eta }{1-\delta } \>0$ and $\frac{\eta -\delta }{1-\delta } <0$. Hence, when k is large enough, the inequality (27) is true. That means there will exist a $k_0$ as the form

$$\begin{aligned} k_0=\bigg \lceil \log _{\delta ^*}{\frac{\epsilon (\frac{\gamma }{\alpha })-(\frac{\delta -\eta }{\delta -1})(\frac{\gamma }{\alpha })}{V^{1-\beta }(t_0)-(\frac{\delta -\eta }{\delta -1})(\frac{\gamma }{\alpha })}} \bigg \rceil \end{aligned}$$

(28)

such that $V(t_{k_0}) \leqslant (\epsilon \frac{\gamma }{\alpha }) ^ \frac{1}{1-\beta }$ holds.

Thirdly, if $\delta ^* \>1$, according to (25), let

$$\begin{aligned} \delta ^{*k}[V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }]+\frac{1-\eta }{1-\delta }\delta ^{k}\frac{\gamma }{\alpha }+\frac{\eta -\delta }{1-\delta }\frac{\gamma }{\alpha } \le \epsilon \frac{\gamma }{\alpha }. \end{aligned}$$

Similar to the discussion in (21), we have d(k) as the form

$$\begin{aligned} d(k)=\delta ^{*k} [V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }] +\frac{1-\eta }{1-\delta }\delta ^{k}\frac{\gamma }{\alpha }+\frac{\eta -\delta }{1-\delta }\frac{\gamma }{\alpha } - \epsilon \frac{\gamma }{\alpha } \end{aligned}$$

and get it derivative $\dot{d}(k)$. By calculation, we have

$$\begin{aligned} k^0=\frac{1}{1-\log _{\delta ^*}\delta }\log _{\delta ^*}{\left( \frac{\eta -1}{1-\delta }\frac{1}{V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }}\frac{\ln {\delta }}{\ln {\delta ^*}}\frac{\gamma }{\alpha }\right) } \end{aligned}$$

as its minimum point. This implies that $d(k^0) \le 0$ for any

$$\begin{aligned} V^{1-\beta }(t_0) \le \root -\log _{\delta ^*}\delta \of {[\frac{\ln \delta }{\ln {\frac{\delta }{\delta ^*}}}\frac{\gamma }{\alpha }(\epsilon +\frac{\delta -\eta }{1-\delta })]^{\log _{\delta ^*}{\frac{\delta ^*}{\delta }}}\frac{1-\delta }{\eta -1}\frac{\ln {\delta ^*}}{\ln \delta }\frac{\alpha }{\gamma }}+\frac{\gamma }{\alpha }. \end{aligned}$$

Meanwhile,

$$\begin{aligned} k_0=\lceil k^0 \rceil = \bigg \lceil \frac{1}{1-\log _{\delta ^*}\delta }\log _{\delta ^*}{\left( \frac{\eta -1}{1-\delta }\frac{1}{V^{1-\beta }(t_0)-\frac{\gamma }{\alpha }}\frac{\ln {\delta }}{\ln {\delta ^*}}\frac{\gamma }{\alpha }\right) } \bigg \rceil \end{aligned}$$

(29)

can satisfy $V(t_{k_0}) \leqslant \left( \epsilon \frac{\gamma }{\alpha }\right) ^ \frac{1}{1-\beta }$. This concludes the proof. $\square$

Remark 2

Lemma 3 demonstrates the impact of delayed impulses on the system’s evolution. It is evident that $\delta$ and $\delta ^*$ are key parameters that influence the radius $\rho$ of the initial value set. It should be noted that $\delta$ and $\delta ^*$ contain the lower and upper bounds of IDI (7), respectively. In fact, they can also be seen as an extension of the $impulsive degree$ defined in [29]. Furthermore, it can be easily deduced that smaller values of $\delta$ and $\delta ^*$ indicate stronger controlled strength. Meanwhile, it needs to be emphasized that large difference between $\delta$ and $\delta ^*$ may result in a smalle allowable set for the initial value.

Remark 3

The framework proposed in Lemma 2 consists of linear and nonlinear terms. Under certain conditions, variable V can converge to 0 in a finite time T. Such a framework can generate many models, from which the logistic regression model is critical for predicting the population size [32]. In the logistic model, V denotes the population number, and the parameters capture the population’s features. The impulsive effect in Lemma 3 represents a sudden shock that accounts for some “accidents” in the population’s growth, such as epidemics, natural disasters, etc. By Lemma 3, we can explore how the population number changes after such shocks.

Remark 4

Lemma 3 studies an impulsive differential system with finite and discrete impulses at times $\{t_k\}$. The control strategy of Lemma 3 uses finite impulses to bring V(t) to a small interval, and then apply Lemma 2 to make the system converge to 0. The $\alpha$, $\beta$, $\gamma$ determine the system’s properties. A large $\alpha$ and small $\beta$, $\gamma$ hinder the system’s convergence to 0. The parameter $\eta$ shows the impulsive strength, and a smaller $\eta$ means a stronger impulse. Our control strategy in Lemma 3 can overcome the initial value restriction, meaning that the differential system can converge to 0 for any initial value under certain conditions. Since the system itself can be used to describe quantitative changes in biological populations. For real population numbers, Lemma 3 implies that any population can die out quickly if the external destructive force is large enough.

3 Main Result

In this section, we will examine the global and local finite-time stability of system (4) under the designed controller, which takes the following form:

$$\begin{aligned} \left\{ \begin{array}{l} I_i(t)=-k_{i1}w_i(t)-k_{i2}{\text {sign}}(w_i(t))|w_i(t)|^{\frac{u}{v}}+\sum _{k=1}^{k_0}{\mu _iw_i(t_k-\tau _k)\delta (t-t_k)},\\ J_i(t)=-\xi _{i1}e_i(t)-\xi _{i2}{\text {sign}}(e_i(t))|e_i(t)|^{\frac{u}{v}}+\sum _{k=1}^{k_0}{\mu _ie_i(t_k-\tau _k)\delta (t-t_k)},\\ \end{array} \right. \end{aligned}$$

(30)

where $k_{i1},k_{i2},\xi _{i1},\xi _{i2} \in \mathbb {R}^+$, $i \in \mathbb {N}^+$, $k \in \mathbb {K}^0$, $k_0 \ge 1$ is the number of impulses that occur, $\mathbb {K}^0=\{1,2,\dots ,k_0\}$. u, v are the constants satisfying $0<u <v$. $w_i(t), \, e_i(t)$ are the error variables of the system. $t_0$ is the initial time and $\delta (\cdot )$ is the Dirac function. The continuous feedback controller terms are crucial to achieve FTS of INNs as shown by many previous studies [14, 22, 29]. The impulsive controller terms depend on the impulsive instants $t_k, \, k \in \mathbb {K}^0$. The value of $k_0$ is influenced by the impulsive strength, controller gain, initial state and other factors. We will discuss these factors in more detail later.

3.1 Finite-Time Stability and Settling-Time

Theorem 1

Under the Assumptions 1 and 2, suppose the average impulsive delay of the impulsive delay sequences $\{\tau _k\}_{k=1,\ldots ,n}$ is $\tilde{\tau }$ and there exists a constant $\eta \in (0,1)$ such that

$$\begin{aligned} (1+\mu _i)^2 <\eta ^{\frac{2v}{v-u}}. \end{aligned}$$

(31)

Then, the following conclusions can be drawn:

• (1) the INNs (2) under the controller (30) can achieve global finte-time stability (GFTS) when $\zeta ^* <1$;

• (2) the INNs (2) under the controller (30) can achieve local finte-time stability (LFTS) when $\zeta ^* \ge 1$.

Furthermore, the settling-time T can be estimated as

$$\begin{aligned} T=\left\{ \begin{array}{ll} \Upsilon \left( \lceil \log _{\zeta ^*}{\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil \right) +\tau ^*+\Theta ln(1-\epsilon ), &{} {\check{V} \&{}gt;\nabla , \zeta ^*<1};\\ \Upsilon \left( \lceil \log _\zeta (\epsilon \check{a}-\frac{\check{a}\check{V}}{\nabla }+1) \rceil \right) +\tau ^*+\Theta ln(1-\epsilon ), &{} {\nabla<\check{V}<\rho ^* ,\zeta ^*=1};\\ \Upsilon \left( \lceil \frac{1}{1-\frac{1}{\tilde{b}}}\log _{\zeta ^*}{(-\frac{1}{\check{a}\tilde{b}}\frac{\nabla }{\check{V}-\nabla })} \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ), &{} {\nabla<\check{V}<\rho ^*, \zeta ^* \&{}gt;1};\\ \Upsilon \left( \lceil \frac{1}{\eta -1}(\epsilon -\frac{1}{\nabla }\check{V}) \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ), &{} {\epsilon \nabla<\check{V}<\nabla ,\zeta =1};\\ \Upsilon \left( \lceil \log _\zeta {\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ), &{} {\epsilon \nabla<\check{V} <\nabla , \zeta \ne 1};\\ \Theta \ln (1-\frac{1}{\nabla }\check{V}), &{} {\check{V} \le \epsilon \nabla }.\\ \end{array} \right. \end{aligned}$$

and $\rho ^*$ can be determined as

$$\begin{aligned} \rho ^*=\left\{ \begin{array}{ll} +\infty , &{} {\zeta ^* <1};\\ (\epsilon +\frac{1}{\check{a}})\nabla , &{} {\zeta ^* = 1};\\ \root -\frac{1}{\tilde{b}} \of {(\frac{\epsilon -\hat{a}}{1-\tilde{b}}\nabla )^{1-\frac{1}{\tilde{b}}}\frac{(-\check{a}\tilde{b})}{\nabla }}+\nabla , &{} {\zeta ^* \&{}gt;1}. \end{array} \right. \end{aligned}$$

where u, v are the constants satisfy $0<u <v$, $\phi _i=(d_i+r_i(r_i+c_i))$, for $i=1,\ldots ,n$, $\varphi =\max _{1 \le i \le n}(\sum _{j=1}^{n}|a_{ij}|l_j)$, $\kappa =\max _{1 \le i \le n}(|1-2r_i-2k_{i1}+\phi _i+\varphi |,|1-2(c_i-r_i)-2\xi _{i1}+\phi _i+\varphi |)$, $\lambda =(\frac{1}{2})^{\frac{2v}{u+v}}\min _{1 \le i \le n}(k_{i2},\xi _{i2})$, $V(t_0)=\frac{1}{2}\sum _{i=1}^{n}{{w_i}^2(t_0)}+\frac{1}{2}\sum _{i=1}^{n}{{e_i}^2(t_0)}$, $\zeta = \eta e^{\kappa \frac{v-u}{2v}\underline{\tau }}$, $\zeta ^*= \eta e^{\kappa \frac{v-u}{2v}\overline{\tau }}$, $\lceil \cdot \rceil$ is the upward rounding function, $\hat{a}=\frac{\zeta -\eta }{\zeta -1}$, $\check{a}=\frac{1-\zeta }{1-\eta }$, $\nabla = \frac{\lambda }{\kappa }$, $\check{V}=V^{\frac{v-u}{2v}}(t_0)$, $\hat{b}=\frac{\epsilon -1}{\eta -1}$, $\check{b}=\ln {\zeta ^*}$, $\tilde{b}=\frac{\ln {\zeta ^*}}{\ln \zeta }$, $\Theta =\frac{v}{\kappa (u-v)}$ and $\Upsilon =\tilde{\tau }+\overline{\tau }$.

Proof

Construct the Lyapunov function:

$$\begin{aligned} V(t)=\frac{1}{2}\sum _{i=1}^{n}{{w_i}^2(t)}+\frac{1}{2}\sum _{i=1}^{n}{{e_i}^2(t)}. \end{aligned}$$

(32)

For $t \in [t_{k-1},t_k)$, it holds that

$$\begin{aligned} \dot{V}(t)&=\sum _{i=1}^{n}{w_i(t)\dot{w}_i(t)}+\sum _{i=1}^{n}{e_i(t)\dot{e}_i(t)}\nonumber \\&=\sum _{i=1}^{n}w_i(t)(e_i(t)-r_iw_i(t)+I_i(t)\nonumber \\&\quad +\sum _{i=1}^{n}e_i(t)(-(c_i-r_i)e_i(t)-(d_i+r_i(r_i-c_i))w_i(t)\nonumber \\&\quad +\sum _{i=1}^{n}\sum _{j=1}^{n}a_{ij}(g_j(x_j(t))-g_j(s))+J_i(t))\nonumber \\&\le \sum _{i=1}^{n}w_i(t)e_i(t)-r_i{w_i}^2(t)\nonumber \\&\quad +(-k_{i1}w_i(t)-k_{i2}sign(w_i(t))|w_i(t)|^{\frac{u}{v}})w_i(t)\nonumber \\&\quad +\sum _{i=1}^{n}-(c_i-r_i){e_i}^2(t)-(d_i+r_i(r_i-c_i))w_i(t)e_i(t)\nonumber \\&\quad +\sum _{i=1}^{n}\sum _{j=1}^{n}|a_{ij}||(g_j(x_j(t))-g_j(s))||e_i(t)|\nonumber \\&\quad +\sum _{i=1}^{n}{(e_i(t)(-\xi _{i1}e_i(t)-\xi _{i2}sign(e_i(t))|e_i(t)|^\frac{u}{v}))}\nonumber \\&\le \sum _{i=1}^{n}{w_i(t)e_i(t)-r_i{w_i}^2(t)-k_{i1}{w_i}^2(t)-k_{i2}|w_i(t)|^{\frac{u+v}{v}}}\nonumber \\&\quad +\sum _{i=1}^{n}{-(c_i-r_i){e_i}^2(t)-(d_i+r_i(r_i-c_i))w_i(t)e_i(t)}\nonumber \\&\quad +\sum _{i=1}^{n}{\rho |w_i(t)||e_i(t)|-\xi _{i1}{e_i}^2(t)-\xi _{i2}|e_i(t)|^{\frac{u+v}{v}}}\nonumber \\&\le \frac{1}{2}\sum _{i=1}^{n}(1-2r_i+\phi _i+\varphi -2k_{i1}){w_i}^2(t)+\frac{1}{2}\sum _{i=1}^{n}(1-2(c_i-r_i)\nonumber \\&\quad +\phi _i+\varphi -2\xi _{i1}){e_i}^2(t)- \sum _{i=1}^{n}{k_{i2}|w_i(t)|^{\frac{u+v}{v}}}-\sum _{i=1}^{n}\xi _{i2}|e_i(t)|^{\frac{u+v}{v}}\nonumber \\ {\le }&\kappa \left( \frac{1}{2}\sum _{i=1}^{n}{w_i}^2(t)+\frac{1}{2}\sum _{i=1}^{n}{e_i}^2(t)\right) \nonumber \\&\quad -\lambda \left[ \left( \frac{1}{2}\right) ^{\frac{u+v}{2v}}\sum _{i=1}^{n}{|{w_i}^2(t)|^{{\frac{u+v}{2v}}}}+\left( \frac{1}{2}\right) ^{\frac{u+v}{2v}}\sum _{i=1}^{n}{|{e_i}^2(t)|^{\frac{u+v}{2v}}}\right] \nonumber \\&\le \kappa \left( \frac{1}{2}\sum _{i=1}^{n}{w_i}^2(t)+\frac{1}{2}\sum _{i=1}^{n}{e_i}^2(t)\right) \nonumber \\&-\lambda \left[ \left( \frac{1}{2}\right) ^{\frac{u+v}{2v}}\left( \sum _{i=1}^{n}|{w_i}^2(t)|\right) ^{\frac{u+v}{2v}}+ \left( \frac{1}{2}\right) ^{\frac{u+v}{2v}}\left( \sum _{i=1}^{n}{|{e_i}^2(t)|}\right) ^{\frac{u+v}{2v}}\right] \nonumber \\&= \kappa \left( \frac{1}{2}\sum _{i=1}^{n}{w_i}^2(t)+\frac{1}{2}\sum _{i=1}^{n}{e_i}^2(t)\right) \nonumber \\&\quad -\lambda \left[ \left( \sum _{i=1}^{n}{\frac{1}{2}{w_i}}^2(t)\right) ^{{\frac{u+v}{2v}}}+\left( \sum _{i=1}^{n}{\frac{1}{2}{e_i}^2(t)}\right) ^{\frac{u+v}{2v}}\right] \nonumber \\&\le \kappa \left( \frac{1}{2}\sum _{i=1}^{n}{w_i}^2(t)+\frac{1}{2}\sum _{i=1}^{n}{e_i}^2(t)\right) \nonumber \\&\quad +\lambda \left[ \frac{1}{2}\sum _{i=1}^{n}{{w_i}^2(t)}+\frac{1}{2}\sum _{i=1}^{n}{{e_i}^2(t)}\right] ^{\frac{u+v}{2v}}\nonumber \\&\le \kappa V(t)-\lambda V^{\frac{u+v}{2v}}(t). \end{aligned}$$

(33)

While $t=t_k$, we can get

$$\begin{aligned} V(t_k)&=\frac{1}{2}\sum _{i=1}^{n}{{w_i}^2(t_k)}+\frac{1}{2}\sum _{i=1}^{n}{{e_i}^2(t_k)}\nonumber \\&=\frac{1}{2}\sum _{i=1}^{n}{(1+\mu _i)^2{w_i}^2(t_k-\tau _k)}+\frac{1}{2}\sum _{i=1}^{n}{(1+\mu _i)^2{e_i}^2(t_k-\tau _k)}\nonumber \\&\le \eta ^{\frac{2v}{v-u}}V(t_k-\tau _k). \end{aligned}$$

(34)

According to Lemma 3, we can conclude that, for any $\epsilon \in [0,1)$ and initial value $0<V(t_0) <\rho$, there exist a $k_0$ such that $V(t_{k_0}) \le (\epsilon \frac{\lambda }{\kappa })^{\frac{2v}{v-u}}$, i.e., $V(t_{k_0}) \le (\epsilon \nabla )^{\frac{2v}{v-u}}$.

Next, we shall calculate the settling-time. Firstly, we will compute how long it takes to achieve $V(t) \le (\epsilon \nabla )^{\frac{2v}{v-u}}$. Note that $k_0$ is the number of impulse occured. Considering the average impulsive delay (5), we can get

$$\begin{aligned} T_I=\tilde{\tau }k_0+\tau ^*+\overline{\tau }k_0. \end{aligned}$$

(35)

Secondly, because of $\epsilon \in [0,1)$, so we have $V(t_{k_0}) \le \nabla ^{\frac{2v}{v-u}}$. Then, Lemma 2 can be applied to determine that the time taking from $t_{k_0}$ to reach the equilibrium point is

$$\begin{aligned} T_o=\Theta ln\left( 1-\frac{1}{\nabla }V^{\frac{v-u}{2v}}(t_{k_0})\right) . \end{aligned}$$

(36)

Therefore, we can deduce that the settling-time T is equal to

$$\begin{aligned} T = T_I+T_o. \end{aligned}$$

(37)

We can now examine the settling-time for each specific case:

• (a.) For any $\check{V} \>\nabla$ and $\zeta ^* <1$, we have $k_0=\lceil \log _{\zeta ^*}{\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil$, which indicates

  $$\begin{aligned} T&= (\tilde{\tau }+\overline{\tau })k_0+\tau ^*+\Theta ln(1-\epsilon )\nonumber \\&= \Upsilon \left( \bigg \lceil \log _{\zeta ^*}{\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ). \end{aligned}$$

  (38)

• (b). For any $\nabla<\check{V} <(\epsilon +\frac{1}{\check{a}})\nabla$ and $\zeta ^*=1$, we have $k_0=\lceil \log _\zeta (\epsilon \check{a}-\frac{\check{a}\check{V}}{\nabla }+1) \rceil$, which indicates

  $$\begin{aligned} T&= (\tilde{\tau }+\overline{\tau })k_0+\tau ^*+\Theta ln(1-\epsilon )\nonumber \\&= \Upsilon \left( \bigg \lceil \log _\zeta (\epsilon \check{a}-\frac{\check{a}\check{V}}{\nabla }+1) \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ). \end{aligned}$$

  (39)

• (c). For any $\nabla<\check{V} <\root -\frac{1}{\tilde{b}} \of {[\frac{\epsilon -\hat{a}}{1-\tilde{b}}\nabla ]^{1-\frac{1}{\tilde{b}}}(-\frac{\check{a}\tilde{b}}{\nabla })}+\nabla$ and $\zeta ^* \>1$, $k_0$ can be calculated as $\lceil \frac{1}{1-\frac{1}{\tilde{b}}}\log _{\zeta ^*}{(-\frac{1}{\check{a}\tilde{b}}\frac{\nabla }{\check{V}-\nabla })} \rceil$, which indicates

  $$\begin{aligned} T&= (\tilde{\tau }+\overline{\tau })k_0+\tau ^*+\Theta ln(1-\epsilon )\nonumber \\&= \Upsilon \left( \bigg \lceil \frac{1}{1-\frac{1}{\tilde{b}}}\log _{\zeta ^*}{(-\frac{1}{\check{a}\tilde{b}}\frac{\nabla }{\check{V}-\nabla })} \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ). \end{aligned}$$

  (40)

• (d). For any $\epsilon \nabla<\check{V} <\nabla$ and $\zeta =1$, we have $k_0=\lceil \frac{1}{\eta -1}(\epsilon -\frac{1}{\nabla }\check{V}) \rceil$, which indicates

  $$\begin{aligned} T&= (\tilde{\tau }+\overline{\tau })k_0+\tau ^*+\Theta \ln (1-\epsilon )\nonumber \\&= \Upsilon \left( \bigg \lceil \frac{1}{\eta -1}(\epsilon -\frac{1}{\nabla }\check{V}) \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ). \end{aligned}$$

  (41)

• (e). For any $\epsilon \nabla<\check{V} <\nabla$ and $\zeta \ne 1$, we have $k_0=\lceil \log _\zeta {\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil$, which indicates

  $$\begin{aligned} T&= (\tilde{\tau }+\overline{\tau })k_0+\tau ^*+\Theta ln(1-\epsilon )\nonumber \\&= \Upsilon \left( \bigg \lceil \log _\zeta {\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ). \end{aligned}$$

  (42)

• (f). For any $\check{V} \le \epsilon \nabla$, we have $k_0=0$, which indicates

  $$\begin{aligned} T=T_o = \Theta \ln (1-\frac{1}{\nabla }\check{V}). \end{aligned}$$

  (43)

Based on the discussion above, we have completed the proof and calculated the settling-time T. $\square$

Remark 5

In Theorem 1, $\zeta$ and $\zeta ^*$ are key parameters in determining whether the INNs (2) can achieve GFTS. Unlike [22], the system does not required to be stable. In other words, even if the system itself is unstable, controllers can still be designed to achieve FTS. This will be demonstrated in Example 2.

Remark 6

This paper studies more general cases of FTS of INNs with impulses than the literature, despite many results have been published [11,12,13,14]. Firstly, many FTS studies of INNs neglect impulsive effect which occurs frequently in nature. For instance, [13] uses a new integral method, but the control is continuous and expensive. Our result achieves GFTS with lower cost. Secondly, unlike [29], this paper considers impulsive delays in the impulsive controller, which is more realistic due to the communication constraints. Moreover, we add a linear term to the differential equation model, i.e., $\dot{V}(t) \le \alpha V(t)-\gamma V^{\beta }(t)$, compared with the model in [33]. The form in this paper has more applications in nature, as [32, 34,35,36] show, so our results are more applicable.

Remark 7

The algorithms or stability criteria in this paper mainly involve solving matrix multiplication by vector and calculating some parameters, such as Cp(t), Dx(t), $\varphi =\max _{1 \le i \le n}(\sum _{j=1}^{n}|a_{ij}|l_j)$ and $\kappa =\max _{1 \le i \le n}(|1-2r_i-2k_{i1}+\phi _i+\varphi |,|1-2(c_i-r_i)-2\xi _{i1}+\phi _i+\varphi |)$. The algorithmic complexity here is generally $O(n^2)$, where n is the order of the matrix. The algorithmic complexity can be completed in polynomial time. Therefore, as long as the matrix dimension is not very large, the complexity is relatively small.

When the impulsive delays $\{\tau _{k}\}$ are 0, we get the following corollary.

Corollary 1

Under the Assumptions 1, suppose the impulsive instants $\{t_k\}$ satisfy

$$\begin{aligned} \underline{\tau } \le t_k-t_{k-1}\le \overline{\tau },\,\,\,\,\,\, k \in \mathbb {N^+}, \, \underline{\tau } \ge 0, \, \overline{\tau } \>0, \end{aligned}$$

and there exists a constant $\eta \in (0,1)$ such that (31) holds. Then, the conclusions of Theorem 1 also can be drawn. Moreover, the settling-time T can be estimated as

$$\begin{aligned} T=\left\{ \begin{array}{ll} \overline{\tau }(\lceil \log _{\zeta ^*}{\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil )+\Theta \ln (1-\epsilon ), &{} {\check{V} \&{}gt;\nabla , \zeta ^*<1};\\ \overline{\tau }(\lceil \log _\zeta (\epsilon \check{a}-\frac{\check{a}\check{V}}{\nabla }+1) \rceil )+\Theta \ln (1-\epsilon ), &{} {\nabla<\check{V}<\rho ^* ,\zeta ^*=1};\\ \overline{\tau }(\lceil \frac{1}{1-\frac{1}{\tilde{b}}}\log _{\zeta ^*}{(-\frac{1}{\check{a}\tilde{b}}\frac{\nabla }{\check{V}-\nabla })} \rceil )+\Theta \ln (1-\epsilon ), &{} {\nabla<\check{V}<\rho ^*, \zeta ^* \&{}gt;1};\\ \overline{\tau }(\lceil \frac{1}{\eta -1}(\epsilon -\frac{1}{\nabla }\check{V}) \rceil )+\Theta \ln (1-\epsilon ), &{} {\epsilon \nabla<\check{V}<\nabla ,\zeta =1};\\ \overline{\tau }(\lceil \log _\zeta {\frac{\epsilon \nabla -\hat{a}\nabla }{\check{V}-\hat{a}\nabla }} \rceil )+\Theta \ln (1-\epsilon ), &{} {\epsilon \nabla<\check{V} <\nabla , \zeta \ne 1};\\ \Theta \ln (1-\frac{1}{\nabla }\check{V}), &{} {\check{V} \le \epsilon \nabla },\\ \end{array} \right. \end{aligned}$$

where the range of initial value $\rho ^*$, u, v, $\phi _i$, $\varphi$, $\kappa$, $\lambda$, $V(t_0)$, $\zeta$, $\zeta ^*$, $\hat{a}$, $\check{a}$, $\nabla$, $\check{V}$, $\hat{b}$, $\check{b}$, $\tilde{b}$ and $\Theta$ are the same as in Theorem 1.

3.2 Optimization Problems

In Theorem 1, both $T_I$ and $T_o$ are dependent on the uncertain parameter $\epsilon$. As a result, we can calculate $\epsilon$ to determine the optimal settling-time.

Denote the $T_I$ and $T_o$ as the functions with respect to parameter $\epsilon$, in the following form:

$$\begin{aligned}&T_I = \tilde{\tau }k_0(\epsilon )+\tau ^*+\overline{\tau }k_0(\epsilon )=: \, \theta _1(\epsilon );\\&T_o =\Theta \ln \left( 1-V^{\frac{v-u}{2v}}(t_{k_0})\right) \le \Theta \ln (1-\epsilon )=: \, \theta _2(\epsilon ). \end{aligned}$$

Then, we have $T = T_I+T_o \le \theta _1(\epsilon )+\theta _2(\epsilon )$. We denote $\theta (\epsilon )=\theta _1(\epsilon )+\theta _2(\epsilon )$. Now let’s consider the following optimization problem:

$$\begin{aligned}&\min \,\,\, \theta (\epsilon ),\nonumber \\&\mathrm{s.t} \left\{ \begin{array}{ll} (1+\mu _i)^2 <\eta ^{\frac{2v}{v-u}};\\ \epsilon \in [0,1);\\ \check{V} \in \rho ^*. \end{array} \right. \end{aligned}$$

(44)

The above optimization problems can be summarized into the following Algorithm 1:

Algorithm 1

Minimize $\theta (\epsilon )$

Then, we have the following cases:

• (a). If $\check{V} \>\nabla$ and $\zeta ^* <1$, from (38), we can get

  $$\begin{aligned} \theta (\epsilon )=\Upsilon \left( \bigg \lceil \log _{\zeta ^*}(\frac{1 }{\frac{\check{V}}{\nabla }-\hat{a}}\epsilon -\frac{\hat{a}\nabla }{\check{V}-\hat{a}\nabla }) \bigg \rceil \right) +\tau ^*+\Theta \ln (1-\epsilon ), \end{aligned}$$

  which implies that

  $$\begin{aligned} \dot{\theta }(\epsilon ) =\frac{\Upsilon }{\check{b}(\epsilon -\hat{a})}+\frac{\Theta }{\epsilon -1}; \end{aligned}$$

  and

  $$\begin{aligned} \ddot{\theta }(\epsilon ) =-\frac{\Upsilon }{\check{b}(\epsilon -\hat{a})^2}-\frac{\Theta }{(\epsilon -1)^2}. \end{aligned}$$

  Then, we solve the equation $\dot{\theta }(\epsilon )=0$ to get the stationary point

  $$\begin{aligned} \epsilon _0=1-\frac{\Theta \check{b}(1-\hat{a})}{\Upsilon +\Theta \check{b}}. \end{aligned}$$

  (45)

  Notice that $\epsilon _0 \in [0,1)$ implies that $\ddot{\theta }(\epsilon _0) \>0$, based on the relationship among parameters. This indicates that the value of $\epsilon _0$ given in (45) is the minimum point, and $T=\theta (\epsilon _0)$ is the optimal settling-time for this situation.

• (b). If $\nabla<\check{V} <(\epsilon +\frac{1}{\check{a}})\nabla$ and $\zeta ^* =1$, similar to (a) above, we can constract $\theta (\epsilon )$ and get $\dot{\theta }(\epsilon )$, $\ddot{\theta }(\epsilon )$. Through simple calculations, the extreme point can be determined as follows:

  $$\begin{aligned} \epsilon _0=1-\frac{(\nabla +\check{a}{\nabla }-\check{a} \check{V})\Theta \ln {\zeta }}{\check{a}\nabla \Upsilon +\Theta \check{a} \nabla \ln {\zeta } }. \end{aligned}$$

  (46)

  Similarly, we can get that $\epsilon _0 \in [0,1)$ implies $\ddot{\theta }(\epsilon _0) \>0$ by computing. In this situation, $T=\theta (\epsilon _0)$ is the solution to the optimization problem.

• (c). If $\nabla<\check{V} <\root -\frac{1}{\tilde{b}} \of {[\frac{\epsilon -\hat{a}}{1-\tilde{b}}\nabla ]^{1-\frac{1}{\tilde{b}}}(-\frac{\check{a}\tilde{b}}{\nabla })}+\nabla$ and $\zeta ^* \>1$, $k_0=\bigg \lceil \frac{1}{1-\frac{1}{\tilde{b}}}\log _{\zeta ^*}{(-\frac{1}{\check{a}\tilde{b}}\frac{\nabla }{\check{V}-\nabla })}\bigg \rceil$ can be obtained, which implies the function $\theta _1(\epsilon )$ is independent on the parameter $\epsilon$ in this situation. Hence, the settling-time $T=\theta (\epsilon )$ is only influenced by $\theta _2(\epsilon )$. The reason for this is that the initial value $\check{V}$ is related to parameter $\epsilon$. By calculation, we have $V^{\frac{v-u}{2v}}(t_{k_0-1}) \ge \nabla$ and $V^{\frac{v-u}{2v}}(t_{k_0}) \le \epsilon \nabla$. Thus, the value of $\theta _1(\epsilon )$ only depends on the initial value $\check{V}$. Due to $\theta _2(\epsilon )$ is monotonically increasing, we choose

  $$\begin{aligned} \epsilon _0=0 \end{aligned}$$

  (47)

  to get the optimal settling-time for this situation.

• (d). If $\check{V} <\nabla$ and $\zeta =1$, we can get

  $$\begin{aligned} \epsilon _0=1-\Theta \frac{\eta -1}{\Upsilon }. \end{aligned}$$

  (48)

  Taking $\epsilon _0$ into $\theta (\epsilon )$, we can get the optimal settling-time T for this situation.

• (e). If $\check{V} <\nabla$ and $\zeta \ne 1$, we can get

  $$\begin{aligned} \epsilon _0=1-\frac{(1-\hat{a})\Theta \ln {\zeta }}{\Upsilon +\Theta \ln {\zeta }}. \end{aligned}$$

  (49)

  Then, $T=\theta (\epsilon _0)$ is the solution of optimization problem for this situation.

4 Numerical Examples

In this section, three numerical examples are given to demonstrate the theoretical results.

Example 1

Suppose the parameters in INNs (2) are chosen as

$$\begin{aligned} R=\begin{pmatrix} 2&{}0&{}0\\ 0&{}2&{}0\\ 0&{}0&{}2 \end{pmatrix}, \, C=\begin{pmatrix} 0.5&{}0&{}0\\ 0&{}0.5&{}0\\ 0&{}0&{}0.5 \end{pmatrix}, \, D=\begin{pmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{pmatrix}, \, A=\begin{pmatrix} 0.3&{}0.15&{}0.4\\ 0.5&{}0.4&{}0.1\\ 0.4&{}0.3&{}0.2 \end{pmatrix}, \end{aligned}$$

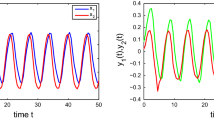
$H=(10,5,-11)^{\textsf{T}}$ and $f(x)=sinx$. The equilibrium point is $(\omega _0, \varsigma _0)^{\textsf{T}}=(5.04523, 2.4$ $2879, -5.5 2197, 10.09046, 4.85758, -11.04394)^{\textsf{T}}$ by simple computation. Figure 1a shows the evolution of the error states of the system (2) without the controller.

Fig. 1

The trajectories of INNs (2) in Examples 1 and 2, without the controllers

We can obsever that the system without the controller takes more than 8s to achieve FTS. Taking the controller (30) into consideration. Suppose the delay sequence and the impulsive sequence satisfy Definition 1 and Assumption 2, respectively, where $\tilde{\tau }=0.1$, $\tau ^*=0.001$, $\underline{\tau }=0.04$, $\overline{\tau }=0.05$. Set the parameters of the controllers as $k_{11}=k_{21}=k_{31}=3$, $k_{12}=k_{22}=k_{32}=4$, $\xi _{11}=\xi _{21}=\xi _{31}=4$, $\xi _{12}=\xi _{22}=\xi _{32}=3$, $\mu _1=\mu _2=\mu _3=-0.5$, $u=1$, $v=5$, $\eta =0.6$, which indicate that $\zeta =0.6397$ and $\zeta ^*=0.65$. We set the initial time $t_0=0$, the initial value $w(t)=(w_1(t), \, w_2(t), \, w_3(t))^{\textsf{T}}=(3,7,10)^{\textsf{T}}$, $e(t)=(e_1(t), \, e_2(t), \, e_3(t))^{\textsf{T}}=(6,14,20)^{\textsf{T}}$ and $\epsilon =0.8$.

By simple calculation, in this simulations, we can get $V(t_0)=786.8139$, which imply that $V(t_0) \>(\frac{\lambda }{\kappa })^{\frac{2v}{v-u}}=0.0271$. Notice that $\zeta<\zeta ^* <1$. Accroding to Theorem 1, the INNs (2) can realize GFTS and the settling-time is $T=1.5529s$, based on (38), where the number of occurrence impulses $k_0$ is 7. Figure 2a, b display the state and error trajectories of system (2) with controller (30), respectively. By comparing Figs. 1a and 2b, it can be seen that the time to achieve stability is significantly reduced after adding the controller (30). This demonstrates that the controller (30) can promote stability. Additionally, it can be observed that the system reaches the equilibrium point at around 1.2s, indicating that our estimation of the settling-time is relatively accurate.

Fig. 2

The state and error trajectories of the INNs (2) in Example 1 with the controllers

By considering the optimization problem, we can determine that $\epsilon _0$ is equal to 0.4749 according to equation (45). The optimal settling-time T is 1.4013s and the number of occurrence impulses $k_0$ is 8. As shown in Fig. 5a, a smaller value of $\epsilon$ implies a higher frequency of impulses. In Fig. 2b, the last impulse occurs at $t=0.8s$, while the previous one occurs at $t=0.7s$. This indicates that the FTS of system (2) can be achieved faster by using the optimal $\epsilon _0$.

Example 2

In this example, consider an unstable INNs (2) with the parameters

$$\begin{aligned} R&=\begin{pmatrix} 0.501&{}0&{}0\\ 0&{}0.501&{}0\\ 0&{}0&{}0.501 \end{pmatrix}, \, C =\begin{pmatrix} -0.5&{}0&{}0\\ 0&{}-0.5&{}0\\ 0&{}0&{}-0.5 \end{pmatrix}, \\ \, D&=\begin{pmatrix} 0.5&{}0&{}0\\ 0&{}0.5&{}0\\ 0&{}0&{}0.5 \end{pmatrix}, \, A =\begin{pmatrix} 0.86&{}0.1&{}0.04\\ 0.2&{}-0.75&{}0.1\\ 0.1&{}0.8&{}-0.3 \end{pmatrix}, \end{aligned}$$

$H=(0,0,0)^{\textsf{T}}$ and $f(x)=sinx$. Figure 1b shows the evolution of the states of the system (2) without the controller.

Set the the delay sequence and the impulsive sequence satisfy Definition 1 and Assumption 2, respectively, where $\tilde{\tau }=0.1$, $\tau ^*=0.001$, $\underline{\tau }=0.03$ and $\overline{\tau }=0.05$. The parameters of the controllers are chosen as $k_{11}=k_{21}=k_{31}=5$, $k_{12}=k_{22}=k_{32}=5$, $\xi _{11}=\xi _{21}=\xi _{31}=2$, $\xi _{12}=\xi _{22}=\xi _{32}=3$, $\mu _1=\mu _2=\mu _3=-0.8$, $u=2$, $v=5$ and $\eta =0.45$, which indicate that $\zeta =0.4849$ and $\zeta ^*=0.5097$. Set $t_0=0$, $w(t)=(w_1(t), \, w_2(t), \, w_3(t))^{\textsf{T}}=(3,7,10)^{\textsf{T}}$, $e(t)=(e_1(t), \, e_2(t), \, e_3(t))^{\textsf{T}}=(1.503,3.507,5.01)^{\textsf{T}}$ and $\epsilon =0.2$ in this simulations.

In this example, our goal is to stabilize the system to the original point. We find that $V(t_0) \>(\frac{\lambda }{\kappa })^{\frac{2v}{v-u}}=0.0012$ and $\zeta<\zeta ^* <1$. According to Theorem 1, the INNs (2) can achieve GFTS with a settling-time of $T=1.5448s$, as determined by equation (38), where the number of occurrence impulses $k_0$ is 10. Figure 3a, b show the state and error trajectories of system (2) with controller (30), respectively. By comparing Figs. 1b and 3a, it can be seen that the addition of controller (30) stabilizes system (2). This demonstrates the effectiveness of controller (30) in promoting stability. Additionally, the system reaches the equilibrium point at around 1s, indicating that our estimation of the settling-time is relatively accurate. We also notice that the values of $\zeta$ and $\zeta ^*$ in this example are smaller than those in Example 1, indicating stronger control strength. As a result, even though the initial value is the same and the system is unstable, after adding controller (30), the INNs (2) can achieve finite-stability in a shorter settling-time and with fewer impulses compared to Example 1.

Fig. 3

The state and error trajectories of the INNs (2) in Example 2 with the controllers

According to Eq. (45), the optimal value for $\epsilon$ is 0.4936 when considering the optimization problem. The optimal settling-time is $T=1.3366s$ and the number of occurrence impulses $k_0$ is 8. Figure 4b shows that a larger value of $\epsilon$ results in a lower frequency of impulses. The last impulse occurs at $t=1s$, while in Fig. 3b it occurs at $t=0.8s$. Using the optimal value of $\epsilon _0$ results in a shorter estimated settling-time.

Example 3

In this example, we assume that the controlled strength is relatively weak, meaning $\zeta ^* \>1$. We also assume that the parameters of INNs (2) are the same as in Example 2, which results in an unstable system as shown in Fig. 1b. The delay sequence and impulsive sequence satisfy both Definition 1 and Assumption 2, where $\tilde{\tau }=0.25$, $\tau ^*=0.001$, $\underline{\tau }=0.2$, $\overline{\tau }=0.25$. The parameters of the controller are chosen as $k_{11}=k_{21}=k_{31}=6$, $k_{12}=k_{22}=k_{32}=30$, $\xi _{11}=\xi _{21}=\xi _{31}=6$, $\xi _{12}=\xi _{22}=\xi _{32}=30$, $\mu _1=\mu _2=\mu _3=-0.65$, $u=1$, $v=25$, $\eta =0.45$, which indicate that $\zeta =1.0753$ and $\zeta ^*=1.3769$. We set $t_0=0$, $w(t)=(w_1(t), \, w_2(t), \, w_3(t))^{\textsf{T}}=(0.6,0.8,1.15)^{\textsf{T}}$, $e(t)=(e_1(t), \, e_2(t), \, e_3(t))^{\textsf{T}}=(0.3006,0.4008,0.5752)^{\textsf{T}}$ and $\epsilon =0.06$ in the simulations.

In this example, the controlled strength is weaker than in Example 2, as indicated by $1<\zeta <\zeta ^*$. By calculation, we find that $0.7680=\frac{\lambda }{\kappa }<V^{\frac{v-u}{2v}}(t_0) <\rho ^*=1.1544$. According to Theorem 1, the INNs (2) can achieve LFTS with a settling-time of $T=3.0063s$. Figure 5a, b show the state and error trajectories of system (2) with controller (30), respectively. The system reaches the equilibrium point at around 2s, indicating that our estimated settling-time is relatively accurate. A comparison of Figs. 5b and 3b shows that a weaker control strength leads to a smaller range of initial values and a longer settling-time.

Fig. 4

The error trajectories of the INNs (2) in Examples 1 and 2 under optimized parameter $\epsilon _0$

Fig. 5

The state and error trajectories of the INNs (2) in Example 3 with the controllers

5 Conclusion

In this paper, we investigated the FTS of INNs with delayed impulses. Through designing new hybrid controllers, we proposed a useful FTS criterion for impulsive nonlinear dynamical systems. Unlike previous works, our criterion takes into account delayed impulses and can achieve GFTS. We then applied these results to INNs to obtain GFTS and LFTS criteria, respectively. Additionally, we estimated the settling-time by choosing optimized parameters. Numerical examples were provided to verify the correctness of our theoretical results.

Some possible directions for future work are as follows. One is to consider the INNs with delay, that is the inertial delayed neural networks (IDNNs), which may have more complex dynamics and stability properties. Another is to relax the restriction of impulsive and delay interval, and allow them to vary randomly or dependently. A third one is to add more complex and even destabilizing impulses, and study how they affect the synchronization of the INNs.