Skip to main content
SpringerLink
Log in

Integral Sliding Mode Exponential Synchronization of Inertial Memristive Neural Networks with Time Varying Delays

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

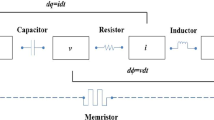
In this article, the exponential synchronization issue for inertial memristive neural networks (IMNNs) with time varying delays is addressed. A new synchronous lemma, Lemma 1, has been obtained through some inequality techniques. Also, inspired by sliding mode control method, a new integral sliding mode control law with mode-dependent integral terms is designed to solve the IMNNs synchronization problem. By using these new lemma and integral sliding mode controller, two theorems of exponential synchronization are proposed and some novel synchronization criteria are given. Finally, numerical examples corresponding to Theorems 1 and 2 respectively are given to show the validity, and the merit of the proposed controller is provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Song Q, Yan H, Zhao Z, Liu Y (2016) Global exponential stability of impulsive complex-valued neural networks with both asynchronous time-varying and continuously distributed delays. Neural Netw 81:1–10

    MATH  Google Scholar 

  2. Song Q, Zhao Z (2015) Impulsive effects on stability of discrete-time complex-valued neural networks with both discrete and distributed time-varying delays. Neurocomputing 168(C):1044–1050

    Google Scholar 

  3. Yang X, Feng Z, Feng J, Cao J (2017) Synchronization of discrete-time neural networks with delays and markov jump topologies based on tracker information. Neural Netw 85(C):157–164

    MATH  Google Scholar 

  4. Song Q, Shu H, Zhao Z, Liu Y, Alsaadi FE (2017) Lagrange stability analysis for complex-valued neural networks with leakage delay and mixed time-varying delays. Neurocomputing 244(JUN.28):33–41

    Google Scholar 

  5. Song Q, Yu Q, Zhao Z, Liu Y, Alsaadi FE (2017) Dynamics of complex-valued neural networks with variable coefficients and proportional delays. Neurocomputing, 0925231217318003

  6. Alimi AM, Aouiti C, Assali EA (2019) Finite-time and fixed-time synchronization of a class of inertial neural networks with multi-proportional delays and its application to secure communication. Neurocomputing 332(MAR.7):29–43

    Google Scholar 

  7. Babcock KL, Westervelt RM (1986) Stability and dynamics of simple electronic neural networks with added inertia. Phys D: Nonlinear Phenomena 23(1):464–469

    Google Scholar 

  8. Angelaki DE, Correia MJ (1991) Models of membrane resonance in pigeon semicircular canal type ii hair cells. Biol Cybernet 65(1):1–10

    Google Scholar 

  9. Mauro A (1970) Subthreshold behavior and phenomenological impedance of the squid giant axon. J Gen Phys 55(4):497–523

    Google Scholar 

  10. Huang D, Jiang M, Jian J (2017) Finite-time synchronization of inertial memristive neural networks with time-varying delays via sampled-date control. Neurocomputing 266:527–539

    Google Scholar 

  11. Zhang R, Zeng D, Park JH, Liu Y, Zhong S (2018) Quantized sampled-data control for synchronization of inertial neural networks with heterogeneous time-varying delays. IEEE Trans Neural Netw Learn Syst 29:6385–6395

    MathSciNet  Google Scholar 

  12. Feng Y, Xiong X, Tang R, Yang X (2018) Exponential synchronization of inertial neural networks with mixed delays via quantized pinning control. Neurocomputing 310:165–171

    Google Scholar 

  13. Cao J, Wan Y (2014) Matrix measure strategies for stability and synchronization of inertial bam neural network with time delays. Neural Netw Official J Int Neural Netw Soc 53:165–172

    MATH  Google Scholar 

  14. Rakkiyappan R, Premalatha S, Chandrasekar A, Cao J (2016) Stability and synchronization analysis of inertial memristive neural networks with time delays. Cogn Neurodynamics 10(5):437–451

    Google Scholar 

  15. Prakash M, Balasubramaniam P, Lakshmanan S (2016) Synchronization of markovian jumping inertial neural networks and its applications in image encryption. Neural Netw 83:86–93

    Google Scholar 

  16. Li X, Li X, Hu C (2017) Some new results on stability and synchronization for delayed inertial neural networks based on non-reduced order method. Neural Netw Official J Int Neural Netw Soc 96:91–100

    MATH  Google Scholar 

  17. Chen C, Li L, Peng H, Yang Y (2018) Fixed-time synchronization of inertial memristor-based neural networks with discrete delay. Neural Netw 109:81–89

    MATH  Google Scholar 

  18. Zhang Z, Cao J (2018) Novel finite-time synchronization criteria for inertial neural networks with time delays via integral inequality method. IEEE Trans Neural Netw Learn Syst 30(5):1476–1485

    MathSciNet  Google Scholar 

  19. Lh A, Sz A, Ks B, Xz A (2020) Further results on finite-time synchronization of delayed inertial memristive neural networks via a novel analysis method - sciencedirect. Neural Netw 127:47–57

    Google Scholar 

  20. Li N, Zheng W (2018) Synchronization criteria for inertial memristor-based neural networks with linear coupling. Neural Netw: Official J Int Neural Netw Soc 106:260–270

    MATH  Google Scholar 

  21. Wei R, Cao J, Alsaedi A (2018) Finite-time and fixed-time synchronization analysis of inertial memristive neural networks with time-varying delays. Cogn Neurodynamics 12(1):121–134

    Google Scholar 

  22. Xu C, Zhang Q (2015) Existence and global exponential stability of anti-periodic solutions for bam neural networks with inertial term and delay. Neurocomputing 153(apr.4):108–116

    Google Scholar 

  23. Xavier GT, Gomez Castaneda F, Flores Nava LM, Moreno Cadenas JA (2017) Memristive recurrent neural network. Neurocomputing 273(jan.17):281–295

    Google Scholar 

  24. Zhang W, Yang S, Li C, Zhang W, Yang X (2018) Stochastic exponential synchronization of memristive neural networks with time-varying delays via quantized control. Neural Netw 104:93–103

    MATH  Google Scholar 

  25. Cai Z, Huang L (2017) Finite-time stabilization of delayed memristive neural networks: Discontinuous state-feedback and adaptive control approach. IEEE Trans Neural Netw Learn Syst 29(4):856–868

    Google Scholar 

  26. Hu C, He H, Jiang H (2022) Edge-based adaptive distributed method for synchronization of intermittently coupled spatiotemporal networks. IEEE Trans Automat Control 67(5):2597–2604

    MathSciNet  MATH  Google Scholar 

  27. Hu C, Jiang H (2022) Special functions-based fixed-time estimation and stabilization for dynamic systems. IEEE Trans Syst, Man, Cybernet: Syst 52(5):3251–3262

    Google Scholar 

  28. Steur E, Tyukin I, Nijmeijer H (2009) Semi-passivity and synchronization of diffusively coupled neuronal oscillators. Phys D: Nonlinear Phenomena 238(21):2119–2128

    MathSciNet  MATH  Google Scholar 

  29. Gray CM (1994) Synchronous oscillations in neuronal systems: Mechanisms and functions. J Comput Neurosci 1(1–2):11–38

    Google Scholar 

  30. Wang J, Feng J, Chen X, Yi Z (2013) Exponential synchronization of stochastic perturbed complex networks with time-varying delays via periodically intermittent pinning. Commun Nonlinear Sci Numer Simul 18(11):3146–3157

    MathSciNet  MATH  Google Scholar 

  31. Huang C, Cao J (2018) Impact of leakage delay on bifurcation in high-order fractional bam neural networks. Neural Netw 98:223–235

    MATH  Google Scholar 

  32. Wu G, Baleanu D, Zeng S (2018) Finite-time stability of discrete fractional delay systems: Gronwall inequality and stability criterion. Commun Nonlinear Sci Numer Simul 57:299–308

    MathSciNet  MATH  Google Scholar 

  33. Edwards C, Spurgeon SK (1998) Sliding mode control: Theory and applications. Crc Press, Boca Raton

    MATH  Google Scholar 

  34. Hu J, Zhang P, Kao Y, Liu H, Chen D (2019) Sliding mode control for markovian jump repeated scalar nonlinear systems with packet dropouts: The uncertain occurrence probabilities case. Appl Math Comput 362:124574

    MathSciNet  MATH  Google Scholar 

  35. Xu J, Zhang D (2010) Projective synchronization of different chaotic time-delayed neural networks based on integral sliding mode controller. Appl Math Comput 217(1):164–174

    MathSciNet  MATH  Google Scholar 

  36. Shi Y, Zhu P, Ke Q (2014) Projective synchronization of different chaotic neural networks with mixed time delays based on an integral sliding mode controller. Neurocomputing 123:443–449

    Google Scholar 

  37. Gan Q, Rui X, Yang P (2012) Synchronization of non-identical chaotic delayed fuzzy cellular neural networks based on sliding mode control. Commun Nonlinear Sci Numer Simul 17(1):433–443

    MathSciNet  MATH  Google Scholar 

  38. Wu H, Wang L, Niu P, Wang Y (2017) Global projective synchronization in finite time of nonidentical fractional-order neural networks based on sliding mode control strategy. Neurocomputing 235(APR.26):264–273

    Google Scholar 

  39. Huang H, Feng G (2009) Synchronization of nonidentical chaotic neural networks with time delays. Neural Netw 22(7):869–874

    MATH  Google Scholar 

  40. Zhang D, Xu J (2010) Projective synchronization of different chaotic time-delayed neural networks based on integral sliding mode controller. Appl Math Comput 217(1):164–174

    MathSciNet  MATH  Google Scholar 

  41. Gan Q, Xu R, Yang P (2012) Synchronization of non-identical chaotic delayed fuzzy cellular neural networks based on sliding mode control. Commun Nonlinear Sci Numer Simul 17(1):433–443

    MathSciNet  MATH  Google Scholar 

  42. Shi Y, Zhu P, Qin K (2014) Projective synchronization of different chaotic neural networks with mixed time delays based on an integral sliding mode controller. Neurocomputing 123:443–449 (Contains Special issue articles: Advances in Pattern Recognition Applications and Methods)

    Google Scholar 

  43. Xiong J, Zhang G, Wang J, Yan T (2020) Improved sliding mode control for finite-time synchronization of nonidentical delayed recurrent neural networks. IEEE Trans Neural Netw Learn Syst 31(6):2209–2216. https://doi.org/10.1109/TNNLS.2019.2927249

    Article  MathSciNet  Google Scholar 

  44. Xiao J, Zeng Z, Wu A, Wen S (2020) Fixed-time synchronization of delayed cohen-grossberg neural networks based on a novel sliding mode. Neural Netw 128:1–12

    MATH  Google Scholar 

  45. Song X, Man J, Song S, Lu J (2020) Integral sliding mode synchronization control for markovian jump inertial memristive neural networks with reaction-diffusion terms. Neurocomputing 378:324–334

    Google Scholar 

  46. Yang S, Yu J, Hu C, Jiang H (2018) Quasi-projective synchronization of fractional-order complex-valued recurrent neural networks. Neural Netw 104:104–113

    MATH  Google Scholar 

  47. Du F, Lu JG (2021) New criterion for finite-time synchronization of fractional order memristor-based neural networks with time delay. Appl Math Comput 389:125616

    MathSciNet  MATH  Google Scholar 

  48. Guo Z, Gong S, Huang T (2018) Finite-time synchronization of inertial memristive neural networks with time delay via delay-dependent control. Neurocomputing 293(JUN.7):100–107

    Google Scholar 

Download references

Funding

This work was supported in partial by the Natural Science Foundation of Shaanxi Province(2020JM-256), Technology Innovation Leading Program of Shaanxi(No.2020QFY03-01) and in part by in part by the Technology Program of Weinan (No. ZDYF-GYCX-81).

Author information

Author notes

  1. Jiefei Yan contributed equally to this work.

Authors and Affiliations

  1. School of Electronic and Control, Chang’an University, Xi’an, 710064, ShaanXi, China

    Meng Hui & Jiefei Yan

Authors
  1. Meng Hui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiefei Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiefei Yan.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hui, M., Yan, J. Integral Sliding Mode Exponential Synchronization of Inertial Memristive Neural Networks with Time Varying Delays. Neural Process Lett 55, 2725–2742 (2023). https://doi.org/10.1007/s11063-022-10981-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-10981-9

Keywords

Search

Navigation