1 Introduction

Redundant manipulators have been widely applied in numerous industry and service scenarios, and heavy labor burdens on operating personnel have been massively pared down. Through taking advantaging of extra degrees of freedom (DOFs) from joint space, fast, flexible and accurate manipulation tasks in Cartesian space can be favorably fulfilled by redundant manipulators during long-term dull and repetitive operations [1, 2].

Before achieving desirable motion control of end-effectors in workspace for redundant manipulators [3], the suitable kinematic control action in joint space is necessary to seek to eventually generate the desired motion. However, as one may know, forward kinematics modeling for redundant manipulators always presents strong coupled nonlinear equations. To find the general analytical inverse kinematic control solutions for redundant manipulators might be impossible, and it still increases considerable computational burdens for conventional numerical methods for getting inverse kinematic control references in joint space. A traditional way of finding the inverse kinematic solutions is to solve pseudoinverse of the Jacobian matrix of a manipulator [4, 5], but it may neglect additional and prerequisite constraints to reflect reasonable performance indices and motion limits.

In order to enhance redundancy resolution with appendant constraints for redundancy manipulators, Optimization-based methods have been proposed and investigated to solve for inverse kinematic resolutions. Such optimization-based methods can involve different levels of physical constraints or other types of constraints, but general analytical solutions for constrained-optimization paradigms are even more difficult to obtain. Numerical methods in a serial-processing manner may be an alternative, but they still suffer from dissatisfactory computational efficiency. In a parallel way of processing in computation, dynamic recurrent neural networks have been developed for redundancy resolution and kinematic control with physical constraints [6,7,8,9,10,11,12], mainly including joint angle limits, joint angular velocity limits and joint angular acceleration limits. In [13], redundancy resolution of manipulators with the joint velocity constraints is solved by a passivity-based approach from an energy perspective. In [14], a repetitive motion planning strategy of manipulator with joint acceleration constraints was designed. In [15], a minimum-acceleration-norm as the optimization objective is proposed for obstacle avoidance of manipulators in the joint-acceleration level. In [16], both velocity-level and acceleration-level constraints are integrated into the redundant resolution of manipulators. In [17], a unified quadratic-programming for joint torque optimization is established by combining the velocity-level and acceleration-level redundancy resolution. In [18], a novel redundancy resolution method is proposed to deal with the joint-drift-free problem with tracking error theoretically eliminated. In [19], an orthogonal projection-based method is proposed for repetitive motion control of manipulators. All of these redundancy resolutions with physical constraints in joints based on constrained-optimization paradigms have received great success, and the computational efficiency of recurrent neural networks was demonstrated.

When redundant manipulators encounter some specific operations such as minimally invasive surgery into the subject’s body through small incisions and industrial implanting with sensors for detecting cracks, they have to satisfy some special constraints like remote center of motion constraints. Remote center of motion (RCM) is a remote fixed point with no physical revolute joint around the location [20]. A RCM usually leaves a sole point for the manipulator performs positioning or/and insertion [21,22,23]. Such applications need to impose additional constraints in joint space to guarantee safe motion generation of the end-effector of the manipulator. Conventional pseudo-inverse based methods may neglect the necessary constraints in the RCM case, which makes it difficult to get the solutions. To remedy this, Su et al. proposed an improved and efficient recurrent neural network for RCM control of manipulators with constrained optimization [24]. Motivated by the aforementioned points, in this paper, we are making breakthroughs to propose a new model-based method based on RNN for redundancy resolution of manipulators with RCM constraints. The contributions of this work are summarized as follows:

  1. (1)

    The proposed RNN for manipulator control with RCM constraints is with a concise and novel neural-network architecture and can get rid of unnecessary modeling and computation, as compared with the conventional zeroing dynamics (ZD) based solvers.

  2. (2)

    Simulation results a 7-DoF redundant manipulator synthesized by the proposed RNN demonstrate the efficiency of the proposed method in kinematic control of manipulators with RCM constraints for different end-effector path tracking tasks.

2 Preliminaries

RCM means a remote static/fixed point near the workspace with no physical revolute joint around the location [21, 22]. In order to achieve manipulation such as minimally invasive surgery into the subject’s body through small incisions or industrial implanting with sensors for detecting cracks, RCM usually leaves a sole point for the manipulator performs positioning or/and insertion. In addition to the joint physical constraints, RCM imposes an additional constraint on the motion planning and control of redundant manipulator.

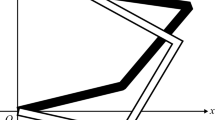
Let us consider a n-link manipulator with its end-effector’s position is remote from the objective RCM position \(r_P\) which is shown in Fig. 1, the redundant manipulator executes its task control operations between the two end points \(r_A\) and \(r_B\) in the workspace. Point \(r_A\) is the distal point of the end-effector, point \(r_B\) is the distal point of the \(n-1\) link. The end-effector of the redundant manipulator has to travel through the objective point \(r_P\) along the line/curve between point \(r_A\) and point \(r_B\). To describe the motion relation between joints and end-effector, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{r}_A=J_1{\dot{\theta }}\\ \dot{r}_B=J_2{\dot{\theta }} \end{array} \right. \end{aligned}$$
(1)

where \(r_A\in R^{m}\) and \(r_B\in R^{m}\) denotes the position vector of the end-effector and the position vector of the end-point of the \(n-1\)th link of the manipulator respectively, \(J_1\in R^{m\times n}\) and \(J_2\in R^{m\times n}\) respectively denotes the Jacobian matrix of the whole manipulator and the Jacobian matrix of the associated \(n-1\) link, and \(\theta \in R^{n}\) denotes the joint angle of the manipulator.

Fig. 1
figure 1

RCM constraint for a redundant manipulator during motion planning and control

Full size image

In Fig. 1, \(r_P\) denotes the position vector of the RCM point P, and it can be within the line \(A-B\) and the corresponding relation among \(r_P\), \(r_A\) and \(r_B\) is depicted by

$$\begin{aligned} r_P-r_B=k(r_A-r_B) \end{aligned}$$
(2)

where \(k\in R\) is a scaling parameter to locate the position \(r_P\) with the RCM constraint. When \(k=0\) is configured, then \(r_P=r_B\); when \(k=1\) is configured, then \(r_P=r_A\); when \(0<k<1\), \(r_P\) is strictly between points \(r_A\) and \(r_B\). The redundancy resolution for kinematic control of the manipulator needs to finish the two tasks, 1) let the end-effector track the desired path accurately; and 2) satisfy the RCM constraint to make \(r_P\) vary in a very small range or almost static during motion planning and control. In an application scenario, the last link (e.g., \(r_A-r_B\)) of the manipulator can penetrate a small hole (e.g., \(r_P\)) and simultaneously make the end-effector (e.g., \(r_A\)) perform the path tracking task.

3 Problem Formulation

As the RCM constraint makes point \(r_P\) is between \(r_A\) and \(r_B\), \(r_P\) can be depicted by the equation \(r_p-r_B=k(r_A-r_B)\). Since \(r_A\) and \(r_B\) are obtained through the forward kinematics with resolved joint angles \(\theta \), thus the state variable pair \((\theta , k)\) can describe the redundancy resolution of the manipulator with RCM constraints. By differentiating the both sides of equation \(r_p-r_B=k(r_A-r_B)\) which depicts the RCM constraint, one can obtain

$$\begin{aligned} \dot{r}_P-\dot{r}_B=\dot{k}(r_A-r_B)+k(\dot{r}_A-\dot{r}_B) \end{aligned}$$
(3)

When combining it with the aforementioned Eq. (1), one can further have

$$\begin{aligned} \dot{r}_P-J_2\dot{\theta }=\dot{k}(r_A-r_B)+k(J_1-J_2)\dot{\theta } \end{aligned}$$
(4)

As the position of RCM point \(r_P\) can be described by the following linear combination between \(r_A\) and \(r_B\)

$$\begin{aligned} r_P=k(r_A-r_B)+r_B \end{aligned}$$
(5)

Combining the aforementioned equations, then we have

$$\begin{aligned} \dot{k}(r_A-r_B)+kJ_1\dot{\theta }+(1-k)J_2\dot{\theta }+\dot{r}_P=0 \end{aligned}$$
(6)

i.e.,

$$\begin{aligned} \begin{aligned} \dot{k}(r_A-r_B)+[kJ_1+(1-k)J_2]\dot{\theta }+\dot{r}_P=0 \end{aligned} \end{aligned}$$
(7)

where we can call the equality above as the RCM constraint for redundancy resolution.

Based on the derivations and discussions above, we propose the quadratic programming formulation for redundancy resolution of manipulators with RCM constraints as follows

$$\begin{aligned} \begin{aligned}&\arg \min _{\theta ,k}~~\dot{\theta }^T\dot{\theta }/2+c_2\dot{k}^2/2\\&\text {s.t.}\left\{ \begin{array}{ll} \dot{k}(r_A-r_B)+[kJ_1+(1-k)J_2]\dot{\theta }+\dot{r}_P=0\\ J_1\dot{\theta }+c_3(r_A-r_d)-\dot{r}_d=0 \end{array} \right. \end{aligned} \end{aligned}$$
(8)

where \(c_2>0\) and \(c_3>0\) denote the scaling parameters for the objective function and the last equality constraint respectively. In order to satisfy RCM constraints during redundancy resolution for kinematic control, the time-derivative \(\dot{r}_P\) of \(r_P\) should follow some rules to make \(r_P\) converge to a constant position value.

As the point \(r_P\) should not hold static as much as possible to sanctify the RCM constraint, then the time derivative of \(r_P\) can be concisely depicted by

$$\begin{aligned} \dot{r}_P=-c_1(r_P-r_P(0)) \end{aligned}$$
(9)

to make the RCM point \(r_P\) converge to a fixed position \(r_P(0)\), where \(c_1\ge 0\) is used to scale the convergence of \(r_P\) which shows how the corresponding RCM constraint’s dynamic response changes.

In the proposed optimization formulation for redundancy resolution with RCM constraints, the position of \(r_P\) is dynamically adjusted by parameter k with simultaneous positions \(r_A\) and \(r_B\). The initial value k(0) is chosen according to the specific scenarios for safe manipulation, e.g., when \(t=0\), \(r_P\) can be chosen in the middle of the line \(A-B\), and thus \(k(0)=0.5\). To maintain the RCM constraint, \({\dot{\theta }}\) and \(\dot{k}\) are used as decision variables, and the variable which really controls the manipulator is \(\dot{\theta }\) as the control input action. In practice, we can therefore solve \(\dot{k}\) and substitute it into the aforementioned proposed optimization formulation and thus the RCM constraint can be satisfied and modulated by resolving the joint angle variable \(\theta \).

4 Simplified RNN for Redundancy Resolution with RCM Constraints

In this section, the modeling and theoretical analysis of the proposed SIMPLIFIED RNN for redundancy resolution with RCM constraints are addressed.

4.1 Optimization Paradigm

In order to deal with the RCM constrained redundancy resolution issue, in this work, Lagrange function which is simultaneously associated with the kinematic objective function and the RCM constraint is defined as follows

$$\begin{aligned} \begin{aligned} L=&\dot{\theta }^T\dot{\theta }/2+c_2\dot{k}^2/2+\lambda _1^T[\dot{k}(r_A-r_B)+kJ_1\dot{\theta }+(1-k)J_2\dot{\theta }\\&+c_1(r_P-r_P(0))]+\lambda _2^T[J_1{\dot{\theta }}+c_3(r_A-r_d)-\dot{r}_d] \end{aligned} \end{aligned}$$
(10)

where \(\lambda _1\) and \(\lambda _2\) denote the Lagrange multiplier vectors. The partial derivatives of the Lagrange function with respect to the unknown variables \(({\dot{\theta }},\dot{k},\lambda _1,\lambda _2)\) are

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial L}{\partial {\dot{\theta }}}={\dot{\theta }}+[kJ_1+(1-k)J_2]^T\lambda _{1}+J_1^T\lambda _2\\ \frac{\partial L}{\partial \dot{k}}=c_2\dot{k}+ \lambda _{1}^T(r_A-r_B)\\ \frac{\partial L}{\partial \lambda _{1}}=(kJ_1+(1-k)J_2)\dot{\theta }+\dot{k}(r_A-r_B)\\ ~~~~~~~+c_1(r_P-r_P(0))\\ \frac{\partial L}{\partial \lambda _{2}}=J_1{\dot{\theta }}+c_3(r_A-r_d)-\dot{r}_d \end{array} \right. \end{aligned}$$
(11)

According to the Karush-Kuhn-Tucker (KKT) conditions [25] , the optimization above can be solved by force the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial L}{\partial {\dot{\theta }}}=0\\ \frac{\partial L}{\partial \dot{k}}=0\\ \frac{\partial L}{\partial \lambda _{1}}=0\\ \frac{\partial L}{\partial \lambda _{2}}=0 \end{array} \right. \end{aligned}$$
(12)

to be zero and obtain the desired solution \(({\dot{\theta }}^*,\dot{k}^*,\lambda _1^*,\lambda _2^*)\) for satisfying the optimization objective and constraints.

4.2 Original ZD-based RNN Method

In order to solve such optimization paradigm which reflects the redundancy resolution with RCM constraints, according to the general design principle of the ZD-based RNN model to make the aforementioned partial derivatives of the Lagrange function being 0, we thus need to construct the following error-monitoring function

$$\begin{aligned} \begin{aligned} \Xi&=\begin{bmatrix} {\dot{\theta }}+[kJ_1+(1-k)J_2]^T\lambda _{1}+J_1^T\lambda _2\\ c_2\dot{k}+ \lambda _{1}^T(r_A-r_B)\\ (kJ_1+(1-k)J_2)\dot{\theta }+\dot{k}(r_A-r_B)+c_1(r_P-r_P(0))\\ J_1{\dot{\theta }}+c_3(r_A-r_d)-\dot{r}_d \end{bmatrix}\\&=AZ+B \end{aligned} \end{aligned}$$
(13)

where

$$\begin{aligned} A= & {} \begin{bmatrix} I_{n\times n} &{} 0_{n\times 1} &{} kJ_1^T+(1-k)J_2^T &{} J_1^T\\ 0 &{} c_2 &{} r_A^T-r_B^T &{} 0_{1\times m} \\ kJ_1+(1-k)J_2 &{} r_A-r_B &{} 0 &{} 0 \\ J_1 &{} 0_{m\times 1} &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$
(14)
$$\begin{aligned} Z= & {} \begin{bmatrix} {\dot{\theta }}\\ \dot{k}\\ \lambda _1\\ \lambda _2 \end{bmatrix}~~\text {and}~~B=\begin{bmatrix} 0_{n\times 1}\\ 0\\ 0_{m\times 1}\\ c_3(r_A-r_d)-\dot{r}_d \end{bmatrix} \end{aligned}$$
(15)

Our goal of applying ZD-based method is to force \(\varXi =0\) eventually and thus the resultant optimal solution of Z can be got.

Based on the design discipline of the ZD method, we have the following error-processing formula for redundancy resolution of manipulator with RCM constraints

$$\begin{aligned} \dot{\varXi }=-\gamma \varPsi (\varXi ) \end{aligned}$$
(16)

where the convergence scaling parameters can be configured as \(\gamma >0\) for unity, \(\varPsi (\cdot ):R^{(n+7)\times (n+7)}\rightarrow R^{(n+7)\times (n+7)}\) denotes the general nonlinear activation function array with its entries being monotonously-increasing odd functions. Therefore, we would have the following ZD-based neural network model for redundancy resolution of manipulator with RCM constraints

$$\begin{aligned} \dot{A}Z+A\dot{Z}+\dot{B}=-\gamma \varPsi (AZ+B) \end{aligned}$$
(17)

Due to existence of time derivative of coefficient matrix A in the system equation above, such ZD model needs to obtain the time-derivatives of Jacobian matrices analytically during its solution to update the model states,i.e., the coefficient matrix \(\dot{A}\) that is consisted of Jacobian matrices \(\dot{J}_1\) and \(\dot{J}_2\). However, the analytical time-derivative expressions of these Jacobian matrices can be rather tough, i.e., the time-derivatives should be obtained as follows

$$\begin{aligned} \dot{J}_1=\frac{\partial J_1}{\partial \theta _1}\dot{\theta }_1+\frac{\partial J_1}{\partial \theta _2}\dot{\theta }_2+\cdots +\frac{\partial J_1}{\partial \theta _n}\dot{\theta }_n \end{aligned}$$
(18)

and

$$\begin{aligned} \dot{J}_2=\frac{\partial J_2}{\partial \theta _1}\dot{\theta }_1+\frac{\partial J_2}{\partial \theta _2}\dot{\theta }_2+\cdots +\frac{\partial J_2}{\partial \theta _n}\dot{\theta }_n \end{aligned}$$
(19)

which makes \(\dot{A}\) rather complicated to compute. Moreover, if the Jacobian matrices \(J_1\) and \(J_2\) become rank-deficient, the coefficient matrices A and \(\dot{A}\) may become singular. In this situation, the resultant ZD-based model for redundancy resolution of manipulator with RCM constraints can fail to converge. Therefore, avoidance of finding the time-derivatives of Jacobian matrices and encountering unexpected singularity is essentially required for the aforementioned ZD-based model.

4.3 Proposed Simplified RNN

In this work, we propose the a new simplified RNN method for redundancy resolution of manipulator with RCM constraints. From the first two equations of the partial derivatives equations of the Lagrange function L, we can get

$$\begin{aligned} \begin{aligned}&{\dot{\theta }}=-[kJ_1+(1-k)J_2]^T\lambda _{1}-J_1^T\lambda _2\\&\dot{k}=-\frac{1}{c_2}\lambda _{1}^T(r_A-r_B) \end{aligned} \end{aligned}$$
(20)

Substitute these two equations above to the other constraints, we have

$$\begin{aligned} \begin{aligned}&-[kJ_1+(1-k)J_2][kJ_1+(1-k)J_2]^T\lambda _1-[kJ_1\\ {}&+(1-k)J_2]J_1^T\lambda _2-\frac{1}{c_1}\lambda _1^T(r_A-r_B)(r_A-r_B)\\&+c_1(r_P-r_P(0))=0 \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} -J_1[kJ_1+(1-k)J_2]^T\lambda _1-J_1J_1^T\lambda _2+c_3(r_A-r_d)-\dot{r}_d=0 \end{aligned}$$
(22)

Defining the coefficient matrix \(W=kJ_1+(1-k)J_2\), therefore the aforementioned two equations can be rewritten as

$$\begin{aligned} \begin{aligned}&WW^T\lambda _1+WJ_1^T\lambda _2+\frac{1}{c_1}\lambda _1^T(r_A-r_B)(r_A-r_B)\\&-c_1(r_P-r_P(0))=0 \end{aligned} \end{aligned}$$
(23)

and

$$\begin{aligned} -J_1W^T\lambda _1-J_1J_1^T\lambda _2+c_3(r_A-r_d)-\dot{r}_d=0 \end{aligned}$$
(24)

Therefore, we can reformulate the equations above to get

$$\begin{aligned} M\varLambda =H \end{aligned}$$
(25)

where

$$\begin{aligned} M= & {} \begin{bmatrix} WW^T+\frac{1}{c_1}(r_A-r_B)(r_A-r_B)^T &{} WJ_1^T\\ J_1W^T &{} J_1J_1^T \end{bmatrix}, \end{aligned}$$
(26)
$$\begin{aligned} \varLambda= & {} \begin{bmatrix} \lambda _1\\ \lambda _2 \end{bmatrix},~~\text {and}~~ H=\begin{bmatrix} c_1(r_P-r_P(0))\\ c_3(r_A-r_d)-\dot{r}_d \end{bmatrix} \end{aligned}$$
(27)

In this work, we propose the following general nonlinear ZD-based model for getting the optimal solution of the simplified RNN

$$\begin{aligned} M\varLambda ={\mathcal {F}}(H) \end{aligned}$$
(28)

where

$$\begin{aligned} {\mathcal {F}}(H)=\begin{bmatrix} c_1\psi (r_P-r_P(0))\\ c_3\psi (r_A-r_d)-\dot{r}_d \end{bmatrix} \end{aligned}$$
(29)

and \(\psi (\cdot )\) is a nonlinear activation function array with its entries being monotonously-increasing odd functions. Correspondingly, we have the following theoretical results.

Theorem 1

Given an initial condition k(0) and \(\theta (0)\), there exists an unique solution \(\varLambda ^*\) for linear Eq. (25), provided that the Jacobian matrices \(J_1\) and \(J_2\) are full-rank.

Proof

As the coefficient matrix

$$\begin{aligned} M=\begin{bmatrix} WW^T+\frac{1}{c_1}(r_A-r_B)(r_A-r_B)^T &{} WJ_1^T\\ J_1W^T &{} J_1J_1^T \end{bmatrix} \end{aligned}$$
(30)

can be rewritten as

$$\begin{aligned} M=\begin{bmatrix} W\\ J_1 \end{bmatrix} \begin{bmatrix} W\\ J_1 \end{bmatrix}^T+\frac{1}{c_2}\begin{bmatrix}r_A-r_B\\ 0_{m\times 1}\end{bmatrix}\begin{bmatrix}r_A-r_B\\ 0_{m\times 1}\end{bmatrix}^T \end{aligned}$$
(31)

Since \(W=kJ_1+(1-k)J_2\), we can further rewrite matrix W as

$$\begin{aligned} W=\begin{bmatrix} kI_{m\times m} &{} (1-k)I_{m\times m}\\ I_{m\times m} &{} 0 \end{bmatrix} \begin{bmatrix} J_1\\ J_2 \end{bmatrix} \end{aligned}$$
(32)

If

$$\begin{aligned} \text {rank}(\begin{bmatrix} J_1\\ J_2\end{bmatrix})=n \end{aligned}$$
(33)

and thus

$$\begin{aligned} \text {rank}(WW^T)=n \end{aligned}$$
(34)

which means that \(WW^T\) is positive definite. In this situation, there exists a unique solution for linear Eq. (25). The proof is thus complete.

Theorem 2

[26]. The nonlinear activation function array \(\psi (u)\) can make the state variable u of the dynamic sub-system \(\dot{u}=-c\psi (u),c>0\) converge to zero, starting from its initial condition.

Proof

Define a Lyapunov function \(V=u^Tu/2\ge 0\) which is positive definite, and its time-derivative is \(\dot{V}=u^T\dot{u}=-cu^T\psi (u)\). As \(\psi (\cdot )\) is monotonously-increasing odd function array, thus we have \(\dot{V}=u^T\dot{u}=-cu^T\psi (u)\le -u^Tu\le 0\) which indicates that it is negative definite. Therefore we can conclude that the u can converge to zero. The proof is complete. \(\square \)

According to Theorem 1, as the Jacobian matrices \(J_1\) and \(J_2\) can be either rank-deficient or full-rank, the general solution of linear Eq. (25) is

$$\begin{aligned} \varLambda =[\lambda _1^T,\lambda _2^T]^T=(W+\sigma I)^{-1}H \end{aligned}$$
(35)

where \(\sigma \ge 0\) is the regularization factor to make the matrix inversion feasible. Next, according to Theorem 2, the partial derivatives equations \(\partial L/\partial \lambda _1=0\) and \(\partial L/\partial \lambda _2=0\) can hold, i.e, \(r_P\rightarrow r_P(0)\) and \(J_1{\dot{\theta }}\rightarrow r_A\) as time t evolves. It means that the end-effector tracking can be done and the RCM constraint can be satisfied with \(r_P\) converge to its initial position.

After \(\varLambda \) is solved and substituted into the aforementioned constraints, we would have the simplified neural network model which is associated with the redundancy resolution under RCM constraints as follows

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{\theta }}=-[kJ_1+(1-k)J_2]^T\lambda _{1}-J_1^T\lambda _2\\ \dot{k}=-\frac{1}{c_2}\lambda _{1}^T(r_A-r_B) \end{array} \right. \end{aligned}$$
(36)

Such simplified neural network model is directly related to the joint variable and the RCM scaling variable, and it makes the modeling more concise and gets rid of computing of time derivative of Jacobian matrices. A variable step Runge-Kutta method as the ordinary-differential-equation (ODE) solver can be used to solve the aforementioned neural network model. Through adjusting convergence scaling parameters \(c_1\), \(c_3\) and choosing different nonlinear activation functions \(\psi (\cdot )\), the resolution convergence for kinematic control with RCM constraints can be modulated as required. We can have the following activation function for ZD models:

  1. (1)

    linear activation function

    $$\begin{aligned} \psi (u)=u \end{aligned}$$
    (37)
  2. (2)

    power-sum activation function

    $$\begin{aligned} \psi (u)=b_1u+b_3u^3+b_5u^5+\cdots +b_Nu^{2N-1}, N\ge 2, b_i>1 \end{aligned}$$
    (38)

    and

  3. (3)

    hyperbolic sine activation function

    $$\begin{aligned} \psi (u)=\frac{\exp (\zeta u)-\exp (-\zeta u)}{2},\zeta \ge 1 \end{aligned}$$
    (39)

As compared with the original complex RNN model (17), the proposed simplified RNN model (28) is with less computational cost due to getting rid of computing the time-derivative of Jacobian matrices and less state vectors of neural network, i.e., the state vectors of (17) include \({\dot{\theta }}\), \(\dot{k}\), \(\lambda _1\) and \(\lambda _2\), while the state vectors of (28) include \(\theta \) and k. Moreover, the proposed simplified RNN model (28) may encounter less singularity that appears in the original complex RNN model (17), as the singularity situation of coefficient matrix A in (17) becomes more uncertain.

5 Simulation Results

In this section, simulation results on kinematic control of the redundant manipulator with RCM constraints are shown to verify the proposed simplified RNN method. The RCM constraint of the manipulator is locating between between the \(r_A\) and \(r_B\), where \(r_A\) is the position of the remote point at an additional link from the end-effector and \(r_B\) is the position of the end-effector. The initial value of k is set as 0.5, parameters \(c_1=100\), \(c_2=0.1\) and \(c_3=100\) are configured. The desired paths are used as targets as follows, 1) a circle path with its radius being 0.15 m, 2) a square with its length being 0.10 m, 3 ) a tetracuspid curve and 4) an ‘8” shape (eight-character) curve. Three types of activation functions are used: 1) pure linear activation function \(\psi (u)=u\); 2) powersum activation functions, i.e., unit-coefficient powersum activation function \(\psi (u)=u+u^3+u^5\), powersum-I activation function \(y=5u+15u^3+25u^5+35u^7\) and powersum-II activation function \(y=10u+30u^3+50u^5+70u^7\); 3) hyperbolic sine (sinh) activation function \(\psi (u)=\sinh (\zeta u)\) with \(\zeta =5\) and \(\zeta =10\).

Fig. 2
figure 2

Comprehensive performance of the proposed method for circle path tracking with the RCM constraint. The linear activation function is used

Full size image
Fig. 3
figure 3

Comprehensive performance of the proposed method for square path tracking with the RCM constraint. The linear activation function is used

Full size image
Fig. 4
figure 4

Comprehensive performance of the proposed method for tetracuspid path tracking with the RCM constraint. The linear activation function is used

Full size image
Fig. 5
figure 5

Comprehensive performance of the proposed method for “8” path tracking with the RCM constraint. The linear activation function is used

Full size image

5.1 Linear Case

Firstly, we utilize the linear activation function \(\psi (u)=u\) for the proposed simplified RNN method and evaluate its performance. Fig. 2 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for circle path tracking. Figure 2a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 2b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(6\times 10^{-3}\) m, which is very small as compared with the radius of the circle path target. Figure 2c shows resolved joint angle for by the proposed simplified RNN method. Figure 2d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Fig. 6
figure 6

Comprehensive performance of the proposed method for circle path tracking with the RCM constraint. The powersum activation function is used

Full size image
Fig. 7
figure 7

Comprehensive performance of the proposed method for square path tracking with the RCM constraint. The powersum activation function is used

Full size image

Figure 3 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for square path tracking. Figure 3a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 3b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(1\times 10^{-3}\) m, which is very small as compared with the length of the square path target. Figure 3c shows resolved joint angle for by the proposed simplified RNN method. Figure 3d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Fig. 8
figure 8

Comprehensive performance of the proposed method for tetracuspid path tracking with the RCM constraint. The powersum activation function is used

Full size image
Fig. 9
figure 9

Comprehensive performance of the proposed method for “8” path tracking with the RCM constraint. The powersum activation function is used

Full size image

Figure 4 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for tetracuspid path tracking. Figure 4a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 4b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(3\times 10^{-3}\) m, which is very small as compared with the size of the tetracuspid path target. Figure 4c shows resolved joint angle for by the proposed simplified RNN method. Figure 4d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Figure 5 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for “8” path tracking. Figure 5a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 5b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(4\times 10^{-3}\) m, which is very small as compared with the size of the “8” path target. Figure 5c shows resolved joint angle for by the proposed simplified RNN method. Figure 5d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

5.2 Nonlinear Case

Next, we utilize the powersum activation function \(\psi (u)=u+u^3+u^5\) for the proposed simplified RNN method and evaluate its performance. Figure 6 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for circle path tracking. Figure 6a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 6b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(6\times 10^{-3}\) m, which is very small as compared with the radius of the circle path target. Figure 6c shows resolved joint angle for by the proposed simplified RNN method. Figure 6d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Figure 7 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for square path tracking. Figure 7a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 7b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(1\times 10^{-3}\) m, which is very small as compared with the length of the square path target. Figure 7c shows resolved joint angle for by the proposed simplified RNN method. Figure 7d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Figure 8 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for tetracuspid path tracking. Figure 8a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 8b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(3\times 10^{-3}\) m, which is very small as compared with the size of the tetracuspid path target. Figure 8c shows resolved joint angle for by the proposed simplified RNN method. Figure 8d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Figure 9 presents the comprehensive performance of the proposed simplified RNN method for the redundant manipulator for “8” path tracking. Figure 9a shows the circle path tracking performance, and we can roughly observe that, the path tracking is well done with RCM constraint satisfied (a point \(r_P\) is obviously seen). Figure 9b shows the position error \([E_x,E_y,E_z]\) for the end-effector of the redundant manipulator, and one can evidently see that the position error \([E_x,E_y,E_z]\) can be lower than \(4\times 10^{-3}\) m, which is very small as compared with the size of the “8” path target. Figure 9c shows resolved joint angle for by the proposed simplified RNN method. Figure 9d shows the convergent process of the 3D coordinates of the \(r_P\) point, and we see that its 3D coordinate \(r_{p}\) can almost hold static from the beginning time instant, which indicates that when finishing the path tracking tasks the point \(r_P\) is almost made fixed. All these results verify the proposed method is efficient for the redundant manipulator on circle path tracking control with the RCM constraint satisfied.

Fig. 10
figure 10

Comparisons on the position errors and RCM tracking error with different activation functions used with \(c_1=c_2=1\)

Full size image
Fig. 11
figure 11

Comparisons on the position errors and RCM tracking error with different activation functions used with \(c_1=c_2=10\)

Full size image

5.3 Comparison

In this subsection, the convergence performances for the redundancy resolution with RCM constraints are compared in both linear and nonlinear cases. The pure linear activation function, powersum-I and powersum-II activation functions, and the hyperbolic sine (sh) activation function with \(\zeta =5\) and \(\zeta =10\), are all used for the proposed simplified RNN method for the purposes of comparisons. The two sets of convergence scaling parameter pairs are used in this comparison, i.e., \(c_1=c_3=1\) and \(c_1=c_3=10\).

Fig. 12
figure 12

Comparisons on the position errors and RCM tracking error with different activation functions used with \(c_1=c_2=1\)

Full size image
Fig. 13
figure 13

Comparisons on the position errors and RCM tracking error with different activation functions used with \(c_1=c_2=10\)

Full size image

Figure 10 shows the position errors of the end-effector and the convergence error of \(r_P\) with \(c_1=c_3=1\) with powersum and linear activation functions utilized. Seen from this figure, when using powersum-I and powersum-II activation functions, better error performance can be achieved as compared with that of using the linear activation function. Figure 11 shows the position errors of the end-effector and the convergence error of \(r_P\) with \(c_1=c_3=10\), and we could observe that, the error performance can be enhanced with larger parameters \(c_1\) and \(c_3\), and still, the error can be lowered by using powersum-I and powersum-II activation functions.

Additionally, Fig. 12 shows the position errors of the end-effector and the convergence error of \(r_P\) with \(c_1=c_3=1\) with hyperbolic sine (sh) and linear activation functions utilized. Seen from this figure, when using the hyperbolic sine activation functions with \(\zeta =5\) and \(\zeta =10\), better error performance can be achieved as compared with that of using the linear activation function. Figure 13 shows the position errors of the end-effector and the convergence error of \(r_P\) with \(c_1=c_3=10\), and we could observe that, the error performance can be enhanced with larger parameters \(c_1\) and \(c_3\), and still, the error can be lowered by using the hyperbolic sine activation function.

6 Conclusion

In this paper, for the first time, a RNN-based approach with a simplified neural network architecture is proposed to solve the redundancy resolution issue with RCM constraints, with a new and general dynamic optimization formulation containing the RCM constraints investigated. Theoretical results analyze and convergence properties of the proposed simplified RNN for redundancy resolution of manipulators with RCM constraints. Simulation results further demonstrate the efficiency of the proposed method in end-effector path tracking control under RCM constraints based on an industrial redundant manipulator model.