Video Synchronization Based on Projective-Invariant Descriptor

Abstract

In this paper, we present a novel trajectory-based method to synchronize two videos shooting the same dynamic scene, which are recorded by stationary un-calibrated cameras from different viewpoints. The core algorithm is carried out in two steps: projective-invariant descriptor construction and trajectory points matching. In the first step, a new five-coplanar-points structure is proposed to compute the cross ratio during the construction of the projective-invariant descriptor. The five points include one trajectory point and four fixed points induced from the background scene, which are co-planar in the 3D coordinate. In the second step, the matched trajectory points are initially estimated by the primitive nearest neighbor method, and are further refined by using epipolar geometric constraints and post processing. Experimental results demonstrate that the proposed method significantly outperforms the existing state-of-the-arts. More importantly, the proposed method is more generic in the sense that it works well for those videos captured under different conditions, including different frame rates, wide baseline, multiple moving objects, planar or non-planar motion trajectories.

1 Introduction

Video synchronization is a technique that temporally aligns two videos, which are recorded for the same dynamic scene by un-calibrated cameras from distinct viewpoints or over different time intervals [1]. The critical goal for video synchronization is to establish temporal correspondences among frames of two input videos, i.e., a reference video and a video to be synchronized. The applications of video synchronization cover a wide range of video analysis tasks [2,3,4,5,6,7,8], such as video surveillance, target identification, human action recognition, saliency detection and fusion.

For simplicity, the temporal alignment is assumed to be modeled by a 1D affine transformation¹ in this paper. The relationship between the frame index $i$ in the reference video and its corresponding frame index $j$ in the video to be synchronized is assumed to satisfy:

$$ j = \alpha \times i + \Delta t $$

(1)

where $\alpha$ is the ratio of the frame rates between the two videos, and $\Delta t$ is the temporal offset between them. Our goal is to recover the parameters $\alpha$ and $\Delta t$ in the 1D affine transformation. We address this problem by exploiting a novel projective-invariant descriptor based on the cross ratio to obtain the matched trajectory points between the two input videos.

So far, numerous video synchronization methods have been presented in the previous works, which are mainly classified into two categories: intensity-based ones [9,10,11,12,13] and feature-based ones [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. The intensity-based methods usually rely on colors, intensities, or intensity gradients to achieve the temporal synchronization of overlapping videos. The feature-based methods, however, rely on some detected features like trajectory points.

Among the feature-based video synchronization methods, the trajectory-based ones are one of the most popular categories [19,20,21,22,23,24,25,26,27,28,29]. These methods generally use some epipolar geometry or homography information among different viewpoints for the purpose of exploiting the matched trajectory points or time pairs between (or among) input videos [21, 22, 26, 28]. For example, Padua F, et al., introduced a concept of the timeline and presented a linear sequence-to-sequence alignment algorithm in [21]. They first performed the epipolar geometric constraint (EGC) on each trajectory point and then searched the matched trajectory points (or time pairs). In [22], a rank constraint-based video synchronization method was presented. Owing to the proposed rank constraint, it was not necessary to compute the fundamental matrix between the two views.

Alternatively, some video synchronization methods were proposed by first constructing a projective or multi-view invariant descriptor for each trajectory point and then finding the matched trajectory points or time pairs between the two videos based on the similarities among those descriptors. For example, Liu and Yang [23] proposed a video synchronization method based on the trajectory curvature (TC), where TCs were adopted as the descriptors and a scale-space scoring method was used to match the trajectory points. Since the curvature-based descriptor is not full-affine or projective invariant, this method only works for the videos that are captured from the slightly different viewpoints. In [24] and [25], two projective-invariant representation based video synchronization methods were presented based on the cross ratio of five coplanar points and four collinear points, respectively. These methods were shown to recover both spatial and temporal alignments with good precision and efficiency for the planar scenes.

However, the five coplanar points or the four collinear points were constructed by using the neighbors of each current trajectory point in [24] and [25]. This leads to the following two facts: (1) In the case of the planar or locally planar trajectories, each trajectory point and its neighbors on the trajectory are coplanar, which is not really true for the scenes containing the non-planar motions. As a result, such methods generally work well for the specific scenes containing planar motions rather than the general non-planar motions; (2) During the computation of the cross ratio, only the local spatial information from the trajectories is employed. The global spatial information of the trajectory point related to the whole scene is easily ignored in these methods. In another words, these methods may achieve some undesirable results or even fail when the trajectories containing numerous segments with the largely similar shapes.

In this paper, a set of five points are first constructed for each trajectory point in each input video, where a trajectory point is used as the reference point and other four fixed points are induced from the background scene. Their corresponding original points in the 3D real-world are co-planar even if the motions of the targets in the scene are non-planar. Then a projective-invariant descriptor is presented for each trajectory point by using the cross ratio induced from the five co-planar points. Finally, a novel synchronization method is proposed to synchronize the multiple videos.

Owing to the proposed five-coplanar-points structure, the proposed video synchronization method works well for the scenes containing the more general non-planar motions as well as the planar motions. Moreover, the spatial information of each trajectory point related to the whole background scene is also considered via computing the cross ratio based on the four fixed points from that scene in the proposed synchronization method. This will further improve the synchronization precision. Experimental results demonstrate the validity of the proposed method.

The main contributions in this paper are listed as follows.

• (1) A novel trajectory-based video synchronization method is proposed, where the proposed projective-invariant descriptor and the epipolar geometric constraint are jointly engaged, rather than just the geometric constraint in [21] or the projective invariant representation in [24, 25].

• (2) A robust and distinctive projective-invariant descriptor is presented for each trajectory point, which consists of multiple cross ratio values rather than single cross ratio value. This greatly improves the matching accuracy of the trajectory points.

• (3) A novel five-coplanar-points structure is constructed for each trajectory point during the computation of the cross ratio. In such structure, the proposed descriptor works well for the scenes with the planar or the general non-planar motions.

The rest of this paper is organized as follows: Sect. 2 describes the proposed projective-invariant descriptor in details. In Sect. 3, the proposed video synchronization method is elaborated. The experimental results and the conclusions are given in Sects. 4 and 5, respectively.

2 Projective-Invariant Description

In this section, we will present a novel method to construct a robust and distinctive projective-invariant descriptor for each trajectory point in the input videos. Firstly, we will briefly introduce the computation of the cross ratio of the five coplanar points. Then we will introduce a five-points construction method for each trajectory point such that their original points in the 3D real-world are coplanar even if the trajectory of the moving target in the scene is non-planar.

Mathematically, if the five coplanar points $\left\{ {{\mathbf{p}}_{i} |i = 1,2,3,4,5} \right\}$ are expressed in the homogeneous coordinates (i.e., ${\mathbf{p}}_{i} = [\lambda x_{i} ,\lambda y_{i} ,\lambda ]^{T}$), their cross ratio can be computed by [24]

$$ \varGamma ({\mathbf{p}}_{1} ,{\mathbf{p}}_{2} ,{\mathbf{p}}_{3} ,{\mathbf{p}}_{4} ,{\mathbf{p}}_{5} ) = \frac{{\left| {m_{125} } \right|\left| {m_{134} } \right|}}{{\left| {m_{124} } \right|\left| {m_{135} } \right|}} $$

(2)

where $m_{ijk}$ is the $3 \times 3$ matrix with ${\mathbf{p}}_{i}$, ${\mathbf{p}}_{j}$ and ${\mathbf{p}}_{k}$ as columns, and $\left| m \right|$ is the determinant of the matrix $m$. Here, ${\mathbf{p}}_{1}$ is viewed as the reference point of the cross ratio.

Based on the cross ratio, we can construct a projective-invariant descriptor for each trajectory point to establish the frame correspondences between the two input videos. However, for each trajectory point to be considered, how to construct a set of five points from every input video to compute its cross ratio such that their corresponding original points in the 3D real-world are coplanar is still an open issue. In addition, there is no ordering ambiguity for the five points under any projective transformation, considering that the cross ratio values depend on the ordering of the five points.

In this paper, the proposed five-points set consists of a moving point from the trajectories and the four fixed points from the background image, where the ordering ambiguity is avoided because of four of the five points are fixed. Moreover, the trajectory point will be taken as the reference point during the computation of the cross ratio. In this case, the remaining problem is how to construct the four fixed points from the background image.

Suppose there are two input videos, denoted by $V$ and $V^{\prime}$, respectively. $V$ is the reference video and $V^{\prime}$ is the video to be synchronized. $I$ and $I^{\prime}$ are their background images, and $\{ ({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} )|i = 1,2, \ldots ,n_{0} ;{\mathbf{b}}_{i} \in I,{\mathbf{b^{\prime}}}_{i} \in I^{\prime}\}$ are a set of matched feature points between the two background images. $\{ {\mathbf{p}}_{i} |i = 1,2, \ldots ,n_{1} \}$ and $\{ {\mathbf{p^{\prime}}}_{j} |j = 1,2, \ldots ,n_{2} \}$ are the trajectory points extracted from the two input videos. ${\mathbf{e}}$ and ${\mathbf{e^{\prime}}}$ are the epipolar points in the two views, and ${\mathbf{F}}$ denotes the fundamental matrix between the two views. ${\mathbf{C}}$ and ${\mathbf{C^{\prime}}}$ are supposed to be the centers of two cameras. The four fixed points are then constructed as follows.

First, three pairs of the matched feature points $\left\{ {({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} )|i = 1,2,3;{\mathbf{b}}_{i} \in I,{\mathbf{b^{\prime}}}_{i} \in I^{\prime}} \right\}$ are randomly selected from the background images of the two input videos.

Secondly, define a line ${\mathbf{l}}_{1}$ passing through points $\{ {\mathbf{b}}_{1} ,{\mathbf{b}}_{2} \}$ and a line ${\mathbf{l}}_{2}$ passing through points $\{ {\mathbf{e}},{\mathbf{b}}_{3} \}$ in the image $I$. A point ${\mathbf{b}}_{c}$ is obtained as the intersection of lines ${\mathbf{l}}_{1}$ and ${\mathbf{l}}_{2}$. Similarly, two lines ${\mathbf{l^{\prime}}}_{1}$ and ${\mathbf{l^{\prime}}}_{2}$ are defined through points $\{ {\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} \}$ and points $\{ {\mathbf{e^{\prime}}},{\mathbf{b^{\prime}}}_{3} \}$ in the image $I^{\prime}$, respectively, and a point ${\mathbf{b^{\prime}}}_{c}$ is also obtained as the intersection of lines ${\mathbf{l^{\prime}}}_{1}$ and ${\mathbf{l^{\prime}}}_{2}$.² Obviously, ${\mathbf{b}}_{c}$ and ${\mathbf{b^{\prime}}}_{c}$ are also a pair of matched feature points. The four points $\{ {\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}}\}$ in the video $V$ and their corresponding points $\{ {\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}}\}$ in the video $V^{\prime}$ are constructed, respectively.

Next, we will prove their original points $\{ {\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{B}}_{c} ,{\mathbf{E}}\}$ of the five points $\{ {\mathbf{p}}_{i} ,{\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}}\}$ or $\{ {\mathbf{p^{\prime}}}_{j} ,{\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}}\}$ are coplanar in the 3D real-world if the trajectory points ${\mathbf{p}}_{i}$ and ${\mathbf{p^{\prime}}}_{j}$ are a pair of the matched ones.

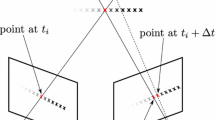
As shown in Fig. 1, the three original points $\left\{ {{\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} } \right\}$ are supposed to be on a plane $\pi_{1}$. The original point ${\mathbf{E}}$ corresponding to the epipolar points $({\mathbf{e}},{\mathbf{e^{\prime}}})$ on the plane $\pi_{1}$ is determined as the intersection of the line passing through points $\left\{ {{\mathbf{C}},{\mathbf{C^{\prime}}}} \right\}$ on the plane $\pi_{1}$. That means the four points $\{ {\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{E}}\}$ are all on the plane $\pi_{1}$ and there is no doubt that they are coplanar.

Fig. 1

Coplanarity of the points $\{ {\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{B}}_{c} ,{\mathbf{E}}\}$. Definitions of those symbols in the figure are seen in the text body

${\mathbf{B}}_{3}$ is not sure to be on the plane $\pi_{1}$, while ${\mathbf{B}}_{c}$ is on the plane $\pi_{1}$. As discussed previously, $\left\{ {{\mathbf{b}}_{1} ,{\mathbf{b^{\prime}}}_{1} } \right\}$ are a pair of the matched feature points, and ${\mathbf{B}}_{1}$ is their original point in the 3D-real world. Also,$\left\{ {{\mathbf{b}}_{2} ,{\mathbf{b^{\prime}}}_{2} } \right\}$ are a pair of the matched feature points, and ${\mathbf{B}}_{2}$ is their original point. Correspondingly, $\left\{ {{\mathbf{l}}_{1} ,{\mathbf{l^{\prime}}}_{1} } \right\}$ are a pair of the matched lines and ${\mathbf{L}}_{1}$ is their original one, which passes through the points ${\mathbf{B}}_{1}$ and ${\mathbf{B}}_{2}$ and is obviously on the plane $\pi_{1}$. The three points $\left\{ {{\mathbf{C}},{\mathbf{b}}_{1} ,{\mathbf{B}}_{1} } \right\}$ are collinear, and the three points $\left\{ {{\mathbf{C}},{\mathbf{b}}_{2} ,{\mathbf{B}}_{2} } \right\}$ are also collinear. A plane $\pi_{2}$, which is not displayed in the Fig. 1, is determined by the two lines. Accordingly, the line ${\mathbf{L}}_{1}$ is also on the plane $\pi_{2}$. Similarly, the three points $\left\{ {{\mathbf{C^{\prime}}},{\mathbf{b^{\prime}}}_{1} ,{\mathbf{B^{\prime}}}_{1} } \right\}$ are collinear, and the three points $\left\{ {{\mathbf{C^{\prime}}},{\mathbf{b^{\prime}}}_{2} ,{\mathbf{B^{\prime}}}_{2} } \right\}$ are also collinear. A plane $\pi^{\prime}_{2}$ is also determined by the two lines, and the line ${\mathbf{L}}_{1}$ is also on the plane $\pi^{\prime}_{2}$. Therefore, ${\mathbf{L}}_{1}$ is the interline of the two planes $\left\{ {\pi_{2} ,\pi^{\prime}_{2} } \right\}$. ${\mathbf{b}}_{c}$ and ${\mathbf{b^{\prime}}}_{c}$ are a pair of the matched points and are on the lines ${\mathbf{l}}_{1}$ and ${\mathbf{l^{\prime}}}_{1}$, respectively. Therefore, their original point ${\mathbf{B}}_{c}$ in the 3D real-world will be on the plane $\pi_{2}$ as well as on the plane $\pi^{\prime}_{2}$. That is to say, the point ${\mathbf{B}}_{c}$ is on the interline, i.e., ${\mathbf{L}}_{1}$, of the two planes $\left\{ {\pi_{2} ,\pi^{\prime}_{2} } \right\}$ and is on the plane $\pi_{1}$. This indicates that the points $\{ {\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{B}}_{c} ,{\mathbf{E}}\}$ are coplanar. It should be also noted that the five points $\{ {\mathbf{P}}_{ij} ,{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{B}}_{c} ,{\mathbf{E}}\}$ are still coplanar, although the plane $\pi_{1}$ and the point ${\mathbf{E}}$ may vary with the moving point ${\mathbf{P}}_{ij}$.

Having constructed the above four points $\{ {\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}}\}$, the cross ratio $\varGamma ({\mathbf{p}}_{i} ,{\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}})$ for each trajectory point ${\mathbf{p}}_{i} (i = 1,2, \ldots ,n_{1} )$ in the video $V$ can be computed by using Eq. (2). Similarly, with the four points $\{ {\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}}\}$, the cross ratio $\varGamma ({\mathbf{p^{\prime}}}_{j} ,{\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}})$ for each trajectory point ${\mathbf{p^{\prime}}}_{j} (j = 1,2, \ldots ,n_{2} )$ in the video $V^{\prime}$ can also be computed by using Eq. (2). Moreover, $\varGamma ({\mathbf{p}}_{i} ,{\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}})$ and $\varGamma ({\mathbf{p^{\prime}}}_{j} ,{\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}})$ will be the same ideally, if ${\mathbf{p}}_{i}$ and ${\mathbf{p^{\prime}}}_{j}$ are a pair of the matched trajectory points between the two input videos. Accordingly, after the two sets of fixed four points $\{ {\mathbf{b}}_{1} ,{\mathbf{b}}_{2} ,{\mathbf{b}}_{c} ,{\mathbf{e}}\}$ and $\{ {\mathbf{b^{\prime}}}_{1} ,{\mathbf{b^{\prime}}}_{2} ,{\mathbf{b^{\prime}}}_{c} ,{\mathbf{e^{\prime}}}\}$ are individually constructed in the videos $V$ and $V^{\prime}$, the matched trajectory points from the two input videos can be simply determined by using their cross ratio values as in [24].

In order to further improve the robustness and accuracy of the subsequent matching of trajectory points, we will use multiple cross ratio values, rather than just single cross ratio value, to describe each trajectory point in this paper. To do so, we will first randomly select three pairs of the matched feature points $({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} ),i = 1,2,3$ for $N$ times, which is set to 4 empirically. For each time, we obtain a cross ratio value for each trajectory point. Then we construct a projective-invariant descriptor ${\mathbf{d}} \in R^{N}$ of dimension $N$ for each trajectory point, each element of which is defined as the cross ratio value computed above. Although its simplicity, the presented descriptor greatly improves the correct matching rate of the proposed method. In summary, the process of building the projective-invariant descriptor is described in Algorithm 1.

From the construction of the five-points set, it is worth noting that their original points in the 3D real-world of those five points remain coplanar even if the motions of the moving targets in the scene are planar or non-planar. As a result of that, the proposed projective-invariant descriptor still works well for the scenes with non-planar motions. Moreover, owing to the four fixed points from the background scene, the spatial position information of each trajectory point related to the whole background scene is integrated into the proposed descriptor. This will further improve the accuracy in the subsequent matching of the trajectory points.

3 Proposed Video Synchronization Method

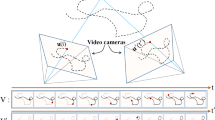
As shown in Fig. 2, the proposed method contains three parts: (I) Trajectory extraction and background image matching; (II) Trajectory point description and matching; (III) Estimation of temporal relationship.

Fig. 2

Diagram of the proposed method

For step I, the backgrounds of input videos are simply assumed to be static and the frame-difference-based methods [30, 31] are performed on the reference video $V$ and the video $V^{\prime}$ to be synchronized, respectively. Some other methods could also be employed here, which are beyond the scope of this paper. Then two background images $I$ and $I^{\prime}$, and two sets of trajectory points³$\left\{ {{\mathbf{p}}_{i} |i = 1,2, \ldots ,n_{1} } \right\}$ and $\left\{ {{\mathbf{p^{\prime}}}_{j} |i = 1,2, \ldots ,n_{2} } \right\}$ are, respectively, extracted from the two input videos. Here, $i$ denotes the frame index of the video $V$, and $j$ denotes the frame index of the video $V^{\prime}$. $n_{1}$ and $n_{2}$ are the total numbers of the frames contained in the two videos, respectively. Consequently, we can obtain the matched feature points $\{ ({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} )|i = 1,2, \ldots ,n_{0} ;{\mathbf{b}}_{i} \in I,{\mathbf{b^{\prime}}}_{i} \in I^{\prime}\}$ by using some image matching methods such as SIFT [32] or ASIFT [33].

The synchronization between the two videos $V$ and $V^{\prime}$, or the estimation of the parameters in the temporal transformation model in Eq. (1), can be achieved by finding the matched trajectory points $({\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} )$ or frame pairs $(i,j)$ between the two videos.

In the following subsections, we will describe step II (i.e., trajectory point description and matching and step III (i.e., temporal relationship estimation) of our proposed method in details.

3.1 Trajectory Point Description and Matching

The procedure of trajectory point description and matching is described as follows:

• (1) Given the matched feature points $\{ ({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} )|i = 1,2, \ldots ,n_{0} ;{\mathbf{b}}_{i} \in I,{\mathbf{b^{\prime}}}_{i} \in I^{\prime}\}$, compute the epipolar geometry between the two views by using the simple-normalized eight-point algorithm [34] or some robust epipolar geometry estimation methods [35, 36] and obtain the Fundamental matrix ${\mathbf{F}}$ as well as the epipolar points $({\mathbf{e}},{\mathbf{e^{\prime}}})$ in the two views.

• (2) Compute the projective-invariant descriptor ${\mathbf{d}}_{i} \, (i = 1,2, \ldots ,n_{1} )$ for each trajectory point ${\mathbf{p}}_{i} \, (i = 1,2, \ldots ,n_{1} )$ in the video $V$ and the projective-invariant descriptor ${\mathbf{d^{\prime}}}_{j} \, (i = 1,2, \ldots ,n_{2} )$ for each trajectory point ${\mathbf{p^{\prime}}}_{j} \, (i = 1,2, \ldots ,n_{2} )$ in the video $V^{\prime}$ based on Algorithm 1, respectively.

• (3) Obtain the initially matched trajectory point pairs set $M_{T}^{(1)} = \left\{ {\left( {{\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} } \right)|{\mathbf{p}}_{i} \in V,{\mathbf{p^{\prime}}}_{j} \in V^{\prime}} \right\}$ via using the nearest neighbor distance ratio based method [37]. More specifically, the trajectory points ${\mathbf{p}}_{i}$ and ${\mathbf{p^{\prime}}}_{j}$ are treated as a pair of the matched ones if they satisfy

  $$ \frac{{D({\mathbf{d}}_{i} ,{\mathbf{d^{\prime}}}_{j} )}}{{D({\mathbf{d}}_{i} ,{\mathbf{d^{\prime}}}_{{j^{\prime}}} )}} \le th1 $$

  (3)

  where $D( \cdot )$ denotes the Euclidean distance between two descriptor vectors. The points ${\mathbf{p^{\prime}}}_{j}$ and ${\mathbf{p^{\prime}}}_{j'}$ are, respectively, the first and second nearest ones to the point ${\mathbf{p}}_{i}$ according to the Euclidean distances of their descriptors. $th1$ is a threshold with a value of 0.85 in this paper.

• (4) Employ the epipolar geometric constraint to remove some obvious mismatches in the set $M_{T}^{(1)}$ and obtain a refined set $M_{T}^{(2)}$. For each pair of the matched points $({\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} )$ in the set $M_{T}^{(1)}$, determine the epipolar line ${\mathbf{l^{\prime}}}_{{{\mathbf{p}}_{i} }}$ of the point ${\mathbf{p}}_{i}$ in the video $V^{\prime}$ and then compute the distance $d\left( {{\mathbf{p^{\prime}}}_{j} ,{\mathbf{l^{\prime}}}_{{{\mathbf{p}}_{i} }} } \right)$ of the point ${\mathbf{p^{\prime}}}_{j}$ to the line ${\mathbf{l^{\prime}}}_{{{\mathbf{p}}_{i} }}$. Similarly, determine the epipolar line ${\mathbf{l}}_{{{\mathbf{p^{\prime}}}_{j} }}$ of the point ${\mathbf{p^{\prime}}}_{j}$ in the video $V$ and compute the distance $d\left( {{\mathbf{p}}_{i} ,{\mathbf{l}}_{{{\mathbf{p^{\prime}}}_{j} }} } \right)$ of the point ${\mathbf{p}}_{i}$ to the line ${\mathbf{l}}_{{{\mathbf{p^{\prime}}}_{j} }}$. If $d\left( {{\mathbf{p^{\prime}}}_{j} ,{\mathbf{l^{\prime}}}_{{{\mathbf{p}}_{i} }} } \right)$ and $d\left( {{\mathbf{p}}_{i} ,{\mathbf{l}}_{{{\mathbf{p^{\prime}}}_{j} }} } \right)$ satisfy Eq. (4), the points $({\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} )$ are viewed as a pair of the correctly matched ones. Otherwise, the points $({\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} )$ are regarded as a pair of the mismatched ones and are removed from $M_{T}^{(1)}$. Then a refined set $M_{T}^{(2)}$ is obtained.

  $$ d\left( {{\mathbf{p^{\prime}}}_{j} ,{\mathbf{l^{\prime}}}_{i} } \right) \le th2 \& d\left( {{\mathbf{p}}_{i} ,{\mathbf{l}}_{j} } \right) \le th2 $$

  (4)

  here the threshold $th2$ is adaptively set as

  $$ th2 = \frac{1}{{2n_{0} }}\sum\limits_{i = 1}^{{n_{0} }} {\left( {d({\mathbf{b}}_{i} ,{\mathbf{l}}_{{{\mathbf{b^{\prime}}}_{i} }} ) + d({\mathbf{b^{\prime}}}_{i} ,{\mathbf{l^{\prime}}}_{{{\mathbf{b}}_{i} }} )} \right)} $$

  (5)

  where ${\mathbf{l^{\prime}}}_{{{\mathbf{b}}_{i} }}$ denotes the epipolar line of the point ${\mathbf{b}}_{i}$ in the video $V^{\prime}$, and ${\mathbf{l}}_{{{\mathbf{b^{\prime}}}_{i} }}$ denotes the epipolar line of the point ${\mathbf{b^{\prime}}}_{i}$ in the video $V$.$n_{0}$ is the total number of the matched feature points between the two background images.

• (5) Extract the frame indices from the matched points $({\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} )$ in the set $M_{T}^{(2)}$ and obtain the matched frame pairs set $M_{F}^{(1)} = \left\{ {(i,j)|\left( {{\mathbf{p}}_{i} ,{\mathbf{p^{\prime}}}_{j} } \right) \in M_{T}^{(2)} } \right\}$.

3.2 Estimation of Temporal Relationship

We can directly perform the Random Sample Consensus (RANSAC) [38] algorithm on the matched frame pairs set $M_{F}^{(1)}$ obtained in the previous subsection to estimate the temporal transformation model between the two input videos. However, there are still many mismatches in the set $M_{F}^{(1)}$ because of the computational errors. This will reduce the final estimation precision, although RANSAC is robust to the mismatches or “outliers” to some extent.

As discussed in the earlier Sect. 2, three pairs of points $({\mathbf{b}}_{i} ,{\mathbf{b^{\prime}}}_{i} ),i = 1,2,3$ are randomly selected from the matched background feature points when the cross ratio for each trajectory point is computed. Accordingly, different sets of matched frame pairs $M_{F}^{(1)}$ are obtained when the trajectory point description and matching method introduced in the previous subsection is performed on the same input videos by several times. Despite of that, we also find that the correctly matched frame pairs generally appear in the set $M_{F}^{(1)}$ with higher probability than those mismatched ones.

Based on such observation, we present a simple but effective temporal parameter or model estimation method in this paper, which is described as follows.

• (1) Perform the trajectory point description and matching method introduced in the previous subsection on the input videos several times (e.g., $S$ times) and obtain $S$ sets of the matched frame pairs $\left\{ {M_{F}^{(s)} |s = 1, \ldots ,S} \right\}$ for the same pair of input videos.

• (2) Define a score matrix $M_{C}$ of orders $n_{1} \times n_{2}$ to count the total times $T_{i,j}$ of each matched frame pair $(i,j)$ appearing in those sets $\left\{ {M_{F}^{(s)} |s = 1, \ldots ,S} \right\}$ with $M_{C} (i,j) = T_{i,j}$. $M_{c} (i,j)$ denotes the $(i,j)$-th entry of the matrix $M_{C}$. A higher value of $M_{c} (i,j)$ means that the i-th frame in the video $V$ and the j-th frame in the video $V^{\prime}$ are more possible to be a pair of the correctly matched frames.

• (3) Compute the final matched frame pairs set $M_{F}$ as

  $$ M_{F} = \{ (i,j)|M_{C} (i,j) \ge \hbox{max} (M_{C} (:)) \times r\} $$

  (6)

  where $\hbox{max} (M_{C} (:))$ denotes the maximum value in matrix $M_{C}$. $r$ is experimentally set to 0.4 in this paper.

• (4) Estimate the parameters $\alpha$ and $\Delta t$ of the temporal transformation model in Eq. (1) by performing RANSAC on the matched frame pairs in $M_{F}$.

In summary, the pseudo code of the proposed video synchronization method is presented in Algorithm 2.

4 Experiments and Analysis

In this section, two sets of experiments are conducted to demonstrate the validity of the proposed video synchronization method. First, the impacts of some parameters are discussed by using a pair of videos. Secondly, several pairs of videos are employed to thoroughly test the effectiveness of the proposed method.

The average temporal alignment error $\varepsilon_{t}$ and the correct matching rate $C_{r}$ are employed to objectively evaluate different algorithms. Here, $\varepsilon_{t}$ is defined by

$$ \varepsilon_{t} = \frac{1}{{n_{1} }}\sum\limits_{i = 1}^{{n_{1} }} {\left| {(\alpha_{0} i + \Delta t_{0} ) - (\alpha_{{^{ *} }} i + \Delta t_{{^{*} }} )} \right|} $$

(8)

where $i$ and $n_{1}$ is the frame index and the total number of the frames in the reference video $V$, respectively. $\alpha_{{^{*} }}$, $\Delta t_{{^{*} }}$ are the estimated parameters for the temporal transformation model between the two input videos. $\alpha_{0}$, $\Delta t_{0}$ are the ground-truth, which are predefined or manually determined in advance. A matched frame pair $(i,j)$ is deemed as a pair of the correct ones if they satisfy

$$ \frac{{\left| {\alpha_{0} i + \Delta t_{0} - j} \right|}}{{\sqrt {\alpha_{0}^{2} + 1} }} \le th3 $$

(9)

where $th3$ is a threshold and is experimentally set to 0.5 in all of the experiments. $C_{r}$ is defined as the ratio between the number of the correct matches and the total number of the matches in the set $M_{F}$. Theoretically, smaller values of $\varepsilon_{t}$ and higher values of $C_{r}$ indicate the better performance of a method.

Table 1 lists several pairs of videos employed in this paper, and Fig. 3 illustrates their background images and the trajectory points extracted from these videos. It should be noted that the motions of the moving targets in the “Toyplay” videos are non-planar.

Table 1 Descriptions of the test input videos

Fig. 3

Background images and trajectory points extracted from the test input videos. aCar; bForkroad; cFootbridge; dToyplay. The images in the top row are the background images of the reference videos, and the images in the bottom row are the background images of the videos to be synchronized. The red points are the trajectory points extracted from the test videos

4.1 Impacts of Some Parameters

In this subsection, we will employ Videos Car in Table 1 to test the impacts on the system performance of some parameters in the proposed method, including the dimension of the descriptor $N$ in Algorithm 1 and the parameter $S$ in Algorithm 2.

The $\varepsilon_{t}$ and $C_{r}$ curves with the two parameters are provided in Fig. 4. Figure 4a, b indicate that the performance of the proposed method varies continuously with $N$ and achieves the best when $N$ is set to 4. As shown in Fig. 4c, d, the values of $\varepsilon_{t}$ decrease dramatically and the values of $C_{r}$ increase obviously with $S$ at the beginning. However, the performance of the proposed method remains nearly unchanged when $S$ is around 100. To facilitate the following experiments, we will set $N$ to 4 and $S$ to 100, respectively.

Fig. 4

Performance of the proposed method with parameters $N$ and $S$, respectively. a$\varepsilon_{t}$ curve with $N$; b$C_{r}$ curve with $N$; c$\varepsilon_{t}$ curve with $S$; d$C_{r}$ curve with $S$

The experimental results in Fig. 4a, b demonstrate the superiority of multiple cross ratio values (i.e., $N = 4$) employed in the proposed descriptor over the single cross ratio value (i.e., $N = 1$). While the experimental results in Fig. 4c, d also indicate that the performance of the proposed method can be greatly improved by using the score matrix despite its simplicity.

4.2 Validity of the Proposed Method

The four pairs of the input videos in Table 1 are employed to thoroughly demonstrate the validity of the proposed method in this subsection. In addition, some previous methods, including RC [22], EGC [21], SPIR [24], MT [25], TC [23], and MB [26], are performed on these videos for comparisons.

The estimation results obtained by different methods on the four pairs of the input videos are shown in Figs. 5, 6, 7 and 8, respectively. These figures demonstrate that the estimated temporal parameters $\alpha_{*}$ and $\Delta t_{*}$ obtained by the proposed method are closer to their corresponding ground truth values than those computed by other methods. Particularly, the estimated temporal parameters $\alpha_{*}$ and $\Delta t_{*}$ obtained by the proposed method are the same as their ground truth values for Videos Footbridge.

Fig. 5

Temporal alignment results on Videos Car. a–g are the alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively. a RC j = 0.9935 * i + 5.3589, b EGC j = 0.9979 * i + 5.9948, c SPIR j = 1.0034 * i + 6.7194, d MT j = 1.015 * i + 1.453, e TC j = 1.011 * i − 0.4463, f MB j = 1.0118 * i + 3.9504, g Proposed j = 0.9982 * i + 5.8486

Fig. 6

Temporal alignment results on Videos Forkroad. a–g are the alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively. a RC j = 0.9901 * i + 49.6535, b EGC j = 0.9932 * i + 51.0856, c SPIR j = 1 * i + 48, d MT j = 1.3045 * i + 17.6967, e TC j = 0.8898 * i + 47.5864, f MB j = 1.0124 * i − 15.1112, g Proposed j = 0.9945 * i + 50.825

Fig. 7

Temporal alignment results on Videos Footbridge. a–g are the alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively. a RC j = 1.999 * i + 9.0093, b EGC j = 1.9971 * i + 8.2176, c SPIR j = 2.042 * i + 4.0875, d MT j = 1.9989 * i + 6.1125, e TC j = 1.9532 * i + 15.4884, f MB j = 2.1459 * i + 7.9369, g Proposed j = 2 * i + 8

Fig. 8

Temporal alignment results on Videos Toyplay. a–g are the alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively. a RC j = 0.9763 * i + 1.9042, b EGC j = 0.9709 * i + 1.8572, c SPIR j = 0.9229 * i − 1.9093, d MT j = 0.5386 * i + 13.4569, e TC j = 0.9301 * i + 0.9917, f MB j = 0.822 * i + 8.3996, g Proposed j = 0.9998 * i + 0.1022

The values of metrics $\varepsilon_{t}$ and $C_{r}$ obtained by different methods are provided in Table 2 and Fig. 9, respectively, which also verify the obvious superiority of our proposed method over others. In addition, the total computing time of different methods is also provided in Table 3, which indicates that the computational efficiency of the proposed method is acceptable. Specifically, for Videos Car and Forkroad, the proposed method achieves the highest computational efficiency.

Table 2 Average temporal alignment errors $\varepsilon_{t}$ obtained by different methods

Fig. 9

Correct matching rate $C_{r}$ obtained by different methods. aCar; bForkroad; cFootbridge; dToyplay

Table 3 Total computing time of different methods (in s)

For better comparisons, we illustrate some visual temporal alignment results of these methods on Videos Footbridge and Toyplay in Figs. 10 and 11, respectively. The first row of Fig. 10 illustrates four representative frames in the reference video of Footbridge. The four matched frames in the video to be synchronized computed by RC, EGC, SPIR, MT, TC, MB and the proposed method are shown in the rest rows. A zoomed version of the representative image block in each frame is also provided in a small window. By comparing these zoomed blocks, there is no doubt that the proposed method obtains the highest temporal alignment precisions among those baselines above.

Fig. 10

Visual temporal alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method on Videos Footbridge. The first row shows the 31st, 60th, 185th, 195th frames in the reference video. The second to eighth rows show the matched frames computed by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively

Fig. 11

Visual temporal alignment results obtained by RC, EGC, SPIR, MT, TC, MB and the proposed method on Videos Toyplay. The first row shows the 8th, 33rd, 71st, 87th frames in the reference video. The second to eighth rows show the matched frames in the video to be synchronized computed by RC, EGC, SPIR, MT, TC, MB and the proposed method, respectively. In each of these sub-figures, the circle denotes the moving target (i.e., playing toy) in the scene, and the red cross (if existed) denotes the centroid location of the playing toy in the corresponding frame of the reference video

For example, as shown in the small window of the 60th frame (row 1, column 2 in Fig. 10) in the reference video, the right foot is behind the left foot. While in the matched frame computed by SPIR (row 4, column 2 in Fig. 10), the right foot is ahead the left foot. In the 185th frame (row 1, column 3 in Fig. 10) of the reference video, the right foot is at the cross of the ground. But in the matched frame computed by MT (row 5, column 3 in Fig. 10), no foot is at the cross of the ground. In contrast, for all of the four frames in the reference video, the proposed method can obtain the correctly matched ones, as shown in the last row of Fig. 10. Similar conclusions can also be made from Fig. 11. Those indicate that our proposed method has achieved better performance for the scenes with both the 3D non-planar and planar motions. This mainly gives credits to the proposed projective invariant descriptor, especially the proposed five-points structure during the computation of the cross ratio.

5 Conclusion

In this paper, we first propose a novel method to construct a robust and distinctive projective-invariant descriptor for each trajectory point by using the cross ratio of the proposed five coplanar points, which consist of a moving point from the trajectories and the four fixed points from the background images. More specifically, the five points remain coplanar in the 3D real-world even if the target motions are non-planar. Then we present a novel video synchronization framework that integrates the proposed projective-invariant descriptor and the constructed five-points structure jointly. The proposed method performs well for the scenes containing the general non-planar motions as well as the planar motions on account of the above novelties. Experimental results demonstrate that the proposed method significantly outperforms some state-of-the-art baselines for those videos being captured under different conditions, including different frame rates, wide baselines, multiple moving objects, planar or non-planar trajectories. In the future work, we will apply the presented approach in this paper to the automated multi-camera surveillance and the co-saliency detection [39,40,41].