Skip to main content
SpringerLink
Log in

Dynamic Analysis of Stochastic Recurrent Neural Networks

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

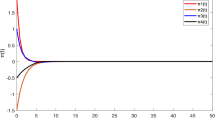
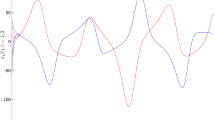
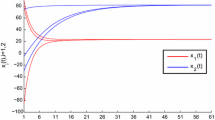
This paper addresses the issue of pth moment exponential stability of stochastic recurrent neural networks (SRNN) with time-varying interconnections and delays. With the help of the Dini derivative of the expectation of V(t, X(t)) “along” the solution X(t) of the model and the technique of Halanay-type inequality, some novel sufficient conditions on pth moment exponential stability of the trivial solution has been established. Conclusions of the development as presented in this paper have gone beyond some published results and are helpful to design stability of networks when stochastic noise is taken into consideration. An example is also given to illustrate the effectiveness of our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Cao J (2003) New results concerning expontential stability and periodic solutions of delayed cellular neural networks. Phys Lett A 307: 136–147

    Article  MATH  ADS  MathSciNet  Google Scholar 

  2. Cao J, Chen T (2004) Globally exponentially robust stability and periodicity of delayed neural networks. Chaos Solitons Fractals 4: 957–963

    Article  MathSciNet  Google Scholar 

  3. Cao J, Song Q (2006) Stability in Cohen-Grossberg-type bidirectional associative memory neural networks with time-varying delays. Nonlinearity 19: 1601–1617

    Article  MATH  ADS  MathSciNet  Google Scholar 

  4. Cao J, Wang J (2004) Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw 17: 379–390

    Article  MATH  Google Scholar 

  5. Chen Y (2007) Network of neurons with delayed feedback: periodical switching of excitation and inhibition. Dyn Contin Discrete Impuls Syst Ser B Appl Algorithms 14: 113–122

    MATH  MathSciNet  Google Scholar 

  6. Chen H (2006) Image-processing algorithms realized by discrete-time cellular neural networks and their circuit implementations. Chaos Solitons Fractals 29: 1100–1108

    Article  MathSciNet  Google Scholar 

  7. Halanay A (1966) Differential equations-stability, oscillations, time lags. Academic Press, NewYork

    MATH  Google Scholar 

  8. Haykin S (1994) Neural Networks. Prentice-Hall, NJ

    MATH  Google Scholar 

  9. Hu J, Zhong S, Liang L (2006) Exponential stability analysis of stochastic delayed cellular neural network. Chaos Solitions Fractals 27: 1006–1010

    Article  MATH  MathSciNet  Google Scholar 

  10. Huang C, Huang L (2007) Dynamics of a class of Cohen–Grossberg neural networks with time-varying delays. Nonlinear Anal RWA 8: 40–52

    Article  MATH  Google Scholar 

  11. Li X, Cao J (2005) Exponential stability of stochastic Cohen–Grossberg neural networks with time-varying delays. ISNN 2005, LNCS 3496, pp 162-167

  12. Liao X, Mao X (1996) Exponential stability and instability of stochastic neural networks. Stochast Anal Appl 14: 165–185

    Article  MATH  MathSciNet  Google Scholar 

  13. Liao X, Mao X (1996) Stability of stochastic neural networks. Neural Parallel Sci Comput 14: 205–224

    MathSciNet  Google Scholar 

  14. Liu B, Huang L (2007) New results of almost periodic solutions for recurrent neural networks. Comput Appl Math 206: 293–305

    Article  MATH  MathSciNet  Google Scholar 

  15. Liu Z, Chen A, Cao J, Huang L (2003) Existence and global exponential stability of periodic solution for BAM neural networks with periodic coefficients and time-varying delays. IEEE Trans Circuits Syst-I 50: 1162–1173

    Article  MathSciNet  Google Scholar 

  16. Luo J (2007) A note on exponential stability in pth mean of solutions of stochastic delay differential equations. Comput Appl Math 198: 143–148

    Article  MATH  MathSciNet  Google Scholar 

  17. Mao X (1997) Stochastic differential equation and application. Horwood Publishing, Chichester

    Google Scholar 

  18. Mohamad S, Gopalsamy K (2000) Continuous and discrete Halanay-type inequalities. Bull AustMathSoc 61: 371–385

    MATH  MathSciNet  Google Scholar 

  19. Sun Y, Cao J (2007) pth moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal RWA 8: 1171–1185

    Article  MATH  MathSciNet  Google Scholar 

  20. Venetianer L, Roska T (1998) Image compression by delayed CNNs. IEEE Trans Circuits Syst I 45: 205–215

    Article  Google Scholar 

  21. Wan L, Sun J (2005) Mean square exponential stability of delayed Hopfield neural networks. Phys Lett A 343: 306–318

    Article  ADS  Google Scholar 

  22. Yuan Z, Yuan L, Huang L (2006) Dynamics of periodic Cohen-Grossberg neural networks with varying delays. Neurocomputing 70: 164–172

    Article  Google Scholar 

  23. Zhao H, Cao J (2005) New conditions for global exponential stability of cellular neural networks with delays. Neural Netw 18: 1332–1340

    Article  MATH  Google Scholar 

  24. Zhao H, Ding N (2006) Dynamic analysis of stochastic Cohen–Grossberg neural networks with time delays. Appl Math Comput 183: 464–470

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematics and Computing Science, Changsha University of Science and Technology, Changsha, Hunan, 410076, P.R. China

    Chuangxia Huang & Ping Chen

  2. College of Electrical and Information Engineering, Hunan University, Changsha, Hunan, 410082, P.R. China

    Chuangxia Huang & Yigang He

Authors
  1. Chuangxia Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yigang He
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ping Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chuangxia Huang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Huang, C., He, Y. & Chen, P. Dynamic Analysis of Stochastic Recurrent Neural Networks. Neural Process Lett 27, 267–276 (2008). https://doi.org/10.1007/s11063-008-9075-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-008-9075-z

Keywords

Search

Navigation