1 Introduction

In the past forty years, there have been plenty of papers written about the neural network dynamics in various application areas [1,2,3,4,5,6,7,8,9,10,11,12]. Particularly, (asymptotically, pseudo) almost neural networks have received great deal of attention in the past decade due to their potential applications in classification, associative memory parallel computation, and other fields. So there have been many research results about the almost periodicity [13,14,15,16,17,18,19], pseudo almost periodicity [20,21,22,23,24,25,26,27,28], and weighted pseudo almost periodicity [29,30,31,32] on neural networks. From the viewpoint of mathematics, let \((x_{1}(t), x_{2}(t), \ldots, x_{n}(t)) \) represent the state vector, recurrent neural networks (RNNs) involving mixed delays can be described as the following nonlinear dynamic system:

$$ \begin{aligned}[b] x'_{i}(t) &= -a_{i}(t)b_{i} \bigl(x_{i}(t)\bigr)+\sum_{j=1}^{n} \alpha_{ij}(t)f _{j}\bigl(x_{j}(t)\bigr)+ \sum _{j=1}^{n}\beta_{ij}(t)h_{j} \bigl(x_{j}\bigl(t-\sigma_{ij}(t)\bigr)\bigr) \\ &\quad {}+ \sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{+\infty }K_{ij}(\mu ) g_{j} \bigl(x _{j}(t-\mu )\bigr)\,d\mu +I_{i}(t),\quad i\in S=\{1, 2, \ldots, n \}, \end{aligned} $$
(1.1)

which includes many kinds of neural networks such as BAM neural networks, Hopfield neural networks, and cellular neural networks. Here the decay function \(b_{i}\) and activation functions \(f_{j}\), \(g_{j}\), \(h_{j}\) are continuous, \(a_{i}(t) \) represents the rate of decay, \(I_{i}(t)\) denotes the external input. Further information on the mixed delays and coefficient parameters is available from [1, 13, 14].

Recently, for \(b_{i}(u)=u\) (\(i\in S\)), by using the exponential dichotomy theorem in semilinear differential systems, the almost periodicity and pseudo almost periodicity have been fully investigated in [15,16,17,18,19] and [20,21,22,23,24,25,26,27,28,29,30,31,32], respectively. Nevertheless, as a nonlinear differential equation, RNNs (1.1) involving that \(b_{i}(u)\neq u \) for some \(i\in S\) has no exponential dichotomy, and there are a few research works on the asymptotically almost periodicity analysis for this case. It is worth pointing out that all results in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] are established under

$$ \text{Assumption (E)}: \quad a_{i}(t) \text{ is almost periodic on } \mathbb{R} \text{ for all } i\in S. $$

Now, a question naturally arises: how about the asymptotically almost periodicity of RNNs (1.1) without assuming (E) and \(b_{i}(u)=u\) (\(i \in S\)). Inspired by the preceding discussions, in this paper, avoiding (E) and \(b_{i}(u)=u\) (\(i\in S\)), we derive some novel criteria to validate the existence and convergence of the asymptotically almost periodic solutions of (1.1). Main contributions and innovation points of this paper are threefold. First, a class of asymptotically almost periodic recurrent neural networks involving mixed delays is established. Second, a novel approach to the problem of the existence on asymptotically almost periodic solutions of RNNs (1.1) is presented. Third, improved results on the global exponential attractivity of all solutions of RNNs (1.1) are obtained. Furthermore, our results not only generalize the results in [20,21,22,23,24,25,26,27,28,29,30,31,32], but also improve them. In truth, one can view the following Remark 3.1 and Remark 4.1 for extensive information.

The rest of this paper is arranged as follows. Some preliminaries and lemmas are supplied in Sect. 2. In Sect. 3, some novel sufficient conditions are gained to evidence the asymptotically almost periodicity of system (1.1). In Sect. 4, an illustrative example is presented to validate the correctness of the proposed theory. In the end, a brief conclusion is presented to summarize and evaluate our work.

2 Preliminary results

Notations

For \(\mathbb{J} \subseteq \mathbb{R}\), \(C_{0}( \mathbb{R}^{+}, \mathbb{J} )=\{\nu:\nu \in C (\mathbb{R}^{+}, \mathbb{J} ), \lim_{t\rightarrow +\infty }\nu (t)=0 \}\). We designate the collections of the almost periodic functions and the asymptotically almost periodic functions from \(\mathbb{R}\) to \(\mathbb{J} \) by \(\operatorname{AP}(\mathbb{R},\mathbb{J} )\) and \(\operatorname{AAP}(\mathbb{R}, \mathbb{J}^{n} )\), respectively. For the definitions of AP and APP, we refer the reader to [33, 34]. For \(i, j\in S\), we suppose that \(a_{i}, \sigma_{ij}\in \operatorname{AAP}(\mathbb{R},\mathbb{R}^{+})\), \(I_{i}, \alpha _{ij}, \beta_{ij}, \gamma_{ij} \in \operatorname{AAP}(\mathbb{R}, \mathbb{R}) \), and

$$ \begin{gathered} a_{i}=a_{i}^{0}+a_{i}^{1},\qquad I_{i}=I_{i}^{0}+I_{i}^{1},\qquad \alpha_{ij}= \alpha_{ij}^{0}+\alpha_{ij}^{1},\\ \beta_{ij}=\beta_{ij}^{0}+\beta_{ij} ^{1},\qquad \gamma_{ij}=\gamma_{ij}^{0}+ \gamma_{ij}^{1},\qquad \sigma_{ij}=\sigma _{ij}^{0}+\sigma_{ij}^{1}, \end{gathered} $$

where \(a_{i}^{0},\sigma_{ij}^{0} \in \operatorname{AP}(\mathbb{R},\mathbb{R}^{+})\), \(I _{i}^{0}, \alpha_{ij}^{0}, \beta_{ij}^{0}, \gamma_{ij}^{0} \in \operatorname{AP}( \mathbb{R}, \mathbb{R})\), \(a_{i}^{1}, \sigma_{ij}^{1}\in C_{0}( \mathbb{R}^{+}, \mathbb{R}^{+} )\), \(I_{i}^{1}, \alpha_{ij}^{1}, \beta _{ij}^{1}, \gamma_{ij}^{1} \in C_{0}(\mathbb{R}^{+}, \mathbb{R} )\).

Assumptions

For \(i, j\in S\) and \(u, v \in \mathbb{R}\), there are constants \(\underline{b}_{i}>0\), \(\overline{b}_{i}>0\), \(L ^{f} _{j}\), \(L^{h}_{j}\), \(L^{g}_{j}\), \(\eta_{1}, \eta_{2}, \ldots, \eta _{n}, \xi \), and λ such that

\((U_{0})\) :

\(b_{i}(0 )=0\), \(\underline{b}_{i}|u -v |\leq \operatorname {sign}(u-v)(b _{i}(u )-b_{i}(v )) \leq \overline{b}_{i}|u -v | \).

\((U_{1})\) :

\(|f_{j}(u )-f_{j}(v )|\leq L^{f} _{j}|u -v |\), \(|h_{j}(u )-h _{j}(v )| \leq L^{h}_{j}|u -v |\), \(|g_{j}(u )-g_{j}(v )| \leq L^{g}_{j}|u -v | \).

\((U_{2})\) :

\(K_{ij}:\mathbb{R}^{+}\rightarrow \mathbb{R}\) is continuous and absolutely integrable.

\((U_{3})\) :
$$ \begin{aligned} &{-}\bigl[a_{i}^{0}(t)\underline{b}_{i}- \lambda \bigr]\eta_{i}+ \sum_{j=1}^{n} \bigl( \bigl\vert \alpha^{0}_{ij}(t) \bigr\vert + \bigl\vert \alpha^{1}_{ij}(t) \bigr\vert \bigr)L ^{f}_{j}\eta_{j}+ \sum _{j=1}^{n}\bigl( \bigl\vert \beta_{ij}^{0}(t) \bigr\vert + \bigl\vert \beta_{ij}^{1}(t) \bigr\vert \bigr)e^{\lambda \sigma } L ^{h}_{j}\eta_{j} \\ &\quad {}+ \sum_{j=1}^{n}\bigl( \bigl\vert \gamma_{ij}^{0}(t) \bigr\vert + \bigl\vert \gamma_{ij}^{1}(t) \bigr\vert \bigr) \int_{0} ^{+\infty } \bigl\vert K_{ij}(s) \bigr\vert e^{\lambda s}\,ds L^{g}_{j}\eta_{j}< -\xi,\\ &\quad t \in \mathbb{R}^{+}, \sigma =\max_{i, j\in S }\sup _{t\in \mathbb{R}}\sigma_{ij}^{0}(t). \end{aligned} $$

For further analysis, we set up the following nonlinear auxiliary system:

$$ \begin{aligned}[b] x'_{i}(t) &= -a_{i}^{0}(t)b_{i} \bigl(x_{i}(t)\bigr)+\sum_{j=1}^{n} \alpha _{ij}^{0}(t)f_{j}\bigl(x_{j}(t) \bigr)+ \sum_{j=1}^{n}\beta_{ij}^{0}(t)h_{j} \bigl(x _{j}\bigl(t-\sigma_{ij}^{0}(t)\bigr)\bigr) \\ &\quad {}+ \sum_{j=1}^{n} \gamma_{ij}^{0}(t) \int_{0}^{+\infty }K_{ij}(u) g_{j} \bigl(x _{j}(t-u)\bigr)\,du+I_{i}^{0}(t),\quad i\in S. \quad (1.1)^{0} \end{aligned} $$

The initial condition involved in systems (1.1) and \((1.1)^{0}\) can be described as follows:

$$ x_{i}(s)=\varphi_{i}(s),\quad s\in (-\infty, 0], i\in S, \varphi \text{ is bounded and continuous on } (-\infty, 0]. $$
(2.1)

Denote \(\|x\|=\max_{i\in S} |x_{i}|\), \(\| x (t)\|_{\eta }= \max_{i\in S}|\eta^{-1}_{i}x_{i}(t) |\), and let \(i_{t}\) be such a designation that

$$ \eta^{-1}_{i_{t}} \bigl\vert x_{i_{t}}(t) \bigr\vert = \bigl\Vert x (t) \bigr\Vert _{\eta }. $$
(2.2)

Lemma 2.1

Designate \(x(t) \) to be a solution of the initial value problem \((1.1)^{0}\) and (2.1). If \((U_{0})\), \((U_{1})\), \((U_{2})\), and \((U_{3})\) hold, then \(x(t)\) is bounded and exists on \([0, +\infty )\).

Proof

Denote \([0, \eta^{*}(\varphi ))\) to be the maximal right existence interval of \(x(t)\). Apparently, we can take \(N_{\varphi }>0\) such that

$$\begin{aligned} N_{\varphi } >&1+\sup_{t\in (-\infty, 0]} \bigl\Vert \varphi (t) \bigr\Vert \\ &{}+\max_{i\in S}\sup_{t\in \mathbb{R}}\Biggl[ \sum _{j=1} ^{n} \bigl\vert \alpha_{ij}^{0}(t ) \bigr\vert \bigl\vert f_{j}(0) \bigr\vert +\sum_{j=1}^{n} \bigl\vert \beta_{ij}^{0}(t ) \bigr\vert \bigl\vert h_{j} (0) \bigr\vert \\ &{} + \sum_{j=1}^{n} \bigl\vert \gamma_{ij}^{0}(t ) \bigr\vert \int_{0}^{+ \infty } \bigl\vert K_{ij}(\mu ) \bigr\vert \,d\mu \bigl\vert g_{j}(0) \bigr\vert \Biggr] \end{aligned}$$

and

$$ \bigl\vert x_{i}(t) \bigr\vert < \eta_{i} \frac{ \Vert I ^{0} \Vert _{\infty }+N_{\varphi }}{\xi } \quad \text{for all } t\in (-\infty, 0], i\in S. $$

We claim that

$$ \bigl\vert x_{i}(t) \bigr\vert < \eta_{i} \frac{ \Vert I^{0} \Vert _{\infty }+N_{\varphi }}{\xi } \quad \text{for all } t\in [0, \eta^{*}(\varphi )),i \in S. $$
(2.3)

Suppose the contrary and choose \(i\in S\) and \(t^{*}\in (0, \eta^{*}( \varphi ))\) such that

$$ \begin{gathered} \bigl\vert x _{i}\bigl(t^{*}\bigr) \bigr\vert = \eta_{i}\frac{ \Vert I^{0} \Vert _{\infty }+N_{\varphi }}{ \xi }, \quad \text{and}\\ \bigl\vert x _{j}(t) \bigr\vert < \eta_{j} \frac{ \Vert I^{0} \Vert _{ \infty }+N_{\varphi }}{\xi } \quad \text{for all } t\in \bigl(-\infty, t ^{*}\bigr), j\in S. \end{gathered} $$
(2.4)

It follows from \((U_{0})\), \((U_{1})\), \((U_{2})\), \((U_{3})\), and (2.4) that

$$\begin{aligned} 0 \leq &D^{-}\bigl( \bigl\vert x_{i} \bigl(t^{*}\bigr) \bigr\vert \bigr) \\ \leq & -a_{i}^{0}\bigl(t^{*}\bigr) \bigl\vert b_{i}\bigl(x_{i}\bigl(t^{*}\bigr)\bigr) \bigr\vert + \Biggl\vert \sum_{j=1}^{n} \alpha_{ij}^{0}\bigl(t^{*}\bigr)f_{j} \bigl(x_{j}\bigl(t^{*}\bigr)\bigr)+\sum _{j=1}^{n}\beta_{ij} ^{0} \bigl(t^{*}\bigr)h_{j}\bigl(x_{j} \bigl(t^{*}-\sigma_{ij}^{0}\bigl(t^{*} \bigr)\bigr)\bigr) \\ &{} + \sum_{j=1}^{n}\gamma_{ij}^{0} \bigl(t^{*}\bigr) \int_{0}^{+\infty }K_{ij}( \mu ) g_{j} \bigl(x_{j}\bigl(t^{*}-\mu \bigr)\bigr)\,d\mu +I_{i}^{0}\bigl(t^{*}\bigr) \Biggr\vert \\ \leq & -a_{i}^{0}\bigl(t^{*}\bigr) \underline{b}_{i}\eta_{i}\frac{ \Vert I^{0} \Vert _{\infty }+N_{\varphi }}{\xi }+ \sum _{j=1}^{n} \bigl\vert \alpha_{ij}^{0} \bigl(t^{*}\bigr) \bigr\vert \bigl( \bigl\vert f _{j} \bigl(x_{j}\bigl(t^{*}\bigr)\bigr)-f_{j}(0) \bigr\vert + \bigl\vert f_{j}(0) \bigr\vert \bigr) \\ &{}+\sum_{j=1}^{n} \bigl\vert \beta_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \bigl( \bigl\vert h_{j}\bigl(x_{j}\bigl(t^{*}- \sigma_{ij}^{0}\bigl(t^{*}\bigr)\bigr) \bigr)-h_{j} (0) \bigr\vert + \bigl\vert h_{j} (0) \bigr\vert \bigr) \\ &{} + \sum_{j=1}^{n} \bigl\vert \gamma_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \int_{0}^{+\infty } \bigl\vert K _{ij}(\mu ) \bigr\vert \bigl( \bigl\vert g_{j}\bigl(x_{j} \bigl(t^{*}-\mu \bigr)\bigr)-g_{j}(0) \bigr\vert + \bigl\vert g_{j}(0) \bigr\vert \bigr)\,d\mu + \bigl\vert I _{i}^{0}\bigl(t^{*}\bigr) \bigr\vert \\ \leq & -a_{i}^{0}\bigl(t^{*}\bigr) \underline{b}_{i}\eta_{i}\frac{ \Vert I^{0} \Vert _{ \infty }+N_{\varphi }}{\xi }+ \sum _{j=1}^{n} \bigl\vert \alpha_{ij}^{0} \bigl(t^{*}\bigr) \bigr\vert L ^{f} _{j} \eta_{j} \frac{ \Vert I^{0} \Vert _{\infty }+N_{\varphi }}{\xi } \\ &{} + \sum_{j=1}^{n} \bigl\vert \beta_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert L^{h} _{j}\eta_{j} \frac{ \Vert I^{0} \Vert _{\infty }+N_{\varphi }}{\xi } \\ &{} + \sum_{j=1}^{n} \bigl\vert \gamma_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \int_{0}^{+\infty } \bigl\vert K _{ij}(\mu ) \bigr\vert \,d\mu L_{j}^{g}\eta_{j} \frac{ \Vert I^{0} \Vert _{\infty }+N_{ \varphi }}{\xi } \\ &{} + \sum_{j=1}^{n} \bigl\vert \alpha_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \bigl\vert f_{j}(0) \bigr\vert +\sum_{j=1} ^{n} \bigl\vert \beta_{ij}^{0} \bigl(t^{*}\bigr) \bigr\vert \bigl\vert h_{j} (0) \bigr\vert \\ &{} + \sum_{j=1}^{n} \bigl\vert \gamma_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \int_{0}^{+\infty } \bigl\vert K _{ij}(\mu ) \bigr\vert \,d\mu \bigl\vert g_{j}(0) \bigr\vert + \bigl\vert I_{i}^{0}\bigl(t^{*}\bigr) \bigr\vert \\ < & \Biggl[-a_{i}^{0}\bigl(t^{*}\bigr) \underline{b}_{i}\eta_{i} + \sum _{j=1}^{n} \bigl\vert \alpha_{ij}^{0} \bigl(t^{*}\bigr) \bigr\vert L^{f} _{j} \eta_{j} + \sum_{j=1}^{n} \bigl\vert \beta_{ij} ^{0}\bigl(t^{*}\bigr) \bigr\vert L^{h} _{j}\eta_{j} \\ &{} + \sum_{j=1}^{n} \bigl\vert \gamma_{ij}^{0}\bigl(t^{*}\bigr) \bigr\vert \int_{0}^{+\infty } \bigl\vert K _{ij}(\mu ) \bigr\vert \,d\mu L_{j}^{g}\eta_{j}\Biggr] \frac{ \Vert I^{0} \Vert _{\infty }+N_{ \varphi }}{\xi } + \bigl\Vert I^{0} \bigr\Vert _{\infty }+N_{\varphi } \\ < & 0, \end{aligned}$$

which derives a contradiction and proves the above claim. Thus, the boundedness and the extension theorem of solution in [35] entail that \(\eta^{*}(\varphi )=+\infty \), which finishes the proof of Lemma 2.1. □

Remark 2.1

Under the assumptions in Lemma 2.1, an argument similar to that applied in Lemma 2.1 shows that each solution of initial value problem (1.1) and (2.1) is bounded on \([0, +\infty )\).

Lemma 2.2

Let \((U_{0})\), \((U_{1})\), \((U_{2})\), and \((U_{3})\) hold. Suppose that \(x(t) \) is a solution of system \((1.1)^{0}\) with the initial function φ satisfying (2.1), and \(\varphi '\) is bounded and continuous on \((-\infty, 0]\). Then, for any \(\epsilon > 0\), one can pick a relatively dense subset \(M_{\epsilon }\) in \(\mathbb{R}\) to satisfy that, for any \(\tau \in M_{\epsilon }\), there is \(N=N(\tau )>0\) obeying

$$ \bigl\Vert x(t+\tau )-x(t) \bigr\Vert _{\eta }< \frac{\epsilon }{2 \max_{i\in S} \eta_{i}} \quad \textit{for all } t> N. $$
(2.5)

Proof

Denote

$$\begin{aligned} &P_{i} (\tau, t) \\ &\quad = -\bigl[a_{i}^{0}(t+\tau )-a_{i}^{0}(t) \bigr]b_{i}\bigl(x_{i}(t+\tau )\bigr)+ \sum _{j=1}^{n}\bigl[\alpha_{ij}^{0}(t+ \tau )-\alpha_{ij}^{0}(t)\bigr]f_{j} \bigl(x_{j}(t+ \tau )\bigr) \\ & \qquad {}+ \sum_{j=1}^{n}\bigl[ \beta_{ij}^{0}(t+\tau )-\beta_{ij}^{0}(t) \bigr]h_{j}\bigl(x _{j}\bigl(t-\sigma^{0}_{ij}(t+ \tau )+\tau \bigr)\bigr) \\ & \qquad {}+ \sum_{j=1}^{n} \beta_{ij}^{0}(t)\bigl[h_{j}\bigl(x_{j} \bigl(t-\sigma_{ij}^{0}(t+ \tau )+\tau \bigr) \bigr)-h_{j}\bigl(x_{j}\bigl(t-\sigma_{ij}^{0}(t )+\tau \bigr)\bigr)\bigr] \\ & \qquad {}+\sum_{j=1}^{n}\bigl[ \gamma_{ij}^{0}(t+\tau )-\gamma_{ij}^{0}(t) \bigr] \int _{0}^{+\infty }K_{ij}(\mu )g_{j} \bigl(x_{j}(t+\tau -\mu )\bigr)\,d\mu + \bigl[I_{i } ^{0}(t+\tau )-I_{i}^{0}(t)\bigr]. \end{aligned}$$

According to Lemma 2.1 and the boundedness of \(x(t) \), one finds that \(x (t)\) is uniformly continuous on \(\mathbb{R}\). Thus, for any \(\epsilon >0\), one can take \(0<\epsilon^{*}<\epsilon \) to obey that

$$ \left . \textstyle\begin{array}{l} \vert a_{i}^{0}(t)-a_{i}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert I_{i}^{0}(t)-I _{i}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert \sigma_{ij}^{0}(t)-\sigma_{ij} ^{0}(t+\tau ) \vert < \epsilon^{*}, \\ \vert \alpha_{ij}^{0}(t)-\alpha_{ij}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert \beta_{ij}^{0}(t)-\beta_{ij}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert \gamma _{ij}^{0}(t)-\gamma_{ij}^{0}(t+\tau ) \vert < \epsilon^{*}, \end{array}\displaystyle \right \} $$

suggests that

$$ \bigl\vert P_{i} (\tau, t) \bigr\vert < \frac{1}{2 \max_{i\in S}\eta_{i}}\xi \epsilon, $$
(2.6)

where \(t\in \mathbb{R}\), \(i, j\in S\).

Note that \(\{a_{i}^{0}, I_{i}^{0}, \alpha_{ij}^{0}, \beta_{ij}^{0}, \gamma_{ij}^{0}, \sigma_{ij}^{0}\in \operatorname{AP}(\mathbb{R}, \mathbb{R})\ (i, j \in S)\}\) is a uniformly almost periodic family. From Corollary 2.3 in [33, p. 19], one can pick a relatively dense subset \(M_{\epsilon^{*}}\) in \(\mathbb{R}\) to satisfy that

$$ \left . \textstyle\begin{array}{l} \vert a_{i}^{0}(t)-a_{i}^{0}(t+\tau ) \vert < \epsilon^{*}, \qquad \vert I_{i}^{0}(t)-I _{i}^{0}(t+\tau ) \vert < \epsilon^{*}, \\ \vert \alpha_{ij}^{0}(t)-\alpha_{ij}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert \sigma_{ij}^{0}(t)-\sigma_{ij}^{0}(t+\tau ) \vert < \epsilon^{*}, \\ \vert \beta_{ij}^{0}(t)-\beta_{ij}^{0}(t+\tau ) \vert < \epsilon^{*},\qquad \vert \gamma_{ij}^{0}(t)-\gamma_{ij}^{0}(t+\tau ) \vert < \epsilon^{*}, \end{array}\displaystyle \right \} \quad \tau \in M_{\epsilon^{*}},t \in \mathbb{R}. $$
(2.7)

Denote \(M_{\epsilon }=M_{\epsilon^{*}}\), for each \(\tau \in M_{\epsilon }\), (2.6) and (2.7) give us

$$ \bigl\vert P_{i} (\tau, t) \bigr\vert < \frac{1}{2 \max_{i\in S}\eta_{i}}\xi \epsilon \quad \text{for all } t \in \mathbb{R}, i\in S. $$
(2.8)

Designate \(t> T_{0}=1+\max \{0, -\tau \}\) and \(z_{i}(t)=x_{i}(t+ \tau )-x_{i}(t)\), one can obtain

$$\begin{aligned} \frac{dz_{i}(t)}{dt} = & -a_{i}^{0}(t)\bigl[b_{i} \bigl(x_{i}(t+\tau )\bigr)-b_{i}\bigl(x _{i}(t) \bigr)\bigr]+ \sum_{j=1}^{n} \alpha_{ij}^{0}(t )\bigl[ f_{j} \bigl(x_{j}(t +\tau )\bigr)-f _{j}\bigl(x_{j}(t ) \bigr)\bigr] \\ &{}+ \sum_{j=1}^{n}\beta_{ij}^{0}(t )\bigl[h_{j} \bigl(x_{j}\bigl(t-\sigma_{ij} ^{0}(t )+\tau \bigr)\bigr) -h_{j}\bigl(x_{j} \bigl(t-\sigma_{ij}^{0}(t)\bigr)\bigr)\bigr] \\ &{}+\sum_{j=1}^{n} \gamma_{ij}^{0}(t) \int_{0}^{+\infty }K_{ij}( \mu ) \bigl[g_{j}\bigl(x_{j}(t+\tau -\mu )\bigr)-g_{j} \bigl(x_{j}(t -\mu )\bigr)\bigr]\,d\mu + P_{i} ( \tau, t), \end{aligned}$$

and

$$\begin{aligned} &D^{-}\bigl(e^{\lambda s} \bigl\vert z_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=t} \\ &\quad \leq \lambda e^{\lambda t} \bigl\vert z_{i_{t}}(t) \bigr\vert +e^{\lambda t} \Biggl\{ -a_{i _{t}}^{0}(t) \bigl\vert b_{i_{t}}\bigl(x_{i_{t}}(t+\tau )\bigr)-b_{i_{t}} \bigl(x_{i_{t}}(t)\bigr) \bigr\vert \\ & \qquad {}+ \Biggl\vert \sum_{j=1}^{n} \alpha_{i_{t}j}^{0}(t )\bigl[ f_{j} \bigl(x_{j}(t +\tau )\bigr)-f _{j}\bigl(x_{j}(t ) \bigr)\bigr] \\ & \qquad {}+ \sum_{j=1}^{n} \beta_{i_{t}j}^{0}(t )\bigl[h_{j} \bigl(x_{j} \bigl(t-\sigma_{i _{t}j}^{0}(t )+\tau \bigr)\bigr) -h_{j}\bigl(x_{j}\bigl(t-\sigma_{i_{t}j}^{0}(t) \bigr)\bigr)\bigr] \\ & \qquad {}+\sum_{j=1}^{n} \gamma_{i_{t}j}^{0}(t) \int_{0}^{\infty }K_{i _{t}j}(\mu ) \bigl[g_{j}\bigl(x_{j}(t+\tau -\mu )\bigr)-g_{j} \bigl(x_{j}(t -\mu )\bigr)\bigr]\,d\mu + P _{i_{t}} (\tau, t) \Biggr\vert \Biggr\} \\ & \quad \leq e^{\lambda t}\Biggl\{ -\bigl[a_{i_{t}}^{0}(t) \underline{b}_{i_{t}}- \lambda \bigr] \bigl\vert z_{i_{t}}(t) \bigr\vert \eta^{-1}_{i_{t}}\eta_{i_{t}}+ \sum _{j=1}^{n} \alpha_{i_{t}j}^{0}(t ) L ^{f}_{j} \bigl\vert z_{j }(t ) \bigr\vert \eta^{-1}_{j }\eta_{j} \\ & \qquad {} + \sum_{j=1}^{n} \beta_{i_{t}j}^{0}(t ) L ^{h}_{j} \bigl\vert z_{j }\bigl(t- \sigma_{i_{t}j}^{0}(t)\bigr) \bigr\vert \eta^{-1}_{j }\eta_{j} \\ & \qquad {} +\sum_{j=1}^{n} \gamma_{i_{t}j}^{0}(t) \int_{0}^{+\infty } \bigl\vert K _{i_{t}j}(\mu ) \bigr\vert L^{g}_{j} \bigl\vert z_{j }(t-\mu ) \bigr\vert \eta^{-1}_{j }\eta_{j}\,d \mu \Biggr\} + e^{\lambda t} \bigl\vert P_{i_{t}} (\tau, t) \bigr\vert . \end{aligned}$$
(2.9)

Denote

$$ Q(t)=\sup_{s\leq t}\bigl\{ e^{\lambda s} \bigl\Vert z (s) \bigr\Vert _{\eta }\bigr\} \quad \text{for all } t\geq T_{0}. $$
(2.10)

Obviously, \(Q(t)\) is nondecreasing.

If \(Q(t)- e^{\lambda t} |z (t) |\) is eventually positive, then one can pick \(T_{1}> T_{0}\) satisfying

$$ Q(t)> e^{\lambda t} \bigl\Vert z (t) \bigr\Vert _{\eta } \quad \text{for all } t\geq T _{1}. $$

Then, for each \(t\geq T_{1}\), there exists \(\varepsilon_{t}>0\) such that

$$ Q(t)> e^{\lambda s} \bigl\Vert z (s) \bigr\Vert _{\eta } \quad \text{for all } s\in (t- \varepsilon_{t}, t+\varepsilon_{t}) $$

and

$$ Q(t) \equiv Q(s)\quad \text{for all } s\in (t-\varepsilon_{t}, t+ \varepsilon_{t}). $$

Therefore,

$$ Q(t)\equiv Q(T_{1})\quad \text{is a constant for all } t \geq T_{1}, $$

and there is \(T_{2}>T_{1}\) satisfying

$$ \bigl\Vert z (t) \bigr\Vert _{\eta } \leq e^{-\lambda t}Q(t)= e^{-\lambda t}Q(T_{1})< \frac{ \epsilon }{2 \max_{i\in S}\eta_{i}}\quad \text{for all } t \geq T_{2}. $$

If \(Q(t)- e^{\lambda t} |z (t) |\) is not eventually positive, then \(A=\{t\geq T_{0}:Q(t)= e^{\lambda t}\|z (t)\|_{\eta }\}\cap [s, + \infty )\neq \emptyset \) for all \(s\geq T_{0}\). Take \(T^{t}\geq T_{0}\) satisfying \(Q(T^{t})= e^{\lambda T^{t}}\|z (T^{t})\|_{\eta }\), \((U_{3})\) and (2.9) yield

$$\begin{aligned} 0&\leq D^{+}\bigl(e^{\lambda s} \bigl\vert z_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=T^{t}} \\ & \leq e^{\lambda T^{t}}\Biggl\{ -\bigl[a_{i_{T^{t}}}^{0} \bigl(T^{t}\bigr)\underline{b} _{i_{T^{t}}}-\lambda \bigr] \bigl\vert z_{i_{T^{t}}}\bigl(T^{t}\bigr) \bigr\vert \eta^{-1}_{i_{T^{t}}} \eta_{i_{T^{t}}}+ \sum _{j=1}^{n}\alpha_{i_{T^{t}}j}^{0} \bigl(T^{t} \bigr) L ^{f}_{j} \bigl\vert z_{j }\bigl(T^{t} \bigr) \bigr\vert \eta^{-1}_{j } \eta_{j} \\ & \quad {} + \sum_{j=1}^{n} \beta_{i_{T^{t}}j}^{0}\bigl(T^{t} \bigr) L ^{h}_{j} \bigl\vert z_{j }\bigl(T ^{t}-\sigma_{i_{T^{t}}j}^{0}\bigl(T^{t}\bigr) \bigr) \bigr\vert \eta^{-1}_{j }\eta_{j} \\ &\quad {} +\sum_{j=1}^{n} \gamma_{i_{T^{t}}j}^{0}\bigl(T^{t}\bigr) \int_{0}^{+ \infty } \bigl\vert K_{i_{T^{t}}j}(\mu ) \bigr\vert L^{g}_{j} \bigl\vert z_{j } \bigl(T^{t}-\mu \bigr) \bigr\vert \eta^{-1} _{j } \eta_{j}\,d\mu \Biggr\} + e^{\lambda T^{t}} \bigl\vert P_{i_{T^{t}}} \bigl(\tau, T^{t}\bigr) \bigr\vert \\ & \leq \Biggl\{ -\bigl[a_{i_{T^{t}}}^{0}\bigl(T^{t}\bigr) \underline{b}_{i_{T^{t}}}-\lambda \bigr] \eta_{i_{T^{t}}} + \sum _{j=1}^{n}\alpha_{i_{T^{t}}j}^{0} \bigl(T^{t} \bigr) L ^{f}_{j} \eta_{j} \\ & \quad {} + \sum_{j=1}^{n} \beta_{i_{T^{t}}j}^{0}\bigl(T^{t} \bigr) L ^{h}_{j} e^{ \lambda \sigma } \eta_{j} \\ & \quad {} +\sum_{j=1}^{n} \gamma_{i_{T^{t}}j}^{0}\bigl(T^{t}\bigr) \int_{0}^{+ \infty } \bigl\vert K_{i_{T^{t}}j}(\mu ) \bigr\vert e^{\lambda \mu } \,d\mu L^{g}_{j} \eta _{j} \Biggr\} Q\bigl(T^{t}\bigr)+ e^{\lambda T^{t}} \bigl\vert P_{i_{T^{t}}} \bigl(\tau, T^{t}\bigr) \bigr\vert \\ & \leq -\xi Q\bigl(T^{t}\bigr)+ e^{\lambda T^{t}} \bigl\vert P_{i_{T^{t}}} \bigl(\tau, T^{t}\bigr) \bigr\vert . \end{aligned}$$
(2.11)

Hence, (2.8) and (2.10) lead to

$$ \bigl\Vert z \bigl(T^{t}\bigr) \bigr\Vert _{\eta } \leq e^{-\lambda T^{t}}Q\bigl(T^{t}\bigr) \leq e^{-\lambda T^{t}}e^{\lambda T^{t}} \frac{1}{\xi } \bigl\vert P_{i_{T^{t}}} \bigl(\tau, T^{t} \bigr) \bigr\vert < \frac{ \epsilon }{2 \max_{i\in S}\eta_{i}}. $$

Similarly, one can derive that \(\|z (\chi )\|_{\eta } <\frac{\epsilon }{2 \max_{i\in S}\eta_{i}} \) provided that \(\chi >T^{t}\) with \(Q(\chi )= e^{\lambda \chi }\|z (\chi )\|_{\eta }\). Therefore, assuming that \(t>T^{t}\) and \(Q(t)> e^{\lambda t} |z (t) | \), one can take \(T^{t}_{*}\in [ T^{t}, t)\) satisfying

$$ Q\bigl(T^{t}_{*}\bigr)= e^{\lambda T^{t}_{*}} \bigl\Vert z \bigl(T^{t}_{*}\bigr) \bigr\Vert _{\eta }, \quad \text{and} \quad Q(s)> e^{\lambda s} \bigl\Vert z (s) \bigr\Vert _{\eta } \quad \text{for all } s \in (T^{t}_{*}, t]. $$

From the fact that \(\|z (T^{t}_{*})\|_{\eta } <\frac{\epsilon }{2 \max_{i\in S}\eta_{i}}\), we get

$$ Q(s)\equiv Q\bigl(T^{t}_{*}\bigr) \quad \text{for all } s \in (T^{t}_{*}, t], \quad \text{and} \quad \bigl\Vert z (t) \bigr\Vert _{\eta } \leq e^{-\lambda t} e^{\lambda T^{t} _{*}} \bigl\Vert z \bigl(T^{t}_{*}\bigr) \bigr\Vert _{\eta } < \frac{\epsilon }{2 \max_{i \in S}\eta_{i}}. $$

Finally, there is \(N=N(\tau )>0\) satisfying that

$$ \bigl\Vert z (t ) \bigr\Vert _{\eta }< \frac{\epsilon }{2 \max_{i\in S}\eta_{i}} \quad \text{for all } t>N. $$

This finishes the proof of Lemma 2.2. □

3 Asymptotically almost periodicity

Theorem 3.1

If \((U_{0})\), \((U_{1})\), \((U_{2})\), and \((U_{3})\) hold, then every solution of (1.1) with initial condition (2.1) is asymptotically almost periodic on \(\mathbb{R}^{+}\) and converges to an almost periodic function \(x^{*}(t)\) as \(t\rightarrow +\infty \), which is a unique almost periodic solution of system \((1.1)^{0}\).

Proof

Denote \(u(t)= (u_{1}(t), u_{2}(t),\ldots, u_{n}(t)) \) to be a solution of system \((1.1)^{0}\) in Lemma 2.2, and

$$\begin{aligned} &P_{i, q} ( t) \\ &\quad = -\bigl[a_{i}^{0}(t+t_{q})-a_{i}^{0}(t) \bigr]b_{i}\bigl(u_{i}(t+t_{q})\bigr)+ \sum _{j=1}^{n}\bigl[\alpha_{ij}^{0}(t+t_{q})- \alpha_{ij}^{0}(t)\bigr]f_{j}\bigl(u_{j}(t+t _{q} )\bigr) \\ & \qquad {}+ \sum_{j=1}^{n}\bigl[ \beta_{ij}^{0}(t+t_{q})-\beta_{ij}^{0}(t) \bigr]h_{j}\bigl(u _{j}\bigl(t-\sigma_{ij}^{0}(t+t_{q})+t_{q} \bigr)\bigr) \\ & \qquad {}+ \sum_{j=1}^{n} \beta_{ij}^{0}(t)\bigl[h_{j}\bigl(u_{j} \bigl(t-\sigma_{ij}^{0}(t+t _{q})+t_{q} \bigr)\bigr)-h_{j}\bigl(u_{j}\bigl(t-\sigma_{ij}^{0}(t )+t_{q}\bigr)\bigr)\bigr] \\ & \qquad {}+\sum_{j=1}^{n}\bigl[ \gamma_{ij}^{0}(t+t_{q})-\gamma_{ij}^{0}(t) \bigr] \int _{0}^{+\infty }K_{ij}(\mu )g_{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,d\mu\\ &\qquad {} + \bigl[I_{i } ^{0}(t+t_{q})-I_{i}^{0}(t)\bigr],\quad i\in S, \end{aligned}$$

where \(\{t_{q}\}_{q\geq 1}\subseteq \mathbb{R} \) is a sequence. Then

$$\begin{aligned} &u'_{i}(t+t_{q}) \\ &\quad = -a_{i}^{0}(t)b_{i}\bigl(u_{i}(t+t_{q}) \bigr)+\sum_{j=1}^{n}\alpha _{ij}^{0}(t)f_{j}\bigl(u_{j}(t+t_{q}) \bigr)+ \sum_{j=1}^{n}\beta_{ij}^{0}(t)h _{j}\bigl(u_{j}\bigl(t-\sigma_{ij}^{0}(t)+ t_{q}\bigr)\bigr) \\ &\qquad {}+ \sum_{j=1}^{n} \gamma_{ij}^{0}(t) \int_{0}^{+\infty }K_{ij}(\mu ) g _{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,d\mu \\ &\qquad {}+I_{i}^{0}(t)+P_{i, q} ( t), \quad i\in S, t+t_{q}\geq 0. \end{aligned}$$
(3.1)

In a similar way to the proof of (2.8), we can take \(\{t_{q}\}_{q \geq 1}\) satisfying

$$ \bigl\vert P_{i, q} ( t) \bigr\vert < \frac{1}{q} \quad \text{for all } i, q, t. $$
(3.2)

Note that \(\{u(t+t_{q})\} _{q\geq 1} \) is uniformly bounded and equiuniformly continuous, from the Arzela–Ascoli lemma, one can select a subsequence \(\{t_{q_{j}}\}_{j\geq 1}\) of \(\{t_{q}\}_{q\geq 1}\) to satisfy that \(\{u(t+t_{q_{j}})\}_{j\geq 1}\) (we also designate it by \(\{u(t+t_{q})\}_{q\geq 1}\)) is convergent uniformly to a bounded and continuous function \(x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\ldots,x ^{*}_{n}(t)) \) in any compact set of \(\mathbb{R}\). Consequently,

$$ \begin{aligned}[b] & \left . \textstyle\begin{array}{l} a_{i}^{0}(t )h_{i}(u_{i}(t+t_{q}))\quad \Rightarrow\quad a_{i}^{0}(t )h_{i}(x _{i}^{*}(t )), \\ \sum_{j=1}^{n}\alpha_{ij}^{0}(t)f_{j}(u_{j}(t +t_{q}))\quad \Rightarrow\quad \sum_{j=1}^{n}\alpha_{ij}^{0}(t)f_{j}(x_{j}^{*}(t )), \\ \sum_{j=1}^{n}\beta_{ij}^{0}(t)h_{j}(u_{j}(t-\sigma^{0}_{ij}(t )+t_{q}))\quad \Rightarrow\quad \sum_{j=1}^{n}\beta_{ij}^{0}(t)h_{j}(x _{j}^{*}(t-\sigma_{ij}^{0}(t ) )), \end{array}\displaystyle \right \}\\ & \quad \text{as } q \rightarrow +\infty \end{aligned} $$
(3.3)

in every compact set of \(\mathbb{R}\). Here, the symbol “⇒” represents “ is convergent uniformly to”. Now, we show that

$$ \begin{aligned}[b] &\sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{+\infty }K_{ij}(\mu )g _{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,d\mu \\ &\quad \Rightarrow \quad \sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{+\infty }K _{ij}(\mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu\\ & \quad (q\rightarrow +\infty ) \text{ on any compact set of $\mathbb{R}$.} \end{aligned} $$
(3.4)

For any \(\varepsilon >0\) and \([a, b]\subseteq \mathbb{R}\), \((U_{2})\) and the boundedness of u and \(x ^{*}\) entail that one can pick \(A^{*}>0\) to satisfy that

$$ \begin{aligned}[b] &\Biggl\vert \sum_{j=1}^{n} \gamma_{ij}(t) \int_{A^{*}}^{+\infty }K_{ij}( \mu )g_{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,d\mu \\ &\quad {}-\sum _{j=1}^{n}\gamma_{ij}(t) \int_{A^{*}}^{+\infty }K_{ij}(\mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu \Biggr\vert < \frac{ \varepsilon }{2} \end{aligned} $$
(3.5)

for all i, t, q. Note that \(\{u(t+t_{q})\}\) is convergent uniformly to \(x^{*}(t) \) on \([a-A^{*}, b]\), one can take a positive integer \(q^{*}\) to satisfy that, for \(q>q^{*}\) and \(t\in [a, b]\),

$$ \Biggl\vert \sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{A^{*}}K_{ij}(\mu )g _{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,du-\sum _{j=1}^{n}\gamma_{ij}(t) \int _{0}^{A^{*}}K_{ij}(\mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu \Biggr\vert < \frac{\varepsilon }{2}. $$

This and (3.5) produce that

$$\begin{aligned} & \Biggl\vert \sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{+\infty }K_{ij}( \mu )g_{j} \bigl(u_{j}(t+t_{q}-\mu )\bigr)\,d\mu -\sum _{j=1}^{n}\gamma_{ij}(t) \int_{0}^{+\infty }K_{ij}(\mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu \Biggr\vert \\ &\quad < \varepsilon,\quad \text{for all } q>q^{*}, t\in [a, b], \end{aligned}$$

which leads to (3.4). Hence, (3.1), (3.2), (3.3), and (3.4) suggest that \(\{u'_{i}(t+t_{q})\}_{q\geq 1}\) is convergent uniformly to

$$\begin{aligned} & {-} a_{i}^{0}(t )h_{i}\bigl(x_{i}^{*}(t )\bigr)+ \sum_{j=1}^{n}\alpha _{ij}^{0}(t)f_{j}\bigl(x_{j}^{*}(t )\bigr) \\ &\quad {}+ \sum_{j=1}^{n} \beta_{ij}^{0}(t)h_{j}\bigl(x_{j}^{*} \bigl(t-\sigma ^{0}_{ij}(t ) \bigr)\bigr)+\sum _{j=1}^{n}\gamma_{ij}(t) \int_{0}^{+ \infty }K_{ij}(\mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu +I_{i}^{0}(t) \end{aligned}$$

on every compact set in \(\mathbb{R}\). Furthermore, one can derive that \(x^{*}(t)\) is a solution of \((1.1)^{0}\) and

$$\begin{aligned} \bigl(x^{*}_{i}(t)\bigr)' & = - a_{i}^{0}(t )h_{i}\bigl(x_{i}^{*}(t )\bigr)+ \sum_{j=1}^{n}\alpha_{ij}^{0}(t)f_{j} \bigl(x_{j}^{*}(t )\bigr)+ \sum _{j=1} ^{n}\beta_{ij}^{0}(t)h_{j} \bigl(x_{j}^{*}\bigl(t-\sigma^{0}_{ij}(t ) \bigr)\bigr) \\ &\quad {}+\sum_{j=1}^{n} \gamma_{ij}(t) \int_{0}^{+\infty }K_{ij}( \mu )g_{j} \bigl(x_{j}^{*}(t -\mu )\bigr)\,d\mu +I_{i}^{0}(t) \quad \text{for all } t\in \mathbb{R}, i\in S. \end{aligned}$$
(3.6)

Hereafter, for any \(\epsilon >0\), according to Lemma 2.2, one can pick a relatively dense subset \(M_{\epsilon }\) in \(\mathbb{R}\) such that, for any \(\tau \in M_{\epsilon }\), there is \(N=N(\tau )>0\) obeying

$$ \bigl\vert u_{i}(s+t_{q}+\tau )-u_{i}(s+t_{q}) \bigr\vert \leq \eta_{i} \bigl\Vert u(s+t_{q}+\tau )-u(s+t _{q}) \bigr\Vert _{\eta }< \frac{\epsilon }{2} \quad \text{for all } s+t_{q}> N, $$

and

$$ \lim_{q\rightarrow +\infty } \bigl\vert u_{i}(s+t_{q}+ \tau )-u_{i}(s+t _{q}) \bigr\vert = \bigl\vert x^{*}_{i}(s +\tau )-x^{*}_{i}(s) \bigr\vert \leq \frac{\epsilon }{2}< \epsilon \quad \text{for all } s\in \mathbb{R}, i\in S, $$
(3.7)

which, together with definitions of AP in [33, 34], proves that \(x^{*}(t)\) is an almost periodic solution of \((1.1)^{0}\).

Now, let \(x(t) \) be an arbitrary solution of the initial value problem (1.1) and (2.1), we turn to demonstrate that \(\lim_{t\rightarrow +\infty }x(t)=x^{*}(t)\). Set \(y(t)=\{y_{ j}(t) \}=\{x_{ j}(t)-x^{*}_{ j}(t) \}=x(t)-x^{*}(t)\) and

$$\begin{aligned} B_{i } ( t) = & - a_{i}^{1}(t ) b_{i}\bigl(x_{i}(t )\bigr)+ \sum _{j=1}^{n} \alpha_{ij}^{1}(t ) f_{j}\bigl(x_{j}(t )\bigr)+ \sum _{j=1}^{n} \beta_{ij}^{1}(t ) h_{j}\bigl(x_{j}\bigl(t-\sigma_{ij}(t ) \bigr) \bigr) \\ &{}+ \sum_{j=1}^{n} \beta_{ij}^{0}(t ) \bigl[h_{j}\bigl(x_{j}\bigl(t-\sigma_{ij}(t ) \bigr)\bigr)-h_{j}\bigl(x_{j}\bigl(t-\sigma_{ij}^{0}(t ) \bigr)\bigr)\bigr] \\ &{}+\sum_{j=1}^{n} \gamma_{ij}^{1}(t ) \int_{0}^{+\infty }K_{ij}( \mu )g_{j} \bigl(x_{j}(t -\mu )\bigr)\,d\mu + I_{i }^{1}(t ), \quad i\in S. \end{aligned}$$

Thus

$$\begin{aligned} y_{i}'(t) =&-a_{i}^{0}(t) \bigl[b_{i}\bigl(x_{i}(t)\bigr)-b_{i} \bigl(x^{*}_{i}(t)\bigr)\bigr]+\sum ^{n}_{j=1}\alpha_{ij}^{0}(t) \bigl(f_{j}\bigl(y_{j}(t )+x^{*}_{j}(t )\bigr) -f_{j}\bigl(x ^{*}_{j}(t )\bigr)\bigr) \\ &{}+\sum^{n}_{j=1}\beta_{ij}^{0}(t) \bigl(h_{j}\bigl(y_{j}\bigl(t-\sigma_{ij}^{0}(t) \bigr)+x ^{*}_{j}\bigl(t-\sigma_{ij}^{0}(t) \bigr)\bigr) -h_{j}\bigl(x^{*}_{j}\bigl(t- \sigma_{ij}^{0}(t)\bigr)\bigr)\bigr) \\ &{}+\sum^{n}_{j=1}\gamma_{ij}^{0}(t) \int_{0}^{+\infty }K_{ij}(\mu ) \bigl(g _{j}\bigl(y_{j}(t-\mu )+x^{*}_{j}(t- \mu )\bigr) -g_{j}\bigl(x^{*}_{j}(t-\mu )\bigr) \bigr)\,d \mu\\ &{} +B_{i } ( t),\quad i\in S. \end{aligned}$$

Since \(a_{i}^{1}, \sigma_{ij}^{1}\in C_{0}(\mathbb{R}^{+}, \mathbb{R} ^{+} )\), \(I_{i}^{1}, \alpha_{ij}^{1}, \beta_{ij}^{1}, \gamma_{ij}^{1} \in C_{0}(\mathbb{R}^{+}, \mathbb{R} )\) and x is uniformly continuous on \(\mathbb{R}\), one can take a constant \(T_{0}^{\varphi }>0\) to satisfy that, for every \(\epsilon >0\),

$$ \bigl\vert B_{i } ( t) \bigr\vert < \xi \frac{\epsilon }{2 \max_{i\in S}\eta_{i}}\quad \text{for all } t>T_{0}^{\varphi }, i\in S, $$

and

$$\begin{aligned} & D^{-}\bigl(e^{\lambda s} \bigl\vert y_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=t} \\ &\quad \leq e^{\lambda t}\Biggl\{ -\bigl[a_{i_{t}}^{0}(t) \underline{b}_{i_{t}}- \lambda \bigr] \bigl\vert y_{i_{t}}(t) \bigr\vert \eta^{-1}_{i_{t}}\eta_{i_{t}}+ \sum _{j=1}^{n} \alpha_{i_{t}j}^{0}(t ) L ^{f}_{j} \bigl\vert y_{j }(t ) \bigr\vert \eta^{-1}_{j }\eta_{j} \\ & \qquad {} + \sum_{j=1}^{n} \beta_{i_{t}j}^{0}(t ) L ^{h}_{j} \bigl\vert y_{j }\bigl(t- \sigma_{i_{t}j}^{0}(t)\bigr) \bigr\vert \eta^{-1}_{j }\eta_{j} \\ & \qquad {} +\sum_{j=1}^{n} \gamma_{i_{t}j}^{0}(t) \int_{0}^{+\infty } \bigl\vert K _{i_{t}j}(\mu ) \bigr\vert L^{g}_{j} \bigl\vert y_{j }(t-\mu ) \bigr\vert \eta^{-1}_{j }\eta_{j}\,d \mu \Biggr\} + e^{\lambda t} \bigl\vert B_{i_{t}} ( t) \bigr\vert \quad \text{for all } t>T_{0} ^{\varphi }. \end{aligned}$$

Define

$$ \varGamma (t)=\sup_{s\leq t}\bigl\{ e^{\lambda s} \bigl\Vert y (s) \bigr\Vert _{\eta }\bigr\} \quad \text{for all } t \in \mathbb{R}. $$

Then, an argument similar to that used in Lemma 2.2 shows that there exists \(T^{\varphi }\geq T_{0}^{\varphi }\) satisfying

$$ \bigl\Vert y (t) \bigr\Vert _{\eta }< \frac{\epsilon }{2 \max_{i\in S}\eta_{i}}\quad \text{for all } t \geq T^{\varphi }, $$

which implies

$$ \lim_{t\rightarrow +\infty } x(t)=x^{*}(t), \quad \text{and} \quad x(t) \in \operatorname{AAP}\bigl(\mathbb{R},\mathbb{R}^{n}\bigr). $$

Therefore, \((1.1)^{0}\) has a unique almost periodic solution \(N^{*}(t)\). The proof is finished. □

Remark 3.1

Under the conditions in Lemma 2.2, from Lemma 2.1 and Lemma 2.2, by applying a similar way as that in Theorem 3.1 of [13], one can show that every solution \(x(t )\) of \((1.1)^{0}\) converges exponentially to \(x ^{* }(t )\) as \(t\rightarrow +\infty \). Since \(\operatorname{AP}(\mathbb{R},\mathbb{R} ) \) is a proper subspace of \(\operatorname{AAP}( \mathbb{R},\mathbb{R} )\), one can easily see that all the results on \((1.1)^{0}\) in [13] are special ones of Theorem 3.1 in this paper. Most recently, the authors in [36] established asymptotically almost periodicity on shunting inhibitory cellular neural networks with time-varying delays and continuously distributed delays. However, the asymptotically almost periodicity on recurrent neural networks without the assumption E and the condition \(b_{i} (u)=u\) has not been explored in [36]. This implies that Theorem 3.1 generalizes and complements the main results of [13, 36].

4 A numerical example

Example 4.1

Regard the following asymptotically almost periodic recurrent neural networks:

$$ \textstyle\begin{cases} x_{1}'(t)=-(10+\cos \sqrt{2}t +\frac{1}{1+ \vert t \vert })(20x_{1}(t)+\arctan x_{1}(t)) \\ \hphantom{x_{1}'(t)=}{}+(\cos \sqrt{3}t+\frac{1}{ \vert t \vert +3})f_{1}(x_{1}(t ))+(\cos \sqrt{3}t+\frac{1}{ \vert t \vert +3}) f_{2}(x_{2}(t )) \\ \hphantom{x_{1}'(t)=}{}+(\cos \sqrt{5}t+\frac{1}{ \vert t \vert +2})h_{1}(x_{1}(t-2))+(\cos \sqrt{5}t+\frac{1}{ \vert t \vert +2}) h_{2}(x_{2}(t-2)) \\ \hphantom{x_{1}'(t)=}{}+(\cos \sqrt{7}t+\frac{1}{ \vert t \vert +2}) \int_{0}^{+\infty } e^{-2\mu } g _{1}(x_{1}(t-\mu ))\,d\mu +(\cos \sqrt{7}t \\ \hphantom{x_{1}'(t)=}{} +\frac{1}{ \vert t \vert +2}) \int_{0}^{+\infty } e^{-2\mu } g_{2}(x_{2}(t- \mu ))\,d\mu +100\sin t+ \frac{1}{5 \vert t \vert +1}, \\ x_{2}'(t)=-(10+\sin \sqrt{2}t +\frac{1}{1+ \vert t \vert })(30x_{2}(t)+\arctan x_{2}(t)) \\ \hphantom{x_{2}'(t)=}{}+(\cos \sqrt{11}t+\frac{1}{ \vert t \vert +3})f_{1}(x_{1}(t ))+(\cos \sqrt{11}t+\frac{1}{ \vert t \vert +3}) f_{2}(x_{2}(t )) \\ \hphantom{x_{2}'(t)=}{}+(\cos \sqrt{15}t+\frac{1}{ \vert t \vert +2})h_{1}(x_{1}(t-2))+(\cos \sqrt{15}t+\frac{1}{ \vert t \vert +2}) h_{2}(x_{2}(t-2)) \\ \hphantom{x_{2}'(t)=}{}+(\cos \sqrt{17}t+\frac{1}{ \vert t \vert +2}) \int_{0}^{+\infty } e^{-2 \mu } g_{1}(x_{1}(t-\mu ))\,d\mu +(\cos \sqrt{17}t \\ \hphantom{x_{2}'(t)=}{} +\frac{1}{ \vert t \vert +2}) \int_{0}^{+\infty } e^{-2\mu } g_{2}(x_{2}(t- \mu ))\,d\mu +100\cos t+ \frac{1}{25 \vert t \vert +1}. \end{cases} $$
(4.1)

Here \(h_{1}(x)=h_{2}(x)= \frac{1}{20}\arctan x\), \(f_{1}(x)=f_{2}(x)=g _{1}(x)=g_{2}(x)=\frac{1}{20}x\),

$$\begin{aligned}& a_{1}(t)=(10+\cos \sqrt{2}t) +\frac{1}{1+ \vert t \vert },\qquad a_{2}(t)= (10+\sin \sqrt{2}t) +\frac{1}{1+ \vert t \vert }, \\& b_{1}(u)=(20u+\arctan u),\qquad b_{2}(u)=(30u+\arctan u) \end{aligned}$$

and

( α 11 ( t ) α 12 ( t ) α 21 ( t ) α 22 ( t ) ) = ( ( cos 3 t + 1 | t | + 3 ) ( cos 3 t + 1 | t | + 3 ) ( cos 11 t + 1 | t | + 3 ) ( cos 11 t + 1 | t | + 3 ) ) , ( β 11 ( t ) β 12 ( t ) β 21 ( t ) β 22 ( t ) ) = ( ( cos 5 t + 1 | t | + 2 ) ( cos 5 t + 1 | t | + 2 ) ( cos 15 t + 1 | t | + 2 ) ( cos 15 t + 1 | t | + 2 ) ) , ( γ 11 ( t ) γ 12 ( t ) γ 21 ( t ) γ 22 ( t ) ) = ( ( cos 7 t + 1 | t | + 2 ) ( cos 7 t + 1 | t | + 2 ) ( cos 17 t + 1 | t | + 2 ) ( cos 17 t + 1 | t | + 2 ) ) .

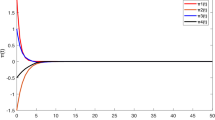
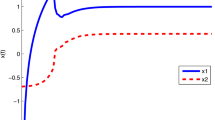
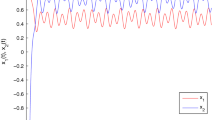
Let \(\eta_{i }=1\), \(L ^{f}_{j}=L^{h}_{j}=L^{g}_{j}=\frac{1}{20}\), \(\underline{b}_{1}=20\), \(\underline{b}_{2}=30\), \(\xi =5\), \(i,j=1,2 \), we can see that system (4.1) obeys all the conditions in Theorem 3.1. Therefore, each solution of (4.1) is convergent to the same almost periodic function as \(t\rightarrow +\infty \), which is also an asymptotically almost periodic function on \(\mathbb{R}^{+}\). This fact can be revealed in Fig. 1: Numerical solutions of system (4.1) with initial values \((10,-30)\), \((-30,40)\), \((30,-60)\), respectively.

Figure 1
figure 1

Numerical solutions of system (4.1) with different initial values

Full size image

Remark 4.1

Clearly,

$$ a_{1}(t)=(10+\cos \sqrt{2}t) +\frac{1}{1+ \vert t \vert } \quad \text{and} \quad a_{2}(t)= (10+\sin \sqrt{2}t) +\frac{1}{1+ \vert t \vert } $$

are not almost periodic functions, and \(b_{1}(u)=(20u+\arctan u)\) and \(b_{2}(u)=(30u+\arctan u)\) do not satisfy that \(b_{i}(u)=u\) (\(i \in S\)). Thus, all the results established in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32, 36] cannot be applied to imply that all the solutions of (4.1) converge globally to the almost periodic solution. On the other hand, to the best of the authors’ knowledge, there is no research work concerning the asymptotically almost periodicity on recurrent neural networks without the assumption E and the condition \(b_{i} (u)=u\). Therefore, the results established in this paper are essentially new.

5 Conclusions

In this paper, avoiding the exponential dichotomy theory, the asymptotically almost periodicity on recurrent neural networks involving mixed delays has been explored. By combining the Lyapunov function method with differential inequality approach, some sufficient assertions have been gained to validate the global convergence of the addressed model. Particularly, our conditions are easily checked in practice by simple inequality methods, and the approach adopted in this paper provides a possible way to research the topic on asymptotically almost periodic dynamics of other nonlinear neural network models. In future research, we will research the dynamics for asymptotically almost periodic Cohen–Grossberg neural network models.