Selection history affects very early expression of wood properties in Pinus radiata

Abstract

Trees in breeding programmes are often selected at 1/4–1/3 of rotation, called ‘early selection’, which is typically between 8 and 10 years in radiata pine. However, differences between populations and genotypes selected for either basic density or wood stiffness are already apparent at age 2. We report the application of very early screening techniques for wood properties in the New Zealand Radiata Pine Breeding Programme deployment populations. Approximately 3000 trees representing three populations with 92 families and 10 clones were grown in a common garden trial, leaning for 21 months to separate compression and opposite wood. The trees were harvested and analysis carried out separately by wood type. The trial showed the existence of large variability in wood properties at early age, in some cases similar to variability near rotation age, and moderate to high degree of genetic control ($0.35 \le h^2 \le 0.71$). The genetic association between traits was strong, particularly between wood stiffness and longitudinal shrinkage ($-\,0.69$) and between longitudinal and volumetric shrinkage (0.83), suggesting that improving stiffness would also have a strong effect on improving dimensional stability. Basic density was also associated with stiffness and shrinkage, but with lower predictive capacity. These results can be used for roguing deployment populations-which already contain superior growing trees-and quickly upgrade the wood quality of seeds and clones currently available to New Zealand forest growers. We discuss necessary modifications to turn this research work into operation to screen any new material before commercial release.

Introduction

Trees are the largest and longest-living organisms in the world, and experience substantial changes in dimensions and structural composition as they age. These changes create obvious patterns for their external attributes (like total height, stem diameter, crown size, biomass, etc.) but also for their wood properties (wood density, stiffness, dimensional stability, chemical composition, etc.).

Variability of wood properties within a tree and within a species can be as large as differences between species. Moreover, tree growth induces typical radial patterns (Lachenbruch et al. 2011) that complicate assessment. Some traits, for example cellulose microfibril angle—which drives wood stiffness in young trees—start with very large between-tree differences that reduce with age. In contrast, other traits like wood density—which drives wood stiffness in older trees—start with small between-tree differences that increase with age (Cave and Walker 1994; Burdon et al. 2004; Chauhan and Walker 2006).

Work on commercial tree species suggests that typical radial patterns possess considerable within-species genetic variability. Some examples are Pinus radiata (Dungey et al. 2006, wood density, modulus of elasticity and microfibril angle), Picea sitchensis (McLean et al. 2016, wood density, modulus of elasticity & rupture, and microfibril angle), Eucalyptus globulus (Downes et al. 2012, pulp yield and cellulose content), Eucalyptus nitens (Hamilton et al. 2007, wood density, decay & gross shrinkage), etc.

Wood properties are often assessed in mature trees or, in breeding programmes, between 1/4 and 1/3 of the economic rotation, which is termed early selection. In the New Zealand Pinus radiata (radiata pine) breeding programme, assessments are traditionally conducted when the trees are 10 m tall, which is between 8 and 10 years of age for an average 26-year commercial rotation. Considering that we are already observing early variability at age 8–10, one might ask if it would be possible to observe it even earlier. Furthermore, we would like to know if selection by the breeding programme is influencing variability of wood properties from much earlier than the selection age.

Studying these changes is often difficult in trees, as it is very time consuming both in the time needed by the trees to achieve the typical assessment age, but also for measuring highly variable properties. We can reframe the problem and instead study genetic variability in very young trees, assuming we want to meet technical product thresholds, and accepting there will be a reduction of age-age correlations with rotation-age performance (Apiolaza 2009). As a thought experiment, we can continue to run earlier assessments up to a point where we break the correlation with typical-age assessments or we are unable to measure the properties of interest.

Apiolaza et al. (2011a) showed that variability of wood properties between clones selected at age 8–10 years could be observed as early as 8 months of age. However, the amount of wood available for evaluation was too small to be practical. Later work measured trees at 2 years of age (Apiolaza et al. 2011b), easily detecting variability and with enough material to simplify mass screening with fast and cheap techniques. The results were promising, but trees were planted directly at a site with more environmental variability than expected, introducing noise in the growth patterns and reducing selection accuracy.

This article reports a replication of the previous experiment with substantial improvements: 1—using both families and clones structured in three populations, 2—planting in bags to achieve better control of the environment, and 3—six times the sample size (assessing more than three thousand radiata pine trees).

The populations were subject to selection with different objectives: higher growth and wood density (Seed Orchard), higher growth and wood stiffness (Clonal Programme), and a combination of traits (New Selections). This permits testing whether selecting on wood properties at 8–10 years affects performance on the next generation from very early age (2 years).

To minimise the role of environmental variability the trees were grown in bags, with slow release fertilisation, irrigation and a compact design. Additional environmental noise was removed by tilting the trees, separating opposite and reaction wood to eliminate random arcs of compression wood.

Very early screening makes feasible using larger sample size, while simultaneously reducing time to assessment. There are obvious trade-offs, like the expected reduction of the age-age correlations with rotation age. Some drawbacks can be solved by changing the problem to rely on first-pass-the-post of technical thresholds, but we still may have to quantify the correlation reduction for other traits (e.g. chemical composition or growth).

In this article we answer the following research questions:

• 1. Can breeding achieve very early differences in wood properties?

• 2. Can we detect very early wood properties differences between populations and trees within populations?

• 3. Is the assessed variability under genetic control?

Materials and methods

Traits of interest

Different end-products have different sets of requirements. Structural wood needs to meet stiffness thresholds which vary between markets. Moreover, dimensional stability has a large effect on recovery of final products, as pieces with defects (e.g. twist or cup) are downgraded to cheaper products.

Wood stiffness (S in GPa), measured as Modulus of Elasticity, is related to both acoustic velocity (V, which in turn is greatly affected by Microfibril Angle, MFA) and wood density ($\rho$):

$$\begin{aligned} S = \rho V^2 \end{aligned}$$

(1)

Stiffness can be calculated at green and dry stages; this article will focus on the latter. There is plenty of variability between trees for V at very early age, when MFA is at its highest and basic density is near its lowest. In outerwood there is little variability for MFA, which has reached its minimum, but plenty of variability for density (Apiolaza et al. 2013). The variability of stiffness in corewood can be better explained by V (and therefore MFA) than by wood density value (Chauhan and Walker 2006). In contrast, outerwood stiffness can be better explained by wood density.

Wood is an anisotropic material, with different shrinkage in the longitudinal, radial and tangential directions. Samples were assessed for longitudinal (LSHR) and volumetric (VSHR) shrinkage, and the analyses emphasize the former as it is quite important in corewood, making sawn timber a less stable product.

Genetic trial

The genetic trial was established in a site owned by the Christchurch City Council, at Harewood, Christchurch. It included 92 families and 10 clones representing 129 parents. There were 54 controlled-pollinated families following an ‘opportunistic’ mating design (that is, not following any crossing rules except for availability of pollen and female cones) and 38 open-pollinated families. The clones are related through the pedigree to the rest of the tested material. In total the trial contained 3059 assessed trees.

Fig. 1

Overview of the Harewood trial at 11 months of age

The experiment was set up to minimize environmental variability, with a flat ground covered with a permeable plastic matting to eliminate the presence of weeds. All trees were planted in 75 L bags filled with potting mix containing slow-release fertilizer and drip irrigated (Fig. 1). Three months after planting the trees were leaned and tied at a 15$^{\circ }$ angle and maintained in that position until they completed 2 years of age (see Fig. 2 for a close-up of the leaning system).

Trees were harvested after 2 years, cutting 100 mm long bolts from the base of the trees. Bolts were sawn lengthwise to separate a compression wood sample (CW) and an opposite wood sample (OW, also known as normal wood). Wood properties were assessed on each of the samples following the protocols and tools described by Chauhan et al. (2013). In summary, samples were weighed to an accuracy of 0.001 g and measured for volume by the water displacement method to an accuracy of 0.01 cm$^3$. Spherical-headed map pins were inserted in the opposite end faces of each specimen, and rested on the concave ends of a micrometer jig, ensuring repeatability of the length measurements. All samples were dried in an oven set at 35 $^{\circ }{\textrm{C}}$ until they achieved a constant weight. Acoustic velocity was measured using WoodSpec, a resonance-based acoustic tool designed for processing small samples. Density, shrinkage and modulus of elasticity were calculated using standard formulas (Walker 2006).

Fig. 2

Detail of leaning tree at 11 months of age

The trial was designed as randomized complete block design with 30 replicates, considering the following terms at the univariate level:

$$\begin{aligned} \varvec{y}_i = \varvec{X}_i \varvec{m}_i + \varvec{Z}_{1i} \varvec{b}_i + \varvec{Z}_{2i} \varvec{a}_i + \varvec{Z}_{3i} \varvec{f}_i + \varvec{Z}_{4i} \varvec{c}_i + \varvec{e}_i \end{aligned}$$

(2)

where $\varvec{y}_i$ is the $i^{th}$ response variable of interest (e.g. wood density, MoE, etc), $\varvec{m}_i$ is the vector of fixed effects for the intercept and population (Breeding Programme, Clonal Programme and Seed Orchard), $\varvec{b}_i$ represents the random effect of a block (replicate), $\varvec{a}_i$ is the vector of random additive genetic effects (introduced via the pedigree of the genetic material), $\varvec{f}_i$ is the vector of random family effects estimating 1/4 of dominance (fitted only for controlled-pollinated families), $\varvec{c}_i$ is the vector of random clonal effects (fitted only for clonal material), and $\varvec{e}_i$ is the vector of random residuals, which include any measurement errors plus environmental and genetic effects not captured by the other terms of the model. The incidence matrices $\varvec{X}_i$, $\varvec{Z}_{1i}$, $\varvec{Z}_{2i}$, $\varvec{Z}_{3i}$ and $\varvec{Z}_{4i}$ relate the phenotypic observations to their respective effects.

The expected value of $\varvec{y}_i$ is $\varvec{X}_i \varvec{m}_i$, while the random effects have a variance of $\varvec{B}_i = \varvec{I} \sigma _{b_i}^2$, $\varvec{G}_i = \varvec{A} \sigma _{a_i}^2$, $\varvec{F}_i = \varvec{I}\sigma _{f_i}^2$, $\varvec{C}_i = \varvec{I} \sigma _{c_i}^2$ and $\varvec{R}_i = \varvec{I} \sigma _{\varepsilon _i}^2$ for blocks, additive genetic, family, clone and residuals respectively. $\varvec{A}$ is the additive genetic numerator relationship matrix among individuals, which summarises the pedigree. All factors are assumed to be independent of each other; that is, with zero covariance.

This model was later extended to a multivariate version, allowing for unstructured correlation matrices for each of the random effects, permitting the direct estimation of the genetic correlations between the traits.

If data are ordered within traits, a multivariate (bivariate as an example) can be expressed as:

$$\begin{aligned} \left[ \begin{array}{cc} \varvec{y}_1\\ \varvec{y}_2 \end{array}\right]&= \left[ \begin{array}{cc} \varvec{X}_1 &{} \varvec{0}\\ \varvec{0} &{} \varvec{X}_2 \end{array}\right] \left[ \begin{array}{cc}\varvec{m}_1\\ \varvec{m}_2 \end{array}\right] + \left[ \begin{array}{cc} \varvec{Z}_{11} &{} \varvec{0}\\ \varvec{0} &{} \varvec{Z}_{12} \end{array}\right] \left[ \begin{array}{cc} \varvec{b}_1\\ \varvec{b}_2 \end{array}\right] + \left[ \begin{array}{cc} \varvec{Z}_{21} &{} \varvec{0}\\ \varvec{0} &{} \varvec{Z}_{22} \end{array}\right] \left[ \begin{array}{cc} \varvec{a}_1\\ \varvec{a}_2 \end{array}\right] \nonumber \\&\quad + \left[ \begin{array}{cc} \varvec{Z}_{31} &{} \varvec{0}\\ \varvec{0} &{} \varvec{Z}_{32} \end{array}\right] \left[ \begin{array}{cc} \varvec{f}_1\\ \varvec{f}_2 \end{array}\right] + \left[ \begin{array}{cc}\varvec{Z}_{41} &{} \varvec{0}\\ \varvec{0} &{} \varvec{Z}_{42}\end{array}\right] \left[ \begin{array}{cc} \varvec{c}_1\\ \varvec{c}_2 \end{array}\right] + \left[ \begin{array}{cc} \varvec{e}_1\\ \varvec{e}_2 \end{array}\right] \end{aligned}$$

(3)

Heritabilities ($h_i^2$) for the ith trait were estimated as the ratio of the additive variance to the sum of all variances fitted for that trait:

$$\begin{aligned} h_i^2 = \frac{\sigma _{a_i}^2}{\sigma _{b_i}^2 + \sigma _{a_i}^2 + \sigma _{f_i}^2 + \sigma _{c_i}^2 + \sigma _{\varepsilon _i}^2} \end{aligned}$$

(4)

where all the variance components are as described before. The genetic correlations between traits 1 and 2 ($r_{a_{12}}$) were estimated directly from the unstructured multivariate additive genetic matrix as:

$$\begin{aligned} r_{a_{12}} = \frac{\sigma _{a_{12}}}{\sqrt{\sigma _{a_1}^2 \sigma _{a_2}^2}} \end{aligned}$$

(5)

where $\sigma _{a_{12}}$ is the additive genetic covariance between traits 1 and 2, and $\sigma _{a_i}^2$ is the additive genetic variance for trait i.

The standard errors for the heritabilities and genetic correlations were obtained using parametric bootstrapping. All statistical analyses were conducted with the R Statistical System (R Core Team 2022), the ASReml-R (Buttler et al. 2017) and asremlPlus (Brien 2021) packages.

Results

Variability

Table 1 presents descriptive statistics for wood density, shrinkage and modulus of elasticity in both compression and opposite wood. In the case of wood density there is increasing variability from green to dry and basic density. In opposite wood there is much more variability for shrinkage (39% longitudinal, 25% volumetric), followed by modulus of elasticity (15%) and, finally, wood density (6%).

Table 1 Descriptive statistics for green density (GDEN in $\mathrm{kg\,m}^{-3}$), dry density (DDEN in $\mathrm{kg\,m}^{-3}$), basic density (BDEN in $\mathrm{kg\,m}^{-3}$), longitudinal shrinkage (LSHR in %), volumetric shrinkage (VSHR in %) and modulus of elasticity (MoE in GPa), presented separately for compression and opposite wood

At age 2 trees display abundant phenotypic variability, which is on par (in terms of Coefficient of Variation) with values at typical selection age (1/4–1/3 of rotation).

Fig. 3

Phenotypic variability for compression wood (CW) and opposite wood (OW), for basic density, longitudinal shrinkage and modulus of elasticity. Each point represents an individual sample, while red boxplots summarize the distribution

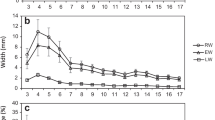
Figure 3 highlights the overall differences for mean and variability between opposite and compression wood for three selection criteria. These differences are behind the rationale of leaning trees and analyzing wood types separately, instead of working with an ‘average’ trait for a stem with intermixed opposite and compression wood. The largest difference between wood types is for basic density.

Fig. 4

Scatterplots for the relationship between longitudinal shrinkage and modulus of elasticity separated by wood type (CW compression wood, OW opposite wood)

The differences do not stop at the individual variable, as they are even more dramatic for the relationships between selection criteria. As an example, Fig. 4 separates the relationship between longitudinal shrinkage and stiffness by wood type, ranging from no association (for compression wood) to strong negative association (for opposite wood).

The proportion of compression wood in small samples from leaning 2-year-old trees is much larger than for standing trees (for example Apiolaza et al. 2011a, Fig. 2). Considering the contrast between compression and opposite wood properties—and the commercial importance of the latter—justifies concentrating the rest of the presentation of results on opposite wood (Chauhan et al. 2013).

Population differences

The genetic material tested in Harewood comes from several populations that were treated as a fixed effect in model (3). Although all the material has been bred for growth and form, there have been different emphases on selection criteria. Seed Orchard material has also been selected for basic density, while the Clonal Programme material has focused more on wood stiffness. Selection for these two wood properties happened in genetic trials at the traditional selection age (around 8–10 years).

The average basic density for Seed Orchard material (296.93 kg m$^{-3}$) is significantly better than for New Selections (292.28 kg m$^{-3}$), but not significantly better than for the Clonal Programme (291.43 kg m$^{-3}$), which although lower on average, also displayed a higher standard error (more uncertainty). In contrast, the Modulus of Elasticity for the Clonal Programme (2.85 GPa) was significantly higher than for the other two populations (2.47 and 2.48 GPa) although also with a higher standard error. These differences in MoE had an impact on shrinkage, with the Clonal Programme showing significantly lower longitudinadinal shrinkage (0.57%) than the other two populations (0.80 and 0.87%), and significantly lower volumetric shrinkage (16.51%) than the Seed Orchard material (18.96%).

Table 2 shows the population means and their standard errors for basic density, modulus of elasticity, longitudinal shrinkage and volumetric shrinkage at 2 years of age. Interestingly, differences in intercepts for trajectories of wood properties resulting from selection at 8 years are already apparent and statistically significant at 95% when progeny are only 2 years old (significantly different population means marked with different letters).

Table 2 Population means (and standard errors) for basic density (BDEN in $\mathrm{kg\, m}^{-3}$), longitudinal shrinkage (LSHR in %), volumetric shrinkage (VSHR in %) and modulus of elasticity (MoE in GPa) at 2 years of age

Genetic control

All wood properties are under substantial additive genetic control (see Table 3). Heritabilities ranged from 0.35 (modulus of elasticity) up to 0.71 (longitudinal shrinkage), with narrow 95% confidence intervals that excluded 0.

Both basic density and predicted modulus of elasticity—selection criteria usually assessed in the breeding programme—displayed strong and negative correlations with shrinkage (Table 3), and a positive correlation between them (0.83). Modulus of elasticity was a better predictor of longitudinal shrinkage than basic density (correlation of $-\,0.69$ vs $-\,0.51$). In contrast, basic density was a better predictor of volumetric shrinkage than modulus of elasticity (correlation of $-\,0.61$ vs $-\,0.34$). There was also a strong positive association between longitudinal and volumetric shrinkage (0.83). None of the 95% confidence intervals included 0.

Table 3 Estimated heritabilities (diagonal) and additive genetic correlations (below diagonal), and their 95% confidence interval (between brackets) for basic density (BDEN), longitudinal shrinkage (LSHR), volumetric shrinkage (VSHR) and modulus of elasticity (MoE) at 2 years of age

As usual, the genetic correlations apply to population level, but exploring the parental breeding values it is possible to see genotypes with large deviations from the overall trend. As an example, Fig. 5 displays a scatterplot of the breeding values for modulus of elasticity versus density, in which a couple of genotypes (new crosses in the breeding programme) express both MoE and BDEN substantially higher than the majority of the population.

Fig. 5

Scatterplots between the breeding values (expressed as deviation from the overall mean) for modulus of elasticity and basic density

Discussion

Variability

There is a common expectation that the properties assessed in younger trees will somewhat display lower variability. Nevertheless, when scaling by differences of mean (that is, using coefficient of variation) there is little difference between 2-year-old trees and adult plantation trees for some traits. For example, Kumar et al. (2007, in Table 2, page 15) point out that in a 20-year-old progeny trial, the variability of basic density and standing-tree acoustic valocity (an estimator of MoE) were 8 and 12%, respectively. These values are similar to the ones presented in Table 1 for opposite wood: 11 and 12%. In contrast, longitudinal shrinkage appears to be lower in our trial, with 20% compared to the results of both similarly aged trees (Apiolaza et al. 2011b, 27%), 20-year-old (Pang and Herritsch 2005, 82%) and 27-year-old (Wang et al. 2008, 85%) trees. There is no single, obvious explanation for this difference, but separating opposite from compression wood and changing spiral grain angle might contribute to this difference. When we assess vertical trees (in contrast with leaning trees) we are modeling an average relationship between variables. This probably partly accounts for the variability observed in the relationship between MoE and BDEN by Apiolaza (2009), as well as the single trait variability differences.

When looking at the parental breeding values (expressed as deviations from the overall mean) for the deployment populations, there were large differences for basic density: $-\,15.5$ and 7.3 kg m$^{-3}$ for the Clonal Programme and Seed Orchard respectively. This 22.8 kg m$^{-3}$ difference is approximately 7% of the overall mean. The differences for modulus of elasticity are smaller: 0.354 and 0.147 GPa for the Clonal Programme and Seed Orchard respectively. These differences are already noticeable at one year of age (Apiolaza et al. 2011a) and obvious by 2 years, as in this trial.

Moving to a progeny trial grown in bags improved the control of environmental noise compared to Apiolaza et al. (2011b), with which the Harewood trial has a substantial pedigree overlap. However, the earlier experiment only included the Seed Orchard population. Heritability estimates and their accuracy increased for all traits, although they still were within the credible intervals produced in the previous article.

There was a strong negative association between basic density and both longitudinal and volumetric shrinkage. There was a moderate positive association between wood density and modulus of elasticity. There was also a negative association between MoE and longitudinal shrinkage, implying that stiffer wood is less likely to shrink. Meylan (1972) and Cave and Walker (1994) made the physical argument for the microfibril angle of cellulose microfibrils (MFA) dominating both stiffness and longitudinal shrinkage variation in corewood. Similar results were observed by Ivković et al. (2008) and Sharma et al. (2016).

It is important to make clear that forest growers should base their choice of genetic material on the breeding values of specific individuals (or total genetic value for clones) not simply on the population means. Despite the significant differences in means, it is possible to do much better within a given population by carefully selecting the best material for the traits of interest. For example, the highest stiffness parent in the Seed Orchard population matches the average stiffness for the Clonal Deployment population. Conversely, the densest clones can compete with the material in the Seed Orchard.

Alternatives

Very early phenotypic screening is not the only option for early selection. The last decade has witnessed an explosion on the application of genomic tools for selection in tree breeding, both as a research tool and lately as an operational process (see Grattapaglia et al. 2018, for a brief review). In some respects, very early screening and genomics could be considered as mutually exclusive; breeders should either use phenotypic selection or train a set of genetic markers to predict later performance.

However, breeders could also consider these approaches as complementary, and train the genomic system to reproduce the results of very early screening, or other fast-screening techniques for wood properties (de Lima et al. 2019). The response variable of the phenotypic data analysis would be the deregressed breeding values for very early expression of wood properties, while the predictors would be systems of genetic markers. This combination of techniques would be appropriate if we consider reframing the problem as selecting trees which are ‘first past the post’ or reach technical thresholds as early as possible. As an example, Apiolaza (2009) proposed selecting trees with a stiffness that qualifies as structural wood as early as possible, instead of looking for the highest stiffness at a traditional selection age.

Trajectories

When performing classical selection for tree growth, we end up selecting trees that differ on growth patterns: they are early bloomers, which initially grow faster, although they may show a slower growth rate after selection age.

Typically, selections in the New Zealand breeding and deployment programmes have been based on phenotypic assessments at 8–10 years of age, technically when the trees are 10 m tall, to account for site productivity differences. In the case of wood properties, the selection criteria are average basic density of an increment core (or, more recently, a resistograph profile) and standing tree velocity. The latter is measured with a time of flight instrument, which captures the velocity of a sound wave in the last 1–2 most external rings, making it an instantaneous trait.

Whether we are assessing a ‘point estimate’ or a cummulative average, we are working with an underlying infinite dimensional trait in the sense of Kirkpatrick et al. (1990), “in which the phenotype of an individual is represented by a continuous function”. These trajectories were originally introduced for growth traits; however, they can be used for wood properties like increment core X-ray densitometry data (Apiolaza and Garrick 2001). Selection on both types of traits in different populations resulted on affecting the ‘intercept’ of the trajectory of wood properties at age 2 in their progeny.

From a practical point of view, the interest in the results of very early screening and particularly on improving the wood properties of corewood is highly related to rotation length. If one is growing short rotation species, corewood can be 50% of the total volume (as in radiata pine, Young et al. 1991) or even 100% as in ‘E. urograndis’ grown for pulp production. However, if one is dealing with longer rotations, say 50 years or longer, the proportion of corewood in the final crop is small and its properties are, likely, inconsequential.

The nearly 4 M ha of radiata pine planted around the world vary in rotation from around 15 years for a pulp regime in Chile to around 35 years in Australia for a solid wood regime (Mead 2013). In that range, the proportion of corewood is very substantial.

The population differences observed in our trial mimic the significant wood properties differences between natural populations (provenances) of the same species, as observed in commonly planted temperate species like Pinus radiata (Burdon and Low 1992), Eucalyptus globulus (Dutkowski and Potts 1999; Apiolaza et al. 2005; Hamilton et al. 2007), Eucalyptus nitens (Purnell 1988), and Pseudotsuga menziesii (Lausberg et al. 1995). In all these examples trees were assessed between 1/4 and 1/2 of rotation length, but it is our expectation that provenance differences will be expressed very early on, as there is evidence of wood properties differences at 1 year of age, both between genotypes of the same species (Apiolaza et al. 2011b) and between species (Goncalves et al. 2018).

Implications

When presenting the idea of very early screening is common to face the question “Where should we use it in a tree improvement programme?” Despite the ability to screen many more small trees, the cost and effort of using this approach at the breeding-population level would still be very high. It is much more likely that these techniques would be more relevant to industry when used to screen deployment populations. In fact, the data for this article was collected while screening the largest seed and clonal deployment populations for radiata pine in New Zealand. This was necessary as the genotypes included in these populations were not originally assessed for all wood properties; for example, typical selection criteria do not include shrinkage. Another implementation point is to include these techniques when training the operational genomic selection models for radiata pine presented by McLean et al. (2023).

Poor (or even lack of) information about corewood properties at the deployment level undermines the ability of breeding programmes to provide the best possible genetic material, and also ignores the investment on research to estimate the value of those wood properties in the first place. Together with the slow flow of genetic material this constitutes one of the major buffers against industry capturing the gains of innovation. This problem coincides with those that inspired Akerlof’s (1970) theory concerning the market problems of ‘quality and uncertainty’, because in the radiata pine structural sawlogs market buyers use basic data with high uncertainty to judge the quality of prospective purchases.

The value of improving corewood quality in radiata pine affects decision-making on stocking, early and intermediate silviculture, and has a strategic impact on economic returns and rotation age (Moore and Cown 2017). As an example, Gavilán et al. (2023) showed that an average increase of 1% in corewood acoustic velocity implies an average increase of structural wood in a log between 8–9% for the second and third logs immediately above the butt log.

Conclusions

• 1. This trial shows that wood properties at very early age meet the criteria to be used as selection criteria; that is, they are measurable, variable and heritable.

• 2. We observed large variability of wood properties at early age, in some cases comparable to coefficients of variation near rotation age.

• 3. While trees in the breeding programme are often selected at age 8–10 years, there were already statistically significant (at $\alpha = 0.05$) differences between populations at age 2 years. Basic density for Seed Orchard material (296.93 kg m$^{-3}$) was significantly higher than for New Selections (292.28 kg m$^{-3}$). In contrast, the Modulus of Elasticity for the Clonal Programme (2.85 GPa) was significantly higher than for the other two populations (2.47 and 2.48 GPa). These differences in MoE had an impact on longitudinal and volumetric shrinkage.

• 4. There was moderate to high degree of genetic control for wood properties (narrow sense heritabilities between 0.35 and 0.71). The genetic correlation between traits was strong, particularly between wood stiffness and longitudinal shrinkage ($-\,0.69$) and between longitudinal and volumetric shrinkage (0.83). Improving stiffness would also improve dimensional stability. Basic density was also associated to stiffness and shrinkage, but with lower predictive capacity.

• 5. The trial also demonstrates that operational deployment populations can be screened a posteriori, particularly if one is willing to use the results as a roguing mechanism.

• 6. Part of the screening cost relates to the large control of environmental conditions in the Harewood trial. Using additional tests we have compared the use of leaning versus standing trees, finding good correlations in the rankings subject to working with a highly trained assessor (in preparation).