Application of Soft Data in Nodule Resource Estimation

Abstract

Minerals and metals are of uttermost importance in our society, and mineral resources on and beneath the deep ocean floor represent a huge potential. Deciding whether mining from the deep ocean floor is financially, environmentally and technologically feasible requires information. Due to great depths and harsh conditions, this information is expensive and time and resource consuming to obtain. It is therefore important to use every piece of data in an optimum way. In this study, data retrieved from images and expert knowledge were used to estimate minimum and maximum nodule abundances at image locations from an area in the Clarion-Clipperton-Zone of the equatorial North East Pacific. From the minimum and maximum values, box cores and the spatial correlation quantified through variogram, a conditional expectation and associated uncertainty were obtained through the Gibbs sampler. The conditional expectation and the uncertainty were used with the assumed certain abundance data from the box cores in a kriging exercise to obtain better informed estimates of the block by block abundance. The quality assessment of the estimations was done based on distance criterion and on kriging quality indicators like the slope of regression and the weight of the mean. From the original image locations, alternative image configurations were tested, and it was shown that such alternatives produce better estimates, without extra costs. Future improvements will focus on improving the estimation of the minimum and the maximum values at image locations.

Introduction

Society needs minerals. Minerals and metals constitute important ingredients in everything from cars, over toothpaste to mobile phones. To replace petroleum-based energy production with renewable energy and e-mobility requires significant amounts of certain metals such as copper, nickel, cobalt and rare earth elements (REEs) to name a few (Månberger and Stenqvist 2018; Teske 2019). Although the remaining metal resources onshore seems to be abundant for, e.g., copper (Singer 2017), the uneven global distribution of minerals and metals as well as the growing ecological pressure on terrestrial deposits call for alternative sources due to high future demand (Elshkaki et al. 2018).

The deep sea offers a great potential for mineral resources (Cathles 2011; Hannington et al. 2011; Hannington 2013; Singer 2014; Ellefmo et al. 2019), but there is still a significant amount of uncertainty associated with any future mining of the deep sea. The uncertainties are linked to social, legal, ecological, technical and geological factors. Mineral resources on the deep ocean floor can roughly be categorized into seafloor massive sulfides, cobalt-rich ferromanganese crusts and manganese nodules (Sharma 2017). These deposits contain significant and varying amounts of copper, zinc, iron, gold, silver, manganese, cobalt, nickel and REEs. The deposits are situated on or beneath the seafloor at depths ranging from 800 to 6000 meters.

According to increasing geological confidence, an identified mineral resource can be classified as an inferred, an indicated or a measured resource (JORC 2012). The classification is performed by a competent or qualified person, and it is dependent on the amount, quality and characteristic of available geodata. The competent person must have at least 5 years of experience relevant to both the style of mineralization, the type of deposit and the performed task. A task can be resource estimation and classification or planning and execution of exploration activities and presentations of the results. Obtaining large amounts of high-quality data from the deep ocean floor is expensive and time- and resource-intensive. It requires exploration cruises with highly skilled scientists and operators and expensive equipment. The necessary support vessel needs to be fitted with accommodation, laboratories and systems to handle launch and recovery of remotely operated and autonomous underwater vehicles used in geodata collection and site inspections. It is of uttermost importance that the time on site is spent efficiently and that the collection of high-quality geodata is maximized. The deep ocean floor is vast and under-explored. Geodata utilization and uncertainty quantification is therefore a key to prioritize exploration efforts and do resource estimations, making the right decision (Eidsvik et al. 2015). This means exploiting all data for potential information.

This study focuses on resource estimation of manganese nodules. Geodata necessary to estimate the abundance of nodules have been collected traditionally with box cores. These squared cores cover roughly an area of 1/4th square meter and are pushed by gravity down into the mud on the ocean floor. A mechanism closes the core to contain the material on the ocean floor covered by the core. One box core takes only one increment per launch and recovery, and with water depths down to 6000 m, such sampling is time consuming. Once the increment is recovered onboard the support vessel, it can be processed and analyzed. A box core increment is associated with low uncertainty where most of the uncertainty is associated with the positioning and the small area of the sampling site. To reduce the required amount of box core data, this study investigates the potential benefit of image data where it is possible to estimate a minimum and maximum nodule abundance based on a combination of expert knowledge and information in the image. Abundance expectations derived through such an approach are termed “soft” and are proxies associated with significant uncertainty. However, image data are relatively cost efficient, and it is possible to collect huge amount of image data from a large area just during few dives. The question that arises is therefore whether a large amount of uncertain data (images) can replace a low amount of certain data (box cores).

Initial tests were run by Ellefmo and Kuhn (2018), but, in that study, it was possible to exploit a direct correlation between the estimated abundance from the images and real abundance measured by the box cores. A similar recent study focused on small nodules and exploited similar correlations (Mucha and Wasilewska-Błaszczyk 2020). The correlation approach, however, collapses once larger nodules are included because the larger nodules are covered with more sediments than the smaller ones (Kuhn and Rathke 2017). Gazis et al. (2018) attempted to use hydroacoustic data in combination with optical imagery and artificial intelligence. They managed to estimate the abundance by using acoustic and optical data and a predictive random forests machine learning model. Yoo et al. (2018) used acoustic backscatter data and reported a good correlation between backscatter intensities and mean nodule abundances.

In the present study, the minimum and maximum abundances are merged with available box core data into the kriging with inequalities algorithm to calculate a conditional expectation at each image location and associated uncertainty (cf. Chilès and Delfiner 2012). The conditional expectations and uncertainties are then plugged into an ordinary kriging algorithm along with the available box core data. This paper illustrates the methodology on a case from the Clarion-Clipperton-Zone of the equatorial North East Pacific. Resource estimation quality indicators were used to assess the effect of introducing the data retrieved from the images. Different image configurations with images at their original location, at random locations and along transects covering the whole area of interest were tested. No attempts were made to classify the resource since more work is needed to improve the quantification of the minimum and maximum abundance values from the images.

Background

Geological Background

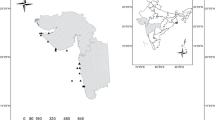
The working area is located about 900 nautical miles (~ 1.700 km) southwest of Manzanillo, Mexico, in the equatorial NE Pacific Ocean (Fig. 1). The seafloor depth of this area ranges between 4000 and 4300 m in general and consists of plateau-like areas, numerous seamounts rising between a few hundred to more than 2000 m above their surroundings as well as NNW–SSE-oriented ridge and graben structures (Fig. 1) (Kuhn et al. 2020). These ridge and graben structures seem to be bounded by faults, and some of those faults may still be active (Kuhn et al. 2017a, b). The seafloor of the plateau-like areas can be smooth and flat, and these are the regions, which are of interest for Mn nodules exploration (Kuhn et al. 2020). The near-surface sediments consist of pelagic clay and siliceous ooze with trace amounts of coarser-grained detrital and volcanic material (Kuhn and Shipboard Scientific Party 2015) and (Heller et al. 2018). The surface sediments contain up to 0.6 wt.% organic carbon associated with sedimentation rates of 0.35–0.5 cm/kyr (Mewes et al. 2014; Kuhn et al. 2017a, b).

Figure 1

General bathymetry of the working area (large figure) and location of the working area in the NE Pacific (small figure). The exemplary data for this study were derived from the plateau area in the NE corner of the large figure

Manganese nodules mainly occur on the sediment surface or within the upper 10 cm of the sediments in the abyssal plains of the working area. They form concretions of different shape and size, but the main shapes are spheroidal or ellipsoidal and the main size class is, in the present case, bimodal with mean values of the long nodule axes being about 3 cm and 6 cm, respectively (Kuhn et al. 2020).

There are two principal processes leading to the formation of manganese nodules in deep-sea abyssal plains, namely hydrogenetic and diagenetic. Hydrogenetic formation means direct precipitation of Fe oxyhydroxides and Mn oxides from oxygen-rich near-bottom seawater (Koschinsky and Hein 2003). Diagenetic precipitation occurs within pore-space of deep-sea sediments because of Mn oxide precipitation from almost oxygen-free (suboxic) pore water upon contact with oxic near-bottom water (Hein et al. 2020). Both processes lead to the formation of different layers around a nucleus forming the Mn nodule. Their alternation is mainly controlled by paleo-climatic conditions in the upper ocean. Hydrogenetic precipitation enriches metals like Co and rare earth elements in the nodules, whereas copper and nickel are enriched mainly by diagenetic processes (Kuhn et al. 2017b).

Mineral Resource Estimation and Classification

Geostatistics is a branch of spatial statistics, and it is a framework to model a spatial or temporal phenomenon. It is the preferred methodology used in mineral resource estimation and classification (Journel and Huijbregts 1978; Rossi and Deutsch 2013), but it has found extensive uses in environmental studies, soil sciences to model nutrients, meteorology and public health (Goovaerts 1997). It is used to estimate values at unsampled locations and the associated uncertainty, and it includes both univariate and multivariate implementations. A mineral resource can be classified as measured, indicated or inferred dependent on the amount and quality of available geodata (JORC 2012). The International Seabed Authority has published their own code (ISA 2015) for publishing nodule estimation results.

In a mining and mine planning context, mineral resource estimation can be used for two purposes (Blom et al. 2019): (1) short-term mine planning or (2) long-term mine planning. In short-term mine planning, the challenge is to estimate the most accurate value in a block in order to decide whether a block that is inside the ultimate pit or mining area should be mined and deposited or mined and sent to the processing plant. Minimizing conditional bias is important in this case (Isaaks 2005), and any estimate of global resource will be significantly smoothed if the conditional bias is minimized. Assuring a minimized conditional bias is achieved by adjusting the kriging search neighborhood until the slope of regression between the estimate and the unknown true value is close to 1 (Armstrong 1998; Isaaks 2005). In long-term mine planning, which is the focus of this work, the challenge is not to find the most accurate value of a specific block, but rather render it possible to estimate some tonnage and grade above some cutoff. The focus on minimizing the conditional bias is not important in this case as argued by Nowak and Leuangthong (2017). Further, Armstrong (1998) warned about using a smoothed block model for long-term mine planning. Kriging quality indicators that can be used to assess the performance of the estimation are summarized in Table 1. Knobloch et al. (2017) used neural networks and classical kriging to estimate nodule resources and used the relative prediction error (RPE) explained in Table 1 to classify the resource.

Table 1 Kriging quality indicators.

Mineral resource classification is a subjective endeavor. The competent or qualified person (CP/QP) assesses the data quality and the amount of data, applies a fit for purpose estimation technique and classifies the mineral resource according to some criteria. Rossi and Deutsch (2013) discussed the use of such criteria summarized in Table 1, and examples are given in Benndorf (2015) and Mucha and Wasilewska-Błaszczyk (2020). Armstrong (1998) argued against the use of the kriging variance as a kriging quality indicator because it is reported to be relatively insensitive to the data configuration. What might add to the use of kriging variance is the co-use of the Lagrange multiplier (Table 1) (Snowden 2017). Armstrong (1998) argued in favor of the weight of mean and the slope, both explained briefly in Table 1, especially when optimizing the search neighborhood to minimize conditional bias. Another option presented by Rossi and Deutsch (2013) is to estimate through more than one kriging pass and vary the requirements from pass to pass, normally from more to fewer requirements. The differences from kriging pass to kriging pass can materialize itself in different number of sectors in the search neighborhood, different number of maximum consecutive empty sectors, the size of the neighborhood and minimum number of samples inside the search neighborhood. Such requirements can be combined with requirements on the slope, the weight of mean and the kriging variance in the final resource classification. In addition, conditional simulation represents an approach that provides a model of local and global uncertainty and which can be used to assess the probability of having a block grade above some cutoff (Boucher and Dimitrakopoulos 2012). Conditional simulation can also be used to quantify the conditional bias (Isaaks 2005).

Using Auxiliary Information in Resource Estimation

Auxiliary data are extra or secondary geodata that have the potential to improve the estimation precision and accuracy in geostatistics. Wackernagel et al. (2002) presented approaches to take advantage of auxiliary information including kriging with external drifts where a primary variable typically at borehole location is combined with a secondary variable providing low(er) frequency/resolution information about the variable(s) under study. Abrahamsen and Benth (2001) presented a methodology to estimate trend coefficients given both exact data and inequality constraints. Omre (1987) developed Bayesian kriging as a generalized form of kriging with an external drift. Cokriging and collocated cokriging is presented in Wackernagel (2010) and Chilès and Delfiner (2012). Cokriging is an approach used if the dataset consists of correlated variables where one variable dominates the other in terms of the number of data points or if the variables must be estimated simultaneously due to relationships between the variables. Collocated cokriging is used if one of the variables is known at the target points. Eidsvik and Ellefmo (2013) looked at the use of uncertain auxiliary data in resource estimation.

Data

“Hard data” for this study were collected using a so-called box corer (Fig. 2). With this device, a block of deep-sea sediment measuring 50 cm by 50 cm of seafloor area and 30–40 cm thickness was sampled at 41 locations. The typical distance between neighboring sampling locations was between 2500 and 3000 m. See Figure 5. The Mn nodules lying on top of the sediments or within the first 10 cm were collected manually from the box corer, and the sum of their weight was measured immediately after recovery of the box core on board the vessel. This way the so-called wet nodule abundance in kg/m² was calculated. This nodule abundance and the metal content of the nodules are the major parameters that control the economic value of the Mn nodule deposit (Knobloch et al. 2017). However, taking box core samples is time consuming and thus expensive. It takes about 4 h to sample one box core increment in about 4200 m water depth. Thus, only about six increments can be taken per day. Kuhn et al. (2016) showed that the average spacing of box corer increments should be in the range of about 1300 to 4700 m in order to reach the indicated resource level of a Mn nodule deposit given that box cores are the only source of information.

Figure 2

Box corer used for sampling of seafloor sediments and nodules (left panel) as well as surface (upper right) and downcore profile (lower right) of the sediment block sampled

Box core sites can be linked by video mapping of the seafloor. For this study, the German video sledge STROMER was used; it is equipped with several high-resolution video and photo cameras (Fig. 3). The sledge is permanently connected with a surface vessel via a fiber optical cable during the deployment. The vessel sailed with a speed of about 1 knot along pre-defined transects, with the STROMER being towed behind the vessel and kept about 3 m above the seafloor. Images were taken automatically every 5 or 10 s, and underwater positions of the video sledge were calculated using a combination of hydroacoustic and inertial navigation systems. In total, 5504 images were taken and included in this analysis. The accuracy of the positioning for each picture is around ± 5 m (Rühlemann and Shipboard Scientific Party 2018).

Figure 3

BGR video sled STROMER used for this study (Photo: S. Sturm)

For the analysis of underwater images, BGR together with the University of Bielefeld developed an automated image analysis software called “Mangan Analyzer.” The objective of this software is to detect manganese nodules automatically and reliably in many seafloor images. The core algorithm for the analysis of seafloor images with special focus on the estimation of manganese nodule coverage is the so-called hyperbolic, self-organizing map (HSOM) as a neural network approach (Schöning et al. 2012). The process to map single nodules within an image requires several steps including illumination correction, feature transformation, machine learning, quantification, and post-processing (Fig. 4).

Figure 4

Working steps of the image processing software MANGAN ANALYZER

Figure 5 shows the box core and the image locations. The area covered by the images followed a slightly skewed distribution that varied between 0.6 m² and about 12 m² with a median area of 5.5 m² and a mean area equal to 5.7 m². This differed from the 0.25 m² covered by the box cores data, but both images and box core data were, in this study, assumed as point data compared to the 1 km² large areas/blocks being estimated.

Figure 5

Base map showing the box core and original image location. Box core increments taken systematically at all squares. Color and size of the squares indicate the abundance. Images were collected along the southeastern (102STR) and the northwestern (131STR) transects. The univariate statistics show the number of samples and the nodule abundance given in kg/m². Number of samples consists of 5504 images and 41 core box increments

The area of each nodule in each image was calculated, and the nodules were divided into different size classes. A mathematical relationship between the number of nodules per size class and their weight was established based on box core stations, and thus the total weight per image in kg/m² can be calculated. The number of nodules per size class and not the measured nodule area was used as a basis for this relationship because it turned out that nodules were arbitrarily covered by sediments and that there was only a weak statistical relationship between coverage and abundance. It was assumed that some part of every nodule was visible in the images. The nodule abundance from images calculated this way still was by factor of 1.1–3.7 lower than the nodule abundance measured in box cores along the video transects. Therefore, the abundance calculated from images was considered minimum abundance only. In this study, the maximum abundance was calculated by multiplying the obtained minimum value by the correction factor 2.21 and 3.71 for the northern and the southern group of images in Figure 5, respectively. These correction factors were the maximum ratios between nodule abundance derived from box core stations and the abundance from the image analysis at the position of each box core station. Summary statistics of the parameter under study is given in Figure 6. There were 41 box cores with an average abundance of 22.8 kg/m², with minimum and maximum values of 10.2 and 36.1 kg/m², respectively.

Figure 6

Summary statistics and histogram showing the characteristics of the abundances collected with the box cores

The minimum and maximum values estimated from the 5504 images are given in Figures 7 and 8. The lowest minimum value was 2.2 kg/m², and the largest minimum value was 17.1 kg/m². Corresponding maximum values were 7.3 kg/m² and 57.3 kg/m². The mean minimum and maximum values were 10 and 28.2 kg/m², respectively. The maximum values varied more than the minimum values due to the use of the two different multipliers (2.21 and 3.71). Figure 9 shows a scatterplot revealing the two populations of minimum and maximum values originating from the application of the two multipliers. The sub-population characterized by the lower slope of the two corresponds to the northernmost (131STR) transect in Figure 5. This indicates that the northernmost transect has a lower maximum abundance for the same minimum abundance and thereby a lower uncertainty due to a smaller nodule size.

Figure 7

Summary statistics characterizing the minimum abundances in kg/m² obtained from images

Figure 8

Summary statistics characterizing the maximum abundances in kg/m² obtained from images

Figure 9

Scatterplot showing two populations of minimum and maximum values

Given the minimum and the maximum values in Figures 7 and 8, a pseudo-standard deviation of a distribution satisfying the minimum and maximum boundaries can be estimated from the range formula (Hozo et al. 2005), thus:

$${\text{Stdv}}_{\text{Pseudo}} = \frac{{{\text{Max}} - {\text{Min}}}}{4}$$

(1)

The pseudo-variance is the squared pseudo-standard deviation calculated from Eq. (1). The histogram of this pseudo-variance is given in Figure 10. The mean was 24.1 (kg/m²)², and the most probable value (the mode) was close to 12 due to the positively skewed distribution. This value was used to validate the quantified uncertainty at images location.

Figure 10

Summary statistics of the pseudo-variance (the pseudo-standard deviation squared) calculated from the minimum and maximum abundance values (kg/m²)

There are studies that reported good correlations between nodule abundance and areal characteristics of nodules retrieved from images (e.g., Felix 1980; Lipton et al. 2016; Mucha and Wasilewska-Błaszczyk 2020). For the area under study, it was difficult to find such reliable correlations due to the multimodal nodule size distribution in the area (Kuhn et al. 2020). Figures 11 and 12 show the relationship between the total nodule coverage in area-% and the calculated minimum abundance in kg/m². Two distinctly different relationships can be identified per transect. The reason is regional differences in nodule size distribution, and to what extent the nodules are covered by sediments. Generally speaking, larger-sized nodules (long nodule axis > 4 cm diameter) are covered by sediments to a higher degree, and if they dominate a location, they may obliterate the relationship between areal nodule coverage and nodule abundance (Kuhn and Rathke 2017).

Figure 11

Relationship between total nodule coverage and calculated minimum abundance in the southeastern transect (102STR). Two distinctly different populations and relationships can be identified. Legend indicates point density in the scatter plot. Coverage varies between 6% and 57.5% with average of 27.5%. Minimum abundance varies from 2.2 to 15.5 with average of 9 kg/m²

Figure 12

Relationship between total nodule coverage and calculated minimum abundance in the northwestern transect (131STR). Two distinctly different populations and relationships can be identified. Legend indicates point density in the scatter plot. Coverage varies between 7.1% and 59.2% with average of 33.2%. Minimum abundance varies from 3.3 to 17.1 with average of 10.8 kg/m²

To study the effects of different data configurations, tests were executed where the images have been placed randomly in the area covering the box core data ± 1000 m and in transects. Images at a random location (Fig. 13) represented an operationally unlikely scenario but can be used to assess how good in terms of the kriging quality indicators given in Table 1 an estimation can be. The scenario with all the images distributed along transects (Fig. 14) that covered the whole area was operationally a more realistic scenario that conceptually can be compared to onshore in-fill drilling in exploration.

Figure 13

Images located randomly in the area of the box core data (black squares). Colors indicate the conditional expectation at each image location. Size of black squares is proportional to abundance

Figure 14

Images located in transects covering the area of the box core data (black squares). Colors indicate the conditional expectation at image location. Size of black squares is proportional to abundance

The minimum and maximum values at images points were kept although the image positions have changed, and new conditional expectations and variances of measurement errors at image locations were estimated using the Gibbs sampler explained in the next section. This is not realistic because new minimum and maximum values should have been estimated at the new locations. Therefore, a comparison between the estimates and the RPE obtained with only box core data and those obtained with images at random location or in transects was not relevant. The slope, the weight of mean, the distances and the kriging standard deviation that do not depend on the prediction can, however, be compared to assess the effects of different data configurations.

Methodology

Linear Geostatistics

The necessary theoretical framework for geostatistics was developed in the 1960s by Matheron (1963) based on empirical work performed by the South-African mining engineer Daniel Krige in 1951. Geostatistics and its application to mining has been described several textbooks, including Journel and Huijbregts (1978), Goovaerts (1997), Armstrong (1998), Grunwald (2005), Buyong (2007) and Chilès and Delfiner (2012). In his publication in 1963, Matheron introduced the term and concept of the regionalized variable and he defined it as “sensu stricto, an actual variable, taking a definite value in each point of space”. The regionalized variable Z(x₀) at location x₀ can be described conceptually by a structured component (m(x₀)), a spatially correlated random component ε′(x₀) and a spatially uncorrelated random component ε″ (x₀), thus:

$$Z\left( {x_{0} } \right) = m\left( {x_{0} } \right) + \varepsilon^{\prime}\left( {x_{0} } \right) + \varepsilon ''\left( {x_{0} } \right)$$

(2)

The structured component m(x₀) is called the drift (Matheron 1963), and it represents the mean of the regionalized variable at location x₀. The spatially correlated random component comprises fluctuations around this drift. Matheron (1963) termed Eq. 2the universal model of spatial variation. Geostatistics has a broad area of use and both the drift, the spatially correlated fluctuations and the spatially uncorrelated random component, are properties that are specific and unique for the investigated phenomenon whether it is geology, meteorology or social sciences.

The regionalized variable is normally so complex that a deterministic formulation is not feasible. A probabilistic framework is required (Hans Wackernagel 2010). In most applications of geostatistics, this probabilistic framework is based on a modeling of the spatial correlation using the variogram, γ. The variogram quantifies the average squared difference between realizations of the regionalized variable, and it is used to find the weights λ_i that minimize the estimation variance of the linear estimator Z^*(x), thus:

$$Z^{*} \left( x \right) = \mathop \sum \limits_{i} \lambda_{i} *Z\left( {x_{i} } \right)$$

(3)

Z(x_i) represents data at locations x_i and λ_i are the associated weights. Different geostatistical implementations make different assumptions on the properties of the drift, m(x₀). Ordinary kriging assumes that the drift is unknown, but constant inside the study area. By introducing the Lagrange multiplier µ that ensures that the estimator Z^*(x) is unbiased, the kriging system used to calculate the optimal weights that minimized the estimation variance can be expressed by Eqs. 4 and 5 (Armstrong 1998):

$$\mathop \sum \limits_{j = 1}^{N} \lambda_{i} \gamma \left( {x_{i} ,x_{j} } \right) + \mu = \bar{\gamma }\left( {x_{i} ,V} \right), \quad i = 1,2, \ldots ,N$$

(4)

$$\mathop \sum \limits_{i = 1}^{N} \lambda_{i} = 1$$

(5)

The γ(x_i,x_j) is the variogram value between the data points at locations x_i and x_j that are used in the prediction of the volume or block V, and the $\bar{\gamma }\left( {x_{i} ,V} \right)$ is the average variogram value between the datapoints and the V. The kriging variance is given by Eq. (6). The kriging standard deviation is the square root of this kriging variance.

$$\sigma_{K}^{2} = \mathop \sum \limits_{j = 1}^{N} \bar{\gamma }\left( {x_{i} ,V} \right) - \bar{\gamma }\left( {V,V} \right) + \mu$$

(6)

Gibbs Sampler

The Gibbs sampler is a variant of the Metropolis–Hastings algorithm (Robert 2015); it is used to sample from multivariate distributions by sampling systematically from the conditional distribution at each sample location. The applications of the Gibbs sampler vary widely from the use in meteorology (Onibon et al. 2004), environmental studies (Michalak 2008) to social sciences (Lynch 2007) and specifically in psychology (Yildirim 2012) and geosciences (Hansen et al. 2012). It was introduced to Bayesian statistics with the work done by Gelfand and Smith (1990).

In the present work, the datasets consist of hard data represented by the box core analyses and soft data represented by the images and the estimated minimum and maximum values. The algorithm used in this work comprises the following the workflow implemented in the geostatistical software Isatis™:

• 1. Transform hard data and n minimum and n maximum values defining the inequalities into Gaussian space (N(0, 1)). Store the anamorphosis for back-transformation into original data space and subsequently the calculation of the conditional expectation and associated uncertainty.

• 2. Calculate the experimental variogram of the Gaussian hard data and fit a variogram model.

• 3. Initialize a vector of length n with values satisfying the minimum and the maximum limits at each soft data location; x^t = x ^t₁ ,…, x ^t_n , t = 0.

• 4. For t = 0, 1, 2,… draw on random an index i between 1 (one) and n.

• 5. Use simple kriging (the expectation is known) to estimate a value (z_i) and the kriging standard deviation (σ_i) at location i from the hard data and x ^t₁ ,…x ^t_i-1 , x ^t_i+1 ,…,x ^t_n . This would be all hard data and all soft data except the value at location i. A unique neighborhood is used to ensure that all data are included in the simple kriging step.

• 6. Draw a value s from the conditional distribution s ~ N(z_i, σ_i) and assign it to location i.

• 7. Assign x^t+1 = x ^t₁ , x ^t₂ ,x ^t_i-1 , s, x ^t_i+1 …x ^t._n

• 8. Back-transform x^t+1 to real data space.

• 9. Store the back-transformed version of x^t+1.

• 10. Repeat steps 4–10 until convergence or the fixed number of simulations has been reached.

• 11. Calculate the conditional expectation as the arithmetic mean of the stored back-transformed values and the associated standard deviation at each soft data location. The conditional expectation is the expected abundance at the image locations given the minimum and maximum constraints, the box core data and the variogram model quantifying the spatial correlation.

In our case, the early values are within boundaries because they have been sampled to satisfy the minimum and maximum limits, but these early values might not be good representatives of the final distribution. Three Gibbs sampler runs were executed to check for consistency. The conditional expectation and the associated standard deviation were used as input with the hard data in kriging with variance of measurement error following the workflow implemented in Isatis™.

Kriging with Variance of Measurement Error

Kriging with variance of measurement error is a procedure that enables the incorporation of data associated with different levels of uncertainty. The ordinary kriging system as used in this study on matrix form is given as

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma_{11} } & {\gamma_{12} } \\ {\gamma_{21} } & {\gamma_{22} } \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {\gamma_{1N} } & 1 \\ {\gamma_{2N} } & 1 \\ \end{array} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} {\gamma_{N1} } & {\gamma_{N2} } \\ 1 & 1 \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {\gamma_{NN} } & 1 \\ 1 & 0 \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\lambda_{1} } \\ {\lambda_{2} } \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\lambda_{N} } \\ \mu \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{\gamma }\left( {x_{1} ,V} \right)} \\ {\bar{\gamma }\left( {x_{2} ,V} \right)} \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\bar{\gamma }\left( {x_{N} ,V} \right)} \\ 1 \\ \end{array} } \\ \end{array} } \right]$$

(7)

Including uncertain data, the extra nugget effect (σ_x) associated with the (more) uncertain data is added to the diagonal of the variance–covariance matrix (Heuvelink et al. 2016):

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma_{11} + \sigma_{x1} } & {\gamma_{12} } \\ {\gamma_{21} } & {\gamma_{22} + \sigma_{x2} } \\ \end{array} } & \cdots & { \begin{array}{*{20}c} {\gamma_{1N} } & 1 \\ {\gamma_{2N} } & 1 \\ \end{array} } \\ { \vdots } & \ddots & \vdots \\ {\begin{array}{*{20}c} {\gamma_{N1} } & {\gamma_{N2} } \\ {1 } & 1 \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {\gamma_{NN} + \sigma_{xN} } & 1 \\ 1 & 0 \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\lambda_{1} } \\ {\lambda_{2} } \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\lambda_{N} } \\ \mu \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{\gamma }\left( {x_{1} ,V} \right)} \\ {\bar{\gamma }\left( {x_{2} ,V} \right)} \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\bar{\gamma }\left( {x_{N} ,V} \right)} \\ 1 \\ \end{array} } \\ \end{array} } \right]$$

(8)

Kang et al. (2017) used a similar approach in their study when they introduce measurement errors in the spatial prediction of soil moisture. Adding the extra nugget effect as indicated by Eq. (8) can be compared to have more data further away from the target block because these points are associated with a higher variogram value.

Kriging Parameterization

Variogram Model

An experimental variogram was estimated for both the original abundance data and its Gaussian transformation. Both were rotated N70E to account for anisotropy. The sills and direction scales are given in Table 2. A graphical representation of Table 2 is shown in Figure 15. The variogram model of the Gaussian transformed hard data is given in Table 3. Given only 41 box core data, the anisotropy can be questioned, but the identified directions correspond well with the NNW–SSE trending ridge and graben structures shown in Figure 1.

Table 2 Variogram model for the original abundance data.

Figure 15

Variogram model for the original abundance data (in kg/m²)

Table 3 Variogram model for the Gaussian transformed hard data.

Block Size and Search Neighborhood

The block size was set to slightly smaller than the distance between the hard data, i.e., block size of 1 km × 1 km. This is in accordance with recommendations by Armstrong (1998) and Hekmat et al. (2013), and it considered out of scope for this study to optimize the block size and the search neighborhood configuration. The search neighborhood used in the kriging step was rotated according to the anisotropies with the long-axis-oriented N160E. The short axis and long axis of the search ellipsoid were set to 2900 m and 11,250 meters, respectively. This corresponds roughly to the ratio between the directional scales for variogram structure 3 in Table 2. The search neighborhood was divided into eight sectors, and the maximum number of consecutive empty sectors was set to 2. This ensured interpolation rather than extrapolation. The optimum number of samples per sector was set to 2 giving an optimum number of samples of 16. The minimum number of samples was fixed to 3.

Results

Conditional Expectations at Image Location

From Figures 16 and 17, it can be seen that the difference between the maximum and the conditional expectation was slightly larger than the difference between the conditional expectation and the minimum. This means that the distribution at each soft data point was slightly skewed with a tail toward higher values.

Figure 16

Histogram showing the difference between the conditional expectation and the minimum value at each image location

Figure 17

Histogram showing the difference between the maximum value and the conditional expectation at each image location

Figures 18 and 19 show the conditional expectation and the associated estimated variance, respectively. It can be seen from Figure 18 that the average conditional expectation was 17 kg/m². The variance of measurement error in Figure 19 at image location was bimodal, and it shows an average value of 9.2 (kg/m²)². This is comparable to the pseudo-variance in Figure 10 calculated from Eq. (1). The two modes in Figure 19 represent the variance of measurement error in the northern and the southern transects with image points shown in Figure 5. The variance of measurement error varied from 1 to 21.8 (kg/m²)², which is 58% of the total sill of 38 (kg/m²)² given in Table 2. The three independent Gibbs sampler runs gave no significant differences in conditional expectations and variance of measurement errors.

Figure 18

Estimated conditional expectation at image location

Figure 19

Estimated variance at image location

Resource Estimation

Resource estimation results using box core data only and box core data and images in different configurations are given in Table 4. The estimated value was higher if only box core data were used. The kriging standard deviation was lower for the estimation that included image data and improved significantly in the alternative image configurations. RPE was higher when images were included because the estimated value on average was significantly lower. The Lagrange multiplier was larger when images were included in their original locations. This indicates that the data points were clustered and/or there were more cases of extrapolation. For this search neighborhood, the slopes and the weight of the mean were practically the same with or without images. This would indicate the same conditional bias. The same parameters were significantly better in the two alternative data configurations. At the same time, the variance of the estimated block values was higher when the image data were included. This is a result of more low-grade blocks.

Table 4 Resource estimation using only box cores (hard data) and box core data and image data in different configurations.

The mean distance to data points included in the estimation was naturally lower when the image data were included and, from a pure data configuration perspective, the estimates with image data were therefore better. The same was the case if one looks at the number of values inside the neighborhood. This indicator was larger for the case where the images were included. In other words, the estimate was “better informed.” Given the requirements on the data points inside the search neighborhood and the sector division of the neighborhood, the number of estimated blocks increases as expected with the introduction of the image points.

The slope that indicates the degree of conditional unbiasedness shows similar results with and without images, with an average slope of 0.76 with images at the original locations and 0.78 without. The kriging standard deviation shows a small improvement from 3.44 without to 3.32 with images. The weight of mean shows significant improvements in the alternative image configurations, dropping down to 0.07 for the operationally unlikely event of having the images points spread at random across the area. The more likely case where the images are placed along transects covering the area of interest, also shows a significant improvement with a drop down to 0.15 from 0.29.

Figures 20 and 21 show estimation results with box core data only and with images in transects covering the whole area. Comparing the results in these figures, the results in Figure 21 appear more noisy indicating that the estimation was to a greater extent controlled by data rather than the global model defined by the variogram. For the slope, the standard deviation was lower when image data were included because the slope was constantly higher. Looking at the number of blocks that were estimated, there was an increase from 215 blocks when only box core data were used to 236 when data from images in transects were included. This was a 10% increase without compromising the estimation quality, just using the available data. Assuming an average abundance of 17.5 kg/m² and the block size of 1 km², the increase in unclassified resource amounted to 367.500 tonnes of nodules.

Figure 20

Estimation and quality indicators with only box core data. From upper left and clockwise: the estimated value, the RPE, the slope and the kriging standard deviation

Figure 21

Estimation and quality indicators with box core and image data. From upper left and clockwise: the estimated value, the RPE, the slope and the kriging standard deviation

Discussion

How can we define a resource and how can the inclusion of uncertain image data influence the resource classification? What parameter should we use to inform the classification? How well suited is the relative prediction error (RPE) as a kriging quality indicator if it depends on the estimated value and uncertain image data are incorporated? Answers to these and other related and relevant questions must be assessed and found by the competent person (CP) who does the resource estimation and the resource classification. The reporting codes must be read and understood. Geological continuity is not necessarily the same as continuity in kriging quality indicators that are dependent on a series of assumption made by the CP. In this work, a methodology was explored where information was retrieved from images, combined with expert knowledge and conditional expectations at image points were calculated. Other methodologies discussed here are available, some of which could potentially have been used for the presented purpose, e.g., kriging with inequalities presented by Abrahamsen and Benth (2001).

None of the kriging indicators can alone be used directly as a classification indicator. The Lagrange multiplier can be used to assess clustering and the amount of extrapolation and can be, in co-use with the kriging variance, an efficient indicator of data configuration. Since the neighborhood was defined using eight sectors and maximum two empty consecutive sectors were allowed, there was little extrapolation. The data coverage was good. Given that the image data were densely organized along rather short transects, we knew that there was clustering because the image points were grouped close together. This explains the higher Lagrange multiplier when the images were included. The kriging variance was also the basic tool in developing confidence intervals and was naturally dependent on the block size. The larger the block size was, the lower was the kriging variance. The selection of block sizes is subjective, but it is often linked to some annual or semi-annual production tonnages. Here, it was fixed according to data density and it was detached from any operational constraints.

Pure distance criteria can be effective, assuming they are derived from the variogram model, but this approach collapses when data of different quality are combined. Slope and weight of mean were good indicators to use in assessing the degree of conditional bias, but the relevance of conditional bias as a criterion was dependent on the purpose of the estimation. The kriged estimates that included the image data were lower than estimates based only on box core data. The reason is that the conditional expectation was lower than the average abundance from the box core data. This is something future activities on predicting the minimum and maximum abundances must focus on. The minimum and maximum values influence naturally the conditional expectations at image location and one could expect that, given representative box core and image sampling, the average conditional expectation should be similar to the average abundance in the material collected with the box cores. In the data presented here, this was not the case; the conditional expectations were lower. Looked from another perspective, box cores might not be able to capture the variability of abundance in the area and the available box cores might seriously over-estimate the abundance.

The degree of improvement when image retrieved information is incorporated is dependent on the uncertainty associated with the conditional expectations at image location. This uncertainty is directly dependent of the defined minimum and maximum values at image locations and the variogram model. There are interesting approaches that can be exploited to improve the minimum and maximum values. These include, for example, the use of backscatter intensity or potentially links between bathymetric expressions. The area under study shows a variable nodule size distribution. In such a case, the simple correlations between coverage and abundance are no longer valid and other approaches must be assessed. The reason for the collapse was primarily because large nodules tend to be covered with more sediments than smaller nodules and it is very difficult to assess the amount of sediment cover. A simple correlation approach followed by ordinary kriging also failed to incorporate the extra uncertainty associated with abundance that was estimated from the correlation. The global extra uncertainty derived from the correlation coefficient can be built-in into the methodologies presented here, but that would not be a location-dependent uncertainty that was achieved with the min/max approach presented here.

The areas covered by the images and the box cores varied, and the support associated with each data point was therefore not consistent. In this study, all data were assumed point data compared to the blocks that were estimated. An extension to what has been tested in this study can be to calculate the dispersion variance within the image areas similar to the study of Castrignanò et al. (2019). This dispersion variance would then affect the total variance of measurement error associated with each image point.

Nodules are formed through both hydrogenetic and diagenetic processes with a dominance of the diagenetic process in almost all nodules. However, in small nodules, the hydrogenetic fraction seems to be higher (Heller et al. 2018), and because hydrogenetic process means direct precipitation from near-bottom seawater it can only be realized under reduced or no sedimentation. This might be the reason why small sized nodules are located on the seafloor with less sediment cover than the larger, more diagenetically formed nodules.

Looking away from the fact that the soft data are associated with higher uncertainty, the estimates using the image data are better informed. The average distance between the target block and the data was smaller and the number of data points involved in the estimation was larger. At the same time, the slope, the weight of mean and the kriging variance were practically the same for the original data configuration with images along northern and southern transects only covering parts of the area of interest. The kriging quality parameters improve significantly if other data configurations are used. Here, tests were made distributing the images randomly and along transects in the area of the box cores. The former is an operationally unlikely scenario, but running photo transects at different orientations covering different parts of the study area is more likely. Both configurations show significant improvements in the kriging quality indicators while having averages of number of points included in the estimation close to the maximum of 16 stemming from the definition of the search neighborhood.

It is out of scope for this study to assess and to incorporate the effect of differences in support between the box cores and the images. The box cores covered an area of about 0.25 m², while the images were taken at different altitudes and they covered an area between 0.6 m² to roughly 12 m² with median area of 5.5 m² and mean area of 5.7 m². All these supports were assessed as being point data compared to the 1000 m² block area. Variograms calculated from the minimum and maximum data (not presented here) showed similar range structures, but naturally both lower (for the minimum data) and higher (for the maximum data) sills. This corresponded well with the fact that the standard deviations of the box core data, the minimum and maximum data presented in Figures 6, 7 and 8, were 6.15, 2.5 and 8.4 kg/m², respectively.

Conclusions

Conditional expectations and associated uncertainty retrieved from images of manganese nodules using the Gibbs sampler have been incorporated with box core data. The difference in the soft and hard data’s ability to quantify correctly the nodule abundance is used in the calculation of the kriging weights. Given the uncertainty in the image data and their original location, the incorporation of the image data does not improve the kriging quality indicators, but it does not worsen it either. From a data configuration point of view, the estimations with images are better informed due to more and closer data points being involved in the estimation. Also given the restricted neighborhood with requirements on the minimum number of data points, the number of sectors and the maximum number of consecutive empty sectors, more target blocks are estimated when the image data are included. Another conclusion is that photo transects should be carried out in different directions covering different parts of the study area rather than following one direction over already known box core locations. Future developments will focus on improving the estimates of the minimum and the maximum values from the images.