Abstract
This paper identifies the drivers of the phenomenal growth in productivity in hydraulically fractured horizontal oil wells producing from the middle member of the Bakken Formation in North Dakota. The data show a strong underlying spatial component and somewhat weaker temporal component. Drivers of the spatial component are favorable reservoir conditions. The temporal component of well productivity growth is driven by increasing the number of fracture treatments and by increasing the volume of proppant and injection fluids used on a per fracture treatment basis. Random Forest, a nonparametric modeling procedure often applied in the context of machine learning, is used to identify the relative importance of geologic and well completion factors that have driven the growth in Bakken well productivity. The findings of this study suggest that a significant part of the well productivity increases during the period from 2010 to 2015 has been the result of improved well site selection. For the more recent period, that is, from 2015 through 2017, part of the improved well productivity has resulted from substantial increases in the proppant and injection fluids used per stage and per well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
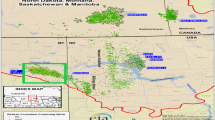
The application of horizontal hydraulically fractured wells to produce “tight” oil, that is, oil from low-permeability geologic formations, has transformed the face of the North American oil industry. The Bakken Formation, located in the Williston Basin in North Dakota and Eastern Montana (Fig. 1), is a leading producer. According to the U.S. Energy Information Administration (USEIA) estimates, the Bakken accounted for just over 11% of total US onshore oil production for 2017 (USEIA 2018), and by the spring of 2019, it had reached nearly 1.4 million barrels per day (1 barrel = 0.159 m3).
Map showing the Bakken total petroleum system (TPS) and the middle member of the Bakken Formation continuous oil assessment units (AUs) after Gaswirth et al. (2013). Inset map shows location of the Bakken TPS (pink)
During the early 1980s, oil producers tried coaxing commercial oil flow rates from vertical Bakken wells that were fractured (stimulated). In the late 1980s and 1990s, operators drilled horizontal wells which produced at commercial flow rates when the wells intersected natural fractures (Lefever 2005). After some experimentation, fractured horizontal wells successfully produced oil from the middle member of the Bakken Formation at the Elm Coulee field, which had been discovered in 2000 in Richland County, Montana (Fitzgerald 2015). Drilling and production of horizontal hydraulically fractured wells have become the standard methods for producing Bakken oil. The relatively high initial production rates for these wells allowed more rapid recovery of the cost of the well. Figure 2a shows the growth in the average of the first 360-day oil production volumes for horizontal hydraulically fractured wells starting production in selected years from 2006 through 2017. These wells were drilled in the North Dakota portion of the play and are all horizontal hydraulically fractured wells.
By way of background, horizontal wells are drilled vertically or directionally to a target formation or “kickoff” location and then horizontally within the formation. The horizontal section or lateral may be drilled for several miles. After drilling operations, the well bores are used in fracturing surrounding rock. A water-based slurry is pumped through the well bore and into a target location so that the high-pressure stream breaks rock to create fractures. Sand, ceramics, or a mixture of the two are added to the pressurized slurry to prop open the fractures with the release of the pressure. The fractures create pathways for fluid to flow to the wellbore.
There has been much speculation relating to the sources of this phenomenal growth in well productivity (Covert 2015; Fitzgerald 2015; Montgomery and O’Sullivan 2017). The increases in average Bakken well productivity could be the result of (1) discrete technological improvements, (2) the application of more intensive investments, evidenced by greater volumes of proppant and injection fluids per well, and longer well laterals, or (3) the result of improved selection of well sites. Figure 2b shows the variation in average initial 360-day oil recovery of wells across Bakken oil-producing counties in North Dakota for 2016. This diversity in productivity likely reflects the spatial variation in reservoir conditions.
Theoretically, innovation and implementation of new or improved technologies have the potential benefits of permitting commercial development of a broad range of hitherto uneconomic resources—similar to what has occurred to oil and gas in low-permeability reservoirs thus far. Alternatively, if the improved productivity is primarily the result of improved selection of well sites, then to maintain production levels over a long period, one should expect extraction costs to increase because increasing inputs will be needed to compensate for declining quality in the sites to be developed in future years. Engineers caution that thresholds exist such that increasing injected proppant and fluids only elevates initial production levels without adding to ultimate well recovery (Barre et al. 2015). Hence, it is important to rank the sources of well productivity growth to properly specify models to predict future supply.
Previous applications of the Random Forest algorithm to petroleum industry problems used it as a predictive tool for well design optimization and also for lithology recognition from well logs. This study considers it as not only a predictive tool, but also an analytical tool at a macro- and economic level to unmask the relative contribution of geologic and technological drivers of the overall increase in well productivity. It shows for the period examined, play-wide productivity improvements are dominated by geologic drivers, which confirms anecdotal evidence that improvements came about because of the convergence of industry drilling to “sweet spots” rather than technological advances.
In particular, productivity of wells in the North Dakota portion of the Bakken oil-producing area is analyzed to make inferences relating to the source of the growth displayed in Figure 2a. The next section describes the data used in the analysis. The Bakken oil-producing area is briefly described, and then, the sources of productivity growth and associated measures are explained. Analysis of the trends in lateral length, number of stages, volumes of proppant and injection fluids, indicators of reservoir quality, and siting of wells permit inferences about the relative importance of drivers of growth. The concluding section explores the implications for future production.
Background
The Bakken petroleum system extends from the western half of North Dakota into eastern Montana and north to Saskatchewan and the southwestern part of Manitoba, Canada. The production target is the middle member of the Bakken Formation which is a mix of siltstone, sandstone, dolomite, and wackestone (Gaswirth and Marra 2015). The middle member generally lies between the upper shale member and lower shale member of the Bakken—the source rocks of the Bakken petroleum system. The Three Forks Formation, another production target, underlies the Bakken Formation. This study, however, focuses on wells that have produced from the middle member. Figure 1 shows the location of the middle member’s continuous accumulation oil and gas production areas that have been subdivided into assessment units by U.S. Geological Survey resource assessment geologists (Gaswirth et al. 2013). A continuous accumulation is a hydrocarbon accumulation that is pervasive throughout a large area that is not significantly affected by hydrodynamic influences. Continuous-type accumulations are also called resource plays. Boundaries that delineate the assessment units are based on geologic properties and are described in some detail in Gaswirth and Marra (2015). Early geologic studies of the Bakken petroleum system established that the upper and lower shale members still contained large in-place volumes of hydrocarbons and that these source rocks had charged the middle member of the Bakken Formation with oil (Dow 1974; Schmoker and Hester 1983; Price 2000).
More recently, geologists have developed a rationale for partitioning the middle member based on indices that reflect the ranking of predicted volumes of oil-in-place, thermal maturity, migration, natural fractures, and factors that contribute to reservoir quality. Theloy and Sonnenberg (2013) reason that the interaction of hydrocarbon generation and thermal maturity results in overpressure and creation of fractures that enhance permeability and porosity. They identified pressure gradients of at least 0.68 lb per square inch per foot as a key indicator of favorable reservoir conditions for drill sites likely to have more highly productive wells. They also created a pressure gradient map of the play. The areas having such gradients were coincident with wells having high oil-to-water ratios (lower water cuts) and were more prevalent in the deeper parts of the formation. Gaswirth and Marra (2015) give a systematic presentation with displays of high-productivity areas based on the criteria considered by Theloy and Sonnenberg (2013). Luo et al. (2018) found high-pressure areas are coincident with high initial gas production. These geologically favorable areas are clustered rather than randomly distributed throughout the extent of the middle member.
Previous Studies on Bakken Well Productivity
In an early study of Bakken oil well productivity, Covert (2015) concentrated on the period before 2010, when operators initiated and modified their facture designs for horizontal wells. That study attributes productivity gains to technology and learning by doing. Fitzgerald (2015) examined just over 3500 wells drilled between 2011 and 2013 and found earlier productivity gains attributed to adaptation of new technology by Covert (2015) had slowed considerably. Montgomery and O’Sullivan (2017) examined wells drilled between the start of 2012 and through the first quarter of 2015 and found unexplained spatial variability a factor as important as technology in the explanation of productivity changes during that period.
Engineering studies focused on improving well productivity by adjusting well completion design factors. An early study by Baihly et al. (2012) examined groups of wells associated with relatively mature fields and concluded the different well groups exhibited a variety of optimal designs. They found, as of the first quarter of 2012, numerous instances where the large number of fracture stages applied to horizontal hydraulically fractured wells could not be justified economically. Lolon et al. (2016) considered a sub-area of the Bakken play in parts of McKenzie and Billings Counties (Fig. 1) and examined factors affecting well productivity. They applied several modeling approaches and found that water cut, volume of injected fluids per foot of lateral length (1 ft = 0.3048 m), and total organic content (TOC) are important predictors of well productivity. Luo et al. (2018) used values of several geologic variables from interpolated maps that were generated from relatively few actual measurements to train a neural network predictive model that they assert enables operators to optimize production.
Vankov et al. (2017) constructed a three-dimensional geo-cellular model for the play used to predict values of oil-in-place from a very limited data set measuring porosity, thickness, and oil saturation. Historical data on the characteristics of well and fracture design (volume of injected fluid, proppant used, lateral length) were used along with the predicted oil in place at drilled locations to calibrate a model to estimate the first 12 months of well production to create play-wide productivity maps. The estimates at undrilled areas were ultimately used to predict future oil supply for the play (see Ikonnikova et al. 2017a, b).
Findings of this study are based on more recent drilling data than other studies, and it examines the relative importance of specific factors underlying the growth in Bakken well productivity rather than focusing on production well optimization strategies or predicting regional production.
Data
For the part of the Bakken play located in North Dakota, the North Dakota Industrial Commission, Oil and Gas Division (NDIC/OGD) publishes individual monthly well production volumes of oil, natural gas, and water along with the number of days the well produced oil (NDIC 2018a). The data are collected by individual wells rather than by leasehold. The Commission also publishes data describing volume of proppant, injection fluids, and number of fracture stages that were applied in well stimulation (NDIC 2018b). The lateral length was estimated by the difference between total length drilled and the drilling length at the lateral kickoff. Only wells that had produced oil for at least 360 days were used in this analysis. IHS Markit (2018) was the source of the vertical depth.
It is widely known and documented that modeling flow characteristics of horizontal hydraulically fractured wells requires a different set of models and generally a longer data series to estimate ultimate well recovery than that required for vertical wells (Kabir et al. 2011). This is because decline-function-forecasting models generally cannot be accurately calibrated until the well flow regime enters a phase of pseudo-steady-state (boundary-dominated) flow (Seidle and O’Conner 2016). The flow regime for horizontal hydraulically fractured wells is initially transient flow (or linear flow). A production decline model calibrated with transient flow data significantly understates the decline that the well will experience once the flow regime changes to boundary-dominated flow. The uncertainty in the change date of a well’s flow regime induces substantial uncertainty in the estimates of ultimate well recovery (EUR).
In this analysis, the 360-day cumulative production total is used to rank the expected individual well recovery. For the wells analyzed, there was a greater than 0.90 correlation between the initial 360-day production total and the cumulative production of wells that had been producing as far out as 9 years (3240 days). Therefore, a well’s initial 360-day cumulative production volume is used as a proxy to represent the relative rank of an individual well’s ultimate recovery.
The NDIC/OGD well stimulation and completion information provide some details relating to the fracture treatments of each well. These include data from which one can estimate the lateral length, number of fracture stages, and volume of proppant and fracture fluids that were injected as part of the fracture treatments. Those wells that had incomplete information were dropped from the analysis leaving about 8345 horizontal hydraulically fractured wells that started production from 2009 through 2017 and produced oil for at least 360 days.
Figure 3 shows boxplots of the distributions of 360-day well production of oil by year in which the well first produces, by the assessment units identified in Figure 1. Except for the Nesson–Little Knife Continuous Oil assessment unit, the distributions for the period from 2010 through 2015 were remarkably stable. Wells that started production in 2016 and 2017 display shifts to higher distributions for several assessment units. A similar trend showing stable distributions from 2010 to the end of 2014 or 2015 is displayed in the boxplots for Billings, Burke, Divide, McKenzie, Mountrail, Stark, and Williams Counties which includes more than 90% of the North Dakota wells starting production during that period (see Appendix Fig. 6).
Boxplots of initial 360-day well productivity for horizontal hydraulically fractured wells producing from the middle member of the Bakken Formation, North Dakota, by continuous oil assessment units (see Fig. 1). (a) Elm Coulee-Billings Nose, (b) Central Basin, (c) Nesson–Little Knife, (d) Eastern Transitional, (e) Northwest Transitional
Table 1 shows the average number of stages, volume of proppant per well, and volume of injection fluids per well gradually increasing until 2015 when there is a more substantial escalation. After 2012, the average lateral length was stable. The rate of increases in the volumes of proppant and injection fluids from 2011 to 2017 more than offset the increase in the number of stages so that proppant and injection fluid per stage increased indicating progressively larger fracture treatments in succeeding years. Corresponding to the noticeable increase in median, well productivities from 2015 through 2017 (see Fig. 3a–e, except in Fig. 3d the productivity change is very subtle), are a 60% increase in proppant per stage, a 40% increase in injection fluids per stage, and an 18% increase in the number of stages per well.
Analysis
Method of Analysis
The investigative approach taken here is a blend of data analytics and statistical modeling. The initial objective is to specify the dependent variable, well productivity, as a function of its determinants or predictor variables. Although values of geologic variables, such as water saturation, porosity, and pressure, determine reservoir conditions and thus productivity, they are not generally available for large numbers of wells because either they are unmeasured or considered propriety. Data analytics and statistical modeling approaches allow the use of closely related variables as predictors if the determining geologic factors cannot be directly observed. The choice of predictive variables can rely on statistical correlations, or alternatively, be selected by the application of modeling techniques such as stepwise regression or various regression tree procedures. The modeling framework is then selected, and the parameters of the model are calculated or fit. If the predictive model does not fall within the parametric regression framework, the criterion for judging the adequacy of the derived model usually rests on the out-of-sample prediction performance. The data are split between training and test samples, the model is calibrated with the training sample, and measures of prediction performance are calculated on the test sample to evaluate the model adequacy.
For this study, the dependent or prediction variable is the initial 360-day cumulative production for individual wells (Fig. 2a). The predictor variables (attributes) that are assumed to influence well productivity relate to characteristics of the horizontal well, the design of the hydraulic fracture treatment, and the geologic characteristics of the well site. Variables that are used to characterize the technology include the lateral length, the number of stages, the proppant volume, and the volume of injected fluids for each well. Additional variables can be constructed from these, such as stages per thousand feet of lateral, and proppant and injected fluids per stage, to capture density and scale of the fracture treatments. Other factors such as fracture length, well orientation, proppant type, and chemical composition of the injection fluids are either propriety or available for a limited number of wells.
Geologic characteristics of drill sites vary spatially. Two possible approaches to studying the influence of well fracture technology factors on well productivity are to control for the spatial variability or try to directly model the variability with proxy variables related to the geology. The pressure gradient and oil saturation have been identified as indicators of reservoir quality (Theloy and Sonnenberg 2013; Gaswirth and Marra 2015; Luo et al. 2018). Their values, if they are measured, are commonly only available to well owners. Models that portray regional trends in these characteristics may have been constructed from a handful of measurements at wells with published information, but these vary in quality and level of documentation.
Rather than rely on predicted measurements from a very small data set, proxy variables representing reservoir quality and state of pressure were constructed. Three proxy variables, used as indicators of reservoir quality, are the initial 180-day water cut (inversely related to the oil-to-water ratio), the vertical depth of the well, and the initial 30-day cumulative gas produced. For the initial 180-day water cut variable, the 180-day period is sufficiently long that distortions introduced by fluid flowback from hydraulic fracture operations are mitigated. Whereas the water cut variable is related to the reservoir’s oil and water saturation (Theloy and Sonnenberg 2013), the initial gas production variable is related to the reservoir pressure regime (Luo et al. 2018). In some environments, vertical depth can be associated with lower porosity and permeability, but in others, such as basin-centered accumulations, greater depth may also be associated with thicker pay zones. The empirical analysis focuses on determination of the relative importance of variables representing fracture treatment design, and the geologic favorability on well productivity as measured by the initial cumulative 360-day oil production and initial 30-day gas production.
Empirical Approaches
The data were fitted with several procedures where some resulting models cannot be expressed in explicit functional forms. The initial 360-day cumulative production (cmpd) for each well is a specified linear function of 12 variables:
where vd is the vertical depth, wc180 is the initial 180-day water cut, g30 is the initial 30-day gas production, ll is the lateral length, stg is the number of stages per well, ppt is the volume of proppant per well, awt is the volume of injected fluid per well, psct is the volume of proppant per stage, wsct is the injected fluids per stage, stlt is the number of stages per thousand feet lateral length, plt is the volume of proppant per lateral foot, wlt is the volume of injected fluids per lateral foot, and ε is the random error. The inclusion of the number of stages standardized on lateral length, and volume of proppant and injected fluids standardized on the number of stages and lateral length attempted to capture the nuances of scale effects associated with each of basic completion variables.
The data were initially fitted to a linear least squares model with no interaction terms. Coefficients and p values of the fitted coefficients are presented in Table 2. About 66% of the variation in well productivity is explained by the linear regression. The extremely large data set resulted in low p values for the coefficients of the explanatory variables, but it also masks the multicollinearity among predictors. It is likely that negative signs on the lateral length, proppant per stage, and number of stages per thousand feet of lateral length are evidence of spurious correlations induced by the multicollinear predictors.
Regression trees (Breiman et al. 1984) and the derivative algorithm, the Random Forest (Breiman 2001), are applicable to nonlinear modeling problems by partitioning the data spaces into smaller subspaces. These modeling algorithms may be used to identify the relative importance of the predictors. Table 2 also presents results of calculations that show the relative importance for the 12 predictor variables for a regression tree calibrated with the entire data set of 8148 horizontal hydraulically fractured wells which started production from 2010 through 2017. The table shows that the six most important predictors account for 78% of the explanatory power of the regression tree. The water cut predictor is the most important followed by volume of injected fluids per well and volume of injected fluids per foot of lateral. These three variables account for almost half of the variation explained by the full (unpruned) regression tree. The large number of observations and the large variation do not allow the display of the initial tree which can have more than 60 splits and more than over 1000 nodes, depending on the when the splitting is cutoff. The pruned tree has 11 splits and is displayed in Appendix Figure 7. The regression tree framework does not immediately allow an evaluation of the statistical significance of the predictor variables.
Application of Random Forest Analysis
The ideas underlying the Random Forest algorithm are the bootstrap aggregation (bagging) of regression trees and the random selection of predictors to introduce randomness and robustness into calculations. In simple “bagging,” bootstrap samples of the training set are taken iteratively with replacement each time a regression tree is built (Breiman 1996). The “Random Forest” procedure as originated by Breiman (2001) not only takes bootstrap samples of the training data but also samples the set of predictors to build a diverse and uncorrelated collection of trees. The collection or ensemble of “trees” (forest) is retained and used to predict the target or dependent variable which is calculated as the average of the predictions of the individual regression trees in the ensemble. The ensemble of trees is thought of as a diverse forest leading to more robust overall predictions.
The computational algorithms for Random Forest provide for generating cross-validation statistics at each node and model subset of predictors sampled. If the original single regression tree is relatively simple, the partitions and values associated with the splits frequently provide additional insight to the analyst (see Appendix Fig. 7). Because a Random Forest represents hundreds or thousands of different trees, one cannot show an explicit regression tree structure for the model, but the predictive power of Random Forest models is much better than a single regression tree (Breiman 2001). For example, for a single tree calibrated with a training data representing 70% of the total data set, the predictive error per well as measured by the root-mean-square error (RMSE) of the test sample of the pruned tree is about 32 thousand barrels per well. The mean value of the initial 360-day cumulative production is 106 thousand barrels for all wells in the test set. In this case, the ensemble procedures reduced the expected root-mean-square error by about 30%. The RMSE calculated with the same training and test samples for the bagging and Random Forest procedures amounted to about 27 thousand barrels.
The bootstrap iterations allow the Random Forest algorithm to incorporate a validation step within the fitting procedure by using out-of-bag (oob) samples which are those samples that are not used in a particular bootstrap iteration to fit the tree that is constructed. The oob error estimate is nearly identical to a cross-validation error. The oob errors are the prediction errors (RMSE) when the fitted model is applied to the oob samples. The variable importance measure is also calculated with the oob samples and measures the relative predictive strength of each predictor (Hastie et al. 2009). The oob errors are also used to calculate the explained variance of values in dependent variables (R2) by the values of the predictor variables in the oob samples.
Recent research by Strobl et al. (2007) shows that computations used to rank variable importance based on the loss of accuracy in Random Forest models’ predictions can be biased when predictors are highly correlated with each other. Later research has developed more rigorous statistical permutation tests (Altmann et al. 2010) that have been implemented within Random Forest software to calculate statistical significance or p values of the predictor variables (Wright et al. 2018).
The implementation of the Random Forest model with the North Dakota Bakken wells which initially used all 12 predictor variables given in Table 2 was reduced to a set of predictors that were not correlated with the geologic proxy variables, that is, the water cut, initial gas production, and vertical depth. The algorithm constructed a forest with a predictor variable set that included 180-day water cut, initial 30-day gas production, vertical depth, lateral length per well, number of fracture stages per well, proppant per stage, and volume of injected fluids per stage. Recall the lateral length, number of stages, volumes of proppants, and injected fluids per stage measure intensity of well completion effort, whereas the vertical depth, 180-day water cut, and 30-day gas production are proxy variables that reflect spatial variability of the geology. For each forest, 1000 trees were generated based on bootstrap samples of four of seven predictors and minimal tree node size of five observations. Alternative numbers of trees or different tuning parameters such as the number of predictors sampled by the bootstrap procedure and individual tree depth setting did not result in significant improvements in predictive performance.
Table 3 shows the order of the importance in ranking and the p values of the primary predictors calculated with the “ranger” implementation of the Random Forest algorithm (Wright and Ziegler 2017). The table shows the ranking of importance as follows: water cut, injected fluids per stage, proppant per stage, initial 30-day gas production, the number of stages, vertical depth, and then lateral length. The water cut, injected fluids, proppant per stage, initial gas production, and numbers of stages predictors have p values less than 0.1% (< 0.001). A p value of 0.1% or less implies a probability that a predictor has no influence on well productivity is not more than 1 chance in 1000, which is low indeed.
The table shows the RMSE and percent of variance explained, denoted as R2, computed from the averages of the oob samples that are part of the training data but not chosen by the bootstrap sample. The algorithm’s training data set consists of 70% of randomly chosen observations; the remaining 30% of the observations represent the test data or out-of-sample data. The similarity in magnitude of RMSE (oob) and RMSE (test) is reassuring and suggests empirical results are not affected by training data idiosyncrasies.
Partial dependence plots are tools for additional analysis which allow the analyst to visualize the partial dependence of the well productivity to a single predictor. Calculations for the partial dependence plots are made after the model has been fit and are critical in understanding the ensemble models. Figure 4a and b shows examples of the plots for water cut (wc180) and the initial 30-day gas production (g30) for the Random Forest model, the two most important geology-related proxy variables. The partial dependence plots depend on density and completeness of the data from which the model was constructed. The full effects of increasing some predictors (such as proppants) may depend on values of other variables (injected fluids and number of stages). For such variables, the data used for calibrating the models may not be sufficiently rich for the calculations of the partial dependencies to produce reasonable plots. Figure 4c shows the partial dependence plot of the response variable to the interaction of these two geologic proxy variables, water cut and initial 30-day gas production.
Partial dependence plots showing response of well productivity to changes in: (a) 180-day water cut (fraction), (b) the initial 30-day natural gas production (millions of ft3), and (c) the combination of the 180-day water cut (fraction) and 30-day gas production (millions of ft3), where the vertical axis is 360-day oil production (thousands of barrels) (1 barrel = 0.159 m3, 1 ft3 = 0.02832 m3)
Analysis of Partitions of Well Data
The incremental productivity improvements resulting from more aggressive well completions depend on the well site’s geologic favorability. The well data set was partitioned into high producers and low producers based on the first and fourth quartiles of 360-day production record of wells initiating production in each year. Table 3(B) and (C) shows the comparison of the ranking of predictor importance, p values, and other model properties for a high and low producer Random Forest models.
The model based on the first quartile (low producers as given in Table 3B) shows the following importance order of predictors: initial 30-day gas production, initial 180-day water cut, number of stages per well, proppant volume per stage, and injected fluid per stage, followed by vertical depth and lateral length. The table also shows the following importance ordering for the 4th quartile (high producers as given in Table 3C): number of stages, water cut, volume of proppant per stage, volume of fluids injected per stage, and initial 30-day gas production, followed by vertical depth and lateral length. Notwithstanding the importance ranking, calculated p values for the first three or four predictors were essentially equivalent. The high producers had more favorable geology; average water cut of high producers was just over half of that of low producers (32% water vs. 59% water) and the average initial 30-day gas production was about three times that of the low producers (28.4 vs. 8.7 million ft3 of gas where 1 ft3 = 0.02832 m3).
The favorable geology works to increase the predicted payoff from boosting well completion inputs. Figure 5 shows the low- and high-producer models’ predicted responses to increasing the number of stages per well. In the figure, the models assumed the same vertical depth, lateral length, and volume of proppant and injected fluids per stage for both high and low producers. The assumed 180-day water cut for the high producers was 32% water and 59% water for the low producers, while the assumed initial 30-day gas production was 28.4 million ft3 for the high producers and 8.7 million ft3 for the low producers. The incremental oil recovery per well for the 360-day production period due to increasing the number of stages from 25 to 50 stages is almost 56 thousand barrels for the high producers vs. the incremental recovery of 20 thousand barrels for the low producing wells.
Random Forest models’ predicted well productivity response (in thousands of barrels, for the initial 360-day cumulative well production) caused by increasing the number of stages per well for wells in first quartile group (low producers) and wells in the fourth quartile group (high producers). Graph represents smoothed predictions from the Random Forest models of the groups. Assumed 180-day water cut for the high-producer group is 32% and for the lower-producer group is 59%, while the assumed initial 30-day gas production for the high-producer group was 28.4 million ft3 and the lower-producer group 8.7 million ft3. The well depth, lateral length, proppant per stage, and the injected fluid per stage were assumed equal for the two groups (1 barrel = 0.159 m3, 1 ft3 = 0.02832 m3)
The substantial increase in well completion inputs (Table 1) after 2015 generally resulted in noticeable increments to well productivity. Models were calibrated using data from the period of 2010 through 2015 (early period) and using data from 2016 through 2017 (late period). Table 3(D) and (E) shows the variable importance, the p values of the predictors, and measures of prediction performance for early start (2010–2015) vs. late start (2016–2017) Random Forest models. In the later period, the number of stages, volume of proppant per stage, and injected fluids per stage had essentially the same p values. From 2015 to 2017, the more aggressive well completion practices (increases in average number of stages per well of 18%, proppant per stage of 60%, and injected fluids per stage of 40%) resulted in an overall increase in well productivity of 11%.
Conclusions
This analysis examined productivities of horizontal hydraulically fractured wells that had begun production from the middle member of the Bakken Formation in North Dakota from the beginning of 2010 though 2017 and that had at least produced for 360 days. Whereas standard operating procedures may have been continuously refined, no dramatic technological improvements were identified to account for the increased productivity shown in Figure 2a. Instead, the location-specific boxplot distributions of well productivities are reasonably stable for the period from 2010 to 2015 when displayed by geographically defined assessment units. Well design inputs such as lateral length, number of stages, volume of proppants, and volume of injection fluids increased but only gradually. The apparent increase in the productivity for 2016 and 2017 appears to be in response to a dramatic increase in these inputs. This evidence is consistent with the hypothesis that much of the overall average increase in productivity shown in Figure 2a was the result of greater concentration of drilling in areas with favorable geology.
The modeling shows the 180-day water cut predictor variable as consistently assigned the highest or second highest rank of importance with the lowest reported p value. Both the 180-day water cut and the initial 30-day gas production predictors were consistently found among the predictors whose influence on well productivity was reasonably affirmed by low p values. Theloy and Sonnenberg (2013) identified the pressure regime and high oil saturation as favorable reservoir properties. As a proxy for modeling the pressure regime, we have used the well’s initial 30-day gas production, and as a proxy for the oil-to-water ratio, we used the 180-day water cut which is roughly inversely related. A regression tree approach was used for modeling well productivity because the requirements of standard parametric regressions such as explicit functional expressions, independence of regressors, homoscedasticity, and normality of errors could not be met. The ensemble regression tree algorithm, Random Forest, out-performed the single regression tree procedure in terms of its predictive ability and consistently pointed to the geologic proxy variables of 180-day water cut and initial 30-day gas production as important; statistical permuation tests confirmed their significance.
There is some evidence that the industry was improving the siting of wells. During the period from 2010 through 2014, the annual mean and annual median values of annual distribution of the 180-day water cut values for wells that began production in each year fluctuated and then began to increase from 2015 through 2017. However, from the period of 2010 through 2017, the standard deviation of the distribution declined by 18% and the interquartile range of the distributions declined by 30%. These data are consistent with an industry more precisely siting wells based on the quality of reservoirs but in the latter part of the period encountering less favorable conditions.
The implications of the findings are that a substantial part of the improved productivity of the Bakken during the period can be attributed to the improved siting of wells. Based on current technology and practices, models that forecast Bakken production will perform best when incorporating the geologic factors that represent the reservoir conditions at undrilled sites to capture the increasing costs that will be incurred if those sites are of lesser quality. Because future tax revenues, infrastructure requirements, and economic activity are based on production rates which will also depend on the competitive cost position of the product, future dynamic changes of Bakken well productivity have broad economic implications to decision and policy makers.
Finally, though Random Forest predictive models have found application in mineral exploration and assessment (Carranza and Laborte 2015a, b, 2016) and to some degree in petroleum assessment (Vankov et al. 2017), their properties remain to be fully exploited. Their robustness for predicting technical recovery of petroleum at undrilled locations using well completion inputs and values of proxy variables that represent the reservoir properties that are only infrequently measured needs further investigation. The values and locations of such proxy variables that are generated in production and often publicly available could provide a more reliable basis for prediction than contoured data based on a very few measurements.
References
Altmann, A., Tolosi, L., Sander, O., & Lengauer, T. (2010). Permutation importance: A corrected feature importance measure. Bioinformatics,26(10), 1340–1347.
Baihly, J. D., Altman, R. M., & Aviles, I. (2012). Has the economic stage count been reached in the Bakken Shale? SPE Paper 159683-MS. In Proceedings of the 2012 SPE hydrocarbon, economics, and evaluation symposium, 24–25 September, Calgary, Alberta. https://doi.org/10.2118/159683-MS.
Barre, R. D., Cox, S. A., Miskimins, J. L., Gilbert, J. V., & Conway, M. W. (2015). Economic optimization of horizontal-well completions in unconventional reservoirs. SPE Production and Operation Journal,30(4), 293–311.
Breiman, L. (1996). Bagging predictors. Machine Learning,24(2), 123–140.
Breiman, L. (2001). Random forests. Machine Learning,45(1), 5–32.
Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and regression trees. Belmont, CA: Wadsworth International Group.
Carranza, E. J. M., & Laborte, A. G. (2015a). Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of random forests algorithm. Ore Geology Reviews,71, 777–787.
Carranza, E. J. M., & Laborte, A. G. (2015b). Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Computers & Geosciences,74, 60–70.
Carranza, E. J. M., & Laborte, A. G. (2016). Data-driven predictive modeling of mineral prospectivity using random forests: A case study in Catanduanes Island (Philippines). Natural Resources Research,25(1), 35–50.
Covert, T. R. (2015). Experiential and social learning in firms: The case of hydraulic fracturing in the Bakken Shale. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2481321.
Dow, W. G. (1974). Application of oil-correlation and source-rock data to exploration in the Williston Basin. American Association of Petroleum Geologists Bulletin,58(7), 253–1262.
Fitzgerald, T. (2015). Experiential gains with a new technology: An empirical investigation of hydraulic fracturing. Agricultural and Resource Economics Review,44(2), 83–105.
Gaswirth, S. B., & Marra, K. R. (2015). U.S. Geological Survey 2013 Assessment of undiscovered resources in the Bakken and Three Forks Formations of the U.S. Williston Basin Province. American Association of Petroleum Geologists Bulletin,99(4), 639–660.
Gaswirth, S. B., Marra, K. R., Cook, T. A., Charpentier, R. R., Gautier, D. L., Higley, D. K., Klett, T. R., Lewan, M. D., Lillis, P. G., Schenk, C. J., Tennyson, M. E., & Whidden, K. J. (2013). Assessment of undiscovered oil resources in the Bakken and Three Forks Formations, Williston Basin Province, Montana, North Dakota, and South Dakota: U.S. Geological Survey Fact Sheet 2013–3013, 4 p. http://pubs.usgs.gov/fs/2013/3013/. Retrieved September 20, 2018.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). Elements of statistical learning—data mining, inference, and prediction (2nd ed.). Berlin: Springer.
IHS Markit. (2018). ENERDEQ U.S. well data: IHS Markit, online database available from IHS Markit Energy Upstream, 15 Inverness Way East, D205, Englewood, CO 80112, U.S.A.. Retrieved July 9, 2018.
Ikonnikova, S., Gülen, G., & Browning, J. (2017a). Well economics and production outlook: Analysis of the Bakken oil play. URTeC Paper 2671319. In Unconventional resources technology conference, 24–26 July, Austin, Texas. https://doi.org/10.15530/urtec-2017-2671319.
Ikonnikova, S., Gülen, G., & Browning, J. (2017b). Summary and conclusions of Bakken and Three Forks Field Study. URTeC Paper 2667925. In Unconventional resources technology conference, 24–26 July, Austin, Texas. https://doi.org/10.15530/urtec-2017-2667925.
Kabir, C. S., Rasdi, F., & Igboalisi, B. (2011). Analyzing production data from tight oil wells. Journal of Canadian Petroleum Technology,50(5), 48–58.
LeFever, J. (2005). Oil production from the Bakken Formation: A short history. North Dakota Geological Survey Newsletter,32(1), 5–10.
Lolon, E. K., Hamidieh, K., Weijers, L., Mayerhofer, M., Melcher, H., & Oduba, O. (2016). Evaluating the relationship between well parameters and production using multivariate statistical models: A Middle Bakken and Three Forks case history. SPE Paper 179171-MS. In SPE hydraulic fracturing technology conference 9–11 February, Woodlands, Texas. 28 p. https://doi.org/10.2118/179171-MS.
Luo, G., Tian, Y., Bychina, M., & Ehlig-Economides, C. (2018). Production optimization using machine learning in Bakken Shale. URTeC Paper 2902505. In Unconventional resources technology conference, 23–25 July, Houston. https://doi.org/10.15530/urtec-2018-2902505.
Montgomery, J. B., & O’Sullivan, F. M. (2017). Spatial variability of tight oil well productivity and the impact of technology. Applied Energy,195, 344–355.
North Dakota Industrial Commission (NDIC), Oil and Gas Division. (2018a). Monthly well production data: Spreadsheet available from North Dakota Industrial Commission, delivered August 23, 2018.
North Dakota Industrial Commission (NDIC), Oil and Gas Division (2018b). Well stimulation dump file data: Spreadsheet available from North Dakota Industrial Commission, delivered January 25, 2018.
Price, L. C. (2000). Origins and characteristics of the basin-centered continuous reservoir unconventional oil-resource base of the Bakken source system, Williston Basin, unpublished. http://www.undeerc.org/Price/. Retrieved October, 2018.
Schmoker, J. W., & Hester, T. C. (1983). Organic carbon in Bakken formation, United States portion of Williston basin. American Association of Petroleum Geologists Bulletin,67(12), 2165–2174.
Seidle, J. P., & O’Conner, L. S. (2016). Estimation of unconventional well recoveries and economics from transient flow data. In Proceedings of SPE/IAEE hydrocarbon economics and evaluation symposium, 17–18 May 2016, Houston, 19 p. https://doi.org/10.2118/179983-MS.
Strobl, C., Boulesteix, A., Zeileis, A., & Hothorn, T. (2007). Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics, 8(1):25, 1–21.
Theloy, C., & Sonnenberg, S. A. (2013). New insights into the Bakken play: What factors control production? In AAPG annual convention and exhibition, Pittsburgh, Pennsylvania, 19–23 May, Pittsburgh, Pennsylvania. http://www.searchanddiscovery.com/abstracts/html/2013/90163ace/abstracts/th.htm. Retrieved September 19, 2018.
U.S. Energy Information Administration (USEIA). (2018). Tight oil remains the leading source of future U.S. crude oil production. Today in Energy. https://www.eia.gov/todayinenergy/detail.php?id=35052. Retrieved August, 2018.
Vankov, E., Ikonnikova, S., Gulen, G., & Medlock, K. (2017). Well productivity analysis of the Bakken Shale Play, URTeC Paper 2671321. In Unconventional resources technology conference, 24–26 July, Austin, Texas. https://doi.org/10.15530/urtec-2017-2671321.
Wright, M. N., Wager, S., & Probst, P. (2018). Ranger: A fast implementation of random forests. R package version 0.11.1. https://cran.r-project.org/web/packages/ranger/ranger.pdf. Retrieved November, 2018.
Wright, M. N., & Ziegler, A. (2017). Ranger: A fast implementation of random forests for high dimensional data in C++ and R. Journal of Statistical Software,77, 1–17. https://doi.org/10.18637/jss.v077.i01.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Boxplots of initial 360-day well productivity for horizontal hydraulically fractured wells producing from the middle member of the Bakken Formation, North Dakota, by county (see Fig. 1). (a) Burke, (b) Divide, (c) Dunn, (d) McKenzie, (e) Stark, (f) Williams
Pruned regression tree for the Bakken well productivity using horizontal hydraulically fractured wells starting production from 2010 through 2017. Variables are awt injected fluids (barrels per well), wc180 initial 180-day water cut (fraction), g30 initial 30-day cumulative gas production (millions of ft3), ppt proppant per well (ton). Numbers at the ends of the leaf are the predicted initial 360-day cumulative well production (thousands of barrels) (1 barrel = 0.159 m3, 1 ton = 0.907 tonne, 1 ft3 = 0.02832 m3)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Attanasi, E.D., Freeman, P.A. Growth Drivers of Bakken Oil Well Productivity. Nat Resour Res 29, 1471–1486 (2020). https://doi.org/10.1007/s11053-019-09559-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11053-019-09559-5