Introduction

Resource managers use scientific data from different disciplines when evaluating federal lands for mining, oil and gas exploration and development, recreation, livestock grazing, conservation, and other uses. For example, in the USA, the Forest and Rangeland Renewable Resources Planning Act of 1974 and the National Forest Management Act of 1976 were enacted to ensure a systematic, interdisciplinary approach to managing Forest Service lands, specifically renewable resources, mining, recreation needs, and their economic effects on local communities. These pieces of legislation require a renewed forecast for potential land assessment every 10 years (http://www.nrs.fs.fed.us/fia/topics/rpa/). One big challenge for scientists is to synthesize, integrate, and present meaningful information to resource managers in a form they will understand and use.

Understanding past and future trends in mineral-related activity is complicated because; for example, the US regulations (e.g., the Securities Act of 1993, the Securities and Exchange Act of 1934, Regulation S-K, Sarbanes–Oxley Act, and Industry Guide 7) do not require the disclosure of exploration results on federally managed lands. The US Securities and Exchange Commission provides guidance for reporting mineral reserves for companies listed on US stock exchanges but does not require the disclosure of the results of exploration activities (Securities and Exchange Commission 2016). In contrast, exploration and mining companies listed on the Canadian stock exchanges have more stringent requirements for reports that support mineral resource and reserve statements (http://www.osc.gov.on.ca/en/15019.htm) although they do not have to provide exploration data that were not used in the estimation of mineral inventory. Privately held companies conducting exploration on federally managed lands are under no obligation to report any information.

Given lack of transparency, determining current and future direction of mining activities or interest, in the USA or elsewhere, is difficult. A useful proxy or surrogate for understanding or predicting future mineral-related activities is to use public records, which show when and where someone or a company was willing to allocate time and resources to take a land position. In the USA, the General Mining Act of 1872 allows its citizens the opportunity to explore for, discover, and purchase valuable mineral deposits on federal lands that are open for mining (Pruitt 1990; Maley 1992; Rohling 2011). These deposits include most metallic, certain nonmetallic, and industrial minerals. A mining claim is a selected parcel of federal land for which someone or a company has asserted a right of possession under the General Mining Law (BLM 2012). Since 1979, the Federal Land Policy and Management Act (FLPMA), or more specifically 90 Stat 2769l 43 USC 1744, requires all holders of an unpatented mining claim to register it with the Bureau of Land Management (BLM) in addition to their local county office. Failure to register (i.e., file a claim and have it accepted) with the BLM results in loss of the claim (Pruitt 1990; Maley 1992). This information is maintained in the BLM’s Legacy Rehost System (LR2000) and is available to the public (http://www.blm.gov/lr2000/). This database provides over 30 years of spatial information on minerals exploration activity.

It is challenging to visualize and analyze datasets with spatiotemporal (i.e., both time and space information) without adequate and proper tools. In 1970, Torsten Hagerstrand, a Swedish geographer, revolutionized the way we look at spatiotemporal data by displaying such data as a three-dimensional (3D) space–time cube (STC) with the spatial data plotted on the x- and y-axes and the temporal data plotted on the z-axis (Kristensson et al. 2009; Bach et al. 2014). Prior to the 1990s and the integration of the personal computer and software that would allow digital rendering of spatiotemporal data, researchers created the complex graphics manually, consuming significant time and effort (Kraak and Koussoulakou 2005). With the increase in computing power and sophisticated programming, spatiotemporal data can be easily rendered in 3D and manipulated and queried in real time. Numerous researchers have used this visualization technique to display and analyze various types of datasets, including movement data for both animals and humans (e.g., Niyogi and Adelson 1994; Demšar and Virrantaus 2010; Ding et al. 2016), eye-tracking data (e.g., Li et al. 2010; Popelka and Voženílek 2013), and crime data in different cities and neighborhoods (e.g., Nakaya and Yano 2010). Esri’s recent (2016) release of ArcPro is equipped with STC functionality and additional analysis tools in the Space Time Pattern Mining toolbox [i.e., Trend, Emerging Hot Spot Analysis (EHSA), Hot Spot Analysis (HSA), and Cluster and Outlier Analysis (COA)], which enable users to conduct statistical analyses on STC data, allowing them to assess trends or changes in the data through time.

This paper explores how to distill 30 years of mining claim data on federal land into products that will give managers insights to types of minerals activity that can be anticipated in the reasonably foreseeable future. As a proof of concept of the utility of using a STC in assessing trends in large datasets, we present several STC analyses and discuss whether they are able to consistently identify and predict future trends in mining claim data. For this test, we chose to use a subset of lode mining claim data around the McDermitt Caldera, an area with multiple commodities (i.e., uranium, gallium, mercury, and lithium) and numerous episodes of exploration and production in a concentrated geographic area.

Background

McDermitt Caldera Geology

The McDermitt Caldera is an approximately 40 by 20 km volcanic collapse structure in northern Nevada and southern Oregon within the Great Basin physiographic province. It is ringed by, and lies within, the Montana Mountains, the Trout Creek Mountains, and the Double H Mountains (Fig. 1). Previous researchers (Rytuba 1976; Rytuba and Glanzman 1978; Rytuba et al. 1979; Rytuba and McKee 1984; Childs 2007) hypothesize that four tuffaceous eruptive events with intermittent rhyolitic lava flows occurred from ~16.1 to 15 Ma, leaving thick deposits of tuff in and around a series of nested and collapsed calderas (i.e., the Older Washburn, the Calavera, the Jordan Meadow, and the Long Ridge calderas) that together, constitute the larger McDermitt Caldera. The tuff deposits conformably overlie mafic volcanic rocks of the Orevada View volcanic series, which is correlative with the Steens Basalt in Oregon (Castor and Henry 2000; Coble and Mahood 2016). Evidence for multiple eruptions and caldera collapse events include the occurrence of multiple vitrophyres and cooling units as well as erosive paleotopography between tuff units and water-reworked air fall tuffs (Rytuba and McKee 1984).

Figure 1
figure 1

McDermitt Caldera and the most notable mines in the area. Areas with significant lithium concentrations are highlighted in brown (Henry et al. 2016)

Full size image

Although previous researchers proposed a resurgent system composed of four tephra eruptions that contributed to the collapse and formation of nested calderas (Rytuba 1976; Rytuba and Glanzman 1978; Rytuba et al. 1979; Rytuba and McKee 1984; Childs 2007), recent research based on 40Ar/39Ar dating found no evidence for multiple eruption events, but rather proposed that the caldera formed from a single eruption responsible for its collapse around 16.35 Ma (Henry et al. 2016). Although the history of caldera formation has been debated for many years (Castor and Henry 2000), it does not affect the analysis presented in this paper and will not be addressed further. The topographically low collapsed structure, however, likely provided a setting for ponding of tuffaceous material, which became a source of lithium-hosted, tuffaceous–lacustrine sediments (Fig. 1) (Rytuba 1976; Glanzman et al. 1978; Rytuba and Glanzman 1978; Henry et al. 2016).

Circa 14 Ma, near-surface hypabyssal rhyolite intrusions were emplaced providing shallow heat and hydrothermal fluids that served to concentrate minerals from previously erupted rhyolitic, dacitic, and tuffaceous country rock (Rytuba et al. 1979; Rytuba and McKee 1984). Accordingly, mercury, lithium, uranium, and gallium occurrences are found in the area. Rytuba and Glanzman (1978) proposed three unique factors that contributed to deposition of highly concentrated metals in this location: (1) the occurrence of volcanic activity in a relatively restricted area, which contributed to a shallow heat source and allowed for near-surface hydrothermal systems to form; (2) earlier deposited rhyolites had high concentrations of uranium, mercury, and lithium—with mercury concentrations as much as two orders of magnitude and lithium as much as one order of magnitude higher than average rhyolites—providing material for later concentration through hydrothermal fluids; and (3) the deposition of tuffaceous deposits into a closed basin. These three factors provided stability, isolation, and an ideal environment for concentration of key mineral resources.

Mineral Commodities, Exploration, and Mines

Although the McDermitt Caldera area hosts numerous deposits of mineral commodities, only gallium, uranium, mercury, and lithium are present in high enough concentrations such that they have been of great interest. The majority of mining claims at McDermitt Caldera, however, were staked for uranium, mercury, and lithium.

Uranium and mercury deposits in the northern portion of the caldera are localized along ring faults and are typically associated with potassium feldspar alteration zones. The faults are thought to have served as conduits for hydrothermal systems that acted to concentrate metals. In the cases of the Bretz, McDermitt, Cordero, Cottonwood, and Opalite mines (Fig. 1), hydrothermal fluids altered and replaced lake sediments with mercury and low concentrations of uranium (Rytuba et al. 1979; Ainsworth 2004). The Cordero Mine (at the northeastern portion of the McDermitt Caldera) was one of the most important mercury mines and produced over 115,000 flasks of mercury before it closed in 1970 (Willden 1964; Rytuba 1976). The nearby McDermitt open-pit mine, produced over 400,000 flasks of mercury before closing in 1989 due to a mercury price crash after the US government divested its strategic reserves (Fig. 2) (Schlottmann 1987; Castor et al. 1996; Castor and Ferdock 2004; Childs 2007). Since 1992, mercury has not been produced as a primary commodity in the USA (USGS 2016).

Figure 2
figure 2

Historic commodity prices for mercury, lithium, and uranium from 1976 to 2010 (blue line) and price altered for inflation to 2016 values (red line). Note, years 1976, 1979, and 1993 correspond to legislation changes (i.e., the Federal Land Policy and Management Act of 1976, the 1979 deadline to registered claims with the Federal Government, and the Omnibus Budget Reconciliation Act of 1993)

Full size image

The presence and abundance of uranium was also of historical interest around McDermitt Caldera (USGS 1946; Castor et al. 1996). The Moonlight Mine, along the western margin of the caldera (Fig. 1), hosts appreciable amounts of uranium associated with fault breccias and breccias linked to rhyolitic dikes that were feeders for the late-stage rhyolitic domes (Rytuba and Glanzman 1978; Rytuba et al. 1979; Castor and Henry 2000). During the late 1970s and early 1980s, uranium became an important commodity (Fig. 2) as a result of the 1970s energy crisis and peak oil. By the late 1970s, interested parties staked all public land thought to have potential for uranium around the caldera (Castor and Ferdock 2004). Although low concentrations of uranium exist in other portions of the caldera, uranium has only been produced from the Moonlight Mine in the southwest.

Lithium is found in tuffaceous, lacustrine sediments that were altered to zeolites and potassium feldspar (Rytuba 1976; Glanzman et al. 1978; Rytuba and McKee 1984; Crocker and Lien 1987). The lacustrine sediments are alteration products of ponded tuff deposits and tuffaceous lithic fragments transported into the caldera by erosion of the surrounding rocks. Lacustrine deposits are present in low-lying areas along the edges of the caldera in an arc extending from the northeast to the southwest. In the northern and western parts of the caldera, lithium occurs in the clay mineral hectorite (Glanzman et al. 1978; Henry et al. 2016).

Gallium is associated with argillic alteration zones proximal to hot-spring mercury deposits at the Cordero and nearby McDermitt Mine. Because gallium is primarily produced as a byproduct in the process of refining bauxite to aluminum and is therefore plentiful, the price of gallium has generally remained at constant levels since the early 1980s (Rytuba et al. 2003; USGS 2010). For a brief period in 2000, however, with a nearly eightfold increase in gallium prices, there was renewed interest in exploration for the commodity which resulted in 17 additional claims staked near the Cordero Mine (Tingley and LaPointe 2002). As a result of this activity, a mineral inventory was defined: Measured and indicated resources are 1,000,000 short tons of rock at 47.7 ppm gallium with an additional inferred resource of 6,600,000 tons at 43.7 ppm gallium (Muntean et al. 2016). The decline in prices between 2001 and 2002 resulted in diminished interest in gallium (USGS 2002; Childs 2007).

Data

Existing summaries of mining claim data were used for the McDermitt Caldera study. Causey (2011) and Dicken and San Juan (2016) extracted mining claim data from BLM’s LR2000 database and summarized the number of mining claims for each meridian, township, range, and section (MTRS) of the Public Land Survey System. Causey’s (2011) compilation encompassed the period from 1976 to 2010; Dicken and San Juan (2016) summarize active claims early in 2016. For the purposes of the analysis using a geographic information system (GIS), the centroid of each MTRS was obtained and the mining claim data were associated with the corresponding centroids (Fig. 1). We restricted our analysis to the number of active lode mining claims per MTRS.

As input for analysis, the lode claim data from Causey (2011) were formatted into five columns: MTRS, latitude, longitude, year, and number of active lode mining claims. The dataset was converted into a shape file and imported into ArcGIS Pro for analysis and testing. Numbers of active lode mining claims per section were reported as rational numbers representing whole or parts of a claim because a claim can fall into more than one mile square section (~1.6 km2). A single lode claim is a rectangle that cannot exceed 1500 feet (457.2 m) in length and 600 feet (182.88 m) in width (Pruitt 1990). If the claims are neatly organized, about 30 claims will fit in a section. However, the number of claims in a section can be much higher because claims may be smaller than the maximum allowed. The formatted McDermitt dataset is provided here as Electronic Supplementary Material.

A regulation enacted in 1993 significantly affects the number of registered claims [Subtitle B of Title X of the Omnibus Budget Reconciliation Act (OBRA) of 1993]. It states that the holder of an unpatented mining claim must pay a yearly claim maintenance fee of $100/claim in lieu of assessment work (Public Law 103-66 August 10, 1993, 107 STAT.403). Before this act was passed, miners could waive the maintenance fee and instead complete assessment work or improvements equaling the maintenance fee amount. The number of registered claims dropped significantly after this new regulation was enacted (Fig. 3). Parties willing to pay the $100 maintenance fee per claim only maintained claims on the western edge of the caldera and areas around active mines in the north and east immediately following the 1993 change in legislation.

Figure 3
figure 3

Total number of active lode claims registered with the Bureau of Land Management per year from 1976 to 2010 and 2016. Years highlighted in gray correspond to the maps in Figure 4. Additionally, years 1976, 1979, and 1993 correspond to legislation changes (i.e., the Federal Land Policy and Management Act of 1976, the 1979 deadline to register claims with the Federal Government, and the Omnibus Budget Reconciliation Act of 1993)

Full size image

Methods

With so many claims registered over the 34-year period according to the Causey (2011) dataset, finding efficient ways to manage, visualize, and describe the data is paramount. Creating a STC is a useful first step to arranging the data into manageable bins. This makes it more efficient to visualize and summarize the data per year. In addition, it is possible to detect trends and possibly predict future activities by arranging and assessing the data by performing analyses on the STC using Trend (to detect monotonically increasing or decreasing trends through time), HSA (to detect statistically significant positive or negative cluster), EHSA (similar to HSA but can group the data into 16 predefined categories), or COA (to distinguish between perfectly dispersed, randomly dispersed, or perfectly clustered data distributions).

Space–Time Cube

The STC was initiated by binning the data into a series of stacked cubes. Easting and northing bins are created either based on a priori-determined size or automatically by the software, which then aggregates data into the bins. Bin sizes for the STC used in these analyses were 1 mile by 1 mile (1.6 km by 1.6 km) (allowing aggregation of data only to nearest MTRS neighbors) by 1 year. Bins that contain the same UTM data are assigned the same location ID and bins that cover the same time period are assigned the same time step ID (Esri 2016). A series of bins that contain the same x and y data and cover the entire time range are referred to as a bin time series. The STC analyses and accompanying displays most useful for our purposes were Trend, EHSA, HSA, and COA.

Trend

Trend analysis, a 2-D representation of the STC, uses the Mann–Kendall trend test to detect patterns (Esri 2016). The Mann–Kendall test is a nonparametric, rank correlation assessment to determine whether there is a monotonic upward or downward trend. At its most basic, it determines whether the value of one variable (e.g., number of mining claims for a STC bin in our case) increases or decreases in relation to another variable (e.g., time in our case). To perform this analysis, the values are arranged in order (a bin time series based on Esri’s nomenclature) and then each later value (e.g., X T3) is compared to all earlier values (e.g., X T2, X T1). For example given [X T1, X T2, …, X Tn−1, X Tn ], X T2–X T1 would produce a value. If the value is positive (i.e., X T2 > X T1) an indicator value of +1 is assigned to the pair. If the value is negative (i.e., X T2 < X T1), an indicator value of -1 is assigned to the pair, and if the values are equal (i.e., X T2 = X T1), an indicator value of 0 is assigned to the pair. By summing indicator values for all pair combinations, a trend can be detected (Gilbert 1987; Kendall and Gibbons 1990). The null hypothesis (H 0) for this test is that there is no trend and that the sum of all indicator values of a bin time series should produce an answer of zero (the expected result for a random process). However, a positive sum indicates an increasing trend with time, whereas a negative sum indicates a decreasing trend with time. To determine to what extent a trend is statistically significant or the product of random chance, a z-score and accompanying probability (p value) are calculated. A positive z-score indicates an increasing trend, a negative z-score indicates a decreasing trend, and a low p value (low probability that the pattern is the result of random processes) indicates the trend is statistically significant and that one can reject the null hypothesis for the alternate hypothesis (H a), meaning the pattern is not random (Gilbert 1987; Kendall and Gibbons 1990).

Emerging Hot Spot and Hot Spot Analyses

The EHSA and HSA tools use the Getis–Ord Gi* statistic to determine whether there are statistically significant positive or negative valued clusters in the data. The Gi* statistic assumes a null hypothesis (H 0) that all data come from the same distribution and the alternative hypothesis (H a) is that statistically significant values higher or lower than the global mean would come from a different distribution. The statistic calculates a mean for a particular location (bin) by averaging the value in that location with values from all adjacent neighbors. It then compares this mean to the global mean of the dataset. The result is a z-score, where a positive score means higher values than the global average (hot spot), a negative score means lower values than the global average (cold spot), and a score of zero indicates that values at that location are equivalent to the global values. In addition to a z-score, an accompanying p value is calculated indicating the intensity or level of statistical significance for the z-score, and if low enough, allows us to reject the null hypothesis and to accept an alternate hypothesis (H a). The algorithm calculates z-scores and p values for each bin and produces a map of hot and cold spots (Getis and Ord 1992; Esri 2016). The key difference between the EHSA and HSA is that the EHSA also uses the Mann–Kendall trend test (discussed above) using the z-scores and associated p values to determine changes in hot spots over time (increasing or decreasing). The results are then categorized into 16 possible pattern types (Table 1). Not all 16 possible categories will be necessary to summarize the data for each analysis and so only the categories that fit the defined criteria are shown.

Table 1 Esri’s EHSA pattern types
Full size table

Cluster and Outlier Analysis

The COA is a valuable tool that determines where there are clusters, not whether there are clusters. This tool identifies statistically significant hot spots, cold spots, and spatial outliers. Unlike the EHSA and HSA tools, the COA tool uses the Anselin Local Moran’s I-statistic to determine relationships between data (Esri 2016). Anselin’s Local Moran I-statistic measures the similarity of particular points to surrounding points. Values for the statistic range from −1, negative spatial correlation (perfectly dispersed), to +1, positive spatial correlation (perfectly clustered), and a value of zero indicates a random spatial pattern. The statistic is a test of local autocorrelation, determining whether there is a relationship between location and value. It is calculated by dividing the deviation from the mean at a given location by the variance of the data and then multiplying that quotient by the weighted sum of the deviation from the mean at other neighboring locations. It is given by:

$$ I_{i} = \frac{{x_{i} - \bar{X}}}{{S_{x}^{2} }}\mathop \sum \limits_{j = 1, j \ne i}^{n - 1} \omega_{i,j} \left( {x_{j} - \bar{X}} \right) $$

where x i is an attribute for feature i, \( \bar{X} \) is the average of the attribute, ω i,j is the weight between features i and neighboring features j, and \( S_{x}^{2} \) is the variance (Anselin 1995; Getis and Ord 1996). The ω i,j is a function of the distance to neighboring data points. The magnitude of ω i,j is commonly the inverse of the distance between points.

Once an I-statistic is obtained, it is converted into a z-score (by subtracting the mean and dividing by the standard deviation) and a pseudo-p value, which is useful for hypothesis testing or making comparisons among datasets. The calculation of a pseudo-p value is preferred as a means of reducing Type I errors (an incorrect rejection of a true null hypothesis or a false positive) over use of the more conservative Sidak or Bonferroni corrections, which may produce Type II errors (failure to reject the null hypothesis when it is false, a false negative) (Anselin 1995). The pseudo-p value is calculated by comparing the I-statistic for a given location to a reference distribution. The reference distribution is created by iteratively shuffling all remaining data randomly into new spatial distributions (maps) and calculating an I-statistic for each map. The I-statistics for all iterations are combined to form the empirically based reference distribution. The location-specific I-statistic is then compared to the reference distribution, and a pseudo-p value is calculated. For the I-statistic, a positive z-score and a low p value is a significant positive autocorrelation (clustering) and a negative z-score with a low p value is a significant negative autocorrelation (dispersion or checkerboard pattern). A p value greater than 0.05 indicates there is no statistical significance and is therefore classified as spatially random despite the sign of the z-scores. After running the statistics on the dataset, the COA tool outputs four categories or clusters of High High (high values surrounded by high values), Low Low (low values surrounded by low values), and two outlier clusters, which are High Low (high values surrounded by low values) and Low High (low values surrounded by high values).

The HSA and the COA tools include an option to use the False Discovery Rate (FDR) Correction. Although Anselin (1995) and Getis and Ord (1996) discuss using a Sidak, Bonferroni, or pseudo-p value to reduce Type I errors in spatial autocorrelation tasks, Caldas de Castro and Singer’s (2006) evaluation of the FDR demonstrates that the FDR is mathematically appropriate for reducing errors, correctly identifies meaningful clusters, and is less conservative than the Bonferroni multiple comparison procedure method. The FDR controls for the number of Type I errors by limiting the number allowed. By setting an α, the proportion of false discovery rates to total discovery rates, to a low value (0.05 or 5%), it ensures that fewer Type I errors will occur. The FDR is calculated by ranking from lowest to highest the p values of all measures that were found to reject the null hypothesis. Each p value is numbered from one to m and then compared to the equation Q = (i/m) α where i is the rank number of a p value, m is the total number of p values that rejected the null hypothesis, and α is the percentage of “allowable” false positives. Traditionally, this value has been 0.05. It is then a systematic process of comparing each p value to its corresponding Q value. The last p value that is less than its corresponding Q value is the maximum p allowed. For all p values higher in the ranking, it is unacceptable to reject the null hypothesis (Benjamin and Hochberg 1995; Maxwell and Delaney 2004; Caldas de Castro and Singer 2006).

To test how well the EHSA, HSA, COA, and Trend tools detect change patterns in the data, the analyses were conducted at various levels of granularity. For each analysis, an ArcGIS Definition Query was conducted on the original data so that a STC could be created for the full dataset, a halved dataset, and a trisected dataset. The full dataset includes mining claim data from the entire 34-year period. The halved dataset was constructed by splitting the data into a 17-year period (1976–1993) and 16-year period (1994–2010). This division of the data coincides with the 1993 OBRA legislation, such that the earlier and later halves of the data pertain to periods, respectively, before and after the enactment of that legislation. The trisected dataset was constructed by splitting the data into two 11-year analyses and a 10-year analysis (1976–1987, 1988–1999, and 2000–2010), roughly corresponding to federal land assessment timing requirements. The STC tool requires a minimum of 10 time step measures to function and, consequently, cubes spanning less time were not created. In total, six STCs were constructed and analyzed using EHSA, HSA, COA, and Trend tools.

Results and Discussion

Space–Time Cube: Mining Claim Data and Trends 1976–2010 and 2016

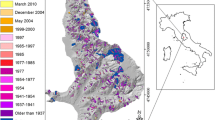
The results of aggregating the lode mining claim data into a STC revealed that in 1976 and 1977, the majority of the sections around the McDermitt Caldera had federally registered mining claims near active and historic mines (i.e., the Opalite, Bretz, and Cordero Mines as well as the McDermitt open pit) and along the west side of the caldera, an area with known and appreciable uranium deposits (Fig. 4a). In 1978, the number of active lode claims increased dramatically from 1601 to more than 9700 across the entire caldera. An additional 1828 claims were registered in 1979, making it the year with the highest number of claims ever registered around the caldera (Figs. 3 and 4b). This sudden increase in claims registered in 1978 and 1979 was most likely a result of the FLPMA act of 1976, which stated that all claims were required to be registered with the BLM by October 1979. Few changes in the number registered of mining claims occurred in 1980 (Fig. 3).

Figure 4
figure 4

Total number and location of active lode mining claims registered with the BLM per section for years 1976, 1979, 1993, 2005, 2010, and 2016. Cooler colors represent less number of claims registered and warmer colors represent higher number of claims registered. Note the 2016 data are arranged by MTRS and have not been processed and subsequently resampled like the other data

Full size image

In 1981, the number of claims decreased in the southeast corner of the caldera rim, and in 1982, the number of claims decreased in the center and the northwest corner of the caldera. The year 1983 saw an increase in claims registered along the south rim of the caldera as well as a block to the north of the caldera. There were few changes in the numbers of claims in 1984 and 1985. In 1986, the claims that had been registered in 1983 in the south and north were almost completely abandoned and additional claims were registered in the west. From 1987 to 1992, the number of claims generally decreased in number and location (i.e., there were fewer claims registered for each section and for less sections) (Fig. 3).

In 1993, a final drastic decrease in number of claims occurred from 1321 to 310 (Figs. 3 and 4Gc). This decrease was most likely the result of the OBRA act, which stated that each claim required a $100 maintenance fee. Although claims were decreasing in the area since 1988, this was the last, large negative change. As expected, the only claims registered were again around mines (e.g., the Cordero, Bretz, Moonlight, and Opalite mines to name a few). The number of claims then either decreased slightly or stayed the same during the rest of the 1990s (Fig. 3).

During the early 2000s, there were modest and gradual increases in the number of claims registered but it was not until 2005 that the significantly large changes occurred with a 34-fold increase in the number of registered claims (Figs. 3 and 4d). Claims were registered in the entire west, south, and most of the southeast rim of the caldera, and more than 60 claims were registered in many sections, most likely the result of an increase in commodity price for uranium (Fig. 2).

From 2007 to 2010, another change occurred and many claims in the southeast were abandoned, and for the first time, claims were staked in the center of the caldera (Fig. 4e). The center of the caldera is an area of known lithium concentration and the staking of claims in this location was probably the result of an increase in interest in lithium driven by the development of smart phones and electric and hybrid vehicles that require lithium batteries (USGS 2010).

In 2016, the majority of mining claims were located along the western and southern edge of the caldera (Fig. 4). Some sections, near the Moonlight Mine, contained as many as 82 active lode mining claims. There were additional active lode mining claims registered around known mines (i.e., the Bretz, the Opalite, and the Cordero mines). The majority of the caldera’s sections (79%), contained zero active lode mining claims in 2016.

Trend

The trend analysis on the STC containing the full dataset resulted in an upward trend in the number of mining claims registered in the center of the caldera, with a large area at the 99% confidence level (p value <0.01) (Fig. 5a). The significant upward trend in the center of the caldera was a result of the increase in mining claims registered in the center of the caldera since 2005. This upward trend is surrounded by either No Significant Trend or downward trend designations scattered discontinuously around it. The northern portion of the caldera, north of the Nevada–Oregon border, is almost entirely designated as a Down Trend at the 99% significance level in the number of claims registered. The remaining 30% of the caldera is designated as No Significant Trend; most likely the result of sporadic increases and decreases in registered mining claims that occurred through time (e.g., an increase in one year, followed by a decrease the next, would produce a zero for the statistics, resulting in a No Significant Trend designation).

Figure 5
figure 5

Trend analysis results showing the change in number of active lode claims per section for (a) the full dataset (1976–2010), (b, c) the halved datasets (1976–1993 and 1994–2010), and (d–f) the trisected datasets (1976–1987, 1988–1999, and 2000–2010). Cooler colors represent a decreasing trend and warmer colors represent an increasing trend

Full size image

By looking at the trend patterns from 1976–1993 to 1994–2010, it is possible to observe additional patterns that help in our interpretation of the 1976–2010 trend data and capture and characterize the impact of decreasing commodity prices through the 1980s and the enactment of the OBRA legislation in 1993. The 1976–1993 trend data shows predominantly decreasing or downward trends around the periphery of the caldera (Fig. 5b). Some upward trends do exist on the west and southwest rim but, for the most part, the majority of locations show a decrease in claims registered during this time period. Conversely, the trend pattern for the 1994–2010 time period shows, for the most part, only an increase in the south, west, and center of the caldera with almost all areas designated at the 99% confidence level (Fig. 5c). The remaining areas are mostly designated as Not Significant. This decreasing trend observed in the first half of the dataset followed by the increasing trend observed in the second half of the dataset mirrors the decrease in commodity pricing of uranium and mercury (Fig. 2), both important commodities in the history of the caldera. These trends most likely led to the No Significant Trend designation that resulted when running the trend analysis on the full dataset described above.

Splitting the full dataset in half and computing trend analyses on each half provided more information than the full dataset. By splitting the mining claim data into roughly 10-year blocks (1976–1987, 1988–1999, and 2000–2010) it was possible to evaluate trends at the scale of prescribed federal land assessments. The trend analysis results for 1976–1987 shows that the majority of the caldera (83%) has no significant trends (Fig. 5d). The significant trends show mostly an increase in registered mining claims in the west and northeast corner, near areas that, at the time, contained active mines (i.e., Cordero, Bretz, Opalite, and McDermitt open-pit mines). These same areas are designated with decreasing trends during the 1988–1999 period (Fig. 5e). Like both the 1976–2010 and the 1994–2010 datasets (Fig. 5a and c), the 2000–2010 dataset shows almost an entirely upward trend in the center and southern areas with the most statistically significant increase (at the 99% confidence level) being in the west (Fig. 5f).

Although different patterns emerged in each of the datasets, there were numerous similarities among the dataset patterns. The most consistent pattern was the upward trend in the center and southwest areas of the crater toward the latter part of the time period (i.e., 1994–2010, and 2000–2010). Another consistent pattern was the decrease or downward trend north of the Nevada–Oregon border. As the data were parsed into smaller timeframes, a greater number of MTRS were designated as no statistical trend (i.e., 187 locations for 1976–2010; 244 locations for 1976–1993; 367 locations for 1994–2010; and 511, 463, and 380 for 1976–1987, 1988–1999, and 2000–2010, respectively). We surmise that these no statistic trend designations occur in areas that have had sustained periods of time with zero mining claims registered (the early 1990s to the early 2000s). Additionally, this lack of significance might be an indication that the Mann–Kendall Trend test is unable to detect changes in this dataset either because too few samples (four is required for the statistic) or due to data changing sporadically rather than monotonically.

When comparing the results of the Trend analyses to the 2016 data in an effort to find a tool to predict future interest, it becomes apparent that the analyses on the full dataset and the halved dataset do a poor job of isolating or highlighting the areas that have claims in 2016. The results for the trisected dataset, however, consistently display activity in the areas that have claims in the 2016 data. All periods of the trisected data display a trend change along the western edge of the caldera, near the Moonlight Mine, as well as around the Cordero, Bretz, and McDermitt mines, all areas with consistent mining activity. If similar assumptions as Raines et al. (2002)—who used a cellular automata in an attempt to forecast future mining activities—are used and commodity prices are assumed to not change drastically from their recent past, no new legislation will be introduced affecting mining interests, and areas where historic mining activities occurred will likely host future exploration and development activities; then, the trisected data provides an indicator for where future mining interests will focus. The 2016 data confirm these results.

In general, the results from the full dataset give a general summary of where robust increases or decreases in mining claims registered through time. The halved dataset, provides a more detailed picture of past mining claim activities, capturing the gradual decrease in mining claims throughout the caldera during the early 1990s, followed by an increase in the western, southern, and central portions of the caldera during the late 1990s and early 2000s. Both of these analyses do a poor job at isolating and predicting future claim locations. Only the trisected datasets displayed trend changes in areas that had consistent activity throughout our data timeframe. Assuming that areas that historically hosted mining activities will most likely be sites for future interest (the locations with highest mineral potential), the results of the trend analyses of the trisected datasets serve as a good indicator of future claim activity.

Emerging Hot Spot Analysis

An EHSA was performed for each STC. As for the trend analyses, a separate EHSA was conducted on the full dataset, the halved dataset, and the trisected dataset. The number of resulting categories ranged from two for the 1988–1999 dataset to more than ten for both the 1994–2010 and the 2000–2010 datasets. Like the trend analysis, each EHSA captured and summarized the data differently. The EHSA for the full dataset (1976–2010) led to five categories (Fig. 6a), namely Intensifying Cold Spot, Oscillating Hot Spot, Oscillating Cold Spot, Sporadic Cold Spot, and Not Emerging. Note that the designation Not Emerging includes the No Pattern Detected and No Trend Detected categories; all are reserved for data that do not fall into any of the 16 predefined categories (for a complete description of each EHSA designation see Esri (2016)). The Intensifying Cold Spot category requires that more than 90% of the data were categorized as a statistically significant cold spot (lower values than the global average), a decrease in values through time, and that the last time step be a cold spot. Both the Oscillating Hot Spot and the Oscillating Cold Spot categories require the final time step to be statistically significant in its sign (hot or cold), to have been a statistically significant designation opposite its sign at some point, and that less than 90% of the time be statistically significant for its own sign historically. The Sporadic Cold Spot is referred to as an “on-again then off-again” category (Esri 2016). This designation requires less than 90% of the data be categorized as a statistically significant cold spot and that there was not a hot spot designation at the location during any time period.

Figure 6
figure 6

EHSA results for (a) the full dataset (1976–2010), (b, c) the halved datasets (1976–1993 and 1994–2010), and (d–f) the trisected datasets (1976–1987, 1988–1999, and 2000–2010) for number of active lode mining claims per section

Full size image

Although the results describe five categories, only three of the categories make up 99% of the map designations. Most of the western, southern, and central areas are designated as Oscillating Hot Spot and are surrounded by Not Emerging designations. In the eastern and northern portions of the caldera these Not Emerging designations are surrounded by Oscillating Cold Spots (Fig. 6a). The Oscillating Hot Spot areas align almost exactly with the locations of upward trends computed by the trend analysis on the 1994–2010 and the 2000–2010 datasets (Fig. 5c and f). The areas designated as Oscillating Cold Spots tend to align with the downward trend computed by the trend analysis on the 1976–2010 and the 1976–1993 datasets (Fig. 5a and b).

Like the Trend analysis, the EHSA for the halved dataset shows more details and tends to preserve general patterns of the two STCs better than the EHSA for the full dataset. The EHSA for the 1976–1993 period displays a general decrease in claims registered by way of multiple cooling-category designations such as New Cold Spot, Intensifying Cold Spot, Persistent Cold Spot, Oscillating Cold Spot, and Sporadic Cold Spot, throughout the caldera (Fig. 6b). The only non-cooling category was Not Emerging seen mostly on the western side of the caldera. The majority of the area is classified as Oscillating Cold Spot. The EHSA for the second portion of the halved data (1994–2010) is mostly covered by warming categories (i.e., Consecutive Hot Spot, New Hot Spot, Oscillating Hot Spot, and Sporadic Hot Spot), which was expected based on the previously discussed trend and STC data (Fig. 6c). Cooling categories (i.e., Consecutive Cold Spot, Diminishing Cold Spot, Intensifying Cold Spot, Oscillating Cold Spot, Persisting Cold Spot, and Sporadic Cold Spot) occur north of the Nevada–Oregon border in the northern portion of the Caldera and in the southeast.

As with the trend analysis, the data was trisected and an EHSA was conducted on each third. This division of the data is preferred over the full and halved datasets as the first third and final third of the data contain the most categories and visually appear to capture more of the variability in the STC data. The middle third, however, has only two categories, which are Not Emerging and Sporadic Hot Spot (Fig. 6e). The Not Emerging categories likely resulted because most of the caldera had zero claims registered, and areas that did have claims registered were decreasing in numbers, especially after the OBRA was enacted in 1993 (Figs. 3 and 4). The Sporadic Hot Spot designation in the middle third of the dataset is around the Bretz Mine, an area in which most claims were abandoned around 1993, when the US divested its strategic mercury reserves (Schlottmann 1987; Castor et al. 1996; Castor and Ferdock 2004; Childs 2007), and then later in 1997 when more mining claims (on average 2.5) were registered. Recall that to meet the Sporadic Hot Spot criteria, less than 90% of the duration of the dataset must be a statistically significant hot spot with no time steps meeting the criteria of a statistically significant cold spot.

The EHSA results for the first and third trisects differ from those of the middle trisect in regard to the number and distribution of categories. The first trisect of the dataset contains 10 categories including Not Emerging (Fig. 6d). The western and northeastern rim of the caldera displays warming patterns (i.e., Consecutive Hot Spot, New Hot Spot, Sporadic Hot Spot, and Oscillating Hot Spot) and the southern, central, and far northeastern areas are mostly designated with Oscillating Cold Spot. The distribution of the diverging pattern types (increasing or decreasing in nature) for the 1976–1987 time period may reflect working mines around the caldera, areas that had active development occurring at the time (Fig. 6d). In contrast, areas that were subject to exploration and not containing working mines would be expected to show sporadic increases and decreases. For all mines except the Ruja Mine, nearby EHSA categories were increasing or warming in nature (possibly because active development was occurring), whereas all other areas featured decreasing or cooling categories (possibly the result of failed exploration programs). The EHSA from the third trisect (2000–2010) (Fig. 6f) contains 11 categories including Not Emerging and produced patterns that were consistent with the trend analysis on the third trisect (Fig. 5f) of the data and for the EHSA and trend analysis on the second half dataset (Figs. 5c and 6c): a pattern of increasing, or warming categories in the south, west, and center and a decrease in the north.

When comparing the EHSA results to the 2016 data, the full dataset seems to capture future potential in areas that are designated as Oscillating Hot Spot. In addition, the second half of the halved dataset, the first trisect, and the third trisect capture the future patterns with the Consecutive Hot Spot, New Hot Spot, Sporadic Hot Spot, and Oscillating Hot Spot designation with the Consecutive and Oscillating designations approximating the 2016 pattern the most closely. Again, this confirms our assumption that locations with historic exploration and development will most likely yield future exploration and development.

Hot Spot Analysis

When evaluating the trend analysis results, splitting the data in half captured large historic changes (e.g., gradual decrease in claims registered during the 1980s and then an increase in claims in the early 2000s) and splitting the data into thirds approximated the 2016 patterns the most closely. When evaluating the EHSA, the second half of the halved dataset and the first and third trisects approximated the 2016 mining claim pattern the most closely. The HSA is a direct byproduct of the EHSA. Consequently, the z-scores and accompanying p value are the basis for evaluating statistical significance for both the EHSA and for the HSA; nevertheless, because the EHSA also requires the data to conform to 16 criteria, patterns between the two can be quite different.

The results of the HSA for the full dataset (1976–2010) show a Down Trend at the 99% confidence level north of the Nevada–Oregon border and in the northeast corner of the caldera, surrounded by No Significant Trend in the center of the caldera, and an additional Down Trend at the 99% confidence level in the southwest (Fig. 7a). Recall that conversely the EHSA results for the full dataset indicated an Oscillating Hot Spot for most of the west, southwest, and center of the caldera (Fig. 6a). These two results, at first, may appear contrary to one another, but based on the definition for the Oscillating Hot Spot (i.e., statistically significant hot spot for the final time step, a history of a statistically significant cold spot at some time, an less than 90% of the time steps have been a statistically significant hot spot)—both results are possible. In addition to the EHSA displaying categories associated with increasing claims, the trend data also showed an upward trend for the center of the caldera (Fig. 5a), and the STC data indicate a notable increase in claims registered in the center of the caldera (Fig. 4e). These changes were not reflected in the HSA, which demonstrate differences between statistical tools and the utility of including and comparing various analyses rather than anchoring on one type of analysis.

Figure 7
figure 7

HSA results showing significant changes in number of active lode claims per section for (a) the full dataset (1976–2010), (b, c) the halved datasets (1976–1993 and 1994–2010), and (d–f) the trisected datasets (1976–1987, 1988–1999, and 2000–2010). Cooler colors represent cold spots and warmer colors represent hot spots

Full size image

In some ways, the HSA might be a more useful tool than the trend analysis and the EHSA to capture and categorize past claim activity. Remember that the trend test uses the Mann–Kendall statistic, a test of monotonically increasing or decreasing data. For data that have variable, temporal changes, Trend analysis may not be the most suitable. The EHSA has value in that it can quickly categorize data based on specific criteria, but some of these criteria might instill misconceptions about increasing or decreasing data over time in circumstances in which only the most recent time period saw an increase. The HSA uses the Getis–Ord Gi* statistic and combines data from neighbors both spatially and temporally before comparing the values to global values. In this way, it could capture subtle changes better than the other two statistics. It appears, as previously discussed, that this analysis works best on data that are split into smaller granules. Splitting the data into halves seems to preserve more variability than computing the analysis on the full dataset, which features downward trends around the rim of the caldera in the north, east, and south and a small area categorizes by upward trends in the west for the first half of the data, and upward trends prevalent in the center, south and west with a small section categorized by downward trends in the northeast for the latter half of the dataset (Fig. 7b and c).

Breaking the data into thirds, like in the EHSA analyses, provides more information about the data than when using the full and halved datasets. The first trisect features an area with an Up Trend on the west side of the caldera and a Down Trend in the northeast (Fig. 7d). The remaining areas are primarily designated as No Significant Trend. The middle trisect features decreasing number of claims around the periphery of the caldera with No Significant Trend in the center, southeast, and northeast-most corner (Fig. 7e). The third trisect primarily features only Up Trends in the west, south, center, and areas surrounding the Cordero and McDermitt Mines, with almost all other areas designated as No Significant Trend (Fig. 7f).

When comparing the HSA results to the 2016 data only the second half of the halved dataset and the third trisect approximate the 2016 patterns with some degrees of similarity and only if the data were limited to the Up Trend at the 99% confidence level. Although the HSA patterns seem similar to the Trend data and capture a lot of variability in the claim data, they do not effectively predict the 2016 data and therefore are not recommended tool for predicting future interest.

Cluster and Local Outlier Analysis

The COA tool uses the STC as the input to perform the Local Moran’s I-statistic calculation. The result is an additional STC in which each bin contains a z-score, p value, I value, and cluster type. This display of data, for our purposes, was difficult to work with. Unlike the STC for the mining claims that could be queried to render only a single year, the cluster STC does not have the ability to display only a single time slice. In an effort to simplify the display to a 2D representation of the data, the Local Outlier Analysis tool was invoked. This tool uses the same Local Moran’s I equation; however, time values are also used as neighbors. The results, in general, were disappointing. For the most part, all maps were dominated by the designation Multiple Types, which results from multiple cluster-type designation (i.e., High High, Low Low, High Low, and Low High) throughout time (Fig. 8a–f). The prevalence of the designation Multiple Types did little to illuminate trends or clusters in the full and halved datasets. The High High designations on the trisected data, however, approximated the 2016 pattern very closely.

Figure 8
figure 8

COA results on number of active lode claims per section for (a) the full dataset (1976–2010), (b, c) the halved datasets (1976–1993 and 1994–2010), and (d–f) the trisected datasets (1976–1987, 1988–1999, and 2000–2010)

Full size image

To determine where statistically significant clusters exist, we recommend using the COA tool to analyze data from previous analyses. Performing the cluster analysis on the EHSA results with the Input Field being Category Type provided patterns that were consistent with the other analyses. Additionally, performing the analysis on the HSA with a Definition Query in place, limiting p values to less than or equal to 0.10 (the 90% confidence level) and using z-scores for the Input Field provided patterns that appeared to capture the data trends (e.g., an increase in claims in the west, south, and center for later years and a decrease in claims during early years).

Conclusions

The ability to visualize data in a space–time cube (STC) and to rotate, pan, zoom, adjust transparency, and query input in real time provides researchers with new methods and opportunities to interrogate their data. Additionally, the various statistical analyses that can be completed with STC datasets can reveal useful insights into increasing or decreasing trends or used to categorize the data. In some cases the results from STC analyses may be used as a predictor of future interests. In an effort to evaluate the utility of STC, we analyzed mining claim data from the McDermitt Caldera in northern Nevada and southern Oregon.

In general, the Trend, EHSA (Emerging Hot Spot Analysis), and HSA (Hot Spot Analysis) adequately detected the major trends in the data. The results of the trend analyses revealed that the full dataset captured big-picture trends and the halved datasets revealed more detail, such as the overwhelming decrease in mining claims registered for the majority of the caldera in the early years and a drastic increase in mining claims during the later years. Trisecting the data and using the trend analyses proved useful for approximating and therefore predicting future mining activities. Unlike the trend analysis, the EHSA was most useful when the data were trisected. By parsing the data into thirds, more categories were included for the first and third trisects, preserving the variability in the data and capturing areas that would continue to hold mining interest. The HSA was useful in capturing historic trends, but a poor predictor of future mining claim activity. Finally, the Cluster and Outlier Analysis (COA) tool provided little information about past or future trends in the mining claim data.

To optimize use of the Space Time Pattern Mining toolbox, we recommend experts in the field review the STC data and analyses in an exploratory data analysis approach by first examining each time step of the STC, developing an appreciation for where trends in the data are increasing, decreasing, or remaining the same, enabling the general characteristics of the raw data through time, to be understood and summarized. Next, parse the data into varying granularities and conduct different analyses to determine the ideal dataset size for each statistic. In most cases, using a combination of portioned datasets may be the ideal method for evaluating data, presenting results, and predicting future claim interest. We recommend using the Trend and EHSA for activities involving future prediction. These analyses can capture data with consistent activity in data and therefore are able to highlight and isolate these areas. With the assumption that areas that had historic activity are likely to be areas that have future activity, these two tools can provide useful insight.

The STC and associated analyses are a useful way to quickly interrogate spatiotemporal mining claims data and develop conclusions about the number of mining claims registered, where they were increasing, decreasing, or staying the same, the nature of the change (e.g., sporadic, reversing, or monotonic), and where future mining activity was likely to occur. We recommend these tools be integrated in federal, state, and local GIS analyses in the future in an effort to better characterize current and future land use needs. With the ease of displaying and creating such data and results, we anticipate an increase in the number and types of applications in which these tools will be included in the future.