Metallic Mineral Resources in the Twenty-First Century: II. Constraints on Future Supply

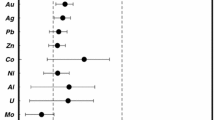
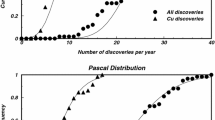
Abstract

Supplying worldwide demand of metallic raw materials throughout the rest of this century may require 5–10 times the amount of metals contained in known ore deposits. This demand can be met only if mineral deposits containing the required masses of metals, in excess of present day ore reserves, exist in the Earth’s crust. It is, by definition, not known whether or not such mineral deposits exist. On the basis of the statistical distribution of metal tonnages contained in known ore deposits, however, it is possible to place constraints on the size distribution of the deposits that must be discovered in order to meet the expected demand. A nondimensional analysis of the distribution of metal tonnages in deposits of 20 metals shows that most of them follow distributions that, although not strictly lognormal, share important characteristics with a lognormal distribution. Chief among these is the observation that frequency falls off symmetrically and geometrically with deposit size, relative to a median deposit size that is approximately equal to the geometric mean deposit size. An immediate consequence of this behavior is that most of the metal endowment is concentrated in deposits that are several orders of magnitude larger than the median deposit size, and that are much rarer than the most common deposits that cluster around the median deposit size. The analysis reveals remarkable similarities among the statistical distributions of most of the metals included in this study, in particular, the fact that distribution of most metals can be fully described with essentially the same value (about 2–3) of the scale parameter, σ, which is the only parameter needed to describe the behavior of a normalized lognormal variable. This observation makes it possible to derive the following general conclusions, which are applicable to most metals—both scarce and abundant. First, it is unlikely that undiscovered mineral deposits of sizes comparable to those that contain most of the known metal endowment exist in sufficient quantities to supply the expected worldwide demand throughout the rest of this century. Second, if the expected demand is to be met, one must hope that very large deposits, perhaps up to one order of magnitude larger than the largest known deposits, exist in accessible portions of the Earth’s crust, and that these deposits are discovered.

Appendix: Lognormal Versus Power-Law Distributions

Consider a rescaled (μ = 0) lognormal PDF, log-transformed as (see Eq. 2):

$$ \ln P\left( z \right) = - \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} - \ln z - \ln \left( {\sigma \sqrt {2\pi } } \right) $$

(46)

and a power-law:

$$ \ln Q\left( z \right) = - \beta \ln z - \gamma . $$

(47)

In a log–log plot, the first function is a curve with negative curvature, and the second function is a straight line. For z > $e^{{ - \sigma^{2} }} ,$ it is d ln P(z)/d ln z < 0. Therefore, the high-end tail of a lognormal distribution and a power law with negative exponent may be related as shown in Figure 15. Assume that the two functions are tangent in a log–log plot at a point z _T , as shown in the figure. We wish to know the distance, δ, between the values of the two functions, as a function of the distance from z _T , and the scale parameter σ (see Fig. 15).

Fig. 15

Schematic relationship between the high-end tail of a lognormal PDF, P(z), and a power-law distribution, Q(z). On a log–log plot the power law is a straight line, and the lognormal PDF is a curve with negative curvature. It is always possible to construct a power law that is tangent to P(z) at any arbitrary point, z _T , see text. One can then ask how the distance between the two curves, δ, varies as a function of the scale parameter of P(z) and the distance from z _T

If the curves are tangent at z _T , then

$$ \ln P\left( {z_{T} } \right) = \ln Q\left( {z_{T} } \right) $$

(48)

and

$$ \left. {\frac{d\ln P\left( z \right)}{d\ln z}} \right|_{{z = z_{T} }} = \left. {\frac{d\ln Q\left( z \right)}{d\ln z}} \right|_{{z = z_{T} }} $$

(49)

From the second equation, we get

$$ \beta = 1 + \frac{{\ln z_{T} }}{{\sigma^{2} }} $$

(50)

Solving the first equation for γ, we find

$$ \gamma = \frac{1}{{2\sigma^{2} }}\left( {\ln z_{T} } \right)^{2} + \left( {1 - \beta } \right)\ln z_{T} + \ln \left( {\sigma \sqrt {2\pi } } \right) $$

(51)

and substituting (50), we find

$$ \gamma = \ln \left( {\sigma \sqrt {2\pi } } \right) - \frac{{\left( {\ln z_{T} } \right)^{2} }}{{2\sigma^{2} }} . $$

(52)

Thus, a power law, Eq. (47), with parameters β and γ given by Eqs. (50) and (52), is tangent at z _T to a normalized lognormal PDF with scale parameter σ. We now wish to know how the distance between the functions varies as the value of the variable z moves away from the point, z _T , where the curves are tangent. Call this distance δ (see Fig. 15):

$$ \delta = \ln Q\left( z \right) - \ln P\left( z \right) = \ln \frac{Q\left( z \right)}{P\left( z \right)} $$

(53)

or, explicitly:

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} + \left( {1 - \beta } \right)\ln z + \ln \left( {\sigma \sqrt {2\pi } } \right) - \gamma . $$

(54)

Substituting Eqs. (50) and (52), we find

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} - \frac{{\ln z_{T} }}{{\sigma^{2} }}\ln z + \frac{{\left( {\ln z_{T} } \right)^{2} }}{{2\sigma^{2} }} $$

(55)

or:

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z - \ln z_{T} } \right)^{2} = \frac{1}{{2\sigma^{2} }}\left( {\ln \frac{z}{{z_{T} }}} \right)^{2} $$

(56)

That is,

$$ \ln \frac{Q\left( z \right)}{P\left( z \right)} = \frac{1}{{2\sigma^{2} }}\left( {\ln \frac{z}{{z_{T} }}} \right)^{2} $$

(57)

The last equation shows an important relationship between the lognormal and power-law distributions: the two functions converge as the scale parameter increases, and they do so quickly, as the convergence goes with the square of the scale parameter. At the limit σ → ∞, the two distributions become indistinguishable. For our purposes, however, it is more relevant to study how the two distributions deviate as a function of the distance from the point of tangency, z _T , for constant values of σ about 2–3 (see text). This is shown in Figure 16.

Fig. 16

The distance between a power law and a lognormal PDF tangent at z _T , given as e ^δ = Q(z)/P(z), as a function of the distance from z _T given as z/z _T . Over a displacement of ~1 order of magnitude from z _T , and for values of σ found here to be characteristic of metallic ore deposits, frequencies predicted by the power law would be less than twice those predicted by a lognormal distribution. The ratio climbs to about 3 to 10 times for a displacement of ~2 orders of magnitude. A power law decays more slowly than an exponential function (such as a lognormal PDF), so it predicts higher frequencies for large deposits. One can interpret this result either as meaning that there are greater chances of finding those large deposits, or as meaning that they do not exist, because, otherwise, we would have already known about them—see text

In this paper, I have modeled the distribution of metal contents in mineral deposits using the lognormal PDF. But suppose that, given the relatively few known mineral deposits in the high-end tail of the distribution, the uncertainty is large enough that power-law behavior cannot be discarded for the largest deposits, i.e., the high-end tail of the distribution can be fitted reasonably well with a straight line in a log–log plot. We saw in the main body of the paper that supplying the world’s metal demand throughout the twenty-first century is likely to require the discovery of deposits 10–100 times larger than the largest known deposits (e.g., assuming that G is ~0.16 in the top panel of Figure 13, see also associated discussion). If deposit size distribution follows a power law, then deposits of this magnitude might be 2–10 times more common than what a lognormal distribution would predict (Fig. 16). Assuming a lognormal distribution, such deposits would make up ~1% of all mineral deposits (bottom panel of Figure 13 with G of ~0.16, and also associated discussion). If, on the other hand, these very large deposits followed a power-law distribution, then we might expect them to be as common as 2–10% of all deposits (Fig. 16). One could use this greater frequency as a source of optimism that the required deposits exist and will be found. Or, following the interpretation that, “if they existed and they were that common we would already have found at least some of them,” one can conclude that assuming a power-law distribution for large deposits should not be a source of greater optimism about meeting future supply of metallic raw materials. The fact remains that statistics cannot answer this question, and that unless and until such giant deposits are discovered we will have no certainty about future supply of metallic raw materials, beyond knowing that smaller deposits will not by themselves be sufficient.