Abstract
We present the use of Multi-angle Dynamic Light Scattering (MADLS®) for the measurement of nanoparticle concentration. We describe the theory of the method and its application to nanoparticles made of gold, silica and polystyrene, with diameters ranging from 30 to 400 nm, and demonstrate some of the limitations with particles of sizes 500 nm and above. We evaluate the method accuracy, linearity and reproducibility, as well as the operational nanoparticle concentration and size range. We show that the concentration working range depends on the material’s optical properties, size and concentration. Here it is shown that the level of accuracy that can be expected for the concentration of particles is typically within 50% of the nominal value across a range of materials and sizes and, for some samples, within 20%. The repeatability of the measurements, in terms of relative standard deviation, is typically below 30%. A linearity of within 40% across a concentration range of 3·108 to 2·1011 mL−1 for concentration measurements was also demonstrated by using gold nanoparticles and gravimetric dilutions for method validation. Overall, we show that MADLS® is a rapid and straightforward method for the reproducible measurement of particle concentration, as well as size, requiring minimal sample preparation, without the need to calibrate using a pre-determined concentration series, and applicable to a broad range of materials. These features make it an ideal tool to support both development and quality control of particle materials for a broad range of applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
High-added value nanoparticles are used in a range of industrial sectors (Stark et al. 2015), including medical (Balasundaram and Webster 2006; Boccaccini et al. 2010), pharmaceutical (Minelli et al. 2010; Schroeder et al. 2011), energy (O'Regan and Grätzel, 1991), catalysis (Corma and Garcia 2008), electronic (Talapin and Steckel 2013) and cosmetic (Indu and Rumjhum 2007; Monteiro-Riviere et al. 2011). Measuring the number concentration of colloidal nanoparticles is of critical importance to industries producing and using high-value nanoparticle materials, as this enables the implementation of effective quality assurance (QA) and quality control (QC) protocols, formulation of related risk assessments and compliance to regulation. For example, the direct measurement of nanoparticle concentration, along with other properties of the materials, is a means to test product stability, lifetime and variability across different batches or production sites. The risk of exposure to nanomaterials is related to their concentration, and similarly, the dose of a nanoparticle-based medicine depends on the concentration of the nanoparticles in solution, as well as their loading with active ingredients. The measurement of nanoparticle concentration also enables compliance with present and future regulation, linked, for example, to the EC Recommendation for the definition of a nanomaterial (2011/696/EU) (European Commission 2011).
A number of instruments are currently available to the community for the measurement of nanoparticle concentration. The choice of the instrument often depends on the materials and the size range of the particle samples. For example, UV-visible spectroscopy (UV-Vis) is widely used to measure the concentration of gold nanoparticles (Haiss et al. 2007; Khlebtsov 2008; Shard et al. 2018b) but its application to other materials is limited by the lack of knowledge of the optical properties of the materials. Small-angle X-ray scattering (SAXS) (ISO 2015), on the contrary, can be used to measure the concentration of a range of different materials, but the measurement of particles that are not spherical, has unknown density or whose size is larger than 100 nm is challenging. Particle tracking analysis (PTA) (ISO 2016) can be used with a wide variety of materials but requires very dilute samples, which imposes some constraints on the preparation of stable samples. The minimum detectable particle size depends on the material and is typically around 10 nm for gold, 40 nm for silica and even higher for liposomes. Tunable resistive pulse sensing (TRPS) (Vaclavek et al. 2019; Vogel et al. 2016) also makes use of diluted samples can detect particles with diameters larger than 50 nm and requires the dispersion of the samples in electrolytes. Condensation particle counters (CPCs) (CEN 2015) can measure the concentration of particles within a broad size range but require these to be aerosolised. Single particle inductively coupled plasma mass spectrometry (spICP-MS) (ISO 2017b) is emerging as a robust method for the measurement of nanoparticle concentration but can only be applied to nanoparticles which contain elements detectable in ICP-MS. Its sensitivity, in terms of the lower size limits of detection, varies from around 10 nm for gold to around 60 nm for silica and is inappropriate for organic nanoparticles.
In this work, we have evaluated a novel method based on dynamic light scattering (DLS) (ISO 2017a) for measuring the concentration of nanoparticles. First demonstrated in 1943 (Ramachandran 1994), DLS has become an invaluable technique in the field of colloid characterisation. Used widely across industrial and research applications, DLS is employed within many sectors, for example in the development and production of biopharmaceuticals, pharmaceuticals, drug delivery products, cosmetics, food, electronics and pigments. The attraction of using DLS for particle size characterisation lies in the speed of measurement, ease of sample preparation—often dispersions can be measured without dilution, and the wide size range—from sub-nanometre up to 10 μm diameter (Ruseva et al. 2019). DLS measures the hydrodynamic size of the sphere with equivalent diffusion coefficient (ISO 2017a). The size resolving power of DLS is typically 3. The sensitivity of DLS to the larger particles can allow, for example, detection of trace levels of protein aggregates or poorly milled pigments. However, the same sensitivity to large particle material can often prevent detection of smaller particles, which may be present in greater number but scatter with less intensity. Here, we demonstrate that multi-angle DLS (MADLS®) can be used for the measurement of both the size and the concentration of nanoparticles with accuracy and precision. We describe the method and validate the approach through the use of well-characterised reference materials.
Theory
Dynamic light scattering
To perform DLS, a dispersed particle system is illuminated by laser light and the scattered radiation is detected as a function of time. Since, micro- and nanometre sized particles undergo continuous Brownian motion when in dispersion, the amplitude of the scattered field continuously evolves over time. Autocorrelation of the detected intensity can be related to the translational diffusion coefficient D of the particles via the Siegert relation:
where g(2)(τ) is the intensity autocorrelation coefficient at lag time, τ; q is the scattering vector; and β is the coherence factor, related to the finite solid angle of detection. The scattering vector is a function of the scattering angle. The translational diffusion coefficient, D, is related to the hydrodynamic diameter, d, through the Stokes-Einstein equation:
where kB is the Boltzmann constant, T is the temperature and η is the dynamic viscosity of the fluid in which the particles are dispersed.
The observed autocorrelation function is the sum of many contributions from all size populations within the sample. Of the numerous methods developed to retrieve the particle size distribution from the measured autocorrelation function, two are in widespread use commercially. The cumulant method (ISO 1996) expands the observed autocorrelation function into a power series where the coefficient of each term is equal to the nth cumulant of the distribution. Usually, the expansion is taken to the second order to derive the so-called Z-average (intensity-weighted harmonic mean hydrodynamic diameter) from the first cumulant and the polydispersity index (PdI) from the second cumulant. The cumulants method is valid if the distribution is monomodal. Polydisperse systems are usually analysed using the second method, a non-negative least squares (NNLS) algorithm (Bloomfield 1987) to derive the particle size distribution, which for DLS is intrinsically weighted by the scattered light intensity (Ford Jr. 1987).
Particle concentration using multi-angle dynamic light scattering
It has been shown that with the use of a reference material, DLS can be used to measure the concentration of a colloidal sample (Makra et al. 2015; Minelli et al. 2019; Schavkan et al. 2019; Vysotskii et al. 2009). However, due, in part, to the lack of such reference materials, this approach was never widely implemented. We show in this paper that the measurement of particle concentration distribution using MADLS® involves measuring just the ensemble time-averaged scattered intensity and the particle size distribution. The operating principle of the particle concentration measurement by DLS is based on a transformation of the intensity-weighted particle size distribution into the absolute concentration distribution using the derived sample-scattered count rate and the optical properties of the material and the dispersant. Critical to the accuracy and repeatability of this technique is the combination of autocorrelation information by MADLS® which is acquired at multiple angles to improve the fidelity of the derived particle size distribution (Malvern Panalytical). A MADLS® measurement involves separately recording scattering data at three angular positions: back-scatter, side-scatter and forward-scatter to form three auto correlation functions. For each measurement angle, an adaptive correlation process (Malvern Panalytical) accumulates the autocorrelation function over many short time periods so that “outlier” runs can be partitioned from those of interest using a statistical basis, improving signal to noise. A non-linear method is employed to invert the measurements into a backscatter-equivalent intensity-weighted particle size distribution (Bryant and Thomas 1995; Cummins and Staples 1987).
The size-dependent particle-scattered photon count rate Ipar(d) is proportional to the total number of particles present in the scattering region according to the following:
where N(d) is the number of particles of size, d, within the scattering volume; \( \frac{d{C}_{sca}}{d\Omega}\left(d,\theta \right) \) is the differential scattering cross section of particles of size, d, at scattering angle, θ; ΔΩ is the solid angle subtended by the detector; and Φp is the incident photon flux (photons per unit area per second).
The differential scattering cross section—the fraction of photons scattered into a unit solid angle as a function of scattering angle—is calculated using Mie theory, with knowledge of the material and dispersant refractive index and absorption. Here, a spherical scattering model is assumed (Boren and Huffman 1983); however, this could be extended to satisfy other particulate systems, for example by using a core-shell model for coated nanoparticles.
The particle number distribution can be represented in terms of the concentration distribution:
where ρ(d) is the particle concentration distribution, A is the cross-sectional area of the scattering volume and L is the interaction length of the scattering volume.
Combining Eqs. (3) and (4), one obtains the following:
where Iin is the photon count rate incident upon the scattering volume (equal to the product qpA).
Instead of measuring Ipar(d) directly, the backscatter time-averaged photon count rate Itot, which is an output of the size measurement autocorrelation process as the derived count rate (kcps), also contains residual background scattering which is light scattered by the medium which the particles are suspended in. The background scattering contribution is removed by subtraction of a separate count rate measurement of the dispersant, such as water or a buffer, only Idis. The size-dependent particle-scattered photon count rate is proportional to the normalised particle size intensity distribution P(d):
Since ΔΩ, Iin and L are unique instrument properties, measurement of a reference material is used to remove the explicit need for knowledge of these parameters. By measuring a molecular scatterer with a known volume scattering function, such as liquid toluene, the instrument sensitivity can be calibrated and the particle concentration distribution can be derived. The count rate of a molecular scatterer, in this case toluene, is given by the following:
where Itol is the detected scattered photon count rate of liquid toluene, Rtol is the Rayleigh ratio of toluene—otherwise known as the volume scattering function since it is equal to the differential scattering cross section per unit volume. The Rayleigh ratio of toluene is known from the literature and is equal to 1.35·10−5 cm−1 at 632.8 nm and 25 °C (Brar and Verma 2011).
Combining Eqs. (5) and (6) and dividing by Eq. (7), rearranging for ρ(d) gives the following:
Equation (8) allows the calculation of the particle concentration distribution from the detected scattered photon count rate (total, corrected for the dispersant contribution), the particle size intensity distribution, the calculated differential scattering cross section, the detected scattered photon count rate from the reference scatterer (toluene) and the Rayleigh ratio of toluene. Simply, the total particle concentration is the integral of the distribution.
This measurement process is analogous to deriving the concentration using UV-Vis: the particle size as measured by MADLS® is used similarly as the extinction cross section in UV-Vis, the total count rate is equivalent to the sample transmitted intensity spectrum and the toluene count rate is used much like the cuvette path length in UV-Vis. The dispersant count rate is subtracted from the total count rate for MADLS®, the same as the transmitted intensity spectrum of the blank is subtracted from that of the sample.
MADLS® particle concentration operating envelope
We address here the theoretical limits between an upper and a lower concentration within which MADLS® particle concentration measurements can be performed. The concentration limits of a MADLS® measurement are dictated by those of the component single-angle DLS measurements. It should be noted that because the particle size is used to compute the concentration, the presence of number fluctuations or multiple scattering creates uncertainty in the result. The lower concentration limit is thus defined by the need to sample an appreciably unchanging number of particles throughout the course of the measurement. The upper limit is instead defined by the requirement that multiply scattered photons are negligibly sampled.
Minimum concentration
When DLS is applied to low concentration systems, with just a few particles diffusing through the scattering volume, measurement artefacts due to particle number fluctuations are observed. The Siegert relation (Eq. (1)) is valid only when the number of particles in the scattering volume is sufficient that the amplitude distribution of the scattered field is Gaussian (Hopcraft et al. 2005). When the number of particles in the scattering volume is small, the amplitude distribution of the scattered field is no longer Gaussian and the intensity autocorrelation function contains an additional term (\( {g}_{\mathrm{N}}^{(2)}\left(\tau \right) \)) caused by particle number fluctuations (Bertolotti 1977):
where \( {g}_{\mathrm{D}}^{(2)}\left(\tau \right) \)and \( {g}_{\mathrm{N}}^{(2)}\left(\tau \right) \) are the diffusive and number fluctuation components, respectively, and α is an amplitude term. The number fluctuation component derives from the transport of particles into and out of the scattering volume. In the low concentration limit, scattered light intensity fluctuations are present as the number of sampled particles changes over time. Given that the particle number follows Poisson probability theory, the relative uncertainty in the expected value increases as the concentration decreases—the relative standard deviation being equal to E(N)−0.5, where E(N) is the expected number of particles in the scattering volume.
The amplitude α of \( {g}_{\mathrm{N}}^{(2)}\left(\tau \right) \) is equal to the reciprocal expected number of particles in the scattering volume, E(N)−1. The probability of number fluctuations for a given sample is calculated using E(N)−1 based on the particle concentration and the scattering volume. We established that a criterion of E(N) ≥ 10 describes the regime for which number fluctuation do not appreciably perturb the measured diffusion coefficient above experimental noise. Values 4 ≤ E(N) < 10 are a transition zone where the impact of the number fluctuation component additionally depends on the rate of transport through the scattering volume and if E(N) < 4 number fluctuations are likely to manifest.
Maximum concentration
The onset of multiple scattering is used to define the maximum concentration permissible for MADLS® measurements. In a single-angle DLS experiment, it is assumed that all photons reaching the detector are scattered only once. As the particle concentration increases, the probability of scattered photons becoming re-scattered increases. The presence of multiple scattering during a DLS measurement leads to uncertainty, with a reduction in the autocorrelation coefficient and a measured size that is smaller than the physical size of the examined particles (Bertolotti 1977).
The size-dependent maximum sample concentration for single scattering can be approximated using a random walk model and Mie theory. According to Pine and Weitz (Weitz and Pine 1993), the diffusive limit of multiple scattering is governed by the photon mean free path, l, which is defined as the average distance between scattering events. In dilute suspensions, this is given by the following:
where ρ is the particle concentration and σ is the total scattering cross section per particle, calculated using Mie theory. If a photon must traverse a distance greater than l, it is likely to be scattered more than once.
The likelihood of detecting re-scattered photons depends on the angular position of the detector and the average scattering angle of the particle system, which is 90° for isotropic scatterers and tends to 0° as the particle size increases. If the particle scatters isotropically, there is no dependence on the detector position and multiple scattering is equally likely in the forward and backscatter directions. If the particle scatters predominantly in the forward direction, photons detected in the forward angle are more likely to have been re-scattered. The probability of detection is increased by the following empirically derived factor k:
where <θs> is the expected scattering angle (weighted by the differential scattered cross section) and θd is the detection angle.
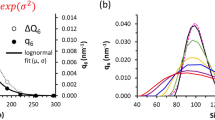
In the MADLS® particle concentration measurement, all measurement angles must be free of multiple scattering effects. Using Eqs. (10) and (11) and the known instrument cuvette dimensions, the theoretical maximum particle concentration for any given particle size can be calculated. Figure 1 a illustrates the maximum measurable particle concentration for polystyrene spheres in deionised water measured in a cuvette with transmission path length equal to 10 mm for detection in backscatter, side-scatter and forward scatter directions. The requirement to measure in the forward angle limits the maximum measurable concentration, because multiply scattered photons are more likely to be detected relative to other angles as soon as their scattering becomes non-isotropic.
By analysing the autocorrelation produced by a DLS measurement, a user can identify if multiple scattering effects are present. If the autocorrelation shows a significantly lowered intercept, this is indicative of multiple scattering. For example, in Fig. 2 is an autocorrelation for a measurement of 60 nm latex in backscatter at a suitable concentration (solid line) which has an intercept of 0.985 and an autocorrelation for a measurement of 60 nm latex at a too high concentration (dashed line). Here the intercept has dropped to 0.869.
Operating particle concentration range
The MADLS® operating envelope is exceeded if any of the angles exhibit either of the two phenomena described: number fluctuations or multiple scattering. In addition, sample related properties such as refractive index and particle size affect the scattering behaviour and therefore the measurable concentration.
Examples of accessible size-dependent concentration ranges for gold and silica nanoparticles are presented in Fig. 1b.
Experimental
Materials
Gold nanoparticles with nominal sizes of 30 nm and 80 nm were purchased from BBI International (Cardiff, UK). The particle manufacturer determined the size of the particles to be 30.7 nm and 76.1 nm, respectively, as measured by transmission electron microscopy (TEM) and a particle concentration of 2.00·1011 mL−1 and 1.10·1010 mL−1, respectively. Their concentrations were measured within the EMPIR InNanoPart 14IND12 project with UV-Vis which yielded results of 1.6 ± 0.3 × 1011 mL−1 and 9.6 ± 1.9 × 109 mL−1, respectively (Shard et al. 2018b).
Silica nanoparticles with nominal sizes of 44 nm and 100 nm were provided by the French Alternative Energies and Atomic Energy Commission (CEA). Their particle concentration was measured within the EMPIR InNanoPart 14IND12 project with SAXS and PTA as 4.7 ± 0.5 × 1013 mL−1 and 3.3 ± 0.4 × 1012 mL−1 (Shard et al. 2018a).
A set of polystyrene nanoparticles with nominal sizes between 60 and 240 nm was synthesized by emulsion polymerization of styrene using sodium dodecyl sulphate as surfactant, as described elsewhere (Minelli et al. 2018). The particle concentration was determined gravimetrically by placing five aliquots of 1.00 mL of nanoparticle suspension in pre-weighed aluminium dishes, drying them in a vacuum oven at 80 °C for 24 h and weighing them to quantify the residual. Standard deviation of their mass resulted of ~ 3%. Another set of polystyrene nanoparticles with nominal sizes between 60 nm and 700 nm was sourced from Thermo Fisher Scientific (3xxxA Series), UK. These polystyrene samples were dispersed in a 10.0-mM NaCl solution (Sigma-Aldrich, UK, ACS reagent grade, > 99%) prepared using ultrapure water (resistivity of 18.2 MΩ).
For all techniques, where sample dilution was required, this was performed gravimetrically to produce accurate dilution factor with uncertainty of less than 1%.
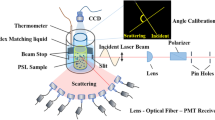
Multi-angle dynamic light scattering
Particle concentration measurements using MADLS® were carried out using a Zetasizer Ultra (Malvern Panalytical Ltd., Malvern, UK) equipped with a He-Ne laser at a wavelength of 633 nm and maximum power of 10 mW. All experiments were performed at 25 °C using a sample volume of 1 mL and disposable cuvettes (DTS0012, Malvern Panalytical Ltd., UK). The instrument settings were optimised automatically by means of the ZS XPLORER software (Malvern Panalytical Ltd., UK). Each concentration result reported is the average of seven or more repeat Malvern Panalytical Better DLS 2018) MADLS® measurements, performed with an acquisition time of approximately 200 s each (Malvern Panalytical Muli Angle 2018). In Table 1 below are the refractive index values used for each material.
Particle concentration by UV-Vis
UV-Vis spectra were acquired in quartz cuvettes using a LAMBDA 850 spectrophotometer (PerkinElmer Inc., MA, USA). The cuvettes’ optical path was 1 cm and the width sufficiently large for the eternity of the beam to traverse the sample. Samples were analysed over the wavelength range 250 to 800 nm. The number concentration N of the particles was derived from the absorption of the particles according to the formula:
where NA is the Avogadro number, A450 is the adsorption measured at 450 nm, L is the optical path (1 cm) and ε450 is the particle molar extinction coefficient calculated according to Mie theory (Haiss et al. 2007). For this calculation, the size of the particles was estimated from the absorption spectra of the particles according to the method described by Khlebtsov (2008). For 30 nm and 80 nm nanoparticles, this method produces an estimate of the diameter of 30.5 nm and 78.3 nm, respectively, in close agreement with the diameter measured by TEM (30.7 nm and 78.8 nm). We used values of the refractive index of gold (Johnson and Christy 1972) at 450 nm of n = 1.38 and k = 1.92 and molar extinction coefficients (Haiss et al. 2007) of 2.07·109 M−1 cm−1 and 3.69·1010 M−1 cm−1 for the 30 nm and 80 nm particles, respectively. The extinction coefficients have a typical uncertainty of 20%, estimated by comparing theoretical and experimental data (Haiss et al. 2007; Khlebtsov 2008). Another potential source of uncertainty is the fact that the position of the local surface plasmon resonance peak depends on the refractive index of the surrounding medium, and, therefore, it is affected by the presence of coatings at the surface of the particles. The particles used in this work are stabilized with citrate molecules, which have been shown to adsorb flat on a gold surface, resulting in a coating thickness of less than 2 nm (Nichols et al. 2004). By applying Mie’s theory, it is estimated that the effect of this coating on the extinction coefficient is below 5%. For this reason, in this work, all gold nanoparticles were treated consistently as uncoated.
Differential centrifugal sedimentation
Differential centrifugal sedimentation (DCS) was performed using a CPS 24000 disc centrifuge (CPS Instruments Inc., Stuart, FL, USA) equipped with an LED laser emitting light with wavelength between 385 and 425 nm and with a spectral intensity peak at 405 nm. The instrument was operated with a sucrose gradient in water according to manufacturer instructions, whose density was selected depending on the particles analysed. Table S1 of the Supporting Information summarises the average densities of the gradients for each type of particles. The sucrose gradient was generated by injections of decreasing sucrose concentration, followed by a final addition of 0.5 mL dodecane as an evaporation barrier. A period of 30 min was allowed prior to measurement acquisition to facilitate thermal equilibrium. Calibration of the instrument was performed before each sample injection by using either polyvinyl alcohol (PVA) or polystyrene (PS) calibration particles with nominal sizes of 237 nm and 522 nm and density 1.385 g cm−3 and 1.052 g cm−3, respectively, provided by the instrument manufacturer. The injected sample volume was measured by weighing the syringe containing the sample before and after each injection and assuming a density of the sample solution of 1 g cm−3. Table S1 summarises the values of materials density, refractive index and absorptions used for the data analysis.
Results and discussion
In this paper, we introduce the MADLS® method for the measurement of nanoparticle concentration and evaluate the accuracy, linearity, size range, repeatability and within-laboratory (intermediate) precision for a range of materials such as gold, amorphous silica and polystyrene nanoparticles, which differ in both size and refractive index. Measurements were performed across a wide range of sample concentrations. The size distributions of these materials were measured with high resolution by DCS and are shown in the Supporting Information in Figures S1, S2 and S3 for gold, silica and polystyrene materials, respectively. The size distributions of the same materials, as measured by MADLS®, are also shown in Figures S4, S5 and S6 of the Supporting Information.
Accuracy
In this section, we investigate the accuracy of the concentration measurements performed by MADLS® in the case of gold, silica and polystyrene nanoparticles of different sizes. To date, nanoparticle reference materials certified for their number concentration do not exist. The EMPIR project 14IND12 Innanopart (Minelli et al. 2019; Schavkan et al. 2019) addressed this gap by developing a range of reference methods that were used to measure the number concentration of different types of nanoparticle materials. These techniques are different for each type of material and are, respectively, UV-Vis for gold nanoparticles, SAXS and PTA for amorphous silica nanoparticles and drying followed by gravimetric measurements for polystyrene nanoparticles. These methods were used to measure the concentration of the stock solutions of the gold, silica and polystyrene nanoparticles used in this work. All samples, including the diluted solutions, were measured by MADLS®, and results are shown in Fig. 3a and Table 2. In Fig. 3a, the dashed line represents the identity relationship, while the dotted lines identify the region of accuracy within a factor 1.5 of the nominal concentration. The concentration measurements performed by MADLS® exhibited excellent agreements with the reference values, with an average deviation of a factor 1.3. It is notable that this is the case for the three types of materials investigated, which have significantly different optical properties and whose size varied from 30 to 240 nm. The measurements are in agreement over a 6 orders of magnitude-wide range of particle concentrations, from ~ 107 to ~ 1013 mL−1.
a Concentration values measured by MADLS® for polystyrene (PS, white), silica (grey) and gold (black) nanoparticle (NPs) samples of various sizes plotted against reference concentrations. The dashed line represents the identity relationship and the dotted lines are a factor of 1.5 deviation. b Percentage difference between the measured MADLS concentration and the nominal concentration for the same samples. The darker shaded region represents 20% discrepancy, and the lighter shaded region represents 50% discrepancy
We note that while the accuracy of the dilute silica samples is typical of the MADLS® measurements of PS and gold, the most concentrated silica samples were underestimated with respect to the reference values. This may be due to the assumption that the viscosity is that of water, while at high particle concentration, the effective viscosity may be higher, resulting in an overestimated particle size. The MADLS® size measurement is used to calculate the expected scattering cross section, and its accuracy is therefore critical to that of the concentration measurement. Since the scattering cross section does not depend linearly on particle size (Boren and Huffman 1983), error in the measured concentration is strongly dependent on the local behaviour of the differential scattering cross section function, \( \frac{d{C}_{sca}}{d\Omega}\left(d,\theta \right) \). For the simple case of a Rayleigh scatterer, the scattering cross section is proportional to the sixth power of the diameter. In this specific case, an overestimation of the particle size by, for example, 10% will give rise to an underestimation in the total particle concentration of 1.1−6 = 56%.
This behaviour indicates the need for optimising the sample concentration for optimal measurement conditions. Some of the differences in the concentration results from the reference values may also be due to sample agglomeration. This was observed, for example, in the high-resolution size distributions of the silica nanoparticle samples measured by DCS, shown in Figure S2 of the supporting information. This is also confirmed by the size measurements reported in Table 2, where MADLS® appears to measure larger diameters of the silica particles with respect to SAXS. The latter is insensitive to agglomeration, while MADLS® measures the hydrodynamic size of the particles, where agglomerates are interpreted as single (larger) particles. As a result, the average particle size of a sample is skewed towards larger sizes in the presence of agglomeration. As previously discussed, the overestimation of the size of the particles leads to an underestimation of the particle concentration. In extreme cases, agglomeration can manifest itself as a large peak in the particle size distribution measured by DLS, whereas minor amounts of agglomeration are more difficult to detect as it only results in an increase in size. By filtering a sample of suspected larger material, a user may then see a change in the size result which would indicate that the sample has agglomeration present.
The reference measurements of the particle diameters of the gold and polystyrene materials are consistent with MADLS® results, and this is reflected in the good agreement achieved in their concentration measurements. The only exception is the most concentrated polystyrene samples with nominal size of 240 nm, whose diameter is measured at 215 nm by MADLS®. A more in-depth analysis of the measurements results for this sample seem to evidence the occurrence of multiple scattering at the side and forward angles, which causes a smaller size to be reported in MADLS®, as discussed in “Theory.”
The accuracy of the measurements of particle number concentration also depends on the accuracy of other parameters that are required for its computation. This is true for all ensemble methods that rely on the use of a model or theory. For example, the accuracy of the number concentration of gold nanoparticles, as measured by UV-Vis, is limited by that of their extinction coefficient, which to date is known with an accuracy of around 20%.
Uncertainties in viscosity, particle size, shape and optical properties are contributing factors to the uncertainty in the concentration measurements. As a result, the accuracy to which these properties are known impacts the accuracy of the number concentration measurement by MADLS®. For a Rayleigh scatterer (particles with diameter at or below approximately one-tenth of the wavelength (633 nm)), the impact of viscosity error will be of the same order as discussed previously. However, for samples larger than this, more complex scattering behaviour occurs which means that error in any given parameter does not translate linearly into error in the concentration. In addition, for simplicity, just as when measuring particle size, we assume a spherical model when calculating the concentration, for non-spherical particles a level of inaccuracy can be expected. Quantifying the error in this case is complex as it is unreliable to relate deviation from sphericity to an error in concentration. Therefore, it is recommended that samples that contain rod-like particles or other structures with a high aspect ratio are not measured using MADLS concentration measurements. It is similarly complex when considering uncertainty in the optical properties; the error in the concentration both increases and decreases as the refractive index increases. Using values readily obtained from the literature is sufficient to achieve the accuracies demonstrated here, of typically within a factor of 1.5 and possibly as good as a factor of 1.2 (approximately ± 20%). It is therefore important to consider and minimise all sources of uncertainty for the attainment of accurate concentration measurements.
Linearity
We demonstrated in the previous section that the MADLS® method allows the accurate measurement of particle concentration for different types of particle materials, sizes and level of dilutions. It should be noted, however, that the optimal operating concentration range will differ depending on the scattering properties of the particle material.
In general, when performing particle concentration measurements, one of the critical parameters to optimise is the operating sample concentration. An instrument with large operating concentration range minimises the need to dilute any samples, which in turn reduces the risk of sample contamination, loss of stability and inaccuracies due to errors in sample dilutions. Furthermore, a large operating concentration range allows contaminants or populations with significantly different concentrations to be quantified during the same measurement.
In Fig. 1b, we have calculated the theoretical linear range measurable by the MALDS® technique. To confirm this, different dilutions of a sample of 30-nm gold nanoparticles were prepared gravimetrically as described in the Experimental section. The stock solution and all the diluted samples were measured using UV-Vis. The results were compared to the concentration measurements performed using MADLS®, as shown in Fig. 4. The MADLS® results are in good agreement with the UV-Vis measurements across particle concentrations between 3·108 and 2·1011 mL−1.
The relative standard deviation of the number concentration measurements performed by MADLS® increases from 10 to 40% with increasing sample dilution. In this specific case, the decrease in repeatability with dilution in water may be as a result of a change in the dynamic equilibrium between the citrate molecules adsorbed at the surface of the particles and those dispersed in solution. This may cause some particle instability or agglomeration at high levels of dilution. This is reflected in the poorer repeatability in the size measurements with increasing dilution where the relative standard deviation increases from 1 to 7%. This information is shown in Table S2 of the Supporting Information.
Size range
As previously discussed, the lower and higher limits of the optimal concentration range for particle concentration measurements by MADLS® depend on the particle size. As the size increases, the concentration range in which neither number fluctuations nor multiple scattering occur narrows and eventually there is no concentration that satisfies these conditions. To demonstrate the effective size range suitable for MADLS® concentration measurements, a range of polystyrene particles with nominal diameters ranging from 60 to 700 nm were measured at nominally the same mass concentration of 0.004% w/v. These are shown below in Fig. 5.
a Average number concentrations measured by MADLS® vs. reference concentrations of a set of polystyrene nanoparticles with size ranging from 60 to 700 nm. Particle concentration increases with decreasing particle size. Error bars represent the standard deviation of repeat measurements (n = 10), while the nominal accuracy of the reference concentration is ± 10%. The dashed line represents the identity relationship, and the dotted lines are a factor of 1.5 deviation. b Relative difference of the concentration measurements as a function of particle size
For particles sizes below 500 nm, the chosen dilutions were suitable for the concentration measurements, which are demonstrated by the accuracy of the size result (Tables S3 and S4 of the Supporting Information). However, we note that MADLS® size measurement repeatability was poor for particles with diameters of 500 nm and 700 nm, resulting in larger uncertainties in the concentration result. For these particle sizes, the samples appeared turbid. Turbidity has the effect of suppressing the total count rate, as well as causing multiple scattering. Both effects introduce error into the derived particle concentration.
Repeatability and intermediate precision
The precision of the MADLS® concentration measurements was evaluated from repeated measurements of the same samples in Fig. 1. This was found to depend on the nature of the sample. The typical relative standard deviation for 7 measurement repeats was 10% or better. This increased to up to 30% for dilution factors greater than 1000-fold. It is interesting to note the case of the agglomerated sample made of 44-nm SiO2 nanoparticles. At the highest sample concentration, the precision, which was measured as the relative standard deviation of 7 repeat measurements, was 80%. However, this decreased to values between 20 and 30% with sample dilution. One of the primary causes for low repeatability in concentration measurements is poor precision in the measurement of particle size. This is typically affected by issues with the sample, such as particle number fluctuations due to large components or the sample concentration being too high or too low. Overall, these results indicate that 10% or better relative precision in number concentration measurements can be achieved with MADLS® for monodisperse and non-agglomerated samples at optimal sample dilution.
The precision achieved with the MADLS® method is of the same order as other laboratory methods available on the market. For example, in the case of 30-nm gold nanoparticles, the relative precision achieved with the MADLS® method is 7%. A recent international interlaboratory study (VAMAS PWA34 Project 10) indicates that the typical relative precision achieved for the measurement of number concentration of 30-nm gold nanoparticles is 3% for PTA, 2% for spICP-MS, 0.2% for UV-Vis and 5% for centrifugal photo-sedimentation.
To evaluate the intermediate precision, defined as a measure of precision performed using the same procedure, instrument and laboratory across a period of time, of the particle concentration measurements using MADLS®, stock solutions of 30-nm gold nanoparticles were measured over a period of 5 days (Fig. 6).
The relative intermediate precision was measured at 10% and the relative intra-day repeatability shows a general increase with time but remains approximately 10%. These results show that the MADLS® particle concentration measurements can achieve both good repeatability and reproducibility with consistent measurements across multiple days.
By providing a high level of intermediate precision, the MADLS® method appears ideal for quality control purposes, enabling, for example, the assessment of the stability of a sample over time or batch to batch variability.
Conclusions
We introduce the MADLS® method for the measurement of particle concentration, and we assessed the accuracy, repeatability and linearity of the Zetasizer Ultra instrument manufactured by Malvern Panalytical Ltd., UK. We applied the method to gold, silica and polystyrene particle samples of different sizes and concentrations and demonstrated accuracies of 50% or better and typical precisions of 10% for monodisperse samples. The different sizes measured showed these levels of accuracy up to sample diameters of 400 nm with samples above this size having data quality issues due to the difficulty in reaching a suitable concentration. The instrument accuracy was evaluated by means of reference materials and methods that were previously developed and assessed within the EMPIR 14IND12 InNanoPart project with the results agreeing with accurate methods such as SAXS, spICPMS and UV-Vis. Both the accuracy and linearity of the instrument were assessed across a threefold concentration range by comparing MADLS® with UV-Vis, the latter having a 20% accuracy for the concentration measurements of gold nanoparticles (Shard et al. 2018b). Results are consistent within uncertainty across a broad concentration range, with MADLS® underestimating the concentration of the particles at high levels of dilutions. The effect of particle size on the accuracy of concentration measurements was also evaluated. We demonstrated that the method can be widely applied across a broad range of sizes. The levels of accuracy shown here have been achieved with measurement times of only a few minutes as part of a simple measurement process, which is carried out much the same as a typical DLS measurement. However, the MADLS® particle concentration measurement does require some characteristics of the particles to be well known such as the particle refractive index and sample viscosity to maintain the levels of accuracy demonstrated here (Malvern Panalytical Measuring 2019).
Overall, we demonstrated that the MADLS® method for the measurement of the size and concentration of particles is straightforward in terms of sample preparation, rapid and versatile, as it can be applied to a range of sample materials, sizes and concentrations. As in the case of the traditional DLS method, MADLS® is also capable of measuring weakly scattering particles at smaller sizes than many other techniques. For example, MADLS® is now being used to measure the concentration of adeno-associated viruses (Malvern Panalytical). These particles are typically around 25 nm in size, and the number concentration is traditionally measured using Capsid ELISA, a laborious technique that is based on the intensity of a colour change due to the number of antibodies binding to the virus (Grimm et al. 1999). However, this means that any fragments or aggregates of the viruses will be included, thus contributing to inaccuracies in the concentration value. As MADLS® can measure the concentration of multiple populations, the number concentration of just the viruses can be accurately determined without influence from other components in the sample.
References
Balasundaram G, Webster TJ (2006) Nanotechnology and biomaterials for orthopedic medical applications. Nanomedicine (London) 1:169–176. https://doi.org/10.2217/17435889.1.2.169
Bertolotti M (1977) Multiple scattering. In: Cummins HZ, Pike ER (eds) Photon correlation spectroscopy and velocimetry. Springer US, Boston, pp 45–141. https://doi.org/10.1007/978-1-4757-1668-9_3
Bloomfield V (1987) Biological applications. In: Pecora R (ed) Dynamic light scattering — applications of photon correlation spectroscopy, vol 91. Plenium Press, New York, pp 372–499. https://doi.org/10.1002/bbpc.19870910455
Boccaccini AR, Erol M, Stark WJ, Mohn D, Hong Z, Mano JF (2010) Polymer/bioactive glass nanocomposites for biomedical applications: a review Compos Sci Technol 70:1764–1776 https://doi.org/10.1016/j.compscitech.2010.06.002
Boren CF, Huffman DR (1983) Absorption and scattering of light by small particles. WILEY-VCH Verlag GmbH & Co KGaA https://doi.org/10.1002/978352761815610.1002/9783527618156
Brar SK, Verma M (2011) Measurement of nanoparticles by light-scattering techniques. TrAC Trends Anal Chem 30:4–17. https://doi.org/10.1016/j.trac.2010.08.008
Bryant G, Thomas JC (1995) Improved particle size distribution measurements using multiangle dynamic light scattering. Langmuir 11:2480–2485. https://doi.org/10.1021/la00007a028
CEN (2015) Workplace exposure - characterization of ultrafine aerosols/nanoaerosols - determination of number concentration using condensation particle counters vol prEN 16897
Corma A, Garcia H (2008) Supported gold nanoparticles as catalysts for organic reactions Chem Soc Rev 37:2096–2126 https://doi.org/10.1039/b707314n
Cummins PG, Staples EJ (1987) Particle size distributions determined by a “multiangle” analysis of photon correlation spectroscopy data. Langmuir 3:1109–1113. https://doi.org/10.1021/la00078a040
European Commission (2011) Commission Recommendation of 18 October 2011 on the definition of nanomaterial Official Journal of the European Union L 275/38
Ford NC Jr (1987) Light scattering apparatus. In: Pecora R (ed) Dynamic light scattering — applications of photon correlation spectroscopy. Plenium Press, New York, p 36
Grimm D, Kern A, Pawlita M, Ferrari FK, Samulski RJ, Kleinschmidt JA (1999) Titration of AAV-2 particles via a novel capsid ELISA: packaging of genomes can limit production of recombinant AAV-2. Gene Ther 6:1322–1330. https://doi.org/10.1038/sj.gt.3300946
Haiss W, Thanh NTK, Aveyard J, Fernig DG (2007) Determination of size and concentration of gold Nanoparticles from UV−Vis spectra. Anal Chem 79:4215–4221. https://doi.org/10.1021/ac0702084
Hopcraft KI, Chang PCY, Jakeman E, Walker JG Polarization fluctuation spectroscopy. In: Videen G, Yatskiv Y, Mishchenko M (eds) Photopolarimetry in remote sensing, Dordrecht, 2005// 2005. Springer Netherlands, pp 137–174
Indu PK, Rumjhum A (2007) Nanotechnology: a new paradigm in cosmeceuticals. Recent Patents on Drug Delivery & Formulation 1:171–182 https://doi.org/10.2174/187221107780831888
ISO (1996) 13321 Methods for determination of particle size distribution. Photon correlation spectroscopy
ISO (2015) 17867:2015: Particle size analysis - small-angle X-ray scattering
ISO (2016) 19430:2016 Particle size analysis - particle tracking analysis (PTA) method
ISO (2017a) 22412:2017
ISO (2017b) TS 19590:2017 Nanotechnologies - size distribution and concentration of inorganic nanoparticles in aqueous media via single particle inductively coupled mass spctrometry
Johnson PB, Christy RW (1972) Optical constants of the noble metals. Phys Rev B 6:4370–4379. https://doi.org/10.1103/PhysRevB.6.4370
Khlebtsov NG (2008) Determination of size and concentration of gold nanoparticles from extinction spectra. Anal Chem 80:6620–6625. https://doi.org/10.1021/ac800834n
Makra I, Terejánszky P, Gyurcsányi RE (2015) A method based on light scattering to estimate the concentration of virus particles without the need for virus particle standards. MethodsX 2:91–99. https://doi.org/10.1016/j.mex.2015.02.003
Malitson IH (1965) Interspecimen comparison of the refractive index of fused silica*,†. J Opt Soc Am 55:1205–1209. https://doi.org/10.1364/josa.55.001205
Malvern Panalytical Better DLS data with less time and effort. https://www.malvernpanalytical.com/en/learn/knowledge-center/application-notes/AN180430IntroAdaptiveCorrelation.html. Accessed 04/09/2018
Malvern Panalytical Measuring the concentration of adeno-associated virus with multi-angle dynamic light scattering (MADLS). https://www.malvernpanalytical.com/en/learn/knowledge-center/application-notes/AN180608AdenoVirusConcentrationMADLS.html. Accessed 24th Jul 2019
Malvern Panalytical Multi-angle dynamic light scattering (MADLS) on the Zetasizer ultra – how it works. https://www.malvernpanalytical.com/en/learn/knowledge-center/technical-notes/TN180719HowItWorksMADLS.html Accessed 04/09/2018
Minelli C, Bartczak D., Peters R., Rissler J., Undas A., Sikora A., Sjöström E., Goenaga-Infante H., Shard A.G. (2019) Sticky measurement problem: number concentration of agglomerated nanoparticles Langmuir 35:4927–4935 https://doi.org/10.1021/acs.langmuir.8b04209
Minelli C, Lowe SB, Stevens MM (2010) Engineering nanocomposite materials for cancer therapy. Small 6:2336–2357. https://doi.org/10.1002/smll.201000523
Minelli C, Sikora A, Garcia-Diez R, Sparnacci K, Gollwitzer C, Krumrey M, Shard AG (2018) Measuring the size and density of nanoparticles by centrifugal sedimentation and flotation. Anal Methods 10:1725–1732. https://doi.org/10.1039/c8ay00237a
Monteiro-Riviere NA, Wiench K, Landsiedel R, Schulte S, Inman AO, Riviere JE (2011) Safety evaluation of sunscreen formulations containing titanium dioxide and zinc oxide nanoparticles in UVB sunburned skin: an in vitro and in vivo study. Toxicol Sci 123:264–280. https://doi.org/10.1093/toxsci/kfr148
Nichols RJ, Burgess I, Young KL, Zamlynny V, Lipkowski J (2004) A quantitative evaluation of the adsorption of citrate on Au(111) using SNIFTIRS. J Electroanal Chem 563:33–39. https://doi.org/10.1016/j.jelechem.2003.08.007
O'Regan B, Grätzel M (1991) A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 353:737–740. https://doi.org/10.1038/353737a0
Ramachandran GN (1994) Fluctuations of light intensity in coron Æ formed by diffraction. J Astrophys Astron 15:357–371. https://doi.org/10.1007/bf02714822
Ruseva V, Jankevics H, Corbett J (2019) An optimized filling method for capillary DLS. MethodsX 6:606–614. https://doi.org/10.1016/j.mex.2019.03.006
Schavkan A et al (2019) Number concentration of gold nanoparticles in suspension: SAXS and spICPMS as traceable methods compared to laboratory methods. nanomaterials 9:502
Schroeder A, Heller D.A., Winslow M.M., Dahlman J.E., Pratt G.W., Langer R., Jacks T., Anderson D.G. (2011) Treating metastatic cancer with nanotechnology Nat Rev Cancer 12:39 https://doi.org/10.1038/nrc3180, 50
Shard AG, Sparnacci K, Sikora A, Wright L, Bartczak D, Goenaga-Infante H, Minelli C (2018a) Measuring the relative concentration of particle populations using differential centrifugal sedimentation Anal Methods 10:2647–2657 https://doi.org/10.1039/c8ay00491a
Shard AG, Wright L, Minelli C (2018b) Robust and accurate measurements of gold nanoparticle concentrations using UV-visible spectrophotometry. Biointerphases 13:061002. https://doi.org/10.1116/1.5054780
Stark WJ, Stoessel PR, Wohlleben W, Hafner A (2015) Industrial applications of nanoparticles. Chem Soc Rev 44:5793–5805. https://doi.org/10.1039/c4cs00362d
Sultanova N, Kasarova S, Nikolov I (2009) Dispersion properties of optical polymers. Acta Phys Pol A 116:585–587. https://doi.org/10.12693/APhysPolA.116.585
Talapin DV, Steckel J (2013) Quantum dot light-emitting devices MRS Bull 38:685–691 https://doi.org/10.1557/mrs.2013.204
Vaclavek T, Prikryl J, Foret F (2019) Resistive pulse sensing as particle counting and sizing method in microfluidic systems: designs and applications review. J Sep Sci 42:445–457. https://doi.org/10.1002/jssc.201800978
Vogel R, Coumans FAW, Maltesen RG, Böing AN, Bonnington KE, Broekman ML, Broom MF, Buzás EI, Christiansen G, Hajji N, Kristensen SR, Kuehn MJ, Lund SM, Maas SLN, Nieuwland R, Osteikoetxea X, Schnoor R, Scicluna BJ, Shambrook M, de Vrij J, Mann SI, Hill AF, Pedersen S (2016) A standardized method to determine the concentration of extracellular vesicles using tunable resistive pulse sensing. J Extracellular Vesicles 5:31242. https://doi.org/10.3402/jev.v5.31242
Vysotskii VV, Uryupina OY, Gusel’nikova AV, Roldugin VI (2009) On the feasibility of determining nanoparticle concentration by the dynamic light scattering method. Colloid J 71:739–744. https://doi.org/10.1134/s1061933x09060027
Weitz D, Pine D (1993) Diffusing-wave spectroscopy. In: Brown W (ed) Dynamic light scattering: the method and some applications. Oxford University Press, pp 652–720
Acknowledgements
CM and MW acknowledge support from the European Metrology Programme for Innovation and Research (EMPIR) as part of the 14IND12 InNanoPart project. The EMPIR initiative is co-funded by the European Union’s Horizon 2020 research and innovation programme and by the EMPIR participating states. CM and MW also acknowledge the Metrology for Advanced Coatings and Formulated Products theme of the UK Department of Business, Energy and Industrial Strategy. The authors acknowledge the partners of the EMPIR project Innanopart for producing a set of particles with information on their concentration and especially Alex Shard and Charles Clifford (NPL, UK), Antoine Thill (CEA, France), Katia Sparnacci (Univeristà del Piemonte Orientale, Italy) and Dorota Bartczak (LGC, UK). The authors would like to thank Valentina Ruseva for support with the accessible concentration range calculations, Kenneth Haber for early development of the algorithm, Matt Ruszala for support and advice and Patrick Hole for beginning this collaboration between NPL and Malvern Panalytical.
Statement of contribution
The MADLS particle concentration analysis was developed by Douglas Hamilton and Jake Austin. The sample preparation was carried out by Magdalena Wywijas and Jake Austin with data collection and analysis carried out by Magdalena Wywijas, Jake Austin, Hanna Jankevics Jones and Caterina Minelli. All authors have contributed to and approved the final manuscript.
Funding
European Metrology Programme for Innovation and Research (EMPIR) as part of the InNanoPart 14IND12 project.
Metrology for Advanced Coatings and Formulated Products theme of the UK Department of Business, Energy and Industrial Strategy.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors Jake Austin, Douglas Hamilton and Hanna Jankevics-Jones are all employed by Malvern Panalytical Ltd. and declare no competing financial interests beyond that.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Austin, J., Minelli, C., Hamilton, D. et al. Nanoparticle number concentration measurements by multi-angle dynamic light scattering. J Nanopart Res 22, 108 (2020). https://doi.org/10.1007/s11051-020-04840-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11051-020-04840-8