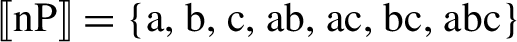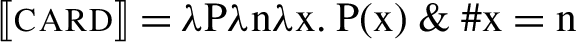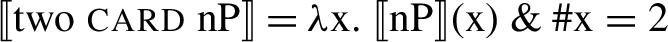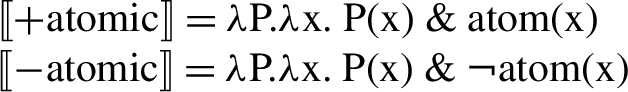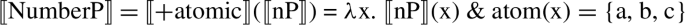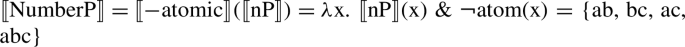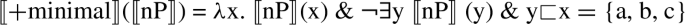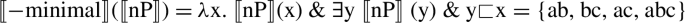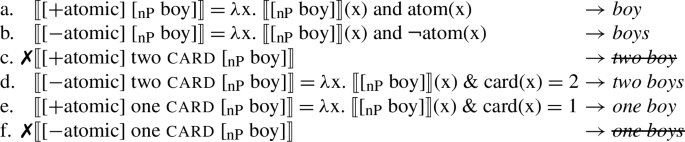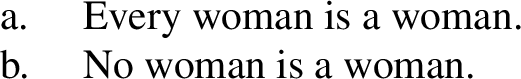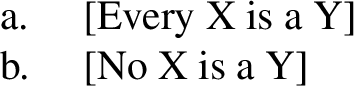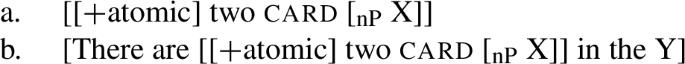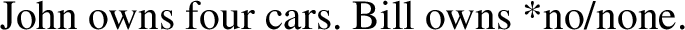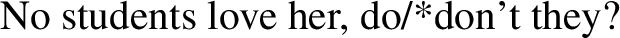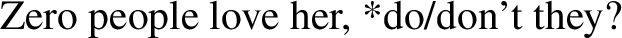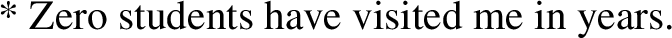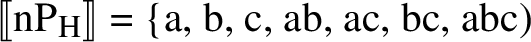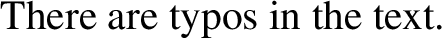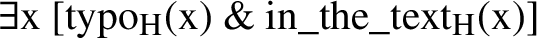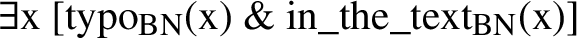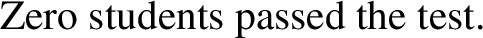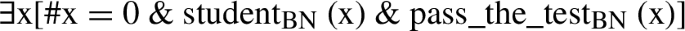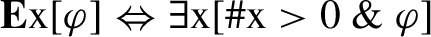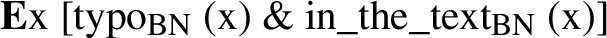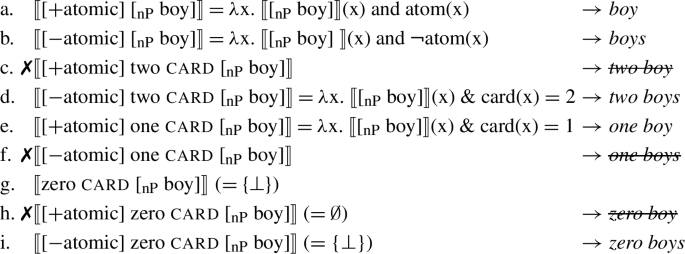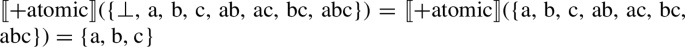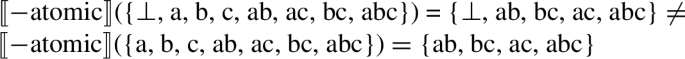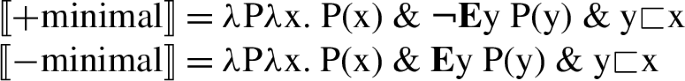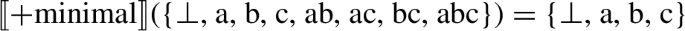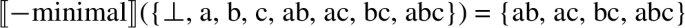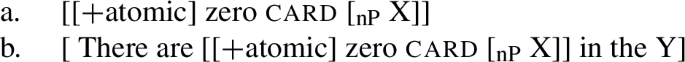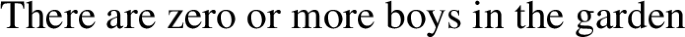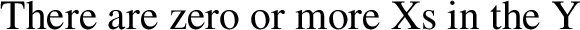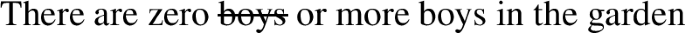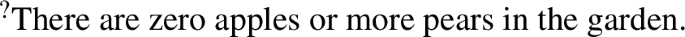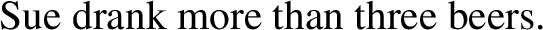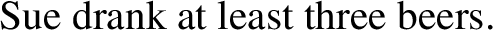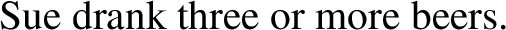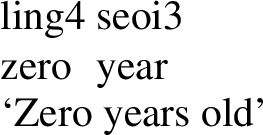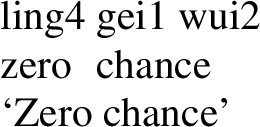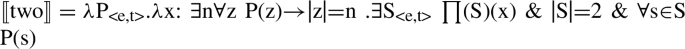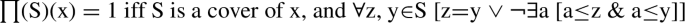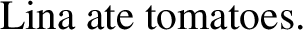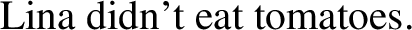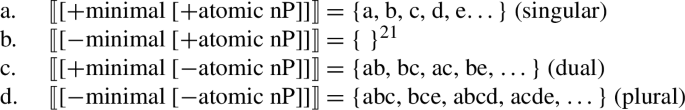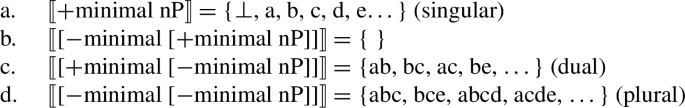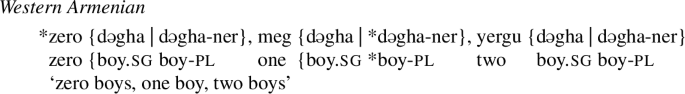Abstract
In this paper I demonstrate that there is an explanation of the number marking we see on nouns when they combine with the numeral zero which combines Martí’s (Semant. Pragmat., 2020a, https://doi.org/10.3765/sp.13.3) account of the morphosyntax and semantics of the numeral-noun construction with Bylinina and Nouwen’s (Glossa 3(1):98, 2018) semantics for zero and which does not need to appeal to any further principles (e.g., agreement).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In some languages, the numeral zero combines with morphologically plural count nouns, as exemplified in (1) for English (cf. Krifka 1989; Borer 2005). In others, such as Turkish (2), it combines with morphologically singular nouns (Turkish requires the use of a morphologically singular noun for all numerals, despite having morphologically plural nouns; Bale et al. 2011; Scontras 2014; Martí 2020a, among others):
-
(1)

-
(2)

In this paper I demonstrate that there is an explanation of these patterns that combines Martí (2020a,b) account of the morphosyntax and semantics of the numeralFootnote 1 + noun construction with Bylinina and Nouwen’s (2018) semantics for zero and that does not need to appeal to any further principles (e.g., agreement). The explanation has the overall advantage of accounting for both the number marking of nouns with zero (and other numerals more generally) and the semantics of the construction using just one set of tools. Included in this set of tools are Harbour’s (2014) semantically contentful number features, which links the present account to his account of the cross-linguistic typology of grammatical number more generally, with potentially far-reaching consequences.
Section 2 introduces the crucial ingredients of Martí’s proposal. Section 3 introduces the semantics for zero argued for in Bylinina and Nouwen (2018). Section 4 puts that together with the technology in Sect. 2 to derive the zero facts. Section 5 discusses issues related to plurality, agreement, and the typology of grammatical number that the account in Sect. 4 raises. Section 6 is the conclusion.
2 Martí (2020a,b) account of the numeral-noun construction
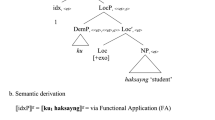
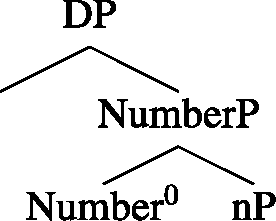
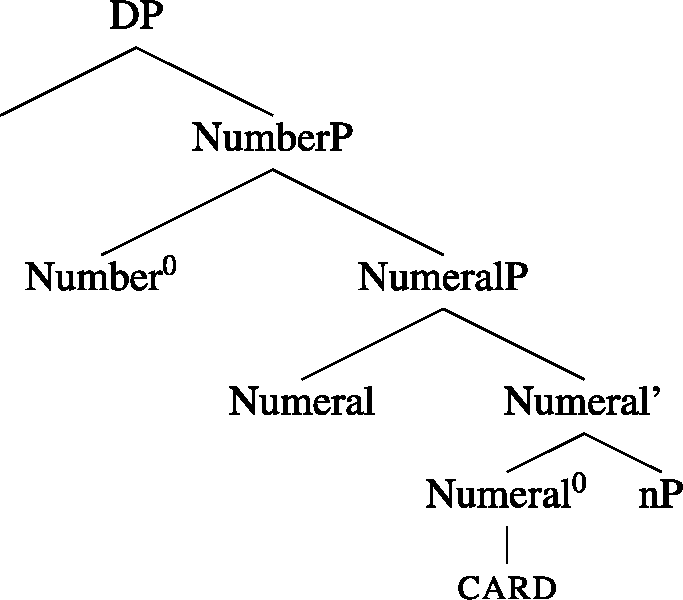
Martí’s (2020a) account of the pattern in (1)-(2) minus the zero facts is as follows (Martí 2020b extends that account to languages with dual number and to complex numerals). Martí assumes the syntax in (3) for noun phrases without numerals, and that in (4) for phrases with numerals (cf. Borer 2005;Footnote 2 Harbour 2014; Scontras 2014, and many others):Footnote 3
-
(3)
-
(4)
Following Harbour (2014), nP in both (3) and (4) denotes a join semilattice (cf. Link 1983) in all cases. For just three individuals, a, b, and c, we have:
-
(5)
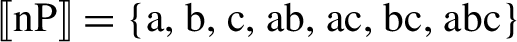
NumeralP is realized only in (4), with a numeral (one, two, etc.) generated as its specifier. Numeral0 hosts Scontras’s (2014) cardinality predicate (cf. Hackl 2001, and others), in (6), a function which takes a predicate P, furnished by nP, and a number, furnished by the numeral, and returns a new predicate such that each of its members is in P and is of that numerosity (‘#x’ stands for ‘the numerosity of x’):
-
(6)
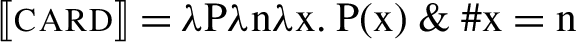
-
(7)
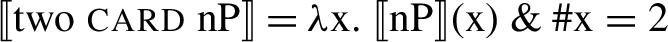
NumberP hosts number features, which, following Harbour (2014), are both semantically contentful and morpho-syntactically relevant. These number features are thus taken to be responsible for the number semantics of nouns (and other nominal entities, such as pronouns or demonstratives in the languages where these show number morphology) and their morphological shape. NumberP is realized in both trees, given that it is necessary in the account of number marking found in noun phrases both with and without a numeral. Martí follows Harbour’s (2014) theory of NumberP-projecting features, where only three features are possible: [±atomic], [±minimal], and [±additive] (for the first two, see also Harbour 2011). With these three features, and a number of additional constraints, Harbour generates all and only the attested grammatical number systems found in the languages of the world—that is, the full cross-linguistic typology of number (see Sect. 5 for more discussion of this point). Only two of those features will be necessary for us, [±atomic] and [±minimal], whose semantics is as follows:Footnote 4
-
(8)
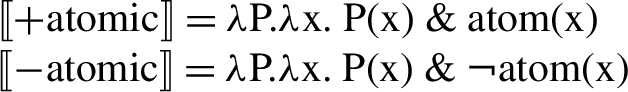
-
(9)

The feature [±atomic] is sensitive to the atomic nature of the members of 〚nP〛:
-
(10)
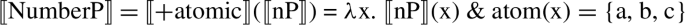
-
(11)
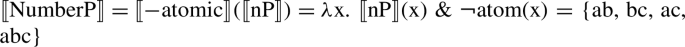
[±Minimal] is sensitive to whether the members of the denotation of its argument have ([−minimal]) or do not have ([+minimal]) proper parts in it:
-
(12)
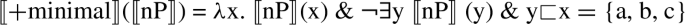
-
(13)
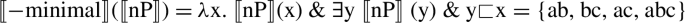
In the simplest case, the argument of [±minimal] is nP, hence (12) and (13), though, as we will see shortly, this is not always the case. The argument of [±atomic] is always nP. [±Atomic] and [±minimal] give rise to the same result whenever their argument is nP. However, Harbour (2011) shows that [±atomic] and [±minimal] come apart in a number of interesting cases, including pronominal systems with an exclusive and inclusive first person distinction (where 〚+atomic〛 (P)≠〚+minimal〛(P)), number systems with a dual (which combine the two features, so that dual number arises from the feature combination 〚+minimal〛(〚−atomic〛(P))), and number systems with a trial (where [±minimal] repeats, so that trial number arises from the feature combination 〚+minimal〛(〚−minimal〛(〚−atomic〛(P)))). Martí (2020a) argues that one further case where [±atomic] and [±minimal] come apart is precisely in their combination with numerals, as shown below. For a more detailed explanation of these arguments, see Martí (2020a, pp. 9–14).
Martí’s account for English is as follows (cf. Scontras 2014), a language in which [+atomic] is realized as ∅ and [−atomic] is realized as -s:Footnote 5
-
(14)
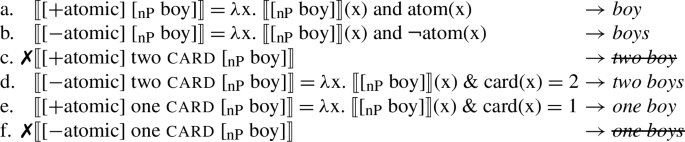
(14a) is the only source for the singular DP boy and gives rise, correctly, to a singular semantics for it. In (14a), the NP boy and the resulting DP boy have different syntactic structures and different semantics, despite sounding the same. This is in part because [+atomic] in English is spelled out as ∅. (14b) gives rise to the plural form boys and assigns it an exclusive plural semantics, more on which in Sect. 5. (14c) is empty, as there are no atoms in a set of, exclusively, plural individuals of numerosity 2 (or ‘twosomes’, for short), so it is assumed to lead to ungrammaticality (more on which below). Thus, two boy is ungrammatical in English. (14d) is the only source for two boys and gives rise, correctly, to a set of boy twosomes as its semantics. (14e) is the only well-formed source for one boy, and also gives rise to the correct semantics. (14f) is ill-formed, since 〚one card nP〛 is a set of atoms, and [−atomic] cannot combine with it. It is the only source for one boys, which is thus correctly predicted to be ungrammatical. Notice that the denotation of nP is assumed to be as in (5) in all cases—whether the noun surfaces in its singular or plural form is determined by the interaction of that denotation with the semantics of the Number0 and Numeral0 heads in (14). The English use of morphologically singular and plural forms in this paradigm thus follows from an interaction between morphological and semantic assumptions. More precisely, the fact that numerals greater than 1 combine with morphologically plural nouns in English follows from the fact that only in the case of such numerals does 〚numeral card [nP boy]〛 satisfy the requirements of [−atomic]. One, on the other hand, is the only numeral where 〚numeral card [nP boy]〛 satisfies [+atomic]—this is how its special status in languages like English is derived.
Martí (2020a, p. 10, ft. 14) follows Gajewski (2002) (see del Pinal 2019; Chierchia 2021 for refinements) in assuming that certain kinds of semantic ill-formedness lead to ungrammaticality, and it is worth being explicit here about what this implies for the treatment of outputs such as (14c) or (14f). Not all informationally trivial sentences are ungrammatical, as illustrated in (15):
-
(15)
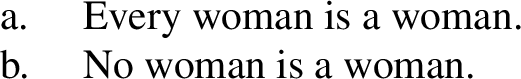
Gajewski argues, however, that there is type of triviality that does lead to ungrammaticality systematically—that is, there are sentences, called L-analytic sentences, whose ungrammaticality is due to their triviality. (14c), (14f) and other cases discussed here involve L-analyticity—the semantics delivers an L-analytic trivial meaning, and the expressions that carry such meanings are ungrammatical. In Gajewski’s framework, any instance of triviality that remains a triviality no matter which content words are used, while keeping function words constant, leads to ungrammaticality. The logical structure of the examples in (15) is as follows:
-
(16)
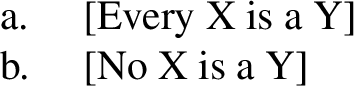
Not all replacements of the variables X and Y lead to triviality. For example, (16a) is not trivial if X is replaced with the predicate woman and Y is replaced with the predicate feminist—indeed, the sentence Every woman is a feminist is informative. Thus, (15a) is not ungrammatical, even if it is uninformative.
Taking (14c) as an illustrative case for our purposes, we have the structure in (17a), where the content word boy has been replaced with the variable X; in (17b), that structure is embedded further into a sentence (assuming that number features, numerals, card, in and the all form part of the functional vocabulary of a language, which seems reasonable):
-
(17)
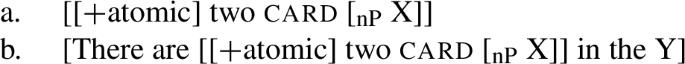
No matter what replaces the variables X and Y, (17b) always leads to a contradiction (since (17a) is always empty by virtue of the semantics of the feature, the numeral and card). Thus, the expressions that spell out (17a) and (17b) are ungrammatical (e.g., *two boy, *There are two boy in the garden). Similar remarks hold for Turkish below (see (18d) and (18f)).
Martí’s analysis of the Turkish pattern (minus the zero facts) in (2) is as follows. Turkish is a [±minimal] system in this account: [+minimal] spells out as ∅ and [−minimal] as –lAr. We have (for iki ‘two’, bir ‘one’, and çocuk ‘boy’):
-
(18)

(18a) and (18b) result, respectively, in a singular semantics for the DP çocuk ‘boy’ and an exclusive plural semantics for the DP çocuklar ‘boys’, as desired.Footnote 6 As Harbour (2011) notes, and as noted above, [±atomic] would have given the same result (see (14a) and (14b)). However, we obtain a different result in combination with numerals. For iki çocuk ‘two boys’ in (18c), we obtain a set of boy twosomes (they have no proper parts in 〚iki card [nP çocuk]〛, which contains only boy twosomes). This is the only possible source for iki çocuk, so its correct morphology and semantics are derived. (18e) denotes a set of boy individuals composed of exactly one atom, these atomic boy individuals having no proper parts in 〚bir card [nP çocuk]〛 (which contains only boy atoms). This is the only possible source for bir çocuk ‘one boy’. [−Minimal] never gives rise to a well-formed result when combined with a numeral, as shown in (18d) and (18f), since [−minimal] selects from its input P those individuals that have proper parts in P, and there are no such parts in 〚iki card [nP çocuk]〛, 〚bir card [nP çocuk]〛, etc. Thus, that all numerals combine with morphologically singular nouns in Turkish follows from the fact that, for any numeral, 〚numeral card [nP çocuk]〛 satisfies the requirements of only [+minimal], not [−minimal].
3 Bylinina and Nouwen’s semantics for zero
Bylinina and Nouwen argue that zero is not an emphatic version of the negative quantifier no (at least when it combines with count nouns; see Chen 2018 and the end of Sect. 4 for more on this). Zero and no differ in distribution ((19)-(20)), polarity ((21)-(22)) and NPI-licensing ((23)-(24)), among other things (Zeijlstra 2007; De Clercq 2011; Gajewski 2011—but see Chen 2018 for more nuance on the issue of NPI licensing):
-
(19)

-
(20)
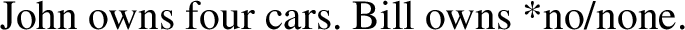
-
(21)
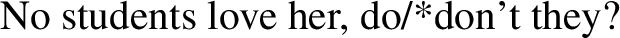
-
(22)
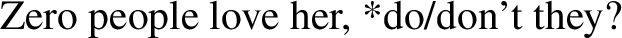
-
(23)

-
(24)
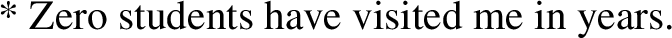
They argue for a treatment of zero in which, just like other numerals, it denotes a number, 0. Bylinina and Nouwen propose that the denotation of count nouns is not a (join) semilattice, as standardly assumed, but a full lattice, which includes the bottommost element, ⊥. ⊥ is of numerosity 0 and has no proper parts. Their proposal is to reconsider our view of pluralization as a full lattice formation. (5), repeated here as (25), is replaced with (26) (in order to keep these denotations distinct, our earlier, Harbour semantics will be referred to with a subscript ‘H’ (see Link 1983); the Bylinina and Nouwen-inspired semantics will be referred to with a subscript ‘BN’):Footnote 7
-
(25)
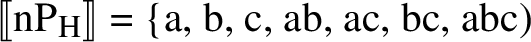
-
(26)

The truth-conditions for a sentence like (27), instead of being those in (28), are now those in (29), where the new version of pluralization is assumed to apply to predicates other than count nouns (e.g., in the text) as well:Footnote 8
-
(27)
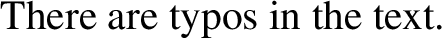
-
(28)
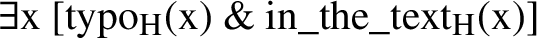
-
(29)
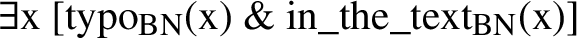
One important issue that Bylinina and Nouwen address is that, while a semantics like that in (28) requires there to be at least one typo in the text, correctly, (29) is a tautology, since for any predicate P, P(⊥) = 1. The same holds for the numeral-noun construction:
-
(30)
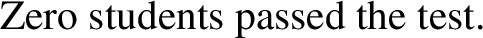
-
(31)
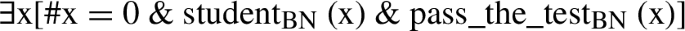
(31) is always true, independently of the number of students who passed the test, since one can always decide that x = ⊥. In informal terms, the problem is that the truth-conditions for (31) are predicted to be those of zero or more students passed the test, which can never be falsified.
The solution proposed for (30) is to note that the semantics that this view provides for numerals is an at least semantics, and that exhaustification can generate the required stronger, exactly readings. Given the truth-conditions in (31), statements with other numerals are stronger. Uttering (30) signals that those stronger statements are false. We thus have, for (30):
-
(32)

Taken together, (31) and (32) result in an exactly reading: there are zero or more students who passed the test, and there are no more than zero students who passed the test—so exactly zero did. Unlike other numerals, exhaustification is obligatory for zero, since no exhaustification leads to a defective, tautological interpretation. And, since the semantics of zero is not stronger in downward-entailing environments (the negation of a tautology is a contradiction), the exactly implicature still obtains in such contexts (cf. Nobody read zero books).
The solution for the more general problem that arises in (27), where there is no numeral to trigger exhaustification, is to assume that the existential quantifier that operates on statements without numerals is not classical ∃ but E, as in (33). This takes into account the fact that the denotation of NP now includes ⊥ and results in the contingent (34) for (27):
-
(33)
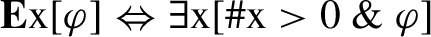
-
(34)
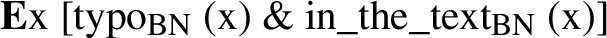
More precisely, Bylinina and Nouwen assume that both the E-operator and the ∃-operator may apply in sentences such as (27), but that, following Landman (2011), a contingent statement is better than a trivial one, that is, that a pragmatic principle against triviality is generally at work in natural language.
The postulation of the E-operator, which is necessary for sentences such as (27) once we assume ⊥, seems rather stipulative. In addition, the classical ∃-operator still needs to be assumed in this system, as use of the E-operator in sentences such as (30) results in a contradiction. Bylinina and Nouwen argue that ⊥ is desirable also in the case of sentences with downward monotone degree quantifiers such as fewer than n, at most n, etc. A sentence like fewer than 10 students passed the exam will fail to come out true in situations in which no students passed the test unless ⊥ is assumed to be part of the denotation of count nouns. Furthermore, the polarity behavior of zero N, as they show, can be explained once ⊥ is assumed. Despite the stipulative flavor of the E-operator, it seems necessary once we include ⊥ in the denotation of common nouns.
Another issue is where the two existential operators are used. While Bylinina and Nouwen, following Hackl (2001), assume that a many predicate has the function of introducing ∃-quantification and combining numerals and predicates, Scontras and Martí, as discussed in Sect. 3, assume that ∃-quantification is introduced elsewhere in the structure (cf. card in (6)). This difference does not have consequences for us. It is still the case in both views that the distribution of the ∃ and E operators is different (∃ for numerals, E in other cases)—embedding the ∃-operator as part of the semantics of many does not change this. Below, I assume (6) and, as far as existential quantification that comes from elsewhere in the structure is concerned, the ∃-operator for numerals, and the E-operator for noun phrases without numerals. As we will see, as far as the denotation of features is concerned, the E-operator is necessary.
Importantly, in full lattices, ⊥ is not considered an atom (for something to count as an atom, it has to have ⊥ as its only proper part; since, ⊥=⊥, ⊥ cannot be a proper part of ⊥) (see Davey and Priestley 2002, p. 113). If ⊥ is not an atom, then it is a non-atom.
4 The morphology and semantics of zero N: a proposal
Given these assumptions, the account proposed here for the full pattern in (1)-(2) is as follows. For English, to the derivations in (14), repeated as (36a)-(36f), we add (36h) and (36i). Recall that we are assuming (26), repeated in (35) for convenience:
-
(35)

-
(36)
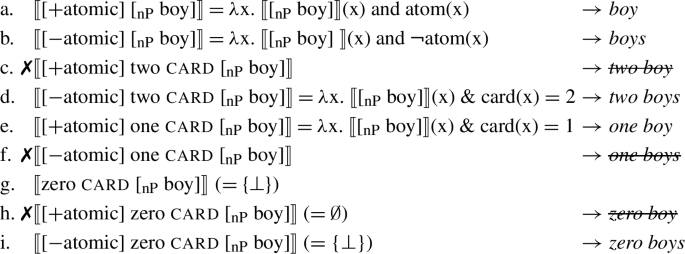
Using (35)/(26) instead of (25)/(5) does not change our earlier results. To see this for a case with just three individuals a, b and c, together with ⊥, we have:
-
(37)
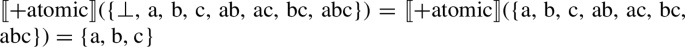
That is, ⊥ is not an atom. We obtain a different result with [−atomic]:
-
(38)
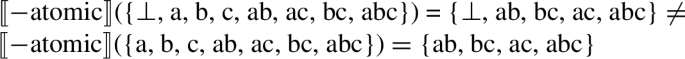
This is unproblematic, however. Exclusive plurals as in (36b) (and inclusive ones) now include ⊥, but the solution Bylinina and Nouwen invoke in (34) applies here. In (36c)/(36d) and (36e)/(36f), since |⊥| = 0, ⊥ is neither in 〚two card [NP boy]〛 nor in 〚one card [NP boy]〛, so the results when the number features get added is as before.Footnote 9
For English zero, we have the following. Just as it was the case for sets of non-atoms, the only member of the set containing {⊥}, which arises from (36g), does not satisfy the requirements of [+atomic] (36h): ⊥ is not an atom. If ⊥ is not an atom, then it is a non-atom, so (36g) satisfies the requirements of [−atomic] (36i). Thus, the reason that with both zero and any numeral greater than 1 English uses the plural morphological marker on the noun is the same: both non-atoms and ⊥ are non-atoms.
Turning now to Turkish, recall that the semantics of Harbour’s feature [±minimal], repeated here, makes use of the ∃-operator:
-
(39)

Since we are adopting Bylinina and Nouwen’s system, the question arises as to whether this semantics needs revision. Given that, with the introduction of ⊥, atoms now have proper parts (⊥ is a proper part of any atom), the semantics for [±minimal] that we need is as in (40), which uses the E-operator:Footnote 10
-
(40)
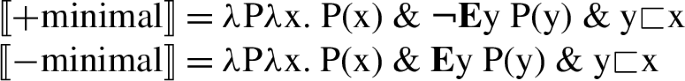
For Turkish we now have (for iki ‘two’, bir ‘one’, sıfır ‘zero’ and çocuk ‘boy’):
-
(41)

Let’s begin with (41a) and (41b). With the semantics in (40), we have, for three elements a, b and c, plus ⊥:
-
(42)
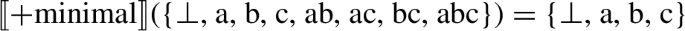
-
(43)
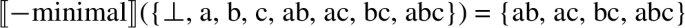
Since both ⊥ and atoms have no proper parts of numerosity greater than 0 (⊥ has no proper parts at all, and atoms have only ⊥ as a proper part, but ⊥ does not have numerosity greater than 0), they count as minimal and are included in (42). Plural individuals are not, since they do have proper parts of numerosity greater than 0. Since neither ⊥ nor atoms have proper parts of numerosity greater than 0, they are excluded in (43). Plural individuals are, on the other hand, included now because they have proper parts of numerosity greater than 0. The denotation of morphologically singular nouns in (41a) now includes ⊥; the use of the E-operator that Bylinina and Nouwen invoke for bare plurals in English is invoked here as well, and we correctly predict that DPs such as çocuk are semantically singular, as before (cf. (18a)). The denotation of morphologically plural DPs such as çocuklar is just as before (cf. (18b)).
In (41c)/(41d) and (41e)/(41f), since |⊥| = 0, ⊥ is neither in 〚iki card [nP çocuk]〛 nor in 〚bir card [nP çocuk]〛, so the results when the number features get added are as before.
Turning now to the account of zero N in Turkish, the only member of the set containing {⊥} (41g) satisfies the requirements of [+minimal], ⊥ has no proper minimal parts at all. Thus (41h) gives rise to the correct morphology and semantics for sıfır çocuk ‘zero boys’. On the other hand, ⊥ is not non-minimal, so [−minimal] cannot successfully apply to {⊥}, and we obtain the result in (41i), namely, *sıfır çocuklar. Thus, the reason why with any numeral including zero Turkish uses the singular morphological marker on the noun stays the same: atoms, non-atoms and ⊥ are all proper-part-less once the numeral has combined with [card [nP çocuk]].
Two important issues about the analysis presented above need addressing before proceeding. The first one has to do with L-analyticity and the role it plays in the analysis of zero—for example, (36h), being L-analytic, leads to ungrammaticality in the analysis of English above (recall also (14c) and (14f)). No matter what replacements of X and Y we carry out in (44), (44a) will always be empty, and sentences of for example the form in (44b) (e.g., *There are zero boy in the garden) will always be a contradiction (and, thus, ungrammatical):
-
(44)
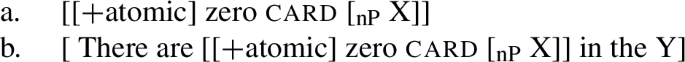
Interestingly, zero seems at first sight to pose a special challenge for this view, as argued by an anonymous reviewer. Indeed, (45) is a trivial, but grammatical, sentence:
-
(45)
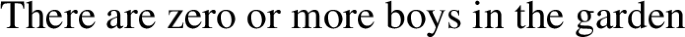
The sentence is clearly uninformative, a tautology. It is equally clear to speakers that the sentence is grammatical. However, the sentence seems L-analytic, because any replacement of the content words in the example renders it still uninformative:
-
(46)
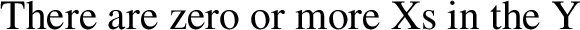
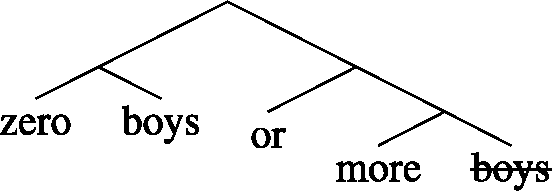
However, whether (45) is indeed a problem for this approach depends on its syntactic analysis, I claim. One possible analysis treats zero or more as a (complex) modifier, on a par perhaps with at least three boys or more than three boys. In that case, we’d have the following basic structure:
-
(47)

Another possibility is as follows:
-
(48)
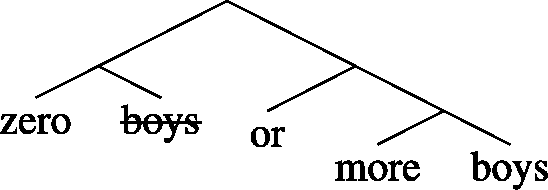
-
(49)
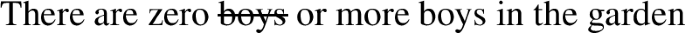
Under this fully compositional analysis, the underlying structure of zero or more boys is more complex than meets the eye and includes a phrase headed by or as well as nominal ellipsis. If (47) is the correct analysis, (45) may indeed be considered an L-analytic sentence which is nevertheless grammatical, a problem for Gajewski’s view and thus also a problem for the analysis of zero defended here. However, if (48) is the correct analysis, then there is no problem, since not every substitution of the lexical material in (48) leads to triviality. (50) doesn’t:
-
(50)
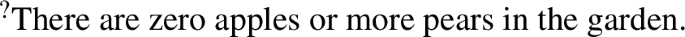
(50) may be odd, particularly out of the blue (since it is necessary to resolve the comparison of more, something which may be alleviated in the right context). But it is certainly not trivial, with a meaning akin to “there are no apples or more than a certain number of pears in the garden” (true in a situation in which there are no apples in the garden, false in a situation in which there are some apples but no pears in the garden). This would make (45) non-L-analytic, and, thus, not a problem for the present account.
The issue is, then, analysis-dependent, and making progress on it involves deciding on the correct analysis. In fact, there are arguments for and against (48). Adopting (48) would presumably entail that the analysis of the related (51) is as in (52):
-
(51)

-
(52)
But zero or more boys and zero boys or more are, interestingly, not equivalent. Zero boys or more conveys that the number of boys was large (if not fully known), which is at odds with there being zero boys in the garden (hence the oddness of (51)), whereas zero or more boys is entirely neutral in that respect.Footnote 11 Conversely, the analysis in (48) sets zero or more apart from numeral modifiers such as at least or more than, which seem genuinely different. For example, both (53) and (54) are true and felicitous in a context in which the speaker is certain that Sue drank three beers and one vodka (and nothing else):
-
(53)
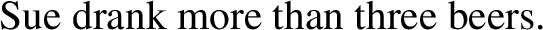
-
(54)
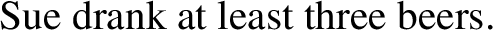
(55) is different in this regard, in a way that suggests that beers plays a role that goes beyond its role in (53) and (54):
-
(55)
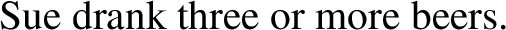
(55) is false if the speaker is certain that all that Sue drank is three beers and one vodka.Footnote 12,Footnote 13 The analysis in (48), extended to numerals such as three, can capture this fact, and is sufficiently different from analyses of at least and more thanFootnote 14 to warrant the contrast with them. I do not pursue the analysis of (45) further here, but I hope to have demonstrated that it is not obvious that such cases necessarily represent a problem for the analysis of zero in terms of L-analyticity pursued here.
The second issue that needs addressing is that zero can combine with mass nouns in English (e.g., zero sugar), as well as with what Chen (2018) calls nominal degree predicates (as in, e.g., zero tolerance), which are typically uncountable. There is an argument to be made, as suggested by a reviewer, that zero shouldn’t be treated as a numeral, since generally numerals cannot combine with mass nouns (*three sugar) or with nominal degree predicates (*two tolerance). Chen (2018), however, suggests that zero might be ambiguous in English between a numeral semantics (which combines with plural count nouns in English), and a degree quantifier semantics. It is the latter that we see in examples with nominal degree predicates, as she argues, and, judging from the behavior shown below on (substance) mass nouns, with these nouns as well. That the zero that appears with regular count nouns (abbreviated to zerocount) and the zero that appears with nominal degree predicates and mass nouns (zerouncount) might be different lexical items is suggested by, for example, the fact that only zerocount (and numerals more generally) is possible in certain comparative constructions or accepts modification by absolutely:
-
(56)

-
(57)

Further evidence for the ambiguity hypothesis for English zero is that not all languages seem to treat their zero as ambiguous in this way—an item that is lexically ambiguous in one language need not be so in the next. Cantonese ling4 might be a case in point. Chow and Morzycki (2021) show that ling4 is compatible (without a classifier) with unit nouns (58) and with ‘chance’ predicates (59), but cannot combine with classifiers and nouns like gau2 ‘dog’, setting it apart from all other numerals in the language (60):
-
(58)
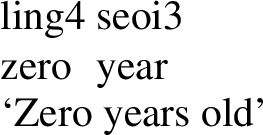
-
(59)
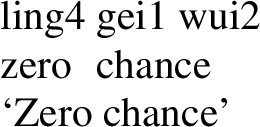
-
(60)

This makes it plausible to think that Cantonese ling4 is unambiguously a degree quantifier, not a cardinality expression/numeral.Footnote 15 Thus, we need not take the appearance of zero with mass nouns or nominal degree predicates in a language like English as evidence against the treatment of zero as a numeral—there are plausibly two zeros in English.Footnote 16,Footnote 17
5 Plurality, agreement and the typology of grammatical number
Two key aspects of the account in Martí (2020a,b) need further discussion and justification: the type of explanation proposed for the facts in (1) and (2) and the semantic contribution assumed for morphological plurality.
Facts such as those in (1) and (2) are often thought of as morpho-syntactic facts, usually in terms of agreement (or concord) between the noun and the numeral. For example, English may be taken to show that nouns agree in the plural with the numeral in this construction, and that the numeral one is special in that it does not support such agreement (or it calls for singular agreement, which is null in English). Turkish can be taken to show that in some languages agreement is lacking, or that it is in the singular by default (see Alexiadou 2019—Ionin and Matushansky 2006, 2018 argue instead for ‘semantic’ agreement, as discussed below). In contrast, no appeal to agreement or any further mechanism is made in Martí’s account, or the account presented above for zero, where compositional semantics plays a crucial role in the explanation. Which account is to be preferred?
The adoption of Martí (2020a,b), and, ultimately, Harbour (2014), also raises the issue of the proper account of the semantics of plurality. To see this, consider that [−atomic] generates only an exclusive semantics for plural forms, that is, a semantics of non-atoms, and non-atoms only, as we saw in (14b). As is well-known, however, many languages have both inclusive and exclusive plurals, inclusive plurals conveying a meaning which involves both atoms and non-atoms. How are inclusive plurals to be accounted for in an approach, like the one pursued here, in which exclusive plural meanings are derived semantically? Indeed, one popular analysis, discussed by Sauerland (2003) and many others,Footnote 18 and which Scontras (2014) uses in his own proposal, takes it that singular features presuppose singularity and plural features are semantically vacuous, which is at odds with (14). In this and other Sauerland-style analyses, there isn’t a feature like [−atomic] alongside [+atomic] that generates an exclusive reading for plural forms. Instead, plural forms are always semantically weak, with exclusive, stronger readings arising pragmatically. As Martí (2020c) argues, however, a Sauerland-style view of plurality is incompatible with Harbour (2014). What arguments are there for the view of plurality in Harbour (2014)?
In this section I argue that there are two important advantages, related to these issues, that Martí’s proposal and, thus, the proposal presented above on zero, has against competitors. The first advantage has to do with theoretical economy, and the second with empirical coverage.
The argument about theoretical economy is that the set of tools needed in the proposal presented here to explain the number morphology of the noun in the numeral-noun construction (singular or plural in the case of English, singular in the case of Turkish) is the same set of tools that accounts for its semantics. This is because Harbour’s number features, which are at the core of the proposal, have both semantic (they are semantically contentful) and morphosyntactic (they are realized morphosyntactically) implications. An explanation that relies on an independent mechanism, such as (semantic) agreement or concord, to explain the morphological make-up of the noun still needs to be complemented by an account of the semantics of the construction. In the proposal above, one and the same set of tools is responsible for both aspects of the construction, which, everything else being equal, is preferable. The same argument applies in the case of zero: there is no need to appeal to agreement, concord or some other morphosyntactic process to explain the zero+noun facts above, as one and the same set of tools accounts for both the semantics and the morphosyntax we observe in this construction.
Contrast this with, e.g., Ionin and Matushansky’s (2006, 2018) account. On that account, numerals have the semantics of modifiers (similarly to our NumeralPs above) and that semantics is such that numerals combine with noun denotations containing atoms only (i.e., singular nouns). Their denotation for a numeral like two is in (61), which makes use of the notions of partition (62) and cover (63) (see Ionin and Matushansky 2018, pp. 13, 78, as well as Higginbotham 1981, p. 110; Gillon 1984; Verkuyl and van der Does 1991; Schwarzschild 1994):
-
(61)
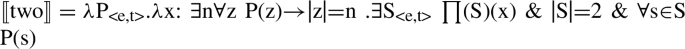
-
(62)
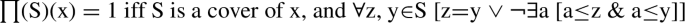
-
(63)

Minus the presupposition, the numeral two takes a set P of individuals as its argument and returns a set of individuals x that complies with the following conditions: there is a set S of non-overlapping individuals such that ⊔S = x, the cardinality of S is 2, and P holds of all members of S. The constraint against overlapping individuals in (62) is crucial to avoid counting an element more than once. Applying two to a set of atoms returns a set of twosomes, each of which is composed of exactly two non-overlapping atoms. The argument of a numeral in this approach is presupposed not to contain plural individuals: if it did, we would not be able to guarantee that, e.g., two boys contains strictly boy twosomes—we’d leave open the possibility of finding a plural boy individual x in its denotation composed of, say, four atoms organized into two non-overlapping plural individuals y and z such that the sum of y and z is x. The presupposition in (61) ensures that P does not contain plural individuals, since different plural individuals will have different cardinality—in a set of atoms, however, all of its members have the same cardinality of 1. Ionin and Matushansky consider the existence of languages like Turkish, where the noun that accompanies a numeral is always morphologically and semantically singular, as direct evidence for their approach. The existence of languages like English prompts them to appeal to semantic agreement: s- marking on boys in three boys reflects, in their analysis, the fact that three boys is a set of plural individuals, not that boys is.
In the approach defended here, there is no need to appeal to a separate mechanism of semantic agreement in languages like English. Nouns in the numeral-noun construction appear marked the way they do across languages because of the number features assumed to operate in NumberP and their combination with a universal numeral semantics (recall (14) for English-like languages, and (18) for Turkish-like languages). Crucially, these assumptions both explain the marking on the noun and generate the correct semantics for numeral-noun phrases. All other things being equal, this should be the preferred approach, as it is much more economical.
Are all other things equal? Some might argue that they are not. After all, as Ionin and Matushansky (2018, pp. 94-109) argue, the numeral-noun construction displays surprising properties in some languages, and sometimes patterns differently from constructions where nouns appear without numerals. Examples they discuss include Miya (where plural marking inside the numeral-noun construction is argued to follow the same pattern as plural agreement on verbs, and is different from plural marking on nouns without numerals; cf. Schuh 1989, 1998), or languages where the number marking on the noun depends on the numeral it combines with (e.g., in Standard Arabic, simplex cardinals greater than 10 use singular marking on the noun, whereas lower numerals combine with plural nouns; see Zabbal 2005). Thus, one might argue that the numeral-noun construction requires special treatment anyway, and, from this perspective, appealing to a special, separate mechanism might seem reasonable. However, I take it that the null hypothesis is that the shape of nouns in the numeral-noun construction is related in some way to the shape of those nouns in other contexts, especially when it is the same. Martí (2020a,b) and the present paper are attempts at explaining the behavior of nouns in the numeral-noun construction as something that is related to the behavior of nouns more generally, and, as such, are, at least, worth considering. It is appealing, as this paper demonstrates, that the properties of zero-phrases can also be understood within the same set of assumptions.Footnote 19
Harbour’s (2014) number features, which are at the core of the explanation proposed here, have ample independent justification in that they help derive the complex set of generalizations that characterize the typology of grammatical number across languages. This typology, known since Greenberg (1966) and discussed in great detail in Corbett (2000), is concerned not just with the number values that are (un)attested cross-linguistically (singular and plural, but also dual, trial, paucal, minimal, augmented, greater plural, global plural, and others), but with the kinds of number systems that are (un)attested in the languages of the world. For example, one cross-linguistically robust generalization is that there is no language that has the dual number value without also having the plural value. Another one is that there is no language that has the trial number value without also having the dual. Thus (see Harbour 2014: p. 186):
-
(64)

Harbour’s proposal accounts for the generalizations in (64)—that is, for the meaning, expression and combination of grammatical number values—with a remarkably small set of tools, which includes the features and assumptions discussed in Sect. 2, in addition to the feature [±additive] and the assumption that one and the same number feature may repeat (neither of which is discussed here because the number values they help to account for, such as paucal or trial, are not expressed in English or Turkish). Thus, the account proposed above allows us to see the numeral-noun construction, including the zero facts, as part of a much larger explanation, that of the semantics and morphosyntax of grammatical number more generally. The advantage of this is not just that the tools used to account for that construction are justified independently, it’s that we now have a series of expectations about, e.g., possible and impossible morphological marking on the noun in the construction as a factor of the grammatical number of the language in question. For singular-plural languages, the facts may be as in (1) or as in (2), with no other combinations allowed. Specific and testable predictions are made for languages with more number values, the details of which are left for future research. I know of no other account of the numeral-noun construction that has the power to make cross-linguistic predictions in this fashion.Footnote 20
Moving on now to the issue of empirical coverage, let’s begin by noting the argument in Martí (2020c) that a Sauerland-style view of plurality is incompatible with Harbour (2014)—note that her argument is concerned both with Sauerland’s (2003) specific proposal and, more generally, with any proposal that postulates an unambiguous approach to the lexical semantics of the plural. The problem is how to account for languages where plurals can be interpreted either inclusively or exclusively, English being one of them, as exemplified in (65) (exclusive interpretation: Lina ate more than one tomato) and (66) (inclusive interpretation: Lina didn’t eat a single tomato):
-
(65)
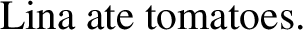
-
(66)
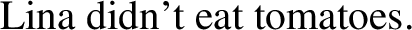
In a Sauerland-style approach, only the inclusive interpretation is lexically/grammatically specified; the exclusive interpretation is derived, e.g., as an implicature.
Martí’s argument is as follows: if a language with inclusive plurals is analyzed as not making use of [−atomic], as one would do in a Sauerland-style approach, the prediction Harbour makes is that such a language should have no number values that are built on [−atomic], such as dual or paucal. This prediction is wrong, since languages with inclusive plurals and duals (or paucals) exist. Therefore, if one is to keep both Harbour’s account of number, which is the only one currently capable of accounting for the crosslinguistic typology of number, and an account of inclusive plurality, one must choose, instead, an ambiguity account of plurality (see Martí 2020c for more on what such an account could look like, following Farkas and de Swart 2010).
As Martí shows, it won’t do to keep [−atomic] but make it semantically empty (or the identity function) across the board, thus allowing plurals to be unambiguously inclusive semantically: it is the exclusive semantics that Harbour gives to [−atomic] that is crucial in deriving other number values. For example, consider the derivation of the dual given the semantics of the features assumed earlier. A singular-dual-plural system uses both [±atomic] and [±minimal], as follows:
-
(67)
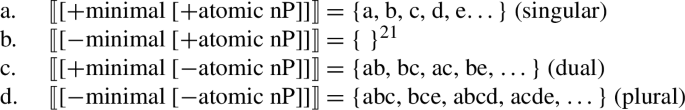
If [−atomic] had no semantic contribution, the dual wouldn’t be assigned the correct semantics—we’d have, as its denotation, not the set of plural individuals of numerosity 2 in (67c), but the set {⊥, a, b, c, d, e…}, which is incorrect as the denotation of the dual. This entails a significant loss of empirical coverage. One might argue against the use of [±atomic] to derive at least some of these systems, using [±minimal] instead, and repeating it to derive number systems with duals, but this will not solve the problem. A singular-dual-plural system would be derived as follows:
-
(68)
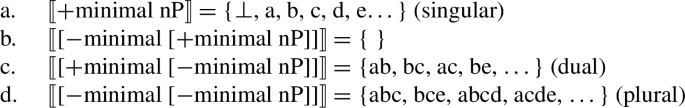
(68) doesn’t help either.Footnote 21 Turkish is, in our Harbour-inspired approach, a [±minimal] language, but it also has inclusive plurals (recall footnote 6). To account for that while adopting the unambiguous treatment of inclusive plurals that takes the relevant feature to be semantically null, we’d have to say that [−minimal] is also semantically empty/the identity function. The earlier problem of empirical inadequacy resurfaces: the correct semantics of the dual can no longer be generated. The same reasoning applies to other number values that are based on [−atomic] in Harbour’s theory, such as paucals. We could give up Harbour altogether, of course, but then we lose the account of the typology of number in (64). The problem is, thus, not which feature is responsible for plurality, but the fact that certain features are used in Harbour’s system, and to great effect, as parts of complex, compositionally-derived, number values, and changing the semantics of those features entails losing the account of those values and/or the typological generalizations from (64) they are involved in.Footnote 22,Footnote 23
Thus, abandoning the non-ambiguity, Sauerland-style view of plurality, Martí shows that it is possible to account for the number marking and semantics of the numeral-noun construction in English and for its exclusive and inclusive plurals by assuming that plural forms are ambiguous between an exclusive, [−atomic]-based semantics, and an inclusive semantics. In this approach, inclusive plurals in English arise from the ability to not generate NumberP in numeral-less noun phrases. That is, English has both inclusive and exclusive plurals because its (numeral-less) plural forms spell out either (69) or (3) (with [−atomic], as in (14b)):
-
(69)

The choice between the two is regulated e.g., by the Strongest Meaning Hypothesis (Farkas and de Swart 2010).
6 Conclusion
In this paper I have added zero to Martí (2020a,b) account of the numeral-noun construction. Two of the main language types that Martí’s framework accounts for are exemplified by English and Turkish, and it is those two types of patterns with zero that the analysis proposed here has been shown to account for. Importantly, the proposal makes use of the same technology (number features, a certain structural relationship between them and numerals) that Martí uses to account for the numeral-noun construction more generally, assumptions that are combined here with Bylinina and Nouwen’s analysis of the semantics of zero. Together with Martí, this paper demonstrates that the theory of grammatical number in Harbour (2014), from which the number features used here are taken, can be extended quite straightforwardly to cover a new empirical domain in a range of languages. That a small number of assumptions can account for such a large array of data, i.e., the numeral-noun construction plus the cross-linguistic typology of grammatical number that the features were originally designed to capture, should be seen as one of its major advantages.
In a nutshell, the noun that accompanies zero in English shows the same number marking (plural) as the noun that combines with numerals greater than 1 because ⊥ is not an atom (like the non-atoms of English plural forms, absent in singular forms). The noun shows the same number marking (singular) as the noun that combines with all numerals in Turkish because ⊥ does not have proper parts of numerosity greater than 0 (like the members of the denotation of Turkish singular forms, absent in plural forms). Crucial to this explanation is the idea that, while English number is sensitive to atomicity, Turkish number is sensitive to minimality, an idea inherited from Scontras’s account. Once these ideas are properly implemented, the number marking on the noun that accompanies zero (and other numerals) follows without further stipulation.
The analysis presented here does not appeal to any agreement mechanism to explain the shape of the noun in the construction, and derives that shape (e.g., marked with -s in English, or not marked with -lAr in Turkish) from the interplay of Harbour’s semantically-contentful number features and a fairly standard syntax and semantics for numerals. The analysis also demonstrates that the Sauerland-style view of plurality is not a necessary ingredient in the account of the full pattern in (1)-(2), and thus, that an account of the numeral-noun construction need not rely on certain views on plurality.
Notes
I focus on cardinals in this discussion and put aside decimals and ordinals. It does not seem difficult to extend the account proposed below to at least decimals, as suggested by Amy Rose Deal (p.c.), but I leave that task for a future occasion.
Borer (2005, pp. 114-118) proposes an explanation of these facts within the exoskeletal approach she defends there. Among other differences, on her account plural morphology is not semantically plural. One can view my proposal here as an alternative to hers. For more discussion on the relationship between morphological and semantic plurality, see Sect. 5.
I assume that these phrases are DPs, though nothing in the account here follows from this choice of label. Material irrelevant for our purposes is possible between DP and NumberP. nP is a nominal sub-constituent that is taken to contain a root and a nominalizer, n0, which converts that root into a noun and gives rise to the denotation in (5).
Anomalous combinations are marked with the symbol ‘✗’ here and throughout.
Turkish has inclusive plurals (see Renans et al. 2020; though see Görgülü 2012 for a different view). Following Martí (2020c), this can be accounted for by allowing NumberP not to be generated in Turkish, and assuming that this configuration is spelled out with the plural form. See Sect. 5 for more.
Bylinina and Nouwen do not decompose nouns into the more complex structures I have assumed here. (26) corresponds to their assumptions about the meaning of NPs.
Just as in other accounts, predicates other than nouns, such as in the text or pass the test, need to be given the appropriate semantics if they are to compose appropriately with arguments whose denotation contains both atomic and non-atomic individuals. In Link (1983) and many others, the *-operator is in charge of this job. Bylinina and Nouwen replace that with an operator, which we can call the x-operator, that takes ⊥ into account. Harbour and Martí are different, since for them the basic denotation of nP already includes atomic and non-atomic individuals. The *-operator (or the x-operator, if we take into account Bylinina and Nouwen’s arguments) is still needed in these accounts for the treatment of predicates that are not nouns (hence, in_the_texth and in_the_textbn in (28)/(29)). Depending on what one assumes to be the internal semantics of nPs, one might still postulate an *-operator (or x-operator) for nouns.
As a reviewer correctly points out, this makes 〚[−atomic] [nP ]〛 pick out a discontinuous area of the lattice (since 〚−atomic〛({⊥, a, b, c, ab, ac, bc, abc}) = {⊥, ab, bc, ac, abc}) and, thus, non-convex (similarly to Link 1983; Landman 2011). This very interesting observation takes us back to Harbour’s (2014, pp. 210–212) discussion of convex meanings. Harbour’s Convexity condition (his (32)), that all basic meanings be convex, might seem at odds with the proposal in the text, but a way out of this problem is to view the condition as applying only to the feature that Harbour is concerned with here, [±additive]. The issue, however, deserves more careful consideration, something that I leave for future research.
Thanks to Greg Scontras for discussion of this point. The question arises as to what consequences this change in the semantics of [±minimal] has in Harbour’s system. I demonstrate below that number systems that use just this feature on nouns can be accounted for as before. Since ⊥ is excluded by [−minimal], any complex number value based on [−minimal] is derived without interference by ⊥, as before. Complex number values where [+minimal] is not the first feature that operates on NP will also work as before. There might be an issue with number values of pronouns based on [+minimal] or [−atomic] (cf. (38)), where ⊥ will be present, since it might be asked whether the E-operator applies with pronouns, but I do not explore this issue here.
Thanks to Sarah Felber, Bruce Morén-Duolljá and Barbara Partee for discussion of these observations.
(54) conveys the idea that the speaker is not completely certain that Sue drank vodka, but both examples are compatible with a state of affairs in which Sue drank it, in addition to the three beers.
Thanks to Rick Nouwen (p.c.) for the examples and the observations just presented.
Chow and Morzycki argue that Cantonese lacks ⊥ in its ontology, which of course has the consequence of preventing ling4 from behaving like a numeral (if Bylinina and Nouwen are right).
In Western Armenian (Bale and Khanjian 2014, p. 5, ft. 4), Hungarian (Csirmaz and Szabolcsi 2012) or Slovenian (Lanko Marušič p.c.), zero never combines with nouns:
-
(i)
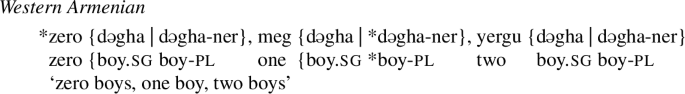
Scontras (2014) and Martí (2020a) account for the zero-less pattern in Western Armenian as well; Martí argues that Western Armenian has access to both the English [±atomic] number system and the Turkish [±minimal] number system. Bylinina and Nouwen suggest that this language does not license zero syntactically in the numeral-noun construction. Another possibility is to assume that, while the language does have the numeral zero (which, as before, denotes 0 and can be used to talk about mathematical calculations), the semantics of its noun phrases never contains ⊥. Yet another possibility is that the ontology of Western Armenian just doesn’t have ⊥ at all, like Chow and Morzycki (2021) argue for Cantonese. I leave further investigation of these options for future research.
-
(i)
The account of the full pattern with zero in (1)-(2) works in Scontras’s (2014) original account as well, which, recall, is based on a Sauerland-style view of plurality. Scontras’s account does not use Harbour’s features but is compatible with Bylinina and Nouwen’s analysis.
See Krifka (1989, 1995), Ivlieva (2013), Lasersohn (1995, 2011), Mayr (2015), Sauerland et al. (2005), Spector (2007), Yatsushiro et al. (2017) and Zweig (2009). Farkas and de Swart (2010) and Grimm (2013) propose an ambiguity account that is compatible with the proposal in Martí (2020a,b) (see Martí 2020c for more on this). Kiparsky and Tonhauser (2012) provide a useful overview of the main issues.
As a reviewer points out, Ionin and Matushansky’s proposal is in principle compatible with Harbour’s account if one assumes that the numeral-noun construction is a special case. Hence, adopting their approach need not entail not capturing the cross-linguistic typology of grammatical number that he achieves. This is true, but my earlier criticism, that Ionin and Matushansky’s hypothesis regarding the number marking on the noun in the numeral-noun construction is not the null hypothesis, still stands.
Harbour (2014, p. 205) proposes a constraint on feature repetition such that combinations like [+F, +F] and [−F, −F] are ruled out, having to do with the need to prevent the system from generating unattested number values such as quadral, quintal, and so on. (68d) would be problematic for this constraint, but this is a smaller problem than the one discussed in the text.
Likewise, Martí (2020c, pp. 55–57) shows that postulating that a language may use [−atomic] in the derivation of the dual (or paucal), but not in the derivation of the plural, is problematic as well.
The interpretation of plurals in exactly-phrases (e.g., exactly one student brought wine bottles to the party) is a well-known problem for ambiguity accounts (see Spector 2007; Farkas and de Swart 2010, p. 34, ft. 25) that the current account inherits. Non-ambiguity accounts deal with such problems more easily. However, non-ambiguity accounts are not compatible with Harbour (2014), as argued above, so giving it up to account for the exactly facts involves giving up the account of the cross-linguistic typology of number that Harbour manages to achieve. Both accounts have their drawbacks. What I think is really interesting here is that a crucial consideration in the assessment of the different options is the cross-linguistic typology of number.
References
Alexiadou, Artemis. 2019. Morphological and semantic markedness revisited: The realization of plurality across languages. Zeitschrift für Sprachwissenschaft 38: 123–154.
Bale, Alan, Michaël Gagnon, and Hrayr Khanjian. 2011. Cross-linguistic representations of numerals and number marking. In Proceedings of Semantics and Linguistic Theory Conference, Vol. 20, 582–598.
Bale, Alan, and Hrayr Khanjian. 2014. Syntactic complexity and competition: The singular-plural distinction in Western Armenian. Linguistic Inquiry 45(1): 1–26. https://doi.org/10.1162/LING_a_00147.
Borer, Hagit. 2005. Structuring sense: In name only. Oxford: Oxford University Press.
Bylinina, Lisa, and Rick Nouwen. 2018. On zero and semantic plurality. Glossa: A Journal of General Linguistics 3(1): 98. https://doi.org/10.5334/gjgl.441.
Chen, Sherry Yong. 2018. Zero degrees: Numerosity, intensification, and negative polarity. In Proceedings of the Chicago Linguistic Society 54, eds. Eszter Ronai, Laura Stigliano, and Yenan Sun, 53–69.
Chierchia, Gennaro. 2021. On being trivial: Grammar vs. logic. In The semantic conception of logic: Essays on consequence, invariance and meaning, eds. Gil Sagi and Jack Woods, 227–248. Cambridge: Cambridge University Press. https://doi.org/10.1017/9781108524919.012.
Chow, Hary, and Marcin Morzycki. 2021. Zero, null individuals, and nominal semantics in Cantonese. Poster presented at Semantics and Linguistic Theory 31. https://osf.io/xc2vr.
Csirmaz, Aniko, and Anna Szabolcsi. 2012. Quantification in Hungarian. In Handbook of quantifiers in natural language, eds. Edward Keenan and Denis Paperno, 399–465. Dordrecht: Springer Netherlands.
Corbett, Greville. 2000. Number. Cambridge: Cambridge University Press.
Davey, B. A., and H. A. Priestley. 2002. Introduction to lattices and order. Cambridge: Cambridge University Press.
De Clercq, Karen. 2011. Squat, zero and no/nothing: Syntactic negation vs. semantic negation. Linguistics in the Netherlands 28: 14–24.
del Pinal, Guillermo. 2019. The logicality of language: A new take on triviality, “ungrammaticality”, and logical form. Noûs 53: 785–818.
Farkas, Donka, and Henriëtte de Swart. 2010. The semantics and pragmatics of plurals. Semantics and Pragmatics 3: 1–54.
Gajewski, Jon. 2002. On analyticity in natural language. University of Connecticut. Unpublished manuscript.
Gajewski, Jon. 2011. Licensing strong NPIs. Natural Language Semantics 19: 109–148.
Geurts, Bart, and Rick Nouwen. 2007. At least et al.: The semantics of scalar modifiers. Language 83(3): 533–559.
Gillon, Brendan. 1984. The logical form of quantification and plurality in natural language. PhD thesis, MIT.
Görgülü, Emrah. 2012. Semantics of nouns and the specification of number in Turkish. PhD thesis, Simon Fraser University.
Greenberg, Joseph. 1966. Language universals, with special reference to feature hierarchies. Vol. 59 of Janua Linguarum. Mouton: The Hague.
Grimm, Scott. 2013. Plurality is distinct from number-neutrality. In Proceedings of NELS 41, eds. Yelena Fainleib, Nicholas LaCara, and Yangsook Park. Vol. 2, 247–258. Amherst: GLSA.
Hackl, Martin. 2001. Comparative quantifiers. PhD thesis, MIT.
Harbour, Daniel. 2011. Descriptive and explanatory markedness. Morphology 21: 223–245.
Harbour, Daniel. 2014. Paucity, abundance and the theory of number. Language 90: 158–229.
Higginbotham, James. 1981. Reciprocal interpretations. Journal of Linguistic Research 1: 97–117.
Ionin, Tania, and Ora Matushansky. 2006. The composition of complex cardinals. Journal of Semantics 23: 315–360.
Ionin, Tania, and Ora Matushansky. 2018. Cardinals. The syntax and semantics of cardinal-containing expressions. Cambridge: MIT Press.
Ivlieva, Natalia. 2013. Scalar implicatures and the grammar of plurality and disjunction. PhD thesis, MIT.
Kiparsky, Paul, and Judith Tonhauser. 2012. Semantics of inflection. In Handbook of semantics, eds. Claudia Maienborn, Klaus von Heusinger, and Paul Portner, 2070–2097. Berlin: de Gruyter.
Krifka, Manfred. 1989. Nominal reference, temporal constitution and quantification in event semantics. In Semantics and contextual expression, eds. Renate Bartsch, Johan van Benthem, and Peter van Emde Boas, 75–116. Dordrecht: de Gruyter.
Krifka, Manfred. 1995. Common nouns: A contrastive analysis of Chinese and English. In The generic book, eds. Greg Carlson and Jeffrey Pelletier, 398–411. Chicago: Chicago University Press.
Landman, Fred. 2011. Boolean pragmatics. In This is not a festschrift, festpage for Martin Stokhof, eds. J. van der Does and C. Dulith Novaes.
Lasersohn, Peter. 1995. Plurality, conjunction, and events. Vol. 55 of Studies in Linguistics and Philosophy. Dordrecht: Springer.
Lasersohn, Peter. 2011. Mass nouns and plurals. In Semantics: An international handbook of natural language meaning, eds. Klaus von Heusinger, Claudia Maienborn, and Paul Portner. Vol. 2, 1131–1153. Berlin: de Gruyter.
Link, Godehard. 1983. The logical analysis of plural and mass terms: A lattice-theoretical approach. In Meaning, use and interpretation of language, eds. Rainer Bäuerle, Christoph Schwarze, and Arnim von Stechow, 302–323. Berlin: de Gruyter.
Martí, Luisa. 2020a. Numerals and the theory of number. Semantics and Pragmatics 13: Article 3. https://doi.org/10.3765/sp.13.3.
Martí, Luisa. 2020b. Dual number and the typology of the numeral-noun construction. Catalan Journal of Linguistics 19: 159–198. https://doi.org/10.5565/rev/catjl.323.
Martí, Luisa. 2020c. Inclusive plurals and the theory of number. Linguistic Inquiry 51(1): 37–74.
Mayr, Clemens. 2015. Plural definite NPs presuppose multiplicity via embedded exhaustification. In Proceedings of the 25th Semantics and Linguistic Theory Conference, eds. Sarah D’Antonio, Mary Moroney, and Carol Rose Little, 204–224. https://doi.org/10.3765/salt.v25i0.3059.
Nouwen, Rick. 2010. Two kinds of modified numerals. Semantics and Pragmatics 3(3). https://doi.org/10.3765/sp.3.3.
Renans, Agata, Yağmur Sağ, F. Nihan Ketrez, Lyn Tieu, George Tsoulas, Hana de Vries, Raffaella Folli, and Jacopo Romoli. 2020. Plurality and cross-linguistic variation: An experimental investigation of the Turkish plural. Natural Language Semantics 28: 307–342.
Sauerland, Uli. 2003. A new semantics for number. In Proceedings of the 13th Semantics and Linguistic Theory Conference, eds. Rob Young and Yuping Zhou, 258–275. Ithaca: Cornell University CLC-Publications.
Sauerland, Uli, Jan Anderssen, and Kazuko Yatsushiro. 2005. The plural is semantically unmarked. In Linguistic evidence, eds. Stefan Kepser and Marga Reis, 409–430. Berlin: de Gruyter.
Schuh, Russell. 1989. Number and gender in Miya. In Current progress in Chadic linguistics: Proceedings of the International Symposium on Chadic Linguistics, ed. Zygmunt Frajzyngier, 171–181. Amsterdam: John Benjamins.
Schuh, Russell. 1998. A grammar of Miya. Los Angeles: University of California Press.
Schwarzschild, Roger. 1994. Plurals, presuppositions, and the sources of distributivity. Natural Language Semantics 2: 201–248.
Scontras, Greg. 2014. The semantics of measurement. PhD thesis, Harvard University.
Spector, Benjamin. 2007. Aspects of the pragmatics of plural morphology: On higher-order implicatures. In Presuppositions and implicatures compositional semantics, eds. Uli Sauerland and Penka Stateva, 243–281. Houndmills: Palgrave-Macmillan
Verkuyl, Henk J., and Jaap van der Does. 1991. The semantics of plural noun phrases. In Quantifiers, logic, and language, eds. Jaap van der Does and Jan van Eijck, 337–374. Stanford: CSLI.
Yatsushiro, Kazuko, Uli Sauerland, and Artemis Alexiadou. 2017. The unmarkedness of plural: Crosslinguistic data. In BUCLD 41: Proceedings of the 41st annual Boston University Conference on Language Development, eds. Maria LaMendola and Jennifer Scott, 753–765. Somerville: Cascadilla.
Zabbal, Youri. 2005. The syntax of numeral expressions. Unpublished manuscript, University of Massachusetts at Amherst.
Zeijlstra, Hedde. 2007. Zero licensers. Snippets 16: 21–22.
Zweig, Eytan. 2009. Number-neutral bare plurals and the multiplicity implicature. Linguistics and Philosophy 32: 353–407.
Acknowledgements
Many thanks to Klaus Abels, Norman Clarke, Amy Rose Deal, Sarah Felber, Nicola Kent, Nathan Klinedinst, Bruce Morén-Duolljá, Rick Nouwen, Barbara Partee, Greg Scontras, Nilüfer Şener, Yasu Sudo and Eytan Zweig for discussion and data, and to several anonymous reviewers, for their very helpful comments and questions, which allowed me to improve the manuscript substantially. All errors are, of course, mine.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martí, L. Zero N: Number features and ⊥. Nat Lang Semantics 30, 215–237 (2022). https://doi.org/10.1007/s11050-022-09193-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11050-022-09193-7