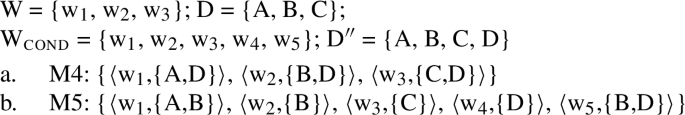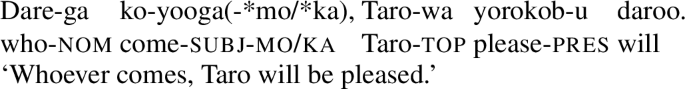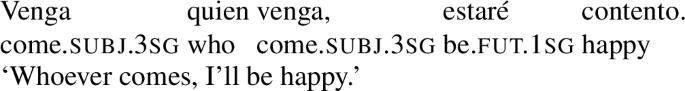Abstract
In this paper, we aim to account for the distribution and interpretation of a novel class of free choice items in Romanian, which we refer to as additive free choice items (ADD-FCIs). We show that the internal composition of ADD-FCIs, as well as their distribution, differs from that attested for other free choice paradigms discussed in the literature. Morphologically, ADD-FCIs are a more complex variant of regular universal FCIs, by virtue of an additional morpheme. This morpheme plays an additive role when it functions as a stand-alone particle, and we propose that its role is similarly additive when it functions as an infix in ADD-FCIs. Couched in an exhaustification framework, we put forward a novel compositional account that can derive the interpretation of these ADD-FCIs. As for their distribution, these elements are only found in the presence of the conditional mood, as well as unconditional structures. We show how our analysis, coupled with the Viability Constraint used to explain the distribution of regular FCIs, can also account for their restricted distribution. In doing so, we further show how the pattern we investigate opens new perspectives regarding the licensing of free choice items in unconditionals.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Data of interest
In many languages free choice items (FCIs), that is, items typically licensed in modal contexts such as (1a) with a possibility modal, can also occur in dislocated clauses known as unconditionals, illustrated in (1b). This is illustrated below with the Hungarian item akárki ‘anyone’ (examples due to Szabolcsi 2019, p. 321):
-
(1)

In this paper, we aim to better understand the connection between the two kinds of contexts in (1) by investigating a novel class of free choice items in Romanian, namely the bolded elements in (2), which we refer to as additive free choice items (ADD-FCIs) for reasons which will become clear shortly.
-
(2)

As first brought up in Fălăuş and Nicolae (2019), ADD-FCIs differ from other free choice paradigms studied to date in two respects: (i) they have a more complex internal composition and (ii) they have a more restricted distribution. We argue that the two properties are connected.
Morphologically, ADD-FCIs have the internal composition in (i), which is a more complex variant of the regular universal free choice items in Romanian, whose composition is given in (ii):
-
(i)
ADD-FCIs: the disjunction ori + the additive/scalar particle şi + a wh-word.
-
(ii)
FCIs: the disjunction ori + a wh-word.
Before we discuss the properties of ADD-FCIs, let us take a closer look at each of their components. Ori is a disjunctive particle that can occur either on its own or be reduplicated to express a disjunctive utterance, as shown in (3); it can disjoin any syntactic constituents, including questions (examples omitted).
-
(3)

As shown in (ii) above, the disjunctive element ori can productively combine on its own with a wh-word, giving rise to universal free choice items (FCIs) like oricine = disj+who ‘anyone’ or orice = disj+what ‘any(thing)’ (e.g., Farkas 2013; Caponigro and Fălăuş 2018).
-
(4)

Note that in Romanian, bare wh-phrases in non-interrogative contexts cannot act as quantifiers, i.e., Romanian doesn’t allow sentences like *Poate veni cine, lit. ‘can come who’ (see Caponigro and Fălăuş 2018 for discussion). A morphologically richer paradigm has to be used instead, e.g., Poate veni oricine ‘Anyone can come’, with the wh-based FCI oricine ‘anyone, whoever’ in (4), or Poate veni cineva ‘Someone can come’, with the wh-based -va existential series such as cineva ‘someone’ (see, e.g., Farkas 2013).
The second element entering the composition of ADD-FCIs is the particle şi. This particle can function as a conjunctive element (which can conjoin any syntactic constituents and can also be reduplicated) as in (5a), but also as an additive particle as in (5b) and as a scalar particle as in (5c).Footnote 1 Anticipating our analysis, we gloss this element as add throughout.
-
(5)

Unlike ori, the particle şi cannot, on its own, morphologically combine with a wh-word (*şi-cine). The particle şi can combine with a wh-word only as long as the disjunctive particle is also present (disj+add+wh). This pattern is fully productive in Romanian—all FCIs double as ADD-FCIs, as shown by the paradigms given in Table 1.
Turning now to their distribution, ADD-FCIs and universal FCIs partially overlap in their distribution, as illustrated by their acceptability in unconditional structures, as shown in (6):
-
(6)

Meaning-wise, the difference is that ADD-FCIs have an emphatic effect, conveying that even extreme or unlikely cases should be considered. For instance, the use of the ADD-FCI in (6a) conveys that even if the queen of England were to call, I still wouldn’t be available.
In addition to this meaning difference, there are also distributional differences. First, unlike regular FCIs, ADD-FCIs are ruled out from typical free choice environments, such as (7a) with a possibility modal verb. Second, even in unconditional constructions, ADD-FCIs require conditional mood marking, as attested by the contrast between their acceptability in (6) and their unacceptability in an unconditional with the indicative future in (7b), where the regular FCI is licensed:Footnote 2
-
(7)

Finally, let us note that for most of our informants the conditional mood on its own is not sufficient to license ADD-FCIs; these speakers find (8) unacceptable, an otherwise ideal licensing environment for a regular FCI.
-
(8)
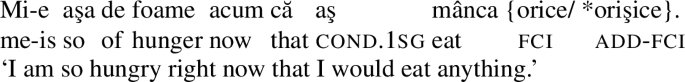
Taking stock, ADD-FCIs contribute an emphatic component to the overall meaning and have two puzzling distributional properties: (i) they are restricted to unconditionals, and (ii) they can only occur in the presence of the conditional mood. In this paper, we offer a compositional account of ADD-FCIs and argue that their restricted distribution and interpretation result from a requirement introduced by the element that sets them apart from regular FCIs, namely the particle şi.
The paper is organized as follows: in Sect. 2, we situate the pattern under investigation with respect to other free choice paradigms discussed in the literature. In Sect. 3, we adopt an alternative-based theory of FCIs and show how their universal meaning can be derived within this framework, followed by a discussion of their licensing in modal environments. In Sect. 4, we focus on the licensing of FCIs in unconditionals. Sect. 5 offers a compositional account for ADD-FCIs, which derives their emphatic meaning and the conditional mood requirement. Finally, Sect. 6 concludes with a number of open questions for future research.
2 The relevance of ADD-FCIs
The properties of ADD-FCIs in Romanian are, to our knowledge, unattested elsewhere in the realm of free choice or wh-based elements. We show that they can further our understanding of the meaning contribution of various kinds of particles across polarity-sensitive paradigms, as well as that of the relation between unconditionals and typical free choice environments. To see the relevance of ADD-FCIs more clearly, it is useful to look briefly at the use of particles in the internal composition of FCIs attested cross-linguistically, as well as the distribution of FCIs in unconditionals discussed in the literature. This helps flesh out the issues raised by the ADD-FCI paradigm investigated in this paper.
2.1 Particles and free choice paradigms
It is by now well-documented that quantificational and polarity-sensitive paradigms cross-linguistically include various connectives, as well as additive and scalar particles (e.g., Haspelmath 1997; Lahiri 1998; Chierchia 2013; Szabolcsi et al. 2014; Szabolcsi 2018; Mitrović 2021). Their frequent use in similar paradigms across typologically unrelated languages has led to compositional analyses which aim to provide a unified semantics for these particles in their various roles. As far as FCIs (some of which double as negative polarity items) are concerned, they fall under two main morphological patterns.Footnote 3 One group is represented by languages with FCIs where a disjunctive particle combines with an indefinite or a wh-word, a pattern we have already illustrated with the Romanian regular FCIs in Table 1. Haspelmath (1997, p. 166) mentions a few other languages where FCIs include a wh-word and an element translatable as ‘or’: Korean, Hungarian, Russian, Basque, Latvian, Ossetic, Hausa, and West Greenlandic. The other group is represented by FCIs that include an indefinite or a wh-word plus a conjunctive or a focus-sensitive particle (additive ‘also, too’ or scalar ‘even’). Well-known examples include Hindi ek bhii lit. ‘also/even+one’ or Malayalam aarum lit. ‘and/also/even+who’ (see, e.g., Haspelmath 1997; Lahiri 1998; Jayaseelan 2001; Slade 2011; Szabolcsi 2018 for discussion and further examples).
Some of the existing analyses of these free choice patterns derive their meaning compositionally and explain the meaning contribution of each particle (see, e.g., Caponigro and Fălăuş 2018 for Romanian FCIs involving a wh-word and a disjunctive particle). A common feature of these analyses is that the free choice behavior is ultimately attributed to the disjunctive particle, although the exact implementation of this idea varies. The pattern we discuss in this paper is more complex and involves a previously unobserved combination of particles, with both a disjunctive and an additive particle. Consequently, none of the current accounts of the semantic contribution of particles across polarity-sensitive paradigms applies straightforwardly, especially since there is no fully compositional account that we know of which explains the role of the conjunctive/focus-sensitive particle in examples such as those mentioned above. If both the disjunctive and the additive particle can trigger free choice behavior, what happens when they combine? The challenge in the case of ADD-FCIs is thus twofold: on the one hand, we need to understand how the different elements combine and end up affecting the restricted distribution of ADD-FCIs; on the other hand, we want to determine how the meaning of the disjunctive and the additive particle at the word-internal level compares with their meaning elsewhere in the language.
Note that it is not uncommon to find free choice and polarity-sensitive paradigms whose morphological makeup includes particle combinations, with one of the particles being an additive element. In Hungarian for example, the additive particle is can optionally participate in the composition of various negative polarity items and FCIs, i.e., akárki (is) lit. ‘or-who too’, bárki (is) lit. ‘or-who too’, valaki (is) lit. ‘some-who too’ (Halm 2016; Szabolcsi 2018). German wer auch (immer) lit. ‘who also always’ and Dutch wie (dan) ook lit. ‘who then also’ or wie ook (maar) lit. ‘who also only’ are other cases in point (Haspelmath 1997). The data available in the literature suggests that these paradigms differ from the ADD-FCIs examined in this paper in at least two respects: first, one of the particles is optional and second, one of the particles (or the particle combination) can be separated from the wh-element. To our knowledge, there is no detailed investigation of the distribution of these morphologically complex paradigms or the way their distribution connects with the presence of the additive particle.
The morphological pattern exhibited by ADD-FCIs, with both a disjunctive and an additive particle present at word-level, enriches the current cross-linguistic picture of particles used in free choice paradigms and may shed new light on their role. We show that the analysis of ADD-FCIs can help further our understanding of whether these particles have a uniform meaning contribution across their various uses, as affixes and stand-alone elements.
2.2 Unconditionals and free choice
In Sect. 1, we saw that both FCIs and ADD-FCIs in Romanian are licensed in unconditionals, i.e., sentences like those in (9):
-
(9)
Whoever comes to the party, it will be fun.
Rawlins (2008, 2013) uses the term ‘constituent unconditional’ to describe this type of structure, while the typological literature (e.g., Haspelmath and König 1998) refers to them as ‘universal concessive clauses’.Footnote 4
There seems to be quite a lot of variation in the way unconditionals are realized cross-linguistically (see Haspelmath and König 1998 for an overview of strategies used in the languages of Europe). However, there are a number of recurring morpho-syntactic elements, which turn out to be relevant for our understanding of ADD-FCIs. The first one is the presence of an adjunct wh-clause, with a (bare or modified) wh-word that is typically fronted. The second ingredient that is pervasive in unconditionals across languages is a focus-sensitive particle akin to ‘also’ or ‘even’, e.g., Dutch ook, German auch, Greek ke, Bulgarian i.Footnote 5 Finally, many languages use conditional or subjunctive mood in unconditionals. These elements do not necessarily co-occur, although they might. For instance, in addition to the fronted (bare) wh-word, the Dutch unconditional in (10a) uses the focus-sensitive particle ook (but no special mood), the French one in (10b) uses the subjunctive mood (but no particle), whereas in Greek and Kannada, we see both the particle and the mood markers (11)[a-b].
-
(10)

-
(11)

The Romanian data we investigate in this paper has all these ingredients, although the internal composition of ADD-FCIs (with an additive particle as an infix in a wh-based free choice item) and the conditional mood requirement are, to our knowledge, previously unobserved. We show that each one of these elements ends up contributing to the interpretation and the restricted distribution of ADD-FCIs.
Moving to the interpretation of unconditionals, Rawlins (2008) identifies a number of key semantic properties in his detailed study of English unconditionals. Most notably, they come with an implication that the choice of alternative in the antecedent does not matter, a property referred to as ‘relational indifference’. A related observation is that unconditionals entail their consequent: the sentence in (9), for example, entails that the party will be fun. Finally, unconditionals can have a speaker-ignorance implication, as evidenced by the incompatibility with a namely continuation (a test first used in Dayal 1997 for -ever free relative clauses), as shown in (12).
-
(12)
Whoever comes to the party (# namely Alfonso), it will be fun.
The way these inferences are derived varies in the literature, depending on whether unconditionals are assumed to be akin to questions (Rawlins 2008, 2013; Hirsch 2016; Šimík 2019, 2020) or akin to free relatives (Izvorski 2000; Bhatt and Pancheva 2017). The compositional details differ, but the standard view is that unconditionals are ultimately equivalent to a set of conditionals, where the consequent remains constant across alternatives: the unconditional in (9) for example comes out as true if all conditionals of the form If x comes to the party, it will be fun (where x ranges over relevant individuals) are true.
The work on the modal inferences characterizing unconditionals has led to a recent line of investigation exploring unified analyses of unconditionals and free choice phenomena across languages (Balusu 2019; Szabolcsi 2019; Gonzalez and Lohiniva 2020). This is empirically supported by the fact that most wh-based indefinites used in unconditionals are also acceptable in typical free choice environments (and sometimes negative polarity contexts as well). In Sect. 1 we already illustrated this for FCIs in Hungarian and Romanian and (13) provides further examples from Italian and French, where the free choice elements qualunque and quoi que ce soit, which can be used in unconditionals, are licensed by a possibility modal.
-
(13)

Interestingly however, the connection between free choice items and unconditionals is not free of restrictions. In particular, it has been observed that free choice any cannot be used, or is at best marginal in unconditionals (Szabolcsi 2019):
-
(14)
-
a.
You may bring anything you like to the potluck.
-
b.
?? Anything you bring to the potluck, the guests will be happy.
-
c.
?? Anyone you invite to the party, it will be fun.
-
a.
This paper brings to light the opposite pattern: Romanian ADD-FCIs are items that are licensed only in unconditionals and are ruled out from typical free choice environments, e.g., modal contexts, generic statements, imperatives. The cross-linguistic picture that needs to be accounted for thus is as in Table 2.
This distribution raises a number of questions: What makes unconditionals such suitable licensing environments for FCIs across languages? What is responsible for the restricted patterns observed for English any and Romanian ADD-FCIs? More generally, can the investigation of free choice items lead to a better understanding of the semantics of unconditionals?Footnote 6
Until recently, free choice items and unconditionals have been studied mostly separately. However, the existence of numerous paradigms across languages occurring in both free choice environments and unconditionals suggests that we need to develop unified analyses. This is the path we pursue as we build our proposal for the restricted distribution of ADD-FCIs. Specifically, we aim to explain the similarities and differences in the interpretation of the following sentences:
-
(15)

The literature on free choice items is vast and complex (see Alonso-Ovalle and Menéndez-Benito 2020 for a recent overview), but to our knowledge, the existing analyses typically do not consider their licensing in unconditionals. The recent proposals in Balusu (2019), Szabolcsi (2019) and Gonzalez and Lohiniva (2020) are notable exceptions in this respect. In what follows, we account for the patterns in (15) by adopting and adapting the analysis in Szabolcsi (2019), which builds on recent alternative-based approaches to free choice and polarity sensitivity (Dayal 2013; Chierchia 2013) to provide a unified treatment for the licensing of the Hungarian akár-paradigm in free choice environments and unconditionals.
3 A compositional account of regular FCIs
In this section, we introduce our assumptions about regular FCIs, providing the ingredients needed for the analysis of ADD-FCIs to be developed in Sect. 5 and staying close to the account in Szabolcsi (2019). We adopt an alternatives-and-exhaustification approach to free choice inferences and focus on two core properties of universal free choice items: (i) the universal-like interpretation (Sect. 3.1) and (ii) the restricted distribution to modal contexts (Sect. 3.2).
3.1 Deriving the universal component
FCIs such as any are known to acquire a universal-like interpretation in most contexts where they are licensed and convey a free choice effect. Accordingly, the modalized statement in (16a) conveys that all (contextually relevant) friends are permitted possibilities (16b), which for a domain of friends that includes Ana, Betty and Carla ends up being equivalent to the conjunctive statement in (16c):
-
(16)
-
a.
Jenny can visit any friend.
-
b.
For every friend x, there is an accessible world where Jenny visits x.
-
c.
Jenny can visit Ana, she can visit Betty and she can visit Carla.
-
a.
To derive this interpretation, we adopt the approach in Fox (2007) to free choice inferences for disjunctions and existential quantifiers (see Meyer 2020 for a more recent overview of the phenomenon). To offer a quick recap, the puzzle posed by free choice inferences is that the use of disjunction with a possibility modal like in (17a) gives rise to a stronger quasi-conjunctive reading, as in (17b). This FC inference cannot be derived by standard semantic or even pragmatic machinery.
-
(17)
-
a.
Jenny can visit Ana or Betty. ◊a ∨ ◊b
-
b.
Jenny can visit Ana and she can visit Betty. ◊a ∧ ◊b
-
a.
Fox (2007) argues that the FC inference can and should be derived in the grammar, on a par with scalar implicatures. Within the grammatical approach to scalar implicatures, as laid out in Chierchia et al. (2012), implicatures arise as the result of a syntactic ambiguity resolution in favor of an LF which contains a covert exhaustivity operator exh (building on work in Groenendijk and Stokhof 1984; Chierchia 2004; Spector 2006; Fox 2007, among others). exh is a two-place operator which takes a proposition as its first argument (‘prejacent’) and a set of alternatives as its second argument. Scalar elements activate alternatives and the grammar integrates these alternatives within the meaning of the utterance by means of this exhaustification operator which is similar to overt only in that it negates all stronger alternatives. There are two important caveats: (i) unlike only, this operator also asserts the truth of its prejacent, and (ii) stronger alternatives are negated but only as long as no contradiction results when their negation is conjoined with the assertion. These two points are encoded in its semantics below where ie(p, Alt(p)) is meant to pick out those alternatives which are innocently excludable, that is, whose negation does not lead to a contradiction when conjoined with the assertion:
-
(18)
〚exh〛(Alt)(p) = pw ∧ ∀q [q∈ie(p, Alt(p))→¬ qw]
where ie(p, Alt(p)) = ∩ {C′⊂Alt(p): C′ is a max subset of Alt(p) s.t.
{¬q : q∈C′} ∪ {p} is consistent}
In the case of a disjunction, the first question to ask is what the relevant alternatives are. In order to derive its scalar implicature, the conjunctive alternative becomes relevant, and the result of applying exh is the strengthened exclusive interpretation that only one of the disjuncts is true.
-
(19)
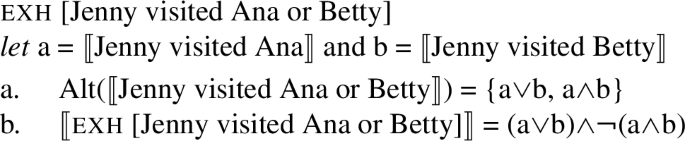
Returning to the FC inference of modalized disjunctive sentences, the relevant alternatives have been argued to be the individual disjuncts (Sauerland 2004; Alonso-Ovalle 2006). Unlike in the case above, however, these alternatives cannot both be negated without giving rise to a contradiction, and neither one is on its own innocently excludable.
Following an insight by Kratzer and Shimoyama (2002) that the strengthened meanings of the individual alternatives are actually relevant, Fox (2007), as well as Alonso-Ovalle (2006) and Chierchia (2006), albeit within a different framework, propose that the relevant alternatives are the enriched, pre-exhaustified alternatives in (20a). These pre-exhaustified alternatives amount to saying that it’s only the case that a is possible, and it’s only the case that b is possible. Taking as a concrete example (17), the alternatives are that Jenny can visit Ana but not Betty and that Jenny can visit Betty but not Ana. Negating these alternatives, in conjunction with the assertion, amounts to the conjunctive FC interpretation that Jenny can visit Ana and she can visit Betty.Footnote 7
-
(20)
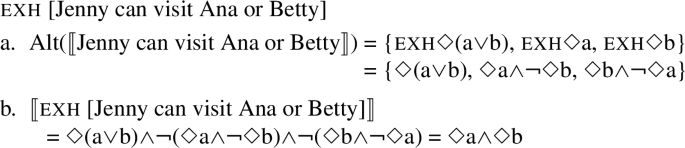
The same strengthening mechanism can be employed to derive the universal inference for existential quantifiers in modalized contexts, an inference that is optional with plain existentials (such as the simple indefinite a in English) and obligatory with FCIs such as any. To illustrate our assumptions about FCIs, let us go through a concrete example. We assume that universal FCIs are, at their base, existential quantifiers following, e.g., Aloni (2007), Chierchia (2013), Dayal (2013) and Szabolcsi (2019) and pace Dayal (2004), Menéndez-Benito (2010) and Aloni (2019) (see Alonso-Ovalle and Menéndez-Benito 2020 for a recent overview on free choice items). In the case of a FCI like any friend, which we take to have the denotation in (21a), the relevant scope configuration is one where the existential quantifier takes scopes above the modal (see Chierchia 2013 for extensive discussion). The interpretation is provided in (21b), which for a domain with three individuals, D = {A, B, C}, amounts to a three-way disjunction, abbreviated as on the last line, where a, b, c stand in for the corresponding propositions.
-
(21)
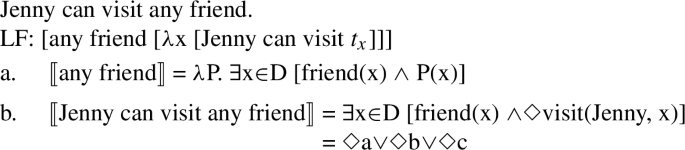
What sets FCIs (and more generally items that are polarity-sensitive) apart from plain existentials is the obligatory activation of alternatives, which, in turn, triggers obligatory exhaustification. The alternatives of existential quantifiers are taken to be sub-domain alternatives: if the existential quantifies over a contextually relevant domain D, the alternatives will be existential propositions where the domain variable is substituted with smaller domains D′, as in (22a). Using the same procedure as above and the pre-exhaustified alternatives in (22b), we derive the strengthened universal interpretation in (22c).
-
(22)
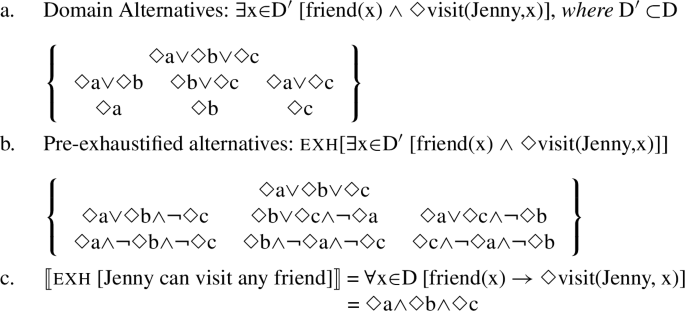
This quick illustration shows how the existential meaning of a FCI gets strengthened to a universal interpretation, using the same ingredients as those responsible for the free choice inferences associated with disjunction.
3.2 Deriving the restricted distribution of FCIs
Let us now turn to the other defining property of FCIs, namely their restricted distribution. Typical environments include possibility modals (as illustrated in the previous section), generic statements and imperatives. Crucially however, they cannot occur in episodic or necessity modal statements, as shown in (23):Footnote 8
-
(23)
-
a.
*Yesterday, Jenny visited any friend.
-
b.
*Jenny must visit any friend.
-
a.
There are different proposals that can account for these distributional restrictions and are compatible with the alternative-based approach to FCIs adopted here. The prevailing intuition in the literature has been that FCIs require the presence of some kind of modal element that leaves room for uncertainty or open-endedness with respect to the individuals that make the sentence true. The key to the licensing of FCIs is to ensure that, on the one hand, there is a modal(izing) operator in the sentence (which is not the case in an episodic environment) and on the other hand, the resulting modal claim is not too strong (which is what happens with a necessity modal). To obtain this result, a number of accounts assume that FCIs are ruled out in cases where the computation of the alternatives they activate would give rise to a contradiction (e.g., Dayal 2009; Menéndez-Benito 2010; Chierchia 2013) or would fail to satisfy a given requirement imposed by FCIs, for example the requirement that the domain widening associated with any lead to strengthening (Kadmon and Landman 1993; Aloni 2007). A critical discussion and detailed comparison of these approaches can be found in Alonso-Ovalle and Menéndez-Benito (2020) (see also Chierchia 2013).
In what follows, we briefly discuss the theory of the licensing of FCIs adopted by Szabolcsi (2019), which she extends to unconditional constructions (to which we turn in Sect. 4). The restricted distribution of FCIs is attributed to the constraint reproduced in (24), a revised version of the Viability Constraint proposed in Dayal (2013), which is itself based on the ‘Fluctuation’ requirement advocated in Dayal (2009).Footnote 9
-
(24)
Viability Constraint (Szabolcsi 2019, p. 328)
∀q∈Alt(p) [◊q ∧ ◊¬q]
[…FCI …] is felicitous if each alternative proposition is true in some world and false in some world.
According to this constraint, each alternative must be true in some but not all worlds. In episodic sentences, namely in the absence of a modal operator, there is only one accessible world, the world of evaluation. Accordingly, Viability cannot be satisfied and the FCI is not licensed. What about modal contexts? Recall from the previous section that the FCI takes scope above the modal (see (21)), meaning that the alternatives are all modalized. After exhaustification (assuming once again a domain with three individuals D = {A,B,C} and the alternatives in (22)), the enriched meaning of the modal statement looks as in (25a) for a sentence with a possibility modal and as in (25b) for a sentence with a necessity modal.
-
(25)
-
a.
∀x∈ D[friendw(x) → ◊visitw(Jenny, x)] ◊a∧◊b∧◊c
-
b.
∀x∈ D[friendw(x) →
 visitw(Jenny, x)]
visitw(Jenny, x)]  a
a b
b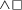 c
c
-
a.
Consider the statement in (25a) first against the models in (26).
-
(26)
W = {w1, w2, w3}; ∀w∈W, friendw = {A, B, C}
-
a.
M1: jenny.visits= {〈w1,{A,C}〉, 〈w2,{A}〉, 〈w3,{A,B,C}〉}
-
b.
M2: jenny.visits= {〈w1,{A,B,C}〉, 〈w2,{A,B,C}〉, 〈w3,{A,B,C}〉}
-
c.
M3: jenny.visits= {〈w1,{A}〉, 〈w2,{B}〉, 〈w3,{C}〉}
-
a.
In a model like M1, (25a) would be true but Viability would not be satisfied since there is an alternative, namely ◊a, for which it does not hold given that A is true in every world in this model, so the second conjunct of the Viability Constraint does not hold for this alternative. Similarly for M2. No such problem arises in M3, however, where the assertion is true and Viability is satisfied since for each alternative there are worlds in which that alternative holds and worlds where it does not. Turning now to a case where the FCI co-occurs with a necessity modal, it is easy to see that none of the three models would work: the assertion is false in M1 and M3, and M2 does not satisfy Viability for the reasons mentioned above. More generally, for a sentence with the enriched interpretation in (25b), there is no model in which the strengthened assertion and Viability can both be satisfied since they are incompatible with each other.
This briefly illustrates how Viability can be used to capture the intuition underlying the restricted distribution of FCIs, namely the fact that they require a plurality of worlds across which alternatives can vary. In addition to overt modal auxiliaries, among the operators that can provide the necessary set of worlds, we also find imperatives, generics, and aspectual and mood markers (see, e.g., Quer 2000, 2001; Giannakidou 2001; Aloni 2007). We do not discuss here further how Viability is satisfied in other environments licensing FCIs, and simply refer the interested reader to Dayal (2013) and Szabolcsi (2019), as well as Chierchia (2013), for a different alternatives-and-exhaustification implementation of a similar licensing constraint.
4 A compositional account of regular FCIs in unconditionals
In the previous section we showed how to derive the universal force of FCIs (via exhaustification with respect to pre-exhaustified alternatives) and how to capture their restricted distribution (via the Viability requirement on the alternatives associated with the FCI). In this section, we build on Szabolcsi (2019) and extend this account to unconditional structures, arguing that the distribution and interpretation of FCIs in such structures can be derived in a parallel manner.
4.1 Spelling out the licensing requirements
Recall the basic intuition behind the interpretation of an unconditional as spelled out by Rawlins (2008) among others: an unconditional amounts to the conjunction of as many conditionals as there are individuals in the domain of the wh-based indefinite (whoever in English, a FCI in Romanian). Specifically, a sentence like (27a) has the same interpretation as the conjunction in (27b):
-
(27)
-
a.
Whoever comes, it will be nice.
-
b.
If Ana comes, it will be nice, and if Betty comes, it will be nice, and if Carla comes, it will be nice.
-
a.
The existing approaches to the interpretation of unconditionals differ with respect to the way they derive the relevant conditional propositions and the way they see the connection between the adjunct clause in unconditionals and other wh-clauses, namely interrogatives and free relative clauses (see Rawlins 2013 for a detailed compositional account, as well as Hirsch 2016; Šimík 2019; Gonzalez and Lohiniva 2020 for recent discussion of the relevant issues).
In this paper we adopt and adapt the approach to unconditionals put forward by Szabolcsi (2019), who tailors her analysis of akár expressions in Hungarian to mirror the analysis outlined earlier for deriving the universal interpretation of free choice items in modal environments. The gist of her proposal is as follows: an unconditional denotes, at its core, an existential statement over conditional propositions, as in (28a), and this existential statement undergoes obligatory exhaustification, delivering the enriched conjunctive interpretation schematized in (28b), representing the conjunction of conditional propositions, as many as there are in the domain of the disjunction/existential statement.
-
(28)
Whoever comes, it will be nice.
-
a.
∃p[p∈{λw. comesw(x)| x∈D} ∧
 (pw→ it will be nicew)]
(pw→ it will be nicew)]If Ana comes, it will be nice, or if Betty comes, it will be nice, or …
-
b.
∀p[p∈{λw. comesw(x)| x∈D} →
 (pw→ it will be nicew)]
(pw→ it will be nicew)]If Ana comes, it will be nice, and if Betty comes, it will be nice, and …
-
a.
We postpone a discussion of the compositional derivation for the next sub-section, turning now instead to the following question: what is it about unconditionals that licenses FCIs? Our answer to this question is based on two assumptions. First, following Szabolcsi (2019), we assume that Viability is checked at the level of the adjunct wh-clause rather than at the level of the entire clause. Second, we take unconditionals to be inherently modalized contexts (a long-standing intuition in the literature on unconditionals). Let us now discuss each of these two assumptions in turn.
In the theory we are assuming, the licensing of FCIs is determined by a requirement on the alternatives associated with the FCI, namely the Viability Constraint in (24). Recall that Viability is evaluated at the level of the constituent containing the FCI, which in the modal environments we considered amounts to checking it at the matrix level. A FCI is licensed if we have models where both the (strengthened) assertion and Viability are satisfied. Since unconditionals are more complex structures, it is not straightforward to determine at what level this requirement is checked.
Szabolcsi (2019) argues that in unconditionals, Viability cannot be checked on the conditional statement underlying each alternative, since if it were, for a sentence like (28) this would end up requiring there to be worlds where if Ana comes, it will be nice is true and worlds where it is not, i.e., worlds in which Ana comes and it will not be nice. Intuitively, however, that is not what Viability seems to be after in unconditionals. Instead, the variation seems to be only with respect to the alternatives made available in the adjunct wh-clause, i.e., the antecedent clause of the relevant conditional structure, thus requiring there to be worlds where Ana comes, and worlds where she doesn’t.
The second key assumption we make is that unconditionals are inherently modalized (see, e.g., Rawlins 2008, 2013 and the discussion in Sect. 2.2). In many languages, the adjunct wh-clause in an unconditional structure involves some form of modality, which manifests itself either through the use of non-indicative mood (as already shown in Sect. 2.2) or through the use of a tense or aspect form that conveys modality. This is illustrated in the Romanian unconditionals in (29), with generic present tense in (29a), imperfective aspect in (29b) or future tense in (29c).
-
(29)

In fact, a similar modal inference is present in unconditional sentences that use an episodic past. For example, just like with unconditionals in other languages (see (12) for English), the adjunct clauses with the wh-based FCIs in the Hungarian or Romanian sentences in (30) could not be followed by namely Paul, indicating that the speaker is ignorant with respect to the identity of the individual who entered or came.
-
(30)

The intuition is that sentences like (30) are interpreted by considering individuals that for all the speaker knows came. This allows room for ignorance, meaning it leaves open the possibility that the speaker may not have full knowledge concerning the set of people who came. One way to formalize the obligatory presence of the modal inference in (30) is to say that the adjunct wh-clause contains a covert modal.Footnote 10 This means that both unconditionals with the FCI oricine in (29c) and (30b) contain a necessity modal in the adjunct wh-clause and have the following interpretation (ignoring tense).Footnote 11
-
(31)
∀p [p∈{λw.
 comew(x)| x∈D} →
comew(x)| x∈D} →  (pw → happyw(Ana))]
(pw → happyw(Ana))]
How then is the FCI oricine licensed in this structure? If, following Szabolcsi (2019), we assume that Viability is checked at the level of the adjunct clause, the set of alternatives relevant for the satisfaction of Viability would be as in (32b).
-
(32)
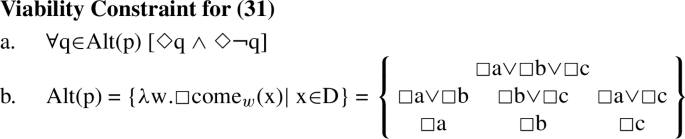
Like before, assuming that the set of worlds compatible with the speaker’s beliefs is W = {w1, w2, w3}, this condition would not be satisfied in M2, but it would be satisfied in M3, as for each individual x in D = {A, B, C}, there are worlds where it’s possible x came and worlds where it’s possible x didn’t come.
-
(33)
-
a.
M2: {〈w1,{A,B,C}〉, 〈w2,{A,B,C}〉, 〈w3,{A,B,C}〉}
-
b.
M3: {〈w1,{A}〉, 〈w2,{B}〉, 〈w3,{C}〉}
-
a.
Summarizing, the mechanism licensing FCIs in typical modal environments and in unconditionals is similar, thus capturing the frequent use of FCIs in unconditionals across languages. It uniformly requires Viability to be satisfied by a set of alternative propositions created on the basis of the elements in the domain of quantification of the FCI. In regular modal contexts, the relevant alternatives are obtained at the level of the matrix clause. In the case of unconditionals, they are obtained at the level of the adjunct wh-clause. Given that the analysis sketched above for unconditionals appears to allow for the licensing of a FCI in a configuration involving a necessity modal, one may wonder what the difference is with a sentence involving a necessity modal as in (34), where the FCI is deviant. Recall from Sect. 3.2 that in the case of (34) we always obtain a clash between the strengthened universal meaning of the FCI in (34a) and the Viability requirement that each alternative in (34b) be true in some worlds and false in others. (For presentational purposes we are assuming a two-membered domain below.)
-
(34)
*Jenny must visit any friend.
-
a.
Strengthened statement
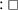 a
a b
b -
b.
Relevant alternatives for Viability: {
 a,
a,  b}
b}
-
a.
Why does no such clash occur in the case of unconditionals such as (35)? This hinges crucially on the fact that the conjuncts making up the strengthened assertion, provided in (35a), are not the ones against which the Viability Constraint is checked, provided in (35b). This difference allows for there to be worlds where the alternatives in (35b) are true and worlds where they are not, without it conflicting with the strengthened interpretation in (35a).
-
(35)

In other words, the richer structure of unconditionals makes it possible to avoid a clash between the universal interpretation associated with FCIs and the Viability requirement regulating their distribution. This may help explain why unconditionals across languages prove to be such hospitable environments for FCIs (as we have already seen in Sect. 2.2).
4.2 Deriving the universal interpretation
We now turn to the compositional derivation of unconditional structures, focusing for the time being on regular FCIs. Recall that we assume, with Szabolcsi (2019), that the conjunction-of-conditionals interpretation of unconditionals comes about similarly to the universal interpretation of other constructions involving FCIs, namely via exhaustification of a disjunctive proposition with respect to a set of pre-exhaustified alternatives; in the case of unconditionals, the pre-exhaustified proposition denotes the disjunction of conditional propositions, as many as there are in the domain of the FCI. Assuming an underlying conditional representation, in order to derive the disjunction-of-conditionals interpretation, the indefinite FCI must scope outside the wh-adjunct island so as to turn it into an existential quantifier over propositions.
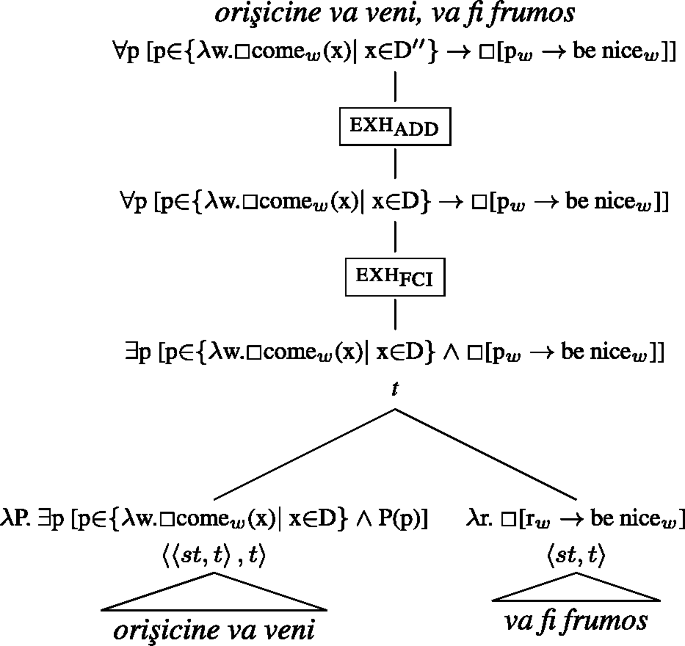
Before we turn to how exactly this is derived, we first illustrate how the wh-adjunct combines with the consequent, which is interpreted as the consequent of a conditional looking for an antecedent. Below in (36b) we provide the derivation of the unconditional in (36a). What is relevant at this step is that the exhaustification associated with the FCI oricine, labeled exh\(_{\text{\textsc{fci}}}\) below, takes place at the topmost level, turning the disjunction over conditional propositions into a conjunction over conditional propositions.
-
(36)
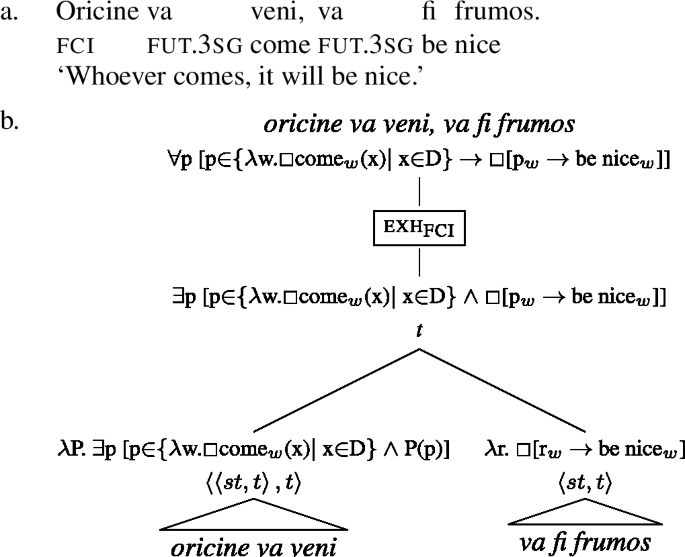
In order for the wh-adjunct clause to denote an existential quantifier, the FCI—an existential—must receive exceptional wide scope. Here we depart somewhat from the specifics of Szabolcsi’s (2019) proposal and instead adopt Demirok’s (2019) proposal for deriving exceptional wide scope for indefinites in conditional structures; the main difference between the two proposals concerns the internal composition of the wh-adjunct (the antecedent) in the unconditional.
Demirok’s (2019) proposal for deriving this exceptional wide scope builds on a recent proposal by Charlow (2019) (itself inspired by Dayal’s (1996) proposal for scope marking in questions).
Demirok (2019) argues that “the essential part of generating exceptional scope is syntactically turning the island into an existential quantifier” (p. 82), the island in our case being the wh-adjunct containing the FCI. In order to accomplish this, a scope position must be created at the edge of the island, above which the existential FCI can QR. At this point a set of propositions is created, which is turned into a scope-taker via merge with an ∃-head. The crux of Demirok’s proposal takes question semantics as a starting point, specifically the compositional tools for giving wh-phrases scope outside the question nucleus. He builds on the indirect method of deriving sets of propositions, as spelled out in Heim (2012) and Fox (2012) (see also von Stechow 2000; Sauerland 1998). Adapting this approach to our case, we derive the exceptional scope of the existential FCI oricine, as illustrated in (38). A crucial piece in the derivation is the interrogative complementizer responsible for creating the set of propositions, id, which has as its semantics (37).
-
(37)
〚id〛 = λp\(_{\left \langle s,t \right \rangle }\). λq\(_{\left \langle s,t \right \rangle }\). p = q
-
(38)

As shown in (38), the sister of id contains a propositional variable which is abstracted over after the quantifying in of the indefinite, thus delivering the set of propositions interpretation. Finally, the ∃-head is merged to deliver the existential quantifier over propositions, which ultimately takes the consequent clause as an argument (shown above in (36b) and omitted above), thus delivering the existential statement over conditional propositions.
On the theory of FCIs we have adopted, the Viability Constraint (and similar conditions posited in the literature) is a global requirement on sentences containing FCIs. In Dayal (2009, 2013), Viability (or its predecessor, Fluctuation) is treated as a presupposition that is triggered by the presence of an element like any, whereas in Szabolcsi (2019) it is triggered by the particle akár that enters the composition of FCIs in Hungarian. We have seen that for typical modal contexts this amounts to checking Viability at the matrix level. For unconditionals, we have followed Szabolcsi (2019) and argued in Sect. 4.1 that Viability needs to be checked at the level of the adjunct wh-clause (rather than on the full conditional statement). To make this concrete, in what follows we propose a compositional implementation of the Viability Constraint by treating it as a presuppositional filter, as in (39a), merged at the level of the adjunct clause, below the ∃-head, as in (39b). Its contribution is simply to check that its sister set satisfies the necessary viability condition.
-
(39)
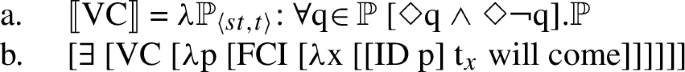
The proposed implementation does not have any impact for the modal contexts considered in Sect. 3.2. It does however play a role in the context of the more complex structure of unconditionals and, as we will see shortly, in the licensing of ADD-FCIs.
5 A compositional account of ADD-FCIs in unconditionals
In this section, we return to the puzzle introduced in Sect. 1, namely the following contrast:
-
(40)

As we have already provided the step-by-step derivation for (40a) with the regular FCI oricine, our remaining task is to introduce our assumptions about the two elements that set apart the structure with the ADD-FCI in (40b), namely the infix şi and the conditional mood. We argue that the presence of şi is responsible for the emphatic meaning associated with ADD-FCIs and the obligatory use of the conditional mood.
5.1 The contribution of şi
In this subsection we discuss the contribution of the particle şi in ADD-FCIs and the way it relates to its uses as a stand-alone particle. We argue that şi makes the same contribution both as an infix and as a stand-alone particle and show how that comes about.
Recall that şi can function as a conjunctive particle as in (41a), as an additive particle as in (41b) and as a scalar particle as in (41c).
-
(41)

We argue that the baseline interpretation of the particle şi is that of an additive, with the conjunctive and the scalar contribution derivable from it. The contribution of the additive particle şi in (41b) is that someone else ate. Following Nicolae (2020) who in turn builds on Mitrović and Sauerland (2016) and Szabolcsi (2017), we propose that this additive inference can be derived via exhaustification of the assertion with respect to its pre-exhaustified variant. The claim is that the alternative to şi p is exh p, its exhaustified variant, as illustrated in (42a) for the sentence in (41b). Since the alternative exh p, which amounts to p and nothing else, is stronger than p itself, it gets negated, as in (42b). The result is the expected conjunctive meaning that both the host proposition and an alternative to it are true: p and not only p. The intuition should be clear: the use of the additive particle is meant to mark that an exclusive interpretation was not intended.Footnote 12 Note crucially that the only contribution of the additive particle is to signal obligatory exhaustification with respect to a pre-exhaustified alternative (exh\(_{\text{\textsc{add}}}\)); it itself makes no other semantic contribution.
-
(42)
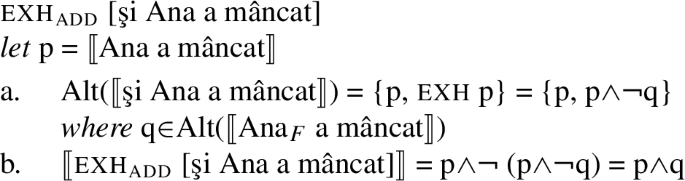
One of the main contributions of this paper rests on showing how the interpretation of orişicine is compositionally transparent, such that the contribution of each morpheme matches its contribution elsewhere. We have already established that the regular FCI oricine, like anyone, makes two main contributions to the overall meaning: (i) existential quantification over individuals and (ii) obligatory exhaustification with respect to its pre-exhaustified sub-domain alternatives (exh\(_{\text{\textsc{fci}}}\)). Turning now to şi, we argue that, like in its stand-alone incarnation, as an infix, şi makes no contribution to the overall meaning except to signal obligatory exhaustification with respect to its pre-exhaustified alternative (exh\(_{\text{\textsc{add}}}\)). When it associates with an individual, as in the example discussed above, the end result is additive. We argue that when it associates with a quantifier, as part of the compound orişicine, its contribution is the widening of the domain of quantification. We can derive this widening effect associated with ADD-FCIs similarly to how we derive the additive effect for şi when it functions as a stand-alone particle, with the only difference being that the associate is not an individual, but rather the domain variable on the quantifier. Intuitively, the reasoning goes as follows: şi signals that the quantification should be not only over the domain with which oricine associates, but over an additional domain as well, which amounts to widening. This means then that the alternatives considered for the pre-exhaustified alternative differ in the contents of the domain: while for the additive stand-alone şi we are considering distinct individuals, in its use as an infix where it associates with a quantifier we are considering distinct domains of individuals. We put forward the LF in (43) as the underlying structure of an unconditional with an ADD-FCI, and propose that exh\(_{\text{\textsc{add}}}\) takes scope over exh\(_{\text{\textsc{fci}}}\).
-
(43)
In (44) we go through the step-by-step derivation of the strengthened interpretation contributed by exh\(_{\text{\textsc{add}}}\). In (44a) we start with the set of alternatives, the prejacent and its exhaustified variant. The relevant alternative for calculating the exhaustified prejacent differs only in terms of its domain value, and we claim that this domain, D′, is distinct from and non-overlapping with the domain D with which the FCI oricine associates; in this sense, this mirrors what happens in the domain of individuals in (42) where we consider an individual distinct from the associate of the additive particle. Finally, in (44b) we calculate the final result of this exhaustification, which amounts to universal quantification over a larger domain D″, consisting of both D and D′.
-
(44)

To recap, the presence of şi signals that the domain of quantification is a domain larger than that corresponding to the regular FCI. The only way to increase the domain of quantification is by including marginal entities, which by their very nature correspond to entities not thought to be relevant or likely. This, in turn, explains straightforwardly the emphatic meaning associated with ADD-FCIs, since the use of ADD-FCIs must be associated with an appeal to a larger domain of individuals.
Lastly, note that there are in principle two possible adjunction sites for exh\(_{\text{\textsc{add}}}\), either below or above exh\(_{\text{\textsc{fci}}}\). We argue that the only way for exh\(_{\text{\textsc{add}}}\) to strengthen the interpretation is by adjoining above exh\(_{\text{\textsc{fci}}}\). If it were to adjoin below, namely at a level where the interpretation corresponds to an existential quantifier, its contribution would be vacuous and thus not licensed, assuming a system whereby only strengthening instances of exh are licensed (Fox and Spector 2018).
Summarizing, we have seen how the emphatic meaning associated with ADD-FCIs can be derived from the semantic contribution of the infix şi, which we take to be the same as when it is used as a stand-alone particle. This in turn has an effect on the licensing of ADD-FCIs. Recall from the previous section that we argued that the Viability Constraint should be encoded as a filter on the set of propositions which make up the adjunct clause of the unconditional, repeated in (45), such that each propositional alternative needs to be true in some worlds and false in other worlds.
-
(45)
〚VC〛 = \(\lambda\mathbb{P}_{\left \langle st,t \right \rangle }\): ∀q\(\in\mathbb{P}\) [◊q ∧ ◊¬q]. ℙ
By encoding this in the underlying representation as a separate projection, the relevant alternatives needed for computing the strengthened interpretation end up carrying this presupposition as well, meaning that the final strengthened interpretation as a whole carries the Viability presupposition. In other words, the widened set of propositions brought about by the ADD-FCI would need to satisfy Viability, a property we argue to be responsible for the conditional mood requirement to which we now turn.
5.2 The mood restriction
Having shown what the meaning contribution of şi is, we can now focus on the conditional mood, whose use is obligatory with ADD-FCIs and possible with regular FCIs, as evidenced by the contrast between (46a) and (46b), repeated from above.
-
(46)

In order to explain why ADD-FCIs require the conditional mood, we first need to understand its meaning contribution. Intuitively, the unconditional with the FCI oricine in (46b) allows for the consideration of more, possibly unlikely, alternatives than what we have in (46a) with the indicative future. To capture this intuition, we take the contribution of the conditional mood to be similar to that commonly attributed to the subjunctive mood. Specifically, we follow Schlenker (2005), who takes the indicative to carry a presupposition that the worlds under consideration (the set of accessible worlds) are only those in the context set, and a non-indicative mood to carry no such presupposition. The idea is that the conditional mood forces us to consider worlds outside of the context set, i.e., worlds not among the speaker’s alternatives, even possibly counterfactual ones.Footnote 13
The consideration of a larger set of worlds does not have any effect on the licensing of regular FCIs: as long as for each alternative there are worlds where that alternative holds and worlds where it doesn’t, Viability is satisfied and the FCI is licensed. The use of the conditional mood rather than the indicative future in (46) simply indicates the availability of this larger set of worlds, a meaning effect that is perfectly compatible with the use of a regular FCI.
What about ADD-FCIs? Why do they require the conditional mood then? The source of the problem in (46a) seems to be the following: we have argued that the additive şi forces us to consider an increased domain of quantification, which includes remote or unlikely alternatives. For ADD-FCIs to be licensed, like for regular FCIs, Viability needs to be satisfied. For the sentence in (46b), with the ADD-FCI, this amounts to the constraint in (47) (where the subscript cond indicates the larger set of worlds brought under consideration by the conditional mood).
-
(47)
Viability Constraint for (46b)
∀q∈Alt(p) [\(\Diamond_{\text{\textsc{cond}}}\) q \(\wedge \Diamond_{\text{\textsc{cond}}}\) ¬q]
where Alt(p) = {λw.
 callw(x)| x∈D″}
callw(x)| x∈D″}
The intuition we pursue is that with the indicative mood there are no worlds in which the unlikely/remote alternatives triggered by the use of şi are true (as indicated by the fact that here we are talking about D″ rather than D). This means that (47) would not be satisfied in a model like M4, where there are no worlds where the individual D (brought about by the presence of şi) does not call. In contrast, with the conditional mood the modal space gets increased, leading to the consideration of more, possibly unlikely worlds. This allows the alternatives associated with those individuals activated by şi to be true in some worlds and false in others, as in the toy model M5 below. Simply put, unlike the indicative mood, the conditional mood provides the variation needed to satisfy Viability for the larger domain D″.
-
(48)
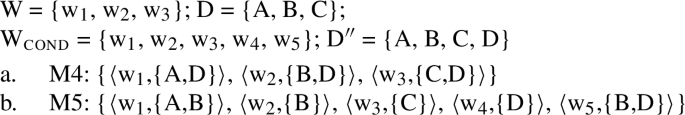
If we think of the contribution of şi as widening the domain of individuals, then its use has to be accompanied by the corresponding widening of the domain of possible worlds. This cannot happen with the indicative mood in (46a), whose use restricts the set of worlds to those in the context set. It can, however, happen with the conditional mood in (46b), which explains its obligatory use with ADD-FCIs.
6 Summary and open issues
Taking stock, in this paper we brought to light a new free choice paradigm, namely ADD-FCIs. We showed that they display a previously unobserved internal composition (i.e., disj+add+wh) and are restricted to unconditionals employing the conditional mood. We provided a compositional account of their meaning, couched in an alternatives-and-exhaustification framework, and we attributed their more restricted distribution to a requirement brought in by the additive particle şi, which combines with the regular (disj+wh) FCI and leads to the consideration of a quantificational domain which includes marginal entities. We argued that this translates into an emphatic meaning, which in turn explains the mood requirement, given that the conditional mood lets us consider remote worlds, which is necessary in order for Viability to be satisfied and thus for the ADD-FCI to be licensed.
Going forward, there are a number of questions and open issues. An obvious question arises: what about sentences like (49), where the conditional mood is present, but the ADD-FCI is outside of an unconditional structure?
-
(49)

Our analysis predicts these to be acceptable. As mentioned in Sect. 1, there is speaker variation with respect to the acceptability of ADD-FCIs in these contexts, but the extent of this variation is still a matter of empirical investigation. However, it is important to note that even for speakers who accept (49), the unconditional variant is a better licensor for ADD-FCIs. No such contrast can be observed for regular FCIs. The question then is regarding what it is about unconditionals that makes them such hospitable environments for ADD-FCIs.
We do not have an answer to this question at this point, but this is clearly a broader question about the semantics of unconditionals, which goes beyond ADD-FCIs. More generally, there is growing cross-linguistic evidence that unconditionals act as licensors of various otherwise ruled out configurations, a tendency which emphasizes the need for a better understanding of the properties of unconditionals. In addition to ADD-FCIs, other examples discussed in the literature include indeterminates in Japanese, which normally need a particle like -ka/-mo to acquire a quantificational meaning, but must occur bare in unconditionals, as shown in (50) (see Hiraiwa and Nakanishi 2020 for details).
-
(50)
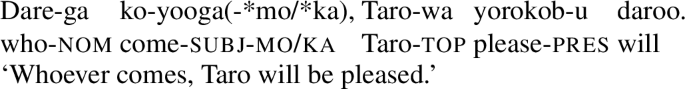
The same is true of Spanish doubling structures, like those in (51), which do not seem to be allowed elsewhere in the language besides unconditionals (more recently analyzed in Šimík 2019).
-
(51)
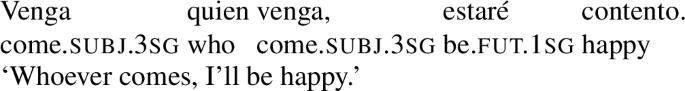
These constructions, like ADD-FCIs, involve alternative-triggering existentials. In order to explain the mechanisms underlying the licensing of the examples in (50)-(51), we need to determine how alternatives get introduced and how they combine in unconditionals, versus other related structures, e.g., conditionals, questions or free relatives. We hope that a closer cross-linguistic investigation of the behavior of free choice elements in unconditionals can further our understanding of these issues.
Another area for future research concerns the contribution of particles to free choice and polarity-sensitive paradigms across languages. The next step in this project is to extend the analysis developed for ADD-FCIs in this paper to the morphologically similar free choice elements described in Sect. 2.1, where the relevant particle combination does not occur at the word level but rather at the phrase level, e.g., German wer auch (immer) lit. ‘who also always’ and Dutch wie (dan) ook lit. ‘who then also’ or wie ook (maar) lit. ‘who also only’. They constitute an interesting intermediate step between the morphologically close unit represented by ADD-FCIs, where the particles function as affixes, and the uses of these elements as stand-alone particles. Their investigation can insightfully contribute to a uniform analysis of these particles across their various uses.
Notes
This scalar meaning can be reinforced via the addition of a concessive particle până/chiar ‘really’.
According to reference grammars, the Romanian verbal system marks the following moods: the indicative, the subjunctive, the conditional, and the imperative (see a full description in Pană Dindelegan 2013, Ch. 2). Present conditional forms are made up of an auxiliary form (which most authors take to originate in the verb a avea ‘to have’), fully inflected for person and number, plus the bare infinitive form of the verb, e.g. aş veni ‘I would come’. The forms of the perfect conditional are made up of the conditional auxiliary, followed by the infinitive of fi ‘be’ and the invariable participle of the verb, e.g. aş fi venit ‘I would have come’.
Here we focus on word-level composition and set aside more complex paradigms, such as free choice constructions involving various verbal forms, e.g., ‘want’ (Spanish cualquiera), ‘it may be’ (French wh + que ce soit, Italian qualsiasi), ‘no matter’ (French n’importe + wh). For further examples and discussion, see, e.g., Haspelmath (1997).
Rawlins also discusses other well-documented types of unconditionals across languages, e.g., so-called headed unconditionals, e.g., No matter/Regardless of who comes to the party, it will be fun, and alternative unconditionals, e.g., Whether Alfonso or Joanna comes to the party, it will be fun. To this, we can add doubling unconditionals, e.g., Venga quien venga, estaré contento ‘Whoever comes, I’ll be happy’, most recently discussed in Šimík (2019). In Romanian, all these types of unconditionals are realized by constructions that are unrelated to free choice items, so we set them aside in the rest of the paper. Accordingly, we use the term ‘unconditionals’ as an abbreviation for ‘constituent unconditionals’.
Constituent unconditionals should also be distinguished from concessive conditional clauses, like those in (i), which contain an overt conditional clause preceded by a scalar particle:
-
(i)
Even if someone uninvited comes, the party will be fun.
We do not discuss the differences between the two constructions in this paper (but see Haspelmath and König 1998; Quer 2001; Balusu 2019; Erlewine 2020 for relevant discussion). We simply note that in Romanian, both FCIs and ADD-FCIs are ruled out from this type of conditional.
-
(i)
The cross-linguistic picture in Table 2 raises the question of where elements like whoever fit in this table, given that they are productively used in unconditionals and give rise to modal inferences when occurring in -ever free relative clauses (ever-FRs). The relation between ever-FRs and FCIs cross-linguistically is an open issue, whose consideration lies beyond the scope of this paper. For references and discussion, see, e.g., Hirsch (2016), Caponigro and Fălăuş (2018) and Šimík (2020).
For the purposes of deriving the FC inference we disregarded the scalar implicature, but note that its presence is crucial. The reason for this is that in its absence we would predict FC implicatures to arise just as easily for non-modalized sentences; in other words, we would derive a conjunctive interpretation for plain disjunctive sentences. If, however, the scalar implicature is computed, the negation of the enriched alternatives cannot be added consistently: not only a and not only b are inconsistent with a or b and not both. Crucially this inconsistency does not arise in the case above where the disjunction is embedded under a possibility modal.
As amply discussed in the literature on FCIs, these sentences can be rescued by the addition of a post-nominal modifier, e.g., Yesterday, Jenny visited any friend that came to the party, a phenomenon dubbed subtrigging (LeGrand 1975).
The Viability Constraint proposed in Dayal (2013) is given in (i) below:
-
(i)
Viability Constraint on alternatives (Dayal 2013, p. 100)
[…FCI…] is felicitous iff there exists a model M, world w, and a conversational background g(w), such that each exhaustified alternative is true at w w.r.t. to some subset of ∩g(w).
Szabolcsi (2019) argues that the requirement that each exhaustified alternative be true in some world is too strong. It would predict for instance that for a sentence with a FCI and a symmetrical predicate like Any bishop may meet a bishop to be true, there would have to be a world where only bishop A meets a bishop, which is intuitively false. This issue relates to a more general problem, namely the requirement in certain theories of donkey anaphora for there to be a minimal situation that provides a unique antecedent for the donkey pronoun. The version in (24) is essentially a way to weaken this requirement, by building in a scalar component into the modal space relevant for the FCI, along the lines of Chierchia (2013).
-
(i)
Szabolcsi (2019) alludes to the presence of a covert modal in unconditionals, but does not formally implement this idea. Instead, she captures variation by resorting to quantification over world-event pairs, without spelling out the details of the proposal.
We abstract away from the fact that the necessity modal operator can quantify over worlds compatible not only with the speaker’s (or the relevant agent’s) beliefs, but also their goals, wishes, preferences etc. For more discussion on the issues raised by the use of covert modals to derive ignorance or free choice readings for seemingly episodic sentences with various kinds of modal indefinites, see, e.g., Chierchia (2013) and Alonso-Ovalle and Menéndez-Benito (2015).
References
Aloni, Maria. 2007. Free choice, modals, and imperatives. Natural Language Semantics 15: 65–94.
Aloni, Maria. 2019. Indefinites as fossils: The case of wh-based free choice. Unpublished manuscript, ILLC, University of Amsterdam.
Alonso-Ovalle, Luis. 2006. Disjunction in alternative semantics, PhD thesis, University of Massachusetts at Amherst.
Alonso-Ovalle, Luis, and Paula Menéndez-Benito. 2015. Epistemic indefinites: An overview. In Epistemic indefinites: Exploring modality beyond the verbal domain, eds. Luis Alonso-Ovalle and Paula Menéndez-Benito, 1–27. Oxford: Oxford University Press.
Alonso-Ovalle, Luis, and Paula Menéndez-Benito. 2020. Free choice items and modal indefinites. In The Wiley Blackwell companion to semantics, eds. Daniel Gutzmann, Lisa Matthewson, Cécile Meier, Hotze Rullmann, and Thomas Ede Zimmermann, 1–33. Hoboken: Wiley Blackwell.
Bade, Nadine. 2015. Obligatory presupposition triggers in discourse, PhD thesis, Universität Tübingen.
Balusu, Rahul. 2019. The anatomy of the Dravidian unconditional. In Proceedings of GLOW in Asia XII, ed. Sae-Youn Cho, 40–59.
Bhatt, Rajesh, and Roumyana Pancheva. 2017. Conditionals, 2nd edn. In The Wiley Blackwell companion to syntax, eds. Martin Everaert and Henk van Riemsdijk, 1–48. Hoboken: Wiley Blackwell.
Caponigro, Ivano, and Anamaria Fălăuş. 2018. Free choice free relatives in Italian and Romanian. Natural Language and Linguistic Theory 36: 323–363.
Charlow, Simon. 2019. The scope of alternatives: Indefiniteness and islands. Linguistics and Philosophy 43: 42–472.
Chierchia, Gennaro. 2004. Scalar implicatures, polarity phenomena, and the syntax/pragmatics interface. In Structures and beyond, ed. Adriana Belletti. Vol. 3, 39–103. London: Oxford University Press.
Chierchia, Gennaro. 2006. Broaden your views: Implicatures of domain widening and the ‘logicality’ of language. Linguistic Inquiry 37: 535–590.
Chierchia, Gennaro. 2013. Logic in grammar. Oxford: Oxford University Press.
Chierchia, Gennaro, Danny Fox, and Benjamin Spector. 2012. Scalar implicatures as a grammatical phenomenon. In Semantics: An international handbook of natural language meaning, eds. Claudia Maienborn, Paul Portner, and Klaus von Heusinger. Vol. 3, 2297–2332. New York: Mouton de Gruyter.
Dayal, Veneeta. 1996. Locality in WH quantification: Questions and relative clauses in Hindi. Dordrecht: Kluwer.
Dayal, Veneeta. 1997. Free relatives and ever: Identity and free choice readings. In Proceedings from the 7th Semantics and Linguistic Theory, ed. Aaron Lawson, 99–116. Ithaca: CLC Publications.
Dayal, Veneeta. 2004. The universal force of free choice any. Linguistic Variation Yearbook 4: 5–40.
Dayal, Veneeta. 2009. Variation in English free choice items. In Universals and variation: Proceedings of GLOW in Asia VII, eds. Rajat Mohanty and Mythili Menon, 237–256. Hyderabad: EFL University Press.
Dayal, Veneeta. 2013. A viability constraint on alternatives for free choice. In Alternatives in semantics, ed. Anamaria Fălăuş, 88–122. London: Palgrave Studies in Pragmatics, Language and Cognition.
Demirok, Ömer. 2019. Scope theory revisited: Lessons from pied-piping in wh-questions, PhD thesis, MIT.
Erlewine, Michael Yoshitaka. 2020. Universal free choice from concessive conditionals. Presentation at Sinn und Bedeutung 25.
Fălăuş, Anamaria, and Andreea C. Nicolae. 2019. Two coordinating particles are better than one: Free choice items in Romanian. Snippets 37: 27–29.
Farkas, Donka. 2013. The semantics of determiners. In A reference grammar of Romanian, eds. Carmen Dobrovie-Sorin and Ion Giurgea, 175–230. Amsterdam: Benjamins.
Fox, Danny. 2007. Free choice disjunction and the theory of scalar implicatures. In Presupposition and implicature in compositional semantics, eds. Uli Sauerland and Penka Stateva, 71–120. New York: Palgrave Macmillan.
Fox, Danny. 2012. The semantics of questions. Class notes. MIT seminar.
Fox, Danny, and Benjamin Spector. 2018. Economy and embedded exhaustification. Natural Language Semantics 26: 1–50.
Giannakidou, Anastasia. 2001. The meaning of free choice. Linguistics and Philosophy 24: 659–735.
Gonzalez, Aurore, and Karoliina Lohiniva. 2020. A compositional semantics for free choice constituent unconditionals. In Sinn und Bedeutung 24, Vol. 1, 223–241. Osnabrück/Berlin: Osnabrück University and Humboldt University of Berlin.
Groenendijk, Jeroen, and Martin Stokhof. 1984. Studies on the semantics of questions and the pragmatics of answers, PhD thesis, University of Amsterdam.
Halm, Tamás. 2016. The grammar of free choice items in Hungarian, PhD thesis, Pázmány Péter Catholic University.
Haspelmath, Martin. 1997. Indefinite pronouns. Oxford: Oxford Studies in Typology and Linguistic Theory.
Haspelmath, Martin, and Ekkehard König. 1998. Concessive conditionals in the languages of Europe. In Adverbial constructions in the languages of Europe, ed. Johan van der Auwera, 563–640. Berlin: de Gruyter.
Heim, Irene. 2012. Notes on questions. MIT class notes for advanced semantics.
Hiraiwa, Ken, and Kimiko Nakanishi. 2020. Bare indeterminates in unconditionals. In Proceedings of the Linguistic Society of America, ed. Patrick Farrell. Vol. 5, 395–409. Washington: Linguistic Society of America.
Hirsch, Aron. 2016. A compositional semantics for wh-ever free relatives. In Sinn und Bedeutung, eds. Nadine Bade, Polina Berezovskaya, and Anthea Schöller. Vol. 20, 341–358.
Howell, Jonathan. 2012. On modal interpretations of the French conditionnel. In Proceedings of the 39th annual North East Linguistics Conference, 401–413. Amherst: GSLA Publications.
Izvorski, Roumyana. 2000. Free adjunct free relatives. In Proceedings of the 19th West Coast Conference on Formal Linguistics, eds. Roger Billerey and Brook Danielle Lillehaugen, 232–245. Somerville: Cascadilla Press.
Jayaseelan, Karattuparambil A. 2001. Questions and question-word incorporating quantifiers in Malayalam. Syntax 4: 63–93.
Kadmon, Nirit, and Fred Landman. 1993. Any. Linguistics and Philosophy 16(4): 353–422.
Kratzer, Angelika, and Junko Shimoyama. 2002. Indeterminate pronouns: The view from Japanese. In Tokyo Conference on Psycholinguistics, ed. Yukio Otso. Vol. 3, 1–25.
Lahiri, Utpal. 1998. Focus and negative polarity in Hindi. Natural Language Semantics 6: 57–123.
LeGrand, Jean Ehrenkranz. 1975. Or and any: The semantics and syntax of two logical operators, PhD thesis, University of Chicago.
Menéndez-Benito, Paula. 2010. On universal free choice items. Natural Language Semantics 18: 33–64.
Meyer, Marie-Christine. 2020. An apple or a pear. Free choice disjunction. In The Wiley Blackwell companion to semantics, eds. Daniel Gutzmann, Lisa Matthewson, Cécile Meier, Hotze Rullmann, and Thomas Ede Zimmermann, 1–44. Hoboken: Wiley Blackwell.
Mitrović, Moreno. 2021. Superparticles: A microsemantic theory, typology, and history of logical atoms. Series in Natural Language & Linguistic Theory. Berlin: Springer.
Mitrović, Moreno, and Uli Sauerland. 2016. Two conjunctions are better than one. Acta Linguistica Hungarica 63: 471–494.
Nicolae, Andreea C. 2020. Negative polarity additive particles. In Monotonicity in logic and language, eds. Dun Deng, Fenrong Liu, Mingming Liu, and Dag Westerstahl, 166–182. Berlin: Springer.
Quer, Josep. 2000. Licensing free choice items in hostile environments: The role of aspect and mood. SKY Journal of Linguistics 13: 251–268.
Pană Dindelegan, Gabriela, ed. 2013. The grammar of Romanian. Oxford: Oxford University Press.
Quer, Josep. 2001. Interpreting mood. Probus 13: 81–111.
Rawlins, Kyle. 2008. (Un)conditionals: An investigation in the syntax and semantics of conditional structures, PhD thesis, UC Santa Cruz.
Rawlins, Kyle. 2013. (Un)conditionals. Natural Language Semantics 21: 117–178.
Saebo, Johan-Kjell. 2004. Conversational contrast and conventional parallel: Topic implicatures and additive presuppositions. Journal of Semantics 2: 199–217.
Sauerland, Uli. 1998. The meaning of chains, PhD thesis, MIT.
Sauerland, Uli. 2004. Scalar implicatures in complex sentences. Linguistics and Philosophy 27: 367–391.
Schlenker, Philippe. 2005. The lazy Frenchman’s approach to the subjunctive. In Proceedings of Going Romance XVII, eds. Twan Geerts, Ivo van Ginneken, and Haike Jacobs, 269–309.
Silk, Alex. 2022. Weak and strong necessity modals. In Meaning, decision, and norms: Themes from the work of Allan Gibbard, eds. Billy Dunaway and David Plunkett. Ann Arbor: Michigan Publishing.
Šimík, Radek. 2019. Doubling unconditionals and relative sluicing. Natural Language Semantics 28: 1–21.
Šimík, Radek. 2020. Free relatives. In The Wiley Blackwell companion to semantics, eds. Daniel Gutzmann, Lisa Matthewson, Cécile Meier, Hotze Rullmann, and Thomas Ede Zimmermann, 1–38. Hoboken: Wiley Blackwell.
Slade, Benjamin. 2011. Formal and philological inquiries into the nature of interrogatives, indefinites, disjunction, and focus in Sinhala and other languages. PhD thesis, University of Illinois.
Spector, Benjamin. 2006. Aspects de la pragmatique des opérateurs logiques. PhD thesis, Université Paris VII.
von Stechow, Armin. 2000. Some remarks on choice functions and LF-movement. In Reference and anaphoric relations, eds. Klaus von Heusinger and Urs Egli, 193–228. Dordrecht: Springer.
Szabolcsi, Anna. 2017. Additive presuppositions are derived through activating focus alternatives. In Proceedings of the 21st Amsterdam colloquium, eds. Alexandre Cremers, Thom van Gessel, and Floris Roelofsen, 455–464.
Szabolcsi, Anna. 2018. Two types of quantifier particles: Quantifier-phrase internal vs. heads on the clausal spine. Glossa: A Journal of General Linguistics 3: 69.
Szabolcsi, Anna. 2019. Unconditionals and free choice unified. In Proceedings from the 29th Semantics and Linguistic Theory, eds. Katherine Blake, Forrest Davis, Kaelyn Lamp, and Joseph Rhyne. Vol. 29, 320–340. Washington: Linguistic Society of America.
Szabolcsi, Anna, James Doh Whang, and Vera Zu. 2014. Quantifier words and their multi-functional(?) parts. Language and Linguistics 15: 115–155.
Acknowledgements
For very helpful discussion and feedback, we would like to thank two anonymous NALS reviewers, as well as Luis Alonso-Ovalle, Veneeta Dayal, Tamás Halm, Paula Menéndez-Benito, Moreno Mitrović and audiences at SinFonIJA 13 and Sinn und Bedeutung 25. We are particularly grateful to Aron Hirsch and Radek Šimík for their invaluable comments on earlier drafts of this paper. The names of the authors are listed in alphabetical order.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported in part by the German Science Foundation (DFG) grant NI 1850/2-1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fălăuş, A., Nicolae, A.C. Additive free choice items. Nat Lang Semantics 30, 185–214 (2022). https://doi.org/10.1007/s11050-022-09192-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11050-022-09192-8











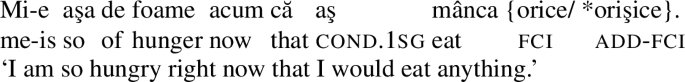




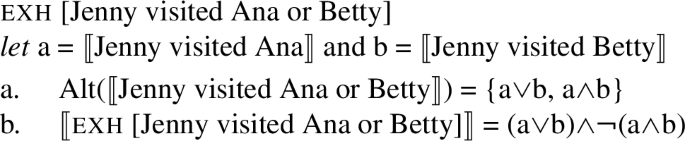
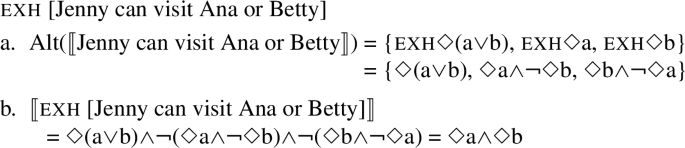
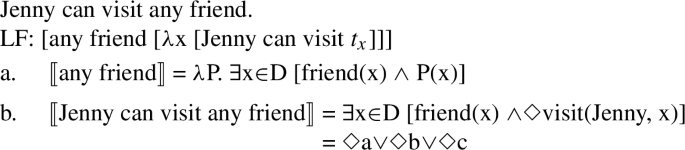
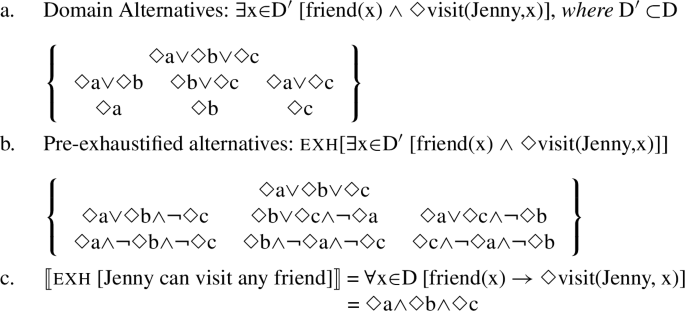
 visitw(Jenny, x)]
visitw(Jenny, x)]  a
a b
b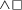 c
c (pw→ it will be nicew)]
(pw→ it will be nicew)] (pw→ it will be nicew)]
(pw→ it will be nicew)]

 comew(x)| x∈D} →
comew(x)| x∈D} →  (pw → happyw(Ana))]
(pw → happyw(Ana))]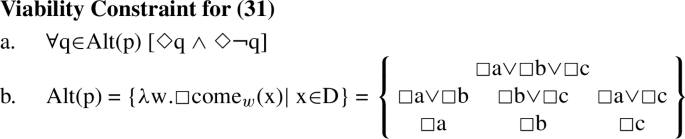
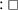 a
a b
b a,
a,  b}
b}


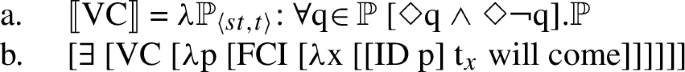


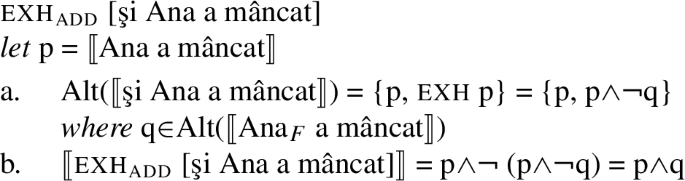



 callw(x)| x∈D″}
callw(x)| x∈D″}