Abstract
Recent work has claimed that (non-tonal) phonological patterns are subregular (Heinz 2011a,b, 2018; Heinz and Idsardi 2013), occupying a delimited proper subregion of the regular functions—the weakly deterministic (WD) functions (Heinz and Lai 2013; Jardine 2016). Whether or not it is correct (McCollum et al. 2020a), this claim can only be properly assessed given a complete and accurate definition of WD functions. We propose such a definition in this article, patching unintended holes in Heinz and Lai’s (2013) original definition that we argue have led to the incorrect classification of some phonological patterns as WD. We start from the observation that WD patterns share a property that we call unbounded semiambience, modeled after the analogous observation by Jardine (2016) about non-deterministic (ND) patterns and their unbounded circumambience. Both ND and WD functions can be broken down into compositions of deterministic (subsequential) functions (Elgot and Mezei 1965; Heinz and Lai 2013) that read an input string from opposite directions; we show that WD functions are those for which these deterministic composands do not interact in a way that is familiar from the theoretical phonology literature. To underscore how this concept of interaction neatly separates the WD class of functions from the strictly more expressive ND class, we provide analyses of the vowel harmony patterns of two Eastern Nilotic languages, Maasai and Turkana, using bimachines, an automaton type that represents unbounded bidirectional dependencies explicitly. These analyses make clear that there is interaction between deterministic composands when (and only when) the output of a given input element of a string is simultaneously dependent on information from both the left and the right: ND functions are those that involve interaction, while WD functions are those that do not.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the past decade, research at the intersection of computational phonology and formal language theory has advanced the subregular hypothesis, which claims that phonological patterns “occupy some area strictly smaller than the regular languages” (Heinz 2011a: 147) and that “the study of the typology of the attested transformations [= input-output maps, henceforth] in the light of the existing categories yields similar conclusions” (Heinz 2018: 198). This work has usefully defined various classes of subregular functions relevant to the description of phonological transformations, all properly included within the regular functionsFootnote 1 in terms of their computational expressivity—the ability of a function defined within that class to describe some otherwise well-defined set(s) of phonological transformations.
Figure 1 is a recent snapshot of the most significant of these subregular function types and their hierarchical inclusion relationships with respect to one another. Johnson (1972) and Kaplan and Kay (1994) showed that the SPE formalism of ordered conditional rewrite rules (Chomsky and Halle 1968) is expressively equivalent to the regular functions; assuming that this formalism is sufficiently expressive to describe all phonological grammars, it follows that phonology is regular and thus that every phonological pattern is able to be described with a non-deterministic (ND) function from the top of the hierarchy in Fig. 1.
A hierarchy of regular function classes, based on Heinz (2018) and Aksënova et al. (2020). All classes define functional string transductions (every input string has at most one output string), and everything below the non-deterministic regular functions are examples of subregular string transductions
One of the aims of recent research in this area is to assess more precisely the minimum degree of computational expressivity required to describe otherwise well-defined sets of phonological patterns, in part to verify whether the full expressive power of the ND class of functions is required to describe phonological grammars. This work has led to results such as “local non-iterative assimilation patterns are input strictly local” (Chandlee 2014; Chandlee and Heinz 2018), “unidirectional iterative assimilation patterns are output strictly local” (Chandlee et al. 2015), and “bidirectional iterative assimilation patterns are weakly deterministic” (Heinz and Lai 2013). These results lead in turn to readily testable hypotheses about the relative complexity and learnability of different types of phonological patterns. Any future results derived from testing hypotheses generated by previous results are of course only as reliable as the previous results on which the hypotheses are based, which are in turn only as reliable as the formal definitions of any subregular function types relevant to those hypotheses. It is thus imperative that these definitions be as meaningfully accurate as possible.
From the perspective of theory development, good mathematical definitions are insightful, may crystalize linguistic intuitions, and often suggest future directions for research or offer an unexpected unification of previously disparate results and hypotheses. Some examples from the relatively recent literature include Oakden (2020), demonstrating that “two competing feature-geometric models of tonal representation are notationally equivalent”; Jardine et al. (2021), showing that “Q-Theory and Autosegmental Phonology are equivalent in terms of the constraints they can express”; and Bennett and DelBusso (2018), establishing that some apparently different constraint sets in the Agreement by Correspondence framework “not only result in the same extensional predictions; they also generate them in identical ways.”
Our focus in this article is on the distinction between sets of phonological patterns that have motivated the postulation of the weakly deterministic (WD) class of functions, at the outer edge of the set of subregular functions depicted in Fig. 1, intermediate between the strictly less expressive subsequential and the strictly more expressive non-deterministic classes of functions. Heinz and Lai (2013) propose the WD class to demarcate the expressivity boundary between two established types of phonological patterns. On the one hand there are amply attested bidirectional harmony patterns, in which the harmonic feature value spreads outward from a designated origin until it reaches a blocking segment or the end of the spreading domain. Bidirectional harmony is illustrated in (1a) with examples from Maasai (Eastern Nilotic; Tucker and Mpaayei 1955—see Sect. 3).Footnote 2 On the other hand are purportedly unattested patterns of so-called “sour grapes” harmony, illustrated with hypothetical examples (based on those from Maasai) in (1b). Sour grapes harmony is a subspecies of non-myopic spreading (Wilson 2003, 2006) in which the harmonic feature value completely fails to spread in a given direction if there is a blocking segment anywhere in that direction.Footnote 3
-
(1)

Heinz and Lai (2013) conjecture that the types of functions required to describe patterns of bidirectional harmony like (1a) are strictly less expressive than those required to describe patterns of sour grapes harmony like (1b). Suppose that a sour grapes harmony function is reading the input form  from right to left. It first encounters the harmony trigger
from right to left. It first encounters the harmony trigger  , and then the potential harmony target /ɔ/. Given that it doesn’t yet “know” that the blocker /ɑ/ is further down the line, the function must entertain either of the two possible outcomes for this target—harmonize to
, and then the potential harmony target /ɔ/. Given that it doesn’t yet “know” that the blocker /ɑ/ is further down the line, the function must entertain either of the two possible outcomes for this target—harmonize to  or remain [ɑ]—until either a blocker or the end of the form is reached. This is the relevant sense in which this function must be non-deterministic: it’s not that one input may result in more than one output, it’s that the output of a given input symbol is not incrementally deterministic in information from one side or from the other.
or remain [ɑ]—until either a blocker or the end of the form is reached. This is the relevant sense in which this function must be non-deterministic: it’s not that one input may result in more than one output, it’s that the output of a given input symbol is not incrementally deterministic in information from one side or from the other.
Now suppose that a bidirectional harmony function is reading the same input form,  , again from right to left. Upon encountering the potential target /ɔ/, the outcome is immediately known: harmonize to
, again from right to left. Upon encountering the potential target /ɔ/, the outcome is immediately known: harmonize to  . Likewise for the next target /ɪ/, which harmonizes to
. Likewise for the next target /ɪ/, which harmonizes to  . When the blocker /ɑ/ is encountered next, only the subsequent potential target—the initial /ɪ/—is affected, and its outcome is likewise immediately known: remain [ɪ]. What makes this function weakly deterministic is that a potential target may be on either side of a trigger or blocker. If this same form is instead read from left to right, the outcome for the initial /ɪ/ cannot be known until the blocker /ɑ/ is reached, and the outcomes for the subsequent targets /ɪ/ and /ɔ/ cannot be known until the trigger
. When the blocker /ɑ/ is encountered next, only the subsequent potential target—the initial /ɪ/—is affected, and its outcome is likewise immediately known: remain [ɪ]. What makes this function weakly deterministic is that a potential target may be on either side of a trigger or blocker. If this same form is instead read from left to right, the outcome for the initial /ɪ/ cannot be known until the blocker /ɑ/ is reached, and the outcomes for the subsequent targets /ɪ/ and /ɔ/ cannot be known until the trigger  is reached. This is the key difference between the ND and WD classes of functions: for patterns requiring the expressivity of the WD class of functions, like bidirectional harmony (1a), the output for any input symbol can be determined based on information on one side or the other, whereas for patterns requiring the expressivity of the ND class of functions, like sour grapes harmony (1b), the output of some input symbols can only be determined based on information on both sides.
is reached. This is the key difference between the ND and WD classes of functions: for patterns requiring the expressivity of the WD class of functions, like bidirectional harmony (1a), the output for any input symbol can be determined based on information on one side or the other, whereas for patterns requiring the expressivity of the ND class of functions, like sour grapes harmony (1b), the output of some input symbols can only be determined based on information on both sides.
Jardine (2016) builds on Heinz and Lai (2013) by demonstrating that attested unbounded tonal plateauing patterns have the relevant descriptive characteristics of non-myopic spreading: a high tone (H) only spreads in a given direction if there is another H somewhere in that direction. Put differently, H completely fails to spread in a given direction if there is no other H anywhere in that direction; compare the definition of non-myopic harmony in (1b). Unbounded tonal plateauing patterns thus require greater expressivity than that afforded by WD functions, leading Jardine to conjecture that the WD class also demarcates the expressivity boundary between non-tonal and tonal phonology. Jardine (2016: 252, (9)) cites the following pair of examples of compounds in Luganda (Bantu) exemplifying unbounded tonal plateauing.
-
(2)

McCollum et al. (2020a) respond by identifying attested non-tonal feature spreading patterns having these same descriptive characteristics and that thus also require crossing the WD expressivity boundary. McCollum et al. (2020a: 217, (1)) cite the following pair of examples in Tutrugbu (Kwa) showing that regressive spreading of [+ATR] from roots is blocked by [−high] vowels only if the initial vowel is [+high].
-
(3)

The WD–ND boundary is thus clearly an important one to define properly, given that it serves as the dividing line between amply attested myopic patterns of bidirectional vowel harmony (1a) and other, non-myopic patterns, ranging from the apparently unattested (1b), to the exclusively tonal (2), to the comparatively rare (3). Heinz and Lai’s (2013) aim is to properly define the WD class of functions, but subsequent work (Graf 2016; McCollum et al. 2018; Lamont et al. 2019; O’Hara and Smith 2019; Smith and O’Hara 2019) has shown that some types of functions technically (and counterintuitively) satisfy Heinz and Lai’s (2013) definition despite clashing with what we feel justified to claim was its intended scope: to include myopic spreading patterns and to exclude non-myopic spreading patterns. We demonstrate in this article how Heinz and Lai’s (2013) definition does not accomplish its intended goal of distinguishing myopic from non-myopic spreading, and we offer a revised definition that accurately distinguishes the intended sets of functions based on a definition of interaction closely related to the notion familiar from the phonological literature.Footnote 4
The article is structured as follows. First, in Sect. 2, we provide some necessary formal background for understanding the problems with Heinz and Lai’s (2013) definition of the WD class of functions and our approach to solving them. In Sect. 3 we turn to the empirical focus of the article, the vowel harmony patterns of two Eastern Nilotic languages, Maasai (Tucker and Mpaayei 1955) and Turkana (Dimmendaal 1983). We devote special attention to the differences that lead these two patterns to be on different sides of the intended WD function boundary, clarifying both the intent and the limits of Heinz and Lai’s (2013) definition. In Sect. 4 we introduce a more precise definition of interaction between string functions, clarify its role in adjudicating the WD–ND boundary, and introduce our proposed definition of weak determinism that properly distinguishes the pattern in Maasai from the pattern in Turkana. We end the article with a discussion of the computational and linguistic naturalness of our revised definition of weak determinism in Sect. 5 and with a brief conclusion in Sect. 6.
2 Formal background
2.1 Scope of relevant claims
We begin here with some clarification of what various results reported in the subregular hypothesis literature mean and what they don’t mean. There is understandable confusion here, due to the fact that the subregular hypothesis itself is intended to be a claim about “phonology” generally—“phonology is subregular”—and the scope of “phonology” in this claim is typically not made sufficiently clear. Reported results within this broad hypothesis often reference individual phenomena (e.g., that bidirectional iterative assimilation is weakly deterministic; Heinz and Lai 2013) or substantive classes thereof (e.g., that non-tonal phonology is subregular while tonal phonology is not; Jardine 2016). However, the statement of these reported results should in and of themselves not be taken as claims about the complexity of phonology in toto.
It is perhaps simplest and most directly useful to clarify this point as follows. The individual components of a phonological analysis—however these may be identified (as the mapping performed by a single rule or by a set of rules in an SPE-style analysis; as the candidates that best-satisfy a single constraint or a set of constraints in an OT analysis, etc.)—are not (typically) the ultimate objects of researchers’ claims within this area of computational phonology. Rather, claims about the complexity of phonology are claims about the nature of the computations required to map any single valid underlying representation (UR) to its grammatical surface representation (SR). The fact that an overall UR↦SR map may be broken down into (possibly) simpler parts has no impact on this notion of overall computational complexity. It is for precisely this reason that results from this approach are of interest to a wide range of phonologists: different analysts may favor different ways of breaking down phonological patterns, but results concerning the minimal necessary computational complexity of the overall UR↦SR map assumed to be performed by the phonological component are fixed.
To perhaps see this more clearly, suppose for example that the functional description of some well-defined set of input-output mappings in a given language is shown to require the expressivity afforded by a defined class of functions \(F_{1}\). Suppose further that this set of input-output mappings has a phonological analysis in terms of two (or more) independently motivated processes, and that the set of input-output mappings individually described by each of those processes can be shown to require the expressivity afforded by some other defined class of functions \(F_{2}\) that is strictly less expressive than \(F_{1}\). The \(F_{1}\) class is still required to express the entire input-output map in such an example; the availability of a phonological analysis whose individual components only require the expressivity afforded by \(F_{2}\) does not alter this fact, regardless of whatever independent linguistic motivation there may be for the componential breakdown in that analysis.
Indeed, this is precisely the situation that we will encounter in our analyses of the vowel harmony patterns in Maasai and Turkana in Sect. 3. Most if not all previous phonological analyses of both patterns have involved the postulation of (at least) two harmonic feature spreading processes, at least one applying from left to right and another applying from right to left, with some amount of independent linguistic motivation for each. Similarly, our analyses break both patterns down into two contradirectional functions, one reading the input string from left to right and the other from right to left. Each of these functions is subsequential, requiring strictly less expressivity than the composition of it with its contradirectional counterpart. The main question that we address in this paper is: what property of these compositions makes some WD and others ND? We argue that the significant difference between functional analyses of WD and ND patterns comes down to whether the two contradirectional functions interact. For brevity and exposition, we give a relatively informal definition of interaction in Def. 1, to be followed up by a more formal definition in Sect. 4.2.
Def. 1
An input-output map (\(X^{*} \rightarrow Y^{*}\)), broken down into two contradirectional functions l and r, requires that l and r interact if there exists some input symbol \(x_{i} \in X\) for which the determination of the corresponding output string \(y_{i} \in Y^{*}\) is dependent on information from both sides of \(x_{i}\), where information from the left is uniquely accessible to l and information from the right is uniquely accessible to r.
As we show in Sects. 3–4 below, the contradirectional functions describing the harmony pattern in Maasai do not interact, and this makes their composition a WD function. By contrast, the contradirectional functions describing the harmony pattern in Turkana do interact, making their composition an ND function.
2.2 Regular functions, composition, and weak determinism: The view “from below”
In general, any regular function can be broken down into two contradirectional subsequential functions (Elgot and Mezei 1965: 60, Prop. 7.4), with one (the “outer” function) composed with and applying to the result of the other (the “inner” function). We refer to all such broken-down regular functions as Elgot-Mezei (EM) compositions. Heinz and Lai (2013) define the subregular WD functions in terms of a restriction on EM compositions. In their initial, informal definition, they state that a WD function “can be decomposed into [an inner] subsequential and [an outer, contradirectional] subsequential function without the [inner] function marking up its output in any special way” (Heinz and Lai 2013: 52, emphasis added). To keep these restricted compositions distinct from EM compositions, we refer to them as Heinz-Lai (HL) compositions.
There are four main, interrelated things to note about EM compositions and HL compositions. The first is that each of the two composand functions is subsequential.Footnote 5 A subsequential function reads its input string incrementally, strictly in one direction or the other, and is able to remember some (finite) amount of what it has already read in the string unboundedly far back in the string but only to look boundedly far ahead to aid in deciding what to write to its output at any given point. A subsequential function is sufficiently expressive to describe a prototypical unidirectional vowel harmony pattern, such as the left-to-right ATR harmony pattern found in Tangale (Kidda 1985), illustrated in (4a), or the right-to-left ATR harmony pattern found in Yoruba (Bamgboṣe 1966), illustrated in (4b). In order to know whether to output a [+ATR] or a [−ATR] vowel for any given affix in each of these cases, the function only needs to know the ATR value of the vowel(s) that it has already read to the left (in Tangale) or to the right (in Yoruba).
-
(4)

The subsequential class of functions is strictly less expressive than the WD or ND classes, as can be seen in Fig. 1, but the composition of two contradirectional subsequential functions may result in an overall function properly belonging to one or the other of the strictly more expressive WD or ND classes. This is the case for the composition of a left-subsequential function and a right-subsequential function needed to describe a bidirectional harmony pattern like the ones in Maasai (1a) and Turkana, as we’ll see in Sects. 3–4.
The second thing to note is that the two functions are contradirectional: one is left-subsequential, reading its input string incrementally starting from the left, and the other is right-subsequential, reading its input string incrementally starting from the right.Footnote 6 The information in the input string to which each of these functions has access differs accordingly: the left-subsequential function has access to information unboundedly far to the left and bounded lookahead access to the right, while the right-subsequential function has access to information unboundedly far to the right and bounded lookahead access to the left. This difference in information access is schematically represented in Fig. 2: string positions enclosed in the solid-line oval and not also in the dashed-line oval are ones that are uniquely accessible to the left-subsequential function, while positions enclosed in the dashed-line oval and not also in the solid-line oval are ones that are uniquely accessible to the right-subsequential function; this is the sense of “uniquely accessible” referenced in Def. 1. As a succinct and direction-agnostic shorthand, we will refer to the side of the string “already read” by a given function at any given point in its traversal of the input word as the causal past of the function at that point, and we will refer to the side of the string that the function has “not yet read” as its causal future.
Information access of an arbitrary string from an arbitrary position (⋄) by two contradirectional subsequential functions. At position ⋄, a right-subsequential function has access to information about all positions (□) enclosed within the dashed-line oval, from position \(\square_{L}\) to the end of the string ⋉, and a left-subsequential function has access to information about all positions enclosed in the solid-line oval, from the beginning of the string ⋊ to position \(\square_{R}\). The maximum distance that \(\square_{R}\) or \(\square_{L}\) can be from ⋄ under any circumstances is an a priori known constant k; k is (arbitrarily) 3 for the left-subsequential function and (again, arbitrarily) 2 for the right-subsequential function
The third thing to note is that the two functions of the composition are (assumed to be) ordered with respect to one another: one is the “inner” function I, applying first, and the other is the “outer” function O, applying to the result of I. In other words, I and O are composed, conventionally represented as O∘I.
The fourth thing to note is the additional restriction of HL compositions: that the inner function I does not “[mark] up its output in any special way.” The intention of this restriction is to prevent I from providing information to the outer function O about what has previously been read on I’s unbounded, causal past side, which is O’s bounded, causal future side. If I is able to provide such information to O, then O would essentially have unbounded access to information on both sides of the string, effectively rendering O more expressive than subsequential, and thus rendering the composition O∘I in general more expressive than an alternative composition in which I did not mark up its output in any special way.
In the discussion leading up to their formal definition of the WD class of functions, Heinz and Lai (2013: 54–55) explicitly identify two forms of inner function markup to be precluded. One is the addition of novel symbols to the output of the inner function I, symbols that aren’t in the original alphabet of I’s input. If I is able to write novel symbols, then those symbols can be strategically deployed in such a way that crucial information about I’s unbounded side is communicated to the outer function O. A function that does not add novel symbols in this way is alphabet-preserving, and a function that does add novel symbols is alphabet-increasing. The other form of explicitly precluded markup is the use of novel sequences of symbols in I’s input alphabet that can also be strategically deployed to communicate crucial information to O about I’s unbounded side. A function that effectively encodes new symbols in this way will necessarily be length-increasing: in general, the length of the output string will be no shorter than the input string and sometimes longer as a result of the insertion of substrings that effectively encode new symbols. A length-preserving function, in contrast, cannot use this particular strategy for encoding novel symbols.
We claim here that what unifies alphabet-increasing and length-increasing inner functions in compositions of contradirectional subsequential functions O∘I is not that both allow particular forms of markup per se, but rather that both enable information from the unbounded, causal past side of I—information that is uniquely accessible to I—to be crucially communicated to O, fundamentally changing O’s behavior by effectively providing O with unbounded access to both sides of the string. When one function changes its contradirectional counterpart’s behavior in this way, the two functions interact as in Def. 1. Information from the unbounded, causal past side of I is information that is uniquely accessible to I; giving O access to that information, whether via these two forms of markup or otherwise, enables the output of a given input symbol to be synergistically dependent both on that information and on information uniquely accessible to O.
Note that, in general, when two functions interact, the order of their composition is important, and—typically—when the order of composition does not matter, they do not interact. Whether any markup introduced by I “matters” in the relevant sense depends on whether it is crucially used by O: if I is alphabet- or length-increasing but O does not make crucial use of that markup, then the composition O∘I may still be WD in the sense that we take to be intended by Heinz and Lai (2013). Conversely, if I is alphabet- and length-preserving but nevertheless I and O interact, then their composition is ND—indeed, this is what we argue is the case for the ATR harmony pattern of Turkana in Sect. 3.2. In other words, whether or not a composition of two contradirectional subsequential functions is a WD or an ND function depends on whether the two functions interact, and not per se on whether the inner function introduces some form of markup.
2.3 Circumambience, semiambience, and weak determinism: The view “from above”
As discussed above, Elgot and Mezei (1965) characterize the ND functions in terms of contradirectional compositions of subseqential functions where the inner function changes the behavior of (= interacts with) the outer function based on information from unboundedly far in the causal future of the outer function. Jardine (2016) offers an essentially phenomenological characterization of properly ND functions in terms of the location of information in the input that is used to determine the output of a given input symbol. In what follows we center Jardine’s framing over Elgot and Mezei’s, and base our revised definition of weak determinism on the WD analogue of Jardine’s phenomenological characterization of the ND functions.
One of Jardine’s (2016) key results is that the minimum level of computational expressivity required to describe unbounded circumambient patterns is that afforded by the class of ND functions, at the outer edge of the class of regular functions and thus strictly more expressive than the class of WD functions (see now also Hao and Andersson 2019; Koser and Jardine 2020; McCollum et al. 2020a). A definition of unbounded circumambience, based on Jardine (2016: 249), is given in Def. 2.Footnote 7
Def. 2
In an unbounded circumambient pattern,
-
a.
the output of at least one input symbol (= a target) is dependent on
information on both sides of the target; and [= circumambient]
-
b.
on both sides, there is no principled a priori bound on how far this
information may be from the target. [= unbounded]
All of the non-myopic spreading patterns mentioned thus far are unbounded circumambient. In the hypothetical case of sour grapes harmony in (1b), whether harmony targets surface as [+ATR] requires both that [+ATR] be present on one side of those targets and that there be no blocking /ɑ/ present on the other side. In the case of unbounded tonal plateauing in Luganda in (2), whether spreading targets surface with H tone requires that H tones be present on both sides of those targets. Lastly, in the case of conditional blocking in Tutrugbu in (3), whether harmony targets surface as [+ATR] requires that [+ATR] be present to the right of those targets and, if a [−high] vowel is also present to the right, that the initial vowel to the left not be [+high]. In all of these cases the need for circumambient information is clear. Their unbounded nature must be inferred from bounded examples, just as the unbounded nature of any iterative spreading pattern must be.
A regular function describing an unbounded circumambient pattern can be broken down into a composition of two contradirectional subsequential functions, with each properly identifying critical information at an a priori unbounded distance on the side of the target in the function’s causal past. Unlike a proper HL composition corresponding to a WD function, however, the inner function of this EM composition must somehow communicate to the outer function whether the critical information is present on the side of the target in the outer function’s causal future in order to correctly describe the unbounded circumambient process. Explained in terms of EM compositions, that is why these patterns require greater computational expressivity than that afforded by the WD functions.
While the literature on weak determinism and its relation to the expressivity of phonology has to date centered on Heinz and Lai’s (2013) initial Elgot and Mezei-derived framing, we suggest instead that Jardine’s definition readily motivates the weakly deterministic parallel to unbounded circumambience in Def. 3. Crucially, this phenomenological characterization of WD functions does not require that the side of the target containing critical information always be the same from word to word or even the same from target to target within the same word; such restrictions hold for the strictly even less expressive subsequential functions.
Def. 3
In an unbounded semiambient pattern,
-
a.
the output of any given input symbol (= any target) is determined
by information from at most one side of the target; and [= semiambient]
-
b.
on any determining side, there is no principled a priori bound on
how far the determining information may be from the target. [= unbounded]
We argue in Sect. 4 that in addition to correctly capturing the intended scope of Heinz and Lai’s (2013) definition of the WD functions, this framing of weak determinism in terms of what information is needed from where is not only equivalent but often simpler to understand and work with than one explicitly grounded in compositions of contradirectional functions. Furthermore, as we will show in Sect. 4, our phenomenological identification of unbounded semiambience with weak determinism is computationally well-founded.
Equipped with this background, we can delve into the details of the vowel harmony patterns of Maasai and Turkana in Sect. 3. As we’ll see, the Turkana pattern is unbounded circumambient, dependent on information on both sides of some targets of harmony, while the Maasai pattern is unbounded semiambient, dependent on information from only one side of every target of harmony (though the side may vary from target to target). Thus, and as will be shown in Sect. 4, the Maasai pattern is weakly deterministic, and the Turkana pattern is not.
3 Maasai and Turkana
Maasai (Tucker and Mpaayei 1955; Hall et al. 1973; Archangeli and Pulleyblank 1994; McCrary 2001; Guion et al. 2004; Quinn-Wriedt 2013) and Turkana (Dimmendaal 1983; Vago and Leder 1987; Albert 1995; Noske 1996, 2000) are closely related Eastern Nilotic languages. Both languages exhibit patterns of ATR harmony operating over an inventory of nine contrastive vowels, four [+ATR]  and five [−ATR] /ɪ ɛ ɑ ɔ ʊ/; in both languages, [+ATR] spreads bidirectionally from root and suffix vowels. Spreading vowels in this type of harmony pattern are called dominant, and alternating vowels are called recessive.
and five [−ATR] /ɪ ɛ ɑ ɔ ʊ/; in both languages, [+ATR] spreads bidirectionally from root and suffix vowels. Spreading vowels in this type of harmony pattern are called dominant, and alternating vowels are called recessive.
Note that there are four direct harmonic [+ATR]∼[−ATR] pairings among the non-low vowels:  ∼ɪ,
∼ɪ,  ∼ɛ,
∼ɛ,  ∼ɔ, and
∼ɔ, and  ∼ʊ. Significantly, the [−ATR] low vowel /ɑ/ does not have a direct harmonic counterpart. In certain [+ATR] contexts, underlying /ɑ/ is raised (and also rounded) to become
∼ʊ. Significantly, the [−ATR] low vowel /ɑ/ does not have a direct harmonic counterpart. In certain [+ATR] contexts, underlying /ɑ/ is raised (and also rounded) to become  , an indirect harmonic relationship dubbed re-pairing in Baković (2000, 2002). This is where the similarities between the Maasai and Turkana vowel harmony patterns end. The key difference between them is the exceptionally dominant behavior of a set of [−ATR] suffix vowels present in the Turkana pattern but absent from the Maasai pattern, with significant consequences for the surface manifestation of re-paired /ɑ/. The presence of these exceptionally dominant [−ATR] suffix vowels in the Turkana case makes the overall Turkana pattern unbounded circumambient and thus non-deterministic, which can only be broken down into an interacting pair of contradirectional subsequential functions. Conversely, the absence of exceptionally dominant [−ATR] vowels in the Maasai case makes the overall Maasai case unbounded semiambient and thus weakly deterministic, which can be broken down into a non-interacting pair of contradirectional subsequential functions.
, an indirect harmonic relationship dubbed re-pairing in Baković (2000, 2002). This is where the similarities between the Maasai and Turkana vowel harmony patterns end. The key difference between them is the exceptionally dominant behavior of a set of [−ATR] suffix vowels present in the Turkana pattern but absent from the Maasai pattern, with significant consequences for the surface manifestation of re-paired /ɑ/. The presence of these exceptionally dominant [−ATR] suffix vowels in the Turkana case makes the overall Turkana pattern unbounded circumambient and thus non-deterministic, which can only be broken down into an interacting pair of contradirectional subsequential functions. Conversely, the absence of exceptionally dominant [−ATR] vowels in the Maasai case makes the overall Maasai case unbounded semiambient and thus weakly deterministic, which can be broken down into a non-interacting pair of contradirectional subsequential functions.
Note that in the discussion that follows, we assume that (non-exceptional) dominant vowels are underlyingly specified for the spreading value of the harmonic feature, [+ATR], and that alternating recessive vowels are underlyingly specified for the opposite value, [−ATR]. Recessive vowels could alternatively be assumed to be underlyingly unspecified for a value of the harmonic feature, and in fact such an analysis has particular appeal in the case of Turkana because [−ATR] can then be reserved for the exceptionally dominant [−ATR] suffix vowels (Noske 1996, 2000). For the purposes of our argument about the differing levels of expressivity necessary to describe these two patterns, however, nothing hinges on this matter of representation.
3.1 Maasai
Examples of [+ATR] spreading from roots in Maasai are shown in (5) below.Footnote 8 The contrast between (5a–5b) shows that [+ATR] spreads leftward from dominant root vowels to preceding recessive prefix vowels, and the contrast between (5c–5d) shows that [+ATR] spreads outward from dominant root vowels both to preceding recessive prefix vowels and to following recessive suffix vowels.
-
(5)

Some suffixes also cause [+ATR] spreading. Examples of suffix-induced harmony are seen in (6). Observe that both the root meaning ‘wash’ and the intransitive suffix surface as [−ATR] in (6a), but in the presence of the dominant applied suffix, all root and prefix vowels surface as [+ATR] in (6b). In the same manner, the dominant instrumental suffix transforms the [−ATR] root and prefixes in (6c) to [+ATR] in (6d).
-
(6)

We focus now on the special behavior of the recessive low vowel /ɑ/. When a [+ATR] dominant vowel occurs to the right of /ɑ/, the low vowel blocks spreading and is output faithfully as [ɑ]. This is evident in (7). Observe that the first-person plural prefix /kɪ/ undergoes harmony under the influence of the following dominant vowel in the root  ‘pull’ in (7a), but when the past tense prefix /tɑ/ occurs between the two (7b), the low vowel /ɑ/ both fails to undergo harmony and prevents the more peripheral /kɪ/ prefix from undergoing harmony. Comparing (7c–7d), we see the same behavior from an /ɑ/ in the root, which blocks leftward spreading originating from the dominant vowel of the /re/ suffix in (7d). Lastly, in (7e–7f) we see that an /ɑ/ in a less peripheral suffix also blocks leftward spreading of [+ATR] from the /ie/ suffix.
‘pull’ in (7a), but when the past tense prefix /tɑ/ occurs between the two (7b), the low vowel /ɑ/ both fails to undergo harmony and prevents the more peripheral /kɪ/ prefix from undergoing harmony. Comparing (7c–7d), we see the same behavior from an /ɑ/ in the root, which blocks leftward spreading originating from the dominant vowel of the /re/ suffix in (7d). Lastly, in (7e–7f) we see that an /ɑ/ in a less peripheral suffix also blocks leftward spreading of [+ATR] from the /ie/ suffix.
-
(7)

However, suffix /ɑ/ alternates depending on whether a dominant [+ATR] vowel occurs to its left. When following other recessive [−ATR] vowels, /ɑ/ is output faithfully, as in (8a–8b). When following dominant [+ATR] vowels, though, /ɑ/ undergoes harmony and is output re-paired as  , as in (8c–8d). Similarly, when /ɑ/ is flanked on either side by dominant [+ATR] vowels, as in (8e–8f)—compare (7e–7f) above—it is output re-paired as
, as in (8c–8d). Similarly, when /ɑ/ is flanked on either side by dominant [+ATR] vowels, as in (8e–8f)—compare (7e–7f) above—it is output re-paired as  due to the presence of the dominant [+ATR] vowel to its left.Footnote 9
due to the presence of the dominant [+ATR] vowel to its left.Footnote 9
-
(8)

The harmony pattern in Maasai can be analyzed with two very similar rules spreading [+ATR] in opposite directions, as in Archangeli and Pulleyblank (1994): a left-to-right rule spreading [+ATR] to all following vowels (and re-pairing /ɑ/ to  ), and a right-to-left [+ATR] spreading rule that is blocked by /ɑ/. These rules do not interact, and thus do not need not be ordered with respect to one another, because the left-to-right rule only affects vowels to the right of a dominant [+ATR] vowel and the right-to-left rule only affects vowels to the left of a dominant [+ATR] vowel. Consider the hypothetical underlying vowel string
), and a right-to-left [+ATR] spreading rule that is blocked by /ɑ/. These rules do not interact, and thus do not need not be ordered with respect to one another, because the left-to-right rule only affects vowels to the right of a dominant [+ATR] vowel and the right-to-left rule only affects vowels to the left of a dominant [+ATR] vowel. Consider the hypothetical underlying vowel string  in Fig. 3, with the
in Fig. 3, with the  being the sole dominant [+ATR] vowel. Left-to-right spreading affects only the final /ɛ ɑ ɪ/ sequence, outputting it as
being the sole dominant [+ATR] vowel. Left-to-right spreading affects only the final /ɛ ɑ ɪ/ sequence, outputting it as  , with re-pairing of /ɑ/ to
, with re-pairing of /ɑ/ to  ; it does not affect the realization of the initial sequence of vowels. Similarly, right-to-left spreading outputs the initial /ɛ ɑ ʊ/ as
; it does not affect the realization of the initial sequence of vowels. Similarly, right-to-left spreading outputs the initial /ɛ ɑ ʊ/ as  , with blocking by /ɑ/, but has nothing to say regarding the realization of the final sequence of vowels.
, with blocking by /ɑ/, but has nothing to say regarding the realization of the final sequence of vowels.
The situation is only superficially different when recessive vowels lie between dominant [+ATR] vowels. When a non-low recessive vowel is flanked by dominant vowels, it is output as [+ATR]. This is consistent with the effect of either of the two rules; in this context, we cannot determine which dominant vowel is responsible for the harmonic assimilation of the non-low vowel. When the low recessive vowel /ɑ/ is flanked by two dominant vowels, it is output as  , but in this context we can uniquely determine that the dominant vowel responsible for the alternation is the one to the left, because /ɑ/ blocks spreading from the right. Since /ɑ/ blocks right-to-left spreading, in a flanking sequence like
, but in this context we can uniquely determine that the dominant vowel responsible for the alternation is the one to the left, because /ɑ/ blocks spreading from the right. Since /ɑ/ blocks right-to-left spreading, in a flanking sequence like  , the
, the  to the right will not cause assimilation (and re-pairing) of the /ɑ/. The
to the right will not cause assimilation (and re-pairing) of the /ɑ/. The  to the left, though, can spread [+ATR] to /ɑ/, and so the string is ultimately output as
to the left, though, can spread [+ATR] to /ɑ/, and so the string is ultimately output as  —regardless of the order of application between the two spreading rules.
—regardless of the order of application between the two spreading rules.
In sum, the output quality of every vowel in Maasai depends on two sources of information. The first source of information is the vowel’s underlying ATR specification, which determines whether it is a dominant (= spreading) or recessive (= alternating) vowel. In the latter case, the second source of information is the output ATR specification of either the preceding or the following vowel. Recessive vowels to the left of a dominant vowel depend on the output ATR value of the following vowel while recessive vowels to the right of a dominant vowel depend on the output ATR value of the preceding vowel. Crucially, no individual vowel’s output quality depends on the ATR specifications of vowels on both sides. In other words, the bidirectional ATR harmony pattern in Maasai is not unbounded circumambient, but rather unbounded semiambient—recall Sect. 2.3, Def. 2 and Def. 3 above. This is of course what makes the Maasai harmony pattern fit comfortably within Heinz and Lai’s (2013) class of WD functions: it can be broken down into an HL composition of two contradirectional subsequential functions, neither one of which marks up its output in such a way that the other function has crucial access to that markup. Or, in the stricter terms that we advocate in this article: the two functions do not interact and can even be composed in either order, because for any given input symbol, its output is determined by information on one side or the other, and never both simultaneously.
3.2 Turkana
As noted at the outset of this section, the bidirectional ATR harmony pattern in Turkana is in relevant respects identical to the pattern in Maasai except for the existence and consequences of a set of exceptionally dominant [−ATR] suffix vowels. We first establish the commonalities with the Maasai pattern. The contrast in (9a–9b) shows that [+ATR] spreads leftward from dominant root vowels to preceding recessive prefix vowels, and the contrast in (9c–9d) shows that [+ATR] spreads outward from dominant root vowels both to preceding recessive prefix vowels and to following recessive suffix vowels.
-
(9)

Dominant suffix vowels also trigger [+ATR] spreading. The voice suffix  and the gerundial suffix
and the gerundial suffix  in (10b, 10d) cause all other, recessive vowels in the word to be output as [+ATR].
in (10b, 10d) cause all other, recessive vowels in the word to be output as [+ATR].
-
(10)

The final parallel between Maasai and Turkana is the behavior of the low vowel /ɑ/ in [+ATR] contexts. Examples (11a–11b) show that the low vowel of the infinitive prefix is output faithfully regardless of the ATR value of the root vowel. In examples (11c–11d), we see that the low vowel of the root ‘beat’ is also output faithfully regardless of the presence of the dominant gerundial suffix vowel  in (11d), blocking spreading to the preceding recessive vowel /ɛ/ of the masculine singular prefix. Examples (11e–11f) further show that the low vowel of the habitual suffix blocks spreading from the dominant nominalizing suffix vowel
in (11d), blocking spreading to the preceding recessive vowel /ɛ/ of the masculine singular prefix. Examples (11e–11f) further show that the low vowel of the habitual suffix blocks spreading from the dominant nominalizing suffix vowel  .
.
-
(11)

However, when a suffix low vowel follows a dominant [+ATR] root vowel, as shown by the contrasts in (12a–12d), or when it is flanked on both sides by dominant [+ATR] vowels (12e–12f), harmony (and re-pairing) obtains, and /ɑ/ is output as  .Footnote 10 Given that leftward harmony is blocked by low vowels, we must assume that rightward spreading from the root is what causes /ɑ/ to be output as
.Footnote 10 Given that leftward harmony is blocked by low vowels, we must assume that rightward spreading from the root is what causes /ɑ/ to be output as  in (12e–12f); compare (11e–11f) above.
in (12e–12f); compare (11e–11f) above.
-
(12)

The harmony patterns in Maasai and Turkana are thus far identical. However, there is one crucial difference between the two: there are exceptionally dominant [−ATR] suffix vowels in Turkana in addition to dominant [+ATR] suffix vowels. We assume that these exceptional suffixes (or the vowels themselves) are lexically specified as dominant and henceforth circle them in cited examples to distinguish them from “normal” recessive [−ATR] suffix vowels. When an exceptionally dominant [−ATR] suffix vowel co-occurs with a dominant [+ATR] vowel, the exceptionally dominant vowel both resists becoming [+ATR] and imposes its own [−ATR] value on all preceding vowels, in a pattern that Baković (2000) refers to as “dominance reversal.”
Observe in (13a) that the dominant [+ATR] vowels of the root  ‘give birth’ spread [+ATR] rightward to the recessive vowels of the ventive and aspect-marking suffixes /ʊn/ and /ɪt/, causing these suffixes to be output as
‘give birth’ spread [+ATR] rightward to the recessive vowels of the ventive and aspect-marking suffixes /ʊn/ and /ɪt/, causing these suffixes to be output as  and
and  , respectively. In the presence of the exceptionally dominant [−ATR] instrumental-locative suffix
, respectively. In the presence of the exceptionally dominant [−ATR] instrumental-locative suffix  (13b), the recessive vowel of the ventive suffix as well as the dominant [+ATR] vowels of the root are all output as [−ATR].
(13b), the recessive vowel of the ventive suffix as well as the dominant [+ATR] vowels of the root are all output as [−ATR].
-
(13)

The remaining examples in (13) illustrate what happens when the low vowel /ɑ/ of the epipatetic suffix is in a fully [−ATR] context (13c), surfacing faithfully as [ɑ]; when it is preceded by dominant [+ATR] vowels (13d), surfacing re-paired as  ; and when it is flanked by dominant [+ATR] vowels to its left and an exceptionally dominant [−ATR] suffix vowel to its right (13e), surfacing in this case as [ɑ]. This is of course the expected harmonic counterpart of
; and when it is flanked by dominant [+ATR] vowels to its left and an exceptionally dominant [−ATR] suffix vowel to its right (13e), surfacing in this case as [ɑ]. This is of course the expected harmonic counterpart of  , indicating that this vowel has in some sense undergone [+ATR] harmony and thus re-pairing. Otherwise it could have surfaced faithfully as [ɑ], which would also harmonically agree with the exceptionally dominant [−ATR] vowel.
, indicating that this vowel has in some sense undergone [+ATR] harmony and thus re-pairing. Otherwise it could have surfaced faithfully as [ɑ], which would also harmonically agree with the exceptionally dominant [−ATR] vowel.
There are some further details to be noted about the behavior of these exceptionally dominant [−ATR] suffix vowels, as well as some differences in the relevant data cited by Dimmendaal (1983) and Noske (2000). First, Dimmendaal (1983: 25–26) notes that if a suffix with an exceptionally dominant [−ATR] mid vowel (/ɔ/ or /ɛ/) is affixed directly to a root with a dominant [+ATR] mid vowel ( or
or  ), a harmony-blocking glide [j] is inserted between them:
), a harmony-blocking glide [j] is inserted between them:  →
→  ‘attempt’; cf. (13b), where a (recessive) suffix intervenes between the same exceptionally dominant [−ATR] suffix and another root with a dominant [+ATR] mid vowel.Footnote 11 Second, Noske (2000: 781–782) claims that only mid vowels, and not high vowels, undergo (leftward) [−ATR] spreading. Noske thus transcribes the form in (13b) as
‘attempt’; cf. (13b), where a (recessive) suffix intervenes between the same exceptionally dominant [−ATR] suffix and another root with a dominant [+ATR] mid vowel.Footnote 11 Second, Noske (2000: 781–782) claims that only mid vowels, and not high vowels, undergo (leftward) [−ATR] spreading. Noske thus transcribes the form in (13b) as  , explicitly noting (2000: 781, fn. 8) that this differs from Dimmendaal (1983); the critical form in (13e)—not cited by Noske—would presumably be
, explicitly noting (2000: 781, fn. 8) that this differs from Dimmendaal (1983); the critical form in (13e)—not cited by Noske—would presumably be  .Footnote 12 We ascribe this difference between Dimmendaal’s (1983) transcriptions and Noske’s to a dialect difference, and stick with Dimmendaal’s. Lastly, Noske (2000: 782, (38)) cites examples with an exceptionally dominant [−ATR] suffix vowel followed by a dominant [+ATR] suffix vowel, e.g.
.Footnote 12 We ascribe this difference between Dimmendaal’s (1983) transcriptions and Noske’s to a dialect difference, and stick with Dimmendaal’s. Lastly, Noske (2000: 782, (38)) cites examples with an exceptionally dominant [−ATR] suffix vowel followed by a dominant [+ATR] suffix vowel, e.g.  ‘way of washing.’ Noske states that this is “[t]he only construction type in which the two types of [dominant] suffixes occur regularly,” but it is at least circumstantial evidence that [−ATR] does not spread rightward from exceptionally dominant [−ATR] suffix vowels. The fact that [+ATR] also does not spread leftward in this example could be due either to the invariance of exceptionally dominant [−ATR] vowels or to the fact that this particular exceptionally dominant [−ATR] vowel is /ɑ/ and thus independently expected to block [+ATR] spreading; for concreteness, we assume that both reasons apply.
‘way of washing.’ Noske states that this is “[t]he only construction type in which the two types of [dominant] suffixes occur regularly,” but it is at least circumstantial evidence that [−ATR] does not spread rightward from exceptionally dominant [−ATR] suffix vowels. The fact that [+ATR] also does not spread leftward in this example could be due either to the invariance of exceptionally dominant [−ATR] vowels or to the fact that this particular exceptionally dominant [−ATR] vowel is /ɑ/ and thus independently expected to block [+ATR] spreading; for concreteness, we assume that both reasons apply.
Two further things are also worth noting here. First, there is no readily apparent phonological information to independently determine whether a given [−ATR] vowel is recessive or exceptionally dominant; compare, for example, the recessive voice-marking suffix /ɑ/ in (11g, 11h) with the distinct, exceptionally dominant voice-marking suffix  in (13e). Second, note in (13e) that the exceptionally dominant [−ATR] vowel may be separated from the affected low vowel by another syllable; we assume that this distance is in principle unbounded, just as we assume—following the extensive literature on the analysis of vowel harmony—that the distance between any trigger and potential target of harmony is in principle unbounded.
in (13e). Second, note in (13e) that the exceptionally dominant [−ATR] vowel may be separated from the affected low vowel by another syllable; we assume that this distance is in principle unbounded, just as we assume—following the extensive literature on the analysis of vowel harmony—that the distance between any trigger and potential target of harmony is in principle unbounded.
Analytically speaking, Maasai and Turkana both exhibit bidirectional [+ATR] spreading, and in addition Turkana exhibits [−ATR] spreading. This additional part of the pattern in Turkana has significant computational repercussions for the analysis. Recall that the output of every alternating vowel in Maasai is dependent on two sources of information: that vowel’s input specification, and the output specification of a neighboring vowel on either side. In Turkana, the output of every alternating vowel depends on additional information: whether there is a preceding dominant [+ATR] vowel and whether there is a following exceptionally dominant [−ATR] vowel. This is the key distinction between the Maasai and Turkana patterns. The output of a recessive low vowel in the input in Turkana is not able to be determined based solely on information about vowels to its left or about vowels to its right; it depends on information from both sides, simultaneously.
Consider the hypothetical underlying vowel string  in Fig. 4, where
in Fig. 4, where  is a dominant [+ATR] vowel and
is a dominant [+ATR] vowel and  is an exceptionally dominant [−ATR] vowel. The output of the vowels in the medial string of recessive vowels /ɛ ɑ ʊ/ depends on both of these flanking sources of information. If only the dominant [+ATR] vowel were to the left, and the exceptionally dominant [−ATR] vowel were not also to the right, then the vowels in this medial string would all be output as [+ATR],
is an exceptionally dominant [−ATR] vowel. The output of the vowels in the medial string of recessive vowels /ɛ ɑ ʊ/ depends on both of these flanking sources of information. If only the dominant [+ATR] vowel were to the left, and the exceptionally dominant [−ATR] vowel were not also to the right, then the vowels in this medial string would all be output as [+ATR],  , with the /ɑ/ re-paired to
, with the /ɑ/ re-paired to  . But because the exceptionally dominant [−ATR] vowel is also to the right, all vowels to its left are instead output as [−ATR], /ɪ ɛ ɔ ʊ/. The fact that both sources of information are critical is made most obvious by the fact that the /ɑ/ is output as [ɑ]: the fact that it is [−low] is due to the dominant [+ATR] vowel to the left, and the fact that it is [−ATR] is due to the exceptionally dominant [−ATR] vowel to the right.
. But because the exceptionally dominant [−ATR] vowel is also to the right, all vowels to its left are instead output as [−ATR], /ɪ ɛ ɔ ʊ/. The fact that both sources of information are critical is made most obvious by the fact that the /ɑ/ is output as [ɑ]: the fact that it is [−low] is due to the dominant [+ATR] vowel to the left, and the fact that it is [−ATR] is due to the exceptionally dominant [−ATR] vowel to the right.
Furthermore, both sources of information could in principle be at an unbounded distance from any of the vowels between them. This dependency is thus consistent with the unbounded circumambient class of patterns; recall Sect. 2.3, Def. 2. The Turkana pattern should thus not be able to be described with an HL composition and to be classified as WD in the way that the Maasai pattern is, and yet an EM composition analysis of the Turkana pattern exists in which the first, inner function of the composition is neither alphabet- nor length-increasing, consistent with Heinz and Lai’s (2013) definition.
We briefly sketch this analysis here before presenting it in more technical detail in Sect. 4.3. The inner, left-subsequential function spreads [+ATR] from underlying dominant [+ATR] vowels from left to right, blocked only by following exceptionally dominant [−ATR] vowels. Underlying /ɑ/ is also re-paired by this function to intermediate  , which of course is representationally identical to an intermediate
, which of course is representationally identical to an intermediate  from underlying
from underlying  or /ɔ/. The outer, right-subsequential function then acts on this intermediate representation, spreading [+ATR] from dominant [+ATR] vowels and now also [−ATR] from exceptionally dominant [−ATR] vowels, this time from right to left. Spreading of [−ATR] is unimpeded, and spreading of [+ATR] is blocked both by low vowels and by exceptionally dominant [−ATR] vowels.Footnote 13 All instances of intermediate
or /ɔ/. The outer, right-subsequential function then acts on this intermediate representation, spreading [+ATR] from dominant [+ATR] vowels and now also [−ATR] from exceptionally dominant [−ATR] vowels, this time from right to left. Spreading of [−ATR] is unimpeded, and spreading of [+ATR] is blocked both by low vowels and by exceptionally dominant [−ATR] vowels.Footnote 13 All instances of intermediate  , whether from underlying /ɑ/,
, whether from underlying /ɑ/,  , or /ɔ/, will surface as [ɑ] if and when this function spreads [−ATR] to them.
, or /ɔ/, will surface as [ɑ] if and when this function spreads [−ATR] to them.
The inner function thus increases neither the size of the input alphabet nor the length of the string, but the two functions do crucially interact. This is most obvious in the case of flanked /ɑ/: it must first be re-paired to  by the inner, left-subsequential function, which crucially enables it to be output as [ɑ] by the outer, right-subsequential function.Footnote 14 We thus maintain that Heinz and Lai’s (2013) reliance on the absence of markup in their definition of weak determinism is insufficient, and that instead the absence of function interaction is key. When the output of a given element in a string depends on information either unboundedly far to the left or unboundedly far to the right, as it does in Maasai, no interaction between composed contradirectional subsequential functions is necessary, but interaction is necessary when it depends on information both unboundedly far to the left and unboundedly far to the right, as it does in Turkana.
by the inner, left-subsequential function, which crucially enables it to be output as [ɑ] by the outer, right-subsequential function.Footnote 14 We thus maintain that Heinz and Lai’s (2013) reliance on the absence of markup in their definition of weak determinism is insufficient, and that instead the absence of function interaction is key. When the output of a given element in a string depends on information either unboundedly far to the left or unboundedly far to the right, as it does in Maasai, no interaction between composed contradirectional subsequential functions is necessary, but interaction is necessary when it depends on information both unboundedly far to the left and unboundedly far to the right, as it does in Turkana.
4 Revising the definition of weak determinism
In the previous section we demonstrated that the nature of the dependencies in the harmony patterns of Maasai and Turkana are distinct: that the Turkana pattern is unbounded circumambient, and that the Maasai pattern is unbounded semiambient. Despite this difference, Heinz and Lai’s (2013) formal definition of weak determinism treats the two patterns as equivalent since they can both be broken down into two contradirectional subsequential functions that involve neither alphabet- nor length-increasing markup.
In Sect. 4.4, Def. 6 below, we offer a formal definition of weak determinism that correctly distinguishes between unbounded semiambient and unbounded circumambient processes and which centers the concept of interaction, defined less formally in Sect. 2.1, Def. 1 above, and to be defined more formally in Sect. 4.2, Def. 5 below. We define the WD functions “from above,” directly in terms of a restriction on ND functions (recall Sect. 2.3), in contrast with Heinz and Lai’s (2013) definition “from below” in terms of restricted compositions of contradirectional subsequential functions following Elgot and Mezei’s (1965) result relating the ND functions to compositions of subsequential functions (recall Sect. 2.2). In doing so, as we shall see, the presence of interaction in ND functions and their absence in WD functions becomes more clear.
In general, an ND function may use information from an unbounded distance in both directions to determine the output for any given input symbol of a given input string. Our proposed restriction for the definition of WD functions requires that for any given output position, the function only ever needs unbounded access in one direction, but that direction may vary from one point in any given string to another. For example, two iterative phonological processes proceeding in opposite directions where neither process changes the conditions or result of (nonvacuous) application of the other (as in the analysis of Maasai) will never result in an input string \(w = x_{1} x_{2} \ldots x_{i} \ldots x_{n}\) where there is some \(x_{i}\) whose associated output depends on information from both directions: either one process will apply, the other will apply, neither process will apply, or if both apply, those applications must result in the same outcome. (These last cases meet the definition because it can be determined that the process applies without considering information only obtainable from both directions.) We formalize this concept using an automaton called a bimachine (Schützenberger 1961; Eilenberg 1974), use it to introduce a more precise definition of interaction, show how interaction cleanly distinguishes the Maasai and Turkana patterns, and then discuss how this relates to previous bottom-up formulations of weak determinism centered on “markup” and interaction of contradirectional subsequential functions.
4.1 Non-deterministic regular functions and bimachines
A bimachine is the canonical machine representation for regular functions (Schützenberger 1961; Eilenberg 1974; Reutenauer and Schützenberger 1991). Briefly, a bimachine is defined by two deterministic finite-state automata, ℒ and ℛ, that read the input from opposite directions and a simple output function ω that, given a tuple containing an input symbol \(x_{i}\) and the state of each automaton before it reads \(x_{i}\) (\(q^{\mathcal{L}}_{j}\) for ℒ and \(q^{\mathcal{R}}_{k}\) for ℛ), maps that tuple to an output string \(w_{i}\). Equivalently, bimachines can be viewed as explicitly determinized versions of functional (one-way) non-deterministic finite-state transducers (NDFSTs)Footnote 15 where determinization is made possible by the summary of information from both directions provided by the contradirectional automata. That is, for a given bimachine, every “joint state” \(\big(q^{\mathcal{L}}_{j}, q^{\mathcal{R}}_{k}\big)\) of the bimachine—at any given point for any given input word—corresponds to some state of the bimachine’s corresponding NDFST (Mihov and Schulz 2019: Ch. 6, Sect. 2; Lhote 2018: Sect. 3.1).Footnote 16 In this sense, bimachines provide expressivity equal to that of NDFSTs. Crucially, for the purposes of this article, bimachines provide clarity and ease of use that are notoriously not offered by NDFSTs, and this is why we employ bimachines here.
Assessing the necessity of unbounded circumambient information is critical to determine membership in the WD vs. the ND classes of functions. Because bimachines make explicit the directionality of all information necessary to determine the output associated with each input symbol, we adopt them here as the clearest representation for defining weak determinism and differentiating it from non-determinism. Bimachines offer not only a correct definition but also a clearer definition of the intended scope of the class of WD functions and how it relates to previous work on the boundary between ND and WD (Heinz and Lai 2013; Jardine 2016). Finally, bimachines are theoretical tools that offer a deterministic representation of regular functions that obviates consideration of new and inventive forms of markup when considering the complexity of a string function. We now provide a more explicit characterization of bimachines and the notation we will adopt here.
Def. 4
A bimachine \((\mathcal{L}, \mathcal{R}, \mathcal{\omega})\) that calculates a regular function \(f \operatorname{ {:} }X^{*} \rightarrow Y^{*}\) is defined by a left-to-right automaton ℒ, a right-to-left automaton ℛ, and an output function \(\mathcal{\omega} \operatorname{ {:} }Q_{\mathcal{L}} \times X \times Q_{ \mathcal{R}} \rightarrow Y^{*}\) that maps triples of a state from ℒ (\(Q_{\mathcal{L}}\)), a symbol of the input X, and a state from ℛ (\(Q_{\mathcal{R}}\)) to a substring of the output \(Y^{*}\).
An inventory of the components that define ℒ, ℛ, and their transition functions is given in Fig. 5.Footnote 17 The computation of an input-output mapping by a bimachine is illustrated schematically in Fig. 6.
Definitions of left (ℒ) and right (ℛ) automata. Each automaton is defined over an input alphabet (X), a set of states (\(Q_{\mathcal{L/R}}\)), a designated initial state (\(\smash{q^{\mathcal{L}}_{i}/q^{\mathcal{R}}_{i}}q^{\mathcal{L}}_{i}/q^{\mathcal{R}}_{i}\)), and a state transition function (\(\Delta _{\mathcal{L/R}}\)). Note that we follow a common stylistic convention for bimachines where the right automaton’s transition function has its argument order flipped (\(\Delta _{\mathcal{R}} \operatorname{ {:} }Q_{ \mathcal{R}} \times X \rightarrow Q_{\mathcal{R}}\)) relative to that of the left automaton (\(\Delta _{\mathcal{L}} \operatorname{ {:} }X \times Q_{ \mathcal{L}} \rightarrow Q_{\mathcal{L}}\))
An example run of a bimachine (\(\mathcal{L,R}\), ω) over an arbitrary string. The i-th output string \(w_{i}\) is the value of ω on (1) the state \(\smash{q^{\mathcal{L}}_{j}}q^{\mathcal{L}}_{j}\) of ℒ after reading input symbols \(x_{< i}\), (2) the i-th input symbol \(x_{i}\), and (3) the state \(\smash{q^{\mathcal{R}}_{k}}q^{\mathcal{R}}_{k}\) of ℛ after reading input symbols \(x_{>i}\). Adapted with permission from Bojańczyk and Czerwiński (2018)
For an input word \(w = x_{1} x_{2}\ldots x_{i} \ldots x_{n-1} x_{n}\), the computation proceeds as follows. First, the series of state transitions of each of the two automata is calculated in the usual fashion. Then the state sequences from each of the two automata are aligned into pairs. Finally, using the definition of the output function ω, the appropriate output string is emitted for each pair of automata states and their associated input symbol. That is, if before reading an input symbol \(x_{i}\) from the left, the left automaton ℒ is in state \(\smash{q^{\mathcal{L}}_{j}}\), and before reading \(x_{i}\) from the right, the right automaton ℛ is in state \(\smash{q^{\mathcal{R}}_{k}}\), then the output of \(x_{i}\) is determined by \(\smash{\omega \big(q^{\mathcal{L}}_{j},x_{i},q^{\mathcal{R}}_{k}\big)}\).
We close this introduction to bimachines and their interpretation with three observations: one on the correspondence between bimachines and more familiar NDFSTs, one on the interpretation of the output function, and one on the relevance of bimachines for formal theories of phonology that do not obviously make use of superficially similar representations. First, as briefly mentioned earlier, the relationship between bimachines and NDFSTs is straightforward. Each pair of automata states of the bimachine can be interpreted as a single state of an NDFST, and the bimachine’s output function performs a function analogous to the NDFST’s transition relation/output function (see e.g. Mihov and Schulz 2019: Ch. 6, Sect. 2 and Lhote 2018: Sect. 3.1 for details). This correspondence between bimachines and NDFSTs highlights that every state of a functional NDFST can be factored into information about prefixes (= substrings originating at the left edge), plus information about suffixes (= substrings originating at the right edge), relative to the position associated with the current state after an NDFST reads some partial input string. This intuition will be useful when considering the relationship of bimachines to EM compositions and hence also when considering the relationship of the definition of the WD functions presented here to the approaches of previous definitions.
Second, note that the output function of a bimachine \(\omega \operatorname{ {:} }Q_{\mathcal{L}} \times X \times Q_{\mathcal{R}} \rightarrow Y^{*}\) implementing a regular function provides a ‘local’ summary of that function’s behavior—it describes everything we need to know about what output each input symbol gets mapped to under what context, described by a pair of states \((q^{\mathcal{L}}_{j}, q^{\mathcal{R}}_{k})\). Because each left-automaton state corresponds to a set of prefixes and each right-automaton state corresponds to a set of suffixes, each of the state pairs that can actually occur together in a given bimachine and define a context for ω corresponds to a set of circumfixes (= contexts). In more linguistically familiar terms, the output function ω of a bimachine is essentially a carefully orchestrated set of rewrite rules defining the contextualized behavior of the regular function associated with the bimachine. Each state of a reachable state pair corresponds directly to the regular expressions of symbols (usually feature vectors) that define a lefthand (or righthand) context in a traditional rewrite rule like  .
.
We close by summarizing the significance of bimachines for phonological formalisms that do not appear to use anything resembling a finite-state transducer (or bimachine) to model string functions. First, recall from Sect. 2.1 that any phonological formalism that involves a function mapping an input string to an output string (usually a UR↦SR map) has some presentation-independent complexity indicating the minimum expressivity required to implement that function; recall also from Sect. 1 that complexity is organized in terms of classes of functions—e.g. input strictly local, subsequential, etc. Each of these classes usually has one or more machine-independent or extensional characterizations and usually has one or more canonical machines that characterize any function in that class. Briefly, a machine-independent or extensional characterization of a function \(f \operatorname{ {:} }X^{*} \rightarrow Y^{*}\) in some class C depends only on properties of the mapping f between input string and output string—not on any specific representation (e.g. phonological formalism) or implementation of that input-output mapping. A canonical machine of some type for f is usually unique, has a minimal number of states relative to all machines in class C that implement f, and has some relatively transparent connection between the definition of its components and at least one machine-independent characterization of f. A machine implementing some function f is a concrete representation for working with or analyzing f, and a machine-independent characterization may be unwieldy: a canonical machine for f offers some of the best of both worlds—concreteness, uniqueness, and interpretability. In the present context, every regular function has an associated canonical bimachine, generally comparable to the status that e.g. a (minimal) deterministic one-way finite-state automaton has for a regular language and that an onward subsequential transducer has for a subsequential function (Oncina et al. 1993: Sect. 3; Choffrut 2003; Heinz and Lai 2013: Sect. 2.1).Footnote 18
4.2 Interaction
Here we discuss a general definition of interaction between regular functions inspired by the linguistic usage of the term, and describe the role of interaction in ordered compositions of contradirectional subsequential functions (EM compositions) that can describe unbounded circumambient patterns.
In an interacting composition the first function f to apply to a word w causes a change in the behavior of the second function g to apply relative to what would have occurred if g had simply been applied to w instead of to f(w); the net result is an ND function g∘f whose behavior is “more than the sum of its parts,” i.e. not simply the union of what one would expect from applying g to w and applying f to w.
As noted at the end of Sect. 4.1, the output function \(\omega \operatorname{ {:} }Q_{\mathcal{L}} \times X \times Q_{\mathcal{R}} \rightarrow Y^{*}\) of a bimachine summarizes the local input-output behavior of the bimachine in any given context, where “context” is completely summarized by the pair of states of the bimachine’s automata reading the string context on each side of a given position within the input string. Recall also that a canonical machine for a given function f offers a concrete, unique, and interpretable representation of f. For these reasons, bimachines provide us with precisely the right machinery to operationalize the concept of interaction. Consequently, as we argue, bimachines enable us to define weak determinism in a way that correctly reflects the difference between unbounded circumambience and unbounded semiambience and that captures the linguistic intuition that an interacting composition involves a “change in behavior” of g∘f relative to the behavior of g and the behavior of f individually. Furthermore, this approach has computational merit, facilitating future exploration of the properties held by the output functions of canonical bimachines, due to its machine-independent foundation, which we describe now.
Bojánczyk (2014: Thm. 2.1 and fn. 3) shows that if we have a specific kind of what a phonologist would call a correspondence relation for a regular function f, then we can define a machine-independent characterization—and therefore a canonical bimachine—for that function. Briefly, a function f augmented with origin semantics is a normal string function equipped with a specific kind of correspondence relation: an origin function \(\mathbbm{o}_{w, f(w)} \operatorname{ {:} }\mathbb{N} \rightarrow \mathbb{N}\) which maps, for every (input word, output word) pair, each position j of the output word f(w) to the position i of the symbol in the input word that caused position j to have the symbol it does (see e.g. Dolatian et al. 2021 for discussion in a linguistic setting). For example, consider the behavior of an unknown regular function f on an input word w = ab such that f(w)=ab. Each of the correspondence relations (“origin graphs”) in Fig. 7 represents a possible origin semantics for how f(w)=ab could be the case for some function f equipped with origin semantics. On the left, f associates input a with output a and input b with output b, in one-to-one fashion. In the middle, f associates input a with output ab and input b with no output symbol. On the right, f associates input a with no output symbol and input b with output ab.
For every regular function, then, if we have an origin semantics for it, we can define a canonical bimachine with a canonical output function \(\omega \operatorname{ {:} }Q_{\mathcal{L}} \times X \times Q_{\mathcal{R}} \rightarrow Y^{*}\) driven by an associated set of canonical state pairs (Bojánczyk 2014: Thm. 2.1 and fn. 3). This means that for every regular function equipped with origin semantics, we have a straightforward path to a machine-independent characterization of that function, which we can manipulate through a canonical bimachine. This machine-independent characterization of regular functions with origin semantics is that every such function f necessarily has a unique finite set of equivalence classes of two-sided contexts, and each of these equivalence classes has a function that maps an input symbol x to an output (Bojánczyk 2014, fn. 3; see also the presentation of origin semantics in Filiot 2015: Sect. 5.4).
The total set of equivalence classes of contexts corresponds to the reachable state pairs of a canonical bimachine for f, which can be used to define the output function \(\omega _{f}:Q_{\mathcal{L}} \times X \times Q_{\mathcal{R}} \rightarrow Y^{*}\). In short, the behavior of an ND function f is summarized by the output function ω and the set of reachable state pairs of f’s canonical bimachine (per Sect. 4.1). Accordingly, we can define a non-interacting composition g∘f as one where the composition’s behavior is exactly the sum (union) of its composands, and an interacting composition as one where something is added or removed relative to the behavior of its composands.
Def. 5
Given length-preserving functions \(g, f, g \operatorname{ \circ }f \operatorname{ {:} }X^{*} \rightarrow X^{*}\) with origin-semantics and canonical bimachines whose output functions are given by \(\omega _{g}\), \(\omega _{f}\), and \(\omega _{g \operatorname{ \circ }f}\), the composition g∘f is a non-interacting composition iff \(\omega _{g \operatorname{ \circ }f}\) reflects all and only the changes that \(\omega _{g}\) makes (in the contexts \(\omega _{g}\) makes them) plus the changes that \(\omega _{f}\) makes (in the contexts \(\omega _{f}\) makes them). If instead for g∘f there exists at least one context (p,s) and input symbol x where the condition above fails to hold, the composition g∘f is an interacting composition at x in the context (p,s).
While the number of unique contexts (p,s) that exists is in principle infinite, bimachines partition the set of contexts into a finite number of equivalence classes, as described above. In this way, the finiteness of bimachines is critical to the operationalization of this definition of (non-)interaction. Once contexts are mapped to the reachable state pairs of some canonical bimachine for the composition, then the reachable state pairs of the composition can be related to the reachable state pairs of each of its composands by applying the definition of bimachine composition (see Peikov 2007: Sect. 4 or Mihov and Schulz 2019: Ch. 6, Sect. 4). The details of this construction lie beyond the scope of this article; importantly, it is precisely the use of bimachines that allows this definition of interaction to be effectively operationalized, casting a solid foundation for the definition of weak determinism that we propose.
4.3 The computational distinction between the Maasai and Turkana harmony patterns
We now show how bimachines bear out the difference between the unbounded semiambience of the Maasai pattern and unbounded circumambience of the Turkana pattern, and in doing so, we demonstrate how bimachines accentuate the necessity of interaction that is core to the Turkana pattern.
Consider the bimachine for Maasai harmony in Fig. 8 and its run in Fig. 9 on an informative underlying form, where the low vowel /ɑ/ is both preceded and followed by dominant [+ATR] vowels.
Left automaton ℒ (top left), right automaton ℛ (top right), and output function ω (bottom) of a bimachine for the Maasai pattern. Transition \(\smash{q^{\mathcal{L}}_{1} \rightarrow q^{\mathcal{L}}_{2}}q^{\mathcal{L}}_{1} \rightarrow q^{\mathcal{L}}_{2}\) initiates left-to-right spreading of [+ATR] and transition \(\smash{q^{\mathcal{R}}_{1} \rightarrow q^{\mathcal{R}}_{2}}q^{\mathcal{R}}_{1} \rightarrow q^{\mathcal{R}}_{2}\) initiates right-to-left spreading of [+ATR]
Run of the Maasai bimachine in Fig. 8 on the input  , resulting in the output
, resulting in the output  ‘3sg-cut-dat-appl’ (8e). The downward arrows indicate the semiambient information needed by the output function ω to determine the output
‘3sg-cut-dat-appl’ (8e). The downward arrows indicate the semiambient information needed by the output function ω to determine the output  from input /ɑ/ in this context
from input /ɑ/ in this context
The top row of Fig. 9 shows the state transitions made by the left automaton ℒ as it reads the input symbols in the second row from left to right, and the third row shows the state transitions made by the right automaton ℛ as it reads the same input symbols from right to left. Each symbol of the surface form, shown on the last row, is determined by the output function ω based on the input symbol (\(x_{i}\)) and the states of ℒ and ℛ (\(q^{\mathcal{L}}_{j}\) and \(q^{\mathcal{R}}_{k}\)) before reading \(x_{i}\). This is highlighted in the figure for the /ɑ/ in the form that is both preceded and followed by dominant [+ATR] vowels. According to the output function ω in Fig. 8, line (a), all that matters when the input symbol is /ɑ/ in Maasai is whether the prior state of ℒ is \(q^{\mathcal{L}}_{2}\)—that is, whether a dominant [+ATR] vowel has already been read to the left of the /ɑ/. In short, only unbounded semiambient information is required in the computation of Maasai harmony.
In the Maasai bimachine representation in Fig. 8, the automata states keep track of whether the information from their causal past (prefixes for the left automaton ℒ, suffixes for the right automaton ℛ) licenses a change or not. The states labeled \(\smash{q^{\mathcal{L}}_{2}}\) (for ℒ) and \(\smash{q^{\mathcal{R}}_{2}}\) (for ℛ) are the states that license spreading; other states bookkeep whether the machine has encountered a spreading trigger, a blocker, or word boundaries. The output function ω is then defined in a piecewise fashion. Crucially, note that the output symbol never depends on both information from the left and information from the right. That is, any conjunction within the conditions of the piecewise-defined output function can be defined using states from at most one of the two automata. The implicit ordering of components of a piecewise function definition means, for example, that line (c) of the output function ω is only used if the conditions for lines (a–b) fail to apply to the current input—i.e. if the negation of conditions for all lines prior to (c) hold. This may superficially appear to suggest that line (c) requires information not only about the righthand side of the string, but also the lefthand side; however, lines (a–c) can be re-ordered without changing the behavior of the string function, demonstrating that information from both sides of the string is not in fact necessary to determine any output string.
In contrast, recall that in the Turkana harmony pattern, the realization of a (suffix) low vowel depends on information on both sides of the vowel: whether there is a preceding dominant [+ATR] vowel and whether there is a following exceptionally dominant [−ATR] suffix vowel. Consider now the bimachine for Turkana harmony in Fig. 10 and its run in Fig. 11 on an informative underlying form, where the low vowel /ɑ/ is preceded by dominant [+ATR] vowels and followed by an exceptionally dominant [−ATR] suffix vowel.
Left automaton ℒ (top left), right automaton ℛ (top right), and output function ω (bottom) of a bimachine for the Turkana harmony pattern. Transition \(\smash{q^{\mathcal{L}}_{1} \rightarrow q^{\mathcal{L}}_{2}}q^{\mathcal{L}}_{1} \rightarrow q^{\mathcal{L}}_{2}\) initiates left-to-right spreading of [+ATR], transition \(\smash{q^{\mathcal{R}}_{1} \rightarrow q^{\mathcal{R}}_{3}}q^{\mathcal{R}}_{1} \rightarrow q^{\mathcal{R}}_{3}\) initiates right-to-left spreading of [+ATR], and transitions \(\smash{q^{\mathcal{R}}_{\{1,3\}} \rightarrow q^{\mathcal{R}}_{2}}q^{\mathcal{R}}_{\{1,3\}} \rightarrow q^{\mathcal{R}}_{2}\) initiate right-to-left spreading of [−ATR]
Run of the Turkana bimachine in Fig. 10 on the input  , resulting in the output
, resulting in the output  ‘ger-drop-epi-dat-voi’ (13e). The downward arrows indicate the circumambient information needed by the output function ω to determine the output [ɑ] from input /ɑ/ in this context
‘ger-drop-epi-dat-voi’ (13e). The downward arrows indicate the circumambient information needed by the output function ω to determine the output [ɑ] from input /ɑ/ in this context
As before, the top row of Fig. 11 shows the state transitions made by the left automaton ℒ as it reads the input symbols in the second row from left to right, the third row shows the state transitions made by the right automaton ℛ as it reads the same input symbols from right to left, and the last row shows the surface form determined by the output function ω based on \(\big(q^{\mathcal{L}}_{j}, x_{i}, q^{\mathcal{R}}_{k}\big)\) triples. This is highlighted in the figure for the /ɑ/ in the form that is preceded by dominant [+ATR] vowels and followed by an exceptionally dominant [−ATR] suffix vowel. According to the output function ω in Fig. 10, lines (a–b), when the input symbol is /ɑ/ in Turkana it matters whether the prior state of ℒ is \(\smash{q^{\mathcal{L}}_{2}}\)—that is, whether a dominant [+ATR] vowel has already been read to the left of the /ɑ/—and whether the prior state of ℛ is \(\smash{q^{\mathcal{R}}_{2}}\)—that is, whether an exceptionally dominant [−ATR] vowel has already been read to the right of the /ɑ/. In short, unbounded circumambient information is crucially required in the computation of Turkana harmony.
The bimachine representation for Turkana harmony in Fig. 10 makes clear the origins of the information necessary to determine any given output symbol. The two-sided context that determines whether an input low vowel /ɑ/ will ultimately be output as [ɑ] can be read directly from the first line (a) of the bimachine output function ω; else-wise, the second and last lines (b, g) determine whether input /ɑ/ will be output as  or faithfully as [ɑ], respectively.Footnote 19 When the left automaton ℒ is in state \(\smash{q^{\mathcal{L}}_{2}}\), the right automaton ℛ is in state \(\smash{q^{\mathcal{R}}_{2}}\), and the current input symbol is /ɑ/, then it will be mapped to [ɑ]. All other lines in the output function require information about the state of only one of the bimachines’s two automata. Crucially, the realization of the low vowel depends on circumambient information, from both the left and the right. Together with the knowledge that the states of the left and right automata encode information from unboundedly far to each side, we can see that this differs from the output function for Maasai in Fig. 8.
or faithfully as [ɑ], respectively.Footnote 19 When the left automaton ℒ is in state \(\smash{q^{\mathcal{L}}_{2}}\), the right automaton ℛ is in state \(\smash{q^{\mathcal{R}}_{2}}\), and the current input symbol is /ɑ/, then it will be mapped to [ɑ]. All other lines in the output function require information about the state of only one of the bimachines’s two automata. Crucially, the realization of the low vowel depends on circumambient information, from both the left and the right. Together with the knowledge that the states of the left and right automata encode information from unboundedly far to each side, we can see that this differs from the output function for Maasai in Fig. 8.
We have focused on the unbounded circumambience required to map /ɑ/ to [ɑ] in this analysis. However, it is also the case that all other input-output ATR mappings in Turkana participate in an unbounded circumambient pattern. Whereas the unbounded circumambience of the low vowel’s realization is easy to see from line (a) of the output function of the bimachine in Fig. 10, the unbounded circumambience of the other vowel mappings is obscured by the implicit ordering of the output function’s top-to-bottom evaluation as a piecewise function. That is, the conditions that license [+ATR] spreading, lines (e–f), depend on unbounded circumambient information because they include not only the determination that there is a dominant [+ATR] vowel to the left of the input index, but also that there is not an exceptionally dominant [−ATR] vowel to the right of the input index—because otherwise, the prior-ordered lines (c–d) would have already ensured leftward [−ATR] spreading. Both the conjunctive internal structure of output condition (a) and the non-trivial ordering of conditions (c–d) and (e–f) belie the unbounded circumambience of the Turkana pattern.
4.4 Weakly deterministic functions and bimachines
To crystallize the intuition that WD ought to be the class that captures unbounded semiambient patterns, we can define the WD functions as the subclass of ND functions definable with a bimachine whose output function meets a specific condition:
Def. 6
A function f is weakly deterministic iff there exists a bimachine implementing f (per Def. 4) such that its output function ω exhibits the following property for all \(q^{\mathcal{L}}\), x, y, and \(q^{\mathcal{R}}\):
In words, Def. 6 states that if ω is the output function of a WD bimachine and it maps x to y when its left automaton is in state \(q^{\mathcal{L}}\) and its right automaton is in state \(q^{\mathcal{R}}\), then either the input-output mapping \(\omega \big(q^{\mathcal{L}}, x, q^{\mathcal{R}}\big) = y\) is explainable by \(q^{\mathcal{L}}\) alone or it is explainable by \(q^{\mathcal{R}}\) alone: either ω mapping x to y is licensed by the left state being \(q^{\mathcal{L}}\) or it is licensed by the right state being \(q^{\mathcal{R}}\). Note that for a given bimachine implementing a WD function and a given input word, the direction to “look” that determines the output for a given input symbol may be leftwards for some symbols and rightwards for others, and it is not in general a priori predictable which direction the determining information will come from.
To be clear, per the semantics of inclusive-or (∨), Def. 6 does not preclude that mapping x to y may be independently licensed by both the current left state and the current right state; it simply forbids bimachines where the output of some symbol x depends on simultaneous knowledge of both the left state and the right state having particular values. The definition also does not require a priori knowledge or computation of which one side (if any) has information that licenses mapping input x to output y. Operationally, in a bimachine known to be weakly deterministic, one may look at the current input symbol x and left automaton state \(q^{\mathcal{L}}\) and check if that state alone licenses mapping x to some y, and if \(q^{\mathcal{L}}\) does not, then one may proceed to check if x and the current right automaton state \(q^{\mathcal{R}}\) alone licenses mapping x to some y. Moreover, again given the semantics of inclusive-or, it will never matter which order one looks at the left vs. right states, or that sometimes one ends up looking at both to check if at least one licenses mapping x to y. Instead, what matters is the directionality of information that licenses mapping input x to output y.
In solidifying the boundary between weak determinism and non-determinism, we have focused exclusively on patterns that require the use of information at an in principle unbounded distance away from the target of a change, and accordingly, we have centered the directionality of information in our discussions of that boundary. This may leave one with questions about how subsequential patterns with bounded bidirectional contexts are handled by our definition. Consider  . While the most intuitive origin semantics for this map does require information from both sides and hence the map may appear superficially non-deterministic, the information required is not unboundedly far in either direction and there are alternative origin semantics that are clearly input strictly local. The relevant left-to-right origin semantics maps every input substring CA to the empty string and then either observes a D and maps it to CBD or observes a non-D symbol X and maps it to CAX; the relevant right-to-left origin semantics is symmetrically analogous, mapping AD to the empty string and then either observing a C and mapping it to CBD or observing a non-C symbol X and mapping it to XAD. In both origin semantics, we know that a function only requires lookahead corresponding to at most one symbol beyond the current “focal” position. The left-to-right origin semantics can be implemented by a bimachine where the left automaton does all the work, while the right automaton has only a single state (i.e. does nothing); similarly, the right-to-left origin semantics can be implemented by a bimachine where the right automaton does all the work. The existence of both of these origin semantics independently shows that the string function defined by
. While the most intuitive origin semantics for this map does require information from both sides and hence the map may appear superficially non-deterministic, the information required is not unboundedly far in either direction and there are alternative origin semantics that are clearly input strictly local. The relevant left-to-right origin semantics maps every input substring CA to the empty string and then either observes a D and maps it to CBD or observes a non-D symbol X and maps it to CAX; the relevant right-to-left origin semantics is symmetrically analogous, mapping AD to the empty string and then either observing a C and mapping it to CBD or observing a non-C symbol X and mapping it to XAD. In both origin semantics, we know that a function only requires lookahead corresponding to at most one symbol beyond the current “focal” position. The left-to-right origin semantics can be implemented by a bimachine where the left automaton does all the work, while the right automaton has only a single state (i.e. does nothing); similarly, the right-to-left origin semantics can be implemented by a bimachine where the right automaton does all the work. The existence of both of these origin semantics independently shows that the string function defined by  is clearly subsequential, and in fact input strictly local. Output mappings for all input words can be performed with information from only one of the bimachine’s automata.
is clearly subsequential, and in fact input strictly local. Output mappings for all input words can be performed with information from only one of the bimachine’s automata.
If the selection of an output symbol only ever depends on information at an unbounded distance from at most a single and consistent direction that is always known a priori, then it is a subsequential function. Alternatively, if the selection of an output symbol only ever depends on information at an unbounded distance from at most a single direction that is not necessarily known a priori and need not in general be uniform from symbol to symbol within the same input word, then it is a weakly deterministic function as defined in Def. 6 and as exemplified by our analysis of Maasai. Alternatively, if the selection of an output symbol sometimes depends on information at an unbounded distance in both directions simultaneously, then it is a non-deterministic regular function, as exemplified by our analysis of Turkana. In this sense, our definition of weak determinism in Def. 6 aligns precisely with the definition of interaction introduced in Def. 1 and crystalized in Def. 5: ND functions involve interaction, while WD functions do not.Footnote 20
5 Discussion
This work presents a novel formal definition of weak determinism, centering interaction as the core property that distinguishes weakly deterministic maps from non-deterministic maps within the computational complexity hierarchy of regular functions illustrated in Fig. 1. Centering interaction as the arbiter of this boundary, rather than markup (Heinz and Lai 2013; McCollum et al. 2018; Lamont et al. 2019; O’Hara and Smith 2019; Smith and O’Hara 2019) or lookahead (Jardine 2016; McCollum et al. 2020a), strengthens the status of weakly deterministic maps as a computational class of linguistic interest because it is a computationally stronger and linguistically more natural concept than those centered in previous formal definitions.
5.1 Interaction is linguistically natural
Interaction meshes well with existing concepts in linguistics. Most obviously, it has a great deal in common with the type of interaction that motivates serial rule ordering in the SPE tradition of Chomsky and Halle (1968) to distinguish e.g. “feeding” from “counterfeeding” and “bleeding” from “counterbleeding” (see Baković 2011; Baković and Blumenfeld to appear; and references therein). After all, a pair of interacting SPE rewrite rules is essentially a specific ordered composition of regular functions g∘f (Johnson 1972; Kaplan and Kay 1994). There is also much in common between our concept of interaction and the type of interaction that motivates constraint ranking and weighting in the traditions of OT (Prince and Smolensky 2004) and HG (Legendre et al. 1990). Insights gained from the study of any of these forms of interaction are thus highly likely to inform the study of the others—as they indeed already have—see for example Norton (2003), Baković (2007, 2011, 2013), and references therein for relevant formal comparisons of the descriptive and explanatory similarities and differences between these serial rule-based and parallel constraint-based theoretical frameworks.Footnote 21
Bringing our focus back to the more immediate concerns of this article, interaction unites all cases of unbounded circumambience and is not limited to those cases that satisfy arbitrary criteria resulting from particular decisions about what counts as markup or about what it means for a function to “look ahead” in the string. The Turkana harmony pattern is an instructive case in point. There is clear linguistic evidence for bidirectional spreading from dominant [+ATR] vowels, for low vowels undergoing left-to-right but not right-to-left spreading of [+ATR], and for right-to-left spreading from exceptionally dominant [−ATR] suffix vowels. Most significantly, left-to-right spreading of [+ATR] interacts with right-to-left spreading of [−ATR], the latter in some sense has the “final say” on the realization of vowels in a string, and each direction of spreading corresponds to one of the contradirectional FSTs of an EM composition or automata of a bimachine. The fact that the surface realization of an underlying low vowel depends on unbounded circumambient information is thus effectively disguised by the independent motivation for each of the interacting spreading processes.
This feels unlike other non-myopic patterns, such as Luganda unbounded tonal plateauing or Tutrugbu ATR harmony mentioned in Sect. 1 (see also Sect. 5.2 below), where the linguistically motivated spreading process only corresponds to one of two contradirectional FSTs of an EM composition or automata of a bimachine, albeit roughly. The other machine must be more indirectly inferred from the information in the causal future of the “primary,” linguistically motivated one, making the overall pattern non-deterministic. In the case of Tutrugbu in (3), for example, the basic pattern of [+ATR] spreading is clearly from right to left (root to prefixes), directly motivating the right-to-left machine, while the conditional blocking of spreading by [−high] vowels only in the presence of an initial [+high] prefix vowel more indirectly motivates the contradirectional machine. This is what makes some obvious form of markup necessary in Tutrugbu (McCollum et al. 2018, 2020a), and similarly for unbounded tonal plateauing in Luganda (Jardine 2016). The total mapping in Turkana is unbounded circumambient and involves lookahead, but precisely because non-myopia is not analytically salient, interaction is a linguistically useful tool for identifying that the subregular complexity of Turkana is the same as other more obviously non-myopic unbounded circumambient maps.
5.2 Interaction subsumes markup
Heinz and Lai’s (2013) vision of weak determinism as a restriction on regular functions implemented through constraints on function composition remains relevant to the reformulation of WD functions presented in Sect. 4. WD functions remain a class of functions that “can be decomposed into [an inner] subsequential and [an outer, contradirectional] subsequential function without the [inner] function marking up its output in any special way”; merely the piecewise nature of initial attempts to formally define “any special way” have been exchanged for the unifying notion of interaction described in this article. And while we argue that bimachines make the identification of interaction far easier than EM compositions do, analysts may still choose to represent WD processes using non-interacting EM compositions. For that reason, we discuss here how even for EM composition representations of the WD class, the use of markup-based definitions of the WD class should be abandoned because interaction subsumes markup.
Heinz and Lai’s (2013) definition of the WD functions identified two possible markup strategies and accordingly stipulated that WD functions be both alphabet- and length-preserving. In identifying and prohibiting strategies case by case, the focus on markup in this definition of weak determinism inspired further work identifying novel variations on these two markup strategies. In these works, an even more clever, third markup strategy has been identified, a form we call phonotactic coding.Footnote 22 In this strategy, substrings of the input alphabet which would otherwise be phonotactically illicit in the language in question are used to smuggle information from an inner function to an outer function via the intermediate form. More specifically, given the input alphabet \(\mathcal{A}\) and a set \(\mathcal{S}\) of non-occurring, phonotactically illicit substrings over \(\mathcal{A}\), the inner function may change some substring of the input to a substring of the same length drawn from \(\mathcal{S}\), conditioned on some motivating property of the input string. If this change is made at a location in the string that the outer function would encounter before it would encounter the motivating property of the input string, then the output of the outer function at that point may be conditioned on information possibly an unbounded distance from that decision point, rendering the composition as a whole non-deterministic. For this to occur, it is only required that each otherwise illicit substring introduced by the inner function be unambiguously interpretable by the outer function (i.e. from the opposite direction) as having been introduced because the inner function encountered particular conditions somewhere in the (unbounded) causal future of the outer function. The result is alphabet-preserving because the set \(\mathcal{S}\) is defined over the input alphabet \(\mathcal{A}\), and it is length-preserving because substrings from \(\mathcal{S}\) only replace substrings of the same length.
Figure 12 illustrates phonotactic coding with a schematic example of unbounded tonal plateauing, with the inner function marking up its output with the phonotactic code suggested by Lamont et al. (2019: 197). In cases of unbounded tonal plateauing, all low (L) tones between two high (H) tones surface as H; other Ls surface as L.Footnote 23 These are quintessential cases of unbounded circumambience: the output of a given L is dependent on information that is unboundedly far to the left and information that is unboundedly far to the right. The phonotactic code in this case is the intermediate HLH substring, written in one fell swoop by the inner function f upon encountering an H preceded by two or more Ls which are themselves preceded by another H. More precisely, after reading and faithfully writing an initial string of some number l of Ls (arrow 1) followed by the first H (arrow 2) in the input string x, the inner function f reads an L. At this point, nothing is written—hence the dotted arrow 3 and the corresponding empty symbol λ in the intermediate string y. If the next symbol to be read were an H, the 2-symbol sequence HH would be emitted: the first H taking the place of the previously unwritten L and the second being the faithful realization of the H just read. Lamont et al. (2019: 197) note that this HLH ↦ HHH mapping “model[s unbounded tonal plateauing] in a local context.” This idiosyncratic treatment of plateaux of length 3 is crucial for this markup strategy to succeed.
The inner function f instead reads another L and once more writes nothing (arrow 4). A subsequent string of some number m of Ls is then written faithfully (arrow 5), and upon reading another H, f writes the sequence HLH (the trio of arrows labeled 6). This compensates for the two previous unwritten Ls, and it does so with the substring HLH which, when present as such in an input string, would have been written by the very same inner function f as HHH (= “unbounded tonal plateauing in a local context”). HLH thus functions as a phonotactic code, informing the outer function g that the conditions for non-local unbounded tonal plateauing were found in the input string x and that the L of this HLH coded substring in y, and all subsequent Ls until another H is read, should surface as H in the ultimate output string z.
To be clear, the works cited above acknowledge that phonotactic coding is a form of markup (see fn. 22), and indeed that “all unbounded circumambient patterns require some sort of markup to be used in the application of a pair of subsequential mappings” (O’Hara and Smith 2019: 10).Footnote 24 Nevertheless, phonotactic coding has been claimed in these works to critically distinguish unbounded circumambient patterns that can be described by WD functions from those requiring more expressive classes of functions because the contradirectional breakdowns of these latter functions crucially require increasing either the alphabet or the length of the string, the only forms of markup explicitly precluded by Heinz and Lai’s (2013) formal definition of WD functions. Perhaps most explicitly, O’Hara and Smith (2019: 6) claim that alphabet- or length-increasing markup is “more powerful” than phonotactic coding of the kind illustrated in Fig. 12 above. As evidence for this claim, these authors argue that the unattested set of “true sour grapes” patterns, illustrated with a hypothetical example in (1b) in Sect. 1 and defined in (14), can be modeled with alphabet- or length-increasing markup but not with phonotactic codes. These true sour grapes patterns are intended to be distinguished from “false sour grapes” patterns, a set which includes attested unbounded tonal plateauing.
-
(14)

O’Hara and Smith (2019) and Smith and O’Hara (2019) show that no length- or alphabet-preserving composition can be devised to correctly describe a true sour grapes pattern, whereas such compositions are possible for false sour grapes patterns (e.g. for unbounded tonal plateauing in Fig. 12). The key difference between unbounded tonal plateauing (qua false sour grapes) and true sour grapes is that unbounded tonal plateauing defines unbounded circumambient conditions for making a change to an input string (spreading H), whereas true sour grapes defines unbounded circumambient conditions for not making a change to an input string. This key difference guarantees the existence of a phonotactic code for unbounded tonal plateauing, as follows. Upon encountering an H in an unbounded tonal plateauing pattern, the inner function will not spread it unless there is another H further down the line, in principle an unbounded distance away. The bounded HLH ↦ HHH mapping is an instance of the more general spreading condition (“unbounded tonal plateauing in the local context”); such bounded maps can be performed by the inner function, guaranteeing that HLH can function as a phonotactic code for unbounded tonal plateauing qua false sour grapes.
There is no such guarantee of a phonotactic code for true sour grapes. Upon encountering a trigger T, the inner function will spread it unless there is a blocker B further down the line, in principle an unbounded distance away. There are thus only bounded instances of the more general non-spreading condition, TUB, which map unchanged to TUB. Thus, no substring can be freed up to function as a phonotactic code. But it is important to keep in mind that all possible substrings of \(\Sigma ^{*}\) are assumed to be equally likely in the toy language of (14): T is just as likely as B or U at every point in the string, leaving no substring of any length capable of both encoding the presence of a blocker elsewhere in the string while preserving the original identity of the substring at the location of the markup. While this toy example neatly demonstrates that phonotactic coding is a non-viable markup strategy for completely unrestricted input languages (that is, input languages where literally any member of \(\Sigma ^{*}\) is a viable word of the language), we argue that this is not a linguistically relevant result at the very least because all languages, human or otherwise, are generally not unrestricted in this way. In other words, while a bounded instance of the more general non-spreading condition in cases of true sour grapes is not guaranteed, it is nevertheless highly probable if not fully guaranteed that some bounded, phonotactically-illicit substring can be recruited to do the necessary markup work (Graf 2016).
This brings us back to O’Hara and Smith’s (2019) claim that alphabet- and length-increasing markup is “more powerful” than phonotactic coding. If “more powerful” is understood to mean “more expressive,” this is in general false, as expressivity is usually defined and considered. In formal language theory, a function class picks out an extensionally-definable equivalence class of functions.Footnote 25 O’Hara and Smith (2019) argue that “true” sour grapes can only be modeled with alphabet- and length-increasing codes while “false” sour grapes can be modeled with either alphabet-/length-increasing codes or phonotactic codes. This is the central logic of their claim that phonotactic codes are not as expressive as alphabet- and length-increasing codes. However, the difference between the mappings of so-called “true” and “false” sour grapes (and thus their difference in “power” as claimed by O’Hara and Smith 2019) lies in a restriction on the input languages of the inner and outer functions that O’Hara and Smith (2019) use to describe these patterns. No complexity class that we are aware of relies so centrally on comparable restrictions of the domain of the input language.
For example, consider a majority-rules function \(f(a^{n} b^{m}) = c^{{max}(n,m)} \) which maps strings of n a’s and m b’s to a string of c’s whose length is either n or m, whichever value is greater. This function—this mapping between input strings and output strings—is not regular. Yet, if we (arbitrarily) restrict the input domain f to the language \(a^{*}\), i.e. where no b’s will ever occur, our function is suddenly regular: mapping \(a^{n}\) to \(c^{n}\) does not require supra-regular computational power. Considering the behavior of f under this domain restriction may tell us something about the relationship between the structure of the input language and the behavior of f, but the usual approach to classifying the complexity of f itself would still indicate the function is not regular.
That the functional descriptions of some language patterns are unable to support phonotactic coding strategies is really a statement about those patterns, not a description of the expressivity of the machinery required to describe a function on those patterns. The exchangability of novel intermediate symbols, length-increasing codes for such symbols, and phonotactic codes for such symbols is apparent from the fact that they all serve the same purpose: creating information about one end of the input string at the other end of the intermediate string. It is the ability of each of these three strategies to accomplish precisely this goal that permits compositions of contradirectional subsequential functions to define ND functions using any of them.
5.3 Machine-independence
In Sect. 1 we alluded to the value that good definitions can provide in crystalizing linguistic intuitions and in offering clarity and confidence about what linguistic formalisms can actually do or how they compare. In Sect. 2.1 and Sect. 4.1, we elaborated more specifically on how machine-independent or extensional characterizations of a language or function class can be used as relatively formalism-agnostic tools for phonological metatheory: each machine-independent characterization of a given class offers a means to completely describe and understand that class and any language or function within that class, as well as a solid foundation to understand and prove results about that class—including e.g. determining whether it is distinct from some other class.
In this article we have extended earlier work expressing the intuitive definition, linguistic motivation, and expected boundary of the WD class (Heinz and Lai 2013) by presenting two distinct classes of phenomena—exemplified by Maasai and Turkana—and then offering a definition of “interaction” between regular string functions and a corrected definition of the WD class that separates those two classes of phenomena. We have chosen a machine-independent characterization of the regular functions transparently related to the unbounded circumambience vs. unbounded semiambience distinction and as a direct result have a definition of the WD class that is simple to understand and whose boundary with respect to ND is clear. The machine-independent characterization we have chosen is also crucial to offering a definition of interaction in regular string functions that can be used to mechanically identify any and all contexts where two string functions interact. The definition of interaction and the revised definition of WD functions also present a unified picture of how any EM composition that defines an ND function does so, regardless of whether it uses novel symbols, length-increasing codes for novel symbols, phonotactic codes for novel symbols, some as-yet unidentified new strategy for encoding novel symbols—or even no codes for novel symbols at all, as in Turkana. In short, we have provided a definition of the WD class of functions that solves the problems of Heinz and Lai’s (2013) original, first-pass definition, matching the spirit of that definition by fixing the letter.
Setting aside the issue of the definition of the WD class, the type of canonical bimachines (and the associated machine-independent characterization) presented here offer an alternative to EM compositions for future work on long-distance processes in phonology. First, when presented with a single independently motivated bidirectional phenomenon, an EM composition-based analysis requires the linguist to engineer two tightly coupled subsequential functions so that they interact in just the right way to define the overall map of interest. As we have shown, there are many strategies to accomplish this, there is not in general anything linguistically interesting or insightful about any particular strategy for doing this, it is often nevertheless difficult to do correctly for analysts, and the resulting analyses are generally harder to read and understand as a consequence. Circumstances where there are two independently motivated contradirectional processes still may justify use and exploration of EM compositions, but identification of interaction or classification of a composition’s complexity will likely remain easier to analyze using representations like what we have presented here: canonical bimachines offer a simpler path to identifying interaction that is otherwise difficult to spot, and to classifying an EM composition’s position on one side of the WD–ND boundary vs. the other.
6 Conclusion
Phonologists have long concerned themselves with the ways that more than one grammatical statement (rules, constraints, etc.) may interact with one another. This article provides a formal definition of function interaction that differentiates properly weakly deterministic functions from the strictly more expressive class of non-deterministic functions. Formal comparison of the functional analyses of the ATR harmony patterns of Maasai and Turkana demonstrates the key difference between weakly deterministic and non-deterministic functions: the contradirectional subsequential functions comprising weakly deterministic functions do not interact because the patterns they describe are unbounded semiambient, while those comprising a non-deterministic function do interact because the patterns they describe are unbounded circumambient. By framing the distinction between weak determinism and non-determinism in this way, our proposal subsumes the various strategies employed in previous work to delimit the subregular class of weakly deterministic functions, thereby offering a single, unified way to characterize the expressivity difference between unbounded circumambient and other, unbounded semiambient bidirectional patterns.
Beyond the temptation to ascribe computational significance to cosmetic differences between markup strategies, viewing weak determinism as a class defined by its resistance to description by a collection of disparate strategies is less parsimonious than the unified account provided by interaction. It also obscures the sense of “intermediateness” that is characteristic of the class. Heinz and Lai (2013: 54) justify the framing of these functions as “weakly” or intermediately deterministic by noting that “they are not necessarily deterministic, but they are ‘more’ deterministic than regular functions.” A more substantive (albeit informal) characterization of the intermediateness of weak determinism is given in (15).
-
(15)
Deterministic, weakly deterministic, and non-deterministic regular functions compared
-
a.
Deterministic (subsequential): There exists a side of the string, for every position in all strings, for which the identity of the output element is determined by elements from that side.
-
b.
Weakly deterministic: For every position in all strings, there exists a side of the string for which the identity of the output element is determined by elements from that side.
-
c.
Non-deterministic: For every position in all strings, both sides of the string may be used to determine the identity of the output element.
-
a.
A weakly deterministic function is intermediate in expressivity because different output positions may require information from different sides of the form (unlike deterministic functions), but no single output position requires information from both sides of the form (unlike non-deterministic functions). In this sense, weakly deterministic functions are “more” deterministic than non-deterministic functions but “less” so than deterministic functions. This intuition is preserved in thinking of determinism in terms of interaction. Deterministic functions are regular functions that can be defined as non-interacting compositions of equi-directional (as opposed to contradirectional) subsequential functions. Weakly deterministic functions are regular functions that can be defined as a non-interacting compositions of contradirectional subsequential functions. And finally, non-deterministic functions are regular functions that can be defined as a interacting compositions of contradirectional subsequential functions. Interaction thus captures the essense of what makes weak determinism not quite deterministic. Defining weakly deterministic functions as the class of EM compositions for which the inner and outer functions do not interact is computationally more sound than attempts to exhaustively list all of the ways one can imagine marking up an intermediate string.
Data Availability
All relevant data and material is included or cited in the manuscript.
Code Availability
Not applicable.
Notes
What we are calling “regular functions” here and throughout are more precisely termed the rational functions in the larger context of formal language theory from the last few decades, where the term “regular” has begun to be reserved for more complex functions that can be expressed by e.g. two-way deterministic finite-state transducers; see e.g. Gauwin (2020: Ch. 2). Because we have no need to make use of this distinction, we keep with older usage and with most of the existing literature in computational phonology and persist in using the term “regular” throughout. We thank a reviewer for advocating that we be upfront about this terminological issue.
Leipzig conventions for abbreviations are used in this article. In all data cited in this article, morpheme boundaries are indicated with hyphens, roots are indicated with a preceding \(\sqrt {}\) symbol, and the presence of the spreading feature value (or tone) in underlying representations (enclosed in
 ), and the extent of its spread in surface representations (enclosed in
), and the extent of its spread in surface representations (enclosed in  ), is indicated with underlining.
), is indicated with underlining.A reviewer takes issue with our characterization of our contribution in relation to Heinz and Lai (2013), suggesting that we are defining a different class of functions than Heinz and Lai (2013) did as opposed to revising Heinz and Lai’s definition of the WD class. We believe that this alternative characterization, while mathematically accurate, risks misrepresenting the fact that our aim here is to build on the phonological significance of (what we take to be) the intention behind Heinz and Lai’s original contribution.
Similar to our discussion of “rational” vs. “regular” in fn. 1, we are using the older term “subsequential” that is also still more prevalent in the computational phonology literature. There is a reasonable argument to be made that the name and meanings of “sequential” and “subsequential” should be swapped, and some movement towards this swap has begun in recent years elsewhere. See e.g. Roche and Schabes (1997: 45–46), Bojańczyk and Czerwiński (2018: Ch. 13, fn. 1), or Heinz and Lai (2013: fn. 3).
Indeed, Heinz and Lai (2013: 52) use “left” and “right” to characterize the two subsequential functions that comprise an HL composition. We use “inner” and “outer, contradirectional” because we find it signals more clearly that the first function to apply may be either left-subsequential or right-subsequential so long as the second function to apply is contradirectional.
Jardine’s (2016) definition of unbounded circumambience references “processes” rather than the “patterns” that we reference in Def. 2. We have changed this wording in an effort to head off misunderstandings about the scope of relevant claims, as discussed in Sect. 2.1—specifically, the misapprehension that unbounded circumambience is (strictly) a property of individual phonological rules.
Note that we omit the transcription of tone on vowels because tone does not play a role in the harmony patterns of Maasai and Turkana. Input-output discrepancies in cited data that are similarly unrelated to harmony are passed over in silence.
Citing the example
 →
→  ‘rafters made of sticks,’ Quinn-Wriedt (2013: 158) concludes that low vowels in roots do not alternate regardless of their position relative to dominant [+ATR] vowels. This is technically inconsistent with the description of the Maasai pattern that we work with in the text, but can be straightforwardly accommodated in the analysis.
‘rafters made of sticks,’ Quinn-Wriedt (2013: 158) concludes that low vowels in roots do not alternate regardless of their position relative to dominant [+ATR] vowels. This is technically inconsistent with the description of the Maasai pattern that we work with in the text, but can be straightforwardly accommodated in the analysis.In his discussion of the Turkana pattern, van der Hulst (2018: 355) states that “[w]ithin morphemes, [the] distribution [of the low vowel] is limited in such a way that it never occurs following an advanced vowel,” and cites the form
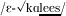 →
→  ‘sg-ostrich’ showing that a low vowel may occur preceding a [+ATR] vowel within a morpheme. This is consistent with our description of the Turkana pattern that we are working with in the text; cf. the inconsistency noted in fn. 9 for Maasai.
‘sg-ostrich’ showing that a low vowel may occur preceding a [+ATR] vowel within a morpheme. This is consistent with our description of the Turkana pattern that we are working with in the text; cf. the inconsistency noted in fn. 9 for Maasai.Glides in general disrupt harmony, such that following vowels “may be [+ATR] or [−ATR] (as with vowels following the vowel /ɑ/)” and preceding vowels “are [+ATR]” (Dimmendaal 1983: 20). This accounts for a notable exception to van der Hulst’s (2018) generalization in fn. 10 that low vowels never follow [+ATR] vowels within morphemes: the form
 ‘the Turkana people’ has a “more frequently used form”
‘the Turkana people’ has a “more frequently used form”  with a harmony-disrupting glide (Dimmendaal 1983: 20).
with a harmony-disrupting glide (Dimmendaal 1983: 20).Noske (2000: 778) also cites the form in (13a), but transcribes the root as
 in this case rather than as
in this case rather than as  .
.But recall from the discussion below example (13) that we know of no examples that crucially require [+ATR] spreading to be blocked by non-low exceptionally dominant [−ATR] vowels.
This
 derivation looks like feeding, but at the level of the individual feature changes it is technically a Duke of York derivation (Pullum 1976; McCarthy 2003). The additional, re-pairing change of /ɑ/→
derivation looks like feeding, but at the level of the individual feature changes it is technically a Duke of York derivation (Pullum 1976; McCarthy 2003). The additional, re-pairing change of /ɑ/→ makes the ultimate segmental result distinct from the prototypical Duke of York derivation A→B→A. But separating re-pairing from harmony reveals a feeding Duke of York derivation (McCarthy 2003; Gleim 2019). With specific feature changes double-underlined: first [+low, −ATR] /ɑ/ changes to [+low, +ATR]
makes the ultimate segmental result distinct from the prototypical Duke of York derivation A→B→A. But separating re-pairing from harmony reveals a feeding Duke of York derivation (McCarthy 2003; Gleim 2019). With specific feature changes double-underlined: first [+low, −ATR] /ɑ/ changes to [+low, +ATR]  , which then feeds the further re-pairing change to [−low, +ATR]
, which then feeds the further re-pairing change to [−low, +ATR]  , which then undergoes the dominance reversal change to [−low, −ATR] [ɑ]. The first change feeds the second—that is, re-pairing applies because [+ATR] harmony creates a non-structure-preserving [+low, +ATR] vowel—but the third change simply reverses the first.
, which then undergoes the dominance reversal change to [−low, −ATR] [ɑ]. The first change feeds the second—that is, re-pairing applies because [+ATR] harmony creates a non-structure-preserving [+low, +ATR] vowel—but the third change simply reverses the first.A one-way NDFST is functional if it maps each complete input string to at most one output string; such a transducer may nevertheless exhibit incremental non-determinism in which state(s) it transitions to as it reads a string from one edge to the other and what the output might be, but by defintion of being functional, by the end of the input string at most a single unique output string must be picked out. Except where noted, every reference to an NDFST henceforth will be to a functional one-way NDFST.
In general, multiple joint-states of a bimachine may correspond to a given state of an equivalent NDFST.
Final states are not included here among the components that define a bimachine’s automata because (without loss of generality) we assume Schützenberger (1961)-style bimachines that implement total functions, meaning that they are defined for every input string. It is conventional in this setting to either omit discussion of final states or to (equivalently) declare that every state is a final state.
See Heinz (2018: Sect. 2) for explicit discussion of the relationship between phonological formalism, formal language theory, and intensional vs. extensional characterizations of a language class or function class; compare this with e.g. McCollum et al. (2020a: Sect. 6) for a differing view of the role and significance of formal language theory in phonological theory with respect to explanation (as opposed to theory qua formalism) and typology.
Note, we have split up the conditions in the output function for [−ATR] and [+ATR] spreading into a base case on one line and a recursive spreading case on another because of typesetting, clarity, and consistency; there is no other significance to this choice.
Proofs are available upon request and will be included in a related manuscript in preparation.
The works cited call this “using phonotactically-illicit intermediate symbol sequences as codes for extra symbols,” (McCollum et al. 2018), “(intermediate) substring markup” (O’Hara and Smith 2019), “using predictable substrings as markup” (Lamont et al. 2019), and “information [that] is smuggled into an intermediate representation using predictable substrings of the symbols already in a language’s alphabet” (Smith and O’Hara 2019). Graf (2016) makes a related proposal, strategically identifying auxiliary symbols from the input alphabet (“green flags”) that can be used as markup.
Jardine (2016: 251ff.) cites Luganda, Digo, Xhosa, Zulu, Yaka, Saramaccan, Papago (Tohono O’odham), and South Kyungsang Korean as examples of languages with some variant of unbounded tonal plateauing; see that work for discussion and references to sources. In some cases the underlying tonal opposition is analyzed as H vs. toneless, rather than H vs. L. This distinction is irrelevant here; all that matters is that there is a two-way opposition, regardless of how it is represented.
Lamont et al. (2019: 197) even go so far as to comment negatively on the result of phonotactic coding from the perspective of substantive and methodological assumptions within phonological theory: “Encoding instructions in intermediate representations is strikingly unphonological and is not intended as a plausible interpretation of the process.”
At the very least, such a function class is expected to have multiple convergent characterizations, including an extensional, machine-independent one, even if we don’t currently know what those are.
References
Aksënova, Alëna, Jonathan Rawski, Thomas Graf, and Jeffrey Heinz. 2020. The computational power of harmony. In Oxford handbook of vowel harmony, ed. Harry van der Hulst. London: Oxford University Press.
Albert, Chris 1995. Derived environments in optimality theory: A case study in Turkana. Unpublished ms., UC Santa Cruz.
Archangeli, Diana B., and Douglas G. Pulleyblank. 1994. Grounded phonology. Cambridge: MIT Press.
Baković, Eric 2000. Harmony, dominance and control. Ph. D. thesis, Rutgers, the State University of New Jersey.
Baković, Eric 2002. Vowel harmony and cyclicity in Eastern Nilotic. In Proceedings of the 27th annual meeting of the Berkeley Linguistics Society, eds. Charles Chang, Michael J. Houser, Yuni Kim, David Mortensen, Mischa Park-Doob, and Maziar Toosarvandani, 1–12. Berkeley: Berkeley Linguistics Society.
Baković, Eric 2007. A revised typology of opaque generalisations. Phonology 24: 217–259. https://doi.org/10.1017/S0952675707001194.
Baković, Eric 2011. Opacity and ordering, 2nd edn. In The handbook of phonological theory, eds. John A. Goldsmith, Jason Riggle, and Alan C. L. Yu, 40–67. Malden: Wiley Blackwell.
Baković, Eric 2013. Blocking and complementarity in phonological theory. London: Equinox.
Baković, Eric, and Lev Blumenfeld. To appear. A formal typology of process interactions. Phonological Data & Analysis.
Bamgboṣe, Ayọ 1966. A grammar of Yoruba. Cambridge: Cambridge University Press.
Bennett, William G., and Natalie DelBusso. 2018. The typological effects of ABC constraint definitions. Phonology 35(1): 1–37. https://doi.org/10.1017/S0952675717000367.
Bojánczyk, Mikołaj 2014. Transducers with origin information. In Proceedings of the 41st international colloquium on automata, languages, and programming, 26–37. https://doi.org/10.1007/978-3-662-43951-7_3.
Bojańczyk, Mikołaj, and Wojciech Czerwiński. 2018. An automata toolbox. Course lecture notes. https://www.mimuw.edu.pl/~bojan/upload/reduced-may-25.pdf.
Chandlee, Jane 2014. Strictly local phonological processes. Ph. D. thesis, University of Delaware.
Chandlee, Jane, Rémi Eyraud, and Jeffrey Heinz. 2015. Output strictly local functions. In Proceedings of the 14th Meeting on the Mathematics of Language (MoL 2015), 112–125. https://doi.org/10.3115/v1/W15-2310.
Chandlee, Jane, and Jeffrey Heinz. 2018. Strict locality and phonological maps. Linguistic Inquiry 49(1): 23–60.
Choffrut, Christian 2003. Minimizing subsequential transducers: A survey. Theoretical Computer Science 292(1): 131–144.
Chomsky, Noam, and Morris Halle. 1968. The sound pattern of English. New York: Harper & Row.
Dimmendaal, Gerrit Jan 1983. The Turkana language. Dordrecht: Foris.
Dolatian, Hossep, Jonathan Rawski, and Jeffrey Heinz. 2021. Strong generative capacity of morphological processes. In Proceedings of the Society for Computation in Linguistics (SCiL) 2021, 228–243.
Eilenberg, Samuel 1974. Automata, languages and machines, Volume A. San Diego: Academic Press.
Elgot, Calvin C., and Jorge E. Mezei. 1965. On relations defined by generalized finite automata. IBM Journal of Research and Development 9(1): 47–68.
Filiot, Emmanuel 2015. Logic-automata connections for transformations. In Indian conference on logic and its applications, 30–57. Berlin: Springer.
Gauwin, Olivier 2020. Transductions: Resources and characterizations. Ph. D. thesis, Université de Bordeaux.
Gleim, Daniel 2019. A feeding Duke-of-York interaction of tone and epenthesis in Arapaho. Glossa: A: Journal of General Linguistics 4(97): 1–27. https://doi.org/10.5334/gjgl.805.
Graf, Thomas 2016. Weak determinism is not too weak: A reply to Jardine (2016). Unpublished ms., Stony Brook University.
Guion, Susan G., Mark W. Post, and Doris L. Payne. 2004. Phonetic correlates of tongue root vowel contrasts in Maa. Journal of Phonetics 32(4): 517–542.
Hall, Beatrice L., Richard M. R. Hall, and Martin D. Pam. 1973. African vowel harmony systems from the vantage point of Kalenjin. Afrika und Übersee: Sprachen, Kulturen 57(4): 241–267.
Hao, Yiding, and Samuel Andersson. 2019. Unbounded stress in subregular phonology. In SIGMORPHON 16, 135–143. ACL.
Heinz, Jeffrey 2011a. Computational phonology—Part I: Foundations. Language and Linguistics Compass 5(4): 140–152.
Heinz, Jeffrey 2011b. Computational phonology—Part II: Grammars, learning, and the future. Language and Linguistics Compass 5(4): 153–168.
Heinz, Jeffrey 2018. The computational nature of phonological generalizations. Phonological Typology 23: 126–195.
Heinz, Jeffrey, and William Idsardi. 2013. What complexity differences reveal about domains in language. Topics in Cognitive Science 5(1): 111–131.
Heinz, Jeffrey, and Regine Lai. 2013. Vowel harmony and subsequentiality. In Proceedings of the 13th Meeting on the Mathematics of Language (MoL 13), 52–63. https://aclanthology.org/W13-3007.
Jardine, Adam 2016. Computationally, tone is different. Phonology 33(2): 247–283. https://doi.org/10.1017/s0952675716000129.
Jardine, Adam, Nick Danis, and Luca Iacoponi. 2021. A formal investigation of Q-theory in comparison to autosegmental representations. Linguistic Inquiry 52(2): 333–358.
Johnson, C. Douglas 1972. Formal aspects of phonological description. Mouton: The Hague.
Kaplan, Ronald M., and Martin Kay. 1994. Regular models of phonological rule systems. Computational Linguistics 20(3): 331–378.
Kidda, Mairo E. 1985. Tangale phonology: A descriptive analysis. Berlin: Reimer.
Kimper, Wendell A. 2012. Harmony is myopic: Reply to Walker (2010). Linguistic Inquiry 43(2): 301–309.
Kiparsky, Paul 2015. Stratal OT: A synopsis and FAQs. In Capturing phonological shades within and across languages, eds. Yuchau E. Hsiao and Lian-Hee Wee, 2–44. Newcastle upon Tyne: Cambridge Scholars Library.
Koser, Nate, and Adam Jardine. 2020. The computational nature of stress assignment. In Proceedings of the 2019 Annual Meeting on Phonology. https://doi.org/10.3765/amp.v8i0.4676.
Lamont, Andrew, Charlie O’Hara, and Caitlin Smith. 2019. Weakly deterministic transformations are subregular. In Proceedings of the 16th Workshop on Computational Research in Phonetics, Phonology, and Morphology, 196–205. https://doi.org/10.18653/v1/W19-4223.
Leduc, Marjorie, and Adam G. McCollum. 2022. Use it or lose it harmony in Komo. Talk presented at the 10th annual meeting on phonology, UCLA.
Legendre, Géraldine, Yoshiro Miyata, and Paul Smolensky. 1990. Harmonic grammar—A formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. In Proceedings of the Twelfth Annual Conference of the Cognitive Science Society, 388–395. Mahwah: Erlbaum.
Lhote, Nathan 2018. Towards an algebraic characterization of rational word functions. CoRR arXiv:1506.06497. https://doi.org/10.48550/arXiv.1506.06497.
Mascaró, Joan 2019. On the lack of evidence for nonmyopic harmony. Linguistic Inquiry 50: 862–872.
McCarthy, John J. 2003. Sympathy, cumulativity, and the Duke-of-York gambit. In The syllable in Optimality Theory, eds. Caroline Féry and Ruben van de Vijver, 23–76. Cambridge: Cambridge University Press.
McCarthy, John J. 2010. An introduction to Harmonic Serialism. Language and Linguistics Compass 4(10): 1001–1018. https://doi.org/10.1111/j.1749-818X.2010.00240.x.
McCollum, Adam G., Eric Baković, Anna Mai, and Eric Meinhardt. 2018. The expressivity of segmental phonology and the definition of weak determinism. Unpublished ms. https://ling.auf.net/lingbuzz/004197.
McCollum, Adam G., Eric Baković, Anna Mai, and Eric Meinhardt. 2020a. Unbounded circumambient patterns in segmental phonology. Phonology 37: 215–255. https://doi.org/10.1017/S095267572000010X.
McCollum, Adam G., Eric Baković, Anna Mai, and Eric Meinhardt. 2020b. On the existence of non-myopic harmony. Unpublished ms., Rutgers University and UC San Diego.
McCrary, Kristie 2001. Low harmony, ATR harmony and verbal morphology in Kisongo Maasai. Papers in Phonology 5: 179–206.
Mihov, Stoyan, and Klaus U. Schulz. 2019. Finite-state techniques: Automata, transducers and bimachines. Cambridge: Cambridge University Press.
Mullin, Kevin, and Joe Pater. 2015. Harmony as iterative domain parsing. Talk presented at the 23rd Manchester Phonology Meeting.
Norton, Russell J. 2003. Derivational phonology and optimality phonology: Formal comparison and synthesis. Ph. D. thesis, Rutgers, the State University of New Jersey.
Noske, Manuela 1996. [ATR] harmony in Turkana. Studies in African Linguistics 25(1): 61–99.
Noske, Manuela 2000. [ATR] harmony in Turkana: A case of Faith Suffix >> Faith Root. Natural Language and Linguistic Theory 18(4): 771–812.
Oakden, Chris 2020. Notational equivalence in tonal geometry. Phonology 37(2): 257–296.
O’Hara, Charlie, and Caitlin Smith. 2019. Computational complexity and sour-grapes-like patterns. In Proceedings of the 2018 Annual Meeting on Phonology. https://doi.org/10.3765/amp.v7i0.4502.
Oncina, José, Pedro García, and Enrique Vidal. 1993. Learning subsequential transducers for pattern recognition interpretation tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence 15(5): 448–458.
Pater, Jeo 2012. Serial harmonic grammar and Berber syllabification. In Prosody matters: Essays in honor of Elisabeth O. Selkirk, eds. Toni Borowsky, Shigeto Kawahara, Takahito Shinya, and Mariko Sugahara, 43–72. London: Equinox.
Peikov, Ivan 2007. Rule Definition Language and a Bimachine Compiler. In Proceedings of the International Workshop on Finite-state Techniques and Approximate Search, 41–48. https://acl-bg.org/proceedings/2007/RANLP_W8%202007.pdf.
Prince, Alan, and Paul Smolensky. 2004. Optimality theory: Constraint interaction in generative grammar. Malden: Wiley-Blackwell.
Pullum, Geoffrey K. 1976. The Duke of York gambit. Journal of Linguistics 12(1): 83–102.
Quinn-Wriedt, Lindsey T. 2013. Vowel harmony in Maasai. Ph. D. thesis, University of Iowa.
Reutenauer, Christophe, and Marcel-Paul Schützenberger. 1991. Minimization of rational word functions. SIAM Journal on Computing 20: 669–685.
Roche, Emmanuel, and Yves Schabes. 1997. Finite-state language processing. Cambridge: MIT Press.
Schützenberger, Marcel-Paul 1961. A remark on finite transducers. Information and Control 4: 185–196. https://doi.org/10.1016/S0019-9958(61)80006-5.
Smith, Caitlin, and Charlie O’Hara. 2019. Formal characterizations of true and false sour grapes. In Proceedings of the Society for Computation in Linguistics (SCiL 2019), 338–341. https://doi.org/10.7275/vd79-kt51.
Tucker, Archibald N., and John T. O. Mpaayei. 1955. A Maasai grammar, with vocabulary. Green: Longmans.
Vago, Robert M., and Harry Leder. 1987. On the autosegmental analysis of vowel harmony in Turkana. In Current approaches to African linguistics, ed. David Odden. Vol. 4, 383–395. Dordrecht: Foris.
van der Hulst, Harry 2018. Asymmetries in vowel harmony. London: Oxford University Press.
Walker, Rachel 2010. Nonmyopic harmony and the nature of derivations. Linguistic Inquiry 41(1): 169–179.
Wilson, Colin 2003. Analyzing unbounded spreading with constraints: Marks, targets, and derivations. Unpublished ms., UCLA.
Wilson, Colin 2006. Unbounded spreading is myopic. Talk presented at the Workshop on Current Perspectives on Phonology, Phonology Fest, Indiana University.
Acknowledgements
For comments and suggestions on this work at various stages of its development, the authors would like to thank Hossep Dolatian, Jeff Heinz, and Jon Rawski, the anonymous reviewers and associate editors, and audiences at the Workshop on Formal Language Theory in Linguistics at SCiL 2020 and at talks delivered at Rutgers University, UC Santa Cruz, and Carleton University. All errors remain ours.
Funding
This work was supported by a UC San Diego Division of Social Sciences and Academic Senate research grants awarded to the authors, and by NSF BCS Award #2021149 awarded to the third author.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meinhardt, E., Mai, A., Baković, E. et al. Weak determinism and the computational consequences of interaction. Nat Lang Linguist Theory (2024). https://doi.org/10.1007/s11049-023-09578-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11049-023-09578-1






























 ), and the extent of its spread in surface representations (enclosed in
), and the extent of its spread in surface representations (enclosed in  ), is indicated with underlining.
), is indicated with underlining. →
→  ‘rafters made of sticks,’ Quinn-Wriedt (
‘rafters made of sticks,’ Quinn-Wriedt (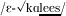 →
→  ‘
‘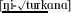 ‘the Turkana people’ has a “more frequently used form”
‘the Turkana people’ has a “more frequently used form”  with a harmony-disrupting glide (Dimmendaal
with a harmony-disrupting glide (Dimmendaal  in this case rather than as
in this case rather than as  .
. derivation looks like feeding, but at the level of the individual feature changes it is technically a Duke of York derivation (Pullum
derivation looks like feeding, but at the level of the individual feature changes it is technically a Duke of York derivation (Pullum  makes the ultimate segmental result distinct from the prototypical Duke of York derivation A→B→A. But separating re-pairing from harmony reveals a feeding Duke of York derivation (McCarthy
makes the ultimate segmental result distinct from the prototypical Duke of York derivation A→B→A. But separating re-pairing from harmony reveals a feeding Duke of York derivation (McCarthy  , which then feeds the further re-pairing change to [−low, +ATR]
, which then feeds the further re-pairing change to [−low, +ATR]  , which then undergoes the dominance reversal change to [−low, −ATR] [ɑ]. The first change feeds the second—that is, re-pairing applies because [+ATR] harmony creates a non-structure-preserving [+low, +ATR] vowel—but the third change simply reverses the first.
, which then undergoes the dominance reversal change to [−low, −ATR] [ɑ]. The first change feeds the second—that is, re-pairing applies because [+ATR] harmony creates a non-structure-preserving [+low, +ATR] vowel—but the third change simply reverses the first.