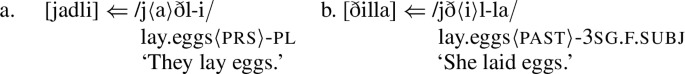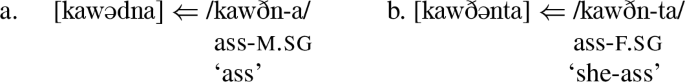Reflexes of exponent movement in inflectional morphology

Abstract

Seemingly non-local phonological operations triggered by inflectional exponents have been observed in a number of languages. Focussing on de-spirantization in Barwar Aramaic, accent shift in Lithuanian, ni-insertion in Quechua, ruki rule application in Sanskrit, and vowel harmony in Kazakh, we argue that these phenomena should be analyzed as strictly local phonological reflexes of movement in a pre-syntactic autonomous morphological component. Such morphological movement is shown to arise without further assumptions under the approach to inflectional morphology based on Harmonic Serialism (McCarthy 2016) developed in Müller 2020. Here, each morphological operation immediately gives rise to an optimization procedure, morphological structure-building is subject to simple alignment constraints, and counter-cyclic operations are precluded. Against this background, phonological reflexes of movement are predicted to show up when a potentially complete word triggers a phonological cycle, which is then followed by morphological movement. Finally, we argue that constraint-driven morphological movement is superior to alternative accounts based on (i) non-local phonology, (ii) base-derivative faithfulness, (iii) phonological movement, (iv) counter-cyclic operations (interfixation, lowering, local dislocation), (v) syntactic movement, and (vi) strata.

1 Introduction

The existence of reflexes of movement is well-documented for syntax. These reflexes reveal syntax-external operations involving some item in a position that does not correspond to the item’s surface position, but that is postulated for independent reasons as a position occupied by this item before it undergoes movement to the surface position. There can be semantic reflexes (see, e.g., Fox 2000 and Nissenbaum 2000), morphological reflexes (see, e.g., McCloskey 1979; Collins 1993; van Urk 2015; Georgi 2017), or phonological reflexes (see, e.g., Clements et al. 1983 and Korsah and Murphy 2020); and these reflexes can in turn be viewed as lending further support to the postulation of a movement operation. Against this background, the question arises whether analogous reflexes of movement can also be established for morphology. Focussing on phonological reflexes of exponent movement in inflectional morphology, we will argue that this is the case.

There are many cases where it looks as though an inflectional exponent can trigger non-local phonological changes. In the present paper, we will consider de-spirantization apparently triggered by non-local agreement exponents in Barwar Aramaic (see Khan 2008), Saussurean accent shift apparently triggered by non-local person/number exponents in Lithuanian (see Kushnir 2018), ni-insertion apparently triggered by non-local possessive markers in Quechua (see Myler 2013), ruki rule application apparently triggered on verb roots by non-local prefixes in Sanskrit (see Kiparsky 1982b), and vowel harmony apparently applying with non-local Q morphemes in Kazakh (see Bowman and Lokshin 2014). We will argue that phonological reflexes involving seemingly non-local morphological exponents can and should be captured in a strictly local way, by movement operations in an autonomous morphological component of grammar. More specifically, we contend that morphological movement of exponents basically comes for free in the approach to inflectional morphology that is developed in Müller 2020. This approach relies on Harmonic Serialism (see McCarthy 2016), a strictly derivational version of Optimality Theory (see Prince and Smolensky 2004). We will show that morphological movement of exponents follows without further ado from the interaction of independently motivated constraints on structure-building and linearization of morphological exponents in Harmonic Serialism, given (i) a certain pattern of ranking of these constraints, and (ii) the general restriction in Harmonic Serialism that competing outputs can differ from their common input by carrying out at most one operation. Morphological movement will in turn be argued to counter-bleed the phonological processes in all the relevant contexts because a phonological cycle is triggered directly upon finishing basic structure-building.

We will proceed as follows. In Sect. 2, we highlight cases of phonological operations apparently triggered by non-local morphological exponents in Aramaic, Lithuanian, Quechua, Sanskrit, and Kazakh. In Sect. 3, the background assumptions about inflectional morphology in Harmonic Serialism are introduced, and it is illustrated how the existence of morphological movement of exponents is predicted. In Sect. 4, we show how the empirical evidence can be straightforwardly analyzed as instances of local phonology followed by morphological movement of exponents in an approach based on Harmonic Serialism, thereby giving rise to a phenomenon of phonological reflexes of morphological movement. In Sect. 5, we discuss alternative accounts of the phenomenon. Section 6 is the conclusion.

2 Seemingly non-local phonological operations

2.1 Non-local de-spirantization in Barwar Aramaic

As observed by Khan (2008), there is a regular phonological process in Barwar Aramaic that turns the dental fricatives /θ/ and /ð/ into dental stops [t] and [d] if they directly precede coronal sonorants, which in the language are the nasal /n/ and the lateral /l/. We will call this process de-spirantization. In (1), the underlying dental fricative of the verb /ʔiθ/ (‘to be there’) precedes a lateral and is thus de-spirantized.¹

• (1)

  

The general, local process of de-spirantization can informally be captured by a rule that changes dental fricatives into stops before coronal /n/ and /l/: l,n.

Interestingly, de-spirantization seems to apply non-locally across the tense/aspect exponent wa (remote); see (1).

• (2)

  

However, there is good evidence that de-spirantization is a genuinely local process that occurs exceptionlessly in a phonologically specified context. In (3a), imperfective 〈a〉 is realized between the first and second radical.² This leaves the second radical /ð/ adjacent to the third one. For the root /jðl/ ‘to lay eggs,’ this yields a dental fricative adjacent to a coronal sonorant, viz., /l/. This creates the local condition for de-spirantization to apply, turning /ð/ into [d]. (3b) shows the same root with perfective 〈i〉, which shows up between the second and third radicals. Here, /ð/ is able to surface faithfully because the lateral is not adjacent. (The first radical /j/ is deleted by a separate process.)

• (3)

  

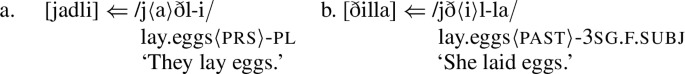
(1) shows the same alternation, albeit with an epenthetic vowel: three-consonant (CCC) clusters must be broken up by a vowel (the site of vowel insertion is variable; Khan 2008: ex. 110). In (4a), the vowel is inserted between the first and second members of the cluster, maintaining adjacency of the dental fricative and the sonorant. This again derives the right context for de-spirantization to apply. In the feminine form for the same root, concatenation creates a four-consonant cluster; cf. (4b). In four-consonant clusters, the locus of epenthesis is no longer optional: it must be between the second and third members of the cluster, in this case between /ð/ and /n/. Here, epenthesis bleeds the application of de-spirantization.

• (4)

  

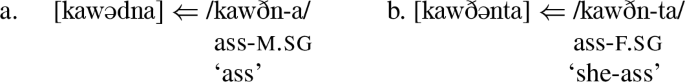
The instances of de-spirantization that apply across morpheme boundaries behave exactly like the ones in roots that we have seen so far. Consider, for instance, the so-called l-suffixes, which indicate subject agreement in the perfective aspect and object agreement in imperfective environments. These exponents are triggers of de-spirantization (however, in the imperfective aspect these affixes are rarely directly adjacent to the root). In (1), the last radical of the verb roots (/θ/ and /ð/, respectively) is adjacent to the l-exponent, and accordingly undergoes de-spirantization.

• (5)

  

If an object agreement suffix intervenes between the root and the l-suffix, de-spirantization is transparently blocked; see (6). The intervening exponent blocks the process exactly like the vowels encoding perfectivity and imperfectivity in (3) and the epenthetic vowel in (4) do.

• (6)

  

However, there is an instance in which de-spirantization unexpectedly applies non-locally across an intervening morphological exponent. The tense/aspect exponent wa (remote) is linearized between the root and the l-suffixes. As (2) has shown for /θ/, and as (1) shows for /ð/, a root-final dental fricative is nonetheless (optionally) de-spirantized in this environment. Since wa intervenes, the phonological context for de-spirantization is not met on the surface. The process thus over-applies non-locally in the context of a remoteness exponent wa.³

• (7)

  

There are no other potential triggers of de-spirantization in (2) and (0) beyond the non-local l-suffix. In particular, the operation does not otherwise take place if a dental fricative precedes a bilabial glide—neither as a general phonological process (see 8a), nor as a phonological process specific to the tense/aspect marker wa (see 8b).⁴

• (8)

  

2.2 Non-local Saussurean accent shift and theme vowels in Lithuanian

A similar phenomenon shows up with accent placement in Lithuanian; cf. Kushnir (2018: Ch. 2 and 4), on which the following discussion is based. Phonological words in Lithuanian have one main pitch accent. Accent can be assigned to any mora (μ) in a word; and there can be up to two moras in the rhyme of a syllable. Depending on where the mora ending up with the main accent is located in a syllable, this produces what Leskien (1919) calls falling vs. rising—or gestoßene (‘pushed’) vs. geschleifte (‘dragged’)—accents, and gives rise to minimal pairs such as ká_μl_μtas (hammer.part.pass) vs. ka_μĺ_μtas (guilty.masc.sg.nom), and lá_μu_μk (wait.imp.2.sg.) vs. la_μú_μk (‘get out!’). Any morphological exponent can bear an inherent lexical accent. Normally, if a stem and an inflectional exponent are both pre-specified for accent, it is the accent on the stem that prevails; i.e., the leftmost accent wins (the Basic Accentuation Principle; cf. Halle and Vergnaud 1987). There is a systematic exception, though, which can be referred to as (the synchronic version of) Saussure’s Law: whenever two underlying accents coincide on two subsequent moras word-finally, the surface accent is aligned with the right edge of the word.⁵ The effect of Saussure’s Law is illustrated for inflected nouns in (1). In (9a), neither mora on the accusative singular long-vowel exponent /a_μa_μ/ is pre-specified for accent, and the word accent ends up on the stem. In (9b), a mora of the locative singular exponent // bears inherent accent, but since the two moras that are associated with accent are separated by an intervening mora that is not, Saussure’s Law does not apply; the accent goes on the stem again. In (9c), there is a mora pre-specified for accent on the dative plural exponent /ó_μo_μms/, but still Saussure’s Law does not spring into action because the clash does not occur word-finally (there is yet another mora further to the right). However, in (9d), with the Saussurean instrumental singular exponent /á/, there are two word-final adjacent moras (/k/ is not moraic), and Saussure’s Law ensures that the pitch accent ends up on the inflectional exponent, rather than on the stem.⁶

• (9)

  

The verbal agreement markers /-u/ (1.sg) and /-i/ (2.sg) are also Saussurean affixes, like the instrumental singular case marker for nominals in (9d). However, with verbs, there is an interesting complication: Between the root and the inflectional exponent encoding ϕ-features, there is a theme vowel; cf., e.g., /a/ in (10a). The short theme vowel /a/ is regularly deleted in front of a following exponent starting with a vowel, as in (10b).

• (10)

  

In (10b), it may look at first sight as though the context for application of Saussure’s Law can be created by theme vowel deletion. However, closer inspection reveals that this cannot be the whole story. In contrast to short theme vowels, long theme vowels in Lithuanian verb inflection are not deleted in front of vowels; they are merely reduced. Thus, long /ee/ becomes [] in front of first and second person singular exponents, and /oo/ becomes [a]. Crucially, the Saussurean effect persists; “the accent shift takes place, disregarding the theme vowel entirely” (Kushnir 2018: 130). This is shown by the examples in (1).

• (11)

  

Thus, just as with de-spirantization in Barwar Aramaic, Saussurean accent shift in Lithuanian verbs appears to be able to apply non-locally; given that the operation can independently be shown to depend on strict locality of the moras involved (see 9b), the conclusion suggests itself that intervening theme vowels behave as if they were not part of the structure at the point where the Saussurean shift takes place.⁷

2.3 Non-local ni-insertion in Quechua

Another piece of evidence which seems to suggest non-local application of a phonological operation comes from Bolivian and Huallaga Quechua; see Bills et al. (1969); Weber (1989) (the source of all data in this section unless indicated otherwise); and Myler (2013). In these languages, illegitimate sequences of phonological segments are repaired by epenthesis of CV.⁸ In some cases, an epenthetic syllable appears even though conditions on its insertion are not met in the surface form and two morphological exponents that would give rise to a banned sequence are separated by other exponents.

The core generalization is that the syllable ni is inserted between two morphological exponents to avoid a creation of super-heavy syllables (see Myler 2013: 191). A syllable is super-heavy if its nucleus and coda consist of three or more moras. Short vowels and simple codas correspond to one mora; long vowels, diphthongs and complex codas correspond to two moras. Thus, V:C or VCC codas create super-heavy syllables and trigger ni-epenthesis. Ni-insertion in Huallaga Quechua is illustrated in (12) and (13). In (12), a third person possessive suffix n is added to different stems of different types. In (12a), it is attached to a stem ending in a short vowel. This creates a bimoraic VC rhyme: The syllable is not super-heavy, and ni-epenthesis does not apply. In (12b), the same suffix n is added to a stem ending in a consonant. This creates a trimoraic VCC rhyme, and the syllable would be super-heavy; so ni-insertion takes place. In (12c), the stem ends in a long vowel. Attachment of the possessive suffix n creates a trimoraic V:C rhyme; again ni-insertion is triggered.

• (12)

  

The same effect is caused by suffixes with the shape CCV(...); see (13). Two consonants at the beginning of an affix cannot be syllabified as the onset of a next syllable due to a restriction on complex onsets in Huallaga Quechua (cf. Weber 1989: 455). This means that the first of the two consonants in the suffix has to belong to the previous syllable. This is unproblematic in (13a), where the stem ends in a vowel. The attachment of the suffix creates a simple CVC syllable here. However, in (13b) the stem ends in a consonant and the attachment of suffix would result in a trimoraic rhyme (consisting of *urn); ni-insertion applies to avoid this.

• (13)

  

Some suffixes do not follow these phonological restrictions. First, epenthesis overapplies with joq, a nominalizer broadly denoting possession. Ni is not inserted if joq is attached to a stem ending in a vowel but insertion is optionally possible if a root ends in a consonant or a long vowel. This is shown in (1). In (14a), joq is added to a stem ending in a vowel, and ni is not inserted. In (14b,c), the stem ends in a consonant and ni-insertion can optionally apply even though there is no super-heavy syllable. The affix thus behaves as if it started with two consonants. Weber (1989: 466) notes that it might indeed be the case that /joq/ diachronically developed from /jjoq/.

• (14)

  

Second, ni does not appear before verbal suffixes, for instance, the aspectual suffixes jka: and jku. The suffix jka: can be added to a stem ending in a long vowel such as wajra: ‘blow,’ and this would create a super-heavy syllable so that the condition for ni-insertion is met. The unacceptable syllable is however repaired by shortening the final vowel of the stem: wajra-jka: ‘blow-ipfv,’ not *wajra:-ni-jka:.⁹

Based on these data, Weber (1976, 1989) analyzes ni-insertion as phonologically conditioned allomorphy of certain affixes. Alternatively, since the affix that leads to overapplication is a possessive nominalizer, one might think that epenthesis is licensed by a [poss] feature rather than by syllable structure. However, while most affixes triggering ni-insertion do indeed have a possessive feature, epenthesis also applies with the caritive nominalizer jnaq and the comitative exponent ntin. More generally, despite the existence of some exceptions we continue to analyze ni-insertion as a regular phonological process that blocks super-heavy syllables and is based on independently attested restrictions on syllable structure in Quechua (also cf. Adelaar and Muysken 2004: 206; Myler 2013).

Syllabic ni can also appear when two exponents that create the environment for its insertion are separated by the exponent ʎa. This exponent denotes “limitation,” and “typically means ‘just’ or ‘only,’ but also has a range of more subtle uses which are much harder to translate” (Myler 2013: 4.2). Example (1) (from Huallaga Quechua) shows that ʎa does not cause insertion of ni on its own if it is attached to a consonant-final stem.

• (15)

  

Non-local application of epenthesis across an intervening exponent ʎa is demonstrated for Huallaga Quechua in (16). In (16a,b), the second person possessive exponent jki is attached to a consonant-final root, and this obligatorily triggers ni-insertion. The possessive exponent surfaces as ki in (16b) due to an independent phonological process that deletes a glide after an i. Importantly, epenthesis also applies in (16c), where the affixes creating its context are separated by an intervening exponent ʎa ‘just.’ (16d) shows that unlike in the local configurations, epenthesis is optional here. (16e) shows that /ʎa/ cannot appear between the root and the epenthesized syllable.

• (16)

  

Next, the examples in (17) (from Myler 2013, citing Bills et al. 1969) show overapplication of epenthesis in Bolivian Quechua: ni is inserted as if ʎa were not present. Unlike in Huallaga Quechua, ni-insertion is obligatory in both local and non-local environments here.

• (17)

  

The intervening suffix ʎa can be in different positions. In Huallaga Quechua, it generally precedes the possessive affix; cf. (18a).¹⁰ Examples where ʎa follows it are significantly degraded, but not completely ungrammatical; cf. (18b). If a noun is marked for both plural and possessive, as in (18c), ʎa appears after both of these exponents. Thus, ʎa precedes a possessive suffix in one case and follows it in another.

• (18)

  

Furthermore, ʎa is not restricted to nouns; it can be attached to verbs or adverbs:

• (19)

  

To sum up the evidence from Quechua, again it looks as though a phonological process which is known to normally operate under strict locality (viz., syllable epenthesis breaking up super-heavy rhymes) can in some cases apply non-locally; and again, under an alternative perspective the data can be taken to indicate that an otherwise intervening exponent behaves as if it were not present at the relevant stage of the derivation where ni-insertion is decided.

2.4 Non-local ruki rule application in Sanskrit

The next pattern comes from Sanskrit; it has been investigated in Kiparsky (1982b), on which the following remarks (and data) are based. In Sanskrit, the so-called ruki rule turns s into retroflex ʂ after high vowels (u, i), velar consonants (e.g., k) and r; see (20)–(22).

• (20)

  

• (21)

  

• (22)

  

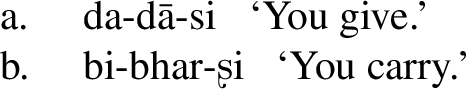
The rule also applies if the past tense prefix (or augment, in the Indo-European tradition) a intervenes; see (23).

• (23)

  

The root without a prefix begins with s; cf. (23a). It is turned into a retroflex sound after the prefix abhi (‘unto’); cf. (23b). The retroflex ʂ also appears in (23c), where the high vowel of the prefix and the root are separated by the past tense exponent a.¹¹

Another example of seemingly non-local application of the ruki rule is given in (24). In (24a), the first two segments of the root are reduplicated, and a retroflex ʂ triggered by the prefix appears in the reduplicant and in the root even though the prefix is not adjacent to the root in the surface form. This, as such, is a regular opaque pattern of reduplication involving (in traditional analyses) a sequence of ruki rule application preceding reduplication. However, more interestingly in the present context, if reduplication and the past tense prefix a co-occur, the ruki rule still applies to the initial consonant of the root, yielding what looks like a doubly opaque pattern of over-generation (alternatively, non-local application of a phonological process followed by reduplication); see (24b).

• (24)

  

2.5 Non-local vowel harmony in Kazakh

As a final example of phonological processes triggered by inflectional exponents which are non-local in surface representations, this section introduces data from non-local vowel harmony in Kazakh. We will consider the pattern of non-local application across the instrumental suffix men before explaining the regular vowel harmony in further detail. Vowel harmony in Kazakh inflectional morphology usually applies locally. In (25) (from Muhamedova 2015), the vowel of the interrogative suffix bA varies between front and back (or between [–back] and [+back]), depending on the backness of the preceding stem vowel.¹²

• (25)

  

The instrumental case suffix men is an exception, since it is transparent to vowel harmony. Vowel harmony applies across this suffix, but the suffix itself does not undergo vowel harmony; see (1) (from Bowman and Lokshin 2014).¹³ The interrogative suffix again varies, but the instrumental suffix stays invariant. Vowel harmony thus applies non-locally.

• (26)

  

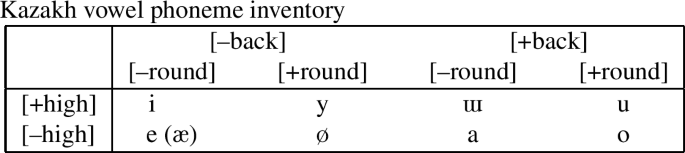
Backness harmony is a regular phonological process and usually affects all suffixes. Suffix vowels assimilate in backness to a preceding stem vowel (cf. Krippes 1996). The rounding and height distinctions between high and non-high vowels are kept constant; see the inventory in (27). The feature [±low] is not relevant for vowel harmony. The low vowel /æ/ mostly occurs in loanwords.

• (27)

  

Vowel harmony is regular and normally applies to case suffixes. As shown in (28), the genitive case suffix nIŋ and the locative suffix dA undergo harmony; they occur with front vowels /i/ and /e/ after front vowel stems and with back vowels /ɯ/ and /a/ after back vowels.¹⁴ They also allow vowel harmony to apply to their left and right. Vowel harmony is restricted to the word domain, since, e.g., the postposition bojɯ in (28e) does not undergo harmony. Vowel harmony is thus a regular and local phonological process in Kazakh.

• (28)

  

The process applying to the question suffix after the instrumental suffix shows the same alternation that we see in other cases of vowel harmony; compare (28c) with (25b). Similarly, this is an argument against deriving exceptional behaviour from properties of the vowel inventory, since /e/ and /a/ generally alternate with each other in regular vowel harmony patterns; cf. the realization of /dA/ in (28c,d). Leaving the backness feature of instrumental /men/ underspecified would allow harmony to propagate through it, but no repair mechanism justified by structure preservation could reverse this change later in the derivation (see van der Hulst 2016: 5–11). Underspecification of /men/ would predict that it undergoes harmony, just like any other /e/ or /a/. For now, we can conclude that idiosyncratic transparency poses a challenge for any purely phonological analysis of the data (cf. Mahanta 2012: 1128; Bowman and Lokshin 2014: 6); we will come back to this issue in Sect. 5.

To sum up this section, we have seen five different pieces of evidence showing that a morphological exponent can be involved in a regular, well-behaved and otherwise strictly local phonological process even though it shows up in a non-local position, separated by an intervening inflectional exponent. In what follows, we will pursue what strikes us as the classical hypothesis in grammatical theory to account for paradoxes of this type: the non-local exponent is in fact a local exponent in an earlier representation, at the point where the phonological operations discussed above take place, but exceptionally ends up in a non-local position as a consequence of subsequent movement. This presupposes a systematic theory of movement of morphological exponents. As we will show in the next section, the approach to inflectional morphology in terms of Harmonic Serialism developed in Müller (2020) predicts the existence of exponent movement in an autonomous morphological component of grammar without any further assumptions specifically designed to bring about displacement.

3 Inflectional morphology in Harmonic Serialism

3.1 Background assumptions

Harmonic Serialism is a derivational version of Optimality Theory which has been envisaged as an alternative to standard parallel Optimality Theory from the very beginning (cf. Prince and Smolensky 2004). In Harmonic Serialism, the generator (Gen) and harmony evaluation (H-Eval) components of the grammar alternate constantly. Basically, the theory works as shown in (1) (see Heck and Müller 2007; McCarthy 2008).

• (29)

  

Harmonic Serialism has been actively pursued over the last decade both for phonology (e.g., McCarthy 2010, 2016; Elfner 2016; and Torres-Tamarit 2016) and for syntax (see Heck and Müller 2007, 2016; Assmann et al. 2015; and Murphy 2017, among others; here the model is sometimes referred to as “extremely local optimization”). In contrast, until very recently there had basically been no work in morphology.¹⁵ This situation has changed with Müller (2020), where the outlines of a harmonic serialist approach are developed according to which inflectional morphology is (i) realizational, (ii) lexical, (iii) Merge-based, and (iv) pre-syntactic. Let us briefly lay out these central assumptions.¹⁶

First, inflectional morphology is realizational, not incremental, in the sense that inflectional exponents realize morpho-syntactic features that are independently available (see Stump 2001); this property is shared with most current approaches to inflectional morphology, like Distributed Morphology (see Halle and Marantz 1993; Noyer 1997), Paradigm Function Morphology (see Stump 2001, 2016) or Network Morphology (see Corbett and Fraser 1993; Brown and Hippisley 2012). Second, inflectional morphology is lexical, not inferential (again, see Stump 2001), which implies that inflectional exponents exist as separate items in the mental lexicon; this property is in accordance with some approaches (e.g., Halle and Marantz 1993; Trommer 2001), and at variance with others (e.g., Anderson 1992; Stump 2001). Third, inflectional morphology is Merge-based, i.e., it involves structure-building via Merge, as in the syntactic component of grammar (see Alexiadou and Müller 2008; Bruening 2017), rather than substitution transformations applying to terminal nodes (‘vocabulary insertion,’ as in Halle and Marantz 1993), or entire subtrees (see Ackema and Neeleman 2003, 2004; Caha 2013; and De Clercq and Vanden Wyngaerd 2017; among others), or spans (see Merchant 2015; Svenonius 2016; and Ermolaeva and Kobele 2019).¹⁷ Like all structure-building operations, morphological Merge is subject to the Strict Cycle Condition (see Chomsky 1973, 1995, 2000; Perlmutter and Soames 1979; Freidin 1992; Pullum 1992), which blocks operations from applying exclusively to embedded domains, and ensures that an exponent can only be merged at the root; cf. (1). We assume that the Strict Cycle Condition is an inviolable constraint, either because it is inherently ranked very high or, more straightforwardly, because it is part of Gen.¹⁸

• (30) Strict Cycle Condition:

  Within the current domain δ, no operation may affect solely a proper subdomain γ that is dominated by δ.

And fourth, inflectional morphology is pre-syntactic, not post-syntactic, parallel to syntax, or syntax-internal: It takes place in the numeration (Chomsky 2000), between lexicon and syntax. While this assumption will actually not play an important role for the gist of what follows, it can be noted that the concept of post-syntactic morphological exponence (either via substitution transformations, as is standardly assumed, or via Merge) is inherently counter-cyclic, and therefore incompatible with (0).

Based on these assumptions, morphological exponence is assumed to proceed as follows. Initially, a stem is taken from the lexicon with its inherent features, and enriched by non-inherent features, yielding a fully specified feature matrix. Together, these features provide the context for underspecified inflection markers, comparable to the fully specified paradigm cell in Paradigm Function Morphology (see Stump 2001), or a fully specified syntactic insertion context in, e.g., Distributed Morphology (see Halle and Marantz 1993). Next, triggered by high-ranked Merge Conditions (MCs) which demand a discharge of structure-building features [•α•], [•β•], etc., on stems, inflectional exponents of type [α], [β], …are then successively merged with the stem (subject to faithfulness constraints demanding maximal compatibility and specificity of underspecified exponents), thereby eventually generating whole words.¹⁹ All of an inflectional exponent’s features are inherent; but they are often underspecified. The morphological categories [α], [β], involved here may or may not correspond directly to syntactic categories (i.e., they can be morphomic; cf. footnote 19). As a general illustration, the MC for the structure-building feature [•T(ense)•] is given in (1); other morphological categories are addressed by MCs in the same way.

• (31) Merge Condition$_{\mathrm{T(ense)}}$ (MC_T):

  A structure-building feature [•T(ense)•] on a stem participates in (and is deleted by) a Merge operation with an inflectional exponent bearing [T].

In addition to the MCs, there are lower-ranked alignment constraints determining the order of exponents, primarily by demanding left-alignment (L⇐α) or right-alignment (α⇒R) of exponents with certain types of features α (see Trommer 2001, 2008). As a an example, consider the right-alignment constraint for [T] in (1). ((1) can be generalized by modulating direction of alignment (R, L) and morphological category.)

• (32) T⇒R:

  Assign * for each item that separates an inflectional exponent bearing [T] from the right edge of the word.

Finally, the fully inflected word is transferred to the syntactic component, which cannot see the internal structure of the word generated in the morphological component but can access all the morpho-syntactic features associated with the stem, and carry out Agree operations with them (cf. Chomsky 2001; Bruening 2017; this tends to suggest a checking—rather than valuation—approach to Agree). Thus, abstracting away from the status of derivational morphology for the time being (but cf. Sect. 4.7 below), the approach conforms to the Strong Lexicalist Hypothesis (see Chomsky 1970, 1993).

Merge operations in syntax have been argued by Chomsky (2008) to underlie both basic structure-building and movement (external vs. internal Merge). Given that inflectional exponence (conceived of as basic structure-building) is brought about by Merge operations in the present approach, there is thus every reason to expect that the very same operation can also give rise to exponent movement in morphology, exactly as in syntax. (In contrast, other morphological theories would minimally need two postulate separate operations, like vocabulary insertion and lowering or local dislocation in Distributed Morphology). In the next section, we show that morphological movement of exponents is automatically predicted under certain rankings of MCs and alignment constraints in the present approach.

3.2 Movement in morphology

Suppose that a stem bears two structure-building features [•α•], [•β•], and that MC_α outranks MC_β. Then, the optimal α-exponent needs to be merged with the stem first (so as to satisfy the higher-ranked MC_α). In the next step, the β-exponent must be merged with the (extended) stem. Now, if the alignment constraints for α and β pull the corresponding exponents in the same direction (say, to the right edge, i.e., into a suffix position), and there is a higher-ranked alignment constraint for the stem precluding a realization of an inflectional exponent at the opposite edge (as a prefix, in the case at hand), a remarkable consequence may arise: if the order of the alignment constraints is identical to the order among the MCs for α and β, the second-merged β-exponent incurs a violation of the higher-ranked alignment constraint (because the peripherality requirement for the α-exponent is not maximally respected, whereas the lower-ranked requirement for the β-exponent is). This introduces a defect into the derivation that must be subsequently be removed by movement of the first-merged α-exponent across the β-exponent. Note that this conclusion depends on two assumptions inherent to the present approach: first, the (inviolable) Strict Cycle Condition holds, so squeezing in the second-merged β-exponent between the first-merged α-exponent and the stem is not an option (this would make subsequent movement of the α-exponent superfluous). Second, the core property of Harmonic Serialism is adopted according to which input and output cannot be separated by more than one operation (otherwise, there would be no optimal intermediate output where the α-exponent is closer to the stem than the β-exponent).

To see this in more detail, let us look at some examples, focussing on (simplified versions of) German verb inflection (where the ranking of MCs and alignment constraints does not produce exponent movement) and Berber verb inflection (where it does).²⁰

Thus, suppose first that initially a German V stem like kauf (‘buy’) is selected from the lexicon that is inherently equipped with morphological structure-building features [•T•] and [•Agr•] identifying tense and subject agreement exponents, respectively. Two relevant exponents for, say, past.2.sg environments are [_T te ] and [_Agr st ], and the eventual output that needs to be derived is kauf-te-st (buy-past-2.sg ‘You bought’). The initial optimization step is shown in (1).

• (33)

  

First, notational conventions need to be clarified: I₁ is the initial input (the V stem and its structure-building features). The second line in the top-left box lists the fully specified feature matrix associated with this stem that is in need of morphological realization (and that can subsequently be accessed in the syntax). The third and fourth lines in this box illustrate the sets of competing T exponents and competing Agr exponents available in the language; only the one that is selected by the faithfulness constraints (from which this optimization abstracts away) is shown here. The morphological exponents pair (↔) a phonological form /  / with a (often underspecified) set of morpho-syntactic features [   ], as in Distributed Morphology. Finally, immediate output descendants of a given input extend the input’s last digit (O₁₃←O₁). With this in mind, let us look at the competition. Since all competing outputs O₁₁–O₁₅ can at most be separated from the input I₁ by one operation, the candidate set is necessarily finite. Output O₁₁ leaves the input intact and is filtered out because of violations of MC_T and MC_Agr. O₁₂ discharges V’s [•T•] feature by merging /te/ as a suffix; this satisfies all constraints, except for MC_Agr. However, if MC_Agr is satisfied by discharging [•Agr•] on V and merging /st/, as in O₁₃, the higher-ranked MC_T is fatally violated. Note that the confinement to at most one operation between input and output ensures that no candidate can be generated in the first step that satisfies both MCs simultaneously, by merging both exponents. Next, O₁₄ is excluded because it fatally violates both the alignment constraint for the stem (L⇐V) and the alignment constraint for the inflectional exponent (T⇒R), by realizing the [T] exponent as a prefix. Finally, O₁₅’s constraint profile is hopeless. It fatally violates MC$_{ \rm T}$, like O₁₃; in addition, like O₁₄, it has gratuitous alignment violations (of L⇐V and Agr⇒R).²¹

In the next optimization, the optimal output O₁₂ of (0) is used as the input; see (1).

• (34)

  

As before, the first competing output O₁₂₁ leaves the input intact. It is filtered out because of the MC_Agr violation that was tolerable in the previous optimization step but has become fatal now. In contrast, O₁₂₂ discharges the [•Agr•] feature by merging /st/ as a suffix; this candidate is optimal. This illustrates a typical property of Harmonic Serialism: there is a continuous, gradual improvement of the constraint profile. Still, O₁₂₂ does not respect all constraints: by satisfying high-ranked MC_Agr, it invariably introduces a new violation of lower-ranked T⇒R: Now /te/ is separated from the right edge of the word by an intervening exponent (viz., /st/). This problem could in principle be solved by merging /st/ as a prefix, as in O₁₂₃; but this fatally violates the two higher-ranked alignment constraints.²² Note that an output which would merge the /st/ exponent counter-cyclically, between the V stem and /te/, and which would (fatally) violate Agr⇒R but not L⇐V, cannot be generated, given the Strict Cycle Condition.

In the third and final optimization step, convergence is reached; see (1).

• (35)

  

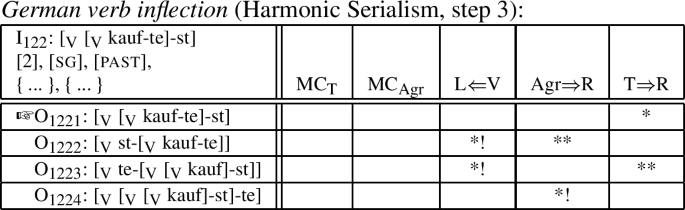
O₁₂₂₁ does not change the input, and thus maintains the previous optimal candidate’s T⇒R violation, but at this point there is no way to improve the constraint profile further by carrying out some operation. In particular, if /st/ shows up in front of the V stem, as in O₁₂₂₂, two higher-ranked alignment constraints are violated, as with O₁₂₃ in (-1); and similar consequences result if /te/ were to be merged in either a prefix or suffix position, as in O₁₂₂₃ and O₁₂₂₄. However, it is worth noting at this point already that O₁₂₂₂–O₁₂₂₄ are outputs that carry out morphological movement: e.g., in O₁₂₂₂, /st/ is moved to the left edge from the right-peripheral position it shows up in I₁₂₂.²³

Let us next look at a scenario that involves movement because the two MCs for [•T•] and [•Agr•] show up in the same order as the two (unidirectional) alignment constraints for [T] and [Agr], which bring about a prefix status of inflectional exponents.²⁴ Consider, e.g., an inflected Berber verb like ad-y-seg (fut-3.masc.sg-buy; ‘He will buy’); cf. Ouhalla (1991). Suppose that the order of MC$_{ \rm T}$ and MC_Agr is the same as in German; in fact, let us generalize this assumption and propose that the order of these two MCs is cross-linguistically invariant, and follows from an independently motivated functional sequence (f-seq; see Starke 2001) of inflectional categories that also predicts a uniform order of functional projections in the syntax. This proposal then derives Mirror Principle effects (see Baker 1985), albeit at an abstract level: Basic structure-building takes place in the same way, determined by f-seq, in morphology and syntax; but the Mirror Principle does not have to be surface-true because, as will be shown momentarily, morphological movement can apply after initial structure-building (we will address the question later of how morphomic features enter the picture). Returning to the constraints that play a role, in addition to the two MCs, there are two alignment constraints L⇐T, L⇐Agr, and a higher-ranked constraint V⇒R ensuring prefix status of the inflectional exponents.²⁵

The first optimization step is shown in (1).

• (36)

  

In (0), the inert output O₁₁ that leaves the input intact violates both MCs; and the outputs O₁₂ and O₁₄ that merge the [Agr] exponent first fatally violate higher-ranked MC_T. The optimal output O₁₅ merges the [T] exponent /ad/ as a prefix, rather than as a suffix, as in O₁₃.

In the following step, based on O₁₅ as the new input, the optimal output merges the [Agr] exponent /y/ as a prefix; see (1). Here, O₁₅₃ emerges as optimal even though it introduces a violation of L⇐T (since /ad/ is now not at the left edge anymore); however, if /y/ is merged as a suffix, as in O₁₅₂, this will give rise not only to (tolerable) violations of lower-ranked L⇐Agr, but also to a fatal violation of higher-ranked V⇒R. An output with the order ad-y-seg would in principle yield the best constraint profile (violating only L⇐Agr). However, this output cannot be generated on the basis of I₁₅ as the input. Here is why. The first option would be to squeeze in /y/ between /ad/ and the V stem /seg/. This would involve only one Merge operation, but it would violate the inviolable Strict Cycle Condition, affecting only a proper subdomain of the existing structure. The second option would be to merge /y/ as a prefix and then directly move /ad/ around it. This would respect the Strict Cycle Condition, but it would involve two operations separating input and output, and such a scenario can never arise because of the core assumption about Gen in (29a), according to which an output can be generated on the basis of a given input by applying at most one operation to the input. Hence, the form ad-y-seg cannot be generated yet in (37).

• (37)

  

In this scenario, the constraint profile can and must be further improved by moving the [T] exponent /ad/ to the front in the next optimization step; see (1).²⁶

• (38)

  

Here, O₁₅₃₂ trades in the input’s L⇐T violation for a less severe L⇐Agr violation, and is therefore optimal. Other outputs carrying out rightward movement also compete but emerge as suboptimal because they incur fatal V⇒R violations: O₁₅₃₃, O₁₅₃₄. This exhausts the candidate set in (0) since the two remaining orders with an initial V stem (viz., seg-ad-y and seg-y-ad) cannot be generated on the basis of O₁₅₃ as the input under present assumptions: In these outputs with a stem-initial order, both inflectional exponents would have to move to the right, i.e., there would have to be two separate movement operations, one for y and one for ad. Again, this is not an option for Gen, given that outputs differ from inputs by applying at most one operation (cf. (29a)).²⁷ Any further movement will deteriorate the constraint profile; hence, convergence is reached in the next step.

To sum up: in the harmonic serialist approach to inflectional morphology outlined in this section, movement of exponents is a natural consequence arising if two MCs and two alignment constraints for two features show up in the same order. Two properties of the approach are worth emphasizing in this context. First, the analysis does not rely on any special assumptions, of whatever type, to bring about movement of exponents. The constraints that trigger such movement are independently motivated, by considerations completely unrelated to movement: every theory of inflectional morphology needs to ensure that morphological exponents show up in words (here this role is played by MC constraints that trigger structure-building), and that stems and inflectional exponents occupy certain positions in words (here it is alignment constraints that achieve this). In an optimality-theoretic approach, all constraints of the H-Eval component must be given some ranking in an individual grammar. And strict cyclicity and the one-edit-away-from-the-input restriction of Harmonic Serialism then automatically predict that there will be rankings that trigger exponent movement (next to many other possible rankings that do not; cf. Sect. 4.7 below). Something comparable does not hold for other theories of morphology that envisage, or might accommodate, displacement operations of various kinds (e.g., Distributed Morphology, or Stratal Morphology); here these operations must be stipulated on a case-by-case basis (we will come back to this issue in Sect. 5). And second, the result that morphological movement comes for free is inherently tied to Harmonic Serialism, and cannot be attained in a standard parallel optimality-theoretic approach. What is crucial here is the restriction that outputs differ from inputs by applying maximally one operation; for this reason, operations may be locally (i.e., at an intermediate stage of the derivation) optimal that can never be optimal from a global perspective. Accordingly, in an optimality-theoretic analysis where this restriction is not in place, a representation like O₁₅₃ in (-1), where the agreement exponent is outside of the tense exponent (/y/-/ad/-/seg/), will ceteris paribus (i.e., under an identical ranking) never emerge; as illustrated in (1), the surface order will be determined directly, without movement.

• (39)

  

Thus, the correct surface order of exponents can be generated under the same constraints, and under an identical ranking, in the harmonic serialist and the standard optimality-theoretic approaches. However, given the same constraints and an identical ranking, it follows from the harmonic serialist analysis that an eventual output order ad-y-seg has to be derived via an intermediate order y-ad-seg, whereas the generation of the parallel optimality-theoretic output order ad-y-seg will at no point have involved the sequence y-ad-seg. This difference is significant from a more general perspective, both conceptually and empirically. A conceptual argument has been given above: the harmonic serialist approach makes it possible to maintain that some version of the Mirror Principle can be satisfied, which (other things being equal) is not possible in the standard parallel approach. Assuming, e.g., that AgrP dominates TP in a clause in syntax, which in turn dominates VP, the Mirror Principle demands that T exponents are closer to the V stem in morphology, and that Agr exponents are attached on the outside of a complex stem consisting of V and T. The Mirror Principle-respecting order does not show up on the surface in Berber, but the harmonic serialist approach makes it possible to assume that it is present at an earlier stage of the derivation, when exponents are first concatenated with the stem in accordance with f-seq, and is subsequently blurred by morphological movement in the same way that, e.g., constraints on linking demanding that objects are merged lower than subjects in the syntax can be respected after initial Merge in the syntax, and may later be blurred by syntactic movement of the object to a higher position. No such reasoning is available in the standard parallel optimality-theoretic approach.²⁸

Turning to empirical arguments next, three pieces of evidence for movement of exponents in the morphological component are presented in Müller (2020). First, the phenomenon of discontinuous exponence (see Harris 1945), including circumfixation, can be accounted for by assuming that the “discontinuous” exponent (like, e.g., ge- -et in the German past participle ge-arbeit-et, ‘worked’) is actually a discrete item initially, part of which gets separated by morphological movement (see Müller 2020: 76–84); it is not obvious how a primitive structure-building operation could take a single object from the lexicon and simultaneously attach parts of it to the stem in two distinct positions.

Second, the phenomenon of partially superfluous extended exponence, where the morpho-syntactic features of two exponents in a single word stand in a proper subset relation, poses a problem for many theories of morphology because the more general (i.e., subset) exponent seems globally unmotivated. Many solutions to this problem predict that the more general exponent has to be closer to the initial stem than the more specific exponent (see Caballero and Harris 2012 and Stiebels 2015; only then can there be a derivational stage without the more specific exponent where the more general exponent is locally motivated). However, in some cases, the surface order is at variance with this requirement. This holds, e.g., for extended exponence of negation on the verb in Swahili, where, in a negated verb like ha-tu-ku-taka (neg-1.pl-neg.past-want, ‘We did not want’), the more general (purely negative) exponent ha shows up further away from the stem taka than the more specific (negative past) exponent tu; cf. Stump (2001). Morphological movement solves this problem: The more general exponent is merged with the stem first, the more specific exponent is merged later, and finally (triggered by an alignment constraint) the former exponent moves across the latter, yielding discontinuous extended exponence (see Müller 2020: 141–153).

Third, non-local stem allomorphy (conditioned by features on exponents that are not next to the stem on the surface) has motivated a number of special devices in the literature (see Merchant 2015; Moskal and Smith 2016; Božič 2019) but can be reinterpreted in the present approach as extremely local stem allomorphy accompanied by subsequent exponent movement. Thus, in a Tamil pronoun like en-ga(l)-ukku (1.dat-pl-dat), the form of the 1 person pronominal stem (en) is conditioned by the dative exponent (a/u)kku, which is not adjacent to it on the surface since the plural exponent (n)ga(l) intervenes. Postulating alignment-driven movement of the dative exponent ensures that strict locality of stem allomorphy can be respected at the initial stage of the derivation (the case exponent (a/u)kku is exceptionally merged closer to the stem than the plural exponent because the stem, which must always be present first, is also specified for case; see Müller 2020: 240–248).

Against this background, the cases of seemingly non-local phonological operations in words discussed in Sect. 2 provide a further argument for movement in morphology.

4 Phonological evidence for movement in morphology

4.1 Cycles

The hypothesis pursued in what follows is that what may at first sight look like a non-local application of a phonological operation can upon closer inspection be shown to be a local phonological operation conditioned by an exponent that eventually shows up in a non-local position as a consequence of morphological movement. At this point, the necessary assumptions to implement this for the five case studies are already in place, except for one: it needs to be determined when phonological operations take place in harmonic serialist derivations.

We would like to suggest that phonological operations apply to the output of a morphological cycle. For the phenomena currently under consideration, we would like to contend that there are two relevant morphological cycles in the present approach to inflectional morphology based on Harmonic Serialism: one morphological cycle is finished when all MC-triggered inflectional Merge operations have applied to a given stem. Intuitively, this is the stage where the word is potentially complete for the first time (this will be minimally modified below). A further morphological cycle is finished when the derivation has converged on a final output. In the above example illustrating German verb inflection, the two morphological cycles converge on O₁₂₂ in (34). However, in the example illustrating Berber verb inflection, the two morphological cycles are not identical: O₁₅₃ in (37) completes one morphological cycle, and O₁₅₃₂ in (38) ends another one.²⁹ We will focus on these two cycles in what follows; however, the present approach is fully compatible with the existence of further cycles. Thus, the literature contains a wealth of empirical arguments for a phonological root cycle applying to forms before derivational or inflectional exponents are attached (see, e.g., Bermúdez-Otero 2008, 2012; Trommer 2011, 2013; and Martínez-Paricio 2012). In line with this, in Müller (2020: Ch. 5) it is argued that “roots” are not in fact primitive but derived on an earlier morphological cycle where category-neutral roots are merged with categorizing heads (see Marantz 1998; Harley 2014; and much related work); this morphological operation can then be assumed to trigger a first phonological cycle. Similar considerations apply in the case of derivational morphology, where there is evidence to postulate a further morphological base cycle (defined by merging derivational affixes) following the root cycle and preceding the first inflectional stem cycle, with an associated phonological cycle. Still, for the data in Sect. 2, root and base cycles can be disregarded; accordingly, we will concentrate on the two stem cycles we have proposed (with morphological movement, for now, establishing the dividing line).³⁰

In such a model, it needs to be ensured that the end of one type of cycle, and the beginning of another type of cycle, can be systematically determined. For morphological cycles, this is unproblematic, given that they are organized according to Harmonic Serialism: The cut-off points are defined by convergence (input-output identity), subject to the requirement that certain kinds of improvements of constraint profiles cannot yet be carried out on a given cycle (e.g., in the case at hand, exponent movement cannot yet be applied to improve the constraint profile on the morphological cycle defined by basic structure-building). As regards the phonological cycles, the answer depends on what kind of approach to phonology is adopted in the first place. If phonology is also organized according to Harmonic Serialism, then the end of a phonological cycle is determined in the same way, via convergence; if it is organized according to standard parallel Optimality Theory, the end of a phonological cycle is determined by selection of the optimal candidate of the unique competition; and if phonology is rule-based, the end of the cycle is determined by finishing the list of ordered rules. For the phenomena addressed in this paper, the exact nature of phonological cycles does not have to be decided—as we have tried to show in Sect. 2, the phonological processes in question are all perfectly simple and well-behaved, can therefore be covered by all the phonological theories just mentioned, and thus do not distinguish between the different approaches.³¹

This general approach to morphology/phonology interactions opens up the possibility that phonological operations may apply after inflectional exponents have been merged with the stem, and before morphological movement takes place. As we will show in the next five subsections, this is what underlies the effects discussed in Sect. 2.

4.2 De-spirantization in Barwar Aramaic

Consider first seemingly non-local de-spirantization in Barwar Aramaic. Recall from (2) and (7) that the tense/aspect exponent /wa/↔[remote] can intervene between the stem and an agreement exponent like /le/↔[3.sg.masc] on the surface but does not block de-spirantization of the final stem consonant triggered by /le/. Given the reasoning in Sect. 3, this implies that /le/ is merged before /wa/ (and the right-alignment constraint for /le/ outranks that for /wa/). At first sight, this might seem to necessitate deviating from the assumption that the order of MCs in the morphological component reflects f-seq. However, closer scrutiny reveals that this is not the case. Although /wa/ has been classified as a “tense/aspect” exponent above, its actual function in the system is not the basic realization of this grammatical category. Rather, the real tense exponent in Barwar Aramaic is the root itself, in the form of non-concatenative root-and-pattern morphology typical of Semitic languages (which may in turn have resulted from earlier Merge of an abstract exponent, perhaps on a prior root cycle; see, e.g., Kastner 2019). The exponent /wa/ has a more adverb-like role; it freely attaches to present or past tense stems to add information of anteriority, or remoteness. Historically, it derives from a separate past tense verb *hwa (cf. Khan 2008: 177). We take this to be a clear indication that /wa/ lies outside the clausal f-seq, which produces a ranking MC$_{ \rm T}$ ≫ MC_Agr in Barwar Aramaic, as in other languages; wa is introduced into words by a MC$_{\mathrm{Adv(erb):T(emp)}}$ that is lower-ranked. Under these assumptions, and zooming in at a stage in the derivation where non-concatenative root morphology has been optimized (in response to MC_T and other constraints), the first optimization step for a form with de-spirantization like (chase.away〈past〉-remote-3sg.sbj, ‘He had chased away’; cf. (7)) is shown in (1). The optimal output O₁₂ merges /le/ as a suffix.³²

• (40)

  

In the next optimization step documented in (1), O₁₂₂ is optimal: /wa/ is added, and it is also added as a suffix (because of the ranking L⇐V ≫ Agr⇒R). As before, placing /wa/ in a position between V and /le/ would in principle give rise to the best constraint profile (because L⇐V and Agr⇒R would be satisfied, and Adv:T⇒R would only be violated once), but this option is not available because of the Strict Cycle Condition.

• (41)

  

At this point, the V stem has discharged all its structure-building features, so a morphological cycle is completed, and phonological operations can be triggered. Thus, de-spirantization applies to O₁₂₂, under strictly local conditions, turning // into //. After this, the next morphological cycle starts; and, as shown in (1), the constraint profile of the word can indeed be further improved by carrying out morphological movement of /le/ to the right edge: O₁₂₂₂ trades in the violation of higher-ranked Agr⇒R incurred by O₁₂₂₁, which leaves the input intact, for a violation of lower-ranked Adv:T⇒R. Outputs that employ movement of one exponent to the left edge (O₁₂₂₃, O₁₂₂₄) can never become optimal; and outputs that move two exponents to the left edge (thereby producing the final two of the six logically possible orders) cannot even be generated (given (29a)).

• (42)

  

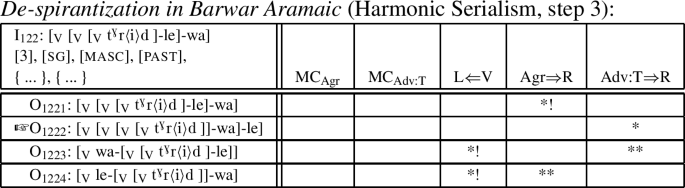
The next step yields convergence, and a second phonological cycle starts which does not affect de-spirantization anymore: morphological movement counter-bleeds de-spirantization.

An immediate prediction of this approach is that exponents which are introduced earlier than the subject agreement marker /le/ in this configuration according to f-seq should ceteris paribus not give rise to de-spirantization. This is indeed the case. For instance, as shown in (6) above, an object agreement exponent intervening between the stem and a subject agreement exponent, as in // (chase.away〈past〉-f.obj-3sg.m.sbj), blocks de-spirantization. Finally, a remark is due on the optionality of the process; recall from (7) that [] and [] co-exist. At least for present purposes, it may suffice to assume that de-spirantization applies without qualification after the second morphological cycle but may or may not apply after the first one; e.g., in Optimality Theory, variation and optionality on the first phonological cycle can be derived by invoking concepts like multiple grammars, partially ordered grammars, or stochastic OT (cf. Anttila 2007).

4.3 Saussurean accent shift in Lithuanian

The problem posed by theme vowels in Lithuanian is that they do not seem to block Saussurean accent shift (such that main accent is placed on the inflectional exponent pre-specified for accent) even though they do seem to intervene on the surface, are associated with a mora themselves, and should thus block this phonological operation; thus, /kás + (see (11)). In what follows, we will show that this phenomenon lends itself to the same kind of analysis as de-spirantization in Barwar Aramaic, with one minor qualification concerning the end of the initial morphological stem cycle.

To begin with, we follow Kushnir (2018) in assuming that (abstracting away from preverbs) the finite Lithuanian verb consists of a stem followed by three inflectional exponents: first, a tense exponent, which is Ø in present and past contexts and realized as /s/ in future contexts; second, a theme vowel; and third, a subject agreement exponent encoding person and number: V-T-Th-Agr. Since the language does not have overt tense exponents for present and past environments, the difference has to be encoded in some other way. This is accomplished by (a) stem alternations, and (b) theme vowel choice—as for the latter, see, e.g., /dírb-Ø-a-u/ (work-1.sg.pres) vs. /dírb-Ø-oo-u/ (work-1.sg.past). However, there is no direct implicational relation between tenses and theme vowels: On the one hand, a given tense can co-occur with various theme vowels (e.g., present tense can co-occur with /a/, /ia/, /i/, and /oo/, depending on the V stem); and on the other hand, a given theme vowel can co-occur with more than one tense (so, /oo/ shows up in the present tense with some verbs, and in the past tense with many other verbs; /i/ occurs in the present tense with some verbs, and in the future tense with all verbs). In view of this state of affairs, we conclude that the theme vowels in Lithuanian are best analyzed as a morphomic (or ‘ornamental’) category [Th] that plays no role in syntax, and is only indirectly related to morpho-syntactic (i.e., non-morphomic) features. In sum, this yields three kinds of exponents for the Lithuanian verb, which are accordingly targetted by three structure-building features on the V stem: [•T•], [•Agr•], and [•Th•]. Given f-seq, we expect MC_T to outrank MC$_{ \rm Agr}$; crucially, MC_Th, being concerned with a morphomic feature, will be lowest-ranked, in the same way that non-f-seq-related MC$_{ \rm Adv:T}$ was argued to be in the previous section. This implies that theme vowels are merged last.³³

The ranking of the respective alignment constraints that produces movement of the agreement exponent across the theme vowel, so that the latter ends up in its surface position between the T exponent and the Agr exponent, then is Agr⇒R ≫ Th⇒R ≫ T⇒R.

Based on these assumptions, the first optimization step in the derivation of a form like (dig-1.sg.past) yields a winning candidate where the T exponent (Ø) has been merged as a suffix; cf. O₁₂ in (1).³⁴

• (43)

  

In the next step, the Agr exponent /ú/ is merged; see (1).

• (44)

  

Importantly, it has to be at this point, before merging the theme vowel in the next step, that the first morphological cycle is concluded, and phonological operations can be triggered: as soon as the theme vowel is part of the representation, the context for Saussurean accent shift is not given anymore, unless additional assumptions are made; recall the example in (9c) above where a mora following the accent-bearing mora in the dative plural exponent /ó_μo_μms/ blocks the process. Hence, the definition of completion of the first morphological stem cycle can be slightly changed: It is not captured by the point where all MC-triggered Merge operations have applied, but rather by the point where all MC-triggered Merge operations involving morpho-syntactic (i.e., non-morphomic) features have taken place. This maintains the original hypothesis that it is the first presence of a morpho-syntactically complete word that defines the option to start phonological operations; morphomic exponents like theme vowels are irrelevant from this perspective. Given this assumption, Saussurean shift applies to O₁₂₂ in (0); this fixes the main accent of the word, which cannot subsequently be undone. In the next step, the theme vowel is merged; cf. (1).³⁵

• (45)

  

Since Agr⇒R outranks Th⇒R, movement of /ú/ to the right edge takes place in the next optimization round. The violation of Agr⇒R that was tolerable in the previous optimization because there was no better alternative becomes fatal as soon as there is one. Thus, an output with the order /kas-Ø-ee-ú/ cannot directly be generated in (0) because counter-cyclic Merge of /ee/ would violate the Strict Cycle Condition, and multiple Merge (one external: /ee/, one internal: /ú/) would violate the prohibition against more than one operation separating input and output (cf. (29a)). However, it can be generated in the next step (because only one movement operation is needed now, with the theme vowel already part of the structure), and consequently becomes optimal; see (1).

• (46)

  

The next optimization step produces convergence. At this point, the second phonological cycle starts, which turns O₁₂₂₂₂, i.e., /kas-Ø-ee-ú/, into the surface representation .³⁶

4.4 Ni-insertion in Quechua

Recall that the phonological operation of ni-epenthesis breaking up super-heavy syllables seems to apply across an intervening exponent ʎa (‘just’) that would normally be expected to destroy the environment for ni-insertion both in Bolivian Quechua, where this process is obligatory (cf. (17d): wawa-s-ni-ʎa-j (child-pl-ni-just-1.poss ‘just my children’)), and in Huallaga Quechua, where it is optional (cf. (16c): kikiç-ni-ʎa-jki armpit-just-2.poss ‘just your armpit’). The basic pattern straightforwardly lends itself to the kind of analysis in terms of morphological movement we have given in the previous two subsections. In fact, the main difference to the analysis proposed for Barwar Aramaic is that the stem that is subject to inflection is of type N now, rather than of type V. Exponents bearing the feature [poss] are clearly subject to the f-seq of nominal categories (possessive marking is a property of nouns in the language); and an exponent like ʎa, which is not restricted to nouns but can be also used with verbs or adverbs and is completely optional, clearly is not. By the same reasoning as in Sect. 4.2 above, we can therefore conclude that there are two MCs, MC_Poss and MC$_{\mathrm{Lim(itation)}}$, and that the former outranks the latter.³⁷

Given, furthermore, a parallel ranking for the alignment constraints Poss⇒R and Lim⇒R and a high-ranked L⇐N, morphological movement of the possessor exponent will be triggered after both MCs have been satisfied. The first optimization step for Bolivian Quechua wawa-s-ni-ʎa-j (child-pl-ni-just-1.poss) is shown in (1).³⁸

• (47)

  

After merging /j/ in (0) because of highest-ranked MC_Poss, the derivation gets rid of the next severe constraint violation (viz., that of MC_Lim) by merging /ʎa/; cf. (1).

• (48)

  

Given the high ranking of L⇐N, /ʎa/ must be merged as a suffix in (0); and given the Strict Cycle Condition, it can only be added at the right edge, in violation of Poss⇒R. At this point, the first morphological cycle is concluded (all non-morphomic MCs have been satisfied), and the phonological operation of ni-epenthesis applies to O₁₂₂, breaking up the super-heavy syllable with a rhyme consisting of a, s, and j: /wawa-s-j-ʎa/ becomes /wawa-s-ni-j-ʎa/; /ʎa/ is already part of the representation but does not intervene because it shows up at the right edge at this stage. After this, the morphological derivation continues; since Poss⇒R outranks Lim⇒R, morphological movement of /j/ across /ʎa/ is triggered; see (1). This movement applies after ni-insertion and counter-bleeds it. Finally, convergence is reached.

• (49)

  

With respect to the optionality of the process in Huallaga Quechua, it can be assumed (essentially as postulated for the optionality of de-spirantization in Sect. 4.2) that since ni-epenthesis is obligatory in configurations that are local on the surface, it always applies after the morphological derivation is complete; but it may or may not apply after the first morphological cycle.

Finally, as regards the contextually determined systematic variation in /ʎa/ placement visible in (18) in Huallaga Quechua (where /ʎa/ follows the possessor exponent if the latter co-occurs with a plural exponent, but not otherwise), we contend that the effect is due to a constraint Coh(erence) that is independently motivated in Trommer (2008), and ranked higher in the variety at hand; Coh demands that two exponents that encode the same argument must show up next to one another. See Müller (2020: Ch. 2) on how Coh can trigger movement of inflectional exponents in the harmonic serialist approach adopted here.

4.5 Ruki rule application in Sanskrit

The core observation here is that an inflected Sanskrit past tense verb shows application of the ruki rule with prefixed verbs where the final segment of the prefix acts as a trigger, turning stem-initial s into retroflex ʂ after r, u, k, and i, even though a past tense (non-ϕ) exponent /a/ intervenes on the surface; cf. (23c) abhy-a-ʂiñc-at (on-past-pour-3.sg). The general logic of the analyses presented so far implies that the prefix /abhi/ (‘unto’) combines with the stem /siñc/ (‘sprinkle’) before the past tense exponent /a/ is added. It turns out that it suffices to make either of the two following traditional assumptions to derive this: (i) Compounding and derivation precede inflection; (ii) Prefix verbs are stored as such in the lexicon. In what follows, we will remain neutral as to the choice between (i) and (ii) (but the above remarks on a possible base cycle would of course favour (i)). Either way, there is a stage of the derivation that looks as in (1), with a complex verb /abhi-siñc/ consisting of prefix and stem as the input. Furthermore, we assume that the past tense prefix /a/↔[past] and the agreement suffix /at/↔[3.sg] are subject to MC_T and MC$_{ \rm Agr}$, respectively. Since three non-stem exponents and one stem exponent are involved, there need to be four alignment constraints; of these, Agr⇒R must be highest-ranked because agreement markers show up as suffixes, in violation of V⇒R; and L⇐P (for the prefix) and L⇐T (for the T exponent) are ranked lower, in this order.

• (50)

  

The optimal output in (0) is O₁₃, which merges the T exponent /a/ in a prefix position, at the cost of a violation of the constraint L⇐P, which requires the verbal prefix to be at the left edge, and which, as such, is ranked higher than L⇐T but cannot be satisfied at this point because of V⇒R and the Strict Cycle Condition. In the next step, the Agr exponent /at/ is merged; see (1).

• (51)

  

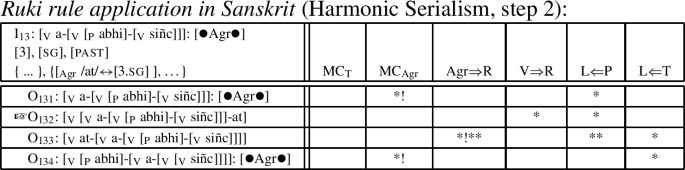
The optimal output O₁₃₂ in (0) violates V⇒R so as to satisfy higher-ranked Agr⇒R; and it inherits the input’s violation of L⇐P because MC_Agr is the higher-ranked constraint; see O₁₃₄, where L⇐P is satisfied by movement of abhi but MC_Agr is violated. However, at this point the word is structurally complete; consequently, a first phonological cycle is initiated, and the ruki rule applies under adjacency of /abhi/ and /siñc/.

Next, the prefix /abhi/ moves to the left edge, because of L⇐P ≫ L⇐T; cf. (1).³⁹

• (52)

  

As before, morphological movement of exponents counter-bleeds a phonological operation: /a/ does not intervene at the relevant stage of the derivation even though it does intervene on the surface.⁴⁰ Finally, convergence is reached, and a second phonological cycle is started.

4.6 Vowel harmony in Kazakh

As shown above (cf. (26)), vowel harmony in Kazakh affects a final Q exponent /bA/ across an intervening instrumental case exponent /men/ that does not participate in the process and should be expected to block spreading of the stem’s backness value to the Q marker; cf. bʊl ʃal nan-men-ba (this old.man bread-instr-q) vs. bʊl ʃal bøbek-men-be (this old.man baby-instr-q). The first thing to note is that, under present assumptions, interrogativity must be a grammatical category for which nouns (like verbs) can be inflected in Kazakh; the feature [C] of which Q is a possible value is part of the f-seq of nominal projections.⁴¹ Next, we propose that the instrumental case exponent /men/ does not belong in a group with the other case exponents in the language, and is introduced into words by a special, designated MC_Instr constraint that is outside of the regular, f-seq-determined order. In line with this special morpho-syntactic behaviour, /men/ also exhibits unusual phonological properties; in particular, it resists vowel harmony. Under these assumptions, the apparently non-local instance of vowel harmony can be derived in a strictly local way: the order of the right-alignment constraints for the C exponent /bA/ and the instrumental exponent /men/ is the same as the order of the two MCs for these items.

Thus, to generate a word like nan-men-ba (bread-instr-q), the noun stem /nan/ is first merged with the Q exponent /bA/, as in O₁₂, which wins the competition in (1).

• (53)

  

In the second step, /men/ is merged as a suffix.

• (54)

  

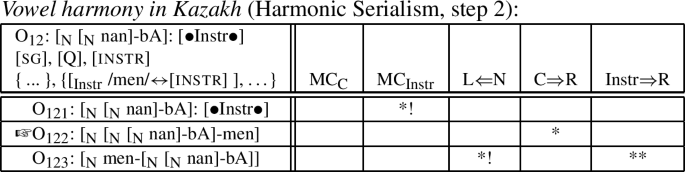
At this point, the first morphological cycle is finished because the N stem has exhausted its structure-building features. Vowel harmony applies, spreading backness from the stem to the adjacent Q suffix /bA/; /men/ is pre-specified for backness, therefore resisting vowel harmony, and so does not change. The output of this round of phonological spell-out is then subjected to the next morphological cycle. Now, movement of the Q exponent /ba/ to the right edge takes place because C⇒R outranks Instr⇒R; see (1) (where outputs with suboptimal movements are ignored, as before).

• (55)

  

The next step is the final step; O₁₂₂₂ as the input is mapped to the same output. As before, a seemingly non-local phonological process (vowel harmony) emerges as a local process that is counter-bled by morphological movement.

4.7 Interim conclusion

To conclude so far, we have looked at five different seemingly non-local phonological operations and have argued that they can all be conceived of as strictly local operations in the harmonic serialist approach to inflectional morphology developed in Müller (2020). In this approach, the defining property of Harmonic Serialism that competing outputs can differ from the input by application of at most one elementary operation, together with the Strict Cycle Condition, automatically yields the consequence that alignment constraints that need to be postulated for reasons entirely unrelated to movement may force exponents to leave the position they are first merged in, and move to an edge position later in the derivation. Given the assumption that phonological operations on the stem cycle can in principle apply as soon as a morphological word is complete (i.e., has all the non-morphomic exponents required by the structure-building constraints), the phonological operations we have investigated here can all be shown to be counter-bled by subsequent morphological movement.⁴²

In this paper, we have focussed on inflectional morphology. We suspect that there may turn out to be many more cases in this area once one starts looking in earnest for the relevant patterns—see, e.g., Embick (2010) on allomorphy in Palauan, where dissimilation forces choice of a verb marker o- instead of the expected verb marker mə- before a labial-initial root like baləʔ ‘shoot’ even if a past exponent il- intervenes on the surface, as in o-il-baləʔ; or Vaux (1994) on vowel raising triggered by seemingly non-local nasal consonants across indicative exponents in Homshetsma Armenian (on which see Gleim et al. 2021). Furthermore, similar phenomena involving apparently non-local phonological effects have also been observed for derivational morphology; see in particular Hyman (1994, 2002, 2003) on frication that seems to be triggered by non-local causative exponents in Bemba and other Bantu languages, as in leef-es-i̧ (lengthen-appl-caus ‘lengthen for/at’), where an underlying root leep is turned into leef by causative i̧ across intervening applicative es; and Hyman et al. (2008) and Myler (2017) on reduplication of a root with a causative affix instead of a closer applicative exponent in Ndebele. Assuming structure-building and linearization in derivational morphology to proceed in the same way as in inflectional morphology, these kinds of data would seem to lend themselves to the same kinds of analyses.⁴³ A somewhat more speculative extension involves the apparent overapplication of l-to-i vocalization in Brazilian Portuguese (cf. Bachrach and Nevins 2008; Rolle 2018a; and references cited there), where a plural exponent s triggers the process not only under adjacency (jornal ‘newspaper’ → jornais), but also if stem and inflection are separated by an intervening diminutive (jornal-zinho vs. jornai-zinho-s); see, again, Gleim et al. (2021) for an analysis in terms of (multiple) exponent movement in Harmonic Serialism.

More generally, then, we take it that the phenomenon under discussion can be viewed as support for a principled approach to morphological movement of exponents. As noted, there are other arguments for this concept detailed in Müller (2020), based on discontinuous exponence, partially superfluous extended exponence, and non-local stem allomorphy. An additional conceptual argument for morphological movement of the type assumed here is that it permits stating, via shared, uniform f-seqs, a version of the Mirror Principle that is not necessarily falsified by deviating surface orders: on this view, what counts for the Mirror Principle in both syntax and morphology (with the qualification in the last footnote) is the initial order in which items are merged; this may then subsequently be undone by movement.

An issue that we have so far been silent about concerns the variation under factorial typology that is predicted under present assumptions. Let us focus on scenarios like the ones in Sect. 3, where there are two Merge Conditions which are active (because the stem is equipped with the features that they hold for)—e.g., MC_T, MC_Agr—and one active alignment constraint each for the stem, the first-merged exponent, and the second-merged exponent—e.g., L⇐V, T⇒R, and Agr⇒R (contrary alignment constraints for these exponents—e.g., L⇐T—exist but are always inactive due to being ranked low, and can therefore be ignored for now). By assumption, the order among MCs is cross-linguistically invariant, given f-seq. Suppose furthermore, at least for present purposes, that all MCs have to outrank all alignment constraints, as assumed in Müller (2020).⁴⁴ Then all relevant rerankings will involve the three alignment constraints, yielding six possible orders. Of these, three converge on V-T-Agr (if Agr⇒R ≫ T⇒R), two predict Agr-V-T (if T⇒R is undominated), and only one will give rise to movement, producing V-Agr-T on the surface (if T⇒R ≫ Agr⇒R and L⇐V ≫ T⇒R). Note that the three remaining combinations T-V-Agr, Agr-T-V, and T-Agr-V are predicted not to arise (with these three alignment constraints active), given the Strict Cycle Condition and the impossibility of moving the stem. Next consider the impact of an additional faithfulness constraint blocking movement (like Shape Conservation or Linearity, cf. footnote 26). Now, with four freely rankable constraints, the system still only predicts the three possible outcomes V-T-Agr, Agr-V-T, and V-Agr-T. The optimal outputs of all 4! = 24 rankings that need to be considered under factorial typology are given in (1) (with constraint violations incurred by optimal outputs in square brackets, greyed out if they arise only temporarily in the derivation, and are subsequently undone by movement).

• (56)

  

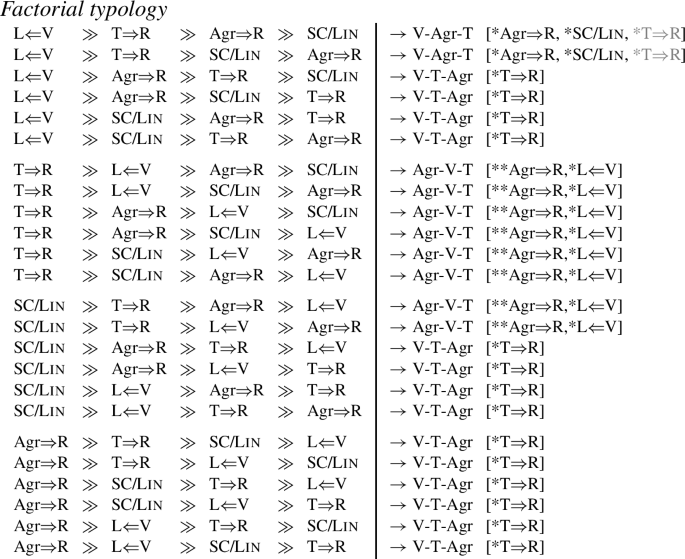
In fact, whereas fourteen rankings give rise to V-T-Agr, and eight rankings produce Agr-V-T, only two rankings out of twenty-four (viz., those with L⇐V ≫ T⇒R, T⇒R ≫ Agr⇒R and T⇒R ≫ SC/Lin) yield the movement output V-Agr-T. Following Anttila (1997), this fact might well be taken to be the source of the apparent markedness of f-seq-violating orders: Morphological movement is systematically predicted in this system, but it is also predicted to be rare (abstracting away from other kinds of constraints that can also trigger movement, like Coh mentioned in Sect. 4.4).

Closer inspection reveals that this result persists when all other logically possible combinations of dominant alignment constraints and their possible rankings are taken into account. E.g., it could be that everything is as in (0), except that Agr⇒R does not outrank the contrary constraint L⇐Agr but is dominated by it, yielding L⇐V, T⇒R, and L⇒Agr as the active constraints. More generally, in the case at hand, there are three categories (V, T, Agr) for which there are two conflicting alignment constraints each (L⇐X, X⇒R). Consequently, there are eight relevant scenarios, each resulting in 4! = 24 rankings (which, among other things, of course also accounts for the existence of the three orders that cannot be produced under any ranking in (0)). Out of these, there are four scenarios where the dominant alignment constraints for T and Agr converge on the same direction (i.e., T⇒R, Agr⇒R and either L⇐V, as in (0), or V⇒R; or L⇐T, L⇐Agr and either L⇐V or V⇒R); in these cases, there are 2 out of 24 rankings that give rise to movement; cf. (57a–d). Next, in those two scenarios where the dominant alignment constraint for Agr converges with the dominant alignment constraint for V but not with that for T (i.e., V⇒R, Agr⇒R and L⇐T; and L⇐V, L⇐Agr and T⇒R), 4 out of 24 rankings will produce movement; cf. (57e–f). And in the remaining two scenarios where the dominant alignment constraint for T converges with the dominant alignment constraint for V but not with that for Agr (i.e., L⇐V, L⇐T and Agr⇒R; and V⇒R, T⇒R and L⇐Agr), not a single ranking triggers movement; cf. (57g–h).

• (57)

  

Thus, all in all, only 16 out of 192 rankings bring about exponent movement, where T and V are separated by Agr on the surface.⁴⁵ These conclusions for patterns with three relevant alignment constraints, as in the case studies of Barwar Aramaic, Bolivian Quechua, and Kazakh, extend, mutatis mutandis, to patterns with four alignment constraints (one for the stem and three for exponents), as in the case studies of Lithuanian and Sanskrit: under certain well-defined rankings, morphological movement is predicted to arise, but under most rankings, it will not occur.

Needless to say, there are many features of the present approach to inflectional morphology that would be in need of further discussion and justification. We cannot possibly do this here; see Müller (2020) for extensive discussion. However, in the final part of the paper, we would like to consider alternatives to morphological movement of inflectional exponents in Harmonic Serialism as the source of the phenomena we have looked at.

5 Alternative approaches

The goal of this final section is to look at alternative approaches to non-local phonological operations that have been proposed in the literature, or could in principle be developed. They can be grouped into six types, the first three of which are phonological in nature. First, some approaches allow for non-local application of phonological processes. Second, other approaches invoke the concept of base-derivative faithfulness. Third, phonological movement might be postulated. Other approaches locate the phenomenon in the morphological component, like we have done; they all maintain the assumption that phonological processes apply locally. Thus, a fourth kind of approach relies on counter-cyclic morphological operations (interfixation, lowering, dislocation); a fifth one is based on syntactic movement; and a final type of approach to be considered here invokes strata. We address these approaches in turn.

5.1 Non-local phonology

One possible approach to the phenomenon of exceptional non-locality in phonological processes is to take the evidence at face value. If phonological processes are potentially non-local, a theory could just allow for all phonological processes to be non-local. Such approaches are rare for reasons that will be discussed below. One such non-local approach to phonology within a more general optimality-theoretic framework is Agreement by Correspondence (ABC; cf. Hansson 2001; Rose and Walker 2004; and Rhodes 2012).

Bowman and Lokshin (2014) propose an account for exceptionally transparent vowels in Kazakh vowel harmony based on ABC. The gist of this analysis is that vowel harmony is always a non-local phenomenon that affects all vowels in a word. If the constraint now applies to all vowels except the instrumental case suffix, we generate the existing pattern. In this subsection, we will first introduce the specific approach and then discuss its application to other cases of exceptionally non-local phonological processes.

The ABC analysis in Bowman and Lokshin (2014: 7) consists of two types of constraints. One constraint type Corr requires all segments of a certain type to be in a correspondence class. Correspondence classes are marked with a subscript index. In the present case, there is a Corr-VV constraint that requires all vowels to be in a correspondence class; cf. (58a). A second constraint type places a certain condition on this correspondence class. In our case, the vowels should agree in backness, so the constraint is Id-VV(back), as given in (58b).

• (58)

  

Ranking these constraints above a general Id(back) constraint already derives the harmony. The directionality of vowel harmony is derived by a high-ranked faithfulness for the initial syllable InitId(back). The analysis is illustrated in the tableau in (59). The Corr-VV constraint excludes all candidates with non-corresponding vowels, e.g., O₁ in (1). Ident-VV(back) on the other hand penalizes candidates with non-agreeing vowels, as shown by O₃. Finally, InitId(back) derives directionality by protecting the first vowel, cf. O₄.

• (59)

  

In order to derive the exceptional transparency of the instrumental case suffix, Bowman and Lokshin (2014) assume a modified system of phonological strength. In their case, strength is based on lexical/morphological marking instead of phonological contrastivity, as in the original proposal by Rhodes (2012). Rhodes proposed that constraints refer to an inventory-based notion of phonological strength, such that non-contrasting features are only weakly specified, and contrastive features are strongly specified. On the other hand, Bowman and Lokshin (2014) assume that vowels can be marked as strong or weak in the underlying representation of a word, independently of the vowel phoneme inventory. In Kazakh, all vowels but the exceptionally transparent one are marked as strong with respect to backness harmony. The Corr-VV constraint is then modified to only apply to strongly specified vowels Corr-V_SV_S. Since this idea of strength is stripped of its phonological meaning in earlier literature, it now only applies lexically to a certain class of morphemes. Thus, it can be seen as a special case of lexical constraint indexation (see Pater 2007), dividing the morphemes into undergoers and non-undergoers for vowel harmony, but with a twist.⁴⁶

The constraint only applies if both targets of the constraint bear an index. This is different from the usual locality conditions in indexed constraint approaches (see Pater 2009). Weak vowels are marked with a superscript obelisk in the tableau in (60). Since the general version of this constraint is now ranked below the Ident(back) constraint, the instrumental suffix vowel cannot undergo vowel harmony; cf. O₅ in (1).

• (60)

  

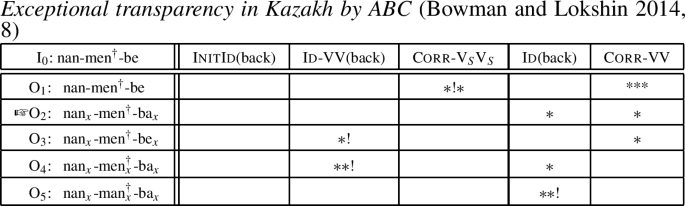
This account works for Kazakh vowel harmony because its domain is large enough. Vowel harmony affects all vowels in a word and ignores intervening consonants. Other processes discussed so far usually operate only under segmental adjacency (Aramaic, Sanskrit) or syllable adjacency (Quechua, Lithuanian). In order to account for these more local processes in other languages, an additional rankable locality constraint would have to be introduced; otherwise, the regular phonological processes would also apply when the adjacency requirements are not met, contrary to fact. One version of this constraint would have to be ranked above, and one below the faithfulness constraint. This constraint would have to penalize intervening segments/syllables, with the higher ranked version of this constraint referring only to morphemes marked as strong and the lower ranked version of this constraint referring to all morphemes. In his early work, Hansson (2001: 237) explicitly denies the possibility of such a constraint. Even the locality constraints later introduced by Rose and Walker (2004) and formalized by Bennett (2015a) do not count intervening segments.⁴⁷ Instead, they are violated for each pair of corresponding segments/syllables as soon as one non-corresponding element intervenes (cf. also Shih and Inkelas 2018, 141). An account of more local phonological processes would thus require either a reformulation of this constraint or the addition of a new constraint type.

ABC has been mostly applied to consonantal and vocalic harmony or dissimilation processes (see Hansson 2001; Rose and Walker 2004; Rhodes 2012; and Bennett 2015a). Therefore, segments in a correspondence class here mostly need to agree with respect to a certain feature, and such constraints do already exist in the system. The processes discussed in the data above however also include other processes, such as epenthesis and accent shift. It is at least not immediately clear how an ABC account would handle these.

There are further conceptual issues raised by this approach. For one thing, the notion of modularity has to be given up or considerably weakened. Constraints in the phonological part of the grammar have to make reference to the identity of certain morphemes. Phonology has to access morphological information. If strength of specification is really a phonological feature, it acts as a diacritic second-order feature. It does not have any other purpose or phonological substance apart from distinguishing undergoers and non-undergoers of vowel harmony. The account thus arguably comes close to merely restating the facts.

Second, non-locality in phonology has to be assumed as a default. Local processes only occur if some locality constraint is ranked high enough. This contrasts with the empirical evidence that can be gained from a cross-linguistic perspective. Most phonological processes are local; non-local processes like consonant harmony are rare. Chandlee and Heinz (2018) find that locality restricts 95% of the approximately 3500 phonological patterns from over 500 languages reported in the P-Base database (Mielke 2008).

5.2 Base-derivative faithfulness

Another phonological account might rely on base-derivative faithfulness (BDF; cf., among others, Benua 1997; Kager 1999; Kenstowicz 2002; and Albright 2002), which has been most concisely formalized as output-output correspondence in Benua (1997). While BDF approaches generally can account for the data, they can only do so by making a very powerful system even less restrictive, arguably without capturing the connection between phonological overapplication (and, crucially, its absence) and morphological structure. In a BDF approach, the phonological computation of a form may refer to a morphologically related but separate existing surface form in the language and transfer some of its phonological properties onto the form under consideration. The derived form thus stands in a relation both with its underlying form, and a separate surface form, the base.⁴⁸ Identifying the correct base is both the most crucial and contested aspect of a BDF analysis, and opinions on what constitutes a licit base are highly divergent in the BDF literature. To the best of our knowledge, the type of base that is necessary for deriving the data at hand—an incoherent, inflectional base—has never been suggested in the literature. First, let us see what a BDF approach to the non-local phenomena could look like, based on the Barwar Aramaic data. On this view, there is a form in which de-spirantization applies regularly, under strict locality. This form serves as the base for the derivation of the form containing the intervening affix /-wa/, where the process applies non-locally; see (1).

• (61)

  

Here faithfulness to the base outranks faithfulness to the input, so that de-spirantization is triggered even if there is no phonological context. The base , however, is incoherent as it is neither a sub- nor a superstring of the derivative. It is different from all the bases that have been proposed in the literature so far: It is not the base of affixation (Input: XY, Base: X), as in Benua (1997) or Kager (1999); nor is the output form the base of affixation whereby the output base contains one unmarked inflectional affix (Input: X, Base: XY, cf. Albright 2002)—this could only be the case if one were to postulate interfixation (for arguments against interfixation, see below); nor is it the unmarked cell of an inflectional paradigm to which the output form also belongs (Input: XY′, Base: XY; cf. Albright 2011). The only precedent for incoherent bases we are aware of is Rolle (2018b); however, here the potentially intervening affixes are explicitly restricted to derivation (Input: XYZ, Base: XZ, where Y is derivational and Z is inflectional). In sum, the addition of yet another novel type of base reduces the restrictivity of BDF further and adds to its problems with overgeneration (cf. Bermúdez-Otero 2011).⁴⁹ Furthermore, there is an arguably even more pressing problem with language-internal overgeneration which is related to the typological overgeneration issue. Given (0), it is unclear why de-spirantization does not overapply with other intervening exponents, like the object agreement suffix /a/ in (6); cf. (1) (☛ indicates a wrong winner, and ✩ accompanies the intended winner that emerges as suboptimal).

• (62)

  

This is not necessarily an unsolvable issue— could either refer to a different base (in violation of Albright’s 2002 single base condition), or the Id-OO[cont] constraint could be lexically indexed to /-wa/. In either case, restrictiveness is further weakened, and the fact that the overapplication is confined to certain exponents remains unexplained.

A final problem for BDF comes from Quechua. While the basic mechanism laid out above can derive the overapplication of epenthesis, it cannot determine its locus; cf. (1).

• (63)

  

There is no standard phonological constraint that could distinguish between O₂ and O₃—Contiguity-OO and Contiguity-IO are both indifferent.⁵⁰

5.3 Movement in phonology

A third possible alternative account would be to postulate that whereas there is indeed a displacement of exponents in the relevant cases, this displacement is a phonological operation that does not change morphological structure, essentially a kind of metathesis operating over strings of segments. There is indeed some potential evidence for the existence of purely phonological displacement. For instance, as argued by Kim (2010), in Huave single-segment affixes alternate between prefixal and suffixal position, and there seems to be a clear phonological trigger for this: The variable placement occurs so as to satisfy syllable structure requirements without altering hierarchical relations. Now, the analysis in Kim (2010) does not actually involve movement (and this is a property shared with other approaches to the phenomenon; cf. Zukoff 2020); rather, the “mobile” exponents show up in either prefix or suffix position. Still, one can conceive of a minimally different version of this approach where the exponents in question are always merged as suffixes in the morphological component, and then undergo movement in the phonological component in certain contexts, triggered by syllable structure constraints (see Grofulović et al. 2021); this is analogous to what has sometimes been argued for phonologically triggered movement in syntax (e.g., Truckenbrodt 1995; Agbayani et al. 2015).

However, the phenomena in Sect. 2 are of a radically different nature: crucially, in none of these cases can a plausible phonological trigger be identified for the displacement. Furthermore, the item that undergoes the displacement is exclusively morphologically defined, and does not lend itself easily to a reinterpretation as an item of the prosodic hierarchy. Finally, even if an account in terms of phonological movement were feasible, it would seem to be inferior to the approach presented above since it would require an additional, designated trigger. In contrast, in the present approach, morphological movement follows in toto from constraints which are independently required: given the one-edit-away-from-the-input restriction, a specific ranking of these constraints gives rise to the effect.

5.4 Counter-cyclic operations: interfixation, lowering, local dislocation

In Distributed Morphology, there are two post-syntactic morphological operations (Lowering, Local Dislocation) that could be invoked for the data in Sect. 2. Interfixation, on the other hand, is a pre-theoretical concept that bears some resemblance to Lowering.

Interfixation is an obvious alternative to our proposal. It stands for a specific morphological process that introduces an exponent between two other exponents that have already been merged in the structure. As noted above, such an approach has been pursued by Hyman (1994, 2002, 2003) for seemingly non-local phonological operations in the derivational morphology of Bantu languages; also see Kiparsky (1982b, 2017); Kushnir (2018); and, to some extent, Myler (2013) for analyses of this type. Interfixing incurs a violation of the Strict Cycle Condition (see (30)): it extends a tree below the root projection. Since interfixation as a grammatical operation has (to the best of our knowledge) so far not been formally made precise, further discussion of the concept is not entirely straightforward; however, we take the problem raised by the inherent violation of the Strict Cycle Condition to be a severe one.

The avatar of interfixation in Distributed Morphology (cf. Halle and Marantz 1993; Embick and Noyer 2001) is Lowering. In contrast to interfixation, where the interfix comes out of the lexicon or the workspace, a lowered morpheme is first merged cyclically in the syntax. At PF, this morpheme undergoes an operation of Lowering which moves the head of a higher phrase downward, onto the head of its complement (see Embick and Noyer 2001: 561). Lowering faces the same problem of counter-cyclicity as interfixation—downward movement violates strict cyclicity because it alters a proper subdomain of the highest cyclic domain.⁵¹ However, Lowering is not only problematic because of the conceptual issue of strict cyclicity, it also fails to derive the patterns discussed in this paper. Lowering is generally assumed to apply before vocabulary insertion, i.e., morphological exponence, in Distributed Morphology (see Embick and Noyer 2001). As a consequence, at the point in the derivation when Lowering applies, there are only abstract morphemes consisting of nothing more than bundles of morpho-syntactic features. This entails that the morphemes in their underlying non-lowered order cannot interact phonologically. Lowering is hence able to account for counter-scopal or otherwise unexpected orders of exponents, but fails to derive the non-local phonological patterns for systematic reasons.

Another mechanism proposed in Distributed Morphology to account for deviant exponent order is Local Dislocation (LD; cf. Embick and Noyer 2001). Unlike Lowering, LD does not operate on hierarchical structures, but on strings of exponents after vocabulary insertion and linearization. It applies at a stage of the derivation where the morphemes have their full morpho-syntactic and phonological features accessible (see Embick 2007). LD is conceived of as a rule that transforms a relation of adjacency into a relation of adjunction, which can result in a change of the order of the two elements. The following discussion is confined to the notion of LD in Embick and Noyer (2001, 2007) and Embick (2007).

Compared to our approach, a LD-based analysis faces three problems. First, like Lowering or interfixation, it is not compatible with strict cyclicity; however, at least at first sight, the problems here might be somewhat less severe: if one follows Embick and Noyer’s (2001) claim that there is no hierarchical structure at the point of LD, the Strict Cycle Condition as defined in (30) (which talks about domains, subdomains, and, most importantly, domination) does not strictly speaking apply. However, Embick and Noyer’s contention seems debatable: their approach to LD relies on (i) the concept of embedding, and (ii) the concept of a head of a morphological constituent during the application of LD. This implies that there is hierarchical structure at this point after all. Embick (2007: 322) explicitly states that different representations, among them hierarchical syntactic structure, exist in parallel at the point of the derivation where LD applies. This makes the Strict Cycle Condition in its original version applicable, as the structure is not yet flattened. If one were to modify LD so that it does indeed exclusively apply on a flattened string, it would not violate the Strict Cycle Condition in the exact form adopted so far, since after flattening there are no domains left that could stand in a structural domination relation. However, if a slightly more general definition of the Strict Cycle Condition is adopted (as in, e.g., Perlmutter and Soames 1979; Freidin 1992; or, for that matter, Pullum 1992), where no outside material can be put into a discrete morpho-syntactic object, the Strict Cycle Condition is violated by any type of LD.

The second problem is the lack of a well-defined trigger for dislocating exponents. The trigger for LD to a position between two words is a constraint that demands that a certain word should morpho-phonologically pattern as an affix. The trigger for LD to a position between affixes is unclear (see Embick and Noyer 2007). Embick (2007: 327) contemplates the idea that LD between affixes might be a different operation altogether. An overarching assumption is that arbitrary and/or unmotivated operations can be tolerated post-syntactically in Distributed Morphology (cf. Embick and Noyer 2007: 321); then again, Embick and Noyer (2007: 320) propose that LD in Huave might be triggered by a linearization constraint that is a bit more complex than, but in fact to some extent comparable to, the alignment constraints employed in the analyses in Sects. 3 and 4 above. More generally, we would like to contend that a systematic formalization of the triggers in an LD-based approach may lead to mechanisms producing effects that are indeed similar to the constraints that we employ.⁵²

The third and most important problem is an empirical one: LD is ultimately not able to account for the phonological long-distance dependencies highlighted in Sect. 2. On the one hand, the scope of LD in Embick’s (2007) version does not extend to the data under discussion. Embick (2007: 325) introduces a Consistency condition, which demands that adjacency requirements may not contradict each other. This condition excludes non-string vacuous LD inside morphological words, or the reordering of affixes (see Embick 2007: 327). This version of LD is thus not able to account for the data because what is needed is clearly a re-ordering of affixes. On the other hand, the version of LD in Embick and Noyer (2001, 2007) does not include Consistency, but it nonetheless fails to derive the data. Its problem lies in the way the morphology-phonology interactions regarding LD are envisioned.

To see this, let us consider, as a representative case study of LD between affixes, the positioning of the reflexive exponent si in Lithuanian (cf. Embick and Noyer 2001, 2007; Embick 2007). This affix appears in second position, between the verb stem and a first prefix if there is one (iš-si-laik-aũ, ‘I hold my stand’). However, if there is no other prefix, si is a suffix to the verb and all other verbal suffixes (laik-aũ-si, ‘I get along’). Prima facie, in the latter case LD is expected to move si from its underlying position preceding the verb to a position between the verb and its inflectional affixes, since this is the available second position. However, this is not what happens: si follows the inflectional affixes in this case (*laik-si-aũ). Embick and Noyer 2001 assume that the reason that LD does not target an intermediate position here is that there has been previous string-vacuous LD of suffixal material onto the verb, so that suffix(es) and stem form a morphologically unbreakable unit. This string-vacuous LD is justified by the ‘closer phonological affinity to the stem’ (Embick and Noyer 2001: 580) of suffixes, as opposed to prefixes, in Lithuanian. Embick (2007: 324) defines a close phonological relationship as exhibiting word-level phonology. Crucially, phonological processes like de-spirantization in Aramaic or vowel harmony in Kazakh are word-level phonology. For them to apply locally, a Distributed Morphology account parallel to the derivation of Lithuanian si must include an operation of string vacuous LD of the underlying inner suffix onto the stem. The exponent cluster created by LD should then be inseparable; it cannot be broken up by later applications of LD (see Embick and Noyer 2001: 580). Thus, the LD operation that is responsible for the application of the phonological process should block the application of LD that would be responsible for the attested affix order. This is shown for Kazakh data like (26) (nan-men-ba, bread-instr-q) in (1).

• (64)

  

First, vocabulary items are inserted. Second, the affix -bA dislocates string-vacuously, so that it forms a morpho-phonological unit with the root nan and can undergo vowel harmony. From now on, nanba has no internal structure anymore. Consequently, subsequent LD can only invert men with this complex unit nanba, yielding *men-nanba instead of nan-men-ba.

Notwithstanding these three problems, it can be noted that a LD-based analysis and the analysis developed in this paper make different empirical predictions. Since LD has access to both phonology and morphology, it can in principle be triggered by both morphological and phonological requirements. In the present approach, morphology and phonology are interleaved, but strict modularity is maintained. Phonological information is thus not expected to be able to trigger movement in morphology.

5.5 Movement in syntax

Another account of seemingly non-local phonological processes is developed in Myler (2017). It shares the idea that these processes may apply locally at some point of the derivation with the present approach. This is derived by a combination of (i) syntactic movement and (ii) a novel algorithm of vocabulary insertion that makes it possible to spell out a specifier before the head of the projection is spelled out. In what follows, we argue that this innovative and elegant proposal nevertheless suffers from two significant problems: first, it predicts phonological interactions between non-adjacent words, which to the best of our knowledge are not attested; second, it employs syntactic movement without a clearly identifiable trigger.

Myler (2017) starts with the observation that seemingly non-local phonological processes can arise if an exponent order violates the Mirror Principle; he suggests that morphemes are first merged in accordance with the Mirror Principle, but the order is then obscured by movement. In this respect, Myler’s (2017) approach is thus a predecessor of the present analysis. The spell-out algorithm is set up in such a way that the resulting structure makes local application of seemingly non-local phonological processes possible. In particular, spell-out proceeds from the bottom to the top of a tree, and depth of embedding is counted by a number of categorially distinct maximal projections; cf. (1) (see Myler 2017: 102):

• (65) Temporal order of vocabulary insertion

  For a pair of terminal nodes x and y:

  If x is the head of a maximal projection M such that M is categorially distinct from y and M dominates y, then y } x.

  If y } x, then y undergoes vocabulary insertion prior to x.

According to this algorithm, the head of a projection undergoes vocabulary insertion after the head of its specifier. For the structure in (66), it generates Z } Y and X } Y, i.e., vocabulary insertion applies to X and Z first, and only then to Y. X and Z are thus adjacent on the vocabulary item level before insertion of Y, and phonological operations applying between them can qualify as local in some sense.

• (66)

  

If Z is the root, X and Y are affixes, and ZP is moved from the complement of X to the specifier of Y, then (65) derives a possible phonological interaction between the root Z and the linearly non-adjacent affix X merged closer to Z in the latter’s base position. So far, so good. However, the spell-out algorithm applies in the same way if the structure is not derived by movement. It predicts phonological interactions between the head of a specifier of Y (i.e., Z in (66)) and a complement of Y (i.e., X in (66)) to be always possible across the intervening head Y. In addition, Z, Y and X may be separate words. The model thus would seem to wrongly predict non-local interactions between non-adjacent words in configurations that are not derived by movement.

Turning to the second potential problem, Myler (2017) shows that (65) correctly derives non-local application of the ruki rule in Sanskrit, where the final vowel of the prefix abhi turns the initial consonant of the root into a retroflex ʂ, across the intervening past tense prefix a. Since Sanskrit data have also been discussed in the present paper (cf. Sects. 2.4 and 4.5), let us compare the two analyses. Myler assumes the structure in (67): a past tense augment is viewed as the head of a designated AugP, and the first prefix abhi is moved to its specifier. According to the spell-out algorithm, abhi undergoes vocabulary insertion before a. This allows seemingly non-local retroflexivization to apply locally. Note that the order in which the affixes are merged, as well as the movement of the first prefix, are more or less exactly as in our approach, and that there is a point in the derivation before movement when there is no intervening material between the prefix abhi and the root. It is the stage at which a first phonological cycle is triggered in our analysis. Myler, however, assumes that phonological interaction between prefixes is postponed to a later stage, where it is derived by manipulating the order of vocabulary insertion operations.

• (67)

  

This (important) difference notwithstanding, a central difference between the two analyses relates to the motivation for movement of abhi in (67). There is general agreement that syntactic movement does not apply without restrictions.⁵³ Myler suggests that abhi is a clitic and should be licensed in the specifier of AugP, but the relation between a past tense augment and syntactic licensing of a clitic is arguably somewhat stipulative. Similarly, an attempt to extend Myler’s (2017) analysis to the other data discussed in Sect. 2 is faced with the challenge of finding a simple syntactic trigger. In effect, then, the approach based on syntactic movement is subject to the same criticism as other approaches discussed above.

5.6 Stratal architecture

Finally, a stratal approach to morphology and phonology (cf. Kiparsky 1982b, 2015; Stiebels 2006; Bermúdez-Otero 2008; Trommer 2011; Rolle 2020; among others) could be developed that would to some extent be similar to the present approach and could in principle derive the patterns. However, there would be one important difference: while the harmonic serialist approach has only one morphological (sub)grammar, employed throughout the morphological module and across different cycles, a stratal account needs several grammars, i.e., it requires re-ranking. To see this, let us consider a stratal approach to seemingly non-local de-spirantization in Barwar Aramaic based on morphological movement. Of course, various technical implementations of such an approach are conceivable; but they will all have to ensure that there are constraints that trigger the concatenation of the exponents with the stem, and constraints that regulate the placement of the exponents in the word. In order to see where the differences are, let us therefore adopt a stratal analysis that leaves as many basic assumptions of the harmonic serialist analysis intact as possible. The (single) competition on the first stratum underlying an eventual output like (chase.away〈past〉-remote-3sg.sbj) then looks as in (1), where the stem // is merged with the Agr exponent /le/ and the Adv:T exponent /wa/.⁵⁴

• (68)

  

O₁₁ exhibits adjacency of /le/ and the V stem. Consequently, given that a cycle of phonology is triggered after this, de-spirantization can take place locally next. However, note that the order in O₁₁ could only be generated under a ranking Adv:T⇒R ≫ Agr⇒R, which is not the ranking that we have assumed so far (and in violation of f-seq). And in fact, in a second morphological stratum, the ranking of these two constraints must be reversed so as to permit /le/ to move across /wa/ and yield the correct surface order; cf. (1).⁵⁵

• (69)

  

Thus, a very basic difference between the two approaches emerges: In the harmonic serialist approach, a given ranking of MCs and alignment constraints (that is determined solely by f-seq and the actual surface positions of exponents, respectively) directly predicts the intermediate representation required for local application of phonological processes, and subsequent morphological movement (because of the one-edit-away-from-the-input restriction and the Strict Cycle Condition); in contrast, in the stratal approach, the required intermediate representation can only be produced if a ranking of alignment constraints is postulated that is not independently motivated by the surface distribution of exponents, and that needs to be subsequently undone via reranking so as to give rise to the actual surface order.

To sum up the results of this section, given that alternative approaches to the phenomena we have been concerned with in the present study all seem to encounter major problems (of different provenance), we take it that there is every reason to look for a new approach that avoids these problems on the one hand, and is conceptually simple and theoretically principled on the other. Morphological movement that is triggered by independently motivated alignment constraints in Harmonic Serialism, and that is systematically interleaved with phonological cycles, strikes us as a promising candidate that meets these requirements.

6 Conclusion

The approach to inflectional morphology based on Harmonic Serialism developed in Müller (2020) predicts the existence of exponent movement in inflected words. This approach is (i) realizational (potentially underspecified inflectional exponents realize fully specified feature matrices associated with stems), (ii) lexical (exponents exist independently of the forms in which they ultimately occur), (iii) based on structure-building via Merge (triggered by MCs which are invariantly ordered among themselves in accordance with f-seq), and (iv) pre-syntactic (thus avoiding insertion transformations, and counter-cyclic operations more generally). Crucially, there are two central features of the approach that, taken together, automatically predict the existence of exponent movement: first, morphological structure-building obeys the Strict Cycle Condition; and second, input and output can only be separated by at most one operation (this is the core principle of Harmonic Serialism). If a second-merged exponent obeys an alignment constraint that is lower-ranked than the parallel alignment constraint for the first-merged exponent, a violation of the latter, higher-ranked alignment constraint is temporarily generated that is subsequently undone by movement of the first-merged exponent; such a scenario arises in a small portion of the rankings that are possible under factorial typology, and it always involves a surface deviation from f-seq.

Against this background, the main point of this article is to argue that the new approach to exponent movement makes it possible to give a principled and simple account of several recalcitrant cases of phonological operations applying in words which may at first sight look exceptionally non-local, and which we reanalyze as reflexes of morphological movement in inflectional morphology, with the phonological operations in question applying under strict adjacency at an earlier step of the derivation: de-spirantization in Barwar Aramaic, accent shift in Lithuanian, ni-insertion in Quechua, ruki rule application in Sanskrit, and vowel harmony in Kazakh.

Finally, we have considered six alternative accounts of the phenomenon: (i) non-local phonology, (ii) base-derivative faithfulness, (iii) phonological movement, (iv) counter-cyclic operations like interfixation, lowering, and local dislocation, (v) syntactic movement, and (vi) strata—and we have argued that the present approach based on exponent movement in an autonomous morphological component is empirically and conceptually superior.