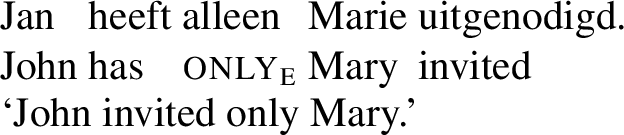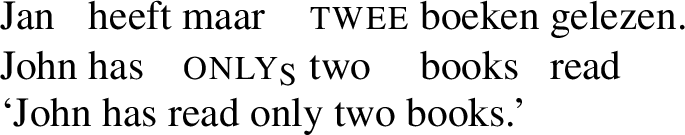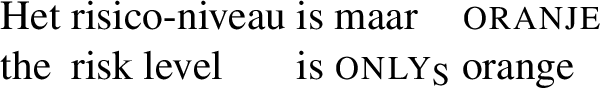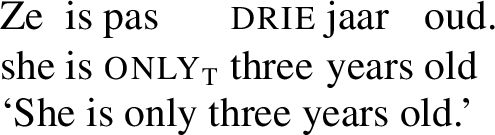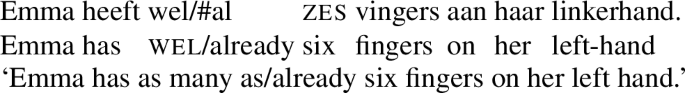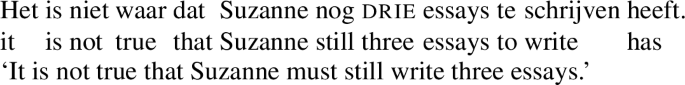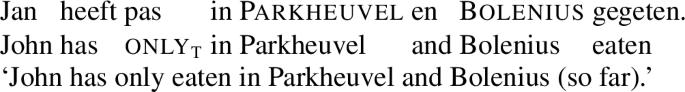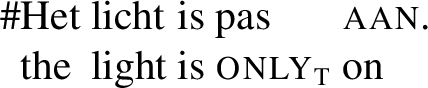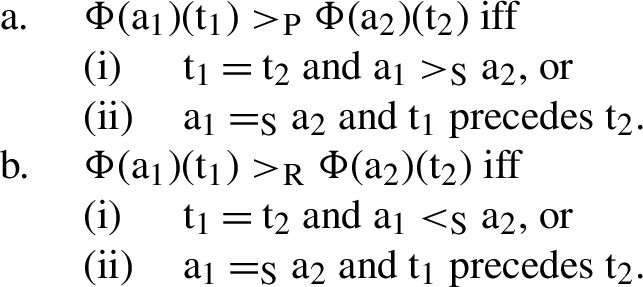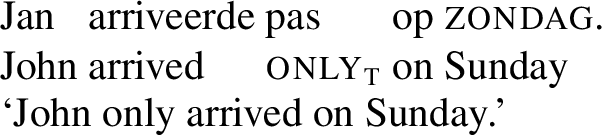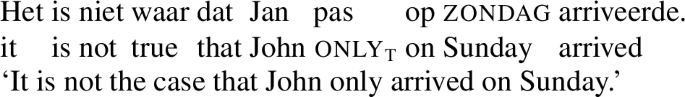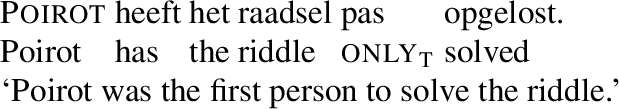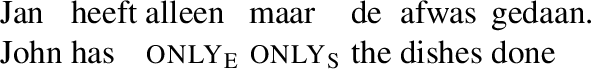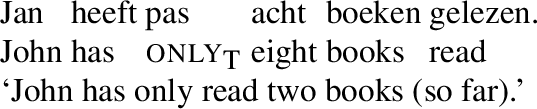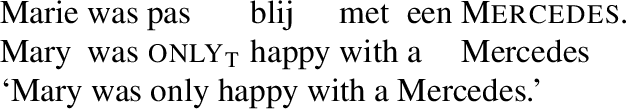Abstract
Among the scalar usages of only, there is one that has a temporal dimension. In Carla understood the problem only on Sunday, for instance, Sunday is considered late for Carla to have understood the problem. In this paper, we explore the interpretation and distribution of temporal only along with other focus particles that permit a temporal reading. We focus on the Dutch counterpart of temporal only, pas (see Barbiers 1995). This particle is formally distinct from both exclusive only (alleen) and non-temporal scalar only (maar). We concentrate on two core issues. The first concerns the observation that temporal focus particles systematically support two modes of interpretation, a purely temporal one and a lack-of-progress reading. The latter is found in an example like Billy has only read three books (so far), which implies that three is a low number of books for Billy to have read at the reference time. The second issue concerns ‘Barbiers’s Generalization,’ the requirement that temporal focus particles immediately c-command the category they interact with. We propose a semantic analysis that captures these observations, building on previous work by König (1979, 1981), Löbner (1989), Krifka (2000) and Klinedinst (2004), among others.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The focus particle only permits at least three readings. Perhaps the best known one is the exclusive reading (see Horn 1969; Rooth 1985; König 1991, among others). On this reading, (1a) means that Susan invited Mary and no one else. Only can also have a scalar reading, as discussed in detail in Klinedinst 2004 (see also Coppock and Beaver 2014 and Hole 2015). The scalar reading of the example in (1b) expresses that three is a low number of fingers for John to have on his left hand. Finally, only can have a temporal reading. The example in (1c) implies that Sunday is late for Carla to have understood the problem. This article is primarily concerned with the temporal reading of only and other focus particles.
-
(1)
-
a.
Susan wanted to invite several people, but in the end invited only Mary.
-
b.
John has only three fingers on his left hand.
-
c.
Carla understood the problem only on Sunday.
-
a.
One might be inclined to deny that the three readings just described are distinct by either unifying the exclusive and scalar readings or the scalar and temporal readings, or indeed by unifying all three. Of course, a unified account is desirable, but it faces the difficulty that in Dutch, among other languages, there are distinct particles for each of the readings of only identified above. Exclusive only translates as alleen, scalar only as maar (or slechts) and temporal only as pas. (2a) has an exclusive reading and hence alleen must be used; (2b) has a nontemporal scalar reading and hence maar must be used; and finally (2c) has a temporal reading, so that pas must be used. (Here and below we use onlye, onlyS and onlyt to gloss alleen, maar and pas, respectively.)
-
(2)

Given that Dutch avoids some of the ambiguities present in English, we will develop a syntax and semantics for temporal focus particles on the basis of the distribution of Dutch pas and its kin.
The problems presented by temporal focus particles are complex. To begin with, temporal focus particles can interact with expressions that do not have an obvious temporal interpretation. For example, if Jeanette is a heavy smoker and we have travelled from Groningen to Amsterdam, we may utter (3a) to indicate that Utrecht was late in the journey for Jeanette to have lit her first cigarette. In other words, pas can interact with a locative PP. Similarly, example (3b) shows that temporal focus particles can interact with argument DPs. The example presupposes that various people had tried to solve the riddle prior to Poirot’s successful attempt, so that the time at which Poirot solved the riddle was late for the riddle to be solved.
-
(3)

Moreover, as discussed by König (1979, 1981), temporal focus particles can give rise to a reading that indicates a high or a low degree of progress, for example when they appear in the context of numerals. König demonstrates this for German erst, but the same is true of Dutch pas (see Barbiers 1995). In (4a), for example, three is lower than the number of books that Paula is supposed to have read at the reference time. Although it is easiest to get low progress readings with numerals, this is not an absolute requirement, as shown by the felicity of (4b). This example requires a context in which we know that Harry is planning to start a distillery and that he must purchase a number of items to bring that plan into effect.
-
(4)

In sum, pas allows two readings. The first we could dub the temporal reading, as it characteristically signifies that the event described happens later than expected. The second we could dub the content reading, as it characteristically signifies that at the reference time less has been achieved or less has happened than expected. Although pas can interact with a wide range of categories, its semantic import can always be described in terms of one of these two readings.
A further dimension to the problem presented by pas is that it belongs to a family of focus particles that have related readings and distributions. For example, in the type of context that licenses (3a), the sentences in (5) are licensed as well.
-
(5)

Despite the fact that these particles share a temporal dimension, they exhibit subtle differences in distribution. In the examples in (6), for instance, the use of pas and al is unproblematic, but nog can only be inserted if accompanied by scalar only (maar).
-
(6)

In addition to the above semantic observations, there is a critical distributional property of pas (and other temporal focus particles) that must be accounted for: as first demonstrated by Barbiers, temporal focus particles must immediately c-command their ‘semantic argument.’ (The semantic argument is the temporal expression, the NP containing the numeral, etc. that the focus particle interacts with.) This is true across the range of usages discussed above. Thus, examples like (7b) and (8b) are ungrammatical, in sharp contrast to examples in which pas is adjacent to its semantic argument (see (7d) and (8d)) and to examples with alleen (exclusive only), which does not require immediate c-command (see (7a) and (8a)). We will refer to this restriction as Barbiers’s Generalization and show that it applies not only to temporal but also to scalar focus particles.Footnote 1
-
(7)

-
(8)

The aim of this paper is to develop a semantic analysis of temporal focus particles that unifies their various usages and that at the same time provides the basis for an analysis of their syntactic distribution. The analysis we propose owes much to König’s (1979) work on German erst, Löbner’s (1989) and Krifka’s (2000) work on temporal focus particles in German, and Klinedinst’s (2004) work on scalar only, although there are differences in a variety of analytical details.
The paper is organized as follows. In Sect. 2 we propose an analysis of temporal only that unifies it with exclusive and scalar only in terms of its core semantics, but distinguishes it in terms of the alternatives it requires. A similar strategy is used in Wiegand’s (2018) analysis of just. The alternatives required for temporal only must lie on a scale whose degrees map onto time. In Sect. 3 we extend this analysis to two other temporal focus particles, namely al ‘already’ and nog ‘still’. In Sect. 4 we consider in more detail what scales temporal focus particles can take as their input. We show that some unexpected interpretations of sentences that contain a temporal focus particle have their origin not in the semantics of the focus particle itself but in the scale to which it applies. For presentational reasons, we limit the discussion in Sects. 2, 3 and 4 to what we have referred to above as low or high progress readings. In Sect. 5, we turn to the other type of interpretation permitted by temporal focus particles, namely one in which the proposition under discussion holds earlier or later than expected. We show that the semantics of the focus particles does not need to be adjusted to deal with these cases, but that it is necessary to develop a proposal that allows nontemporal expressions to assume an additional temporal reading. Section 6 provides an account of Barbiers’s Generalization based on the selectional requirements of temporal focus particles in conjunction with the mechanisms by which alternatives are inherited under merger. We conclude the paper in Sect. 7.
2 Temporal only
We take as our point of departure the semantics of exclusive only. Since Horn 1969, it has been widely assumed that the prejacent of a sentence like (9) (John invited Mary) is presupposed, while the assertion is something like John invited no one other than Mary (see also König 1991, Rooth 1992, Guerzoni 2003).
-
(9)
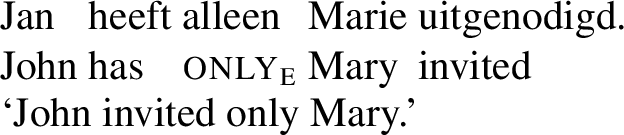
However, there is reason to think that the presupposition is in fact more complex. Let Φ be the lambda formula obtained when the focus constituent f is abstracted. Then the presupposition can be characterized as in (10). It subsumes two possibilities, namely that Φ(f) is true (if a=f) or that Φ applied to an alternative other than the focus is true (see Horn 1996; Klinedinst 2004).
-
(10)
Exclusive only (Dutch alleen)
Presupposition: ∃a [a ∈ ALT ∧ Φ(a) = 1]
Assertion: ¬∃a [a ∈ ALT ∧ a ≠ f ∧ Φ(a) = 1]
Consider the behaviour of (9) in downward-entailing contexts. The example in (11) permits the continuation in (11a), but also the one in (11b). The continuation in (11a) is compatible with the traditional assumption that (9) presupposes its prejacent, but the continuation in (11b) is not. This problem is fixed by the more permissive presupposition we have adopted in (10). In affirmative sentences the permissive nature of presupposition remains hidden because it is asserted that Φ(a) is untrue unless a=f. For instance, the example in (9) asserts that John invited noone but Mary and presupposes that John invited Mary or someone other than Mary. The second part of this disjunction cannot hold, given what is asserted, and so the sentence must presuppose that John invited Mary.
-
(11)

The key difference between exclusive only and scalar only is that the latter requires that the alternatives it is presented with form a scale and that on this scale the focus is weaker than the selected alternatives (the strength relation is expressed in (12) by \(>_{\mathrm{S}}\)). For relevant discussion of non-exclusive interpretations of only, see König 1991; Guerzoni 2003; Klinedinst 2004; Beaver and Clark 2008, and Coppock and Beaver 2011, 2014). We assume that the requirement for a scale with appropriate characteristics takes the form of a presupposition (compare the notion of ‘discourse presupposition’ in Coppock and Beaver 2011). In the lexical items described below we give the relevant presupposition as a condition on alternatives.Footnote 2
-
(12)
Scalar only (Dutch maar)
Condition on alternatives: ∀a [a ∈ ALT ∧ a ≠ f ⇒ a \(>_{\mathrm{S}}\) f]
Presupposition: ∃a [a ∈ ALT ∧ Φ(a) = 1]
Assertion: ¬∃a [a ∈ ALT ∧ a ≠ f ∧ Φ(a) = 1]
We assume that scales are created by applying a contextually defined measure M to the focus and each of its alternatives and ordering them on the basis of the values thus obtained. It stands to reason that this ordering is part of the function of Rooth’s squiggle operator, which after all is responsible for constructing a set of contextually relevant alternatives:
-
(13)
Strength of alternatives (\(>_{\mathrm{S}}\))
M(a1) > M(a2) \(\Rightarrow\ \mathrm{a}_{1} >_{\mathrm{S}}\) a2
We adopt Riester and Kamp’s 2010 proposal that the squiggle operator attaches to the focus constituent, a decision we will motivate in Sect. 6.
With the above in mind, consider the example in (14), where maar is the Dutch counterpart of scalar only. Here two books is the focus constituent, so that the focus and its alternatives form a set {one book, two books, three books, …}. The measuring function is based on cardinality, which implies that three books is a stronger alternative than two books, and so on.
-
(14)
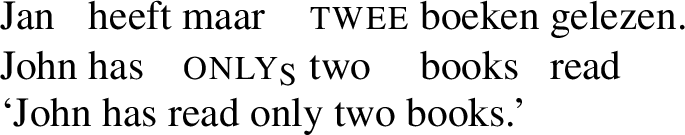
The definition in (12) now yields the following interpretation for (14):
-
(15)
Input: John has read ∼[two books]
Abstract: λx. John has read x
Ranked alternatives: 〈two books, three books, …〉
Presupposition: John has read two books or John has read more than two books.
Assertion: John has not read more than two books.
Note that we use angled brackets to indicate sets whose members are ordered rather than the more usual parentheses. This is a matter of notational convenience, as parentheses already have other roles, such as marking the arguments of functions and the scope of operators.
The choice of alternatives in (15) must fit the context and will therefore have pragmatic effects. In the case at hand, the alternatives to the focus all fit situations in which John has read more books than two and therefore the context must come with the expectation that a variant of (14) with one of these stronger alternatives might reasonably have been true. This leads to the inference that two is a low number of books for John to have read. We borrow this analysis from Krifka (2000), who proposed it for temporal focus particles; see below.
A potential alternative characterization of scalar only would state that the focus is low on the scale of alternatives (rather than it being the lowest of the contextually relevant alternatives). This cannot work, however, for an example like (16). This example is fully acceptable, despite the fact that the number of fingers on one’s left hand will in the typical case not exceed five, so that four is high on the scale that is input to maar (scalar only). The acceptability of the example follows on the proposed account, which only requires that there is a stronger contextually relevant alternative.
-
(16)

The contextually determined function in (13) can measure more complex notions than cardinality. Suppose that a certain type of risk is assessed through a traffic light system, so that there are three values: green, orange and red. In this situation, one can felicitously utter (17).
-
(17)
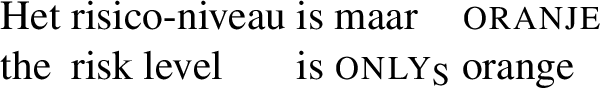
Here maar indicates that the risk level is lower than one might have expected. This effect comes about because M maps the alternatives to the ranking implied by the traffic light system (〈green, orange, red〉), a mapping which is clearly distinct from one based on cardinality. Once this ranking is in place, the interpretation of the example is straightforward:
-
(18)
Input: The risk level is ∼[orange]
Abstract: λP.the risk level is P
Ranked alternatives: 〈orange, red〉
Presupposition: The risk level is orange or red.
Assertion: The risk level is not red.
As a final illustration of the context sensitivity of M, consider the example in (19). Here the measure applied to the focus and its alternatives reflects a qualitative judgement (see Klinedinst 2004 and Coppock and Beaver 2014 for comparable observations).
-
(19)

The use of this sentence requires that one is able to rank cars on the basis of their prestige, and that one understands that een Dafje is a low-prestige car. Hence, M in this case must order cars on the basis of a subjective criterion. Other than this, the interpretation of (19) runs parallel to that of (14) (see (20)). The fact that the focus is the weakest alternative has the pragmatic effect that the car John possesses is considered less desirable than the car one might have expected him to possess.
-
(20)
Input: John has ∼[a Dafje]
Abstract: λx. John has x
Ranked alternatives: 〈a Dafje, a Fiat, a Ford, …〉
Presupposition: John has a Dafje or a car more prestigious than a Dafje.
Assertion: John does not have a car more prestigious than a Dafje.
As in the case of exclusive only, the permissive nature of the presupposition of maar (scalar only) remains hidden in affirmative sentences, but in a downward-entailing context like (21), it correctly predicts the potential continuations given (see Klinedinst 2004).
-
(21)

There is a strand in the literature that aims to unify exclusive and scalar only. This can be achieved in more than one way. The first is to argue that there is a single scalar lexical item whose semantics always involves exclusion of higher ranked members of a scale (see e.g. Klinedinst 2004 and Hole 2015). This proposal might work for English, but is problematic for languages like Dutch, which has distinct lexical items for the exclusive and scalar variant of only. A second option is to argue that exclusive and scalar only select scales that are different in type (see Beaver and Clark 2008, Coppock and Beaver 2011a, 2011b, Orenstein 2015; Wiegand 2018, a.o.). The key question for such proposals is: what distinguishes the scales selected by exclusive and scalar only? A third option, which we adopt in this paper, is to assign a unified semantics to exclusive and scalar only, distinguishing the two by having scalar only select a scale and exclusive only an unordered set of alternatives. Some independent evidence for this distinction will be presented in Sect. 6, where we show that the distribution of exclusive only differs from that of scalar versions of only in a way that can be understood if exclusive only does not in fact require ordering of the alternatives it applies to. (Note that this proposal presupposes that the squiggle operator can order alternatives but does not have to do so, which is our understanding of the position adopted by Rooth 1992.)Footnote 3
An anonymous reviewer suggests the following argument for assuming that exclusive only is scalar. A sentence like Martha invited only John and Fred would be incoherent in the presence of the alternative proposition Martha invited John. This is because the presence of this alternative would lead to the presupposition and assertion contradicting each other. In the case at hand, exclusive only presupposes the prejacent (Martha invited John and Fred) and asserts that all alternative propositions are false. Hence, Martha must at the same time have invited John and not have invited John. This difficulty can be overcome by saying that exclusive only operates on an implicational scale and asserts that all alternative propositions stronger than the prejacent are false. As Martha invited John is implied by and therefore weaker than Martha invited John and Fred, this alternative is not asserted to be false, as required.
We do not think that scales are required to solve this problem. The problem is based on the assumption that a focus particle operates on an unrestricted set of alternatives. However, there is convincing evidence that alternatives are in fact contextually selected, as already argued in some detail by Rooth (1992) (see also Wagner 2006). Consider an example like (22).
-
(22)
Martha only grills seafood.
Without the exclusion of contextually irrelevant alternatives, the focus semantics for (22) would imply that Martha has no relationship with seafood other than that she grills it. As Rooth points out for a comparable example, this is wrong. The example in (22) does not entail that Martha does not buy or eat seafood. Thus, what is required to interpret it is that one restricts the selection of alternatives to cooking methods (in other words, Martha does not, say, boil, steam or pan-fry seafood). But this selection cannot be achieved by saying that exclusive only operates on an implicational scale. We may therefore conclude that contextual selection of alternatives is unavoidable. But if there is selection of alternatives, it seems reasonable to require that no alternatives are selected that contradict the assertion. Since the assertion says that there is no alternative a to the focus such that Φ(a) is true, it follows that any potential alternative to the focus that gives rise to a proposition entailed by the prejacent must not in fact be included in the set of focus alternatives.
We now turn to temporal only. The interpretation of sentences with pas is subtly different from that of sentences with maar in that some notion of progression seems to play a role (as observed for German erst by König 1979; Löbner 1989, and Krifka 2000, among others). Progression is concerned with how events develop over time. In other words, it involves a mapping between a course of events and a temporal scale. The example in (23) involves reading books and so the natural course of events is that over time John will have read an increasing number of books. The use of pas implies that at the reference time eight falls below the number of books that one might reasonably expect John to have read. But eight is not considered to be a low number of books in absolute terms, since it might have met expectations at an earlier point in time. For example, if John is supposed to read ten books in total for an exam, and he has three weeks of preparation time, then eight might be a reasonable number of books to have read in week 2, but falls below expectations in week 3.
-
(23)

Thus, progression is not concerned with the strength of the focus and its alternatives per se, but rather with a notion of strength relative to time. More specifically, it demands that strength grows with time. The use of pas requires a context of progression and a sentence containing this particle is concerned with the point in time at which a particular (timeless) proposition becomes true. In the case of (23) we are concerned with the point in time at which John has managed to read eight books. This leads us to adopt the following felicity condition on the use of progression particles like pas (for related ideas, see Rombouts 1979; Krifka 2000; Smessaert and Ter Meulen 2004):
-
(24)
Felicity condition for progression particles
Expected development from ¬p to p.
That this felicity condition must hold can be demonstrated by considering a situation in which Mary travels from her home in Utrecht to her friend in Amsterdam. If her friend enquires about her progress, then pas cannot be used in the answer if p represents the starting point of the expected development (Mary’s home); it can be used if Mary is in Maarssen, a town on the route to Amsterdam that is close to Utrecht:
-
(25)

That we are dealing with expected development rather than actual development is demonstrated by the example in (26), where the speaker’s evaluation of the two rooms is concerned with the amount of work required to get them ready for the meeting. The development must be expected development because there is no stage in this context at which ¬p is true.
-
(26)

With (24) in place, we can define relative progression as follows:
-
(27)
Φ(a1)(t1) \(>_{\mathrm{P}}\) Φ(a2)(t2) iff
(i) \(\mathrm{t}_{1} = \mathrm{t}_{2}\) and \(\mathrm{a}_{1} >_{\mathrm{S}}\) a2, or
(ii) \(\mathrm{a}_{1} =_{\mathrm{S}}\) a2 and t1 precedes t2.
This definition states that a timed proposition expresses a higher degree of progression than some other timed proposition if either they are specified for the same time and the former contains a stronger alternative, or the alternatives they contain are deemed to be of equal strength but the former holds at an earlier time. This definition implies that the squiggle operator can construct progression scales in two ways. Either it ranks alternatives by strength, or it maps alternatives to a time scale (see Löbner 1989; Krifka 2000 and Declerck 1994 for similar ideas). We will refer to these two modes of ranking as the content mode (strength varies, but time remains the same) and the temporal mode (time varies, but strength remains the same). Ranking in the content mode is relatively easy to understand and all examples discussed in this section and Sects. 3 and 4 will use this type of ranking. We will turn to ranking in the temporal mode in Sect. 5, where we will show that what determines ranking in this mode is when a contextually relevant proposition becomes true.
With (27) in place, we can characterize the semantics of pas (temporal only) as a variant of exclusive only, with the alternatives ordered by progression (we will show in Sect. 5 that the presupposition is as indicated):
-
(28)
Temporal only (pas)
Condition on alternatives: ∀a [a ∈ ALT ∧ a ≠ f ⇒ Φ(a) \(>_{\mathrm{P}}\) Φ(f)]
Presupposition: ∃a [a ∈ ALT ∧ Φ(a) = 1]
Assertion: ¬∃a [a ∈ ALT ∧ a ≠ f ∧ Φ(a) = 1]
Given this definition, the example in (23) receives the interpretation below.
-
(29)
Input: John has read ∼[eight books]
Abstract: λx. John has read x at tr
Ranked alternatives: 〈eight books, nine books, …〉
Presupposition: John has read eight or more books at tr.
Assertion: John has not read more than eight books at tr.
Pas gives rise to a pragmatic effect familiar from our discussion of maar (scalar only): as pointed out by Krifka (2000), the fact that in (29) the focus is the weakest of the alternatives implies that the context must come with the expectation that a proposition based on another alternative might reasonably have been true. In (23)/(29), where the alternatives are ranked by progression, this leads to the inference that eight is a low number of books for John to have read at the reference time.
Pas is a progression particle, which means that it must be used in a context in which strength is evaluated with regard to time (as stated in the definition of progression in (27) and the felicity condition in (24)). This predicts that where strength is evaluated independently of time, pas cannot be used. As a first example of this, consider (30). The oddity of this example follows from the fact that pas forces evaluation of strength relative to time, which is only possible in a world in which people grow more fingers as time passes.Footnote 4
-
(30)

Even variation of strength over time is not a sufficient precondition for the use of pas if it is not the case that time plays a role in the evaluation of strength. In (31), for example, the number of tasks completed grows, but this is accidental as evaluation is not bound to time. Consequently, maar can be used, but insertion of pas is ungrammatical.
-
(31)

The definition in (28) is sparse. In psychology, the concept of progress presumably involves comparison, given some relevant time scale, of the actual situation with alternative hypothetical situations. The linguistic implementation we advocate, however, is much simpler and does not rely on comparison of states of affairs in possible worlds. In this regard it differs from the proposal in Krifka (2000), according to which temporal focus particles explicitly encode such comparison. For example, Krifka argues that a sentence like (23) is felicitous only if the rate of progress in the actual world falls below or is equal to the rate of progress in alternative worlds (that is, one may have expected John to have been able to read more books than he has). This situation is depicted in (32), where the rate of progress in the actual world is given by the solid line, while the dashed line represents the rate of progress in some alternative world.
-
(32)

However, we do not believe that temporal focus particles compare rates of progress across possible worlds. To begin with, there are examples for which such a comparison seems artificial. Consider a situation in which a father is in a toy shop and needs advice on what to buy for his daughter. In that context, he may utter (33) in order to narrow down what toys may be suitable.
-
(33)
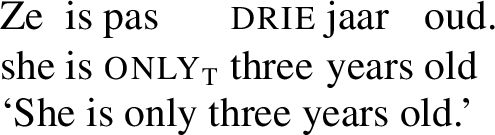
This example does not seem to involve a comparison of growth rates. All that matters is that the daughter is three and that this is at the lower end of the age range for which the shop caters.
Moreover, there is direct evidence that pas is not directly sensitive to the rate of progress, but only to values reached. Consider the following examples:
-
(34)

The situation in (34a) is represented in (35a), where John’s pace of reading in the actual world is given as a solid line, while the contextual alternative (i.e. his pace of reading if he had behaved like other students in his class) is shown as a dotted curve. The use of pas is felicitous in this context, despite the fact that the rate of progress of John’s reading at tr, if taken as a derivative, exceeds that of the other students.
-
(35)

Krifka does not define rate of progress as a derivative, but rather requires that at no time before tr the value yielded by the growth function in the actual world is exceeded by the value yielded by the growth function in any alternative world.Footnote 5 This view of the rate of progress is incompatible with the situation in (34b), as represented in (35b). Here John’s pace of reading is given as a solid curve, while the contextual alternative is shown as a dotted line. The use of pas is felicitous in this context, despite the fact that the solid line yields higher values than the dotted curve at most points before tr.
On our proposal the only requirement imposed by temporal only is that at tr the focus is outranked by all its alternatives, so that alternative propositions represent more progress than the prejacent. Hence, our proposal predicts that the use of temporal focus particles is insensitive to the rate of growth that has led to the values that are being compared. It follows straightforwardly that pas can be used in the situations depicted in (35).
To summarize the main results of this section, all three variants of only have the same core semantics, but they impose different requirements on the alternatives they are presented with. Alleen (exclusive only) operates on an unordered set of alternatives, maar (scalar only) takes as its input a set of alternatives ordered by strength, while pas (temporal only) requires alternatives ordered by progression.
3 A typology of temporal focus particles
Scalar and temporal only belong to a larger family of focus particles whose properties vary along parameters implied by our proposal (for related discussion on only and even as pragmatic opposites, see Beaver and Clark 2008: 71-72).
To begin, one would expect a counterpart to scalar only in which the focus is the strongest among the alternatives, with the consequence that the prejacent is interpreted as exceeding contextual expectations. Such particles indeed exist. Dutch wel differs from maar in exactly this way. The example in (36) suggests that one hundred is a high number of books for John to have read.
-
(36)

We may assume the following semantics for sentences containing wel:
-
(37)
Wel (Dutch)
Condition on alternatives: ∀a [a ∈ ALTS ∧ a ≠ f ⇒ f \(>_{\mathrm{S}}\) a]
Assertion: Φ(f) = 1
Given this characterization of wel, the example in (36) receives the following analysis:
-
(38)
Input: John has read ∼[a hundred books]
Abstract: λx. John has read x
Ranked alternatives: 〈…, 99 books, 100 books〉
Assertion: John has read a hundred books.
As before, the choice of alternatives must be licensed by the context. Therefore, (36) implies that John has read more books than one might have assumed.
Consider what happens if wel is used in the scope of negation, as in (39). This sentence implies that John has read fewer than a hundred books, but still suggests that a hundred would be a relatively high number of books for John to have read. This follows from the semantics in (37), since the assertion is negated, while the alternatives on which wel operates remain.
-
(39)

The semantics proposed for wel is simpler than what we previously assumed for its counterpart maar, repeated below as (40). The more complex semantics assumed for scalar only requires some justification: why can scalar only not be specified as in (41)?
-
(40)
Scalar only (Dutch maar)
Condition on alternatives: ∀a [a ∈ ALTS ∧ a ≠ f ⇒ a \(>_{\mathrm{S}}\) f]
Presupposition: ∃a [a ∈ ALT ∧ Φ(a) = 1]
Assertion: ¬∃a [a ∈ ALT ∧ a ≠ f ∧ Φ(a) = 1]
-
(41)
Condition on alternatives: ∀a [a ∈ ALTS ∧ a ≠ f ⇒ a \(>_{\mathrm{S}}\) f]
Assertion: Φ(f) = 1
The problem with (41) is that it is uninformative in contexts in which ordering among alternatives relies on quantities. This is because in such contexts any proposition of the form Φ(a) implies Φ(f). Since Φ applied to the alternatives represents what can reasonably be expected in the context, asserting Φ(f) does not update the hearer’s background knowledge. The specification in (40) does not suffer from this shortcoming. As it explicitly rejects that any proposition of the form Φ(a) is true, it provides the hearer with information not already compatible with previous assumptions.
The representation for wel (see (37)) can be simpler because the alternatives to the focus are weaker, which means that a proposition Φ(a) will not imply Φ(f). Consequently, a sentence with wel provides information not already present in the hearer’s background knowledge.
Let us now turn to temporal focus particles. The semantics of temporal focus particles is more complex than that of scalar focus particles in that ranking takes place on the basis of progression, which we have defined as a relation between timed propositions, sensitive to the strength of the focus and its alternatives and the time at which the propositions hold. Just like maar has a high-degree counterpart in wel, we might expect pas to have a counterpart with a high degree reading. This reading should of course involve progression rather than just strength and will be subject to the felicity condition on progression in (24). Such a particle indeed exists. The example in (42) implies that five is a high number of books for John to have read at this moment in time (although it is not necessarily a high number of books in absolute terms).
-
(42)

The semantic representation of sentences with al ‘already’ parallels that of sentences with wel, but relies on an ordering of alternatives in terms of progression (so time matters). Since the assertion is stronger than the alternatives, use of al suggests that Φ(f) exceeds reasonable expectations in the context at hand.
-
(43)
Already (al)
Condition on alternatives: ∀a [a ∈ ALTP ∧ a ≠ f ⇒ Φ(f) \(>_{\mathrm{P}}\) Φ(a)]
Assertion: Φ(f) = 1
On this characterization of al, the example in (42) receives the analysis in (44).Footnote 6
-
(44)
Input: John has read ∼[five books].
Abstract: λx. John has read x at tr
Ranked alternatives: 〈…, four books, five books〉
Assertion: John has read five books at tr.
That al differs from wel in requiring reference to time is confirmed by the contrast in (45). Six exceeds the number of fingers one would expect on anyone’s hand no matter the time. Therefore, wel can be used, but al is only appropriate in a very strange context in which one acquires more fingers over time. This is because the use of al is subject to the felicity condition in (24).
-
(45)
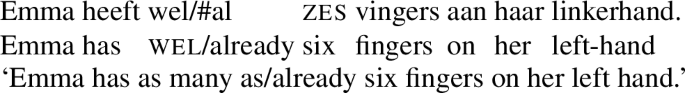
Recall that the felicity condition on progression requires expected, rather than actual, development. It is in fact well-known that use of already does not presuppose that ¬p is true prior to p being true (see Mittwoch 1993; Krifka 2000 and Ippolito 2007 for discussion). The same is true of Dutch al, as can be seen in (26) above, where al is felicitously used in a context where p holds throughout.
As was the case with wel, the behaviour of al under negation follows straightforwardly from the proposed semantic representation. The example in (46) implies that John has read fewer than five books at the reference time and suggests that five would be a high number of books for John to have read at that time.
-
(46)

The temporal particles pas and al have in common that they are evaluated in contexts in which strength increases over time. However, it is also possible for strength to decrease with time. We may refer to this relationship as regression. Its definition in (47) says that a timed proposition expresses more regression than some other timed proposition if either the two propositions are specified for the same time and the former contains a weaker alternative, or the alternatives are deemed to be equal in strength but the former holds at an earlier time.
-
(47)
Φ(a1)(t1) \(>_{\mathrm{R}}\) Φ(a2)(t2) iff
(i) \(\mathrm{t}_{1} = \mathrm{t}_{2}\) and \(\mathrm{a}_{1} <_{\mathrm{S}}\) a2, or
(ii) \(\mathrm{a}_{1} =_{\mathrm{S}}\) a2 and \(\mathrm{t}_{1} < \mathrm{t}_{2}\).
It may seem surprising that the second part of this definition is identical to the second part of the definition of progression. But note that in progression strength increases with time, while in regression it decreases. If you regress to a particular value earlier, then there is a higher degree of regression than when you regress to that value later.
That regression is the mirror image of progression is implied by the felicity condition in (48), which requires a context in which there is an expected development from p to ¬p (see Smessaert and Ter Meulen 2004 for a similar idea). The development is only expected because even in circumstances where we know that p is true, we cannot guarantee that subsequently ¬p will become true.
-
(48)
Felicity condition for regression particles
Expected development from p to ¬p.
As with the notion of progression, regression comes in two modes: the content and the temporal mode. In the content mode, time is fixed, so that the question under discussion is about quantity or strength. In the temporal mode, strength is fixed, so that the question under discussion is when a certain proposition ceases to be true. We postpone definition of the temporal mode to Sect. 5.
The notion of regression allows us to distinguish pas (temporal only), which is a low progression particle, from nog ‘still’, which signals low regression. The use of nog as a temporal focus particle can be exemplified as follows. Suppose that Suzanne has to write five essays in a particular period and that she has written two so far. One can describe this situation in terms of progression (if one concentrates on the number of essays Suzanne has written), or in terms of regression (if one concentrates on the number of essays she has left to write). In the former case, the number of essays increases with time (meeting the felicity condition for progression), while in the latter case, it decreases with time (meeting the felicity condition for regression). As it turns out, in such a context nog can only be used if the situation is framed as involving regression. Thus, in the essay-writing context described above, (49a) is grammatical, but (49b) is not.Footnote 7 By contrast, as shown in (50), pas and al can only be used if the situation is framed in terms of progression.Footnote 8
-
(49)

-
(50)

Nog can be characterized as in (51). Since Φ(f) represents a lower degree of regression than Φ applied to any of the alternatives, and since the latter correspond to contextual expectations, use of nog implies that Φ(f) represents an underwhelming degree of regression.
-
(51)
Still (nog)
Condition on alternatives: ∀a [a ∈ ALTR ∧ a ≠ f ⇒ Φ(a) \(>_{\mathrm{R}}\) Φ(f)]
Assertion: Φ(f) = 1
This definition yields (52) as the analysis for (49a). Notice that the alternatives in (52) are ranked by decreasing strength, given that we are dealing with regression rather than progression.
-
(52)
Input: Suzanne has ∼[three essays] left to write.
Abstract: λx. Suzanne has x left to write at tr
Ranked alternatives: 〈three essays, two essays, …〉
Assertion: Suzanne has three essays left to write at tr.
The behaviour of nog under negation is illustrated by (53). Since Φ(f) is negated, this example means that Suzanne has fewer than three essays left to write. However, the fact that the alternatives remain constant means that the example still suggests that three would be a relatively high number of essays for Suzanne to have left to write at the reference time.Footnote 9
-
(53)
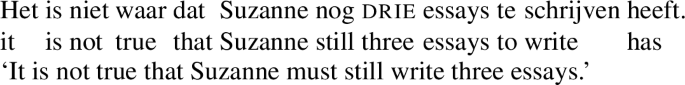
This concludes the discussion of the family of scalar particles to which pas belongs. In the following section we look in more detail at the kind of scales these particles apply to.
4 Articulated scales and two-point scales
So far, we have not elaborated on the nature of the scales that enter into the notions of progression and regression, and most of the examples we have considered involve straightforward scales with multiple members. However, temporal focus particles can operate on alternatives ordered on the basis of more complex criteria, as well as on the basis of simpler ones.
As a first example of a more complex case, we look at scales constructed from intervals that share an end point but vary in length. A relevant example is given in (54), where the focus and its alternatives identify starting points of intervals that end in the reference time. It is the length of these intervals that determines the strength of the focus and its alternatives.
-
(54)

Such intervals are a suitable basis for an ordering of the focus and its alternatives. Recall that strength is determined by applying a contextually defined measure to the focus and each of its alternatives. In the case at hand, the measuring function is trivial: it simply returns the length of the interval yielded by since; that is, the interval that starts at the time indicated by the focus and its alternatives and terminates in the reference time. Ordering can proceed on the basis of the values thus obtained, so that (54) is interpreted as follows:
-
(55)
Input: John has been working in Amsterdam ∼[since Friday].
Abstract: λx. John has been working in Amsterdam during i ∧ \(i = [x,t_{\mathrm{r}}]\)
Ranked alternatives: 〈Friday, Thursday, …〉
Presupposition: At tr, John has been working in Amsterdam since Friday or longer.
Assertion: At tr, John has not been working in Amsterdam since before Friday.
Strictly speaking, the alternatives in (55) should all have the form “λP.P since Friday,” “λP.P since Thursday,” etc. For presentational purposes, however, we have integrated the material shared by the alternatives into the lambda abstract and we will do the same for other examples that involve modifiers below. We provide a more accurate representation for some examples involving focused modifiers in Sect. 6.
With this proviso, the example in (54) yields an interpretation containing the presupposition that John has worked in Amsterdam since Friday or for longer and the assertion that John has not worked in Amsterdam for longer than since Friday. Given the contextually determined alternatives, it is implied that the period in which John has worked in Amsterdam is relatively short.
Ranking on the basis of intervals also captures the interpretation of examples like (56), where what is at stake is the degree of temperature change. Unlike (54), (56) does not contain a preposition that directly delivers an interval. Therefore, the contextually determined measuring function is more complex in this case. It measures the distance between the starting temperature and the value given by the focus and its alternatives. Since the starting temperature is not linguistically given, it may be either higher or lower than twenty. This explains an observation by König (1979), namely that examples like (56) are ambiguous and can be used to express progression in either a heating or a cooling context.
-
(56)

For concreteness, let us assume a heating context, so that the alternatives are ordered from smaller to larger implied increases in temperature. The interpretation of (56) can then be represented as in (57), where the choice of alternatives implies that the extent of temperature change is small for the reference time.
-
(57)
Input: The water is ∼[twenty degrees].
Abstract: λP. The water is P at tr
Ranked alternatives: 〈20 degrees, 21 degrees, …〉
Presupposition: The water is 20 degrees or warmer at tr.
Assertion: The water is not warmer than 20 degrees at tr.
A final example requiring ordering on a more complex scale is given in (58). We assume that it is uttered in a context in which John is a restaurant critic who has been tasked with reviewing all restaurants in the Netherlands with one or more Michelin stars. In this context A can ask B in how many restaurants John has eaten so far, and B can utter in reply:
-
(58)
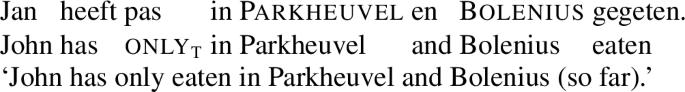
The focus (Parkheuvel en Bolenius) and its alternatives vary in strength, as determined by the number of restaurants John has visited. This is because A is interested in this number rather than in the identity of the restaurants. The focus alternatives must therefore make up a semi-lattice:Footnote 10
-
(59)

Hence, the alternatives to the focus under consideration in this context are sets containing more than two restaurants with Michelin stars. These sets may or may not contain Parkheuvel and Bolenius. In other words, (58) presupposes that John has eaten in Parkheuvel and Bolenius, or in more than two restaurants with Michelin stars, and asserts that John has not eaten in more than two such restaurants. When placed in a context of negation, the sentence implies that John has eaten in more than two restaurants with Michelin stars, but these need not include Parkheuvel and Bolenius. Thus, the following is not a contradiction:
-
(60)

It is easy to demonstrate that in addition to the more articulated scales reviewed above, focus particles can also operate on two-point scales. Consider the examples in (61).
-
(61)

As argued in detail by Löbner (1989), the interpretation of the examples in (61) involves two phases: ¬the light is on and the light is on (for related discussion, see Krifka 2000, who recasts these phases as focus alternatives).Footnote 11 Example (61a) contains a progression particle. It follows from the felicity condition in (24) that the alternatives in (61a) must be ranked 〈¬on, on〉, yielding the semantics in (62a). Example (61b) contains a regression particle, which implies that the alternatives must be ranked 〈on, ¬on〉, given that the felicity condition in (48) implies that ¬p expresses a higher degree of regression than its positive counterpart. This yields the semantics in (62b).
-
(62)
-
a.
Input: The light is ∼[on].
Abstract: λP. The light is P at tr
Ranked alternatives: 〈¬on, on〉
Assertion: The light is on at tr.
-
b.
Input: The light is ∼[on].
Abstract: λP. The light is P at tr
Ranked alternatives: 〈on, ¬on〉
Assertion: The light is on at tr.
-
a.
It follows that the example in (61a) is felicitous in a context in which the light needs to be turned on and was potentially off. Conversely, the example in (61b) requires a context in which the light needs to be turned off and is currently on.
The proposal predicts that pas (temporal only) cannot be used with two-point scales. This is because pas is a low-progression particle, which by definition means that the focus must be ranked below its alternative. But since the prejacent is based on the positive phase, there can be no such alternative. After all, the felicity condition in (24) implies that progression must proceed from the negative to the positive phase. Indeed, as observed by Löbner (1989) for parallel examples in German, the following is unacceptable in a context in which the light was off and is now on (the desired end state):
-
(63)
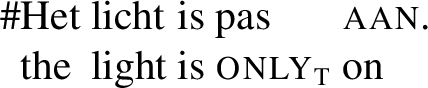
The example in (63) has the interpretive effect that there must be a third state of the light that follows its being on. For example, the sentence could be used in a situation where the light was off, is now on, and will subsequently change colour. Pas then indicates that we have not yet reached this third stage. These observations corroborate, of course, that pas can only operate on articulated scales.
The fact that nog and al can operate on a two-point scale, but pas cannot, explains why it is possible to attach nog and al, but not pas, in a position c-commanding a scalar focus particle. We illustrate this contrast in (64).
-
(64)

The analysis of the example in (64a) runs as follows. The squiggle operator attached to the focus constituent ‘three books’ delivers an articulated scale that maar can apply to. This yields the interpretation that three is a low number of books for Kim to have left to read. Subsequent to this, a second squiggle operator is attached to the verbal constituent maar drie boeken te lezen. This second squiggle operator introduces a two-point regression scale 〈[three books left to read], ¬[three books left to read]〉, which is a suitable input for nog.
-
(65)
Kim heeft nog ∼[maar ∼[drie boeken] te lezen]
The same thing happens in (64b). The particle wel operates on an articulated scale, with ten books being the strongest alternative, and hence triggering the presupposition that ten is a high number of books for Kim to have read. Subsequently, al operates on a two-point progression scale 〈¬[read ten books], [read ten books]〉 and indicates that we have reached the positive phase.
The example in (64c) is ungrammatical. As before, maar operates on an articulated scale and indicates that three is a low number of books for Kim to have read. Subsequent to this, a two-point progression scale of the form 〈¬[read three books], [read three books]〉 may be constructed, but this is not enough for the derivation to converge, since pas cannot apply to two-point scales.Footnote 12
A further contrast in the distribution of pas, as compared to al and nog, can also be understood from its inability to operate on a two-point scale. Perhaps surprisingly, nog can be used in a progression context and al can be used in a regression context (despite the fact that nog is a regression particle and al a progression particle). First consider (66). This example is felicitous in a context in which Suzanne has to write five essays and has written none so far. This is a typical progression context (it allows the use of pas). So why is it possible to use nog?
-
(66)

The solution to this puzzle lies in the fact that nog can operate on the two-point regression scale 〈[written no essays], ¬[written no essays]〉. This scale fits the use of nog but it also fits a context in which the number of essays that Suzanne has written increases with time. This is because the statement “Suzanne has not written no essays” entails that she has written some. In other words, it is possible for nog to masquerade as a progression particle if it can operate on what is formally a two-point regression scale, but pragmatically a scale that expresses progression.
This type of masquerading is also possible with al. Consider the example in (67). This example is felicitous in a typical regression context, where we are counting down to zero. However, al is a progression particle and therefore its occurrence in this context seems unexpected.
-
(67)

The felicity of (67) can be understood if al applies to a two-point progression scale 〈¬[has no essays left to write], [has no essays left to write]〉. While this is formally a progression scale, it is compatible with a regression context, because the statement “Suzanne doesn’t have no essays left to write” entails that she has some left to write.
We showed earlier that pas cannot operate on a two-point progression scale, but only on an articulated scale. This predicts that the kind of masquerading found in (66) and (67) is impossible with pas, a prediction borne out by the data. For example, in (67) al cannot be replaced by pas:
-
(68)

There is a final puzzle whose solution involves masquerading. In order to characterize the puzzle we must briefly return to the example in (19), repeated here as (69a). We used this example to illustrate that scalar focus particles can operate on alternatives ranked by prestige: the sentence implies that John owns a low-prestige car. Example (69b) shows that the same criterion can be used to rank alternatives in sentences with a temporal focus particle. The sentence is felicitous in a context in which we expect John to progress to ever more prestigious cars. It implies that so far he has not managed to progress beyond owning a low-prestige car.
-
(69)

With this background, we can make sense of an intricate pattern involving quality scales exemplified in (70). The core observation is that in a progression context like (70a) all three temporal focus particles can be used, while in a regression context like (70b) use of pas (temporal only) is excluded.
-
(70)

Given that al and pas operate on a progression scale, it is unsurprising that they can be used in (70a). The acceptability of nog in this context is more puzzling, but can be understood if we construe the regression scale it operates on as the two-point scale 〈[drives around in a Ford Focus], ¬[drives around in a Ford Focus]〉. In the context at hand, not driving around in a Ford Focus can be equated with driving a more powerful car. Hence, this is a case of masquerading, where a two-point regression scale fits a progression context.
Example (70b) is placed in a regression context. Hence, the felicity of nog ‘still’ is in line with expectations. The felicity of al ‘already’ can be understood as a further instance of masquerading. In this context, al can operate on the two-point progression scale 〈¬[drives around in a Ford Focus], [drives around in a Ford Focus]〉. In the given context, ¬[drives around in a Ford Focus] is easily interpreted as “drives around in a more polluting car than a Ford Focus.” The fact that pas, in contrast to al, is unacceptable in this context now falls into place. Like al, pas has to operate on a progression scale, which in the context at hand can only be the two-point scale already mentioned. However, as we have demonstrated, a two-point progression scale does not provide a suitable input for pas (because it does not find a stronger alternative than the focus).
In sum, we have shown that temporal focus particles can operate on articuled scales as well as two-place scales. An important implication of this hypothesis is that progression particles can be used in a regression context and vice versa, as long as a two-point scale can be constructed that fits their formal requirements and that is compatible with the situation.
5 Interpretation in the temporal mode
All the examples with temporal focus particles considered so far received an interpretation based either on clause (i) of the definition in (71a)—in case of progression—or clause (i) of the definition in (71b)—in case of regression.
-
(71)
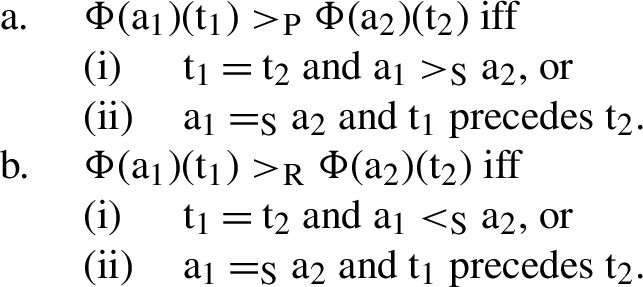
We have referred to this type of interpretation as interpretation in the content mode: the alternative propositions are all specified for the same time but differ in the strength of the focus and its alternatives. In this section we will be concerned with the interpretation of temporal focus particles based on clause (ii) of (71a) and (71b). We have dubbed this the temporal mode because it is concerned with propositions that are specified for different times but which contain focus alternatives that are deemed to be of equal strength. In this mode, the question under discussion is when a relevant proposition becomes true (in case of progression) or when it ceases to be true (in case of regression).
In the first instance we will consider progression particles. In order to understand how interpretation in the temporal mode works, we need to ask ourselves what the proposition is that becomes true. Given that the various alternatives are deemed to be of equal strength, the relevant proposition must abstract away from the focus. For a first illustration of interpretation in the temporal mode, consider the example in (72). Here the question under discussion is when John arrived, so that progression is from ¬[John arrived] to [John arrived]. Crucially, the sentence cannot be interpreted in the content mode, as that would imply progression from ¬[John arrived on Sunday] to [John arrived on Sunday], with Sunday a weak alternative for the reference time tr. This is a nonsensical interpretation, as it implies that while the reference time is part of Sunday, John could nevertheless have arrived at the reference time on days other than Sunday.
-
(72)
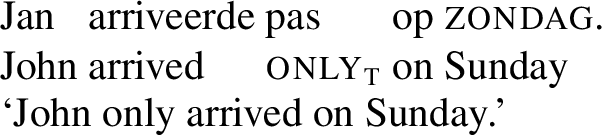
The focused constituent, on Sunday, represents an interval, as do the alternatives (days of the week that precede Sunday). As before, the interpretation relies on a ranking of alternatives that fit a lambda expression created by abstracting the focus constituent. What is different about interpretation in the temporal mode, however, is that the alternatives are specified for times different from tr and that these times are used to create a ranking. In this ranking later times represent weaker alternatives, because if a proposition becomes true later, then there is a lower degree of progression. In order to make this ranking possible, the lambda abstract must contain an existentially bound time variable rather than a constant time tr.Footnote 13 The values for this time variable are constrained by the focus and its alternatives (in each case, t must be contained in the relevant interval). Note that in (73) t must also precede the speech time, since the verb is inflected for past tense. Other than that, the interpretation of pas follows the same procedure as before:
-
(73)
Input: John arrived ∼[on Sunday]
Abstract: λi ∃t [John arrived at t, t ⊆ i ∧ t < ts]
Ranked alternatives: 〈Friday, Saturday, Sunday〉
Presupposition: ∃t [John arrived at t, t ⊆ Sunday ∧ t < ts], or there is an alternative daya such that ∃t [John arrived at t, t ⊆ daya ∧ t < ts]
Assertion: There is no alternative daya such that ∃t [John arrived at t, t ⊆ daya ∧ t < ts].
Since the focus is ranked later than the alternatives, Sunday—and therefore tr—is interpreted as late for John to arrive (see Karttunen 1974 for a similar analysis of not until, which also triggers a presupposition of lateness).Footnote 14
Examples like (74) below allow us to demonstrate that the presupposition in (73) survives under negation. The matrix negation in this example cancels out the negation in the assertion in (73). Therefore, the example asserts that there is an alternative daya such that John arrived on that day. As all the alternative days are earlier than Sunday, this implies that John arrived earlier than Sunday, which is indeed the interpretation the example has. This interpretation is immediately compatible with the proposed presupposition, which simply states that Φ applied to some alternative must be true (see Karttunen 1974; Declerck 1995; Condoravdi 2008 and Iatridou and Zeijlstra 2021 for related discussion on not until).
-
(74)
Temporal intervals are not always given by temporal modifiers. For example, the following discourse is entirely coherent if we are talking about a journey that passes through several cities, including Utrecht, because in such a scenario different locations correspond to different times.
-
(75)
Q: When did Jeanette light her first cigarette?
A: Jeanette lit her first cigarette in Utrecht.
In the answer in (75), Utrecht is interpreted as referring to the temporal interval during which Jeanette was in Utrecht. We can represent this as in (76), where temporal information has been added to the normal representation of a locational modifier through a function τ that maps locations to intervals. (For concreteness’ sake, we adopt the analysis of locational modifiers in Pustejovsky 2013; nothing hinges on this.)
-
(76)
∃t ∃l [Jeanette lit her first cigarette in l, l ⊆ Utrecht, at t, t ⊆ τ(Utrecht) ∧ t < ts]
Given that this is possible, it is hardly surprising that temporal focus particles can associate with locational expressions. In the context of a journey, the following is perfectly acceptable:
-
(77)

The focused constituent, Utrecht, and its alternatives are ranked on the basis of the order in which they come in the journey. However, in the lambda abstract used to compute the semantic contribution of pas these locations are mapped to temporal intervals using the function τ. The order of these intervals is not determined by τ but inherited from the input to τ (which is a contextually ordered set of cities). With this much in place, the interpretation of the example in (77), given in (78) below, runs parallel to (73). Utrecht is the weakest alternative (it refers to the city furthest into the journey). Therefore, the interval associated with it is the latest interval under consideration. Hence we obtain the interpretation that a time in that interval was late for Jeanette to light a cigarette.
-
(78)
Input: Jeanette lit a cigarette ∼[in Utrecht]
Abstract: λx ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ x, at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈Leeuwarden, Lelystad, Utrecht〉
Presupposition: ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ Utrecht, at t, t ⊆ τ(Utrecht) ∧ t < ts] or there is an alternative citya such that ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ citya, at t, t ⊆ τ (citya) ∧ t < ts].
Assertion: There is no alternative citya such that ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ citya, at t, t ⊆ τ(citya) ∧ t < ts].
As we noted in the introduction, temporal focus particles can also interact with argument DPs. The relevant example is repeated below.
-
(79)

This example is interpretable if various people tried and failed to solve the riddle before Poirot arrived on the scene. In such a context Poirot and the alternative investigators can be construed as ordered in time:
-
(80)
Input: ∼[Poirot] solved the riddle.
Abstract: λx ∃t [x solved the riddle at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈Chief Inspector Japp, Mrs Ariadne Oliver, Poirot〉
Presupposition: ∃t [Poirot solved the riddle at t, t ⊆ τ(Poirot) ∧ t < ts], or there is an alternative persona such that ∃t [persona solved the riddle at t, t ⊆ τ(persona) ∧ t < ts]
Assertion: There is no alternative persona such that ∃t [persona solved the riddle at t, t ⊆ τ(persona) ∧ t < ts]
The reading obtained from this semantics is that any time in the interval associated with Poirot was late for the riddle to be solved. This is because Poirot is the weakest alternative (it refers to the investigator ranked last in the sequence). Hence, the interval associated with Poirot is the latest interval under consideration.Footnote 15 Although it is natural, given our knowledge of Agatha Christie’s novels, to rank Poirot and the alternative detectives in terms of their intellectual abilities, it is not this ranking that makes the example work. Indeed, the alternatives could be equal to or higher than the focus in intellectual ability without this affecting the acceptability of the example.
The progression particle al also permits interpretation in the temporal mode. With this particle, the focus is the strongest alternative. Consider (81). As before, the ranking of the alternatives corresponds to the order of cities in the journey. However, the reading obtained for (81) differs from the one that would be triggered by pas, in that the time indexed by the focus precedes the times indexed by the alternatives.
-
(81)

-
(82)
Input: Jeanette lit a cigarette ∼[in Lelystad].
Abstract: λx ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ x, at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈Lelystad, Utrecht, Amsterdam〉
Assertion: ∃t ∃l [Jeanette lit a cigarette in l, l ⊆ Lelystad, at t, t ⊆ τ(Lelystad) ∧ t < ts].
Thus, the example in (81) asserts that Jeanette lit a cigarette at some time during the interval that she was in Lelystad and implies that this time was early for Jeanette to do so.
We now turn to the regression particle nog. Like progression, regression in the temporal mode is concerned with when a given proposition is true. But while progression involves a transition from a negative to a positive phase, regression involves the opposite transition (see (71b)). We can illustrate how the contrast between progression and regression works out in the temporal mode by considering a scenario in which we assess the weight of a piano by checking how many boys are needed to lift it. This can be done in two ways. We can begin with a few boys and consider what the tipping point is when we gradually increase their number. This is a progression scenario, because the question under discussion is when the proposition “the piano can be lifted” becomes true. Alternatively, we can work in the opposite direction, starting with a large number of boys and working our way down to the tipping point. This is a regression scenario, as the question under discussion is when the proposition “the piano can be lifted” ceases to be true. Indeed, pas and al are appropriate in the first scenario, but not in the second, while nog is appropriate in the second scenario but not the first:
-
(83)

Pas, al and nog yield the following interpretations for the example in (83):
-
(84)
-
a.
Input: ∼[Ten boys] could lift the piano.
Abstract: λx ∃t [x could lift the piano at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈eight boys, nine boys, ten boys〉
Presupposition: ∃t [ten boys could lift the piano at t, t ⊆ τ(ten boys) ∧ t < ts], or there is an alternative number n of boys, such that ∃t [n boys could lift the piano at t, t ⊆ τ(n boys) ∧ t < ts]
Assertion: There is no alternative number n of boys, such that ∃t [n boys could lift the piano at t, t ⊆ τ(n boys) ∧ t < ts]
-
b.
Input: ∼[Ten boys] could lift the piano.
Abstract: λx ∃t [x could lift the piano at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈ten boys, eleven boys, twelve boys〉
Assertion: ∃t [ten boys could lift the piano at t, t ⊆ τ(ten boys) ∧ t < ts]
-
c.
Input: ∼[Ten boys] could lift the piano.
Abstract: λx ∃t [x could lift the piano at t, t ⊆ τ(x) ∧ t < ts]
Ranked alternatives: 〈ten boys, nine boys, eight boys〉
Assertion: ∃t [ten boys could lift the piano at t, t ⊆ τ(ten boys) ∧ t < ts]
-
a.
The example with pas is interpreted as follows. It presupposes that at the reference time ten boys could lift the piano or that a smaller group of boys could lift the piano at an earlier time. It asserts that no earlier group of boys could lift the piano. Given that pas requires stronger (i.e. earlier) alternatives, the example further implies that the reference time was late for the piano to be lifted. The example with al asserts that ten boys could lift the piano at the reference time and implies that this time was early for the piano to be lifted, given that al requires weaker (i.e. later) alternatives. Finally, the example with nog requires regression, so that we must be dealing with a transition from the piano being lifted to the piano not being lifted (and hence the number of boys attempting to lift the piano must decrease with time). The example asserts that ten boys could lift the piano at the reference time and implies that there are times following the reference time at which the piano may not have been lifted.
We have analyzed these examples in the temporal mode. In other words, we have mapped different numbers of boys to different temporal intervals. One might wonder whether it would not be more appropriate to analyze these examples in the content mode, given that they contain numerals. It is easy to see, however, that this cannot work without additional assumptions, such as ‘scale reversal’ (see e.g. König 1991). A typical effect of using pas in the content mode is that the numeral is signalled to be low for the reference time, given contextual expectations. For instance, if John has read only three books, then three is a low number of books for John to have read at the reference time. But if only ten boys could lift the piano, then ten is not a low number of boys for the piano to be lifted at the reference time. If anything, ten is construed as a high number. This falls out from an analysis in the temporal mode. In this mode we get the interpretation that the piano is lifted late and hence by a relatively high number of boys.
To sum up, we have extended our analysis of temporal focus particles in this section to interpretations that involve clause (ii) of the definitions of progression and regression. The question under discussion with such interpretations is when a given proposition becomes true or ceases to be true. The proposition in question is not the prejacent, but an existentially closed version of the prejacent from which the focus is removed. The focus and its alternatives are linked to temporal intervals that make it possible to provide information relevant to the question under discussion.
6 Deriving Barbiers’s Generalization
We now turn to the core generalization about the distribution of pas, namely that this particle must immediately c-commandFootnote 16 its semantic argument (we have dubbed this rule Barbiers’s Generalization).Footnote 17 Part of the evidence for this generalization comes from the observation that pas must be adjacent to the category it interacts with if that category precedes the verb (or its trace, in main clauses). In the structure [pas [XP [YP V]]], pas can interact with XP but not with YP:
-
(85)

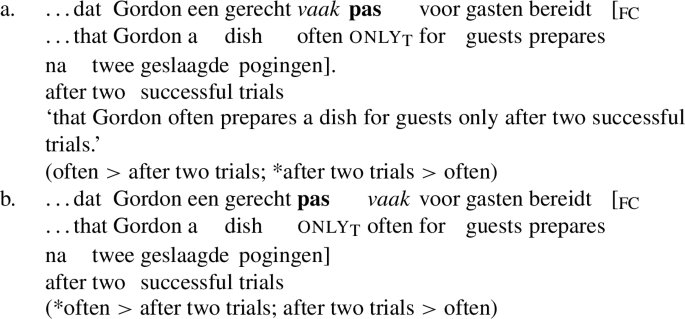
However, Barbiers’s Generalization does not imply that pas must always be adjacent to the category it interacts with. For example, if pas’s semantic argument follows the verb, immediate c-command can obtain even though pas and its semantic argument are not adjacent. In Dutch, non-adjacency is possible when pas takes a postverbal PP as its semantic argument, because pas immediately c-commands such a PP in a structure [pas [ […V] PP]]. That pas must indeed immediately c-command the PP is apparent from the fact that the scopal relation between vaak ‘often’ and the PP is determined by the position of pas with respect to vaak. Thus, (86a) has the same interpretation as (87a) and (86b) has the same interpretation as (87b). (The semantic argument of pas appears between brackets, marked FC for ‘focus constituent’.)
-
(86)
-
(87)

A second way in which pas and its semantic argument can be separated is through movement of the latter. In such cases pas interacts with its semantic argument following reconstruction (see Barbiers 1995, 2002 and Erlewine 2014 for discussion). The immediate c-command requirement still holds, as confirmed by the examples in (88), where the scopal construal of the fronted temporal modifier with regard to vaak ‘often’ is determined by the position of pas. Thus, (88a) has the same scopal construal as (86a) and (87a), while (88b) has the same construal as (86b) and (87b).
-
(88)

As was discussed at length in Sect. 2, it is crucial for the semantic interpretation of pas that it has access to a set of ordered alternatives. The basis of our account is the hypothesis that the process by which focus alternatives percolate up the tree does not preserve order. Therefore, if pas is not local to the node in which order is introduced it cannot be interpreted. In order to work out this idea we need to adopt two assumptions regarding the way focus alternatives are ordered.
The first is that the squiggle operator does not only filter alternatives on the basis of context, but may also order them, as already argued in Rooth (1992) (see also fn. 3). Our second assumption involves the attachment site of the squiggle operator. Rooth claims that this operator is uniformly introduced immediately below any focus particle present. While widely adopted, this claim makes it impossible to account for the strict locality between pas and its semantic argument. But such an account is within reach if we follow Riester and Kamp 2010 in attaching the squiggle operator not directly below the focus particle but immediately above the focus constituent, a practice we have adopted throughout. Riester and Kamp’s key motivation is provided by exchanges like (89) (adapted from their (7)).
-
(89)
Speaker A: I noticed that at Mary’s party there were several people that Sue didn’t know, including Alex, Bill, and Carl.
Speaker B: Oh, Mary must not have known that because she only introduced BILLF to Sue.
Speaker A’s utterance makes no mention of introduction events. It therefore seems wrong to assume that speaker B’s reply involves anaphoric retrieval of a set of VP meanings of the form [introduced z to Sue]. On the other hand, it is highly likely that retrieval is of a set of alternatives to the focus constituent Bill. But in that case it is more intuitive for the squiggle operator to attach to this DP (that is, to the focus constituent).
If these assumptions are on the right track, then the hypothesis that percolation of focus alternatives cannot preserve order has the desired consequences: focus particles can be separated from the focus constituent just in case they do not rely on order for their interpretation. This captures contrasts like the following, as alleen (exclusive only) does not rely on order for its interpretation, whereas pas (temporal only) does:
-
(90)

In order to implement this approach, we need to make explicit what semantic representation we assign to pas. In the preceding sections we have sidestepped this issue by only discussing the semantics of full sentences containing pas. In order to give a detailed semantics for pas we must consider it in one of its potential structural positions. Here, we concentrate on an instance of pas that associates with a focused modifier in a position below the external argument (so something like dat Jan pas op zondag arriveerde ‘that John arrived only on Sunday’). Recall that pas must have access to an ordered context set C consisting of the focused modifier and its alternatives, as well as a lambda abstract φ that represents its scope. In the case at hand, each member of the context set is a lambda abstract that applies to φ. Thus, we propose the following semantics (where l is a locational variable):Footnote 18
-
(91)
〚pas〛 =
λC.λφ.λx.λl.λt.λw [(C is a set such that (alternatives)
-
(91)
∀a [a ∈ C ∧ a ≠ f ⇒ a(φ)(x)(l)(t)(w) \(>_{\mathrm{P}}\) f(φ)(x)(l)(t)(w)]) ∧
-
(91)
(∃a [a ∈ C ∧ a(φ)(x)(l)(t)(w) = 1]) ∧ (presupposition)
-
(91)
(¬∃a [a ∈ C ∧ a ≠ f ∧ a(φ)(x)(l)(t)(w) = 1])] (assertion)
As proposed for exclusive only by Büring (2016: Chap. 10) there must be variants of pas that can be used in different syntactic contexts. These are related to each other via type shifting, with all variants selecting categories of a conjoinable type (i.e. a type that ‘ends in’ t). We will not go into details here, as these do not bear on the central issue in this section (the derivation of Barbiers’s Generalization).
We assume that the focus semantics of a node can be written either as a context set C and a formula that the members of C can combine with, or as a set of expressions that result from pointwise merger of each of the members of C with the formula. For example, a VP like introduced Bill to Sue, where Bill is the focused constituent, has the ordinary value in (92a); its focus value can be represented as either (92b) or (92c):
-
(92)
-
a.
λx.λl.λt.λw.x introduced Bill to Sue in l at t in w
-
b.
{Alex, Bill, Carl}, λy.λx.λl.λt.λw.x introduced y to Sue in l at t in w
-
c.
{λx.λl.λt.λw.x introduced Alex to Sue in l at t in w, λx.λl.λt.λw.x introduced Bill to Sue in l at t in w, λx.λl.λt.λw.x introduced Carl to Sue in l at t in w}
-
a.
Our contention is that the focus semantics must be represented as in (92b) if it is to combine with a focus particle, whereas it must be represented as (92c) if percolation of focus alternatives is necessary. The first requirement follows from the semantics of focus particles, which select a context set and a scope. This is exemplified for VP-adjoined pas in (91). The second requirement is standard and follows from the general assumption that focus alternatives percolate through pointwise merger.
Crucially, any order in a set of alternatives will be lost under pointwise merger. Imagine a situation in which the alternatives in (92b) are ordered (for example, on the basis of their social status):
-
(93)
-
a.
λx.λl.λt.λw.x introduced Bill to Sue in l at t in w
-
b.
〈Alex, Bill, Carl〉, λy.λx.λl.λt.λw.x introduced y to Sue in l at t in w
-
c.
{λx.λl.λt.λw.x introduced Alex to Sue in l at t in w, λx.λl.λt.λw.x introduced Bill to Sue in l at t in w, λx.λl.λt.λw.x introduced Carl to Sue in l at t in w}
-
a.
In the conversion from (93b) to (93c) the order of alternatives is lost. This is a consequence of the fact that order in one set (here a set of individuals) does not entail order in another set (here a set of predicates). Following pointwise merger of an adjunct, we may arrive at the ordinary and focus values in (94a,b). At this point, it is possible to convert (94b) to (94c), but the abstracted set of individuals cannot be (re-)ordered, as the squiggle operator was attached lower down (namely to the focus constituent Bill).
-
(94)
-
a.
λx.λt.λl.λw.x politely introduced Bill to Sue in l at t in w
-
b.
{λx.λt.λl.λw.x politely introduced Alex to Sue in l at t in w, λx.λt.λl.λw.x politely introduced Bill to Sue in l at t in w, λx.λt.λl.λw.x politely introduced Carl to Sue in l at t in w}
-
c.
{Alex, Bill, Carl}, λy.λx.λt.λl.λw.x politely introduced y to Sue in l at t in w
-
a.
In other words, order once lost cannot be regained. The consequence is that following pointwise merger, exclusive only can be interpreted, but scalar or temporal only cannot, as their interpretation requires that C is an ordered set. This, in essence, is our account of Barbiers’s Generalization. For concreteness sake we give partial derivations for three examples.
Consider first a grammatical structure with pas, as given in (95), where the numbered constituents have he semantic representations given in the derivation below the example. The application of the squiggle operator to the modifier vanuit Almere involves two steps. The first is the generation of a set of contextually appropriate alternatives to vanuit Almere, which are ordered based on the sequence of cities in a journey. The second is a transformation of each these alternatives through the function τ into a temporal interval during which Mary was in the location denoted by the alternative. In other words, vanuit Almere does not only determine the location from which Mary telephoned but also the time at which she did so. The ordered set of alternatives and the denotation of the verb are inherited as components of the focus semantics of node 2 (represented below the line). As a consequence, pas finds the input it is looking for: an ordered context set and a scope. We give the resulting focus semantics in 3, where the input condition on C has been dropped, because C meets it. Once this focus semantics combines with the remaining modifier on two days and the external argument she, we obtain the presupposition that for two days Mary telephoned while she was in Almere or earlier and the assertion that on these days she did not telephone before she got to Almere. Furthermore, given the ranking of alternatives, we also obtain the inference that any time contained in the interval during which she was in Almere was late for Mary to call.
-
(95)

As shown in (96), the derivation crashes if pas is structurally separated from the focus constituent. As before, node 2 inherits an ordered set of alternatives and the semantics of the verb. However, pointwise merger of ‘on two days’ requires that this information is converted into an unordered set of predicates, as in 2′. Following pointwise merger, it is possible to extract a set of alternatives, as in 3′, but no order can be established among these alternatives in the absence of the squiggle operator. As a consequence, pas does not find the input it is looking for.
-
(96)

Finally, consider a case in which exclusive only associates with a focus constituent at a distance, as in (97). As before, two representational modes are available for the focus semantics. Presumably alleen—like pas—selects a set of alternatives plus a formula that represents its scope. However, since alleen does not require ordered alternatives, pointwise merger can take place following attachment of the squiggle operator and preceding attachment of alleen (see also (90a)).
-
(97)

This account of Barbiers’s Generalization ties the immediate c-command requirement to the ordering of alternatives. We therefore predict this requirement should also be present with scalar only. There is evidence that this is indeed the case. Consider first the examples in (98). In contrast to what we observed for exclusive only, it is not possible to separate scalar only from the focus constituent.
-
(98)

The same point can be made with biclausal examples. We have already shown that alleen (exclusive only), but not pas (temporal only), can take scope in the matrix clause while interacting with a focus in the embedded clause (see (8)). In this regard, scalar only behaves like pas. We demonstrate this using the examples in (99) and (100), which contain slechts rather than maar for reasons discussed in fn. 2. For these examples two rankings are relevant. To begin with, universities can be ranked by perceived standing, in which case Stanford outranks Cal State. Second, in the case at hand, what is said can be ranked by its negative effect on Mary’s application, in which case saying that she has studied at Cal State outranks saying that she has studied at Stanford. The judgements in (99) and (100) can only be understood if slechts, when merged in the matrix clause, must operate on the strength of what is said rather than on the perceived standing of the universities. In other words, it is possible for an embedded focus to give rise to a set of alternative clausal complements and for the squiggle operator to order those complements. But it is not possible for focus alternatives to be ordered internally to the clausal complement and for that order to be inherited by the node on which matrix slechts operates.
-
(99)

-
(100)

We conclude that Barbiers’s Generalization can be understood in terms of two factors: the fact that scalar focus particles select a set of ordered alternatives alongside a scope and the fact that order cannot be preserved under pointwise merger.
7 Conclusion
In this paper we have argued that exclusive, scalar and temporal instances of only share a core semantics but differ as regards the set of alternatives they operate on. Exclusive only selects unordered alternatives, scalar only selects alternatives ordered by some contextually determined notion of strength, and temporal only selects alternatives ordered by progression, which is a relation that requires increasing strength over time. Like scalar only, temporal only identifies the focus as the weakest alternative.
The literature has identified two other temporal focus particles, already and still. Already, like temporal only, selects alternatives ordered by progression, but unlike temporal only it identifies the focus as the strongest alternative. Still selects alternatives ordered by regression, which is a relation that requires decreasing strength over time. Like temporal only it identifies the focus as the weakest alternative.
All temporal focus particles have two modes of interpretation, which we have dubbed the content and the temporal mode. In the content mode, time is kept constant across alternatives of varying strength; in the temporal mode, strength is kept constant and the alternatives index different temporal intervals. It is inherent in the notions of progression and regression that these two modes of interpretation are available as different perspectives on checking development over time. Once we acknowledge that these two modes of interpretation exist, a uniform analysis of focus particles is possible.
The sets of alternatives on which temporal focus particles operate can be either articulated or binary. Binary scales are of particular interest because they can be used to explain why the progression particle al ‘already’ can sometimes be used in contexts of regression, while the regression particle nog ‘still’ can sometimes be used in contexts of progression. This phenomenon, which we have dubbed ‘masquerading’ can be observed when the particle operates on a binary scale that is formally progressive but compatible with a context of regression, or vice versa. It follows from our analysis that temporal only cannot operate on a binary scale and it is therefore predicted—correctly—that temporal only cannot masquerade as a regression particle.
Finally, we have shown that it can be derived from our account why temporal and scalar only must immediately c-command the category they interact with, in opposition to exclusive only.
Notes
The distributional pattern is more complicated than this, however. Pas can also occur in the c-command domain of its semantic argument (see Barbiers 1995):
-
(i)
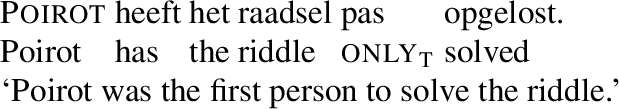
What is particularly remarkable about examples like (i) is that pas is attached below the object, and therefore occupies a position to which the subject does not normally reconstruct. A similar pattern exists with floating quantifiers, where it is also possible for a subject to be interpreted as the restrictor of a floating quantifier that is merged below the object. We will leave discussion of the type of reconstruction required to deal with such examples for future research.
-
(i)
There are two instantiations of scalar only in Dutch, namely slechts and maar. As far as we can tell these differ in two ways. Slechts belongs to a higher register than maar and slechts can interact with VP, which maar cannot. Throughout we use examples with maar, except in Sect. 6, where it is important that scalar only can interact with VP.
One of the examples that Rooth gives to motivate that the squiggle operator can order alternatives is the following:
-
(i)
[Context: My roommates Steve and Paul and I took a quiz in our self-paced calculus class, which was graded right away by the TA. Afterwards, George asked me how it went. My answer was:]
Well, I [passed]F.
One way to interpret this answer is that the speaker did no better than pass the exam (he did not ace it). This interpretation requires that the alternatives fail the exam, pass the exam and ace the exam are ordered by strength, based on the numerical values of fail marks, ordinary pass marks and high pass marks. Since the example in (i) does not contain a focus particle, it seems likely that the order is introduced by the squiggle operator.
-
(i)
Pas requires an expected development from ¬p to p. In the case at hand, p = “John has four fingers on his left hand.” In a scenario where John starts off with 3 fingers and gains one, there is a development from ¬p to p, as “John has four fingers on his left hand” is not true before the change. By contrast, in a scenario where John starts with five fingers and loses one, the felicity condition is not met, because if John has five fingers, he also has four fingers.
Krifka (2000) defines the rate of growth of a background B as in (i). This condition says that B displays a weaker or equal rate of growth in world i than in world i’ if the time at which B reaches a given value in world i’ will always precede or be equal to the time at which B reaches that value in world i. Therefore, at no point in time the growth function in i can yield a value higher than the growth function in i’. This definition of rate of growth is incorporated into the definition of temporal focus particles.
-
(i)
B(i) ≤ B(i’) ⇔ ∀x∀t,t’[B(i)[t,x] ∧ B(i’)[t’,x] → t’ ≤ t]
-
(i)
Some authors (Horn 1970; König 1977 and Ippolito 2007, a.o.) say that already(p) presupposes that there is a time after the reference time at which p is true. This presupposition is not part of the semantics of al proposed here, because there are contexts in which al can be used felicitously, while the reference time is the last time at which p is true. For example, by uttering (i) Susan may complain that Jack has woken up the baby. The most natural construal of the example is one in which the baby wakes as a result of Jack’s noisy entrance.
-
(i)

-
(i)
The particle nog has a second meaning, which requires focus on the particle itself. On this reading, nog can be translated as additionally. Thus, (49b) has a grammatical parse with the interpretation that Suzanne has written another two essays. We will leave analysis of this use of nog to future research.
Example (50a) is acceptable in a progression context in which the number of essays Suzanne has to write grows with time. For example, if the number of assignments on her university course increases as the term progresses, it is perfectly fine to utter (50a) if so far she has been assigned three essays to write (of which she has written none).
Note that we are left with an asymmetry in the typology of temporal focus particles. We have discussed examples of low and high degree progression particles, as well as a particle that expresses a low degree of regression. However, we are not aware of particles that can successfully be characterized as expressing regression to a high degree. The missing particle, which we might refer to as still*, would have the semantics in (i). It shares with al that Φfoc exceeds its alternatives and it shares with nog that it operates on a regression scale. This particle would map Φfoc to the presupposition for reasons that will be familiar by now.
-
(i)
Still* (nog*)
Condition on alternatives: ∀a [a ∈ ALT ∧ a ≠ f ⇒ Φ(f) \(>_{\mathrm{R}}\ \Phi\)(a)]
Presupposition: ∃a [a ∈ ALT ∧ Φ(a) = 1]
Assertion: ¬∃a [a ∈ ALT ∧ a ≠ f ∧ Φ(a) = 1]
The proposal developed here does not account for the absence of still*.
-
(i)
The use of semi-lattices to order alternatives by implicational strength can also be found in Rooth (1992).
As an anonymous reviewer points out, many predicates that permit a construal as a two-point scale also permit a construal as a bounded scale. This is largely context-dependent. For example, pregnant is not a gradable property in a medical context, but you can say She is very pregnant if you mean that she is very close to giving birth. Note, however, that on and off do not seem to permit such construals (*The light is almost on/off). Apparent cases like The light will almost go on have a temporal construal of almost. The example means that the light will soon go to a state of being on, not that it will go to a state of being on to a high degree.
Although we cannot discuss this here, in general stacking of focus particles in Dutch seems to have a compositional semantics, as we have shown in the main text for combinations of a temporal and a scalar focus particle. There is one apparent exception. In the example below, the sequence alleen maar is interpreted with the scalar focus particle applied after the exclusive focus particle. Thus, the example means that the only thing that John did was the dishes and that this is less than what might have been expected.
-
(i)
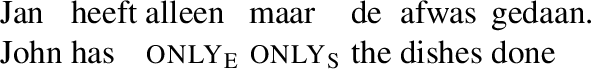
One observation that appears to confirm that scalar only is interpreted outside of exclusive only in (i) comes from the asymmetry in (ii): fronting of the object may pied-pipe alleen and strand maar, but not the other way around.
-
(ii)

The strength of this argument cannot be assessed without evaluating various other complications with the distribution of focus particles in topicalization structures (see Barbiers 2014).
-
(i)
The reference time is always an existentially bound variable rather than a constant (it can vary in the scope of a universal). That time is constant across alternatives in the content mode must therefore be the result of picking the same time for each alternative. We have abstracted away from this in our discussion of the content mode.
It is worth emphasizing that the notion of lateness that pas gives rise to is not absolute. The only thing that pas does is indicate that the time indexed by the focus is late compared to the alternatives. For example, suppose that the coronation of Queen Catharina-Amalia happens on a Sunday and that guests are asked to arrive in Amsterdam no earlier than Monday and no later than Friday. In that context it is possible to utter (i), even though Tuesday is still early in the arrival period.
-
(i)

A similar observation can be made about the interpretation of pas in the content mode. Consider the example in (23), repeated as (ii) below. This example is felicitous in a context where John is required to read ten books but has read only eight. Therefore, eight is not a low number in the context, but it is low compared to the alternatives (nine or ten books).
-
(ii)
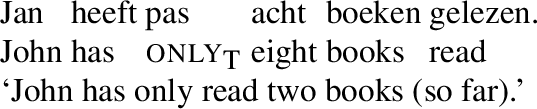
These facts are hard to account for in a theory according to which the semantics of pas expresses that an event happens late in a contextually defined interval, or involves a number low in a contextually defined range (see Barbiers 1995 for a proposal along these lines).
-
(i)
Some examples that we would analyze as involving ranking in the temporal mode do not appear to involve progression at all. The sentence in (i) is a case in point. It appears to express a state rather an element in a temporally ordered set of alternative states. We believe that this is only apparent, however, and caused by the fact that the present tense allows a generic reading.
-
(i)

Once examples of this type are rendered with the past tense, as in (ii), the dominant interpretation is one in which Mary is presented with a sequence of cars and that only a car late in the sequence (a Mercedes) pleases her. If this is on the right track, then the example in (i) can be analyzed as saying that in general when Mary is presented with a sequence of cars, she is only happy once she is offered a Mercedes (or a better car). This generalization over situations obscures the temporality of pas in (i).
-
(ii)
-
(i)
A immediately c-command B iff there is no C such that A asymmetrically c-commands C and C asymmetrically c-commands B. A asymmetrically c-commands B iff A c-commands B and B does not c-command A.
The semantic argument is the constituent to which the squiggle operator is attached. This constituent may coincide with the focus, but must at least contain the focus. For example, in (i), drie ‘three’ is the focus, but the squiggle operator is attached to drie boeken ‘three books’. See Barbiers 1995 for further discussion of the distinction between the focus and the semantic argument of pas.
-
(i)

-
(i)
It may be unexpected that f takes φ as its (first) argument rather than the other way around, but this is because f is modifier and therefore it selects the category it attaches to.
References
Barbiers, Sjef. 1995. The syntax of interpretation. PhD diss., Rijksuniversiteit Leiden.
Barbiers, Sjef. 2002. Remnant stranding and the theory of movement. In Dimensions of movement, eds. Artemis Alexiadou, Elena Anagnostopoulou, Sjef Barbiers, and Hans-Martin Gärtner. Vol. 48 of Linguistics today, 47–67. Amsterdam: Benjamins
Barbiers, Sjef. 2014. Syntactic doubling and deletion as a source of variation. In Linguistics variation in the minimalist framework, ed. Carme M. Picallo. Oxford: Oxfordt University Press.
Beaver, David, and Brady Clark. 2008. Sense and sensitivity. Malden: Blackwell Sci..
Büring, Daniel. 2016. Intonation and meaning. Oxford: Oxford University Press.
Condoravdi, Cleo. 2008. Punctual until as a scalar NPI. In The nature of the word, eds. Kristin Hanson and Sharon Inkelas. Cambridge: MIT Press.
Coppock, Elizabeth, and David Beaver. 2011a. Mere-ology. Alternatives in semantics.
Coppock, Elizabeth, and David Beaver. 2011b. Sole sisters. In Semantics and Linguistic Theory (SALT) 21, 197–217.
Coppock, Elizabeth, and David Beaver. 2014. Principles of the exclusive muddle. Journal of Semantics 31(3): 371–432.
Declerck, Renaat 1995. The problem of “not...until”. Linguistics 33: 51–98.
Declerck, Renaat. 1994. The only/already puzzle: A question of perspective. Cognitive Linguistics 5: 307–350.
Erlewine, Michael Yoshitaka. 2014. Movement out of focus. PhD diss., MIT.
Guerzoni, Elena. 2003. Why even ask? On the pragmatics of questions and the semantics of answers. PhD diss., Cambridge: MIT.
Hole, Daniel. 2015. A distributed syntax for evaluative “only” sentences. Zeitschrift für Sprachwissenschaft 34(1): 43–77.
Horn, Laurence. 1969. A presuppositional analysis of only and even. In The 5th annual meeting of the Chicago Linguistic Society 4, 97–108. Chicago: Chicago Linguistic Society.
Horn, Laurence. 1970. Ain’t it hard (anymore). In Papers from the sixth regional meeting of the Chicago Linguistic Society, eds. M. A. Campbell et al., 318–327. Chicago: Chicago Linguistic Society.
Horn, Laurence. 1996. Exclusive company: Only and the dynamics of vertical inference. Journal of Semantics 13: 1–40.
Iatridou, Sabine, and Hedde Zeijlstra. 2021. The complex beauty of boundary adverbials: in years and until. Linguistic Inquiry 52(1): 89–142.
Ippolito, Michela. 2007. On the meaning of some focus-sensitive particles. Natural Language Semantics 15(1): 1–34.
Karttunen, Lauri. 1974. Until. In Chicago Linguistic Society 10.
Klinedinst, Nathan. 2004. Only Scalar Only. Presented at the presupposition & implicature workshop, Université Paris Diderot, October 5. http://www.linguist.univ-paris-diderot.fr/~amsili/Rech/jpi04/nklinedinst_only_paris.pdf, last accessed 30 August 2021.
König, Ekkehard. 1977. Temporal and non-temporal uses of “noch” and “schon” in German. Linguistics and Philosophy 1(2): 173–198.
König, Ekkehard. 1979. A semantic analysis of German “erst”. In Semantics from different points of view, eds. Rainer Bäuerle, Urs Egli, and Arnim von Stechow, 148–160. Berlin: Springer.
König, Ekkehard. 1981. The meaning of scalar particles. In Words, worlds, and contexts: New approaches in word semantics, eds. Hans-Jurgen Eikmeyer and Hannes Rieser, 107–132. Berlin: de Gruyter.
König, Ekkehard. 1991. The meaning of focus particles: A comparative perspective. London: Routledge.
Krifka, Manfred. 2000. Alternatives for aspectual particles: Semantics of still and already. Annual Meeting of the Berkeley Linguistics Society 26(1): 401. https://doi.org/10.3765/bls.v26i1.1125.
Löbner, Sebastian. 1989. German schon – erst – noch: An integrated analysis. Linguistics and Philosophy 12(2): 167–212. https://doi.org/10.1007/BF00627659.
Mittwoch, Anita. 1993. The relationship between schon/already and noch/still: A reply to Löbner. Natural Language Semantics 2(1): 71–82.
Orenstein, Dina. 2015. A family of exclusives in Hebrew. In ESSLLI 2015 student session, eds. Miriam Kaeshammer and Philip Schulz, 96–106.
Pustejovsky, James. 2013. Where things happen: On the semantics of event localization. In Proceedings of the IWCS 2013 workshop on Computational Models of Spatial Language Interpretation and Generation (CoSLI-3), 29–39. Stroudsburg: Association for Computational Linguistics.
Riester, Arndt, and Hans Kamp. 2010. Squiggly issues: Alternative sets, complex DPs, and intensionality. In Logic, language and meaning, eds. Maria Aloni, Harald Bastiaanse, Tikitu de Jager, and Katrin Schultz. Vol. 6042 of Lecture notes in computer science, 374–383. Berlin: Springer.
Rombouts, Jos. 1979. Dutch nog and al as degree particles. In Bedeutung, Sprechakte und Texte. Akten Des 13. Linguistischen Kolloquiums, Band 2. (= Linguistische Arbeiten 77), eds. Willy Vandeweghe and Marc van de Velde. Tübingen: Niemeyer.
Rooth, Mats Edward. 1985. Association with focus. PhD diss., University of Massachusetts.
Rooth, Mats. 1992. A theory of focus interpretation. Natural Language Semantics 1: 75–116. https://doi.org/10.1007/BF02342617.
Smessaert, Hans, and Alice G. B. Ter Meulen. 2004. Temporal reasoning with aspectual adverbs. Linguistics and Philosophy 27(2): 209–261.
Wagner, Michael. 2006. Association by movement: Evidence from NPI-licensing. Natural Language Semantics 14(4): 297–324.
Wiegand, Mia. 2018. Exclusive morphosemantics: Just and covert quantification. In West Coast Conference on Formal Linguistics (WCCFL) 35, eds. William G. Bennett, Lindsay Hracs, and Dennis Ryan Storoshenko, 419–429. Somervile: Cascadilla Proceedings Project.
Acknowledgements
This paper started with an apparently syntactic question—why should Barbiers’s generalization hold?—that turned out to have a semantic answer (we think). We would like to thank Nathan Klinedinst and Yasutada Sudo for helpful input while we were trying to navigate a landscape only partly familiar to us. We would like to thank associate editor Hedde Zeijlstra and three anonymous reviewers for detailed and constructive comments that led to significant improvements in presentation and content. The distribution of temporal focus particles and its implications were discussed during a BA/MA course, Current Issues in Syntax, at UCL in 2016 and 2018. It was also the topic of a talk given at Queen Mary University of London in December 2019. We would like to thank the attendees of these events for useful suggestions and criticism.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neeleman, A., van de Koot, H. The interpretation and distribution of temporal focus particles. Nat Lang Linguist Theory 40, 793–835 (2022). https://doi.org/10.1007/s11049-021-09526-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11049-021-09526-x