Deriving the Constant Rate Effect

Abstract

The Constant Rate Hypothesis (Kroch 1989) states that when grammar competition leads to language change, the rate of replacement is the same in all contexts affected by the change (the Constant Rate Effect, or CRE). Despite nearly three decades of empirical work into this hypothesis, the theoretical foundations of the CRE remain problematic: it can be shown that the standard way of operationalizing the CRE via sets of independent logistic curves is neither sufficient nor necessary for assuming that a single change has occurred. To address this problem, we introduce a mathematical model of the CRE by augmenting Yang’s (2000) variational learner with production biases over an arbitrary number of linguistic contexts. We show that this model naturally gives rise to the CRE and prove that under our model the time separation possible between any two reflexes of a single underlying change necessarily has a finite upper bound, inversely proportional to the rate of the underlying change. Testing the predictions of this time separation theorem against three case studies, we find that our model gives fits which are no worse than regressions conducted using the standard operationalization of CREs. However, unlike the standard operationalization, our more constrained model can correctly differentiate between actual CREs and pseudo-CREs—patterns in usage data which are superficially connected by similar rates of change yet clearly not unified by a single underlying cause. More generally, we probe the effects of introducing context-specific production biases by conducting a full bifurcation analysis of the proposed model. In particular, this analysis implies that a difference in the weak generative capacity of two competing grammars is neither a sufficient nor a necessary condition of language change when contextual effects are present.

1 Introduction

1.1 The Constant Rate Effect

In a seminal paper in historical syntax, Kroch (1989) proposed the Constant Rate Hypothesis:

[W]hen one grammatical option replaces another with which it is in competition across a set of linguistic contexts, the rate of replacement, properly measured, is the same in all of them. (Kroch 1989:200)

Initially (and still logically) a hypothesis, the notion of a constant rate has accumulated enough support over the last three decades for this to be referred to as the Constant Rate Effect, or CRE (see e.g. Pintzuk 2003:511).

The logic behind CREs is as follows: if a variant replaces another variant in two or more different contexts and the rate of change is the same in each of these contexts, then we should assume that only a single change has occurred. CREs have therefore been deployed to argue that two or more apparently unrelated surface changes are in fact manifestations of a single underlying change (Fig. 1). Unifying changes in this way provides strong support for approaches to language in which syntactic variation consists not primarily in lexical or contextual idiosyncrasies but in the values of a finite number of universal parameters, as in the classical Principles & Parameters approach (Chomsky 1981; Chomsky and Lasnik 1993). There is no necessary link between Principles & Parameters and CREs, as Pintzuk (2003:511) emphasizes; the variationist approach within which the Constant Rate Hypothesis is couched is theory-neutral. However, CREs are a useful tool in the armoury of diachronic syntacticians who wish to argue for “the controlling effect of abstract grammatical analyses on patterns in usage data” (Kroch 1989:239).

Fig. 1

A classical example of a CRE: the emergence of do-support in Early Modern English in negative declarative and four types of interrogative sentences; data from Kroch (1989:224, Table 3). Periphrastic do is adopted at slightly different times in the different contexts, but the rate of adoption appears to be similar across contexts. Kroch (1989) identified loss of V-to-T movement as the underlying parametric change responsible for this constant rate

CREs offer a fresh perspective on the causation of changes. Kroch (1989:238) criticizes the approach to causation in which “the finding that a given context is most favourable to the use of an innovation is taken to show that the innovation is an accommodation to the linguistic functionality of that context.” Where there is a disparity between contexts that share the same rate of change, this “reflects functional effects, discourse and processing, on the choices speakers make among the alternatives available to them in the language as they know it; and the strength of these effects remains constant as the change proceeds” (Kroch 1989:238). In other words: surface changes are to be thought of as reflexes of underlying grammatical changes; the discrepancies in frequencies seen at the surface level are due to extra-grammatical factors, or contextual effects, which are independent of the underlying change itself and constant across time.

The usual procedure for detecting a CRE in some diachronic data is to fit a logistic curve (1) to each of the contexts separately and then to compare the growth rates of these curves against each other.

$$ p_{t} = \frac{e^{s(t-k)}}{1 + e^{s(t-k)}} = \frac{1}{1 + e^{-s(t-k)}} $$

(1)

Here, $p_{t}$ is the frequency of either the innovatory or the receding variant (or parameter value) in a given context at time t, and s is the (time-independent) rate of change in that context. The k parameter serves to translate the curve along the time axis, indicating the point of greatest growth, or the tipping point, of $p_{t}$ (Fig. 2). With this operationalization, we have the following procedure for establishing a CRE: a logistic curve of the form (1) is first fit to each of the contexts of interest separately and independently. Then, if variation among the s or ‘slope’ parameters for these curves is found to fall within a reasonable confidence interval, the change is said to proceed at the same (‘constant’) rate in all contexts. Variation among the k or ‘intercept’ parameters, on the other hand, is allowed and is where the contextual effects, independent of the underlying grammatical change, are thought to manifest themselves. This is the procedure used in a number of studies that have sought to establish CREs in various processes of change across a number of languages (e.g. Kroch 1989; Santorini 1993; Pintzuk 1995; Kallel 2005; Pintzuk and Taylor 2006; Kallel 2007; Fruehwald et al. 2009; Postma 2010; Durham et al. 2012; Wallage 2013; Gardiner 2015). Henceforth, we shall refer to it as the standard operationalization.¹

Fig. 2

Three logistic curves (1) with identical s (‘slope’) parameters but differing k (‘intercept’) parameters

1.2 The non-linking problem

Initially, the logistic function (1) was adopted because of its practicability and its success in other disciplines such as population genetics, not because it followed from any established first principles:

[G]iven the mathematical simplicity and widespread use of the logistic, its use in the study of language change seems justified, even though, unlike in the population genetic case, no mechanism of change has yet been proposed from which the logistic form can be deduced. (Kroch 1989:204)

The logistic has since been derived from mathematical models of language acquisition independently by Niyogi and Berwick (1997) and Yang (2000); Ingason et al. (2013) provide a particularly clear illustration of how syntactic acquisition in successive generations can give rise to logistic change at population level. What has never been explicated in detail, however, is why different contextual reflexes of a single underlying change should be governed by logistics agreeing in their s parameters but freely varying in their k parameters: even though this operationalization has proved useful in gathering empirical support for the Constant Rate Hypothesis, it is not a model of the CRE itself.² In short, while the standard operationalization may adequately describe historical data, it fails to explain it, suggesting no mechanism for how contextual reflexes spring from underlying changes. The fact that under the standard formulation the independent contextual reflexes are not linked to each other, or to anything else, in this stronger sense we call the non-linking problem, and there are a number of reasons to believe that the problem is serious enough to warrant that the standard operationalization of CREs should be rejected.

Firstly, note that fitting a number of independent logistics to a number of contexts in some data leaves variation among the k parameters entirely unexplained, even if we assume that the logistics agree in their s parameters as required by the standard operationalization. In principle, it is possible for this variation in k to be arbitrarily large, and it is therefore in principle possible to ‘connect’ two clearly unrelated changes—possibly separated by millennia on the time axis—as long as they happen to share the same growth rate. In principle, then, it is possible to be led to the absurd conclusion that a single change runs to completion in one context before it even takes off in another (Fig. 2).

Secondly, there are reasons to think that not all instances of logistics agreeing in their s parameters are in fact CREs in the sense that a single underlying grammatical change is being modulated in the usage of a speaker or group of speakers by constant contextual (functional, discourse-related, etc.) effects. The relevant evidence comes from studies in which the ‘contextual effects’ are not within-speaker but between-speaker effects or even outright contingencies. Wallenberg (2016) shows that relative clause extraposition is a gradually declining option across the histories of both English and Icelandic, and that the s parameters of the two curves do not differ significantly. Similarly, Willis (2017), in his study of the spread of the innovative second-person pronoun chdi in the recent history of Welsh, finds that in different regions of Wales the change is more or less advanced (i.e. different intercepts) but that the slopes of the changes are not significantly different. Corley (2014) tests for a CRE in the usage of negative concord between female and male speakers of Early Modern English, using data from Nevalainen and Raumolin-Brunberg (2003), and again finds no significant difference in slopes. What these case studies show is that the s parameters of two different changes may be similar for reasons other than being reflexes of a single abstract grammatical pattern, and thus that identity of slope parameters is not a sufficient condition for the assumption of a single underlying change. Wallenberg (2016:e244), for instance, notes explicitly that these are different populations, and suggests that the similarity of slopes may indicate that “the same forces are underlying the change” in both the English and the Icelandic populations—but however these forces are to be understood, we cannot be dealing with a CRE in the traditional sense, as all these authors recognize.³

These two problems are in most cases only technical in the sense that a researcher will usually have independent reasons for ruling out such fantastical hypotheses: in particular, the inference that two apparently separate changes are reflexes of the same underlying phenomenon is usually motivated by a particular structural analysis which is arrived at on independent grounds. However, the theoretical importance of these problems is great: they demonstrate that the standard independent logistics formulation of the CRE can serve at most as a proxy to CREs, not as a model of them. If the CRE is a phenomenon—and the empirical support gathered for it over the last three decades suggests it is—this means we have so far failed to model one of the more well-established facts about language diachrony. Consequently, we have only a very approximate understanding of the dynamics of language change in the presence of contextual factors, and a number of questions remain wide open: if underlying changes are to be thought of as competition between two or more parametric options or grammars, and if CREs are thought to appear because of some sort of performance effects operating over that process of competition, how, exactly, do the two processes interact? What role does the magnitude of the performance effects play in the overall change? Could contexts that favour the innovatory variant be so favouring as to accelerate the change, and if so, can this accelerating effect be quantified and measured? Similarly, could disfavouring contexts slow the change down? Could they even block change in certain cases? These questions can only be answered with the help of mathematical models of change that accommodate mechanisms for both grammatical competition and contextual effects, and also define, without equivocation, the possible interactions between these two mechanisms over time.

The non-linking problem has, of course, not gone unnoticed in the literature. As Roberts (2007) puts it:

One might wonder why [the CRE] should hold. It is unlikely to be a fact about the grammars themselves. Instead, it is plausible that it may be a fact either about speech communities or about the ways in which individuals choose among grammars available to them. As such, it may be attributable to sociolinguistic factors or to the dynamics of populations, or both factors acting in tandem. (Roberts 2007:313)

Our aim in this paper is to propose a solution to the non-linking problem, and our concrete proposal is that the CRE occurs because of context-specific production biases which serve either to promote or to hinder an underlying change in progress. That is to say, we will argue that the CRE is indeed a fact about the ways in which individuals choose among grammars available to them, and propose a rigorous mathematical model of this kind of speaker behaviour. The result is a first step towards a mechanistic model of the CRE that not only describes the diachronic phenomenon but explains it by deriving it from independently plausible first principles of language acquisition and use.

1.3 Plan

The paper is structured as follows. In Sect. 2, we augment Yang’s (2000) mathematical model of grammar competition with production biases to account for variability across contexts. This results in a dynamical system in which the evolution of the underlying change—a parameter switch for us—and the evolution of the usage frequencies in a number of linguistic contexts feed into each other iteratively. We then derive analytical expressions for the time evolution of this system and show in Sect. 3 that in most cases it can be approximated by a constrained set of equations based on one logistic. In Sect. 4, this approximation is used to derive a theorem concerning the possible temporal separation between two reflexes of one underlying change: we show analytically that under our proposed model the time separation between contexts always has a finite upper bound which is inversely proportional to the rate of the underlying change. This solves the problem of unconstrained variation in the k parameters: under our model, it is no longer possible for the curves of different contexts to be radically distant from each other in time. In the remainder of Sect. 4, we proceed to test the model empirically from two complementary angles: (1) by investigating whether time separations observed in a number of previously established CREs agree with the predictions of our time separation theorem, and (2) by testing whether our model is able to distinguish actual CREs from pseudo-CREs, that is, surface changes that proceed at similar rates accidentally but that are clearly not reflexes of one and the same underlying change.

A side product of this investigation is an extension of some of the analytical results in Yang (2000). In Sect. 3, we uncover all possible outcomes of the dynamical interplay between grammatical competition and production biases. A full bifurcation analysis of the two-grammar case shows that production biases can both induce change in settings where Yang’s (2000) model outlaws change, and block change in settings where Yang’s (2000) model predicts change. On the assumption that a model which incorporates the possibility of production biases is more realistic than one that does not, then, the assumption that language change is driven (solely) by distributional differences in the proportion of sentences parsed by different competing grammars is shown to be too simple. A theorem resulting from our analysis of the extended model shows that, when production biases are in operation, such differences are neither necessary nor sufficient for change, though they continue to play an important role in any given change process in a way that can be quantified exactly. In Sect. 5, we offer a brief account of the nature of production biases; Sect. 6 concludes.

2 Grammar competition and production biases

2.1 Learning competing grammars

Empirical work on language variation and change has demonstrated the limitations of the traditional view of parameter setting as a once-and-for-all process which leaves the learner with a unique grammar at the point of maturation: speakers have, at least during periods of change, access to more than one grammar (Kroch 1989, 1994, 2000; Santorini 1992; Pintzuk 2003). As pointed out by Santorini (1992:619), this intra-individual co-existence of multiple grammatical systems is “an ability for which the phenomena of multilingualism, diglossia and intrasentential code-switching provide independent and incontrovertible evidence”; see also the discussion in Roberts (2007:319–331). This notion has been formalized by Yang (2000, 2002) in his mathematical model of competition-driven change, on which our model of the CRE is based. We therefore begin by reviewing the operating principles behind this model, focussing on the presentation in Yang (2000).

This model construes language change as a learning process in a homogeneous, well-mixing population with non-overlapping generations. At each iteration, we can therefore think of the population as a single individual who sets parameters based on the linguistic output of the previous generation, abstracting away entirely from the social and geographical structure of that population. In the competing grammars framework, each biologically possible grammar of human language $G_{i}$ is associated with a weight which gives the probability of an individual using that grammar. The framework allows any number of those grammars to compete; however, during well-studied and relatively well-understood periods of language change, it usually seems to be the case that two grammars are in competition. Since, additionally, this renders the mathematics of the model particularly tractable, we focus on the two-grammar case in all that follows.

Let $G_{1}$ and $G_{2}$ be these two grammars, and denote their weights with $p_{t}$ and $q_{t}$, respectively, indexed for generational time t.⁴ The basic insight behind Yang’s (2000) model is that each grammar has its time-independent (parsing) advantage, which is simply the proportion of sentences the other grammar cannot parse (out of all sentences generated, in abstracto, by either grammar). There are then fundamentally three kinds of sentence: sentences of type $L_{1}$, which $G_{1}$ but not $G_{2}$ parses; sentences of type $L_{2}$, which $G_{2}$ but not $G_{1}$ parses; and sentences of type $L_{X}$, which both grammars parse (Fig. 3). The language learner receives primary linguistic data (PLD)—the linguistic output of the generation at time step t—and his task is to arrive at weights $p_{t+1}$ and $q_{t+1}$ for the two competing grammars in his own generation. Letting α denote the advantage of $G_{1}$ and β that of $G_{2}$, then (assuming he samples his environment uniformly) the learner is confronted with a number of sentences drawn from the following distribution:

$$ \begin{matrix} & L_{1} & L_{2} & L_{X} \\ G_{1} & \alpha p_{t} & 0 & (1-\alpha)p_{t} \\ G_{2} & 0 & \beta q_{t} & (1-\beta)q_{t} \end{matrix} $$

(2)

Based on this input, the learner is assumed to set parameters in accordance with linear reward–penalty learning, an off-the-shelf learning algorithm from mathematical psychology (Bush and Mosteller 1951, 1958; Narendra and Thathachar 1989). Of crucial importance here are the two quantities $c_{t} = \beta q_{t}$ and $d_{t} = \alpha p_{t} = \alpha (1-q_{t})$, known as the penalty probabilities of the two grammars: $c_{t}$ is the probability of the learner encountering a sentence which $G_{1}$ cannot parse and $d_{t}$ the probability of a sentence which $G_{2}$ cannot parse. It can be shown (Narendra and Thathachar 1989:162–163) that, if the learner’s training sample is large enough, eventually he ends up with a weight $q_{t+1}$ which is well approximated by

$$ q_{t+1} = \frac{c_{t}}{c_{t} + d_{t}}. $$

(3)

Assuming $c_{t} \neq 0$ and $d_{t} \neq 0$ without loss of generality, this equation may be reduced to the more useful form

$$ q_{t+1} = \biggl(1 + \frac{d_{t}}{c_{t}} \biggr)^{-1} = \biggl(1 + \rho \frac{1-q_{t}}{q_{t}} \biggr)^{-1}, $$

(4)

where we write ρ = α/β for the ratio of the parsing advantages. Equation (4), then, relates the grammar weights of the (t + 1)th generation to those of the tth generation, thereby defining the inter-generational or diachronic dynamics of a sequence of (reliable) linear reward–penalty learners.⁵

Fig. 3

Venn diagram of the sentences generated by $G_{1}$ (the set $L_{1}\cup L_{X}$) and by $G_{2}$ (the set $L_{2}\cup L_{X}$). Here, $L_{2}$ represents a greater proportion of sentences than $L_{1}$, and so the advantage of $G_{2}$ is greater than that of $G_{1}$

It follows that α<β, or ρ<1, is a sufficient condition for grammar $G_{2}$ to overtake grammar $G_{1}$:

Theorem 1

(The Fundamental Theorem of Language Change; Yang 2000:239)

Assume reliable learners, so that (4) holds. Then $q_{t} \to 1$ as t→∞ if α<β, and $q_{t} \to 0$ as t→∞ if α>β.

In other words, the grammar with the greater parsing advantage will necessarily win out in the long term. The difference equation (4) may in fact be solved for t to yield

$$ q_{t} = \biggl(1 + \rho^{t}\frac{1-q_{0}}{q_{0}} \biggr)^{-1}, $$

(5)

where $q_{0}$ is the weight of $G_{2}$ at the point of actuation of the change (Appendix A.1, Corollary 4): hence as soon as the value of $q_{0}$ is known, the entire change trajectory can be predicted. Furthermore, it is not difficult to show that this solution is equivalent to

$$ q_{t} = \bigl(1 + e^{-s(t-k)} \bigr)^{-1} $$

(6)

with s = −log(ρ) and $k=-\log(\rho)^{-1}\log (q_{0}^{-1} - 1)$. Thus, assuming that learners receive representative samples of their linguistic environments, a diachronic sequence of such learners exhibits logistic evolution. In particular, the slope of the trajectory is directly dependent on the advantage ratio ρ such that the smaller ρ (the more advantageous $G_{2}$ is), the faster the change from $G_{1}$ to $G_{2}$, and vice versa.

This is the gist of the competing grammars model of language change; for more details, see Kroch (1994), Yang (2002), Pintzuk (2003) and especially Heycock and Wallenberg (2013), who apply the model to a concrete case study involving the loss of verb movement in Scandinavian.

2.2 Competing grammars and contextual biases

To account for contextual effects and the CRE, we now assume the existence of K linguistic contexts 1,…,K, with each sentence generated by $G_{1}$ or $G_{2}$ belonging to one and only one of these contexts.⁶ Each context i is equipped with a context weight $\lambda_{i}$ that gives the proportion of sentences that fall in that context (out of all sentences generated by either $G_{1}$ or $G_{2}$); clearly, since we are dealing with proportions, we require $\lambda_{1} + \dots + \lambda_{K} = 1$ (Fig. 4). In addition to these weights, each context is associated with a fixed (constant over time) production bias $b_{i}$ which can be positive, negative or zero. In the first case, the context favours $G_{2}$; in the second, it favours $G_{1}$; and in the third case, the context is neutral with respect to the two grammars.⁷

Fig. 4

Venn diagram of the sentences generated by $G_{1}$ and $G_{2}$, partitioned by four contexts

Now consider a language learner acquiring his grammar weights based on the output of generation t of speakers. With Yang (2000), we assume that the tth generation has internalized grammar weights $p_{t}$ and $q_{t}$. Where our treatment diverges is the effect these weights have on the language acquisition process of the (t + 1)th generation. Rather than assuming that $p_{t}$ and $q_{t}$ feed directly into the acquisition process in the following generation, we assume that speakers of the tth generation may promote or demote the two weights $p_{t}$ and $q_{t}$ in different linguistic contexts in different ways, subject to the context-specific production biases $b_{i}$. It is then on the basis of this usage, modulated by the contextual biases $b_{i}$ and the context weights $\lambda_{i}$, that the next generation of learners must infer their grammar weights.

Letting $q^{(i)}_{t}$ denote the probability with which a speaker of the tth generation uses grammar $G_{2}$ in context i, and similarly for $p^{(i)}_{t}$ and $G_{1}$, a general form of this biasing is

$$ \left\{ \begin{aligned} p^{(i)}_{t} &= p_{t} + F(b_{i}, p_{t}) \\ q^{(i)}_{t} &= q_{t} + G(b_{i}, q_{t}) \end{aligned} \right. $$

(7)

where F and G are some (yet undetermined) functions which modulate the effect of the bias $b_{i}$ on production. These functions must satisfy two requirements:

$$ \left\{ \begin{aligned} p^{(i)}_{t} + q^{(i)}_{t} &= 1 \quad\text{(as $G_{1}$ and $G_{2}$ are the only grammars)} \\ 0 \leq p^{(i)}_{t}, q^{(i)}_{t} &\leq 1 \quad\text{(as the two quantities are probabilities)} \end{aligned} \right. $$

(8)

and the following is a theorem.

Theorem 2

Functions $F = F(b_{i}, p_{t})$ and $G=G(b_{i}, q_{t})$ satisfy the conditions (7) and (8) if, and only if, they satisfy

$$ \left\{ \begin{aligned} F &= -G \\ |F|, |G| &\leq \min\{p_{t}, q_{t}\} \end{aligned} \right. $$

(9)

Proof

Appendix A.2. □

Theorem 2 thus implies that the functions F and G are necessarily the additive inverse of each other, and that their absolute value is necessarily bounded from above by the minimum of $p_{t}$ and $q_{t}$. Technically an infinite number of functions satisfy this pair of conditions, so we need to ask what these functions actually are (Fig. 5). The simplest, most parsimonious choice is to consider the product $p_{t}q_{t}$, which is guaranteed to be bounded from above by both $p_{t}$ and $q_{t}$ whenever $0 \leq p_{t},q_{t} \leq 1$. In other words, we suggest setting

$$ F= -b_{i}p_{t}q_{t} \quad \text{and}\quad G = b_{i}p_{t}q_{t} $$

(10)

with $-1\leq b_{i} \leq 1$. The contextual usage probabilities in (7) then assume the definite forms

$$ \left\{ \begin{aligned} p^{(i)}_{t} &= p_{t} - b_{i}p_{t}q_{t} = p_{t} - b_{i}p_{t}(1-p_{t}) \\ q^{(i)}_{t} &= q_{t} + b_{i}p_{t}q_{t} = q_{t} + b_{i}q_{t}(1-q_{t}) \end{aligned} \right. $$

(11)

where the contextual biases $b_{i}$ range from −1 (maximally $G_{1}$-favouring) through 0 (neutral) to 1 (maximally $G_{2}$-favouring).

Fig. 5

The biasing functions F and G have to satisfy the requirement $|F|,|G|\leq \min\{p_{t},q_{t}\}= \min\{q_{t},1-q_{t}\}$ (see Appendix A.2 for a proof) and thus land in the shaded region of this plot. The parabolic curve shown here gives the most parsimonious such upper bound, the product $p_{t}q_{t} = q_{t}(1 - q_{t})$

This choice for the functions F and G has a number of intuitively satisfying features. For example, (10) implies that if either $p_{t}=1$ or $q_{t}=1$, then F = G = 0 (since in the first case $q_{t}=0$ and in the second case $p_{t}=0$ and consequently $p_{t}q_{t}=0$) and no biasing will apply. Empirically, this means that if a grammar has been acquired categorically, no contextual biases will be able to skew usage in the direction of the other grammar. This is intuitively right: if a grammatical option has been acquired categorically, then by definition the competing option does not exist for the speaker and no grammar-external biasing ought to be able to apply. This behaviour of our biasing mechanism in the limits $q_{t}\to 1$ and $q_{t} \to 0$ is just one manifestation of a more general feature of the model: that while the biases $b_{i}$ themselves are constant and do not change over time, the magnitude of the effect of these biases on usage does depend on the state of the underlying change: the effect is the strongest midway through the change (from Fig. 5, we see that the effect is the strongest when $q_{t}=0.5$) and tails off to zero in the limits $q_{t} \to 1$ (completion) and $q_{t} \to 0$ (actuation). As we will see in Sect. 4, this is what the empirical data also show.⁸

With (11) in place, it is possible to work out the diachronic, inter-generational dynamics of our model (assuming, again, that learners receive large input samples). What generation t outputs in this extended model is not the distribution given in (2), but a combination of grammar advantages (α and β), grammar weights ($p_{t}$ and $q_{t}$), context weights ($\lambda_{i}$) and context biases ($b_{i}$). The penalty probability for grammar $G_{1}$ now becomes

$$ c_{t} = \beta\sum_{i=1}^{K} \lambda_{i} q^{(i)}_{t} = \beta \sum _{i=1}^{K} \lambda_{i} (q_{t} + b_{i}p_{t}q_{t}) = \beta \Biggl(q_{t} + \sum_{i=1}^{K} \lambda_{i} b_{i} p_{t}q_{t} \Biggr) = \beta (q_{t} + Bp_{t}q_{t}), $$

(12)

where the index i runs through the contexts i = 1,…,K and where we write $B = \sum_{i=1}^{K} \lambda_{i} b_{i}$ for convenience.⁹ The quantity B, which may be regarded as the net bias operating on the language acquisition process weighted by the context proportions $\lambda_{i}$, turns out to be a decisive quantity in our model: from (12), we immediately see that if B = 0, the penalty $c_{t}$ reduces to the Yangian penalty $c_{t} = \beta q_{t}$. Our model, then, generalizes Yang’s (2000) model and reduces to the latter in the special case that the contextual biases are ‘in balance’—if either all the biases are zero or if $G_{2}$-favouring (positive) biases cancel out the effect of $G_{1}$-favouring (negative) biases.

Entirely symmetrically, the penalty for grammar $G_{2}$ reads

$$ d_{t} = \alpha \sum_{i=1}^{K} \lambda_{i} p^{(i)}_{t} = \alpha (p_{t} - Bp_{t}q_{t}). $$

(13)

Assuming reliable learners, we may now use these penalty probabilities to write down the inter-generational difference equation that relates $q_{t+1}$ to $q_{t}$ for the extended model: equation (4) becomes

$$ q_{t+1} = \biggl(1 + \frac{d_{t}}{c_{t}} \biggr)^{-1} = \biggl(1 + \frac{\alpha (p_{t} - Bp_{t}q_{t})}{\beta (q_{t} + Bp_{t}q_{t})} \biggr)^{-1}. $$

(14)

Recalling that $p_{t} = 1 - q_{t}$, this may be written as

$$ q_{t+1} = \biggl(1 + \Lambda_{t} \rho \frac{1-q_{t}}{q_{t}} \biggr)^{-1}, $$

(15)

where ρ = α/β as before and

$$ \Lambda_{t} = \frac{1 - Bq_{t}}{1 + B(1-q_{t})}. $$

(16)

2.3 The Constant Rate Effect

To summarize, we propose to augment Yang’s (2000) model of grammar competition with a set of production biases $b_{i}$ which modulate the grammar weights $p_{t}$ and $q_{t}$ in actual linguistic production. This modulation is implemented by a mechanism which, we have shown, has to operate within certain analytical bounds. Within those bounds, we have suggested that the most parsimonious mechanism be adopted, corresponding to our particular choice of the bias-modulating functions F and G, as explained above. The diachronic behaviour of this extended model is characterized by equations (11) and (15): the difference equation (15) gives the evolution of the underlying grammar weight $q_{t}$, whilst equation (11) supplies the context-specific value of this probability, modulated by the contextual production biases. The flowchart in Fig. 6 illustrates the inter-generational dynamics that result from this mechanism, comparing our extension of Yang’s (2000) model to the original.

Fig. 6

Inter-generational change in Yang’s (2000) model (top) and our model (bottom). After parameter setting, the learner ends up with a weight $q_{t}$ for grammar $G_{2}$ (and $p_{t}$ for grammar $G_{1}$). In our model, this weight is then attenuated in production by the context-specific production biases $b_{i}$ so that the actual probability of using $G_{2}$ in the ith context is $q_{t}^{(i)} = q_{i} + b_{i}p_{t}q_{t}$ (see text for details). This biased probability, together with the advantage ratio ρ = α/β and the context weight $\lambda_{i}$, then determines the PLD for the following generation

Before moving on to an empirical evaluation of our proposed model, we first ask whether it produces, in broad qualitative terms, the right kind of behaviour. To this end, Fig. 7 shows the behaviour of our model in two different situations involving three arbitrarily chosen contexts: in a situation in which the contextual biases are in balance and cancel each other out (B = 0; Fig. 7a), and in a situation in which the net effect of biases in favour of the conventional variant $G_{1}$ conspire against the propagation of the innovative variant $G_{2}$ (B<0; Fig. 7b). Impressionistically, our model produces a CRE in both cases: the probability of use of $G_{2}$ increases roughly at the same rate in each context, with a characteristic temporal shift between the propagation curves of the individual contexts. This suggests that our model is able to replicate the central intuition of Kroch (1989) that different reflexes of one underlying change ought to proceed at similar rates, and that the output of our model can, in principle, approximate the empirical situations that have been suggested as CREs in the literature.

Fig. 7

The behaviour of our model with two different sets of production biases, for advantage ratio ρ = 0.5 and initial value $q_{0} = 0.01$ (1% usage of $G_{2}$ at the point of actuation): the evolution of both the underlying probability $q_{t}$ (•) as well as that of the contextual usage probabilities $q^{(1)}_{t}$ (○), $q^{(2)}_{t}$ (×) and $q^{(3)}_{t}$ (□) is shown up to $q_{t} = 1-q_{0} = 0.99$. In each case, the context weights are set at $\lambda_{1} = 0.2$, $\lambda_{2} = 0.4$ and $\lambda_{3} = 0.4$. (a) Here the biases are $b_{1} = 1$, $b_{2} = -1$ and $b_{3} = 0.5$. With these choices, $B=\lambda_{1} b_{1} + \lambda_{2} b_{2} + \lambda_{3} b_{3} = 0$, and consequently the positively-biased contexts (○ and □) cancel out the effect of the negatively-biased context (×), resulting in logistic evolution of the underlying probability $q_{t}$ (•). (b) Here the biases are $b_{1} = 1$, $b_{2}=-1$ and $b_{3}=-0.5$. Now $B = \lambda_{1} b_{1} + \lambda_{2} b_{2} + \lambda_{3} b_{3} = -0.4 < 0$. The two negatively-biased contexts (□ and ×) outweigh the one positively-biased context (○), and as a consequence, the change from $G_{1}$ to $G_{2}$ takes much longer than in (a). The trajectory of $q_{t}$ is also not strictly logistic in this case, as is evident from the fact that it is not symmetric about the midpoint $q_{t}=0.5$: passage from $q_{0} = 0.01$ to $q_{t} = 0.5$ takes longer than passage from $q_{t}=0.5$ to the final value $q_{t}=0.99$

In these two cases, the evolution of the underlying probability $q_{t}$ is different, however, because of the different biasing that applies in each case. In Fig. 7a the contexts are ‘in balance’ (B = 0), which by the preceding analysis implies that the evolution of $q_{t}$ itself is logistic. In Fig. 7b, on the other hand, $G_{1}$-favouring biases outweigh $G_{2}$-favouring biases (B<0), hindering the propagation of $G_{2}$. This is reflected in the fact that the evolution of the underlying $q_{t}$ is slowed down. Even though $G_{2}$ still overtakes $G_{1}$ in the limit, the trajectory of $q_{t}$ is no longer strictly logistic (careful examination shows that it is not symmetric about the midpoint $q_{t}=0.5$, but rather exhibits slower change for $q_{t} < 0.5$ and faster change for $q_{t} > 0.5$). This motivates us to consider extreme model parameter regimes, particularly the subspace where B is negative, in more detail.

In equation (15), the factor $\Lambda_{t}$ depends on $q_{t}$ whenever B ≠ 0. This complicates the analysis of the extended model significantly: while the Yangian equation (4) can be solved for t to yield the logistic function, we are not aware of a closed-form solution to the more complex nonlinear difference equation (15) except in the singular case B = 0, where the equation reduces to (4). This has the undesirable practical consequence that there is no trivial way of fitting our model to data—lacking a closed-form curve for the underlying probability $q_{t}$ from which to derive curves for the contextual reflexes $q^{(i)}_{t}$, there simply are no closed-form contextual curves to fit. The best one can do is to iterate the model for various choices of model parameter values and initial conditions and compare the resulting trajectories against empirical data, an approach which soon becomes computationally prohibitive as the number of logically possible model parameter combinations grows as a superlinear function of the number of model parameters. To tackle this problem, we will in the next section conduct a full analysis of the behaviour of our model in the limit t→∞ and show that, under most empirically meaningful combinations of model parameter values, the underlying trajectory $q_{t}$ is well approximated by a logistic curve. Thus, even though we cannot write down the solution of $q_{t}$ for arbitrary times t, and even though we know that for some parameter values (such as when B<0) the evolution of $q_{t}$ is not logistic, we can use logistic functions to approximate the true value of $q_{t}$. This will form the basis of our curve-fitting procedure in Sect. 4. A reader who is willing to skip the technicalities of the logistic approximation may advance straight to Sect. 4.

3 Dynamics of the extended model

3.1 Advantage versus bias

As we have noted above, the Fundamental Theorem of Yang’s (2000) model is that a more advantageous grammar will necessarily overtake a less advantageous one: if ρ<1 (α<β) and learners are reliable, then $q_{t}\to 1$ as t→∞, and thus grammar $G_{2}$ overtakes $G_{1}$ (Theorem 1). A nontrivial consequence of extending the model with production biases is that this theorem no longer holds: a difference in the proportion of input parsed by the two competing grammars is neither sufficient nor necessary for language change. While this is a minor observation from the point of view of the CRE, which is the main focus of the present paper, the failure of the Fundamental Theorem under suitable combinations of grammar advantages and production biases is an interesting finding from the vantage point of the theory of language change in general, and we will therefore pursue it briefly in this section. The bifurcation scenario here outlined will also play a role in the logistic approximation that we develop in the following subsection for model evaluation purposes.

The production biases $b_{i}$ can be positive, negative or zero. In the first case, the context in question favours $G_{2}$ over $G_{1}$; in the second case, $G_{1}$ is favoured; and in the third case, the context is neutral. The scalar product $B = \sum_{i=1}^{K} \lambda_{i}b_{i}$ of context weights and production biases turns out to play a critical role in determining how, and if, change from $G_{1}$ to $G_{2}$ happens. If there are negatively biased ($G_{2}$-disfavouring) contexts, and if their share of all sentences in the language learner’s PLD is large enough, change from $G_{1}$ to $G_{2}$ can be blocked even if the advantage of $G_{2}$ is greater than the advantage of $G_{1}$. On the other hand, if there are sufficiently strong positively biased ($G_{2}$-favouring) contexts, $G_{2}$ may overtake $G_{1}$ even if the latter’s advantage exceeds that of the former. A critical value $B_{c}$ of the net bias B in fact exists such that change from $G_{1}$ to $G_{2}$ is guaranteed whenever $B > B_{c}$ but is blocked whenever $B \leq B_{c}$:

Theorem 3

(The Extended Fundamental Theorem of Language Change)

Assume reliable learners, so that (15) holds. Let $q_{0}$ be the weight of grammar $G_{2}$ at the point of actuation, let $B=\sum_{i=1}^{K} \lambda_{i}b_{i}$, and let

$$ B_{c} = \frac{\rho - 1}{1 + q_{0}(\rho - 1)}. $$

(17)

Then

• 1. $q_{t} \to 1$ as t→∞, if $B > B_{c}$;

• 2. $q_{t} = q_{0}$ for all t, if $B = B_{c}$;

• 3. $q_{t} \to 0$ as t→∞, if $B < B_{c}$.

In other words, $G_{2}$ overtakes $G_{1}$ if, and only if, $B > B_{c}$.

Proof

Appendix A.3. □

In dynamical-systems terminology, the production bias mechanism induces a bifurcation in the parameter space of the extended model: small tweaks made to either the biases ($b_{i}$) or to the proportion of input falling in each context ($\lambda_{i}$) can alter the trajectory of language change entirely by determining which of the two grammars will win out (Fig. 8). An immediate consequence of Theorem 3 is that if no context is negatively biased, $G_{2}$ will overtake $G_{1}$ whenever ρ<1:

Fig. 8

The outcome of language change for different combinations of advantage ratio ρ and net bias B, for two different initial weights for $G_{2}$: $q_{0} = 0.001$ (left) and $q_{0} = 0.9$ (right). The thick curve corresponds to the subset of this parameter space where $B=B_{c}$, the critical bifurcation value. If $B > B_{c}$, grammar $G_{2}$ overtakes; if $B < B_{c}$, grammar $G_{1}$ prevails; and if $B = B_{c}$, the system falls in an equilibrium where $q_{t} = q_{0}$ for all t (Theorem 3). Yang’s (2000) model corresponds to the dashed line running at B = 0 (no contextual effects, or contexts wholly in balance) and thus predicts that $G_{2}$ wins for any 0<ρ<1 and loses for any ρ>1. Since B has both a lower and an upper limit (−1 ≤ B ≤ 1), the advantage ratio ρ has critical values, dependent on the boundary condition $q_{0}$, such that if ρ lands beyond one of these values, no amount of out-of-balance bias can overthrow the advantage-induced dynamical outcome (Corollary 2). In the figure on the left, for instance, any ratio ρ greater than about 2 guarantees $G_{2}$ to fail. In the figure on the right, any ratio ρ smaller than about 0.5 guarantees $G_{2}$ to succeed, no matter what the combination and magnitude of contextual biases

Corollary 1

If ρ<1 and $b_{i} \geq 0$ for all contexts i, $q_{t}\to 1$ as t→∞.

Proof

Since $B_{c} < 0$ for any choice of $q_{0}$, if ρ<1. □

Even though production biases, then, can induce or block change in parameter regimes where such behaviour is impossible in Yang’s (2000) original model, there are limits to how much of an effect the biases can have over grammar advantages. Briefly put, if $G_{2}$ is much more advantageous than $G_{1}$ (0<ρ≪1), then no amount of negative bias can block change, and, on the other hand, if $G_{1}$ is much more advantageous than $G_{2}$ (ρ≫1), no amount of positive bias can make $G_{2}$ overtake $G_{1}$. How much is much depends on the boundary condition $q_{0}$:

Corollary 2

If $\rho < q_{0}/(1+q_{0})$, then $q_{t} \to 1$ as t→∞, regardless of the value of B. If $\rho > (2-q_{0})/(1-q_{0})$, then $q_{t} \to 0$ as t→∞, regardless of the value of B.

Proof

Clearly −1 ≤ B ≤ 1 since $-1 \leq b_{i} \leq 1$ and $0 \leq \lambda_{i} \leq 1$. If $\rho < q_{0}/(1+q_{0})$, then $B_{c} < -1$. If $\rho > (2-q_{0})/(1-q_{0})$, then $B_{c} > 1$. □

Figure 8 illustrates.

3.2 Logistic approximation

The above results show that the outcome of grammar competition in the presence of context-specific production biases is determined by a complicated interaction between these biases ($b_{i}$), the proportion of input that falls in each context ($\lambda_{i}$) and the ratio of the parsing advantages of the two competing grammars (ρ). This is because in our model the language acquisition mechanism and the production bias mechanism constitute a feedback loop across iterated applications over multiple generations of language learners, the production biases modulating the acquisition of the grammatical weights $p_{t}$ and $q_{t}$. As we noted in Sect. 2.3 (Fig. 7), this feature of the model also implies that when the production biases are particularly strong, they will cause the evolution of the underlying grammar weights to be non-logistic. The feedback loop gives rise to a nonlinear difference equation for which we have no solution in the general case, and the following problem immediately arises: how can the predictions of our model be tested against empirical data if there is no closed-form curve which to fit?

Even though the evolution of $q_{t}$ is, strictly speaking, logistic only when B = 0, eyeballing trajectories such as the one in Fig. 7b suggests that these trajectories are still S-shaped and perhaps well approximated by logistics. To explore this possibility, we performed a sweep across the model parameter space, generating trajectories of $q_{t}$ from the initial condition $q_{0} = 0.01$ (1% usage of $G_{2}$ at the point of actuation) in the regime $B > B_{c}$ (i.e. in the parameter regime where $G_{2}$ is guaranteed to oust $G_{1}$ by Theorem 3), until $q_{t}$ had reached the value $q_{t} = 1-q_{0} = 0.99$. We then proceeded to fit a logistic curve to each of these trajectories in order to investigate how well the trajectory may be approximated by a logistic. Figure 9a gives the errors of these fits, showing that the trajectories are closely approximated by logistics whenever ρ is not too large and B is not too close to the critical bifurcation threshold $B_{c}$.

Fig. 9

(a) Error of fit (sum of squared residuals; nonlinear least squares regression) of a logistic function to trajectories of the underlying probability $q_{t}$ generated by our model for various combinations of advantage ratio ρ and net bias B, for initial condition $q_{0} = 0.01$ (1% usage of $G_{2}$ at the point of actuation). The dashed vertical lines give the critical value $B_{c}$ of the bifurcation parameter for each selection of ρ. We find that trajectories of $q_{t}$ are closely approximated by logistics except in the immediate vicinity of the bifurcation threshold $B_{c}$ at which change from $G_{1}$ to $G_{2}$ is blocked. (b–c) Best-fitting slope (s) and intercept (k) values found by these regressions

Figures 9b–c supply the best slope (s) and intercept (k) coefficients found by these regressions. We find that s is a decreasing function of ρ and an increasing function of B: the more advantageous $G_{2}$ is, and the more $G_{2}$ is favoured by the production biases, the steeper the underlying change, as one would expect. The intercept coefficient k, in turn, is an increasing function of ρ and a decreasing function of B: the less advantage $G_{2}$ has and the more the production biases tend to disfavour $G_{2}$, the more the curve of the underlying change is shifted towards positive time.

4 Evaluation

4.1 The Time Separation Theorem

Under the logistic approximation from Sect. 3, the usage of grammar $G_{2}$ in the contexts i = 1,…,K is described by a set of K equations

$$ \left\{ \textstyle\begin{array}{rcl} q_{t}^{(1)} &=& \tilde{q}_{t} + b_{1}\tilde{q}_{t}(1 - \tilde{q}_{t})\\ &\vdots &\\ q_{t}^{(K)} &=& \tilde{q}_{t} + b_{K}\tilde{q}_{t}(1 - \tilde{q}_{t}) \end{array}\displaystyle \right. $$

(18)

where $\tilde{q}_{t}$ is a logistic function approximating the true underlying probability $q_{t}$. What historical language corpora give us are usage frequencies in various contexts, and we therefore wish to fit curves of the form (18) to such data. The fact that under the logistic approximation all such curves are tied to $\tilde{q}_{t}$, which itself has a closed-form solution, now facilitates this empirical evaluation: even though the individual context curves $q_{t}^{(i)}$ themselves are not logistic (unless $b_{i}=0$), they are easily derived from one that is. In what follows, we will take a look at a number of case studies, fitting context curves with the help of a nonlinear least squares optimization algorithm.

Estimating the goodness of fit of these regressions is one important goal of this exercise. However, our main aim is to solve the non-linking problem identified in Sect. 1.2. Specifically, we wish to demonstrate that our model does not allow arbitrarily large time separations between contexts, operationalized as the difference between the points in time at which different context curves reach their tipping point, or the point in time at which the context frequency of the overtaking grammar equals 0.5 when (18) is generalized for real-valued t. The logistic approximation gives us a straightforward proof of this.

Theorem 4

(The Time Separation Theorem)

For any two contextual reflexes of an underlying change from $G_{1}$ to $G_{2}$ approximated by a logistic $\tilde{q}_{t}$ with slope s, the maximal time separation at tipping points is

$$ \Delta (s) = \frac{2}{|s|}\log \biggl(\frac{1}{\sqrt{2} - 1} \biggr) \approx 1.76 \frac{1}{|s|}. $$

(19)

Proof

Appendix A.4. □

It is to be noted that Δ(s) is inversely proportional to s—the slower the rate of change, the more time separation is allowed between any two contexts and vice versa.

To fit the system (18) to a set of data points, we first define reasonable ranges of variation for the s and k parameters of the logistic $\tilde{q}_{t}$ that we wish to probe. We then loop through the values contained in these ranges, finding the best fitting bias parameters $b_{i}$ for each pair (s,k) using a nonlinear least squares optimization algorithm such as the Gauss–Newton procedure (Bates and Watts 1988), bearing in mind the bounds $-1 \leq b_{i} \leq 1$. Finally, out of all these regressions, we pick the combination of s, k and $b_{i}$ that provides the best fit to the data in question. The whole procedure is detailed in pseudocode in Appendix A.5.¹⁰

We now proceed to an evaluation of the model by comparing its predictions against three historical changes for which a CRE has been reported in the literature: the emergence of periphrastic do in the history of English (Kroch 1989), the earliest stages of the English Jespersen Cycle (Wallage 2013), and, to take a phonological example to illustrate the generality of the procedure, the loss of final fortition in Early New High German (Fruehwald et al. 2009). In Sects. 4.2–4.4 we first briefly summarize the linguistics of each change, reproduce the relevant empirical data, and visualize the fit of our model to the data when the regression is conducted using the procedure outlined above. In Sect. 4.5, we take a more quantitative angle and report the numerical errors of these fits, comparing them to the errors that an application of the standard procedure based on individual logistics (cf. Sect. 1.1) would produce. Finally, in Sect. 4.6, we take a look at a pseudo-CRE—a case where the standard independent logistics operationalization reports a CRE but where this conclusion is patently absurd from other considerations (cf. Sect. 1.2)—in order to investigate whether or not our model, too, is prone to report false positives in such cases.

4.2 Periphrastic do in English

The first case study we will consider is perhaps the best known instance of a CRE: Kroch’s (1989) interpretation of Ellegård’s (1953) data on the rise of periphrastic do in Early Modern English. The variable in question is whether a form of do is used in certain contexts, as in (20a), or not, as in (20b) (examples from Kroch 1989:216).

• (20)

  

In modern standard English, a form of do is required in a number of contexts, including all interrogatives as well as negative declaratives. What Ellegård’s (1953) data show is that, on the surface, the use of do appears to ‘take off’ in the different contexts at different rates: for instance, between around 1500 and 1650, negative questions exhibit a much higher proportion of do than affirmative wh-object questions or negative declaratives, though the latter contexts eventually catch up (Table 1). Kroch (1989) conducted a regression on these contexts and showed that logistic curves fitted to them individually did not differ much in their slope (s) parameters, although they did differ in terms of the intercept (k) parameter. This particular example, while perhaps the most celebrated instance of a CRE, is in fact not the most straightforward instance found in the literature, primarily due to a ‘dip’ in the later portion of the change in some contexts, which makes the progression of do non-monotonic; see Warner (2005) and Ecay (2015) for detailed discussion, concluding that other factors (and possibly another grammar) are at play. Kroch (1989) also identifies the dip and consequently focusses on the first seven data points of Ellegård’s (1953) data only; we follow his practice here.

Table 1 Proportion of do in five different contexts: negative declaratives, negative questions, affirmative transitive questions, affirmative intransitive questions, affirmative wh-object questions. From Kroch (1989:224, Table 3)

When the algorithm from Appendix A.5 is used to fit a model of the form (18) to these data, the picture in Fig. 10 emerges. On visual inspection, the fit is a good one. Crucially, our model is constrained to allow only so much time separation between any two contexts of one change (Theorem 4), illustrated in Fig. 10 as the horizontal bar extending both ways from the tipping point of the curve of the underlying grammar probability. We find that fitting the model to Ellegård’s (1953) data drives two of the context curves (negative questions and affirmative object questions) to the very extremes of the range licensed by the model—in other words, for these contexts, the production biases need to be maximal in order for the model to fit the data. Crucially, however, the data are described well by the regression curves so obtained, an observation which we back up quantitatively in Sect. 4.5.

Fig. 10

Fit of our model to the data on English periphrastic do (curves: model; points: data from Table 1, first seven periods). On visual inspection, the fit to each context is a good one. Theorem 4 implies a maximal time separation, illustrated here as the horizontal bar extending both ways from the tipping point of the theoretical curve for the underlying grammatical change (no production biases). The best-fitting parameters found by the regression are s = 0.031, k = 1547.677, with bias sizes $b_{i}$ as follows: −0.885 for negative declaratives, 1.000 for negative questions, 0.656 for affirmative transitive questions, −0.647 for affirmative intransitive questions, and −1.000 for affirmative wh-object questions. With s = 0.031, the maximal time separation licensed by the model is roughly 56.5 years

4.3 English Jespersen Cycle

Our second case study, also from the history of English, involves the replacement of preverbal ne/ni by postverbal not during the Middle English period. This change involves an intermediate stage in which both ne and not co-occur. The three stages are illustrated in (21a)–(21c) (examples from Wallage 2008:644).

• (21)

  

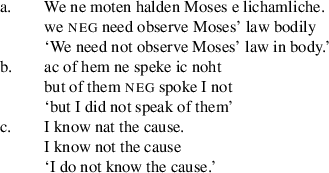
This replacement of negators, a cross-linguistically common diachronic pathway, is referred to as Jespersen’s Cycle; see Wallage (2008) and Ingham (2013) for detailed discussion of the English development. For our purposes, the change that is important is the replacement of Stage 1 of Jespersen’s Cycle—negation by ne alone, as in (21a)—with Stage 2, bipartite negation, as exemplified by (21b). Wallage (2013) shows that Stage 2 is favoured with discourse-old propositions during the middle of the change, but that a CRE obtains (Table 2). Again, on purely visual inspection, our model fits the data well, and the variation observed between discourse-old and discourse-new propositions falls, roughly, within the time bounds prescribed by the Time Separation Theorem (Fig. 11).

Fig. 11

Fit of our model to the data on the first two stages of the English Jespersen Cycle (curves: model; points: data from Table 2). On visual inspection, the fit to each context is a good one, though the poor time resolution of the data is a problem. Theorem 4 implies a maximal time separation, illustrated here as the horizontal bar extending both ways from the tipping point of the theoretical curve for the underlying grammatical change (no production biases). The best-fitting parameters found by the regression are s = −0.016, k = 1203.788, with bias sizes $b_{i}$ as follows: −1.000 for discourse-old propositions and 1.000 for discourse-new propositions. (Note that in a case like this where the slope s is negative, a negative context bias means a preference for the overtaking grammar, whereas a positive bias indicates preference for the receding one.) With s = −0.016, the maximal time separation licensed by the model is roughly 110 years

Table 2 Proportion of Stage 1 negation (preverbal ne) in the English Jespersen Cycle in discourse-old and discourse-new contexts. From Wallage (2013:12, Table 1)

4.4 Loss of final fortition in Early New High German

CREs are not found only with syntactic variables. Fruehwald et al. (2009) reanalyse data from Glaser (1985) on the loss of final fortition in (Bavarian) Early New High German, which is observable in orthographic variation of the period, e.g. tak vs. tag ‘day (acc. sg.)’, rat vs. rad ‘counsel (acc. sg.)’. They argue that the orthographic variation clearly represents a phonological change in progress rather than shifting scribal tradition, and that fortition is the result of a single phonological rule whose loss is visible to different degrees in different contexts during the period of the change: /d/ exhibits fortition the most and /g/ the least, with /b/ showing an intermediate pattern (Table 3). Our model describes the data well, with the observed CRE again falling within the time bounds implied by the model (Fig. 12).

Fig. 12

Fit of our model to the data on loss of final fortition in Early New High German (curves: model; points: data from Table 3). On visual inspection, the fit to each context is a good one. Theorem 4 implies a maximal time separation, illustrated here as the horizontal bar extending both ways from the tipping point of the theoretical curve for the underlying grammatical change (no production biases). The best-fitting parameters found by the regression are s = −0.019, k = 1374.747, with bias sizes $b_{i}$ as follows: 0.353 for /b/, 1.000 for /d/, and −1.000 for /g/. With s = −0.019, the maximal time separation licensed by the model is roughly 93 years

Table 3 Proportion of fortition of the three plosives /b/, /d/ and /g/ in Early New High German. From Fruehwald et al. (2009:4, Table 1)

This example illustrates that even though our model is based on the variational learner in Yang (2000), which is essentially a hypothesis about parameter setting in syntax, the logistic approximation (18) which underlies the curve-fitting procedure can legitimately be used to model CREs in any domain as long as the assumption of an underlying logistic change is justifiable. As Fruehwald et al. (2009:9) point out, “[t]he discovery of the Constant Rate Effect in phonological change is perfectly expected under normal generative theories of phonology when the mechanism of change is grammar or rule competition”—the learning algorithm a language learner uses in this case may (or may not) be different from the one assumed in Yang’s (2000) model, but this notwithstanding, as long as some sort of underlying representation similar to the Yangian weights $p_{t}$ and $q_{t}$ can be assumed to exist, our production bias mechanism may be applied.

4.5 Comparison with standard procedure

Sections 4.2–4.4 have adduced evidence to the effect that the model introduced in this paper can account for the CRE: the model gives fair fits to historical data even though it is constrained by the chronological bounds set by the Time Separation Theorem (Theorem 4). To make this argument more quantitatively, in this section we compare these three fits to the standard operationalization of the CRE: that is, logistic curves agreeing in the s (slope) parameter but differing in their k (intercept) parameters. For each of the three case studies considered in Sects. 4.2–4.4, then, we carry out two fits: one for our model, and another one for a model consisting of a set of logistic curves (one per context) where the s parameter is not allowed to vary between contexts but where such variation is allowed for the k parameter.

We quantify the goodness of fit of these regressions in the usual way, by the normalized sum of squared residuals: in other words, for each context of a given change, for each time period, we calculate the displacement between the empirically attested frequency and the value predicted by the model, square this displacement, sum over all time periods and over all contexts, and divide by the number of data points. Thus, the better the fit, the closer the sum of squared residuals is to zero. Some deviance from zero is always to be expected because of the noisy nature of historical language data. However, this measure is still able to capture the difference between models which are good fits, but subject to noise, from models which are simply bad fits to the data in question.

Figure 13 shows a comparison of the goodness of fit of the two models for each of the three case studies, operationalized using the sum of squared residuals. The crucial finding is that our model, which places more constraints on the shape and placement of the regression curves, fares no worse than the standard procedure in two out of three cases: in other words, a more constrained, theoretically motivated model which generates empirical predictions (in the form of the Time Separation Theorem) performs no worse than a less constrained, theoretically unmotivated model. The exception to this are the data on the English Jespersen Cycle, where the less constrained standard formulation reports a very low error. This appears to be a result of the very small number of data points—just three time periods and two contexts—for this particular case study. Low data resolution necessarily gives a disproportionate advantage to the less constrained model over any model that incorporates more assumptions.

Fig. 13

Error (sum of squared residuals normalized by number of data points) of the fit of our model (grey) and the standard procedure (black) for the three changes examined in Sects. 4.2–4.4: periphrastic do in Early Modern English, Jespersen Cycle in Middle English, and loss of final fortition in Early New High German. Generally speaking, the more constrained model defined in this paper does not fare worse than the less constrained, theoretically unmotivated standard operationalization. We suspect that the exceptionally good fit of the standard operationalization for the Jespersen Cycle is accounted for by sparsity of data (6 data points only), which means that any model that is little constrained will be favoured disproportionately

4.6 A pseudo-CRE

Above, we have shown that the proposed model can account for the CRE, in the sense that it gives good fits to three historical changes—fits which are, in two of these cases, no worse than fits conducted using the standard operationalization of CREs. It remains to be shown that introducing this more constrained model can actually solve some of the underspecification issues the standard operationalization suffers from. As discussed in Sect. 1.2, the method of ‘same slopes, different intercepts’ is susceptible to false positives: the fact that a number of logistics agree in their s or slope parameters is insufficient evidence that a single underlying change is at hand (see Corley 2014; Wallenberg 2016; Willis 2017 for examples where the ‘contexts’ cannot possibly be assumed to be evidence of underlying grammatical unity).

Here, we construct a pseudo-CRE by combining the two changes investigated in Sections 4.3 and 4.4: the early stages of the English Jespersen Cycle and loss of fortition in Early New High German. As it turns out, these two changes happen to propagate at very similar paces by accident (Fig. 14). The standard operationalization of CREs is, then, expected to report a CRE between changes to English sentential negation and Bavarian phonology, a conclusion which is clearly absurd.

Fig. 14

An ‘Anglo-Bavarian pseudo-CRE’ that attempts to combine Jespersen’s Cycle in Middle English with loss of final fortition in Early New High German: data from Tables 2 and 3. The different contexts exhibit similar rates of change across the two historical changes by accident: the slope of the underlying change is −0.016 for the English Jespersen Cycle and −0.019 for Early New High German fortition (see captions to Figs. 11 and 12). This means that the standard ‘same slope, different intercepts’ procedure for detecting CREs in historical data is liable to produce a false positive in this case. Our model, which implies an upper bound on the time separation possible between any two contexts of one underlying change (Theorem 4), can help to diagnose a ‘change’ such as this as a pseudo-change

The fact that the two changes are separated in time, however, means that the more constrained model introduced in this paper can correctly diagnose the pseudo-CRE. Figure 15 gives the residual errors of both the present model and the standard one for this pseudo-CRE, along with the errors for the actual CREs investigated above. The pattern that emerges is striking: for each of the actual CREs, our model reports an error on the order of 0.005, whereas for the Anglo-Bavarian pseudo-CRE the model generates an error that surpasses 0.03. The standard operationalization, by contrast, reports similar errors for all changes, failing to distinguish between the pseudo-CRE and the actual CREs.

Fig. 15

Error (sum of squared residuals normalized by number of data points) of the fit of our model (grey) and the standard procedure (black) for the three changes examined in Sects. 4.2–4.4, plus the pseudo-CRE of Fig. 14. Our model correctly distinguishes the pseudo-CRE from the actual CREs

The pseudo-CRE thus sheds light on the manner in which our model constrains variation in the time dimension—a constraint that is not built into the model as a premise but that follows from first principles in the form of the Time Separation Theorem. Ultimately, the amount of time separation allowed between any two contextual reflexes of a single underlying change depends on s, the slope of the underlying logistic $\tilde{q}_{t}$. To obtain a more intuitive interpretation of the relationship between contextual time separations and the rate of the underlying change, it is useful to convert the slope parameter into a quantity that measures the time the change needs to go from actuation to completion, using the time-to-completion calculations proposed by Ingason et al. (2013:96–97). Namely, it can be shown that for slope s,

$$ T_{\tilde{q}_{0}}(s) = \frac{2}{|s|}\log \biggl( \frac{1-\tilde{q}_{0}}{\tilde{q}_{0}} \biggr) $$

(22)

gives the time it takes for a change to proceed from initial frequency $\tilde{q}_{0}$ to final frequency $1-\tilde{q}_{0}$, for any (small) $\tilde{q}_{0}$ with $0< \tilde{q}_{0} \leq 0.5$. Choosing $\tilde{q}_{0} = 0.01$, a reasonable choice corresponding to 1% usage of the new variant at the point of actuation, this ‘inverse slope’ then gives a time-to-completion of

$$ T_{0.01}(s) = \frac{2}{|s|}\log \biggl(\frac{0.99}{0.01} \biggr) = \frac{2}{|s|}\log(99) \approx 9.2 \frac{1}{|s|} $$

(23)

time units (e.g. years) for any slope s. Theorem 4, on the other hand, implies a maximal time separation of

$$ \Delta (s) = \frac{2}{|s|}\log \biggl(\frac{1}{\sqrt{2} - 1} \biggr) \approx 1.8 \frac{1}{|s|} $$

(24)

units between any two contexts of a change proceeding at rate s. Since 1.8/9.2 ≈ 0.2, this means that the maximal time separation between any two contexts of a single underlying change is roughly a fifth of the time it takes for the change to go to completion in any context individually.

This fact can be used as a heuristic to evaluate purported CREs. For the Anglo-Bavarian pseudo-CRE, for instance, the time-to-completion for $\tilde{q}_{0} =0.01$ is

$$ T_{0.01}(-0.0175) = \frac{2}{0.0175}\log(99) \approx 525 $$

(25)

years when calculated for slope s = −0.0175, which is the arithmetic mean of the slopes found by our regressions for the two changes previously (see captions to Figs. 11 and 12). This implies that the time separation between any two contexts should be no more than 0.2⋅525 = 105 years. On visual inspection, however, the empirical time separation between the discourse-old and /d/ ‘contexts’ must be at least 300 years (Fig. 14). This, essentially, is why the model is able to diagnose the pseudo-CRE.

5 Discussion

In this paper, we have augmented Yang’s (2000, 2002) variational learner with production biases that vary by context—the first time, to our knowledge, that this has been done.¹¹ We have used this model to make precise the important intuition of Kroch (1989) that variation between contexts in the increasing use of a new variant may, under certain circumstances, be due to the interaction of a single underlying change with fixed contextual biases. Two important issues remain to be discussed: the diachronic implications of the interaction between language acquisition and production biases, and the nature of the production biases themselves.

5.1 Which grammar wins?

Yang’s (2000) Fundamental Theorem of Language Change, given earlier as Theorem 1, can be paraphrased as follows: when grammars compete, the one with the greater parsing advantage will win. In Sect. 3 we have shown that this result does not hold in our model. Instead, bias and advantage together determine which grammar will triumph: the precise way in which this works is given in our Extended Fundamental Theorem (Theorem 3).

In one sense this result is unsurprising: one of the great virtues of Yang’s (2000, 2002) model of the learner and of diachronic change is its simplicity, and our model introduces additional complexity. It is therefore not a particular surprise that our more complex model does not yield the same intuitive generalization. On the other hand, it is not a necessary consequence of this complication that the Fundamental Theorem fails to hold. As Fig. 8 shows, if we add to our model the stipulation that contextual weights must always be precisely in balance (B = 0), then Yang’s Fundamental Theorem does hold. Such a stipulation would be wholly unmotivated, as far as we are aware, and represents a more complex model than ours.

Moreover, we have not, of course, shown that the Fundamental Theorem of Language Change is false—merely that it is false under the assumptions we make. Whether or not it is false, empirically speaking, depends on how well our model, and Yang’s (2000, 2002) model, correspond to reality: specifically, whether a model that incorporates the effect of contextual biases as ours does is more realistic than one that does not, and more realistic than one that constrains the net bias. We think that is right, but it is likely that a full consideration of the facts of real-life acquisition and change will require a model that is substantially more complex than any that has been proposed thus far. One feature of Yang’s model, with or without our extension, is that it is completely impossible for a grammar $G_{2}$ to overtake and defeat another grammar $G_{1}$ if the weak generative capacity of $G_{2}$ is a proper subset of that of $G_{1}$; yet a preference for exactly this kind of subset is often invoked in the context of acquisition in the form of the Subset Principle (Berwick 1985; Manzini and Wexler 1987), and, in the domain of phonology at least, retreat to the subset is a frequently-attested diachronic pathway, since unconditioned mergers are well-attested and have precisely the effect of reducing the number of forms generated by the grammar (see e.g. Labov 1994:551). Future work will need to address these questions of realism, as well as pursuing further analytical consequences of simpler (and thus more tractable) models like this one.

5.2 The nature of production biases

Up to now we have remained mute with respect to the ontology of production biases, beyond stating that they are biases that affect production. In principle, such biases could assume a number of forms. In a word order change such as OV to VO, for instance, one possibility for interpreting the fixed biases we have proposed is as a reflection of performance pressures in the sense of Hawkins (1994, 2004). Hawkins’s (2004:38) principle of Minimize Domains states that “[t]he human processor prefers to minimise the connected sequences of linguistic forms and their conventionally associated syntactic and semantic properties in which relations of combination and/or dependency are processed.” This general principle is made concrete using a metric of Early Immediate Constituents (EIC), which serves to favour syntactic structures with a uniform directionality of branching. Importantly, EIC does not penalize right-branching (e.g. VO) or left-branching (e.g. OV) grammars directly, instead disfavouring individual structures with a disharmonic directionality of branching, for instance when a head-final VP is embedded under a head-initial TP. This is equivalent to a context-specific production bias in our sense. Hawkins conceptualizes Minimize Domains and EIC as principles of parsing rather than of production, but notes that there is evidence that EIC might be involved in production too (Hawkins 2004:106), and states that “if EIC can be systematically generalized from a model of comprehension to a model of production […] then so much the better” (Hawkins 1994:427). Hawkins’s principles have also been reformulated as principles of derivational/computational complexity by Mobbs (2008) and Walkden (2009).

In phonological change, meanwhile, the biases can be interpreted as well established articulatory phonetic effects. Final fortition, for example, is known to be more likely to apply to velar consonants than to coronal consonants and more likely to apply to coronal consonants than labial consonants (Ohala 1983), and this order of preference seems to be observed diachronically as final fortition emerged in the history of Frisian (Tiersma 1985).¹² These two phonological and syntactic examples are intended to give a flavour of how contextual production biases can be interpreted, not to exhaust the range of possibilities. For other changes, other biases might be necessary: for instance, in Wallage’s (2013) data, discourse-old propositions favour Stage 2 of the Jespersen Cycle during the change, and the biases here could plausibly reflect Gricean maxims of cooperative communication.

The above-mentioned biases—constraints on syntactic processing, articulatory pressures, pragmatic principles—are plausibly innate in the sense that they are shared by all speakers across all languages and are not subject to change. This is why in our model definition we maintained that the biases $b_{i}$ be diachronically constant. Note that the logic here is not just that constant biases imply Constant Rate Effects—we are actually defending the stronger claim that Constant Rate Effects occur if, and only if, diachronically constant biases impinge on an underlying change. Time-dependent biases, or random biases, would result in change processes in which the trajectories of different linguistic contexts are not parallel to each other—something we might refer to as an ‘Inconstant Rate Effect.’ Having said that, it is not inconceivable that some non-innate biases are constant on sufficiently long timescales so that they may give rise to Constant Rate Effects: this will be the case when the underlying change itself is fast enough to be carried to completion within the timeframe in which the biases stay fixed. This could be true of certain sociolinguistic biases, and here the biasing mechanism of our model is in agreement with sociolinguistic work (e.g. Labov 2001:ch. 9) which has found some types of sociolinguistic bias modulation to be strongest midway through the change, just as in our model (cf. Fig. 5).¹³

6 Conclusion

Building on earlier work that derives logistic evolution as a population-level property of language change (Niyogi and Berwick 1997; Yang 2000, 2002), we have provided a mechanism for the Constant Rate Effect proposed by Kroch (1989). We have done this by enriching Yang’s (2000, 2002) model of acquisition and change with a contextual bias mechanism that links different context curves to a single underlying change. The work also provides a method of testing for CREs that is demonstrably superior to the traditional method of ‘same slope, different intercepts,’ since it is a consequence of the model that there is a fixed upper bound on the time separation of contextual curves. We have shown that this enables us to distinguish certain types of pseudo-CREs from instances in which a single underlying grammatical change is actually plausible. We have also shown that advantage, in the Yangian sense, is not the only factor at play in determining the ultimate outcome of a situation of grammatical competition, if the basic assumptions of our model hold true.

The upshot of all this is that it is now possible to test whether divergent usage frequencies in corpora across different contexts during the course of a change in fact mask a deeper underlying grammatical homogeneity, and to do so in a more restricted and principled way than has been possible to date. Crucially, the method we propose is not only methodologically superior to the standard operationalization of CRE testing: our model in fact derives the possibility of CREs, and sets tight bounds on the kind of empirically observed situation that can be said to constitute a CRE.

Appendix:  Derivations

1.1 A.1 Evolution of $q_{t}$

Theorem 5

Let $\Lambda_{0} = 1$ and

$$ q_{t+1} = \biggl(1 + \Lambda_{t}\rho \frac{1-q_{t}}{q_{t}} \biggr)^{-1}. $$

(A.1)

Then, for all t,

$$ q_{t} = \frac{q_{0}}{q_{0} + \mathcal{L}_{t}\rho^{t}(1-q_{0})}, $$

(A.2)

where $\mathcal{L}_{t} = \prod_{\tau=0}^{t-1} \Lambda_{\tau}$ for t ≥ 1 and $\mathcal{L}_{0} = 1$.

Proof

Induction. For t = 0,

$$ q_{0} = \frac{q_{0}}{q_{0} + \mathcal{L}_{0}\rho^{0}(1-q_{0})} = \frac{q_{0}}{q_{0} + 1 - q_{0}} = q_{0}. $$

(A.3)

Now assume that the claim holds for t. Then

$$ \begin{aligned} q_{t+1} &= \biggl(1 + \Lambda_{t}\rho \frac{1-q_{t}}{q_{t}} \biggr)^{-1} \\ &= \frac{q_{t}}{q_{t} + \Lambda_{t}\rho(1-q_{t})} \\ &= \frac{\frac{q_{0}}{q_{0} + \mathcal{L}_{t}\rho^{t}(1-q_{0})}}{\frac{q_{0}}{q_{0} + \mathcal{L}_{t}\rho^{t}(1-q_{0})} + \Lambda_{t}\rho (1 - \frac{q_{0}}{q_{0} + \mathcal{L}_{t}\rho^{t}(1-q_{0})} )} \\ &= \frac{q_{0}}{q_{0} + \Lambda_{t}\rho(q_{0} + \mathcal{L}_{t}\rho^{t}(1-q_{0}) - q_{0})} \\ &= \frac{q_{0}}{q_{0} + \Lambda_{t}\mathcal{L}_{t}\rho\rho^{t}(1-q_{0})} \\ &= \frac{q_{0}}{q_{0} + \mathcal{L}_{t+1}\rho^{t+1}(1-q_{0})} \end{aligned} $$

(A.4)

as desired. □

Corollary 3

Let B = 0. Then the evolution of $q_{t}$ is logistic.

Proof

Let B = 0. Then from equation (16) $\Lambda_{t} = 1$ for all t, so that

$$ q_{t+1} = \biggl(1 + \rho\frac{1-q_{t}}{q_{t}} \biggr)^{-1}. $$

(A.5)

Theorem 5 now implies

$$ q_{t} = \frac{q_{0}}{q_{0} + \rho^{t}(1-q_{0})}. $$

(A.6)

Now assume $q_{t}\neq 0$ and divide both the numerator and the denominator by $q_{0}$:

$$ \begin{aligned} q_{t} &= \biggl(1 + \rho^{t} \frac{1-q_{0}}{q_{0}} \biggr)^{-1} \\ &= \biggl(1 + \exp \biggl(\log \biggl(\rho^{t}\frac{1-q_{0}}{q_{0}} \biggr) \biggr) \biggr)^{-1} \\ &= \biggl(1 + \exp \biggl(\log \bigl(\rho^{t} \bigr) + \log \biggl( \frac{1-q_{0}}{q_{0}} \biggr) \biggr) \biggr)^{-1} \\ &= \biggl(1 + \exp \biggl(t\log(\rho) + \log \biggl(\frac{1-q_{0}}{q_{0}} \biggr) \biggr) \biggr)^{-1} \\ &= \biggl(1 + \exp \biggl(\log(\rho) \biggl(t + \frac{1}{\log(\rho)}\log \biggl( \frac{1-q_{0}}{q_{0}} \biggr) \biggr) \biggr) \biggr)^{-1}. \end{aligned} $$

(A.7)

Hence, $q_{t}$ is logistic with s = −log(ρ) and $k = -\frac{1}{\log(\rho)}\log (\frac{1-q_{0}}{q_{0}} )$. □

Corollary 4

In Yang’s (2000) model, the weight $q_{t}$ evolves as

$$ q_{t} = \biggl(1 + \rho^{t}\frac{1-q_{0}}{q_{0}} \biggr)^{-1}, $$

(A.8)

which is a logistic function of t.

Proof

In this model, $q_{t}$ obeys (A.1) with $\Lambda_{t} = 1$ for all t. From Theorem 5,

$$ q_{t} = \frac{q_{0}}{q_{0} + \rho^{t}(1-q_{0})}. $$

(A.9)

Assuming, without loss of generality, that $q_{0} \neq 0$, we derive

$$ q_{t} = \biggl(1 + \rho^{t}\frac{1-q_{0}}{q_{0}} \biggr)^{-1}. $$

(A.10)

This is a logistic function by Corollary 3. □

1.2 A.2 The bias-modulating functions F and G

Theorem 6

Let

$$ \left\{ \begin{aligned} p^{(i)}_{t} &= p_{t} + F(b_{i}, p_{t}) \\ q^{(i)}_{t} &= q_{t} + G(b_{i}, q_{t}) \end{aligned} \right.. $$

(A.11)

Then

$$ \left \{ \begin{aligned} p^{(i)}_{t} + q^{(i)}_{t} &= 1 \\ 0 \leq p^{(i)}_{t}, q^{(i)}_{t} &\leq 1 \end{aligned} \right. $$

(A.12)

if and only if

$$ \left\{ \begin{aligned} F &= -G \\ |F|, |G| &\leq \min\{p_{t}, q_{t}\} \end{aligned} \right.. $$

(A.13)

Proof

Writing $F = F(b_{i},p_{t})$, $G=G(b_{i},q_{t})$, $p=p_{t}$ and $q=q_{t}$, the first requirement in (A.12) implies that

$$ F = -G, $$

(A.14)

since

$$ p + F + q + G = 1\quad \text{only if}\quad p + F + 1 - p + G = 1\quad \text{only if}\quad F+G=0. $$

(A.15)

The second requirement in (A.12), on the other hand, implies F ≤ q and −F ≤ p, since

$$ p + F \leq 1\quad\text{only if}\quad F \leq 1 - p = q $$

(A.16)

and

$$ 0 \leq p + F\quad\text{only if}\quad -F \leq p; $$

(A.17)

hence

$$ |F| \leq \min\{p, q\}, $$

(A.18)

and an exactly symmetric argument shows that

$$ |G| \leq \min\{p, q\}. $$

(A.19)

Thus

$$ \left\{ \begin{aligned} F &= -G \\ |F|, |G| &\leq \min\{p, q\} \end{aligned} \right.. $$

(A.20)

On the other hand, if (A.20) holds, then

$$ p_{t}^{(t)} + q_{t}^{(i)} = p + F + q + G = p + F + q - F = p + q = 1, $$

(A.21)

and

$$ |F| \leq \min\{p,q\} \quad\text{only if}\quad -F \leq p \quad \text{only if}\quad 0 \leq p + F = p_{t}^{(i)}. $$

(A.22)

Similarly,

$$ |F| \leq \min\{p,q\} \quad\text{only if}\quad F \leq q \quad \text{only if}\quad F \leq 1-p \quad\text{only if}\quad p_{t}^{(i)} \leq 1, $$

(A.23)

and an analogous argument shows that $0 \leq q_{t}^{(i)} \leq 1$. □

1.3 A.3 Proof of the Extended Fundamental Theorem

Let

$$ B_{c}(\rho, q_{t}) = \frac{\rho - 1}{1 + q_{t}(\rho - 1)}. $$

(A.24)

To prove Theorem 3, we make use of the following auxiliary result:

Theorem 7

For all t:

• (1) $q_{t+1} > q_{t}$ if $B > B_{c}(\rho, q_{t})$;

• (2) $q_{t+1} = q_{t}$ if $B = B_{c}(\rho, q_{t})$;

• (3) $q_{t+1} < q_{t}$ if $B < B_{c}(\rho, q_{t})$.

Proof

From (14) and (16),

$$ q_{t+1} = \frac{1}{1 + \Lambda_{t}\rho\frac{1-q_{t}}{q_{t}}} $$

(A.25)

with

$$ \Lambda_{t} = \frac{1 - q_{t}B}{1 + (1-q_{t})B}. $$

(A.26)

To prove the first claim, we examine the difference $q_{t+1} - q_{t}$. Now $q_{t+1} - q_{t} > 0$ if and only if

$$ \begin{aligned} \frac{1 - q_{t} - \Lambda_{t}\rho(1-q_{t})}{1 + \Lambda_{t}\rho\frac{1-q_{t}}{q_{t}}} > 0 & \quad \quad \text{iff}\\ 1 - q_{t} - \Lambda_{t}\rho(1-q_{t}) > 0 & \quad \quad \text{iff}\\ \Lambda_{t}\rho(1-q_{t}) < 1 - q_{t} & \quad \quad \text{iff}\\ \Lambda_{t} < \frac{1}{\rho} & \quad \quad \text{iff}\\ \frac{1 - q_{t}B}{1 + (1-q_{t})B} < \frac{1}{\rho}. & \end{aligned} $$

(A.27)

Now, −1 ≤ B ≤ 1, so always $1 - q_{t}B > 0$ and $1 + (1-q_{t})B \geq q_{t} > 0$. Hence

$$ \begin{aligned} \frac{1 - q_{t}B}{1 + (1-q_{t})B} < \frac{1}{\rho} & \quad \quad \text{iff}\\ \rho(1 - q_{t}B) < 1 + (1-q_{t})B & \quad \quad \text{iff}\\ \rho - \rho q_{t}B < 1 + (1-q_{t})B & \quad \quad \text{iff}\\ B(1 - q_{t} + \rho q_{t}) > \rho - 1 & \quad \quad \text{iff}\\ B\bigl(1 + q_{t}(\rho - 1)\bigr) > \rho - 1 & \quad \quad \text{iff}\\ B > \frac{\rho - 1}{1 + q_{t}(\rho - 1)} & \end{aligned} $$

(A.28)

as desired. Claims 2 and 3 are handled similarly. □

Corollary 5

For all t:

• (1) $q_{t+1} > q_{t}$ if $B > B_{c}(\rho, q_{0})$;

• (2) $q_{t+1} = q_{t}$ if $B = B_{c}(\rho, q_{0})$;

• (3) $q_{t+1} < q_{t}$ if $B < B_{c}(\rho, q_{0})$.

Proof

First, we note that $B_{c}(\rho, q_{t})$ is a decreasing function of $q_{t}$: if q<Q, then $B_{c}(\rho, q) \geq B_{c}(\rho, Q)$.

Now let $B > B_{c}(\rho, q_{0})$. Then by Theorem 7 $q_{1} > q_{0}$. Since $B_{c}$ is decreasing, $B_{c}(\rho, q_{1}) \leq B_{c}(\rho, q_{0}) < B$. Hence $q_{2} > q_{1}$ by Theorem 7. By full induction, $q_{t+1} > q_{t}$ for all t.

Let $B = B_{c}(\rho, q_{0})$. Then by Theorem 7 $q_{1} = q_{0}$. Then $B_{c}(\rho, q_{1}) = B_{c}(\rho, q_{0}) = B$, so that $q_{2} = q_{1}$ by Theorem 7. By full induction, $q_{t+1} = q_{t}$ for all t.

Finally, let $B < B_{c}(\rho, q_{0})$. Then by Theorem 7 $q_{1} < q_{0}$. Since $B_{c}$ is decreasing, $B_{c}(\rho, q_{1}) \geq B_{c}(\rho, q_{0}) > B$, so that $q_{2} < q_{1}$ by Theorem 7. By full induction, $q_{t+1} < q_{t}$ for all t. □

Theorem 3 now follows from Corollary 5: since $q_{t}$ is bounded between 0 and 1 and $q_{0}$ may be chosen arbitrarily close to 1 or 0, $q_{t} \to 1$ if $B > B_{c}(\rho, q_{0})$ and $q_{t} \to 0$ if $B < B_{c}(\rho, q_{0})$ in the limit t→∞.

1.4 A.4 Proof of the Time Separation Theorem

We shall now prove Theorem 4, reproduced here as Theorem 8:

Theorem 8

For any two contextual reflexes of an underlying change from $G_{1}$ to $G_{2}$ approximated by a logistic $\tilde{q}_{t}$ with slope s, the maximal time separation at tipping points is

$$ \Delta (s) = \frac{2}{|s|}\log \biggl(\frac{1}{\sqrt{2} - 1} \biggr). $$

(A.29)

Proof

Assume two contexts 1 and 2. The maximal separation will of course be attained with maximal biases $b_{1} = 1$ and $b_{2} = -1$ (or vice versa). Assume this. Then $q^{(2)}_{t} = \tilde{q}_{t} - \tilde{q}_{t}(1-\tilde{q}_{t}) = \tilde{q}_{t}^{2}$, and so $q^{(2)}_{t} = 1/2$ when $\tilde{q}_{t} = 1/\sqrt{2}$. On the other hand, $\tilde{q}_{t}$ is given by the logistic

$$ \tilde{q}_{t} = \frac{1}{1 + e^{-st}}, $$

(A.30)

where we assume k = 0 because translation along the time axis obviously makes no difference to the argument here. A little algebra now shows that $\tilde{q}_{t} = 1/\sqrt{2}$ if and only if $t = -\frac{1}{s}\log(\sqrt{2}-1)$. Thus, $q_{t}^{(2)}$ attains its tipping point at time $t_{2}^{*} =-\frac{1}{s}\log(\sqrt{2}-1)$. Since the logistic $\tilde{q}_{t}$ itself attains its tipping point at t = 0 and since $b_{1} = -b_{2}$, symmetry implies that $q_{t}^{(1)}$ attains its tipping point at $t_{1}^{*} = 0 - t_{2}^{*} = \frac{1}{s}\log(\sqrt{2}-1)$. Hence

$$\begin{aligned} \Delta (s) &= |t_{1}^{*} - t_{2}^{*}| = |2t_{1}^{*}| = \frac{2}{|s|}|\log(\sqrt{2} - 1)| \\ &= -\frac{2}{|s|}\log(\sqrt{2} - 1) = \frac{2}{|s|}\log \biggl( \frac{1}{\sqrt{2} - 1} \biggr) \end{aligned}$$

(A.31)

as wished. □

1.5 A.5 Curve-fitting algorithm for the extended model

This appendix provides the curve-fitting algorithm used for model evaluation in Sect. 4, in pseudocode. We assume the existence of three subroutines: Regress, Param and Error. The first of these can be any optimization algorithm that performs nonlinear regression on the ith context for given s and k, fitting a curve of the form (18) subject to the lower and upper bounds $-1 \leq b_{i} \leq 1$. The second routine is assumed to return the bias size $b_{i}$ found by this regression, and the third to give the error (in terms of the normalized sum of squared residuals) of the fit.