Abstract
A cellular automata model has been developed to study the sintering behavior of ceramic particles. In this model, the only physical rule that drives the evolution of the system is to reduce the energy at the interface between the mass cells and the void cells. The meaning of several computational parameters, such as particle size or computational temperature, were investigated. Experiments of partial sintering of spherical particles of silica were performed and it was verified that this model successfully mimics the neck formation. Moreover, other experimental evidences of the stages of the densification, such as the formation of the intermediate vermicular microstructure or the dependence of porosity with temperature, were also qualitatively simulated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ceramic materials have been the subject of considerable scientific study for centuries due to their exceptional combination of physical, mechanical, and chemical properties. Nowadays, ceramics, or ceramic matrix composites, are used in a variety of everyday technologies. Some of the most studied ceramic materials are silica, \(SiO_{2}\), and alumina, \(Al_{2}O_{3}\), which are currently used in a wide range of applications, including mechanical, high-temperature, and biomaterials (Kingery 1976; Gocha et al. 2016; Gonzalez-Sanchez et al. 2022). The fabrication procedures of ceramics require a high-temperature treatment for the sintering process (also known as consolidation or densification) of the precursor compacted powders to obtain a fully dense bulk material. Many different techniques have been thought for the sintering of ceramics, such as pressureless sintering, hot isostatic pressure sintering, spark plasma sintering (SPS), ultra-fast high temperature sintering (UHS), or reactive sintering (Orrù et al. 2009; Wang 2020; Rivero-Antúnez et al. 2021; Morales-Florez and Domínguez-Rodríguez 2022). Usually, the objective of the improvements is to get the fully dense material employing the least amount of energy and time. Therefore, the fundamentals and physical features of this essential step are still of significant scientific and technological interest in order to achieve more efficient sintering protocols.
Sintering is a process that results in the material being denser by reducing porosity through viscous flow and diffusion (Brinker and Scherrer 1990). Additional steps, such as surface dehydroxylation, grain boundary creation, crystallization, or phase transitions, may also appear. As a general rule, sintering is driven by the tendency of the system to reduce its energy by decreasing the interface between solid particles and gas (or vacuum). Hence, viscous flow occurs, promoted by the gained energy through interface surface reduction. The dependence of the viscosity \(\eta \) with temperature obeys an Arrhenius-type relationship:
where \(T_{th}\) is a threshold temperature, k is the Boltzman constant, \(\eta _0\) is the nominal viscosity, and Q the characteristic energy of the process. In the case of crystalline materials, the formation of the grain boundaries and external interface solid-gas are additional mechanisms that take up time and energy during densification. The relationship between each process with time and temperature, the temperatures at which each process begins, and the impact of the microstructure and chemical configuration of the precursor powders are still being researched. Thus, the sintering of powders is a complicated phenomenon involving numerous concurrent and conflicting physical processes that control the microstructure of the ceramics, the size of the crystals and grains, the disappearance of the porosity, and, consequently, the physical properties of the final material.
From a technological point of view, the success of the sintering techniques is discussed based on the relative density (or final residual porosity) after sintering. This is usually assessed in terms of the ratio of the actual sample density with respect to the theoretical bulk density of the material, e.g., 3.98 g/cm\(^3\) for alumina. In all cases, a direct relation between decreasing porosity with time and temperature has been confirmed (Kingery 1976; Brinker and Scherrer 1990; Jagota and Raj 1992; Tan et al. 2022). Numerous investigations on the sintering process can be found in the literature. Mainly on the development of the microstructure of the precursor powders and on the reduction of porosity during the consolidation process. Several stages have been observed along the gradual densification, such as neck formation, vermicular microstructure formation, and final removing of remaining porosity for achieving total densification. For example, vermicular structures are created in heated boehmite (AlOOH) precursor powders (Rivero-Antúnez et al. 2022), and they were investigated by electron microscopy revealing the peculiar structural patterns that emerge during densification (Dutta et al. 2011).
There are two reasons for using simulation methods in the study of materials. One is the enhancement of the material’s qualities for industrial use, and the other is the theoretical interest in understanding the underlying physical processes. Monte Carlo simulation techniques have historically been taken into consideration, but their sequential update of randomly chosen points may not be able to capture the simultaneous evolution of grains and the realistic representation of physical processes. Besides, it is also known that it is very inefficient when applied to large datasets (Maazi and Boulechfar 2019). Instead, the simultaneous updating of every single cell in the lattice of the discretized system in Cellular Automata (CA) models seems to more accurately reflect the underlying physical phenomena throughout natural processes. Models built utilizing CA have recently been used in many studies in the field (He et al. 2006; Wang et al. 2021; Li et al. 2019; Raabe 2002; Contieri et al. 2017; Ji and Shi 2020). The majority of these models concentrate on the kinetics and analysis of the dynamic recrystallization process.
In this work, we extend the preliminary results of the model (Jiménez-Morales et al. 2022) already performed on this subject towards the achievement of more comprehension of the physical meaning of the relevant computing parameters. We have also carried out some experiments of partial sintering of spherical particles of silica to test the correspondence between simulations and real behavior, and finally we point out some of its limitations.
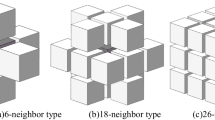
The neighborhood cells considered to evaluate the interface energy of one block. The star may be an empty site or one occupied by matter. The energy of the block is given by \(e=\sum _{ij}J( 1-\delta _{ij})\), where i and j are 0 or 1 for the \(2 \times 2\) cells block, \(\delta _{ij}=1\) if \(i=j\) and \(\delta _{ij}=0\) if \(i\ne j\)
2 Methods
2.1 The cellular automata model
To simulate the synthesis of alumina we have used the cellular automata technique. In this simulation method, both space and time are discrete quantities and the evolution of the system is carried out synchronously in all the cells that make up the material. In a formal way, a cellular automaton (CA) is defined by the following elements:
-
1.
The space in which the simulation is developed, which in our case is a two-dimensional network of \(N=500\times 500\) cells with periodic boundary conditions to avoid edge problems.
-
2.
The set \(\sigma =\{ 0,1 \}\) of states in which each cell can be. In our model, zero represents vacuum and \(\sigma =1\) the presence of matter.
-
3.
The neighborhood or set of adjacent cells. Contrary to other simulation techniques, CAs are local and only the neighborhood is taken into account to determine the next state of the considered cell. In our model we take the Margolus neighborhood and thus the basic unit is built with \(2 \times 2\) cells that evolve simultaneously. The network is divided into two sublattices which are updated in successive time steps. In this way, the conservation of the number of particles is guaranteed. Also we assign an energy to each block and for this purpose, we take into account the set shown in the Fig. 1. The energy of one block is defined by:
$$\begin{aligned} e=\sum _{ij}J( 1-\delta _{ij}) \end{aligned}$$(2)where the summation considers all the cells in the block, namely, both i and j take the value 0 and 1. Two neighboring cells in the same state give zero while there is a positive contribution to the energy when they are in different states. J is the surface energy of one elemental interface which, for simplicity, we take \(J=1\). The total energy E of the system is obtained by adding the energy of each individual block.
-
4.
The transition function f will assign to each block a probability, \(p_i\), that at time \(t+1\) it can change depending exclusively on the difference in energy \(\Delta e_i\) between the possible configurations and the original one. For each of them, the factor \(q_i = e^{\frac{-\Delta e_i}{kT}}\) is calculated, and the probability \(p_i\) of each case is obtained by normalizing between the different configurations \(p_i=q_i/ \left( \sum _j q_j\right) \). Fig. 2 shows the look up table of the transition function, and Fig. 3 shows and example of transition function with the corresponding probability values at two different temperatures. Starting with random initial conditions of concentration 0.6 (porosity = 0.4) the system evolves for at least over \(10^4\) time steps when different data are collected. We have performed multiple simulations changing the size and the shape of the initial particles.
2.2 Partial sintering of spherical particles
Experiments of partial sintering of spherical particles of silica were performed in order to test the correspondence between simulations and real neck formation. Random packings of spherical particles were prepared with monodisperse silicon dioxide (SiO\(_{2}\)) spheres with a diameter of 3.34 \(\mu \)m, purchased as a commercial suspension from MicroParticles GmbH, Inc. The suspension was in deionized water at a concentration of 5 wt.%. A Teflon die of 8 mm was clamped on alumina disc-shaped substrates, where 0.5 mL of the suspension was dropped with a micropipete. The system was then placed on a hot plate at 80 \(^\circ \)C to allow the water to evaporate and the particles to self-assemble into close-packed structure. When the suspension was totally dry, the Teflon die was removed, leaving a thin layer of particles on the alumina substrate. The thin layers of silica particles were then sintered at different temperatures in an tubular furnace in air, with a heating ramp of 5 \(^\circ \)C/min. The sintering temperatures and dwell times used were in the range of 1000–1300 \(^\circ \)C and 0.5–5 h, respectively. For the study of the morphology of the silica microspheres after the heat treatment, the samples were observed by scanning electron microscopy (SEM) using an FEI model Teneo with an acceleration voltage of 5 kV. Previously the samples were metallized with Pt whose thickness is around 10 nm, using a Leica ACE600 sputtering.
3 Results and discussion
3.1 Computing parameters
The sintering experiments simulated by the CA showed the evolution of the starting particulate system towards densified structures. With the exclusive aim of reducing the surface energy of the system, different configurations were tested to explore the relevant parameters of the algorithm, such as the size of the starting particles and the temperature.
3.1.1 Size of the starting particles
The first analysis of the parameters of the simulation algorithm was focused on the effect of the size of the starting particles. Thus, different simulations were run with analogous systems, namely, with the same porosity of P = 40% and the same mass but in randomly distributed squared particles of the following sizes: 1, 4, 9 and 16 cells. The evolution of the decrease of the energy of the system, in relative terms to the starting energy is shown in Fig. 4a, as a function of the temperature of the simulation. All the curves for different starting particle sizes exhibit analogous behavior, although each curve started from different value of energy, \(E_{0}\), according to their starting particle size. Hence, the comparison confirms that the effect of the size of the starting particles is not qualitatively relevant for the simulation of the energy reduction process. Therefore, the choice of the number of cells selected for simulate any real system will be a matter of resolution, reliability and accuracy, and it will not affect the fundamental conclusions.
a Dependence of the relative variation of the equilibrium energy (\(\Delta E/E_{0}\)) with the simulation temperature, for different starting sizes: the legend shows the size (number of cells) of the starting squared particles. b Effect of the size of the starting particles on \(T_{s}\), the temperature above which (\(\Delta E/E_{0}\)) is higher than zero
In particular, all the simulations confirm the presence of a \(T_{min}\) for which the reduction of the energy is maximum, and, interestingly, this value is the same for all cases, \(T_{min} = 0.5\). It should be recalled that temperature is the parameter that modulates the probability distribution of the evolution states through the Arrhenius type function. Some values of the transition probability and the effect of the temperature can be seen in Fig. 3. Interestingly, above an specific temperature, \(T = T_{s}\), the final equilibrium state is found with an energy higher than the starting one, namely, \(\Delta E/E_{0}\) is higher than zero. In Fig. 4b, the estimated values of \(T_{s}\) are plotted as a function of the size of the starting particles. It is verified that for starting particles of \(4 \times 4\) cells of size or more, this \(T_{s}\) seems to be size-independent. This can be understood in terms that there is a minimum surface-to-perimeter ratio (volume-to-surface ratio, in 3D) of the shape of the particles, or ’critical resolution’, equal to 1 cell, above which the results are size-independent.
3.1.2 Temperature
The effect of the temperature in the sintering simulation was explored for selected values of T. In Fig. 5, the sintering behavior of a random packing of hard spheres of porosity P = 40% is shown for the indicated temperatures, and for two different simulation times. The selected temperatures cover the different regions found in the reduction energy curve (Fig. 4, left), namely, \(T < T_{min}\), being \(T_{min}=0.5\), \(T_{min}<T<T_{s}\), being \(T_{s}\) dependent on the system, and \(T>T_{s}\). The two snapshots of the sintering states at \(T = 0.25\), \(T < T_{min}\) show the formation of the necks at the contact point of the original hard spheres. Nevertheless, after such a long time as 300,000, the particulate nature of the original system has not disappear yet and only the thickening of the necks can be seen. On the other hand, at \(T=T_{min}\), the system exhibits well formed necks even at the first stages of sintering (t = 10,000) and, at the equilibrium, a unique continuous bulk structure has formed with the characteristic vermicular features.
The original system is 500 x 500 cells size filled with a random packing of spherical particles (disks in 2D). The radius of the disks is 20 cells and the porosity is \(P=40\%\). The grid of snapshots shows two different states at four selected temperatures: an intermediate state at 10,000 CA steps, and the equilibrium state at 300,000 CA steps. Note that, while working below the \(T_{min}\) of 0.5 leads to the formation of the sintering necks and the typical vermicular structures, for high T, the system evolves towards a non-condensed equilibrium
At slightly higher temperatures, e.g., \(T=0.80\), neck formation and vermicular formation is even faster. But, at this temperature, some isolated black points can be seen segregated from the bulk. This single points remain disconnected from the bulk at the final equilibrium state. Correspondingly, the bulk also exhibits selected white points. This result suggests that, above the \(T_{min}\), there is a set of segregated points in equilibrium with the bulk. This phenomenon is totally confirmed when working at high temperatures, that is, at \(T=1.50\), three times the \(T_{min}\). In this case, the first snapshot taken at \(t=10,000\) steps, already shows how the set of disks has started its dissolution into individual cells.
Therefore, although the algorithm is aimed to reduce the total energy E at each step, it should be recalled that the evolution is based on a random nature biased through an Arrhenius-like probability distribution. That is, there is always a non-null probability to evolve to an state with higher energy which increases with the temperature.
3.2 Partial sintering behavior for spherical particles
In order to explore the reliability of the simulated process, partial sintering of spherical particles were performed and the intermediate states of densification could be compared with CA simulation results. In Fig. 6 partial sintering of real and simulated spherical systems can be compared. Colloidal silica was considered for experimental comparison as it densifies in amorphous state and no influence of possible grain formation is expected, similarly to the CA algorithm, which does not consider crystalline orientation and grain formations. Firstly, it was confirmed that the silica spheres exhibited a very good monodisperse size distribution around 3 \(\mu \)m (Fig. 6, a). Once the system of random packing of silica spheres was submitted to heat treatment, neck formation clearly appeared between neighbors spheres (Fig. 6, b).
Top: SEM images showing experimental evidences of the neck formation between silica spherical particles as the first step of the sintering behavior: a original system; b the system after 3 h at \(1300^\circ \)C. Below: simulation of the partial sintering silica spheres and experimental results: c original system of 500 pixel side, with two disks of 150 pixel radius in hard contact; d) neck formation can be clearly seen after 1,000,000 steps at T = 0.35
Accordingly, the 2D CA simulation algorithm is able to emulate the realistic behavior of the neck formation. The original particles (Fig. 6, c), which were in hard contact at the beginning, evolves towards the formation of a joining neck (Fig. 6, d). Hence, this simple algorithm based exclusively on the surface energy reduction is able to reproduce this first step of the sintering without the need of any additional consideration. Therefore, the formation of the necks in real systems could be explained just in terms of heat-driven Arrhenius viscous flow. Note that the radius-to-cell ratio is well above the critical value for avoiding any possible size-induced artifact (see Sect. 3.1.1 for details).
Despite this encouraging results, some limitations of the model arose. For example, real pressureless sintering process takes several hours above a given temperature threshold, and, finally, bulk 100% dense samples can be obtained. On the contrary, in the simplest version of this simulation algorithm, the number of cells of the system assigned with mass is always the same, and the porosity is thereby constant along the process. Additionally, nor gravity nor other external forces are considered in this model, so full densification cannot be reproduced. In addition, it is known that the diffusion of mass that takes place at the surfaces and the contact points between particles involves energy dissipation as the movement of the mass has to overcome energy barriers (Redanz and MackMeeking 2003). Moreover, the curvature of the interface is also established as a critical parameter that promotes local diffusion (Mason 2015), and other numerical simulations of the sintering of two spherical particles considering two driving mechanisms, namely, surface energy and grain boundary energy reductions, achieved total sintering of the system of two spherical in hard contact (Pan et al. 1998).
3.3 Porosity and vermicular structures
To measure the porosity of the sample with the CA model, we make temporary averages in the occupancy of the network sites. In the event that \(\left\langle \sigma \right\rangle \) is greater than 0.5, that site is considered occupied, while otherwise the site is considered empty. In Fig. 7a the evolution of the final porosity shows the existence of a temperature threshold, beyond which, the final porosity of the systems goes to zero. Moreover, comparing the behavior of porosity with temperature of the simulations with the experimental data plotted in the figure, confirms that the simulated behavior fits reasonably well the behavior of the real systems. Additionally, the possible size effect in this extension of the model was also checked. In Fig. 7b, the porosity behavior with the temperature was researched for systems with different starting sizes. Note that the curves were vertically shifted for clarity. Thus, it was verified that the behavior was exactly the same in all cases, neglecting any possible size-induced artifacts.
Vermicular structures. Comparison between real intermediate sintering steps of alumina [from Ref. Dutta et al. (2011) with permission] and their simulated corresponding systems
Finally, experimental and simulated evolution of the vermicular structures along the sintering can be compared in Figs. 8. In this images series, the scanning electron images of different densification states of alumina powders, taken after different heat treatments, are shown together their simulated counterparts, and the similarity of the simulated structures is evident. Therefore, the capacity of this simple algorithm to simulate the sintering behavior of particulate systems is confirmed.
4 Conclusions
This work has extended a probabilistic model of cellular automata, in which one single physical rule governs the evolution of the system: the reduction of the surface energy according to an Arrhenius function. In this model, the probability of transition depends on the ratio of the interface energy with the temperature. The size of the particles has been revealed as a critical parameter only in the case of very small particles, very coarsely defined, build with very few cells, less than 16. Interestingly, the temperature is modulating the transition probability in such a way that, under high temperature regime, the system can evolve rising their energy.
On the other hand, some limitations were discussed such as the absence of gravity or other external forces that enhance densification, energy barriers to be solved during viscous flow, or the effect of the curvature. However, although this CA-based model lacks of all this relevant information, the implementation of the evolution of the system driven by a surface energy under a probabilistic Arrhenius function leads to consistent physical results. For example, the neck formation process observed in experiments of partial sintering of spherical microparticles was successfully reproduced by simulation. In addition, the extension of the model to simulate the full densification leads to microstructural patterns that outstandingly mimic the classical vermicular structures of real systems for various temperatures. Finally, the variation of sample porosity as a function of temperature is also in good agreement with experimental results.
Data availability
Datasets will be supplied upon request.
Change history
18 December 2023
A Correction to this paper has been published: https://doi.org/10.1007/s11047-023-09970-1
References
Brinker CJ, Scherrer GW (1990) The physics and chemistry of sol-gel processing. Academic Press, Inc., Cambridge
Contieri RJ, Zanotello M, Caram R (2017) Simulation of CP-Ti recrystallization and grain growth by a cellular automata algorithm: simulated versus experimental results. Mater Res 20(3):688–701
Dutta Sreya, Kim Taek Bo, Krentz Timothy, Vinci Richard P, Chan Helen M (2011) Sol-gel-derived single-crystal alumina coatings with vermicular structure. J Am Ceram Soc 94(2):340–343
Gocha A, Liverani S, De Guire E (2016) Ceramics and glass-materials for diverse industries A 2016 industry profile and manufacturing forecast. Am Ceram Soc Bull 95:10–20
Gonzalez-Sanchez M, Rivero-Antunez P, Cano-Crespo R, Morales-Florez V (2022) Fabrication of porous alumina structures by SPS and carbon sacrificial template for bone regeneration. Materials 15:1754
He Y, Ding H, Liu L, Shin K (2006) Computer simulation of 2D grain growth using a cellular automata model based on the lowest energy principle. Mater Sci Eng A429:236–246
Jagota S, Raj R (1992) Model for the crystallization and sintering of unseeded and seeded boehmite gels. J Mater Sci 27:2251–2257
Ji Xiang, Shi Yabei (2020) Simulation of the microstructural evolution during dynamic recrystallisation with a modified cellular automaton. Philos Mag Lett 100(3):105–115
Jiménez-Morales F, Rivero-Antúnez P, González-Sánchez M, Garrido-Regife L, Morales-Flórez V (2022) The evolution of vermicular structures and sintering behavior of alumina. Lect Notes Comput Sci 13402:153–162
Kingery WD (1976) Introduction to ceramics. Wiley, Hoboken
Li Zhiqiang, Wang Junsheng, Huang Houbing (2019) Grain boundary curvature based 2D cellular automata simulation of grain coarsening. J Alloy Compd 791:411–422
Maazi N, Boulechfar R (2019) A modified grain growth Monte Carlo algorithm for increase calculation speed in the presence of Zener drag effect. Mater Sci Eng B 242:52–62
Mason JK (2015) Grain boundary energy and curvature in Monte Carlo and cellular automata simulations of grain boundary motion. Acta Mater 94:162–171
Morales-Florez V, Domínguez-Rodríguez A (2022) Mechanical properties of ceramics reinforced with allotropic forms of carbon. Prog Mater Sci 128:100966
Orrù R, Licheri R, Locci AM, Cincotti A, Cao G (2009) Consolidation/synthesis of materials by electric current activated/assisted sintering. Mater Sci Eng, R 63:127–287
Pan J, Le H, Kucherenko S-, Yeomas JA (1998) A model for the sintering of spherical particles of different sizes by solid state diffusion. Acta Mater 46(13):4671–4690
Raabe Dierk (2002) Cellular automata in materials science with particular reference to recrystallization simulation. Annu Rev Matter Res 32:53–76
Redanz P, MackMeeking RM (2003) Sintering of a bcc structure of spherical particles of equal and different sizes. Phylosophical Mag 83(23):2693–2714
Rivero-Antúnez P, Cano-Crespo R, Sánchez-Bajo F, Domínguez-Rodríguez A, Morales-Flórez V (2021) Reactive SPS for sol-gel alumina samples: structure, sintering behavior, and mechanical properties. J Eur Ceram Soc 41:5548–5557
Rivero-Antúnez P, Morales-Flórez V, Cumbrera FL, Esquivias Luis (2022) In situ formed La-\(\beta -Al_2O_3\)/\(Al_2O_3\) composites by sol-gel method: XRD analysis and mechanical properties. Ceram Int 48(17):24462–24470
Tan H, Zhang H, Salamon D (2022) Densification behavior and mechanical properties of nano-alumina ceramics prepared by spark plasma sintering with pressure applied at different sintering stages. Ceram Int 48:30224–30228
Wang C et al (2020) A general method to synthesize and sinter bulk ceramics in seconds. Science 368:521–526
Wang Dong, Bai Yifan, Xue Chao, Cao Yan, Yan Zhenghu (2021) Optimization of sintering parameters for fabrication of \(Al_2 O_3 /TiN/TiC\) micro-nano-composite ceramic tool material based on microstructure evolution simulation. Ceram Int 47:5776–5785
Acknowledgements
M. G-S. acknowledges European Social Fund from the Empleo Juvenil European Plan. Consuelo Cerrillos, from the technical staff of the CITIUS central services of the University of Seville is deeply acknowledged.
Funding
Funding for open access publishing: Universidad de Sevilla/CBUA. Consejería de Transformación Económica, Industria, Conocimiento y Universidades (Junta de Andalucía, Spain), P20 01121. Ministerio de Ciencia, Innovación y Universidades (Spanis government), PGC2018- 094952-B-I00. Special action I.9 from the VI-PPITUS (Universidad de Sevilla, Spain).
Author information
Authors and Affiliations
Contributions
LG-R and FJ-M made the cellular automata model. MG-S, PR-A and VM-F made the experiments. FJ-M and VM-F wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
the authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to the wrong figure appeared as Fig. 1 and the figure has been corrected.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Laura, GR., Francisco, JM., Manuela, GS. et al. Cellular automata simulations of the sintering behavior of ceramics driven by surface energy reduction. Nat Comput 23, 61–68 (2024). https://doi.org/10.1007/s11047-023-09958-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-023-09958-x