1 Introduction

Large-scale optimization problems are often solved by decomposing them into several subproblems or by using dimensionality reduction methods. The cooperative coevolution (CC) framework (Potter and De Jong (1994) is the most common framework used to decompose the problems. As for dimensionality reduction, Yang et al. introduced EACC-G No definition in the paper, simply they want to call the algorithm with this namein (Yang et al. 2008). The EACC-G framework is based on the CC framework but instead of optimizing the subproblems created by grouping, the EACC-G optimizes weights that are associated with the groups. The framework effectively reduces the dimensionality to the number of groups created which is less than or equal to the number of variables.

These techniques for large-scale optimization are also used when there are several objectives to be optimized simultaneously, i.e., in a large-scale multi-objective (LSMO) optimization problem. Some examples are the cooperative coevolution with generalized differential evolution (CCGDE3) (Antonio and Coello 2013) and the weighted optimization framework (WOF) (Zille et al. 2017) which are based on the CC framework and EACC-G, respectively. In addition to those, new frameworks designed for LSMO optimization problems are also available, such as the multiobjective evolutionary algorithm based on decision variable analysis (MOEA/DVA) (Ma et al. 2016) as well as algorithms that utilize machine learning techniques such as the SVM + NSGA-II (Zhang et al. 2019) and PCA-MOEA (Liu et al. 2020).

In most of the mentioned frameworks and algorithms, variable decomposition/grouping plays a major role. In regards to grouping, there are many ways of specifying groups for the framework/algorithm. There are simple methods like random grouping which allocate variables to groups randomly to a fixed size, but there also exist more sophisticated methods. As an example, the random dynamic grouping (Liu et al. 2020) uses varying group sizes at each iteration which is determined by a roulette wheel selection based on the quality of the groups. Combined with the WOF and using MMOPSO as the optimizer, the random dynamic grouping shows good performance on WFG (Huband et al. 2006) and UF (Zhang et al. 2009) test problems.

Other common methods used to group variables are based on variable interactions or separability. A problem is called partially separable iff:

$$\begin{aligned} \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{\mathbf {x}} f({\mathbf {x}}) = (\mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{x_1} f({\mathbf {x}}), \ldots , \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{x_n} f({\mathbf {x}})) \end{aligned}$$
(1)

Further, a function is additively separable iff:

$$\begin{aligned} f({\mathbf {x}}) = \sum _{s=1}^{|S|} f_s(x_s) \; , \; |S|>1 \end{aligned}$$
(2)

The variables are grouped together when they do not fulfill the above criteria for separability, i.e., they are non-separable. This ensures that variables that affect each other are optimized together. The differential grouping (DG) family (Omidvar et al. 2014, 2017; Sun et al. 2019) focuses on grouping based on this additive separability. Another method that has been used to group variables is differential analysis (DA). These methods will be discussed further in Sect. 3.

In LSMO problems, such variable interactions must be checked for each objective function. Variables that are separable with respect to one objective can be non-separable on other objectives and it is non-trivial on how to process such variables. To define how such variables are being considered separable or non-separable, the so-called transfer strategies are used (Sander et al. 2018).

As an alternative to grouping based on interaction, variables can be grouped based on whether they affect convergence or diversity of solutions in the objective space. Some examples of such grouping methods are the control variable analysis (CVA) (Ma et al. 2016), and decision variable clustering (Zhang et al. 2018). The advantage of these methods is that no transfer strategies are needed. To summarize, the different grouping methods are listed in Table 1.

Table 1 Commonly used grouping/decomposition methods
Full size table

This paper provides studies on extensions and modifications to existing methods for solving LSMO problems. The topics covered are:

  • an improvement on the CVA grouping method;

  • implementing the improved CVA in a cooperative coevolution framework;

  • implementing the novel mirrored orthogonal sampling method introduced in Wang et al. (2019) to solve LSMO problems.

This paper is organized as follows: Sect. 2 introduces several existing frameworks for large scale optimization that use grouping in their routine, Sect. 3 discusses existing grouping methods that have been used to solve LS optimization problems, Sect. 4 introduces a modification to the CVA grouping method to improve its accuracy, Sect. 5 discusses the implementation of the CVA and orthogonal sampling in a CC framework, and lastly, Sect. 6 summarizes the work.

2 Large-scale optimization frameworks

In this section, existing frameworks for solving large-scale problems are described. The frameworks discussed in this section are based on decomposition. Discussion on the decomposition methods is available in Sect. 3.

2.1 Cooperative coevolution

The challenge with large-scale optimization problems is that common solver’s performances deteriorate rapidly as the number of variables increases due to the exponential expansion of the search space (Li et al. 2013). The cooperative coevolution (CC) framework (Potter and De Jong 1994) is intended to scale up these solvers by decomposing the large-scale problem into several smaller subproblems that are solved cooperatively.

The first step of the CC framework is the grouping of the variables. The grouping methods will be discussed further in Sect. 3.

After grouping, the second step is the optimization itself. The variables in different groups are optimized separately, while variables in the same group will be optimized together in one subproblem. Each subproblem optimizes a subvector \({\mathbf {x}}_\mathcal{S}\) from the large-scale problem, with \({\mathcal {S}}\) being the index set defining the subproblem, \({{\mathcal {S}}} \subseteq \{1,\ldots ,n\}\).

The optimization subproblems are constructed as optimizing \({\mathbf {x}}_{{\mathcal {S}}}\) while all other variables \({\mathbf {x}}_\mathcal{{\bar{S}}}\) are filled with the so-called context vector (CV) and kept constant (with \(\mathcal {\bar{S}}\) the complement of the index set \(\mathcal S\)). The subproblems’ formulation can be seen in Eq. 3.

$$\begin{aligned} \underset{{\mathbf {x}}_\mathcal{S}}{\text {min}}f({\mathbf {x}}') \; , \;x_i' = {\left\{ \begin{array}{ll} x_i &{} \text {if } i \in {{\mathcal {S}}} \\ x_i^{(cv)} &{} \text {otherwise } \end{array}\right. } \end{aligned}$$
(3)

In Eq. 3, the CV denoted as \({\mathbf {x}}^{(cv)}\) and variable whose index is in \({{\mathcal {S}}}\) are substituted with \({\mathbf {x}}_{{\mathcal {S}}}\). The CV is built from the representative individuals of each subproblem, e.g. the best individuals of each subvector (Trunfio 2015).

After \({\mathbf {x}}_{{\mathcal {S}}}\) is optimized with respect to the current CV, the CV is updated with the optimized \({\mathbf {x}}_{{\mathcal {S}}}\). This concept is illustrated in Fig. 1. The process is then repeated for several iterations (known as cycles) until a stopping criterion is triggered.

Fig. 1
figure 1

Optimization and update of the context vector. In each cycle, each subproblem is optimized consecutively. In the example above, a 4-variable problem is decomposed into two subproblems. Subproblem 1 optimizes the first two variables, while the other two variables are taken from the context vector. Solving subproblem 1 yields optimized \(x_1\) and \(x_2\) which are used to update the context vector. Subsequently, subproblem 2 will optimize \(x_3\) and \(x_4\) while the value for \(x_1\) and \(x_2\) are taken from the updated context vector

Full size image

2.2 MOEA/DVA

The difficulties of solving LSMO problems are two-fold. There are challenges related to the multi-objectivity and also challenges related to the large number of variables involved. Common solvers for multi-objective optimization problems (MOPs) struggle due to these challenges. Similar to the CC framework, the MOEA/DVA is intended to scale up these solvers (Ma et al. 2016).

The MOEA/DVA also uses grouping in its routine. There are two stages of grouping, first, it groups variables using control variable analysis (CVA, see Sect. 3.3), and then it creates subgroups on the convergence and mixed variables based on interaction using differential grouping (DG, see Sect. 3.1). Decomposing large scale optimization problems using several grouping methods are common to control group sizes and interaction sensitivity (e.g., Zhenyu et al. 2008; Yue and Sun 2021), or increase grouping efficiency (e.g., Irawan et al. 2020). The two-stage grouping in MOEA/DVA differs in that the first stage is to address the multi-objective nature of the problem. Additionally, as mentioned in Sect. 1, when dealing with LSMO problems, non-separability can happen differently in each objective. In MOEA/DVA, variables interacting indirectly on different objectives must be grouped together. In MOEA/DVA, the optimization is divided into two big phases. In the first phase, several points are sampled uniformly on the diversity variables subspace and will be kept static during this phase. During this phase, optimization effort is focused on convergence and mixed variable groups to push the solution closer to the Pareto front.

After a certain stopping criterion is fulfilled, the second phase of MOEA/DVA is to optimize all variables together. The primary aim of this last phase is to uniformly spread solutions in the objective space. Ma et al. (2016) tested MOEA/DVA on various large-scale test problems with good results although the number of function evaluations is very high, mainly due to the DG.

2.3 Weighted optimization framework

The weighted optimization framework (WOF) reduces the problem’s dimensionality by changing the values of a group of decision variables simultaneously. This is achieved by utilizing the transformation function, \(\psi \) which specifies a search direction for a group of variables. The offspring are generated along this search direction from an individual \({\mathbf {x}}^{(k)}\) in the population by varying a weight vector \({\mathbf {W}}\). The optimization problem is then transformed into finding a weight vector that produces good objective values, i.e.

$$\begin{aligned} \begin{aligned} \min _{\mathbf {W}} {\mathbf {f}}_k({\mathbf {W}})&= \min _{\mathbf {W}}{\mathbf {f}}(\psi ({\mathbf {W}},{\mathbf {x}}^{(k)})) \\ \psi ({\mathbf {W}},{\mathbf {x}}^{(k)})&= \{W_1x^{(k)}_1,\ldots ,W_1x^{(k)}_l,\ldots ,\\&\qquad W_\gamma x^{(k)}_{n-l+1},\ldots ,W_\gamma x^{(k)}_{n}\} \end{aligned} \end{aligned}$$
(4)

In Eq. 4 it is assumed that the variables are grouped into \(\gamma \) groups with the same size \(l=n/\gamma \). The transformed problem is created with the hope that the search directions intersect with the Pareto set. The transformed problem and the original problem are solved in a loop, one after the other.

To summarize, in the WOF, the problem is transformed into optimizing weights to a specific search direction where each group of variables is represented with a straight line. These search directions are defined by a good candidate solution position and random grouping of variables. Other algorithms have also emerged based on this concept. He et al. (2019) used a similar method with two search directions. Qin et al. (2021) further increased the number of search directions for the directed sampling in their LMOEA-DS to increase the chance for the direction vectors to intersect with the Pareto set in the decision space. The search directions in LMOEA-DS are generated based on the solutions closest to the ideal point of the objective space.

3 Grouping methods

As mentioned before, in solving large-scale problems, the use of grouping to decompose the large-scale problem is prominent. This section will discuss several well-known grouping methods in more detail.

3.1 Differential grouping

Recall that one of the most common methods used to group variables is based on separability. Detecting additive separability in a function is possible by evaluating the second-order differentials of the function. The second-order differential is computed following Eq. 5.

$$\begin{aligned} \begin{aligned}&\Delta _i = f(\ldots ,x_i',\ldots )-f(\ldots ,x_i,\ldots )\\&\Delta _{i,j} = f(\ldots ,x_i',\ldots ,x_j',\ldots )-f(\ldots ,x_i,\ldots ,x_j',\ldots )\\&\Theta _{i,j}= {\left\{ \begin{array}{ll} 1 &{} \quad {\Delta _i \ne \Delta _{i,j}}\\ 0 &{} \quad {\Delta _i = \Delta _{i,j}} \end{array}\right. } \\&i,j \in (1,\ldots ,n) \end{aligned} \end{aligned}$$
(5)

In Eq. 5, \(\Delta _i\) is the effect of perturbation on \(x_i\) while \(\Delta _{i,j}\) is the effect of perturbation on \(x_i\) after an initial perturbation on \(x_j\). The \(\Theta _{i,j}\) is a binary matrix which indicates whether the variables interact with each other. A complete \(\Theta _{i,j}\) with i and j spanning all variables yields what is called a Design Structure Matrix (DSM) (Omidvar et al. 2017). Two variables \(x_i\) and \(x_j\) are additively separable when \(\Theta _{i,j}=0\). A full DSM can be constructed using the so-called DG2 method, consuming \(\frac{n^2-n}{2}\) function evaluations (Omidvar et al. 2017).

For multi-objective problems, the DG must be conducted on each objective function. The computational cost is then multiplied by the number of objectives. Variables may be separable on one objective, but not on other objectives. Care should be taken as indirect interactions across different objectives are possible. As an example, suppose that \(x_1\) interacts with \(x_2\) on the first objective, and \(x_2\) interacts with \(x_3\) on the second objective. This implies \(x_1\) is indirectly interacting with \(x_3\).

3.2 Differential analysis

While the DG uses second-order differentials, another method, known as differential analysis (DA) (Morris 1991; Campolongo et al. 2005), uses the first-order differential. In DA, multiple samples of the first-order differentials are drawn and the mean and variance of the differences are taken as scores (known as sensitivity indices) for each variable. It is important to note that the DA by itself does not produce groups. The groups are created separately after the analysis. In Mahdavi et al. (2017), the groups are created based on the scores using a clustering method, while in Irawan et al. (2020) the groups are created based on the ranking of one of the scores.

For DA, each variable in the search space is divided into p intervals. The scores are then calculated based on the elementary effects (EE). The elementary effect of variable \(x_j\) is calculated according to Eq. 6.

$$\begin{aligned} EE_i({\mathbf {x}}) = \frac{f(\ldots ,x_i+\Delta ,\ldots ) - f({\mathbf {x}})}{\Delta } \; ,\; i=1,\ldots ,n \end{aligned}$$
(6)

\(\Delta > 0\) is a grid jump which is chosen from a multiple of \(1/(p-1)\), \({\mathbf {x}}\) is a random point in the search space such that \({\mathbf {x}}+ \Delta \) is still within the search space which we refer to as base points. Several samples of \(EE_i\) are collected. If r samples are desired for each variable then \(N=r(n+1)\) function evaluations are required. The mean \(\mu _i\) and variance \(\sigma _i\) of \(EE_i\) are used in Mahdavi et al. (2017) for grouping, while Irawan et al. (2020) used the mean of absolute values of \(EE_i\), i.e. the \(\mu ^*\) as defined in Campolongo et al. (2005).

3.3 Control variable analysis

In MOPs, several objectives need to be considered simultaneously. The control variable analysis (CVA) is used in MOEA/DVA (Ma et al. 2016) to detect whether the variables affect convergence or diversity (or both) with respect to the Pareto front. CVA is based on the first-order effects of the variables.

For CVA, a base solution \({{\textbf {x}}}\) is evaluated. Afterwards, one variable \(x_i\), \(i\in \{1,\ldots ,n\}\), is shifted and new objective values are evaluated at the shifted position, thus \({{\textbf {x}}}'=(\ldots ,x_i+\delta ,\ldots )\). Several \(\delta \) values are used such that the whole range of \(x_i\) is filled uniformly. The sampling is then followed by non-dominated sorting to identify the order of non-domination levels (see Deb 2001 for further details on dominance and non-dominated sorting). The variable is then classified based on 3 possible results of non-dominated sorting on the set of objective vectors obtained from shifting \(x_i\) several times:

  1. 1.

    If all solutions belong to the same non-dominated front, then \(x_i\) is affecting diversity (will be referred to as diversity variable).

  2. 2.

    If each non-dominated front only contains one objective vector then \(x_i\) is affecting convergence (will be referred to as convergence variable).

  3. 3.

    If none of the previous two criteria is fulfilled, then \(x_i\) is affecting both diversity and convergence (will be referred to as mixed variable).

The CVA as proposed by Ma et al. (2016) was tested on WFG problems. The WFG problems have a parameter k which specifies the number of diversity variables; however, these variables can act as mixed variables instead of only affecting diversity.

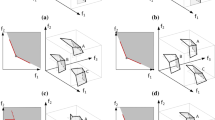
In Fig. 2 we show that the traditional CVA is inconsistent. Figure 2 shows how solutions for two-dimensional WFG2 are distributed over the objective space when only the diversity variables are varied. Based on the function definition in Huband et al. (2006), the objective values are determined by the average of the diversity variables. The CVA samples around the lower bound of the variables which means that it will only sample the left side of Fig. 2. When the number of variables is low, the effect of each diversity variable on their average is high and solutions will spread over a large part of the objective space and most likely will be identified as a mixed variable. However, when the number of diversity variables is high, each variable has only a minuscule effect on the average and the CVA will only identify a small portion of Fig. 2. By adding a shift to the first sampled point, the variables may be identified as any of the three possible types irrespective of how many samples are being taken. This can happen on any problem with mixed variables.

Fig. 2
figure 2

Distribution of solutions in the objective space of 2 objective WFG2 by changing only the diversity variables. Depending on where diversity variables are being sampled, the variables can be identified as diversity, convergence, or even mixed variables

Full size image

3.4 Decision variable clustering

The decision variable clustering (DVC) takes off from the same idea as the CVA, it attempts to identify which variables affect diversity and which variables affect convergence. Zhang, et al. (2018) identified some optimization problems where the diversity variables should be considered as convergence variables to guarantee convergence to the Pareto set. An example of such a problem is as follows:

$$\begin{aligned} \begin{aligned}&f_1(x_1,x_2)= x_1x_2\\&f_2(x_1,x_2)= \frac{(1-x_1x_2)+1-x_2}{2}\\&0 \le x_1 \le 1, 0\le x_2 \le 1 \end{aligned} \end{aligned}$$
(7)

If CVA is used in the problem in Eq. 7, both \(x_1\) and \(x_2\) will be considered diversity variables. Perturbing \(x_1\) while keeping \(x_2\) generates points that do not dominate each other in the objective space, under CVA, \(x_1\) is a diversity variable (see Fig. 3). The same also applies to \(x_2\). However, it should be noted that as \(x_2\) approaches 1, the objectives actually get closer to the Pareto front. In fact, the Pareto front can only be achieved if \(x_2\) is equal to 1, therefore, \(x_2\) is a variable that affects convergence.

To take such a case into account, the DVC starts similarly to CVA where it perturbs the value of a variable while keeping all other variables constant. It then follows up by creating a line fit on the sampled points, one line for each variable. Finally, the angle between the normal vector of the (normalized) hyperplane \(f_1+f_2+\cdots +f_m=1\) and the fitted lines are measured and a k-means clustering method is used to determine which variables have small angles (convergence variables) and which variables have large angles (diversity variables).

Fig. 3
figure 3

The objective values obtained by using various \(x_1\) and \(x_2\) on the problem described in Eq. 7. Objective vectors obtained by varying \(x_1\) while keeping \(x_2\) at 0.2, 0.5, or 1 are depicted with solid circles where each value of \(x_2\) forms the top, middle, and bottom row of circles, respectively. Similarly, objective vectors obtained by varying \(x_2\) while keeping \(x_1\) at 0.2, 0.5, or 1 are depicted with empty circles making the left, middle, and right column of circles, respectively. The solid line is the Pareto front, while the dashed line is the normal of the line \(f_1+f_2=1\)

Full size image

4 Proposed grouping method: CVA–DA

4.1 Method description

Let us recall the inconsistency issue on CVA. The inconsistency occurs because the CVA only samples a small portion of the search space, around the lower bound. This issue was addressed in DVC (Zhang et al. 2018) by taking several base points in the search space and perturbing the variables around these base points, similar to how the DA is performed. In this work, we propose to improve the CVA in a similar way to DVC; however, we keep the usage of domination levels as the base for grouping. Domination levels must be checked separately for each base point because the control variables are different. The modified CVA is presented in Algorithm 1 and referred to as CVA–DA.

The CVA–DA differs from the DVC firstly by having an additional third category, similar to the traditional CVA: the mixed variables. In DVC, this category is deemed not informative and forced to fall into either diversity or convergence category through the clustering. However, we would argue that there are indeed variables that should be regarded as mixed variables as seen in Fig. 2. Secondly, the CVA–DA relies on domination levels using non-dominated sorting. The domination level is chosen here because the k-means clustering used in DVC has several weaknesses, such as the implicit assumption that the clusters have equal radii and the sensitivity to outliers (Raykov et al. 2016). For example, let us modify and generalize the problem in Eq. 7 into the following:

$$\begin{aligned} \begin{aligned}&f_1(x_1,x_2,x_3)= x_1x_2-x_3+1\\&f_2(x_1,x_2,x_3)= a(-x_1x_2)-bx_2-cx_3+a+b+c\\&0 \le x_1 \le 1, \\&0\le x_2 \le 1, \\ {}&0 \le x_3 \le 1,\\&a,b,c>0 \end{aligned} \end{aligned}$$
(8)

In Eq. 8, variable \(x_1\) will only affect diversity, while variable \(x_2\) and \(x_3\) is important for convergence to the Pareto front as the front can only be achieved if both \(x_2\) and \(x_3\) are equal to 1. However, using the DVC, the measured angle used for clustering the variables will depend on the values of a, b, and c thus the k-means clustering will produce different results. This means that the identified roles of the variables can change despite no change to their actual role. In the end, the DVC does not perfectly solve the issue of misclassification.

In terms of time complexity, the DVC and CVA–DA use the same amount of resources for sampling the points; however, they differ in the classification phase. The non-dominated sorting used in CVA–DA depends more on the number of objectives and the number of points being sorted, N, typically in the order of \(\mathcal {O}(mN^2)\) in most implementations (Roy et al. 2016). However, there exist some fast algorithms which have \(\mathcal {O}(N \text {log}^{m-1}N)\) time complexity (Buzdalov and Shalyto 2014). On the other hand, the time complexity for DVC scales with the number of variables as it uses \(\mathcal {O}(n)\) in the typical implementation of k-means clustering.

figure a

In CVA–DA, samples are taken for each base point, therefore the cost will be multiplied by the number of base points. The main improvement in using this CVA–DA is that mixed variables are more likely to be correctly classified (recall Fig. 2). However, because we are only taking samples, it is still possible to obtain the wrong classifications. In a many-objective optimization problem, this sampling poses a greater challenge because non-dominated solutions are easier to obtain. This means the variables are more likely to be classified as distribution variables.

4.2 Numerical experiment

The performance of CVA–DA is compared against the original CVA. The algorithms are tested on the WFG test suite (Huband et al. 2006) with 3 different settings. The first setting follows Ma et al. (2016) where 24 input variables are used with the number of diversity variables, k, set to 4. The other settings test the algorithms’ performances on larger input size, at 100 input variables, with \(k=20\) and \(k=80\).

For both algorithms, the number of samples taken is varied with a multiplier r and scaled with respect to the number of objectives, \(m\in \{2,3,5\}\). The rationale for scaling it with m is that the domination can expand in any direction in the objective space, so it should be scaled by \(2m^2\). The total number of samples used is therefore \(2rm^2\), with \(r\in \{2,5,10\}\). The correct classification is determined from all samples in the experiment. If one method classifies a variable as one type while other methods classify it as another type, then the classification for the variable is ”mixed”. The accuracy is measured as the number of correct classifications by the CVA or CVA–DA divided by the number of variables. The results are presented in Figs. 4, 5, and 6, where results for those test problems on which not all algorithms consistently obtained an accuracy of 1.0.

The test results show that the number of samples does not affect the accuracy of the original CVA because the randomness in the sampling only causes a small, local perturbation. Therefore, for CVA, only a single value is reported for each setting of the test problems. The CVA–DA, on the other hand, is sensitive to the number of samples as the randomness affects both the base points and the size of the perturbation. Despite the sensitivity to the number of samples, the CVA–DA always outperforms CVA on all WFG functions, except WFG1.

Fig. 4
figure 4

Accuracy on WFG test problems with 24 variables and \(k=4\). Results are only presented for those test problems on which not all algorithms consistently obtained an accuracy of 1.0

Full size image
Fig. 5
figure 5

Accuracy on WFG test problems with 100 variables and \(k=20\). Results are only presented for those test problems on which not all algorithms consistently obtained an accuracy of 1.0

Full size image
Fig. 6
figure 6

Accuracy on WFG test problems with 100 variables and \(k=80\). Results are only presented for those test problems on which not all algorithms consistently obtained an accuracy of 1.0

Full size image

In all figures, it can be seen that the CVA always struggles in WFG7, WFG8, and WFG9. These are problems where parameter-dependent biases are used. This means that in these problems, the diversity variables may interact with the convergence variables and change the type of the variables from either diversity- or convergence-related to mixed variables. In CVA, the parameter-dependent biases are not properly recognized and they are left to be detected in the second phase grouping by the interaction analysis (DG). In CVA–DA, the type-switch can be properly detected provided that enough samples are taken.

The CVA fails to correctly classify variables in the WFG2 problems with 100 variables and \(k=80\). These are the cases discussed in Sect. 3.3 where the CVA struggles to detect mixed variables. The CVA–DA, on the other hand, correctly classifies the variables because it takes samples around several base points and easily recognizes the mixed variables. With the performance improvement confirmed, we can move forward to apply CVA–DA in an MOEA based on the cooperative coevolution framework.

5 Cooperative coevolution SMS-EMOA

In our study, we further use the CVA–DA in an MOEA using the same grouping rule as MOEA/DVA, i.e. CVA–DA followed by DG. The DG used will be the recursive variant (RDG3 Sun et al. 2019) because it is very efficient as it only costs \(\mathcal {O}(n \log n)\) function evaluations. The framework used here is the CC framework. This means that the diversity variables are included and are optimized from the start as opposed to being kept constant as in MOEA/DVA. The variable groups are generated exclusively for each class (diversity, convergence, or mixed).

The solver is based on SMS-EMOA (Beume et al. 2007) where one offspring is added to the population, and the least contributor to the hypervolume is removed (see Algorithm 2) to keep the population size at 100. The algorithms are also compared against a basic SMS-EMOA algorithm without any grouping. In all experiments, the maximum number of function evaluations is set at 100,000 and ncv is set at 3.

For all algorithms, a minimum group size is also imposed. If the group size is below the minimum, it will be merged with another group. The minimum group size is set to 100 variables. This is used because currently, no budget allocation methods are implemented and each group is set to use the same number of function evaluations (20) in each cycle. The minimum group size will then limit the number of groups generated so each cycle will not take too much resources.

To generate offspring, the genetic operator used is only a mutation based on the mirrored orthogonal sampling (Wang et al. 2019). Similar to search directions in WOF, the search directions for orthogonal sampling used here are also defined based on the variable groups; however, the number of search directions can be varied from one up to the number of variables in the group. If the upper limit is used, then the problem size is not reduced. By using the orthogonal sampling, the problems are not explicitly transformed into a weight optimization problem; however, as we are generating offspring only in the subspace spanned by the search directions, it is effectively equivalent to weight optimization. The samples are generated around a parent using truncated normal distribution so that the offspring always stays within the box constraint. For a truncated normal distribution, if the standard deviation is too large, the distribution will be more flat; if the standard deviation is too small, the probability that the offspring will be generated near the boundary will be minuscule, limiting the search to very close proximity around the parent. By setting the standard deviation to 0.3 multiplied by the possible range, we found that the offspring have a reasonable chance to be generated near the boundaries while also maintaining the bell-shaped curve in the probability distribution.

figure b
figure c
figure d
figure e
figure f

The orthogonal sampling is more flexible as more than one search direction can be generated for each group. So, instead of line search along different directions as done in WOF, LMOEA-DS, and other similar algorithms, the orthogonal sampling allows us to search on hyperplanes in each of the subproblems. With respect to the WOF algorithm, we can think of each additional search direction as an additional weight to be optimized and it is guaranteed that the search directions are orthogonal to each other. This also means that the extent of dimensionality reduction in each group can be controlled. The search directions are generated following Algorithms 4 and 5.

In this section, two numerical experiments are conducted. The first numerical experiment is to assess the algorithm sensitivity to the number of samples used in CVA–DA. The purpose of these experiments is to check whether CVA–DA grouping is beneficial for the optimization. The grouping itself has some associated costs and may deteriorate performance when the budget is limited. After all, the final goal is obtaining the Pareto front, not the grouping. To assess this, the groups obtained from CVA–DA are used in a CC framework and compared against the same algorithm with random grouping.

The second set of numerical experiments is focused on the EA instead of the grouping. In these experiments, we evaluate the algorithm performance with different numbers of search directions for the mirrored orthogonal sampling. The performances from this set of experiments are also compared against the performances of the WOF algorithm.

The WFG Huband et al. (2006) and UF Zhang et al. (2009) test problems are used for benchmarking. The problems are chosen because they represent problems with different diversity types (Hong et al. 2019). The UF problems also represent problems with complex Pareto set topology. Additionally, the problems are also chosen because the performance data for WOF is available in Zille et al. (2017) for these particular problems.

5.1 Sensitivity to the Number of Samples for CVA–DA

Recall that the number of samples and the number of base points affect the accuracy of CVA–DA (see Sect. 4.2). However, these numbers also affect how many function evaluations will be used for the CVA–DA. While more samples and bases improve the grouping accuracy, more resources are also required for CVA–DA and the optimization phase will have a more limited budget. As an example, using a total number of samples \(2rm^2d\), with \(r=5\), 1000-variable problems will require 90,000 function evaluations (90% of the budget) for 3-objective problems and 250.000 function evaluations (not feasible) for 5-objective problems only for classifying variables. If instead we set \(r=1\), the CVA–DA will only consume 18,000 and 50,000 function evaluations for 3- and 5-objective problems, respectively.

To check how the budget for CVA–DA affects optimization performance, the algorithms are tested using various values of r, including testing against random grouping and SMS-EMOA without grouping which can be considered as the cases where \(r=0\). In this set of experiments, only a single search direction is used. The results are shown in Table 2. It can be seen that the base SMS-EMOA never performed best in all tests which implies that grouping/decomposition is crucial and improves performance on LSMO problems.

Table 2 Sensitivity of CC-SMS-EMOA to the number of samples taken for grouping
Full size table

Table 2 shows that the CVA–DA dominates the best median performances. This indicates that the grouping using CVA–DA and RDG3 is better than random grouping. However, it can also be seen that CVA–DA with \(r=5\) does not perform well on 3 objective problems. This is because the grouping consumes more than 90% of the budget so it may be better to sacrifice grouping accuracy to allow more iterations for the solver. A potential solution to reduce the CVA–DA cost is to stop the analysis of a variable when it is found that the variable should be classified as a mixed variable. In cases where there are mixed variables, this can significantly reduce the CVA–DA cost and in the worst-case scenario, where there are no mixed variables, there will be no extra cost.

Table 2 also shows that the random grouping performs best on UF1, UF2, UF6, UF7, UF8, and UF9. In UF1-UF7, all variables interact with the first variable but not with others. On UF1–UF7, both the algorithms based on CVA–DA and random grouping behave very similarly. The main difference is that in the algorithm based on random grouping the search directions are repeatedly changed. This indicates a potential strength of dynamic grouping on these types of problems.

In UF8-UF10, only the first two variables interact with other variables. This means the problems are separable except for one or two variables so there are no disadvantages for random grouping. On these problems, both CVA–DA and random grouping behave differently. The CVA–DA detected interactions between the first two variables with each other, as well as the interactions between them with other variables. This results in the RDG3 assigning all variables into a single big group; in other words: no decomposition even after some computation budget is used for grouping. Random grouping, on the other hand, keeps on doing decomposition with no cost which leads to superior performance.

5.2 Sensitivity to the number of search directions

As mentioned before, the orthogonal sampling is more flexible because the number of search directions can be configured. However, more search directions will lead to a more complex search space and may reduce convergence rate.

In this section, the performances of CC-SMS-EMOA with different numbers of search directions are compared against the best results from the WOF. For these experiments, r is set to 1 following the best results obtained in the previous section. In addition to that, the directed sampling method from Qin et al. (2021) is also implemented on CC-SMS-EMOA to see how multiple line search fares against orthogonal search directions. The directed sampling is set similar to how it was used in Qin et al. (2021). First, \(10+m\) clusters are generated in the objective space and a representative solution is taken from each cluster as the basis for search directions. For each representative solution, two search directions are generated, one pointing to the lower bound, the other pointing to the upper bound, creating \(2(10+m)\) search directions. In each search direction, 30 points are sampled.

The data for WOF are not generated from our own tests but rather taken directly from the table in Zille et al. (2017).

The results of the experiments are presented in Table 3. These show that the proposed CC-SMS-EMOA can outperform the WOF on some test problems. Despite having less budget for the optimization due to the grouping steps, the CC-SMS-EMOA is competitive on most test problems. This further shows how good grouping can improve performance as opposed to random grouping.

Table 3 Sensitivity of CC-SMS-EMOA to the number of orthogonal search directions
Full size table

Table 3 also shows an interesting pattern. It can be seen that on WFG test problems the median performances drop significantly as the number of search directions increases. On the UF test problems, on the other hand, there are cases where the performances improve as the number of orthogonal search directions increases. This may be attributed to the fact that some of the UF problems are designed to have complicated Pareto set structures as opposed to the straight lines for each diversity variable in the WFG test problems. A single search direction may struggle to get close to this Pareto set. With more search directions, larger parts of the search space can be explored. The orthogonal sampling method allows for flexibility in this regard. However, it is difficult to determine the optimum number of search directions beforehand because the shape of the Pareto set is unknown before optimization. It may be beneficial to tune/adapt the number of search directions as the search space is being explored.

Another observed result is that in most test problems in the experiments, directed sampling is outperformed by orthogonal sampling. Multiple line search is inferior to using orthogonal sampling in CC-SMS-EMOA.

6 Conclusion and future work

In this paper, an improved control variable analysis is proposed resembling the decision variable clustering and differential analysis which is referred to as CVA–DA. The method has higher accuracy than CVA, but it is also sensitive to the number of samples drawn.

It is also shown that, in a cooperative coevolution framework, the CVA–DA combined with the RDG3 can achieve higher performance than random grouping when the variables are strongly interacting. As the computational costs for the grouping methods are low, the weighted optimization framework may also benefit from using the proposed method, as opposed to random grouping, in problems with strong variable interactions.

For orthogonal sampling, in problems with a simple Pareto set, a single search direction is sufficient. However, in problems with a more complicated Pareto set, the optimal number of search directions cannot be determined easily. An adaptive scheme can potentially be applied to determine this. Additionally, the step size of the mutation can also be adapted to balance the exploration and exploitation of the search space.

For future work, Ma et al. (2021) mentioned that the decision variable clustering (and similarly, CVA–DA) cannot discern how much each variable affects convergence and/or diversity. It should be noted that the samples used in decision variable clustering and CVA–DA are suitable for DA and the purpose of doing DA is exactly to measure how much each variable affects the objectives. The only issue is that the DA normally can only process scalar functions. For a vectorial output, pre-processing is needed. An example of how DA is used on vectorial output is available in Strachan et al. (2015), Monari and Strachan (2017) where principal component analysis (PCA) is used to summarize the output. By using these techniques, the sensitivity indices can be exploited, e.g., as a basis for budget allocation.

It would also be compelling to implement mirrored orthogonal sampling in other frameworks such as the LMOEA-DS. The orthogonal sampling samples the offspring on sub-hyperplanes of the original problem instead of one-dimensional search directions as in LMOEA-DS and WOF. Such experiments would allow us to determine on which problems multiple line search directions are preferred and on which problems the orthogonal sampling is performing better.