Abstract
Quantum annealing, a method of computing where optimization and machine learning problems are mapped to physically implemented energy landscapes subject to quantum fluctuations, allows for these fluctuations to be used to assist in finding the solution to some of the world’s most challenging computational problems. Recently, this field has attracted much interest because of the construction of large-scale flux-qubit based quantum annealing devices. These devices have since implemented a technique known as reverse annealing which allows the solution space to be searched locally, and algorithms based on these techniques have been tested. In this paper, I develop a formalism for algorithmic design in quantum annealers, which I call the ‘inference primitive’ formalism. This formalism naturally lends itself to expressing algorithms which are structurally similar to genetic algorithms, but where the annealing processor performs a combined crossover/mutation step. I demonstrate how these methods can be used to understand the algorithms which have already been implemented and the compatibility of such controls with a wide variety of other current efforts to improve the performance of quantum annealers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The quantum annealing algorithm (QAA) (Finilla et al. 1994; Kadowaki and Nishimori 1998; Kaminsky and Lloyd 2002, 2004; Kaminsky et al. 2004) has been demonstrated to be a promising candidate for a vast number of real-world problems. The potential applications are too numerous to list here, but include fields as diverse as aerospace (Coxson et al. 2014), computational biology (Perdomo-Ortiz et al. 2012), neural networks (Amin et al. 2018; Benedetti et al. 2016, 2017; Adachi and Henderson 2015), pure computer science (Chancellor et al. 2016), and economics (Marzec 2016). In this manuscript, I discuss a formalism which can represent general control of quantum annealers. I demonstrate how this formalism can be used to design new algorithms based on multiple calls to a quantum annealer. More generally, this formalism represents hybrid analog-digital computation, but I restrict the discussion in this paper to quantum annealing applications, except for a brief discussion on how it can be related to classical Monte Carlo algorithms. For a review of quantum annealing, and the related field of adiabatic quantum computation, see Albash and Lidar (2018). For an outlook on the opportunities and challenges for quantum annealing, see Biswas et al. (2017).
The QAA as it is usually structured starts from a superposition state representing all possible solutions. The system is then annealed and quantum fluctuations are introduced through competition between a problem Hamiltonian and a ‘driver’ Hamiltonian which does not commute with the problem Hamiltonian
where \(0\le s \le 1\) is the annealing parameter which controls the annealing schedule, A(s(t)), B(s(t)), which are chosen such that \(\frac{A(0)}{B(0)}\gg 1\) and \(\frac{B(1)}{A(1)}\gg 1\), and both A and B behave monotonically with s. In traditionally formulated quantum annealing, s is also a monotonic function of t, but to construct the protocols here, I will consider cases where s is a non-monotonic function of t, as was discussed in Chancellor (2017). The problem Hamiltonian is usually chosen to be an Ising model,
with field variables \(h_i\) and coupler variables \(J_{ij}\). Ising model-based annealing architectures were first proposed in the context of closed quantum systems by Kadowaki and Nishimori (1998) and later generalized to open quantum systems by Kaminski et al. (2002, 2004). In this paper I consider open system quantum annealing, where tunneling mediated by these fluctuations is driven by a low temperature thermal bath. One example of a driver Hamiltonian is the transverse field driver which is currently implemented on the annealers produced by D-Wave Systems Inc. (2018).
I also consider more general multi-body driver Hamiltonians of the form
where, \(c_i\) is a positive real number which determines the strength of the coupling, \(R_i\) is a set of qubits, and
where \(a=\left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array} \right)\) is a lowering operator operator such that \(\sigma ^x=a+a^\dagger\). The reason such drivers are of interest is that they are able to introduce a sign problem in quantum Monte Carlo simulations if no basis exists for which all off diagonal terms are negative (Bravyi et al. 2008; Bravyi and Tehral 2009). No other method is known for large scale low temperature simulations of this class of Hamiltonians, which is called non-stoquastic (Bravyi 2014) (conversely, Hamiltonians where a basis exists with all negative off diagonal elements is called stoquastic). Because of this increased difficulty in simulation, it is widely suspected that quantum annealing with non-stoquastic drivers is more powerful than quantum annealing with stoquastic drivers. However recent work has emphasized the computational power of stoquastic drivers (Hastings 2020), and obstructions to complete emulation using quantum Monte Carlo have been known for some time (Andriyash and Amin 2017; Hastings 2013).
Recall that the QAA as it is usually formulated starts from an equal superposition of all classical solutions, meaning that there is no way to incorporate existing knowledge about the solution, neither from previous annealing runs nor from different algorithms. One way around this deficiency is to use algorithms based on local searches (Chancellor 2017; Amin and Johnson 2015) around a candidate solution rather than global searches which start from a superposition of all classical solutions. In particular, Chancellor (2017) includes proof-of-principle numerical experiments which demonstrated how such techniques may assist in a search. Reverse annealing has now been added as a feature of D-Wave devices which is available to remote users (D-Wave Systems Inc. 2019).
Since the introduction of the reverse annealing feature, there have been many promising proof-of-concept experiments to demonstrate its computational power. For example priming a reverse annealing algorithm with the result of a gradient decent algorithm (Venturelli and Kondratyev 2019) found that portfolio optimisation problems could be solved about 100 times faster. In Ottaviani and Amendola (2018) it was found that using a simple iterative strategy with reverse annealing D-Wave devices were able to solve non-negative matrix factorization problems which were not solved by simple forward annealing. A similar improvement for the same problem has also recently been observed in Golden and O’Malley (2020). Finally, it has been observed that by using reverse annealing to aid with mutation (as opposed to the methods discussed later which perform both mutation and crossover), the performance of a genetic algorithm in finding global optimum of spin glasses can be improved (King et al. 2019). The algorithm proposal have been called Quantum Assisted Genetic Algorithms (QAGA) With the exception of the last example, these are all incredibly simple applications of the protocol, as I demonstrate later using the inference primitive formalism developed in this paper. In spite of their simplicity these still could yield a large improvement, hinting at the potential power of more sophisticated algorithms and more control.
There are also alternate formulations which pre-dates the proposals in Chancellor (2017), Amin and Johnson (2015) which allow an initial guess (Perdomo-Ortiz et al. 2011; Duan et al. 2013; Graß 2019) to be incorporated into a closed system adiabatic quantum protocol. While protocols based on these techniques can also be represented with the inference primitive formalism, for this paper I will restrict the discussion to the local search formulation in Chancellor (2017). It also may be fruitful to explore connections to recent work exploring the use of a reinforcement algorithm (Ramezanpour 2017) in quantum optimization, although such a study is beyond the scope of this work.
In addition to representing the protocols in Chancellor (2017), I show that the formalism demonstrated here represents a more generalized control strategy which includes annealing the qubits independently. Such additional freedom allows for the annealer to accept individual uncertainty values for each bit, or cluster of bits in the case of multi-body drivers.
This formalism can be used to demonstrate a new way in which a combined crossover mutation step for genetic-like algorithms can be constructed using these individual uncertainty values. Generic algorithms, originally proposed by Holland (1975) are a powerful optimization tool based on combining different solutions to difficult optimization problems to obtain a solution with the best features of both. For an overview of the field, see Vikhar (2016), Srinivas and Patnaik (1994), MacKay (2003), and for some examples of applications see Deng and Fan (1999), Fogel (1994).
The idea of using an annealer for genetic algorithms is not new: in addition to the QAGA proposal in King et al. (2019), Coxson et al. (2014) experimentally demonstrated that a D-Wave device can successfully aid these algorithms in finding radar waveforms before the development of reverse annealing. The method I propose for genetic like algorithms, however, is completely general, and only requires that an annealer be able to realize a problem Hamiltonian, rather than a potentially more complex directed mutation Hamiltonian (the details of the methods used in Coxson et al. (2014) were not published, so it is not possible to know what the precise requirements would be).
The structure of this paper is as follows. In Sect. 2 I discuss the inference primitive formalism, how it relates to quantum annealers, and demonstrate how previously known algorithms such as the traditional QAA and those proposed in Chancellor (2017) may be represented using inference primitives. I also discuss how the recent experiments can be represented using this formalism. In Sect. 3 I discuss how annealer based genetic-like algorithms may be represented in this formalism and how it may be used to add genetic components to the algorithms proposed in Chancellor (2017). I also contrast my formulation (which combines mutation and crossover as a call to the annealing processor followed by post-processing) with traditional genetic algorithms and the QAGA methods (King et al. 2019). This is followed by a discussion in Sect. 4 about how the control represented in the inference primitive formalism is compatible many other recent advances in the field, including synchronization of freezing 4.1, higher order drivers, including non-stoquastic drivers 4.2, and belief propagation methods used to represent graphs larger than the hardware 4.3. Finally in Sect. 5 I conclude with some overall discussion.
2 Inference primitive
Consider a high level description of a subroutine \(\Phi\) which performs a guided search of an energy landscape based on known information about likely solutions. I will call such a subroutine an inference primitive, as it is designed to infer the correct solution based on input information. The inference primitive will be supplemented by information processing which determines the parameters to give each call to the primitive, I will call this the processing function \(\mathcal {F}\). I will demonstrate later in this section that \(\Phi\) can be a high level description of a call to a quantum annealer, with \(\mathcal {F}\) representing classical information processing used within a hybrid algorithms. I will also formally define both \(\Phi\) and \(\mathcal {F}\).
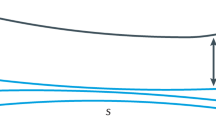
Before discussing the formalism further, I will motivate the use of this formalism to represent control of quantum annealers. It has recently been demonstrated in Chancellor (2017), that global transverse fields can be used to control the range of local search in solution space. Building on this idea, application of different transverse fields locally will cause an algorithm to search different ranges in different directions in solution space. In this way, the strength of local transverse fields can encode bitwise certainty of a solution. In fact, algorithms based on an extreme version of this have already been implemented (Karimi and Rosenberg 2017; Karimi et al. 2017), in which, based on previous solution statistics, qubits are either treated as taking fixed values (absolute certainty), or annealed using a traditional protocol (absolute uncertainty). To implement a protocol which incorporates local uncertainty, I generalize the methods given in Chancellor (2017), to allow different qubits to be annealed to different points \(s_i'\), as depicted in Fig. 1.
Annealing schedule for inference primitive protocol. This is the same as in Chancellor (2017) except that individual qubits are annealed back to different values of s. Qubits are annealed first with a simple Hamiltonian to program an initial state, then the Hamiltonian is reprogrammed to the problem Hamiltonian and each qubit (or multi-qubit driver) is annealed back to \(s'(P_i)\), where \(P_i\) is a measure of the uncertainty of a qubit value. The qubits are then annealed back toward \(s=1\), each starting its anneal when the other bits reach the same value of s. For \(s_i'=0\) (red, light gray in print), setting the initial value is unnecessary, as no information about the qubit value is known
In this paper, I will not focus on how to construct heuristics which relate uncertainty to transverse field strengths, but rather examine how algorithms can be designed and represented, assuming a suitable heuristic has been developed. I provide an example of a very simple heuristic in appendix 1. This heuristic is only intended as an example of how these quantities can be related, and may be too simplified to perform well in the real world. Alternative heuristics could be based on experimental local temperature estimates using the methods of Raymond et al. (2016), or by adaptations of the methods to estimate a global effective temperature used in Benedetti et al. (2016). For the remainder of this work, I will assume that a suitable heuristic, \(s_i'(\{P\})\), where the set notation has been used to emphasize that in general this parameter may also depend on the uncertainty \(P_i \in [0,0.5]\) of neighbouring qubits as well.
I have motivated the high level description of a quantum annealer as an inference primitive \(\Phi\), now I must further motivate that suitably chosen processing functions \(\mathcal {F}\) will be able to appropriately extract uncertainty information from the output data of a quantum annealer. To do this, I consider the problem of finding the ground state of a Sherrington-Kirkpatrick like spin glass (Sherrington and Kirkpatrick 1975):
where each \(J_{ij}\) is selected uniformly randomly from the range \([-1,1]\). All energy eigenstates of such Hamiltonians will be at least two fold degenerate because of total spin inversion symmetry. To break this symmetry I fix the last spin to be in the down orientation. This transformation results in the following effective \(n-1\) spin Hamiltonian.
where \(h_i=J_{in}\). For the proof-of-principle I generate 1500 such Hamiltonians with \(n=17\). I then run Path Integral Quantum Annealing (PIQA) 1001 times for each such Hamiltonian, following the methods used in Chancellor (2017), which were adapted from those in Martonak et al. (2002), but with \(T=0.8246\), \(\tau =20\) and \(P=30\). For each spin within each Hamiltonian, I compare the average value of the annealer output to a simple certainty value \(P_i\) calculated using
where G consists of the list of the 1001 solutions returned by PIQA (\(G_i \in \{1,-1\}\)). I then break these spins up into two categories, those where \(S_i\) found by Eq. (7) agrees with the true solution found by exhaustive classical search, and those where it does not. As Fig. 2 clearly shows, the larger the value of \(P_i\) becomes, the more likely it is that the bit value is incorrect. Therefore the statistics of our simulated quantum annealer outputs not only information about the probable value of a bit in a given solution, but also about the relative certainty of different bit values. How effectively this information is used depends on the heuristic used in \(\mathcal {F}\), I discuss a few examples of how \(\mathcal {F}\) could be constructed in Sect. 3.1.
Historgam of \(P_i\) for spin values obtained by the ‘traditional’ QAA on 1500 instances of spin glass problems described by Eq. (6) with \(n=17\), (\(1500\times (n-1)=24,000\) data points). Data are based on PIQA runs with \(T=0.8246\) and \(\tau =20\) using the same numerical methods as the proof of principle in Chancellor (2017). Blue (light gray in print) bars are cases where \(S_i\) found by Eq. (7) agrees with the true ground state, red (dark gray in print) are cases where it does not, and unfilled bars are total counts
2.1 Definitions
I now define a mathematical representation of the computational subroutine I have described earlier. Firstly I consider a system of \(N_{\mathrm {bits}}\) bits. To simplify some mathematical definitions which I will give later and for consistency with spin Hamiltonian definitions, I allow these bits to take values \(\{1,-1\}\), rather than \(\{1,0\}\). I further define clusters \(R_i\) which each consist of a unique, non-empty set of these bits, as represented in Fig. 3a.
I also define an inference primitive \(\Phi\), which takes as inputs a list of guesses for the value of the bits, S, as well as uncertainty values P for each cluster in R. An inference primitive in turn outputs a list of solution candidates G, and a list of associated energies for each candidate E. Each solution candidate consists of \(N_{\mathrm {bits}}\) numbers, each corresponding to a bit value of \(\{1,-1\}\). The energy value \(E_i=\left\langle G_i \mid H_{problem} \mid G_i \right\rangle\) tells how optimal each solution value is, where lower values indicate a higher level of optimality. Lists G and E must have the same length, which I refer to as \(N_{\mathrm {out}}\). Figure 3b represents an inference primitive visually. In practice, the role of \(\Phi\) will be played by a call to an analog computational element, in the case of this paper, a quantum annealer.
Visual explanation of functions used within an inference primitive protocol. a Sets of one or more bits (black circles) \(\{R\}\) represented by green ovals, b inference primitive \(\Phi\), c processing function \(\mathcal {F}\). All quantities are defined in Table 1.
In the absence of multi-bit clusters, S and P could be defined as a single ‘mean’ bit value for each bit which could be written as \(v_i=(1-P_i)\,S_i\in [-1,1]\). However, this notation does not easily generalize to include multi-bit clusters, and therefore I represent S and P as distinct quantities where \(|S|\le |P|\). Parametrizing in terms of S and P is natural as these two quantities map to different control parameters within an annealing protocol.
In addition to the inference primitive, I also define a mathematical function which I call the processing function \(\mathcal {F}\). This function takes as its input a list of lists \(\mathcal {G}\), each element of which is a list G of solution candidates. This function likewise takes \(\mathcal {E}\) as an input, which is a list of lists E of the associated energies for each solution candidate. The lists \(\mathcal {G}\) and \(\mathcal {E}\) must have the same length which I call \(N_{\mathrm {inputs}}\). Generally, \(\mathcal {G}\) and \(\mathcal {E}\) will be allowed to be empty (\(N_{\mathrm {inputs}}=0\)). This function outputs a list of guesses for the values of each of the bits S, and an uncertainty value P for each cluster in R. A processing function is represented visually in Fig. 3c.
I have now defined an inference primitive \(\Phi\), the outputs of which can be used to construct the inputs of a processing function \(\mathcal {F}\), in turn the outputs of \(\mathcal {F}\) can be used as the inputs of \(\Phi\). The mathematical functions and their associated inputs and outputs define the basic structure of the inference primitive framework, these mathematical functions can be expressed diagrammatically as depicted in Fig. 3 and this diagrammatic representation can be used to express sophisticated protocols as discussed in Sects. 2.2 and 3.2.
It is useful to give a few more definitions of mathematical quantities which will become important in specific examples which I will give later in this paper. In particular, to define ways in which \(\mathcal {G}\) and \(\mathcal {E}\) can be reduced to lists, rather than lists of lists. I first consider ‘flattened’ versions of the lists \(\mathcal {G}\) and \(\mathcal {E}\), \(\tilde{G}=\mathcal {G}_1\cup \mathcal {G}_2 \cup ...\) and \(\tilde{E}=\mathcal {E}_1\cup \mathcal {E}_2 \cup ...\), both will have length \(N_{\mathrm {flat}}=N_{\mathrm {inputs}}\,N_{\mathrm {out}}\). These flattened versions contain all of the information within the original lists \(\mathcal {G}\) and \(\mathcal {E}\) except for information about where each solution candidate came from. As I will discuss later, many processing functions may be constructed for which information about where each solution candidate originated is not important. A second pair of useful quantities is the list of unique solution candidates in \(\tilde{G}\), and their associated energies. I label these quantities \(\tilde{G}^{(u)}\) and \(\tilde{E}^{(u)}\), with a new length \(N_u\le N_{\mathrm {flat}}\).
As a convention, for \(\tilde{G}\) and \(\tilde{G}^{(u)}\), which are both solution candidate lists, I use a subscript to refer to the solution number and put the list of bits to be considered as a functional argument. For instance \(\tilde{G}_j(i)\) is the value of the ith bit in solution candidate number j. Alternatively, \(\tilde{G}_j[R_i]\) is the list of all of the bit values over the cluster \(R_i\) in solution candidate number j. For S, which only has a bit index, I use the subscript to refer to the bit cluster, so for instance \(S_i\) refers to the value of the inferred bit value of bit i and while \(S_{R_i}\) refers to the list of inferred bit values on the cluster \(R_i\), expressed mathematically \(S_{R_i}=\{S_x: x \in R_i\}\).
For single bit clusters, the solution candidates can be divided into two groups based on the value of the bit. For multi-bit clusters the picture is more complicated, one quantity which I will demonstrate later is convenient to define is a weighting factor, \(W(\tilde{E}_j,\tilde{G}_j[R_i],S_j)\) which weights the importance of each state to calculating P for the cluster. Based on these weighting factors, I define
where \(M_j=\sum _{k\in R_j} S_k \frac{\tilde{G}_j(k)}{|R_j|}\), and the minimum value is taken to guarantee that \(P_i \in [0,0.5]\). Here, I use piping symbols \(|\star |\) to refer to the length of a list, so for instance |R| means the number of elements in the list R. For simplicity, one can further restrict this study to functions W which can be decomposed into two parts, one which depends purely on \(\tilde{E}\), and one which depends purely on S such that
2.2 Examples with existing protocols
Let us now discuss in more detail how to construct algorithms based on inference primitives from quantum annealers. As an example, I will first explicitly demonstrate how both the traditional QAA and the simplest local search method of Chancellor (2017) can be re-expressed in terms of inference primitives.
The traditionally formulated QAA is not biased toward a particular state, we formulate a processing function \(\mathcal {F}_{\mathrm {init}}\) which takes no inputs and returns \(P_i=0.5\,\forall i\). For these values of P, the values of S do not matter, so we set them to be all 1 without loss of generality,
In general, the traditional QAA can be augmented by sophisticated post processing, (Nishimura et al. 2016; Douglass et al. 2017; Bian et al. 2014, 2016), and therefore after the inference primitive, we should include a second processing function \(\mathcal {F}_{\mathrm {post}}(G,E,R)\) to include all of these possibilities. This representation is depicted on the left of Fig. 4. This diagram can also represent more sophisticated initialization, such as choosing a classical state to bias toward, as was done in Venturelli and Kondratyev (2019), this would only require the substitution of a more complicated \(\mathcal {F}_{\mathrm {init}}\) which produces the initial guess. The hybrid methods used in Douglass et al. (2017), Bian et al. (2014, 2016) actually use multiple runs with changing problem definitions to solve a problem, and therefore constitute many repeated runs of the protocol depicted on the left of Fig. 4. The reverse annealing protocols in Ottaviani and Amendola (2018), Golden and O’Malley (2020) fall into the category of algorithms represented by the right side of this diagram. I discuss in Sect. 4.3 how such existing hybrid techniques may be combined with more sophisticated inference primitive protocols.
Left: Traditional QAA or reverse annealing initialised based on the outcome of a classical algorithm formulated in terms of inference primitives and processing functions, where \(\mathcal {F}_{init}\) is defined in Eq. (11). Right: local search protocol formulated in terms of inference primitives and processing functions, the general for \(\mathcal {F}_{ls}\) is given in Eq. (12)
For the local search protocols considered in Chancellor (2017), the results of previous calls to the inference primitive are used sequentially, with the result of a previous call being fed into the next iteration of the protocol, as depicted on the right of Fig. 4. In this case, however, there is only one global value of \(P_i=p\,\forall i\) which defines the uncertainty, the processing function which is run at each step can therefore be defined as
where \(p'\) is the global value of P to be used for the next local search, and the protocol is run iteratively with \(p\leftarrow p'\) and \(S\leftarrow S'\) at each step. This formalsim can further be generalized to represent another class of hybrid annealer based algorithms, which can be used without any reverse annealing capabilities. These algorithms, which have been shown to be successful in Karimi and Rosenberg (2017), Karimi et al. (2017) work by ‘fixing’ some qubits by removing them from the problem description and replacing them with appropriate field terms to match the state which they are assumed to take. This kind of process allows an annealer without reverse annealing to be represented by an inferrence primitive where \(p_i\) is restricted to only take values of either 0, indicating that a spin is to be ‘fixed’ or 0.5 for those which are not removed and will be annealed normally. The representation of these algorithms in the inferrence primitive formalism are therefore exactly the same as the ones for the local search given in Fig. 4, but with
where \(P'_i \in \{0,0.5\}\).
Structure of the poplution annealing inspired protocols from Chancellor (2017) expressed in the inference primitive formalism
Going beyond simple local search (Chancellor 2017), protocols incorporating local search that are inspired by the state-of-the-art optimization techniques of parallel tempering (Swendsen and Wang 1968; Earl and Deem 2005) and population annealing (Hukushima and Iba 2003; Matcha 2010; Wang et al. 2015; Barzegar et al. 2017), these algorithms can be represented in this framework. The processing function and inference primitives will still have the general local search structure in Eq. 12, but generally allow \(\{G,E\}\) to be copied (in the case of population annealing) or exchanged between sets of inferrence primitives with different p values. The structure of the population annealing inspired protocol is depicted in Fig. 5, while the structure of a parallel tempering inspired protocol is depicted in Fig. 6.
Structure of the parallel tempering inspired protocols from Chancellor (2017) expressed in the inference primitive formalism
Since quantum annealing is often considered a quantum analog to simulated annealing, it is worth briefly considering how those methods could be interpreted using the formalism introduced here. This is especially appropriate considering that much of the work in hybrid quantum annealing algorithms, particularly in Chancellor (2017) could be thought of as bringing intuition developed for classical Monte Carlo methods into use for quantum annealing. The most faithful way to translate the methods here to more traditional Monte Carlo methods is to consider each call to the inference primitive \(\Phi\) to be a call to a Metropolis Hastings algorithm (Metropolis et al. 1953; Rosenbluth 2003) at a given temperature and number of updates. The processing function \(\mathcal {F}\) can in turn be viewed as passing the initial state and the temperature (which can be viewed as global certainty as expressed in Eq. 12). A simple call to Metropolis Hastings at a fixed temperature therefore has the structure given in Fig. 4 (left) since the algorithm is called with a fixed set of parameters, although it could also be viewed as a call to the algorithm depicted in the right figure, but where each processing function acts trivially and does not change the parameters.
Since simulated annealing sweeps the temperature rather than leaving it fixed, it must be represented as a diagram in the form of Fig. 4 (right). Furthermore, the more advanced Monte Carlo algorithms of population annealing and parallel tempering in this analogy would directly take the form of Figs. 5 and 6 respectively, but with probability replaced with temperature. The fact that a simple adaptation of the formalism here can be used to express powerful classical Monte Carlo algorithms helps demonstrate its potential for developing hybrid quantum/classical algorithms.
3 Algorithmic design
As well as being a powerful tool for expressing currently proposed algorithms, the intended purpose of the inference primitive formalism is to design new algorithms. This formalism depicts the different possible ways for information to flow between classical processing and a quantum ‘inference primitive’ subroutine in a high level way, and therefore can be used to express different algorithmic possibilities in terms of information flow. Thus far, we have only considered processing functions which take outputs from a single call to an inference primitive, however, processing functions can be constructed which take information from multiple inference primitive calls. Using processing functions in this way represents a combined crossover and mutation step in a genetic-like algorithm. While the focus of this paper is on developing the inference primitive formalism for design of annealer algorithms, rather than to design specific heuristics, it is still useful to discuss examples how different processing function heuristics can be constructed, which I do in the next subsection.
3.1 Processing function heuristics
Although the primary purpose of this paper is not to design algorithms, it is worth briefly discussing what form the heuristics in the processing function could take, including some examples which are direct extensions of work which has already been done. While testing these heuristics would be useful, doing it properly would be quite an involved task, and therefore beyond the scope of the current work. The focus of this work is to examine how new algorithms can be designed for a quantum annealer with generalized controls, not to study relative algorithm performance.
Recall that I have already discussed heuristics to convert probability values for each qubit into the actual \(s'\) values which will be supplied to the annealer. In the inference primitive formalism details of the exact experimental implementation are contained with the inference primitive \(\Phi\) itself, rather than the processing function \(\mathcal {F}\). In this subsection however, I focus on the processing function \(\mathcal {F}\) which provides uncertainty information which can then be converted to experimental parameters in the inference primitive.
For simplicity, let us start with cases where the processing function \(\mathcal {F}\) only has a single stream of input values from the inference primitive \(\{G,E\}\). In this case, the simplest thing to do is just to take statistics over the raw data, calculating the probability that a bit will take a certain value directly by averaging over G with no regard for E, as was done in Eqs. 7 and 8. Such a simplistic approach relies on the ability of the inference primitive, for instance a quantum annealer, to always find highly optimal states. However, in practice real devices may only occasionally sample very high quality solutions and often return ones of low quality.
One approach to mitigate the fact that some solutions in G may not be very optimal is to only consider candidates which have an energy below an ‘elite threshold’, this approach has already proved useful in hybrid algorithms used in Karimi and Rosenberg (2017), Karimi et al. (2017) which do not require an initial state to be seeded. Those papers, however, were based on annealers which did not have reverse annealing capabilities. With reverse annealing capabilities (and independent annealing controls of individual qubits), their method can be extended to include the possibility where the direction of a state of a qubit is suspected but should not be assigned with \(100\%\) certainty. A simple generalized processing function in this case could take the form:
where \(\Theta\) is the Heaviside step function defined so that \(\Theta (a)=1\) if \(a>0\) and \(\Theta (a)=0\) otherwise, and \(E_{\mathrm {elite}}\) is the elite energy threshold, as assigned in Karimi and Rosenberg (2017), Karimi et al. (2017). Note that, as implemented in those papers, any qubit with \(P_i=0\) can be excluded from the actual annealer run and replaced with field terms.
Rather than using a hard cutoff, another way to give preference to low energy solution candidates when calculating S and P is to thermally reweight each of the unique candidates
where the (u) superscript indicates a set of solution candidates and energies where duplicate candidates in \(G_i\) have been removed. In this case, T can be thought of as a meta-parameter which controls the effective range of the search that will be performed by the inference primitive. This suggests that one algorithmic possibility could be to run a series of inference primitive calls as depicted in Fig. 4 (right), but with successively decreasing T as a simulated annealing analogue.
Thus far we have only considered processing functions \(\mathcal {F}\) which take a single \(\{G,E\}\), however, for genetic-like algorithms, we need to define processing functions which take sets of inference primitive outputs \(\{\mathcal {G},\mathcal {E}\}\). One way to construct such processing function heuristics is to create flattened lists, which treat all solution candidates as if they came from a single inference primitive, these flattened data \(\{\tilde{G},\tilde{E}\}\) can then be used directly in heuristics such as those discussed earlier in this section. Not all processing functions can be represented in this way, however, for example a processing function \(\mathcal {F}\) could take the lowest energy solution candidate from two different \(\mathcal {G_i}\in \mathcal {G}\) and assign \(P_i=0.5\) to bits which disagree between the two and \(P_i=p\) where \(0<p<0.5\) to those which do.
3.2 Algorithm structure
Now that I have given examples of how processing function heuristics can be constructed, it is worth briefly considering how the inference primitive formalism can be used as a graphical tool to understand algorithmic applications. To start out, let us contrast a traditionally formulated genetic algorithm with a simple genetic-like algorithm built using the inference primitive formalism. Let us start by reviewing a simple traditionally formulated genetic algorithm, which starts with a population, which is a pool of solution candidates which have either been generated randomly, or have come from a previous iteration of the algorithm, this pool of states undergoes the following three steps:
- Selection:
-
The most fit solution candidates are chosen to breed and form the next generation, discarding the less fit candidates.
- Crossover:
-
Pairs of solution candidates are spliced together to form a pool of new solutions.
- Mutation:
-
Small random changes are made after crossover to ensure diversity in the pool of states.
These steps are then applied repeatedly on the population until the algorithm converges or until a solution candidate of sufficient quality is observed. A genetic like algorithm which uses a quantum annealer as an inference primitive would similarly start with a population, made either of single states or ensembles of states output by the annealer. This population similarly undergoes three steps:
- Selection:
-
The most fit solution candidates are chosen to breed and form the next generation, discarding the less fit candidates. This is performed in the same way as in a traditional genetic algorithm.
- Processing function:
-
Annealer inputs constructed based on a pair of inputs, recall that this can be done in a variety of ways.
- Inference primitive:
-
Annealer is called based on output of processing function, the outputs make the new population.
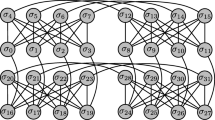
As with a traditional genetic algorithm, these steps can be repeatedly applied until the algorithm converges or until a solution candidate of sufficient quality is observed. To some extent, the processing function can be thought of as analogous to crossover, while the inference primitive itself, or the call to the annealer can be thought of as analogous to mutation. This analogy is appropriate in one sense, because like crossover in a traditional genetic algorithm, the processing function is responsible for determining how the information from each annealer output is combined, and is a deterministic processFootnote 1. The call to the inference primitive, in other words the annealer itself, is non-deterministic in nature, and this superficially similar to mutation, in that it produces a variety of states randomly based on the input from the processing function. This analogy breaks down when considering the details of how the information is being processed however, the output of the processing function is not of the same form as the population, it is a set of control inputs for the annealer, therefore it does not exactly perform a crossover, it combines the information in such a way that the inference primitive can perform a randomized crossover which has mutation built in. Since the inference primitive is also performing part of the crossover as well as the mutation, it is likewise not appropriate to think of this step as only a mutation step. A visualization of this process using the inference primitive formalism appears in Fig. 7.
Although the protocol is different, the structure in Fig. 7 is also shared by the QAGA proposed in King et al. (2019). The key difference between these algorithms is that the annealer is only used for mutation in that algorithm rather than mutation and crossover as proposed here. One important observation about this structural similarity is that it means that the QAGA methods could also be applied to the more complicated algorithmic structures discussed later in this paper
Structure of an analogue of a genetic algorithm constructed using the inference primitive formalism (right labelling). This diagram also represents the structure of the QAGA proposed in King et al. (2019) with the left labelling
Now that we have discussed how to build an analogue of a standard genetic algorithm, it is worth discussing more advanced usage of the formalism, for instance how a genetic component can be added to the population annealing algorithm depicted in Fig. 5 by allowing multiple edges to be incident on each processing function, as depicted in Fig. 8. Because of the way the total population is controlled in these algorithms (see Hukushima and Iba 2003), adding a fixed number of extra processing functions which accept two or more inputs to produce offspring will not cause the population to grow (or shrink) uncontrollably. In this example, which inference primitive outputs get to produce extra offspring could be chosen for instance by drawing two or more from a Boltzmann probability distribution constructed from the lowest energy given by each inference primitive call (as was suggested in Chancellor (2017) \(P_j=\exp (-\min (\mathcal {E}_j)/T_{\mathrm {eff}})/Z\) without replacement. The genetic like component could also be replaced by a QAGA type call, where the qubits are not individually biased, and the reverse annealing step is used for only mutation rather than crossover and mutation, in this case crossover would have to be performed as it is in traditional genetic algorithms.
The inference primitive formalism can also demonstrate how we can add a genetic component to a parallel tempering inspired algorithm. In such an algorithm one can replace each single call to an inference primitive at an effective temperature with a pair of calls, and than combine these outputs in a ‘hybridization pool’ consisting of inference primitive calls based on pairs of inference primitive outputs as depicted in Fig. 9. As with the population annealing methods, the genetic component could be replaced with a QAGA type call, with crossover performed using more traditional methods. These hybridization results could then be reinserted into the main pool of inference primitive calls probabilistically, one way to accomplish this is to use the process outlined below:
-
1
Produce ‘genetic pool’ of inference primitive outputs, for instance using some of the methods discussed in the previous subsection.
-
2
For each set of inference primitive outputs in the genetic pool, \(\{G^{\mathrm {hyb}},E^{\mathrm {hyb}}\}\), starting from the lowest \(T_{\mathrm {eff}}\) and increasing, have this set of outputs replace a set in the standard inference primitive pool probabilistically with a probability determined by
$$\begin{aligned} P_{\mathrm {ex}}=\min \left( \exp (\frac{\min (E^{\mathrm {hyb}})-\min (E)}{T_{\mathrm {eff}}}),1\right) , \end{aligned}$$where \(T_{\mathrm {eff}}\) is the effective temperature which has been used on the inference primitive in the parallel tempering pool. If either a replacement has been performed, or all inference primitive outputs in the regular parallel tempering pool have been tested and none have been replaced, move on to the next set of hybridzation outputs. In the case where a replacement has been successfully performed discard the inference primitive outputs which have been replaced, otherwise, discard the outputs in the genetic pool. Once all outputs in the gentic pool have been either discarded or used as replacements, move on to the next step.
-
3
Perform parallel tempering inspired swaps using the standard update rules as described in Chancellor (2017).
Step 2 could also be performed using the QAGA methodology, and the inference primitive diagram would remain the same, however the inference primitive and processing function used within the genetic pools would function differently than in the genetic-like algorithm I have described in this paper. There are also many other algorithms which can be discovered using the inference primitive formalism. The two ideas here are included to give examples of how the inference primitive formalism can be used as a tool to visualize information flow in annealer based algorithm design.
4 Compatibility with other methods
Now that I have demonstrated the power of the inference primitive formalism in terms of designing algorithms based on quantum annealers with generalized classical controls (and representing those which have already been used), I turn my attention to how these methods are compatible with many methods which currently represent the state of the art, as well as techniques which are now on the horizon. This section is not supposed to be an exhaustive list, but rather to give the reader an idea of the versatility of inference primitive based annealer computation.
4.1 Protocol modifications
The first techniques which I discuss are techniques developed by D-Wave Systems Inc. to advance or retard individual qubits to synchronize freezing (Lanting et al. 2016) using an effective local temperature estimated using the methods in Raymond et al. (2016). These methods apply to the relative values of the annealing parameter s during the final forward anneal, a parameter which is not fixed by the inference primitive protocol described in Sect. 2, and therefore freezing can be synchronized by advancing or retarding the point at which one qubit begins its final forward anneal relative to the other qubits, as depicted in Fig. 10.
The anneal offset feature, as implemented on D-Wave devices Andriyash et al. (2016) combined with reverse annealing performs a combination of the protocol depicted in Fig. 10 and the variation of \(s'\) depicted in Fig. 1. In principle this feature could be used to create inference primitives as described in this paper, but also with potentially unintentional consequences from varying the qubit freeze time. The use anneal offsets to perform biased searching will be explored experimentally in Chancellor (2020).
4.2 Higher order drivers
Let us now consider generalizations of inference primitive protocols for multi-body drivers, which are necessary to realize non-stoquastic drivers, for example. Previously, R has just been a list of every qubit, but now will also include some clusters of qubits which are flipped simultaneously by multibody drivers. To determine the strength at which multibody drivers are applied, one should consider statistics over the overlap of each of the members of \(G_j\) with the solution candidate S over the relevant cluster, \(M_j=\sum _{k\in R_j} S_k \frac{\tilde{G}_j(k)}{|R_j|}\) where \(|R_j|\) is the number of elements in \(R_j\). When \(M_j=1\), then the cluster agrees exactly for the candidate solution and the \(\tilde{G}_j[R_i]\). The value \(M_j=-1\) indicates perfect disagreement. The uncertainty value \(P_i\) for the cluster \(R_i\) corresponds to the probability that \(S_{R_j}\) is closer in Hamming distance to the correct solution than \(\lnot S_{R_j}\). Positive \(M_j\) indicates that \(S_{R_j}\) is the closer of the two, whereas negative indicates that \(\lnot S_{R_j}\) is closer.
For each cluster, we formulate a weighted sum to determine the probability that \(S_{(R_i)}\) is closer. To achieve this, I define P in terms of a weighting factor W using Eq. (9). For simplicity, I assume that W can be decomposed into two terms such that \(W(\tilde{E}_j,\tilde{G}_j[R_i],S_{(R_i)})= \hat{W}(\tilde{E}_i)\bar{W}(\tilde{G}_j(R_i),S_{(R_i)})\). For the energy dependent part, one could for example define \(\hat{W}(\tilde{E}_i)=\exp (\frac{-\tilde{E}_i}{T})\) corresponding to the thermal weighting as in Eq. (17), \(\hat{W}(\tilde{E}_i)=1\) for unweighted averages as in Eq. (8), or finally \(\hat{W}(\tilde{E}_i)=\Theta (\tilde{E}_{elite}-E_i)\) for a multi-bit analogue of the elite averages used in Eq. (15). As for \(\bar{W}(\tilde{G}_j[R_i],S_{(R_i)})\), it should be weighted to favor \(|M_j|\) close to 1, as these are the values for which cluster flips will make the largest difference. A logical choice is therefore to choose weights which are inversely proportional to the number of states within the same Hamming distance from either \(S_{(R_j)}\) or \(\lnot S_{(R_j)}\),
where \(|R_j|\) indicates the number of elements in the set, and \(\mathcal {D}(S_{(R_i)},\tilde{G}_j[R_i])\) indicates the Hamming distance between the two lists.
4.3 Belief propagation
For the current generation of annealers, with hardware graphs which are relatively small compared to the size of many relevant problems, it is important to be able to solve problems which are larger than the available hardware graph. The general method to do this is to solve problems on modified subgraphs of the hardware graph in an algorithmic way (Bian et al. 2014, 2016; Douglass et al. 2017), eventually converging on a single consistent solution. In this paper I will focus on one particular method, the generalized belief propagation method proposed in Bian et al. (2016) based on earlier work in Yedidia et al. (2005). Although only exact for tree graphs, belief propagation has proven to be an important tool for solving a host of important real world problems, most notably decoding Low Density Parity Check Codes (LDPC) (Kschischang et al. 2006; Mceliece et al. 1998). The belief propagation method described in Bian et al. (2016) performs belief propagation between hardware-sized subgraphs to obtain an approximate thermal distribution.
Because this method obtains a distribution, rather than a single state, it can be used effectively as an inference primitive and therefore can be used as a subroutine in all of the previously discussed algorithms, using the same \(\{R, S,P\}\) throughout the protocol until either convergence is found or a timeout occurs. However, the marginals which are calculated throughout the protocol carry beliefs about the likely value of a bit and its uncertainty. The protocol can be made more efficient by using this information to update \(\{S,P\}\), whenever the beliefs are updated. With fixed \(\{S,P\}\) new information about bit values is wasted. If one of the bit values \(S_i\) with a low value of \(P_i\), became inconsistent with the others during the course of this protocol it would likely not be able to correct for this inconsistency and may either fail to converge or return a low quality solution.
In the algorithm proposed in Bian et al. (2016), each bit has an associated marginal, \(b_i(z_i)\), which contains information about the relative likelihood of a bit having a value of 1 or \(-1\). Based on a normalized version of this marginal, we can find an approximate value for \(S_i\) and \(P_i\) which dynamically updates at each step of the protocol:
5 Conclusions
In this paper I have proposed a new way of thinking about algorithms based on a quantum annealer with generalized classical controls. I have given examples both of how existing quantum annealer based algorithms can be represented in this formalism and how this formalism can be used to design new algorithms, including algorithms with genetic components. While the algorithms proposed here will not in general obey detailed balance, they could allow for a more complete accounting of the low energy local minima of an energy landscape, and therefore may be useful for calculating thermal distributions if used with appropriate post processing. To motivate this formalism I have given a proof-of-principle demonstration that the output of annealer runs contain information not only about the likely solution to a problem Hamiltonian, but also the relative bitwise uncertainty.
Although a full analysis is beyond the scope of this paper, it would likely be interesting to explore the connection between the methods proposed here and quantum inspired diffusion Monte Carlo algorithms as discussed in Jarret et al. (2016, 2017), which show similar structure in the methods with which they solve problems. It would likewise be interesting to develop inference primitives based on other physical mechanisms, such as closed system adiabatic quantum computing, or quantum walks. It would also be interesting to run comparisons of algorithms designed with this formalism on real devices to determine their performance, and to design more algorithms. The algorithms given in this paper are only intended as examples of how the design techniques I have developed can be used, this paper has only scratched the surface of the algorithmic possibilities for this functionality of a quantum annealer.
Notes
Up to the fact that where the two genomes are spliced together may be chosen randomly.
References
Alejandro P-O, Venegas-Andraca Salvador E, Alán A-G (2011) A study of heuristic guesses for adiabatic quantum computation. Quant Inform Process 10(1):33–52
Amin Mohammad H, Evgeny A, Jason R, Bohdan K, Roger M (2018) Quantum boltzmann machine. Phys Rev X 8:021050
Benedetti M, Realpe-Gómez J, Biswas R, Perdomo-Ortiz A (2016) Estimation of effective temperatures in quantum annealers for sampling applications: a case study with possible applications in deep learning. Phys Rev A 94:022308
Berger AL et al (1996) A maximum entropy approach to natural language processing. Comput Linguist 22:39
Bian Z et al (2014) Discrete optimization using quantum annealing on sparse Ising models. Front Phys 2:56
Bravyi S, Tehral BM (2009) Complexity of stoquastic frustration-free Hamiltonians. SIAM J Comput 39(4):1462
Bravyi S, DiVincenzo DP, Oliveira RI, Terhal BM (2008) The complexity of stoquastic local Hamiltonian problems. Quant Inf Comp 8(5):0361–0385
Chancellor N (2017) Modernizing quantum annealing using local searches. New J Phys 19(2):023024
Chancellor N, Zohren S, Warburton P, Benjamin S, Roberts S (2016) A direct mapping of max k-SAT and high order parity checks to a chimera graph. Sci Rep 6:37107
Davide V, Alexei K (2019) Reverse quantum annealing approach to portfolio optimization problems. Quant Mach Intell 1(1):17–30
Deng X, Fan P (1999) New binary sequences with good aperiodic autocorrelations obtained by evolutionary algorithm. IEEE Commun Lett 3(10):288–290
Earl DJ, Deem MW (2005) Parallel tempering: theory, applications, and new perspectives. Phys Chem Chem Phys 7:3910–3916
Finilla AB, Gomez MA, Sebenik C, Doll DJ (1994) Quantum annealing: a new method for minimizing multidimensional functions. Chem Phys Lett 219:343–348
Fogel DB (1994) An introduction to simulated evolutionary optimization. IEEE Trans Neural Netw 5(1):3–14
Frieden BR (1972) Restoring with maximum likelihood and maximum entropy. J Opt Soc Am 62:511
Gilmore CJ (1996) Maximum entropy and Bayesian statistics in crystallography: a review of practical applications. Acta Crystallogr A 52:561
Hamed K, Gili R, Katzgraber Helmut G (2017) Effective optimization using sample persistence: a case study on quantum annealers and various monte carlo optimization methods. Phys Rev E 96:043312
Hastings MB (2013) Obstructions to classically simulating the quantum adiabatic algorithm. Quantum Info Comput 13(11–12):1038–1076
Jarret M, Jordan SP, Lackey B (2016) Adiabatic optimization versus diffusion Monte Carlo methods. Phys Rev A 94:042318
Kadowaki T, Nishimori H (1998) Quantum annealing in the transverse Ising model. Phys Rev E 58:5355
Karimi H, Rosenberg G (2017) Boosting quantum annealer performance via sample persistence. Quant Inform Process 16(7):166
Kohji N, Hidetoshi N, Ochoa Andrew J, Katzgraber Helmut G (2016) Retrieving the ground state of spin glasses using thermal noise: Performance of quantum annealing at finite temperatures. Phys Rev E 94:032105
Kschischang FR, Frey BJ, Loeliger HA (2006) Factor graphs and the sum-product algorithm. IEEE Trans Inf Theor 47:498–519
Marcello B, John R-G, Rupak B, Alejandro P-O (2017) Quantum-assisted learning of hardware-embedded probabilistic graphical models. Phys Rev X 7:041052
Martonak R, Santoro GE, Tosatti E (2002) Quantum annealing by the path-integral monte carlo method: The two-dimensional random Ising model. Phys Rev B 66:094203
Matcha J (2010) Population annealing with weighted averages: a Monte Carlo method for rough free energy landscapes. Phys Rev E 82:026704
Mceliece RJ, Mackay DJC, Cheng J (1998) Turbo decoding as an instance of Pearls belief propagation algorithm. IEEE J Select Areas Commun 16:140–152
Mistrulli PE (2011) Assessing financial contagion in the interbank market: maximum entropy versus observed interbank lending patterns. J Bank Finance 35:1114
Nicholas M, Rosenbluth Arianna W, Rosenbluth Marshall N, Teller Augusta H, Edward T (1953) Equation of state calculations by fast computing machines. The J Chem Phys 21(6):1087–1092
Nishimori H (1980) Exact results and critical properties of the Ising model with competing interactions. J Phys C: Solid State Phys 13:4071
Otsubo Y et al (2012) Effect of quantum fluctuation in error-correcting codes. Phys Rev E 86:051138
Perdomo-Ortiz A, Dickson N, Drew-Brook M, Rose G, Aspuru-Guzik A (2012) Finding low-energy conformations of lattice protein models by quantum annealing. Sci Rep 2(571):1–7
Phillips SJ et al (2006) Maximum entropy modeling of species geographic distributions. Ecol Model 190:231
Qian-Heng D, Shuo Z, Wei W, Ping-Xing C (2013) An alternative approach to construct the initial hamiltonian of the adiabatic quantum computation. Chin Phys Lett 30(1):010302
Ramezanpour A (2017) Optimization by a quantum reinforcement algorithm. Phys Rev A 96:052307
Raychaudhur S et al (2002) Associating genes with gene ontology codes using a maximum entropy analysis of biomedical literature. Genome Res 12:203
Rosenbluth Marshall N (2003) Genesis of the monte carlo algorithm for statistical mechanics. AIP Conf Proc 690(1):22–30
Ruján P (1993) Finite temperature error-correcting codes. Phys Rev Lett 70:2968–2971
Sherrington D, Kirkpatrick S (1975) Solvable model of a spin-glass. Phys Rev Lett 35:1792–1796
Srinivas M, Patnaik LM (1994) Genetic algorithms: a survey. Computer 27(6):17–26
Swendsen RH, Wang JS (1968) Replica monte carlo simulation of spin-glasses. Phys Rev Lett 57:2607
Tameem A, Daniel L (2018) Adiabatic quantum computation. Rev Mod Phys 90:015002
Tobias G (2019) Quantum annealing with longitudinal bias fields. Phys Rev Lett 123:120501
Wang W, Machta J, Katzgraber HG (2015) Population annealing: theory and application in spin glasses. Phys Rev E 92:063307
Yedidia JS, Freeman WT, Weiss Y (2005) Constructing free-energy approximations and generalized belief propagation algorithms. Inform Theory, IEEE Trans 51(7):2282–2312
Adachi SH, Henderson MO (2015) Application of quantum annealing to training of deep neural networks. arXiv:1510.06356
Amin MHS, Johnson WM (2015) Systems and methods employing new evolution schedules in an analog computer with applications to determining isomorphic graphs and post-processing solutions. Patent number: 20150363708
Andriyash E and Amin MH (2017) Can quantum monte carlo simulate quantum annealing? ar\(\chi\)iv:1703.09277
Andriyash E, Bian Z, Chudak F, Drew-Brook M, King AD, Macready WG, and Roy A (2016) Boosting integer factoring performance via quantum annealing offsets. https://www.dwavesys.com/sites/default/files/14-1002A_B_tr_Boosting_integer_factorization_via_quantum_annealing_offsets.pdf. Technical Report, Accessed: 2020-29-07
Bian Z, Chudak F, Israel RB, Lackey B, Macready WG, and Roy A (2016) Mapping constrained optimization problems to quantum annealing with application to fault diagnosis. Frontiers in ICT, 3:14. ISSN 2297-198X. 10.3389/fict.2016.00014. https://www.frontiersin.org/article/10.3389/fict.2016.00014
Biswas R et al (2017) A NASA perspective on quantum computing: Opportunities and challenges. ar\(\chi\)iv:1704.04836
Bravyi S (2014) Monte Carlo simulation of stoquastic Hamiltonians. arXiv:quant-ph:1402.2295
Chancellor N (2020) Fluctuation guided search with quantum annealing. in preparation
Coxson GE, Hill CR and Russo JC (2014) Adiabatic quantum computing for finding low-peak-sidelobe codes. Presented at the 2014 IEEE High Performance Extreme Computing conference
D-Wave (2018) D-wave systems inc. website. http://www.dwavesys.com/. Accessed: 2018-01-10
D-Wave Systems Inc. (2019) Reverse quantum annealing for local refinement of solutions. https://www.dwavesys.com/sites/default/files/14-1018A-A_Reverse_Quantum_Annealing_for_Local_Refinement_of_Solutions.pdf. Accessed: 2019-05-03
Douglass A et al (2017) qbsolve. https://github.com/dwavesystems/qbsolv. accessed: Nov. 28
Golden J and O’Malley D (2020) Reverse annealing for nonnegative/binary matrix factorization. ar\(\chi\)iv:2007.05565
Hastings MB (2020) The power of adiabatic quantum computation with no sign problem. ar\(\chi\)iv:2005.03791
Holland JH (1975) Adaptation in Natural and Artificial Systems. Univ. of Michigan Press, Ann Arbor, Mich
Hukushima K and Iba Y (2003) The Monte Carlo Method in the physical sciences: celebrating the 50th anniversary of the metropolis algorithm, volume 690. AIP
Kaminsky WM and Lloyd S (2002) Scalable architecture for adiabatic quantum computing of NP-hard problems. arXiv:quant-ph/0211152
Kaminsky WM and Lloyd S (2004) Scalable architecture for adiabatic quantum computing of np-hard problems. In A. J. Leggett, B. Ruggiero, and P. Silvestrini, editors, Quantum Computing and Quantum Bits in Mesoscopic Systems, pp 229–236. Springer US. 10.1007/978-1-4419-9092-1 25
Kaminsky WM, Lloyd S, and Orlando TP (2004) Scalable superconducting architecture for adiabatic quantum computation. arXiv:quant-ph/0403090
King J, Mohseni M, Bernoudy W, Frechette A, Sadeghi H, Isakov SV, Neven H, and Amin MH (2019) Quantum-assisted genetic algorithm. ar\(\chi\)iv:1907.00707
Lanting T et al (2016) Techniques for modifying annealing trajectories in quantum annealing processors. https://aqccreg2016.eventfarm.com /events/index/7fff5387-0000-456c-a4da-3f0389a7aa72?page=7fff46cb-0000-4577-a218-60207dca65cd. Presented at: AQC 2016
Lackey B, Jarret M (2017) Substochastic Monte Carlo algorithms. arXiv:1704.09014
MacKay DJC (2003) Information theory, inference, and learning algorithms. Cambridge University Press
Marzec M (2016) Portfolio Optimization: applications in quantum computing, pp 73–106. John Wiley & Sons, Inc. ISBN 9781118593486. 10.1002/9781118593486.ch4. http://dx.doi.org/10.1002/9781118593486.ch4
Nishimori H (2001) Statistical Physics of spin glasses and information processing. Clarindon Press
Ottaviani D and Amendola A (2018) Low rank non-negative matrix factorization with D-wave 2000Q. ar\(\chi\)iv:1808.08721
Pattison BC, Wang W, and Katzgraber HG (2017) Optimization of population annealing Monte Carlo for large-scale spin-glass simulations. ar\(\chi\)iv:1710.09025
Raymond J, Yarkoni S, and Andriyash E (2016) Global warming: temperature estimation in annealers. arXiv:quant-ph/1606.00919
Vikhar PA (2016) Evolutionary algorithms: A critical review and its future prospects. In 2016 international conference on global trends in signal processing, information computing and communication (ICGTSPICC), pp 261–265. 10.1109/ICGTSPICC.2016.7955308
Acknowledgements
The author was supported by EPSRC (grant refs: EP/L022303/1 and EP/S00114X/1), and would like to thank Viv Kendon, Joschka Roffe, and Dominic Horsman for critical reads of the paper and useful discussions. The author would also like to thank Alejandro Perdomo-Ortiz for making me aware of the alternative protocol in Perdomo-Ortiz et al. (2011).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Example of a heuristic to relate uncertainty to transverse field
Appendix 1: Example of a heuristic to relate uncertainty to transverse field
There are many potential heuristics which could be used to relate the probabilites P which are passed to an inference primitive to the annealing \(s'\) parameter which is use in a reverse annealing protocol. While the focus of this paper is not on how to actually relate these two parameters, it is instructive to give a simple example of what one such heuristic could look like. Whether or not this heuristic works well in practice is beyond the scope of this current work, and almost certainly more sophisticated heuristics, for instance based on the local temperture estimates given in Raymond et al. (2016) are likely to perform better.
To start with, I make use of the fact that it has been numerically demonstrated that quantum fluctuations moderated by a transverse field can be used as a proxy for thermal fluctuations for inference problems (Otsubo et al. 2012). In this spirit I define an approximate effective temperature related to a transverse field strength, which is set by a chosen value of s in Eq. (1) which I denote as \(s'\). This can be done using the method suggested in Chancellor (2017) by analytically diagonalizing the Hamiltonian at the appropriate point in the annealing schedule with a“problem”Hamiltonian consisting of a single bit Hamiltonian with a longitudinal field of unit strength, \(H_{1}(s')=-A(s')\,\sigma ^{x}+B(s')\,\sigma ^{z}\). This ratio is then compared to a Boltzmann distribution, and the equation inverted to solve for temperature. This approach yields
In situations where coupling is present, rather than the single qubit case examined here, the effective picture becomes more complicated. To correctly determine the effect of a coupler on a single qubit, one must take into account the fact that all other qubits within the coupler are also fluctuating in a way which is generally complicated and correlated both with each other and the qubit we are examining. The results in Otsubo et al. (2012) suggest, however, that these complicated effects will be very similar for both quantum and thermal fluctuations. Based on these similarities, a simple first approximation is to apply relationships between temperature and driver strength which are derived in the single qubit case to larger multi-qubit systems, based on the reasoning that the effects of correlations with neighbors may be qualitatively similar in both cases. While this is a rather crude approximation, the heuristic given here is only intended as a minimal example, single qubit dynamics provide one of the simplest ways to relate temperature to transverse field. Alternatively, a local temperature could be estimated experimentally using the methods of Raymond et al. (2016), or by adapting the methods to estimate a global effective temperature used in Benedetti et al. (2016).
Now I use the seminal result by Nishimori (1980, 2001, 2016) that a temperature can be related to an error probability via the Nishimori temperature, \(T_N\). This relationship is mathematically rigorous and is the underlying principle behind maximum entropy inference, which has many practical applications (Frieden 1972; Berger et al. 1996; Phillips et al. 2006; Raychaudhur et al. 2002; Gilmore 1996; Mistrulli 2011; Ruján 1993). In these applications, the Nishimori temperature
serves to match a temperature to an effective uncertainty, expressed as a probability P. The quantity could be, for instance, an error rate in the context of decoding of communications as in Ruján (1993). In the context of inference primitive protocols, P should be taken as \(P_i\) for a given bit or cluster of bits a simple approximate heuristic to relate the probailities to the effective temperature \(T'\) is to set it to be proportional to the Nishimori temperature
By plugging in the approximate formula in Eq. 21 and inverting the equation, I obtain the approximate uncertainty value,
The relationship I have just derived allows a direct definition of the uncertainty values defined in \(\{P\}\) in Sect. 2 in terms of real device parameters. Expressed in these term, the algorithms in Chancellor (2017) assign the same probability of being incorrect to every bit value.
Thus far, I have assumed that the annealer is exposed to a bath with a temperature which is low compared with the relevant energy scales \(A(s')\) and \(B(s')\). However, this may not be the case in a real annealer. In this case we can make the approximation that the themal and quantum fluctuations act in a statistically independent way and add them in quadrature,
where \(T_{phys}\) is the physical temperature. Carrying this result through, we arrive at,
It is worth discussing briefly a special subclass of problem Hamiltonians for which \(h_i=0 \forall i\) in Eq. (2). For the quantum annealing algorithm applied to such a problem Hamiltoninan, the mean orientation of a bit is zero \(\left< \sigma ^z_i \right>=0\) and similarly for any cluster of bits \(\left<\sum _{j\in R _i} \sigma ^z_j\right>=0\) by the fact that these Hamiltonians have a \(\mathbb {Z}_2\) symmetry with respect to flipping all of the qubits (global bit inversion). However, the candidate solution breaks this symmetry, meaning that solution refinement will still work. If multiple sets of annealer outputs are being combined (i.e. \(|\mathcal {G}|>1\)) for such a problem Hamiltonian, then we should consider the possibility of performing global spin inversions on some of the sets of outputs before applying the processing function. Ideally this should be chosen as the one which yields the highest possible bitwise correlation between all of the candidates.
Because the space of possible global spin inversions of candidate solutions will be \(2^{N_{inputs}}\), performing an exhaustive search over all possible inversions may not be possible if \(N_{inputs}\) is moderately large. However a heuristic search method such a simulated annealing could be used to find choices which yield high correlations. Alternatively, one could break the spin inversion symmetry by taking a ‘majority vote’, and performing a global bit inversion on all solution candidates in \(\mathcal {G}_k\) if more bits are in the \(-1\) state than the 1 state.
A simple alternative approach for problems where \(h_i=0 \forall i\) is to effectively fix a single spin arbitrarily, and replace coupling to that spin with fields. While mathematically correct, this approach has the disadvantage that it gives one spin a ‘privileged’ role in that quantum fluctuations damp out the effect of couplers much more strongly then they do fields because the effect of a coupler is moderated by the fluctuations of two qubits, while the effect of a field is moderated only by the fluctuations of the single qubit it is coupled to.
The methods which I have derived in this section to relate the local annealing parameter on the real device \(s'\) to the uncertainty value \(P_i\) are not necessarily unique, there will be other suitable mathematical ways to relate these quantities. For real applications the preferred method may actually be to try different heuristics until one is found which works well, or to try to work out this relationship directly experimentally, for instance by adapting the bisection methods used to find the range of local searches proposed in Chancellor (2017).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chancellor, N. Modernizing quantum annealing II: genetic algorithms with the inference primitive formalism. Nat Comput 22, 737–752 (2023). https://doi.org/10.1007/s11047-022-09905-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-022-09905-2