Regularized restoration for two dimensional band-limited signals

Abstract

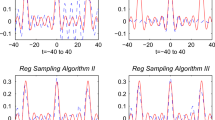
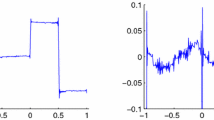
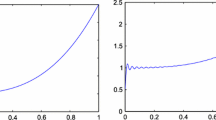
In this paper the ill-posedness of restoring lost samples is discussed in the two dimensional case. The restoration algorithm by Shannon’s Sampling Theorem is analyzed. A regularized restoring algorithm for two dimensional band-limited signals is presented. The convergence of the regularized restoring algorithm is studied and compared with the restoration algorithm by Shannon’s sampling theorem in the two dimensional case.

Appendix

Proof of Theorem 1.2

In (1) we take the convolution with

$$\begin{aligned} \frac{\sin \Omega _0t_1}{\Omega _0t_1} \frac{\sin \Omega _0t_2}{\Omega _0t_2} \end{aligned}$$

we obtain

$$\begin{aligned} f(t_1, t_2)=r_1r_2\sum _{n_1=-\infty }^\infty ~\sum _{n_2=-\infty }^\infty \frac{\sin \Omega _0(t_1-n_1h_1)}{\Omega _0(t_1-n_1h_1)} \frac{\sin \Omega _0(t_2-n_2h_2)}{\Omega _0(t_2-n_2h_2)} f(n_1h_1, n_2h_2). \end{aligned}$$

Let $t_1=0, ~t_2=0$, solve for $f(0, 0)$, then we obtain the formula (2).

Proof of Lemma 3.3

By the Cauchy inequality and Lemma 3.2

$$\begin{aligned} S_1^2\le \sum _{n_1\not =0} \left| \frac{[2\pi \alpha +2\pi \alpha (n_1h_1)^2]}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2] n_1h_1}\right| ^2 \left( \frac{h_1}{r_1\pi }\right) ^2 \sum _{n_1\not =0} |f(n_1h_1, 0)|^2 =O\left( \alpha ^{\frac{1}{2}}\right) . \end{aligned}$$

Proof of Lemma 3.4

$$\begin{aligned} S_2&= \sum _{n_1\not =0}~\sum _{ n_2=0} \frac{\eta (n_1h_1, n_2h_2)}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } \\&+\sum _{n_1=0}~\sum _{n_2\not =0} \frac{\eta (n_1h_1, n_2h_2)}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi }\\&+\sum _{n_1\not =0}~\sum _{n_2\not =0} \frac{\eta (n_1h_1, n_2h_2)}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } \end{aligned}$$

By Lemma 3.1, the first two terms are of the order $O(\delta )+O(\delta \ln \frac{1}{\alpha })$. By using the estimation (6) the third term is of the order $O(\delta \ln ^2 \frac{1}{\alpha })$.

Proof of Lemma 3.5

By the Cauchy inequality

$$\begin{aligned}&I^2\le \sum _{n_1\not =0} ~\sum _{n_2\not =0} \left| \frac{2\pi \alpha + 2\pi \alpha (n_1h_1)^2}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2] n_1h_1} \frac{2\pi \alpha + 2\pi \alpha (n_2h_2)^2}{[1+2\pi \alpha +2\pi \alpha (n_2h_2)^2] n_2h_2}\right| ^2 \\&\cdot \left( \frac{h_1}{r_1\pi }\right) ^2 \left( \frac{h_2}{r_2\pi }\right) ^2 \sum _{n_1\not =0} ~\sum _{n_2\not =0} |f(n_1h_1, n_2h_2)|^2. \end{aligned}$$

Then by Lemma 3.2, $I^2=O(\alpha )$.

Proof of Lemma 3.6

By the Cauchy inequality

$$\begin{aligned}&J_1^2\le \sum _{n_1\not =0} ~\sum _{n_2\not =0} \left| \frac{2\pi \alpha + 2\pi \alpha (n_1h_1)^2}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2] n_1h_1} \frac{1}{[1+2\pi \alpha +2\pi \alpha (n_2h_2)^2] n_2h_2} \right| ^2 \\&\cdot \left( \frac{h_1}{r_1\pi }\right) ^2 \left( \frac{h_2}{r_2\pi }\right) ^2\sum _{n_1\not =0} \sum _{n_2\not =0} |f(n_1h_1, n_2h_2)|^2. \end{aligned}$$

Then by Lemma 3.2, $J_1^2=O(\alpha ^\frac{1}{2})$.

Proof of Lemma 3.7

$J_2=I_1+I_2+I_3$ where

$$\begin{aligned} I_1&= \sum _{n_1\not =0}~\sum _{n_2=0} \frac{\left\{ [1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]-1\right\} }{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]} \\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2)\\ I_2&= \sum _{n_1=0}~\sum _{n_2\not =0} \frac{\left\{ [1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]-1\right\} }{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2)\\ I_3&= \sum _{n_1\not =0}~\sum _{n_2\not =0} \frac{\left\{ [1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]-1\right\} }{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]} \\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2) \end{aligned}$$

Here

$$\begin{aligned} I_1&= \sum _{n_1\not =0} \frac{\left\{ [1+2\pi \alpha +2\pi \alpha (n_1h_1)^2](1+2\pi \alpha )-1\right\} }{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2](1+2\pi \alpha )} \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } f(n_1h_1, 0)\\&= \frac{1}{1+2\pi \alpha } \sum _{n_1\not =0} \frac{[2\pi \alpha +2\pi \alpha (n_1h_1)^2]}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2]} \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } f(n_1h_1, 0)\\&+\frac{2\pi \alpha }{1+2\pi \alpha } \sum _{n_1\not =0} \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } f(n_1h_1, 0) =O(\alpha ^{\frac{1}{4}}) \end{aligned}$$

by Lemma 3.3. For the same reason $I_2=O(\alpha ^{\frac{1}{4}})$.

$$\begin{aligned} I_3&= \sum _{n_1\not =0}~\sum _{n_2\not =0} \frac{[2\pi \alpha +2\pi \alpha (n_1h_1)^2][2\pi \alpha +2\pi \alpha (n_2h_2)^2]}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]} \\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2)\\&+\sum _{n_1\not =0}~\sum _{n_2\not =0} \frac{[2\pi \alpha +2\pi \alpha (n_1h_1)^2]}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2)\\&+\sum _{n_1\not =0}~\sum _{n_2\not =0} \frac{[2\pi \alpha +2\pi \alpha (n_2h_2)^2]}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]}\\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2) =O(\alpha ^{\frac{1}{4}}) \end{aligned}$$

by Lemma 3.5 and by Lemma 3.6.

Proof of Theorem 3.1

$f_\alpha (0, 0)-f_E(0, 0)$

$$\begin{aligned}&= \frac{r_1r_2}{1-r_1r_2}\sum _{n_1\not =0}~\sum _{\mathrm{or} ~n_2\not =0} \frac{f(n_1h_1, n_2h_2)+\eta (n_1h_1, n_2h_2)}{[1+2\pi \alpha +2\pi \alpha (n_1h_1)^2][1+2\pi \alpha +2\pi \alpha (n_2h_2)^2]} \\&\cdot \frac{\sin (n_1r_1\pi )}{n_1r_1\pi } \frac{\sin (n_2r_2\pi )}{n_2r_2\pi } \\&\quad -\frac{r_1r_2}{1-r_1r_2} \sum _{n_1\not = 0} ~\sum _{\mathrm{or} ~n_2\not =0} \frac{\sin (n_1r_1\pi )}{n_1r_1\pi }\frac{\sin (n_2r_2\pi )}{n_2r_2\pi } f(n_1h_1, n_2h_2) =\frac{r_1r_2}{1-r_1r_2}(J_2+S_2) \end{aligned}$$

where $J_2=O(\alpha ^{\frac{1}{4}})$ is the same as in Lemma 3.7 and

$$\begin{aligned} S_2=O(\delta )+O\left( \delta \ln \frac{1}{\alpha }\right) +O\left( \delta \ln ^2 \frac{1}{\alpha }\right) \end{aligned}$$

is the same as in Lemma 3.4.