Proportional plus integral control of ladder circuits modeled in the form of two-dimensional (2D) systems

Abstract

In this paper, a 2D systems setting is used to develop new results on control of active electrical ladder circuits. In particular, the proportional plus integral control method has been extended to this case and the problem of how to obtain some distributed along the circuit nodes desired (reference) signal, and how to completely decouple distributed disturbances has been solved.

1 Introduction

Spatially interconnected systems are the series of similar subsystems distributed in space according to some rule, for example in a cascade way, which directly interact with their nearest neighbors. Despite the fact that these subsystems can be very simple and can interact with neighbors in a simple way, the resulting system can display rich and complex behavior when viewed as a whole (D’Andrea and Dullerud 2003). There are many applications for such systems, as for example, automated highway systems (Raza and Ioannou 1996), airplane formation flight (Wolfe et al. 1996) satellite constellations (Graeme 1998), cross-directional control in paper processing applications (Stewart 2000), and e.g. micro-cantilever arrays for massively parallel data storage (King et al. 2002). One of the methods for consideration of systems governed by partial differential equations (PDEs) is an application of PDE’s lumped approximations which is used in the analysis of, for example, the deflection of beams, plates, and membranes, and the temperature distribution of thermally conductive materials (Taylor 1996; Cichy et al. 2011).

It is also frequently assumed that every subsystem of overall system possesses sensing and actuation capabilities as, for example, for automated highway systems, airplane formation flight, satellite constellations, and cross–directional control systems. Due to the rapid advances in micro electromechanical actuators and sensors, distributed control can be applied to systems governed by partial differential equations.

The electric ladder networks or circuits (also known as the ladder systems or series-shunt networks) formed by the repetition of identical components (cells), which are realized by longitudinal and transversal resistance or reactance (or, in general, impedance) can be also considered as a sub–class of spatially interconnected systems where except temporal indeterminate we assume the node number as a space indeterminate. Hence, there is a possibility to employ two-dimensional setting, with time and space information propagation directions to investigate such systems. The ladder circuits find multiple applications in the analysis of transmission and delay lines, chains of transmission gates or long wire interconnections, see e.g. Alioto et al. (2004) and also are useful in the approximation of distributed parameter systems classes e.g. Schanbacher (1989), in the analysis of dynamic DNA chains e.g. Swierniak et al. (1999) and in the simulation of physical systems such as mechanical, chemical, thermal, e.g. Indulkar (2005). Hence, there is the significant interest in the general area of the analysis and the synthesis of electric ladder circuits, e.g. Mitkowski (2003).

In this paper, we consider a class of active ladder circuits whose activity and also distributed control are realized in the form of controlled sources applied to each ladder node. Due to the aforementioned applications of ladder circuits in modeling and analysis of physical systems, the study of two–dimensional (2D) nature, i.e. spatial distribution of this system class has a great potential. Representing their dynamics in the 2D framework leads to various control problems, as e.g. considered in this paper distributed control towards obtaining a particular time and space (node) distribution of voltage and/or current signals, which in this case can be treated as 2D (variable in time and nodes) signals, against distributed disturbances. The same refers to the active control of passive or lossless ladder circuits, where no controlled sources being the intrinsic circuit parts, in which case there is no need of stabilization as uncontrolled circuits cannot be unstable but obtaining a requested system behaviour is still an option. Hence, the presented theoretical study can find an impact for solving many engineering problems.

For example, ladder circuits of the similar form occur in the power supply systems for white or color LED strips (Light Energy Source Co). Such strips contain series of emitting elements used to form series of different intensity and/or color light sources that produce the required, specific view. This results in using one output for white LEDs or three for color LED (RGB representation) at the state-space model. The intensity of light emitted at the specific node of the strip is controlled by the value of the voltage applied to the given LED. Since LEDs in the stripe work only at the conductive range of elements the non-linear part of the their characteristics can be omitted. The control goal here is to obtain a requested intensity/color distribution along the strip, which is realized by applying controlled voltage sources distributed along the emitting elements and ladder circuits based distributed control algorithms can be applicable.

Another possible application area for ladder circuits refers to the use of electronic RC ladders in modeling of distributed thermal processes (Tockhorn et al. 2010). In such a case, the process information flow is represented by the current distribution in the electrical circuit. A particular interest of using ladder circuits arises in modeling and control of a tunnel brick kiln (Schalk 2010; Stojanovski and Stankovski 2011), where the main purpose is on ensuring the required temperature profile at various sections of a kiln. Also, since the material being burned (bricks) accumulates the energy supplied at previous sections of the kiln, this can cause the occurrence of the additional energy sources at the particular section, which can be modeled by using the active circuit in the model. Since the temperature profile along sections in the brick kiln is required to follow the reference one defined as a 2D signal (space–temporal) the appropriate distributed control scheme has to be applied.

It is also expected that ladder circuits control can be useful in biotechnological applications, e.g. in evolution control of cancer cells drug resistance, see Kimmel et al. (1998), as mathematical models used there are very similar.

The last but not least advantage of using the ladder circuits is a relative simplicity of building the experimental, physical setups for reliable simulations. Also control implementation is rather straightforward in both software and hardware realizations, due to that controlled sources are well studied electrical circuits components.

The past decades, in particular, have seen a continually growing interest in so-called two-dimensional (2D) or, more generally, multi-dimensional (nD) systems. This is clearly related to the wide variety of applications of both practical and/or theoretical interest. The key unique feature of an nD system is that the plant or process dynamics (input, output and state variables) depend on more than one indeterminate and hence information is propagated in many independent directions. Many physical processes have a clear nD structure. Also, the nD approach is frequently used as an analysis tool to assist, or in some cases enable, the solution of a wide variety of problems. A key point is that the applications areas for nD systems theory/engineering can be found within the general areas of Circuits, Control and Signal Processing (and many others).

It is straightforward to see that ladder circuits can be modeled as 2D systems where the time variable and the node number are the two indeterminates. However, due to the left–right and right–left dependence between neighboring cells there is the need to use models that capture features of the dynamics which are excluded from the most frequently used 2D models as the Roesser (1975) and the Fornasini and Marchesini (1978) models. The similar situation occurs frequently for repetitive processes, see e.g. Cichy et al. (2013). In particular, the classic 2D causality, which is defined in the right upper quadrant sense, does not apply in this case. (Note that in many other applications such causality is too strong requirement, and may not always be physically motivated).

In Palucki et al. (2012), discretization of naturally continuous ladder circuits has been applied, which has resulted in obtaining the so-called discrete, linear, ”wave” repetitive processes. However, it turns out that there are significant problems with the proper discretization of this system class. The first limitation is that only the simplest $0$-order method could be applied to avoid obtaining very complicated, hard for analysis, models. The next problem is the requirement to use very small time discretization periods and even then only thing possible to achieve is stability invariance between a continuous model and a discrete approximation but the discrete approximation performance turns out to be poor in comparison to the differential original.

This paper shows how ladder circuits can be modeled as hybrid, discrete–continuous 2D systems. However, for “a’causal” hybrid 2D systems considered here, there are no direct 2D stability analysis and control methods, as for their discrete approximations of the form of discrete, linear wave repetitive process, which is a subject of ongoing work. Hence, we apply the so-called “lifting” approach, which yields an equivalent 1-D model, for which stability and analysis and control can be performed. Finally, we present an extension to the controller design, where the goal is to achieve a desired performance, i.e. a prescribed reference output signal and also disturbance decoupling, which both can be variable along the circuit nodes but constant in time. To solve this problem, the proportional plus integral (PI) control scheme is extended. Then, the illustrative simulation example is given to show the effectiveness of the proposed method.

Throughout this paper $M\succ 0$ (respectively $\prec 0$) denotes a real symmetric positive (respectively negative) definite matrix. The null matrix with the required dimensions are denoted by $0$. The symbol ${\mathrm {diag}}\{W_1, W_2, \ldots , W_M\}$ denotes a block diagonal matrix with diagonal blocks $W_1, W_2, \ldots , W_M$, and also

2 Ladder circuits in the 2-D framework

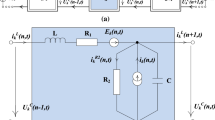
For the presentation issues, we start with the consideration of the particular ladder circuit presented in Fig. 1, where $E(p,t)\hbox { and }i(p,t)$ are the voltage and current controlled sources respectively, added to each $p$th node, which can be used to obtain an active circuit and/or can represent possible control input variables.

Fig. 1

The ladder chain: a Ladder circuit of the identical blocks $S_p,\;p=0,\ldots ,\alpha -1$. b Structure of the block $S_p$

The Kirchoff’s laws equations for $p$th node yield the state-space model of the whole 2-D network, which can be written over nodes $p=0,1,\ldots , \alpha -1\hbox { and }t\ge 0$ in the form of

$$\begin{aligned} \begin{aligned} \frac{d}{dt}x(p,t) = {\mathcal {A}}^{*}_{1}x(p-1,t) + {\mathcal {A}}_2x(p,t)+ {\mathcal {A}}_3x(p+1,t)+ {\mathcal {B}}^{*} \begin{bmatrix} i(p,t) \\ E(p,t) \\ \end{bmatrix}, \end{aligned} \end{aligned}$$

(1)

where the local state of the $p$th cell is

$$\begin{aligned} x(p,t)= \begin{bmatrix} U_c(p,t)\\ i_L(p,t) \\ \end{bmatrix}, \end{aligned}$$

(2)

$i(p,t)\hbox { and }E(p,t)$ denote current and voltage controlled sources respectively and

$$\begin{aligned} \begin{aligned} {\mathcal {A}}^{*}_{1}&= \begin{bmatrix} 0&0 \\ \frac{1}{L}&0 \\ \end{bmatrix} ,&{\mathcal {A}}_2&= \begin{bmatrix} -\frac{1}{R_2 C}&\frac{1}{C} \\ -\frac{1}{L}&-\frac{R_1}{L} \\ \end{bmatrix} ,\\ {\mathcal {A}}_3&= \begin{bmatrix} 0&-\frac{1}{C} \\ 0&0 \\ \end{bmatrix} ,&{\mathcal {B}}^{*}&= \begin{bmatrix} \frac{1}{C}&0\\ 0&-\frac{1}{L} \end{bmatrix}. \end{aligned} \end{aligned}$$

(3)

The controlled sources $i(p,t)\hbox { and }E(p,t)$, assumed the same for each circuit node $p$, are used as the intrinsic part of the active circuit or to create the external input signal through a feedback. Note that for forward control respective sources would be autonomic.

To complete the model description, it is necessary to specify the boundary conditions, which for the purposes of this article are assumed to be

$$\begin{aligned} \begin{aligned} x(-1,t)&= \begin{bmatrix} U(t) \\ 0 \\ \end{bmatrix} ,&x(\alpha ,t)&= \begin{bmatrix} 0 \\ i (t) \\ \end{bmatrix},\\ x(p,0)&= 0,\;0\le p\le \alpha -1. \end{aligned} \end{aligned}$$

(4)

It is straightforward to see that (1) represents the hybrid (differential–discrete) system characterized by the lack of causality in the indeterminate $p$, which however is not a physical problem as $p$ represents the node number and causality in this indeterminate would even create serious drawbacks as it would require that only left-hand neighbor cell could act to the right-hand side one, but not reversely.

As aforementioned, the differential model of the form of (1) can be discretized, see Palucki et al. (2012), which leads to the class of discrete 2D systems, so called ’wave’ discrete linear repetitive processes, for which stability and stabilization techniques are known. This however has turned out to be a very troublesome task with respect to achieving the required discrete approximation accuracy and hence, in this paper we consider an original hybrid (continuous–discrete) model. However, it is to note that there are strong premises to apply effectively for discretization of such circuits the so-called “wave” filters, see Fettweis (1986), which is a subject of ongoing work.

Note now that the circuit with no controlled sources is passive and hence cannot be unstable. The proposed method for control towards achieving the prescribed distributed reference signal against disturbances is valid however also for a general case where the controlled system is unstable. This can be realized for ladder circuits by means of applying controlled sources which can cause instability of the obtained in that way active circuit. Consider hence the active circuit of (1), where a controlled source of each $p$th circuit node is of the form of

$$\begin{aligned} i(p,t)=\gamma U_c(p-1,t) \end{aligned}$$

(5)

and is treated as an intrinsic part of the overall active circuit. Note that these voltage controlled current sources represent internal feedback loops and are not the system inputs. Then, the resulted active circuit state-space model becomes

$$\begin{aligned} \begin{aligned} \frac{d}{dt}x(p,t)&= {\mathcal {A}}_{1}x(p-1,t) + {\mathcal {A}}_2x(p,t)\\&\quad + {\mathcal {A}}_3x(p+1,t)+{\mathcal {B}}u(p,t), \end{aligned} \end{aligned}$$

(6)

where

$$\begin{aligned} {\mathcal {A}}_1=\mathcal {A}^{*}_1 + \begin{bmatrix} \frac{\gamma }{C}&0 \\ 0&0 \\ \end{bmatrix},\; {\mathcal {B}}= \begin{bmatrix} 0 \\ -\frac{1}{L} \\ \end{bmatrix} \end{aligned}$$

(7)

and the rest of the matrices remain the same as in (1) and now a voltage sources $E(p,t), p=1,2,\ldots ,\alpha$ serve as distributed control inputs, i.e.

$$\begin{aligned} u(p,t)=E(p,t). \end{aligned}$$

(8)

Hence, we see that both the active circuits and the control action are realized in a distributed way by applying controlled sources to each circuit node. Such an approach can be used only for the cases where it is possible to apply distributed actuators, for example, except electrical circuits for aforementioned LED chain or tunnel brick kiln control. Otherwise boundary control is only the solution.

2.1 1D equivalent model and stability analysis

On the contrary to the discrete circuits discussed in Palucki et al. (2012) there are not known yet direct 2D methods for stabilty/stabilization analysis of hybrid a’causal models of the form of (6), which is however the subject of ongoing work. Although systems considered in this paper belong to the class of continuous-discrete 2D systems but cannot be analyzed by using the methods related to the commonly used upper, right quadrant causal 2D systems, i.e. the Roesser (1975) or the Fornasini and Marchesini (1978) type models, see e.g. Gałkowski et al. (2003) or Busłowicz and Ruszewski (2012). Hence, first we transform the models into the equivalent 1D form by applying “lifting” along the circuit nodes to build an equivalent 1-D dynamical model where the space dynamics along the spatial variable $p$ has been subsumed in the model structure. Define the so-called state and input super-vectors $\mathbf {x}(t)\hbox { and }\mathbf {u}(t)$ as

$$\begin{aligned} \mathbf {x}(t)=\left[ x(0,t)^T,\;x(1,t)^T,\;\ldots ,\; x(\alpha -1,t)^T\right] ^T \end{aligned}$$

(9)

and

$$\begin{aligned} \mathbf {u}(t)=\left[ u(0,t),\;u(1,t),\;\ldots ,\; u(\alpha -1,t)\right] ^T. \end{aligned}$$

(10)

Then the augmented state equation based on (6) takes the following form

$$\begin{aligned} \frac{d}{dt}\mathbf {x}(t)= \varPhi \mathbf {x}(t) + \varPsi \mathbf {u}(t), \end{aligned}$$

(11)

where

$$\begin{aligned} \varPhi = {\mathrm {tri}}\{{\mathcal {A}}_3,\mathcal {A}_2,{\mathcal {A}}_1\},\;\varPsi ={\mathrm {diag}}\{{\mathcal {B}}, \mathcal {B}, \ldots , {\mathcal {B}}\}. \end{aligned}$$

(12)

Applying Lyapunov stability theory to this last model gives the following result.

Lemma 1

The ladder circuit described by (11) with no control inputs, i.e. $\mathbf {u}(t)=0$, is stable if and only if $\exists \; {\mathcal {P}}\succ 0$ such that the following holds

$$\begin{aligned} \varPhi {\mathcal {P}}+ \mathcal {P} \varPhi ^T \prec 0. \end{aligned}$$

(13)

In application to circuit stabilization, a fully populated matrix P means that each node directly influences all others and this is not necessary in most cases. Hence the following sufficient stability condition is developed, which also eases implementation.

Theorem 1

The ladder circuit described by (11) with no control inputs, i.e. $\mathbf {u}(t)=0$ is stable if $\exists \; P\succ 0$ such that the following holds

$$\begin{aligned} {\mathrm {tri}}\left\{ P{\mathcal {A}}_1^T +\mathcal {A}_3 P,P{\mathcal {A}}_2^T +\mathcal {A}_2 P,P{\mathcal {A}}_3^T +\mathcal {A}_1 P\right\} \prec 0. \end{aligned}$$

(14)

Proof

The proof is straightforward when assuming in Lemma 1 that ${\mathcal {P}}={\mathrm {diag}}\{P,P,\ldots , P\}$ $\square$

Remark 1

Note that for lossless circuits, where no resistances, the circuit is stable but not asymptotically stable and hence instead of $\prec$ we should use in Lemma 1 and Theorem 1 $\preceq$.

2.2 Stabilization of a ladder circuit

Again consider the ladder circuit of Fig. 1 described by the equation (6). Introduce the following state feedback law $\forall \; p=0,1,\ldots , \alpha -1$

$$\begin{aligned} u(p,t)=K_1 x(p-1,t) + K_2 x(p,t) + K_3 x(p+1,t), \end{aligned}$$

(15)

where the controls $u(p,t)$ are represented by voltage sources $E(p,t)$ as in (8). A control law of (15) can be equally represented in the equivalent 1D form as

$$\begin{aligned} \mathbf {u}(t)=\mathbf {K}\mathbf {x}(t), \end{aligned}$$

(16)

where

$$\begin{aligned} \mathbf {K}={\mathrm {tri}}\{K_3,K_2,K_1\}. \end{aligned}$$

(17)

Due to that the state vector entries are capacitor voltages and inductor currents, the control law of (15) is realised by appropriate voltage and current controlled voltage sources. Then we have the following result.

Theorem 2

Suppose that a control law of the form (16) is applied to the circuit described by (11) having $\alpha$ nodes $(p=1,2,\ldots , \alpha )$. Then the closed loop circuit is stable if $\exists \hbox { matrices }P\succ 0,\,N_1,\,N_2\hbox { and }N_3$ such that the following LMI holds

$$\begin{aligned} {\varvec{\Omega }}_{\alpha } \,\widehat{=}\,\,{\mathrm {tri}}\{\varOmega _1,\varOmega _2,\varOmega _1^T\} \prec 0, \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{aligned} \varOmega _2&=P{\mathcal {A}}_2^T+N_2^T{\mathcal {B}}^T +\mathcal {A}_2 P+{\mathcal {B}} N_2 ,\\ \varOmega _1&=P{\mathcal {A}}_1^T+N_1^T{\mathcal {B}}^T +\mathcal {A}_3 P+{\mathcal {B}} N_3.\\ \end{aligned} \end{aligned}$$

(19)

If this condition holds, the stabilizing controllers are given by

$$\begin{aligned} \begin{aligned} K_1&=N_1 P^{-1}, \\ K_2&=N_2 P^{-1} ,\\ K_3&=N_3 P^{-1}. \\ \end{aligned} \end{aligned}$$

(20)

Proof

The proof is straightforward when inserting in (14) the closed loop matrices ${\mathcal {A}}_{i}+\mathcal {B}K_i\hbox { instead }$ of ${\mathcal {A}}_{i}$ followed by assuming $K_iP=N_i,\hbox { for }i=1,2,3.$ $\square$

Remark 2

It is well known that controllability of a system is the sufficient condition for its stabilizability. It is straightforward to see that the considered circuit is controllable under the defined above controls independently on the values of the circuit elements. This can be concluded from that the matrix pair $\{{\mathcal {A}}_2,\;\mathcal {B}\}$ of (3) is always controllable which implies that the general controllability requirement for a circuit described by (11), i.e.

$$\begin{aligned} rank\begin{bmatrix} zI-\varPhi&\varPsi \\ \end{bmatrix}=2\alpha \end{aligned}$$

(21)

holds $\forall z\in {\mathcal {C}}.$

3 Proportional plus integral (PI) control of ladder circuits

In the remainder, we solve the problem of how to design the control law (15) matrices $K_{i},i=1,2,3$ to obtain a specified reference signal even in the presence of disturbance terms.

Recall hence the state equation of the considered ladder circuit model of (6) with additional disturbances and add the output equation to obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt}x(p,t)&= {\mathcal {A}}_{1}x(p-1,t) + {\mathcal {A}}_2x(p,t) + {\mathcal {A}}_3x(p+1,t) + {\mathcal {B}} u(p,t) + {\mathcal {E}} w(p), \\ y(p,t)&= {\mathcal {C}} x(p,t), \end{aligned}\qquad \end{aligned}$$

(22)

where $w(p)\in R^v,\;v\le n$ is the constant in time disturbance vector acting at the node $p,\,{\mathcal {E}}\in R^{n \times v}, \,{\mathcal {C}}$ is an $R^{m \times n}\;\; (m \le n)$ matrix that contains zeros and ones to select the state vector entries that are simultaneously the output vector entries (in this case the capacitor voltages $U_c(p,t)$ are assumed to be outputs and hence ${\mathcal {C}}=\begin{bmatrix} 1&0 \\ \end{bmatrix}$)

Next, define the reference signal $y_{ref}(p),\; 0\le p \le \alpha -1$ which also due to the requirements of the PI control scheme is constant in time.

The PI control scheme has the following objectives:

• (a) assure the stability of the closed loop system,

• (b) drive the model output to the constant in time reference signal $y_{ref}(p)$,

• (c) reject the influence of constant in time disturbances.

Note that both reference signal and disturbances can be variable in the space indeterminate $p$.

First, define the so-called total tracking error at the node $p$ as

$$\begin{aligned} e(p,t) = \int \limits _0^{t} \left( y(p,\tau ) - y_{ref}(p) \right) d \tau \end{aligned}$$

(23)

or

$$\begin{aligned} \frac{d}{dt}e(p,t) = y(p,t) - y_{ref}(p)={\mathcal {C}} x(p,t) - y_{ref}(p). \end{aligned}$$

(24)

Next, introduce the extended state vector

$$\begin{aligned} z(p,t)= \left[ x(p,t)^T,\; e(p,t)^T \right] ^T, \end{aligned}$$

(25)

which leads to the following augmented state space model

$$\begin{aligned} \begin{aligned} \frac{d}{dt}z(p,t)&= \left[ \begin{array}{cc} {\mathcal {A}}_{1} &{} 0 \\ 0 &{} 0 \end{array}\right] z(p-1,t) + \left[ \begin{array}{cc} {\mathcal {A}}_{2} &{} 0 \\ {\mathcal {C}} &{} 0 \end{array}\right] z(p,t)\\&\quad + \left[ \begin{array}{cc} {\mathcal {A}}_{3} &{} 0 \\ 0 &{} 0 \end{array}\right] z (p+1,t) + \left[ \begin{array}{c} {\mathcal {B}} \\ 0 \end{array}\right] u(p,t) \\&\quad + \left[ \begin{array}{c} {\mathcal {E}} \\ 0 \end{array}\right] w(p) - \left[ \begin{array}{c} 0 \\ I \end{array}\right] y_{ref}(p) ,\\ y(p,t)&= \left[ \begin{array}{cc} {\mathcal {C}}&0 \end{array}\right] z(p,t). \end{aligned} \end{aligned}$$

(26)

Assume now that the system is stable. Then $\frac{d}{dt}z(p,t) \rightarrow 0$ and hence $z(p,\infty ) \rightarrow \text{ const }\;\;(x(p,\infty ) \rightarrow \text{ const },\; e(p,\infty ) \rightarrow \text{ const })$ and $y(p,\infty ) \rightarrow \text{ const }$. We also require that $y(p,\infty ) = y_{ref}(p)$, which is guaranteed by $\frac{d}{dt}z(p,t) \rightarrow 0$. Hence, (26) can be written in the steady state as

$$\begin{aligned} \begin{aligned} 0 = \left[ \begin{array}{cc} {\mathcal {A}}_{1} &{} 0 \\ 0 &{} 0 \end{array}\right] z(p-1,\infty ) + \left[ \begin{array}{cc} {\mathcal {A}}_{2} &{} 0 \\ {\mathcal {C}} &{} 0 \end{array}\right] z(p,\infty )\\+ \left[ \begin{array}{cc} {\mathcal {A}}_{3} &{} 0 \\ 0 &{} 0 \end{array}\right] z (p+1,\infty ) + \left[ \begin{array}{c} {\mathcal {B}} \\ 0 \end{array}\right] u(p,\infty ) \\+ \left[ \begin{array}{c} {\mathcal {E}} \\ 0 \end{array}\right] w(p) - \left[ \begin{array}{c} 0 \\ I \end{array}\right] y_{ref}(p), \\ y_{ref}(p) = \left[ \begin{array}{cc} {\mathcal {C}}&0 \end{array}\right] z(p,\infty ). \end{aligned} \end{aligned}$$

(27)

Now introduce the following incremental vectors

$$\begin{aligned} \begin{aligned} \widehat{z}(p,t)&= z(p,t) - z(p,\infty ),\\ \widehat{u}(p,t)&= u(p,t) - u(p,\infty ),\\ \widehat{y}(p,t)&= y(p,t) - y_{ref}(p),\\ \end{aligned} \end{aligned}$$

(28)

which yields the following incremental state space model

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\widehat{z}(p,t)&= \left[ \begin{array}{cc} {\mathcal {A}}_{1} &{} 0 \\ 0 &{} 0 \end{array}\right] \widehat{z}(p-1,t) + \left[ \begin{array}{cc} {\mathcal {A}}_{2} &{} 0 \\ {\mathcal {C}} &{} 0 \end{array}\right] \widehat{z}(p,t)\\&\quad + \left[ \begin{array}{cc} {\mathcal {A}}_{3} &{} 0 \\ 0 &{} 0 \end{array}\right] \widehat{z} (p+1,t) + \left[ \begin{array}{c} {\mathcal {B}} \\ 0 \end{array}\right] \widehat{u}(p,t), \\ \widehat{y}(p,t)&= \left[ \begin{array}{cc} {\mathcal {C}}&0 \end{array}\right] \widehat{z}(p,t), \end{aligned} \end{aligned}$$

(29)

where the disturbances has been decoupled. Note that the model of (29) has a “structure” of (6) and hence the stability/controller design theory developed for this case can be applied also now.

Introduce hence the following state feedback law $\forall \; p=0,1,\ldots , \alpha -1$

$$\begin{aligned} \widehat{u}(p,t)&= \widehat{u}^1(p,t)+\widehat{u}^2(p,t)+\widehat{u}^3(p,t)=\widetilde{K}_1 \widehat{z}(p-1,t)\nonumber \\&+ \widetilde{K}_2 \widehat{z}(p,t) + \widetilde{K}_3 \widehat{z}(p-1,t), \end{aligned}$$

(30)

which can be rewritten in the form of

$$\begin{aligned} \begin{aligned} u^1(p,t)&=\widetilde{K}_{1x} \left( x(p-1,t) - x(p-1,\infty ) \right) + u^1(p,\infty ) ,\\ u^2(p,t)&=\widetilde{K}_{2x} \left( x(p,t) - x(p,\infty ) \right) \\&\quad + \widetilde{K}_{2e} \left( e(p,t) - e(p,\infty ) \right) + u^2(p,\infty ) ,\\ u^3(p,t)&=\widetilde{K}_{3x} \left( x(p+1,t) - x(p+1,\infty ) \right) + u^3(p,\infty ). \end{aligned} \end{aligned}$$

(31)

Since

$$\begin{aligned} \begin{aligned} u^1(p,\infty )&=\widetilde{K}_{1x} x(p-1,\infty ), \\ u^2(p,\infty )&=\widetilde{K}_{2x} x(p,\infty ) + \widetilde{K}_{2e} e(p,\infty ), \\ u^3(p,\infty )&=\widetilde{K}_{3x} x(p+1,\infty ), \end{aligned} \end{aligned}$$

(32)

the “steady–state” parts cancel each other in (31), which yields

$$\begin{aligned} \begin{aligned} u^1(p,t)&=\widetilde{K}_{1x} x(p-1,t),\\ u^2(p,t)&=\widetilde{K}_{2x} x(p,t) + \widetilde{K}_{2e} e(p,t),\\ u^3(p,t)&=\widetilde{K}_{3x} x(p+1,t) \end{aligned} \end{aligned}$$

(33)

or (using (23))

$$\begin{aligned} \begin{aligned} u^1(p,t)&=\widetilde{K}_{1x} x(p-1,t),\\ u^2(p,t)&=\widetilde{K}_{2x} x(p,t) + \widetilde{K}_{2e} \int \limits _0^t \left( {\mathcal {C}} x(p,t) - y_{ref}(p) \right) d \tau ,\\ u^3(p,t)&=\widetilde{K}_{3x} x(p+1,t). \end{aligned} \end{aligned}$$

(34)

It is straightforward to see that $u^2(p,t)$ contains the proportional and integral parts.

The following is the major result of this article and gives LMI-based controller design method.

Theorem 3

Suppose that a control law of the form (34) is applied to the circuit described by (22) having $\alpha$ nodes ($p=0,1,\ldots , \alpha -1$). Then the resulting closed loop circuit is stable, its output is driven to $y_{ref}(p), \; 0\le p \le \alpha -1$ and the influence of disturbances is decoupled if $\exists \hbox { matrices }\hat{P}\succ 0,\,\hat{N}_1=\begin{bmatrix} \bar{N_1}&0 \\ \end{bmatrix}$, $\hat{N}_2$ and $\hat{N}_3=\begin{bmatrix} \bar{N_3}&0 \\ \end{bmatrix}$ such that the following LMI holds

$$\begin{aligned} {\varvec{\hat{\Omega }}}_{\alpha }\,\widehat{=}\,tri\{\hat{\varOmega }_1, \hat{\varOmega }_2, \hat{\varOmega }_1^T\} \prec 0, \end{aligned}$$

(35)

where

$$\begin{aligned} \begin{aligned} \hat{\varOmega }_2&=\hat{P}\hat{\mathcal {A}}_2^T+\hat{N}_2^T\hat{\mathcal {B}}^T +\hat{\mathcal {A}}_2 \hat{P}+\hat{\mathcal {B}} \hat{N}_2 ,\\ \hat{\varOmega }_1&=\hat{P}\hat{\mathcal {A}}_1^T+\hat{N}_1^T\hat{\mathcal {B}}^T +\hat{\mathcal {A}}_3 \hat{P}+\hat{\mathcal {B}} \hat{N}_3 \\ \text{ and }&\\ \hat{\mathcal {A}}_1&=\left[ \begin{array}{cc} {\mathcal {A}}_{1} &{} 0 \\ 0 &{} 0 \end{array}\right] ,\; \hat{\mathcal {A}}_2=\left[ \begin{array}{cc} {\mathcal {A}}_{2} &{} 0 \\ {\mathcal {C}} &{} 0 \end{array}\right] ,\; \\ \hat{\mathcal {A}}_3&=\left[ \begin{array}{cc} {\mathcal {A}}_{3} &{} 0 \\ 0 &{} 0 \end{array}\right] ,\; \hat{\mathcal {B}}=\left[ \begin{array}{c} {\mathcal {B}} \\ 0 \end{array}\right] . \end{aligned} \end{aligned}$$

(36)

If this condition holds, the stabilizing controllers are given by

$$\begin{aligned} \begin{aligned} \widetilde{K}_1&=\left[ \widetilde{K}_{1x}\; 0\right] = \hat{N}_1 \hat{P}^{-1} ,\\ \widetilde{K}_2&=\left[ \widetilde{K}_{2x}\; \widetilde{K}_{2e}\right] = \hat{N}_2 \hat{P}^{-1} ,\\ \widetilde{K}_3&=\left[ \widetilde{K}_{3x}\; 0\right] = \hat{N}_3 \hat{P}^{-1} .\\ \end{aligned} \end{aligned}$$

(37)

Proof

Note that (29) is of the form (1) and hence Theorem 2 can be applied for this augmented model. $\square$

3.1 Controller robustness against nodes number

The LMI matrix ${\varvec{\Omega }}_{\alpha }$ of (18) or $\hat{{\varvec{\Omega }}}_{\alpha }$ of (35) is possibly of the very large dimension, which is the case when ladder circuit consists of the large number of cells, i.e. when $\alpha$ is large. Although, LMI matrix is tridiagonal Toeplitz it can be the source of numerical problems when solving (18) or (35). The question hence arises whether the controller calculated for a circuit with $\alpha _1$ identical cells can be applied to an augmented circuit of $\alpha _2\gg \alpha _1$ the same cells, i.e. whether the control law (33) or (34) matrices $\widetilde{K}_{ix},\;\;i=1,2,3\hbox { and }\widetilde{K}_{2e}$ calculated from Theorem 3 for a given $\alpha =\alpha _1$ satisfy the LMIs of Theorem 3 for larger value of $\alpha$. This is equivalent to the question of whether $\hat{{\varvec{\Omega }}}_{\alpha _2}\prec 0$ if $\hat{\varvec{\Omega }}_{\alpha _1}\prec 0\hbox { for }\alpha _1\ll \alpha _2$. It is however very difficult task to develop a simple numerical iterative method for finding the maximum $\alpha _2$, for which the controller calculated for a smaller value $\alpha =\alpha _1<\alpha _2$ still works properly.

To highlight this problem first assume that $\hat{\varvec{\Omega }}_{\alpha }\prec 0$ and consider $\hat{\varvec{\Omega }}_{\alpha +1}.$ Note that

$$\begin{aligned} \hat{\varvec{\Omega }}_{\alpha +1}=\left[ \begin{array}{c|c} \hat{\varvec{\Omega }}_{\alpha } &{} \begin{array}{c} 0 \\ \vdots \\ 0 \\ \hat{\varOmega }_1 \end{array} \\ \hline \begin{array}{cccc} 0 &{} \cdots &{} 0 &{} \hat{\varOmega }_1^T \end{array} &{} \hat{\varOmega }_2 \\ \end{array}\right] \end{aligned}$$

(38)

and hence the necessary condition for $\hat{\varvec{\Omega }}_{\alpha +1 }\prec 0$ is that $\hat{\varvec{\Omega }}_{\alpha }\prec 0$ and $\hat{\varOmega }_2\prec 0$ hold.

Corollary 1

Given the negative definite matrix $\hat{\varvec{\Omega }}_{\alpha }$, the matrix $\hat{\varvec{\Omega }}_{\alpha +1 }$ is also negative definite if and only if

$$\begin{aligned} \hat{\varOmega }_2- \left[ \begin{array}{cccc} 0&\cdots&0&\hat{\varOmega }_1^T \end{array} \right] \hat{\varvec{\Omega }}_{\alpha }^{-1} \left[ \begin{array}{c} 0 \\ \vdots \\ 0 \\ \hat{\varOmega }_1 \end{array} \right] \prec 0. \end{aligned}$$

(39)

This result can be immediately proved when applying appropriate elementary operations to the matrix $\hat{\varvec{\Omega }}_{\alpha +1}$ and shows that ${\varvec{\Omega }}_{\alpha }\prec 0$ can cause ${\varvec{\Omega }}_{\alpha }\prec 0$ but it is not necessary. Hence, as is shown in the next section devoted to the numerical validation of the obtained results, it is possible to design the controllers for some value of $\alpha$ and check the feasibility of LMI (18) for larger values of $\alpha$. The algorithmic solution of this problem is the subject of ongoing work.

4 Numerical example

Consider the ladder circuit presented on Fig. 1 with $L=0.0477[ H ],\;C=42.4\times 10^{-4} [F ],\; R_1=50 [\varOmega ],\; R_2=200 [\varOmega ]$. Here the active circuit with $\gamma =0.006$ is considered. The preliminary number of nodes has been chosen as $\alpha =50$. The model matrices of (1) take the following form:

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_1= \left[ \begin{array}{cc} 2.36 &{} 0 \\ 20.96 &{} 0 \\ \end{array}\right] ,\; {\mathcal {A}}_2=\left[ \begin{array}{cc} -1.18 &{} 235.85 \\ -20.96 &{} -1048.22 \\ \end{array}\right] ,\; \\ {\mathcal {A}}_3=\left[ \begin{array}{cc} 0 &{} -235.85 \\ 0 &{} 0 \\ \end{array}\right] ,\; {\mathcal {B}}=\left[ \begin{array}{c} 0 \\ 20.96 \\ \end{array}\right] ,\;{\mathcal {C}}=\begin{bmatrix} 1&0 \\ \end{bmatrix} \end{aligned} \end{aligned}$$

(40)

and ${\mathcal {E}}=\left[ 0.1\; 0.1\right] ^T.$ The boundary conditions are assumed to be

$$\begin{aligned} \begin{aligned} x(-1,t)&= \begin{bmatrix} -5 \\ 0 \\ \end{bmatrix} ,&x(\alpha ,t)&= \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix},\\ x(p,0)&= 0,\;0\le p\le \alpha -1. \end{aligned} \end{aligned}$$

(41)

The active circuit is clearly unstable which can be seen at Fig. 2.

Fig. 2

The simulation results of the active uncontrolled circuit—$U_c(p,t)$

Note that using the Theorem 3 result we may obtain not satisfactory result, as e.g. the control action can be too excessive or the error convergence can be very slow. To avoid such a situation we introduce the additional decision matrix $Q$, such that

$$\begin{aligned} Q>0, \; \hat{P}-Q-I<0,\; \hat{P}+Q-I>0 \end{aligned}$$

(42)

and propose solving the following minimization problem

$$\begin{aligned} \begin{aligned} \text{ min } f(Q,\hat{N}_1,\hat{N}_2,\hat{N}_3),\;\; \\ \text{ where }\\ f(Q,\hat{N}_1,\hat{N}_2,\hat{N}_3) = r_1\cdot \text{ trace }(Q)+r_2\cdot \hat{N}_1\cdot \hat{N}_1^T \\ \qquad +\, r_3\cdot \hat{N}_2\cdot \hat{N}_2^T + r_4\cdot \hat{N}_3\cdot \hat{N}_3^T \\ \text{ subject } \text{ to } \text{(35) } \end{aligned} \end{aligned}$$

(43)

where $r_1,\; r_2,\;r_3 ,\;r_4$ are scalar parameters to be selected. In the remainder of this section, we show the developed method effectiveness for two different reference signals and two different node numbers $\alpha =50\hbox { and }\alpha =100$.

4.1 Scenario 1: The first choice of the reference signal ($\alpha =50$)

Assume the following disturbance vector acting across the ladder nodes

$$\begin{aligned} \begin{aligned} w(i)=\frac{1}{2}sin\left( \frac{8\pi \;i }{\alpha -1} \; -\; 4\pi \right) \;+\frac{1}{2}r(i) , \quad i=0,1,\ldots ,\alpha -1, \; \end{aligned} \end{aligned}$$

(44)

and $r(i)$ is a random variable with uniform distribution with expected value $E(r(i))=0\hbox { and }r(i) \in (-0.5, 0.5)$. The exemplary disturbance vector has been presented on Fig. 3. The reference signal is shown on Fig. 4.

Fig. 3

Disturbances along the ladder—Scenario 1

Fig. 4

The reference signal for $U_C(p,t)$—Scenario 1

The application of Theorem 3 together with the optimization procedure (43) for $\alpha =50$ and optimization parameters chosen as

$$\begin{aligned} r_1=100,\;r_2=10,\;r_3=1,\;r_4=1 \end{aligned}$$

(45)

yields the controller matrices of the following form:

$$\begin{aligned} \widetilde{K}_{1x}&= \left[ \begin{array}{cc} -0.27 &{} -0.06\\ \end{array}\right] ,\nonumber \\ \widetilde{K}_{2x}&= \left[ \begin{array}{cc} 22.74 &{} \;\; 9.99\\ \end{array}\right] ,\nonumber \\ \widetilde{K}_{3x}&= \left[ \begin{array}{cc} -0.1 &{} -0.06 \\ \end{array}\right] ,\; \widetilde{K}_{e2}= 10.35. \end{aligned}$$

(46)

Figure 5 presents the dynamics of the distributed along circuit nodes $p\hbox { output }U_C(p,t)$ and shows that it converges quickly to the required referencee signal with no excessive oscillations at the transients and also disturbances are perfectly decoupled. Figure 6 presents the distributed state variable $i_L(p,t)$ and shows no instability or strong oscillations occurrence. Mean square error (MSE) convergence in time is highlighted by Fig. 7, which shows that the error after being damped is kept at the small value and does not build up again. Additionally, Fig. 8 shows how the distributed output signal approaches to the desired one. Finally, Figs. 9, 10, and 11 present the distributed control actions and it is seen that there is no need of the excessive control action.

Fig. 5

The dynamics of $U_C(p,t)$ with PI control scheme applied—Scenario 1

Fig. 6

The dynamics of $i_L(p,t)$ with PI control scheme applied—Scenario 1

Fig. 7

Mean squared error along circuit nodes as a time function—Scenario 1

Fig. 8

Approaching the reference signal at the consecutive time moments $(t=1,\; 5,\; 20\; [s])$—Scenario 1

Fig. 9

Input $u^1(p,t)$—Scenario 1

Fig. 10

Input $u^2(p,t)$—Scenario 1

Fig. 11

Input $u^3(p,t$)—Scenario 1

4.2 Scenario 2: The second choice of the reference signal ($\alpha = 50$)

Since the control law (30) matrices of Theorem 3 together with the optimization procedure (43) are computed independently of the reference signal one can suppose that they can be applied to the given circuit also for different distributed reference signals. It is checked for the distributed reference signal given in Fig. 12 when the disturbances remains the same as in Scenario 1. Below, in Figs. 13, 14, 15, 16, 17, 18 and 19, there are shown simulations resulted when applied the control law (30) with the matrices of (46). It is seen that the closed loop dynamics remains very similar to this of Scenario 1, i.e. the output signals converge quickly (in about 10 sec) to the required new reference signal with no oscillations at the transients and with disturbances perfectly decoupled and also that there is no need of applying the excessive control action. Also, the second state vector entry $i_L(p,t)$ dynamics is stable. Additionally, Fig. 15 shows how the distributed output signal approaches to the desired one.

Fig. 12

The reference signal used for Scenario 2

Fig. 13

The dynamics of $U_C(p,t)$ for Scenario 2

Fig. 14

The dynamics of $i_L(p,t)$ for Scenario 2

Fig. 15

Approaching the reference signal at the consecutive time moments ($t=1,\; 5,\; 20\; [s]$) for Scenario 2

Fig. 16

Mean squared error along circuit nodes as a time function for Scenario 2

Fig. 17

Input $u^1(p,t)$ for Scenario 2

Fig. 18

Input $u^2(p,t)$ for Scenario 2

Fig. 19

Input $u^3(p,t$) for Scenario 2

4.3 Scenario 3: Ladder circuit with doubled number of nodes

Now we check what happens when the control law (30) matrices calculated for the circuit with $\alpha =50$ is applied to the augmented ladder circuit with $\alpha =100.$ This is a partial solution of the problem of the obtained controllers robustness against nodes number, considered in the Sect. 3.1. Clearly, although the control law matrices remain the same as in the case of Scenario 1, the control action distribution can be different. The augmented disturbance and reference signals adjusted to the new ladder “length” are given in Figs. 20 and 21 respectively. To highlight the circuit behavior, the mean square error dynamics is presented in Fig. 22. Additionally, Fig. 23 shows how the distributed output signal approaches to the desired one. Finally, Figs. 24, 25 and 26 present the distributed control action. These simulations show again that closed loop circuit dynamics are quite similar to the previous scenarios, i.e. the respective signals converge quickly to the desired one with no excessive oscillations at the transient response and with disturbances perfectly decoupled and only the required control action increases. Similar results have been achieved for the modified signals of Scenario 2. This shows that having a ladder circuit of some possibly large number of nodes $\alpha$ we can frequently calculate the control law matrices for the much shorter ladder circuit (smaller $\alpha$) and apply to the desired one, which can greatly reduce numerical efforts.

Fig. 20

Disturbances along the ladder—Scenario 3

Fig. 21

The reference signal for $U_C(p,t)$ of the type of Scenario 1 updated to Scenario 3

Fig. 22

Mean squared error along circuit nodes as a time function—Scenario 3

Fig. 23

Approaching the reference signal at the consecutive time moments $(t=1,\; 5,\; 20\; [s])$—Scenario 3

Fig. 24

Input $u^1(p,t)$—Scenario 3

Fig. 25

Input $u^2(p,t)$—Scenario 3

Fig. 26

Input $u^3(p,t)$—Scenario 3

5 Conclusions

This paper presents new results on application of the hybrid (continuous–discrete) two-dimensional systems approach to modeling, stability analysis and stabilization together with performance requirements to the class of so-called spatially distributed systems, particularly ladder circuits. The goal is to obtain a required spatially distributed reference signal and to completely decouple disturbances of the similar character. Proportional plus Integral control strategy has been extended to this case and applied, which requires constant in time steady state signals and hence has limited our interest only to constant in time reference and disturbance signals. They however can vary along the space variable, i.e. with node number. The results presented here express the potential of the proposed techniques for spatially distributed systems and can be applied to the variety of the systems from this class. Also, numerous problems arising for spatially distributed systems modeling and control have been identified to be the subject of future work.

The motivation for the analysis of controlled ladder circuits has been discussed intensively in the introductory part of the paper. Again it should be stressed that such structures, although of interest for its own from a theoretical point of view, can be used as a model for the description of spatially-temporal physical systems and materials, where the spatial behaviour has been discretized, as e.g. when the discretized spatial coordinate describes the position of a section in the ladder chain. There are already some ideas for which kind of physical effects and structures (like heat transfer in certain materials) our model can be applied. However, this is still work in progress and needs further detailed analysis and simulation.

Future work hence are planned to be twofold, i.e. in the applications to real physical systems, as e.g. to heating systems or LED chains control and for developing new approaches that can be used in different cases and requirements. The crucial here is the lack of spatial causality, which extends the class of possible models. For example, a ladder circuit of the form of Fig. 1 cannot be modeled in the form of Eq. (1) and the resulted model is of the form of

$$\begin{aligned} {\mathcal {E}}_1 \frac{d}{dt}x(p-1,t) +{\mathcal {E}}_2\frac{d}{dt}x(p,t)+{\mathcal {E}}_3\frac{d}{dt}x(p,t)={\mathcal {A}}x(p,t), \end{aligned}$$

(47)

which in fact is not a state equation but in the form of descriptor equation with rectangular singularity matrix. The direct 2D approach is not known for such systems and only the option seems to be using the lifting procedure as in this paper. Also, the extension to time variable reference and disturbance signals is planned where the use of Iterative Learning Control schemes can be fruitful. The extension to the case of uncertain model parameters, which topic is much more complicated for 2D systems in comparison to 1D (Ghamgui et al. 2013), to obtain robust control schemes can be done too.

Another problem that appears to be very important is to develop the proper discrete models of ladder circuit, where the “wave” filters approach seems to be effective. Another promising area related to the ladder systems are circuits described by fractional differential relationship, e.g. super–capacitors, see Kaczorek (2011) and the literature therein. Here it should be mentioned that “fractional” systems stability can be analyzed in the multidimensional (nD) framework leading to the efficient results, see Bachelier et al. (2012).