Mutual information-based feature selection for inverse mapping parameter updating of dynamical systems

Abstract

A digital twin should be and remain an accurate model representation of a physical system throughout its operational life. To this end, we aim to update (physically interpretable) parameters of such a model in an online fashion. Hereto, we employ the inverse mapping parameter updating (IMPU) method that uses an artificial neural network (ANN) to map features, extracted from measurement data, to parameter estimates. This is achieved by training the ANN offline on simulated data, i.e., pairs of known parameter value sets and sets of features extracted from corresponding simulations. Since a plethora of features (and feature types) can be extracted from simulated time domain data, feature selection (FS) strategies are investigated. These strategies employ the mutual information between features and parameters to select an informative subset of features. Hereby, accuracy of the parameters estimated by the ANN is increased and, at the same time, ANN training and inference computation times are decreased. Additionally, Bayesian search-based hyperparameter tuning is employed to enhance performance of the ANNs and to optimize the ANN structure for various FS strategies. Finally, the IMPU method is applied to a high-tech industrial use case of a semi-conductor machine, for which measurements are performed in closed-loop on the controlled physical system. This system is modeled as a nonlinear multibody model in the Simscape multibody environment. It is shown that the model updated using the IMPU method simulates the measured system more accurately than a reference model of which the parameter values have been determined manually.

1 Introduction

As part of the fourth industrial revolution, digital twins have the potential to monitor the structural health and improve the performance of a physical system, e.g., via model-based control. To achieve this, the digital twin, e.g., a dynamical multibody model, should accurately represent the true physical system. In practice, however, it may be difficult to accurately and efficiently tune the model parameter values for a fleet of systems due to manufacturing tolerances. Moreover, due to, e.g., wear, the system dynamics may change over time. Consequently, there is a need for updating methods that update physically interpretable parameter values and are applicable in an online setting. Furthermore, to allow for fast fault detection (e.g., important in the scope of diagnostics), the updating procedure should be computationally efficient. Finally, we aim for a method that can update a broad range of nonlinear dynamics models.

As a solution to the problem posed here, in previous work, the authors have proposed the inverse mapping parameter updating (IMPU) method [1]. This method employs an artificial neural network (ANN) that infers (online) a set of parameter values from a set of features extracted from measured data. Here, the ANN is trained in an offline phase using supervised learning on simulated data, where the features and parameter values serve as inputs and outputs to the ANN, respectively. By using simulated training data, direct access to the (physically interpretable) updating parameter values is obtained, which on a physical system are typically unmeasurable. By shifting the majority of the computation time to the offline phase, parameter values can be inferred in the order of microseconds in the online (or parameter estimation) phase. Due to the use of input (features) and output (parameter values) data only, this methodology is applicable to a large variety of (dynamic) models, i.e., models in closed form derived from first principles or opaque simulation models (such as those constructed in software, e.g., in Simscape Multibody [2]).

In contrast, other popular model (parameter) updating methods, e.g., the extended Kalman filter (EKF) [3–7], typically require the explicit equations of motion (EoMs) of a model. Although the main advantages of the IMPU method over the EKF are mostly of a qualitative nature, the interested reader is referred to [1] for a quantitative comparison (using simulated measurements, polluted with artificial noise). Other conventional (sensitivity-based) parameter updating techniques [8–10] require costly iterative computations, which are undesirable. Moreover, these sensitivity-based updating techniques (as well as EKF) require initial guesses for the parameter values, where an incorrect guess may result in suboptimal parameter estimates. Furthermore, traditional system identification methods typically yield models in a generic form, due to which some physical interpretability (which is valuable for intelligible health monitoring) is lost [11].

In the IMPU method, a wide range of response features can be used: multiple (combinations of) transient-based types, i.e., sampled values of a time-signal, the extrema thereof, and (complex) values of the Fourier-transformed signal, see [1]. In practice, however, some features might be irrelevant as they are barely influenced by the updated parameters. As a result, the ANN may become unnecessarily large, which causes slower (offline) training and (online) inference. Additionally, the accuracy of the inferred parameters might suffer from these irrelevant (noisy) features since it is affected by these features that make training more difficult [12, 13].

Therefore, feature selection (FS) techniques that determine which features should be retained and which features should be omitted can be employed [14]. Within FS, methods are available for supervised, semi-supervised, and unsupervised learning [15]. Since the IMPU method is based on supervised learning, we will only consider supervised FS methods. Furthermore, a distinction is made between embedded, wrapper, and filter FS methods [16]. Since only filter methods allow for feature selection prior to training an ANN, and are consequently computationally less demanding, this type of methods is used in this work. To determine if a feature is relevant for the accurate updating of a particular parameter, the mutual information (MI) [17] score between a feature and a parameter is calculated using the training data. Then, a user-defined number of features with the highest MI scores is selected. An advantage of MI is that this metric can deal with nonmonotonic and nonlinear relations between the assessed variables. This is in contrast to other filter methods, such as the Pearson’s correlation coefficient, Spearman’s rank correlation coefficient, and Kendall’s tau coefficient [18].

Additionally, manual tuning of training- and topology-related settings of an ANN is both difficult and time consuming. Therefore, ANN hyperparameter tuning (HPT) is employed to automatically tune these hyperparameters such that performance is improved and online inference time is decreased.

Finally, in previous work [1], the IMPU method has only been applied to academic demonstrators that operate in open loop. In this work, this application is extended to an industrial use case. Specifically, parameters of the closed-loop controlled motion stages of a high-tech wire bonder system [19] are updated. Additionally, in contrast to previous work in which measurements were simulated, in this paper, model updating is performed based on data that is measured on a physical wire bonder machine.

To summarize, the main contributions of this work are:

• 1. Extension of the inverse mapping parameter updating method with mutual-information-based feature selection, thereby improving efficiency and accuracy of the parameter updating approach. Herein, the effectiveness of different FS approaches is investigated.

• 2. The use of hyperparameter tuning for the inverse mapping parameter updating method. Hyperparameter tuning is, for example, used to optimize the artificial neural network topology for different sets of selected features.

• 3. The application and analysis of the proposed method on a multibody model of an industrial system that is measured in closed-loop with feedback and feedforward control.

The outline of this paper is as follows. In Sect. 2, some preliminaries for the IMPU method and HPT are provided. Section 3 discusses feature selection by introducing the concept of MI, and introducing various MI-based FS strategies. Subsequently, Sect. 4 shows the industrial application of the discussed methodologies. Results are shown based on simulated and physical measurements of the wire bonder machine. Finally, conclusions and recommendations for future work are discussed in Sect. 5.

2 Preliminaries

2.1 Inverse mapping parameter updating method

In the IMPU method [1], the goal is to update parameter values, stored in $\boldsymbol{p}\in \mathbb{R}^{n_{p}}$ such that the output $\boldsymbol{y}\in \mathbb{R}^{n_{\textrm{out}}}$ of a generic nonlinear dynamical model,

$$ \begin{aligned} \boldsymbol{\dot{x}}(t) &= \boldsymbol{g}(\boldsymbol{x}(t), \boldsymbol{u}(t), \boldsymbol{p}) \\ \boldsymbol{y}(t) &= \boldsymbol{h}(\boldsymbol{x}(t), \boldsymbol{u}(t), \boldsymbol{p}) + \boldsymbol{w}, \end{aligned} $$

(1)

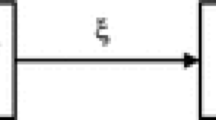
best corresponds to (sampled) measured data $\boldsymbol{\bar{\texttt{y}}}$ obtained on a physical system. For this comparison, $\boldsymbol{y}$ needs to be sampled in the same way as the sampled measurement $\boldsymbol{\bar{\texttt{y}}}$, see (4) for the sampled version of $\boldsymbol{y}$. Here, $\boldsymbol{x}\in \mathbb{R}^{n_{x}}$ and $\boldsymbol{u}\in \mathbb{R}^{n_{\textrm{in}}}$ represent the state and input vector, respectively. Furthermore, $\boldsymbol{g}$ is the nonlinear vector field, $\boldsymbol{h}$ is the output function, and $\boldsymbol{w}$ is zero-mean additive sensor output noise. The number of states, outputs, inputs, and updating parameters is given by $n_{x}$, $n_{\textrm{out}}$, $n_{\textrm{in}}$, and $n_{p}$, respectively.

Given some $\boldsymbol{u}(t)$ and initial conditions, the dynamical (or forward) model in (1) yields output signals for some choice of updating parameter values. Since the relation between the output signals and updating parameters is complex, updating the parameter values typically requires iterative methodologies that employ the sensitivity of the forward model, resulting in high online computational cost. As an alternative, the IMPU method proposes to use an inverse mapping model (IMM, constituted by some generic regression model) to capture this complex relation. This is achieved by training the IMM in an offline phase (which will be discussed below Equation (3)) such that the computational burden in the online phase is reduced to a minimum. After training, the IMM ℐ maps a set of $n_{\psi}$ measured features $\boldsymbol{\bar{\psi}}\in \mathbb{R}^{n_{\psi}}$ (related to the measured output $\boldsymbol{\bar{\texttt{y}}}$) to a set of estimated parameter values $\boldsymbol{\hat{p}}\in \mathbb{R}^{n_{p}}$ and thus serves as an inverse of the forward model [1]:

$$ \boldsymbol{\hat{p}} = \mathcal{I}(\boldsymbol{\bar{\psi}}). $$

(2)

Here, features are extracted and selected from the measured transient data $\overline{\mathbf{\text{y}}}$ using some function ℒ:

For the IMM, which is constituted by an ANN, to learn the correct mapping ℐ, supervised learning is used. Therefore, pairs (or samples) of training parameters $\boldsymbol{p}_{s}$ and corresponding training features $\boldsymbol{\psi}(\boldsymbol{p}_{s})$ are utilized, where $s=1,\dots ,n_{s}$ indicates the training sample. The training features $\boldsymbol{\psi}(\boldsymbol{p}_{s})$ are extracted using (3) from simulated output data that is obtained using the model (e.g., (1)), parameterized using $\boldsymbol{p}_{s}$ (i.e., ). Note that this simulated output data is polluted with artificial noise ($\boldsymbol{w}$ in (1)) to mimic real measurements. Furthermore,

represents a set of sampled (or discretized) simulated output signals, where each row corresponds to an individual output signal, with $N$ (time) samples. For a more elaborate general introduction to ANNs and training thereof using supervised learning, please consult [20] or, in the context of the IMPU method, see [1].

The ANN is trained on data generated in the offline phase using the model in (1) for a particular updating experiment, i.e., for a particular choice of $\boldsymbol{u}(t)$ and initial conditions $\boldsymbol{x}_{0}$. As a result, the ANN only ‘knows’ how to infer parameter values from features that are obtained for this specific experiment. Since the ANN thus implicitly assumes an invariable updating experiment, the measured data provided to the ANN in the online phase should be obtained with the same $\boldsymbol{u}(t)$ and $\boldsymbol{x}_{0}$ as used in the offline phase. A schematic overview of the IMPU method is provided in Fig. 1. Finally, it is remarked that the IMPU method implicitly assumes that the model structure, i.e., its EoMs, is rich enough to capture all relevant dynamics of the measured system and that measurement errors are limited to zero mean output sensor noise.

Fig. 1

Schematic overview of the IMPU method with the offline (top) and online (bottom) phases, including FS (see Sect. 3). The selected set of features is indicated by the subscript $\mathcal{S}$. Furthermore, $\boldsymbol{P}$ and $\boldsymbol{\Psi}$ represent the collection of all $n_{s}$ training parameters $\boldsymbol{p}_{s}$ and features $\boldsymbol{\psi}_{s}$, respectively, as defined in (5)

2.2 ANN hyperparameter tuning

During training of an ANN, the training parameter settings (e.g., learning rate and batch size) and structure (e.g., the number of layers and the number of neurons in each layer) of an ANN directly influence its training time and, more importantly, its inference accuracy. Therefore, these so-called hyperparameters can be tuned such that some metric, e.g., the validation loss, is minimized. Since the (validation) loss varies in each epoch during training, the instance of the ANN with the lowest validation loss during its training is saved and evaluated.

Remark 1

The validation loss is the loss (in our case defined as the mean squared error between parameter values inferred based on sets of features and the actual parameter values) calculated using the validation data. For training and inference, both the inferred and actual parameter values are normalized (between 0 and 1) as this improves the conditioning for the training of the ANN [21]. This type of ‘normalization for training’ is not to be confused with ‘normalization for confidentiality’ as used in Sect. 4. Hence, the validation loss is measured on a distinct scale. Validation data is similar to, yet independent from, the training data such that an unbiased evaluation of ANN performance is achieved.

Manually tuning hyperparameters can prove both difficult and time consuming, although some directions can be found in [22]. Therefore, different automated HPT search methods have been developed [23]. In such searches, ANNs are trained and evaluated for different configurations of hyperparameter values. The most popular search methods are grid, random, and Bayesian searches [24]. Since in a grid search all possible configurations of hyperparameter values are evaluated for a predefined discretized set of values, this is typically a computationally intensive search. In contrast, random and Bayesian searches allow for continuous hyperparameter values. Random searches tend to be less costly but suffer significantly from uncertainty. In a Bayesian search, a Gaussian process that models the relationship between hyperparameter values and the validation loss such that the probability of improvement is optimized is used [25]. Since Bayesian searches compromise well between accuracy, efficiency, and reliability, this search type is employed for this research. As is the case for any Bayesian method, a prior on the hyperparameter values is required. In this work, we do not assume any hyperparameter values to be more likely than others. Therefore, uniform priors are employed.

3 Feature selection

In this section, the underlying theory for mutual information-based feature selection is provided. First, Sect. 3.1 explains how the (conditional) MI score between two variables is calculated from training data. Subsequently, Sect. 3.2 discusses three popular FS strategies that employ MI.

3.1 Mutual information

The MI score $I$ between two variables, e.g., the $i$^th feature and $k$^th parameter, quantifies how much information is shared between these two variables. This score is calculated based on the values these individual variables take on for all $n_{s}$ training samples. Therefore, the values of all features for all training samples are collected in $\boldsymbol{\Psi}\in \mathbb{R}^{n_{\psi}\times n_{s}}$, where the $i$^th row, denoted as $\boldsymbol{\Psi}_{i}$, contains the values for feature $i$ for all $n_{s}$ training samples:

$$ \boldsymbol{\Psi} = \begin{bmatrix} \boldsymbol{\psi}^{(1)}, \dots , \boldsymbol{\psi}^{(n_{s})}\end{bmatrix} = \begin{bmatrix} \boldsymbol{\Psi}_{1} \\ \vdots \\ \boldsymbol{\Psi}_{n_{\psi}} \end{bmatrix} . $$

(5)

Similarly, we define $\boldsymbol{P}\in \mathbb{R}^{n_{p}\times n_{s}}$ for the $n_{p}$ model parameters. The MI score, $I\geq 0$ [26], is then calculated as follows [17]:

$$ I\left (\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{P}}_{k} \right ) = \sum ^{n_{\textrm{bins}}}_{a=1} \sum ^{n_{\textrm{bins}}}_{c=1} \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{P}}_{k}^{(c)}\right ) \log \left ( \frac{\phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)},\boldsymbol{\check{P}}_{k}^{(c)}\right )}{\phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}\right )\phi \left (\boldsymbol{\check{P}}_{k}^{(c)}\right )} \right ), $$

(6)

where the check in $\boldsymbol{\check{\Psi}}_{i}$ indicates that the continuous feature $i$ stored in $\boldsymbol{\Psi}_{i}$ is partitioned in $n_{\textrm{bins}}$ (chosen by the user) discrete bins of equal width,¹ with the value of each bin $a$ indexed by $\boldsymbol{\check{\Psi}}_{i}^{(a)}$. A similar notation convention is used for the partitioned (or discretized) values for parameter $k$ stored in $\boldsymbol{\check{P}}_{k}$. Furthermore, $\phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}\right )$ represents the (approximated) probability that the value of a discretized feature equals $\boldsymbol{\check{\Psi}}_{i}^{(a)}$. A mathematical explanation on the computation of (joint) probabilities for a finite dataset is given in Appendix A. Note that the MI score can also be calculated between two features to prevent that multiple features that carry approximately the same information are selected.

Moreover, the conditional mutual information (CMI) between features $i$ and $j$, conditioned on parameter $k$, is defined as [17]

$$ \begin{aligned} I^{\textrm{con}}\left (\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{\Psi}}_{j} \left |\boldsymbol{\check{P}}_{k} \right .\right ) &= \sum ^{n_{\textrm{bins}}}_{c=1} \phi \left ( \boldsymbol{\check{P}}_{k}^{(c)} \right ) \sum ^{n_{\textrm{bins}}}_{a=1} \sum ^{n_{\textrm{bins}}}_{b=1} \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{\Psi}}_{j}^{(b)} \left |\boldsymbol{\check{P}}_{k}^{(c)} \right .\right ) \\ &\times \log \left ( \frac{ \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{\Psi}}_{j}^{(b)} \left |\boldsymbol{\check{P}}_{k}^{(c)}\right . \right ) }{ \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}\left | \boldsymbol{\check{P}}_{k}^{(c)}\right . \right ) \phi \left (\boldsymbol{\check{\Psi}}_{j}^{(b)}\left | \boldsymbol{\check{P}}_{k}^{(c)}\right . \right ) } \right ). \end{aligned} $$

(7)

Here, vertical bars indicate conditioning on a value for the $k$^th parameter. The CMI in (7) can be regarded as the amount of information that two features share when the parameter value is known. In this work, all MI and CMI scores are computed using the MI toolbox [28] with $n_{\textrm{bins}}=50$.

3.2 MI-based FS strategies

To select features based on their MI, they are ranked based on a relevance score $J$. This score is calculated per feature (indexed by $i$) to quantify the importance of that feature with respect to the $k^{\textrm{th}}$ parameter. Although a large variety of definitions for this score exist, here, we will limit ourselves to three strategies: (1) the mutual information maximization (MIM) [29, 30], (2) max-relevance min-redundancy (MRMR) [31], and (3) joint mutual information (JMI) [32]. For these strategies, the relevance score for candidate feature $i$ with respect to parameter $k$ are given by

$$ J(\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{P}}_{k}, \mathcal{S}) = J_{\textrm{REL},ik} - \gamma _{1} J_{\textrm{RED},i} + \gamma _{2} J_{\textrm{CRED},ik}, $$

(8)

where for $\gamma _{1}=\gamma _{2}=0$ we obtain MIM, for $\gamma _{1}=1$ and $\gamma _{2}=0$ we get MRMR, and for $\gamma _{1}=\gamma _{2}=1$ JMI is obtained. Furthermore,

$$\begin{aligned} J_{\textrm{REL},ik} &= I \left (\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{P}}_{k}\right ) , \end{aligned}$$

(9)

$$\begin{aligned} J_{\textrm{RED},i} &= \frac{1}{|\mathcal{S}|}\sum _{j\in \mathcal{S}} I \left (\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{\Psi}}_{j} \right ), \end{aligned}$$

(10)

$$\begin{aligned} J_{\textrm{CRED},ik} &= \frac{1}{|\mathcal{S}|}\sum _{j\in \mathcal{S}} I^{\textrm{con}}\left (\boldsymbol{\check{\Psi}}_{i}, \boldsymbol{\check{\Psi}}_{j} \left |\boldsymbol{\check{P}}_{k} \right .\right ), \end{aligned}$$

(11)

where $\mathcal{S}$ denotes the set of (already) selected features (hence, $i\notin \mathcal{S}$), with $|\mathcal{S}|$ its cardinality, i.e., the number of elements in $\mathcal{S}$ [17].

All three strategies employ $J_{\textrm{REL},ik}$ which quantifies the relevance of feature $i$ to parameter $k$ using their MI score. The second term $J_{\textrm{RED},i}$ penalizes redundancy between features, i.e., feature $i$ is penalized if it contains information similar to the information carried by features that have already been selected. The third term $J_{\textrm{CRED},ik}$ (conditional redundancy) can partly mitigate the second term. This term recognizes that the correlation between two similar features, i.e., between feature $i$ and any of the already selected features, can be useful. Suppose that, for some combination of features, this correlation is stronger given some knowledge about the parameter $k$ than the correlation when this knowledge is absent. Then, if we indeed see strong correlation, we still obtain some information about the parameter, and it is therefore valuable to select both features [17]. In other words, JMI promotes the complementary information between features and acknowledges that “correlation between features does not imply redundancy” [33].

For MIM, only $J_{\textrm{REL}}$ contributes to $J$. Consequently, the relevance score $J$ does not depend on the set of (already) selected features. Thus, MIM is, in contrast to MRMR and JMI, a noniterative strategy and, hence, computationally more efficient. Therefore, $J$ is calculated for all features with respect to parameter $k$. Then, the (user-specified) $n_{\psi ,\textrm{sel}, k}$ highest scoring features are concurrently collected in $\mathcal{S}_{k}$ for the MIM strategy. If $n_{p}$ parameters are updated, then the set of all kept features (across all parameters) $\mathcal{S}$ is given by the unique union of the selected sets per parameter, i.e., $\mathcal{S}= \mathcal{S}_{1} \cup \mathcal{S}_{2} \cup \cdots \cup \mathcal{S}_{n_{p}}$. As a result, for MIM, the total number of features selected for all $n_{p}$ parameters $n_{\psi ,\textrm{sel},\textrm{MIM}}=|\mathcal{S}_{\textrm{MIM}}|\leq \sum _{k=1}^{n_{p}}n_{\psi ,\textrm{sel}, k}$.

For the MRMR and JMI strategy, $J$ does depend on the already selected features in the current set $\mathcal{S}$ that have been selected with respect to any of the parameters. Consequently, after having selected one additional feature for a certain parameter, $J$ has to be recalculated for all features to select the next feature to be added to $\mathcal{S}$ in an iterative manner, even if this feature is selected with respect to a different parameter. The MRMR and JMI strategies are initiated by defining an empty set $\mathcal{S}$ (which in the end will contain selected features for all $n_{p}$ parameters). Then, relevance scores are calculated for all features with respect to the first parameter. Note that, since in the first iteration $|\mathcal{S}|=0$, for this iteration only, the contributions of $J_{\textrm{RED}}$ and $J_{\textrm{CRED}}$ are manually set to zero. The feature with the highest relevance score is selected and added to $\mathcal{S}$. Subsequently, the same procedure is performed for the second parameter and so on. Having selected one feature per parameter, this process is repeated until $n_{\psi , \textrm{sel}, k}$ features are selected for all parameters.² As a consequence, for MRMR and JMI, when all features have been selected $n_{\psi ,\textrm{sel},\textrm{MRMR}} = n_{\psi ,\textrm{sel}, \textrm{JMI}} = \sum _{k=1}^{n_{p}}n_{\psi ,\textrm{sel}, k} \geq n_{ \psi , \textrm{sel}, \textrm{MIM}}$. The MRMR and JMI strategies are summarized in Algorithm 1. Note that, in this work, for simplicity, the number of features selected per parameter $n_{\psi ,\textrm{sel}, k}$ is chosen equal for all parameters for all three discussed FS strategies.

Algorithm 1

Algorithm to select features using MRMR and JMI

4 Application to an industrial multibody system

In this section, the effectiveness of the methodologies explained in the previous sections are demonstrated on an industrial use case. Firstly, the use case and its multibody model are introduced in Sect. 4.1. Then, in Sect. 4.2, offline aspects of the IMPU method, e.g., training data generation, feature selection results, and training (using HPT), are discussed briefly. Finally, in Sects. 4.3 and 4.4, (online) inference results are shown and analyzed for simulated and physical measurements, respectively.

4.1 System and model description

As an industrial use case, the XYZ-motion stage of a wire bonder machine of the commercial company ASMPT is used, see Fig. 2. This is a high-tech system used to connect integrated circuits to other electronic components with high accuracy ((sub-)micrometer range) and high throughput (realized by motion stage accelerations exceeding $1500\textrm{m}/\textrm{s}^{2}$). This multibody motion stage consists of four stacked bodies: a BaseFrame (BF), and an X-, Y-, and Z-stage, as indicated in Fig. 2 and shown schematically in Fig. 3. Here, each stage allows for movement along one axis which is measured and controlled via feedback and feedforward control to follow a position setpoint profile. This system is modeled in Simscape Multibody [2] and, consequently, explicit EoMs are not available. From the total of ten degrees of freedom (DoFs) in the model, seven DoFs are parasitic and induced by, among others, machine feet and linear bearings with finite stiffnesses. The other three DoFs are the motion directions of the three stages, which are measured using encoders. For the model of this system, artificial, white zero-mean Gaussian sensor noise is added with similar noise characteristics, i.e., signal to noise ratio, as observed on the real system.

Fig. 2

XYZ-motion stage of wire bonder machine [19]. Different parts of the system are marked following a color code: , , , . Furthermore, the principal directions of motion of the stages are indicated in their corresponding colors. Note that a color version of the article is given online

Fig. 3

Simplified representation of stacked bodies in wire bonder motion stage model. (Connections to other) bodies are color coded: , , , and . The updating parameters are indicated in . The DoFs are indicated per body by colored arrows, where an open colored arrow head () indicates a parasitic degree of freedom, and a solid colored arrow head () indicates the DoFs related to the principle motion direction of the X-, Y-, and Z-stage

Parameter values of this model have originally been determined by engineers of the commercial company. Specifically, the parameter values of this model related to dimensions and inertia (of all four bodies, i.e., the BF and three motion stages) are obtained from a high-fidelity computer aided design model. The other parameter values (e.g., stiffness and damping) are tuned manually based on frequency response function measurements. In the following, however, it is assumed that the values of some of these parameters are originally determined with relatively high uncertainty, expected to change over time (due to, e.g., wear), and/or have a significant influence on the system’s dynamic behavior, in general. Regarding the latter point, the influence of the parameters on the (output of the) system has been determined in a brief (numerical) parameter sensitivity study (not shown here for brevity). As a result, $n_{p}=10$ parameters are selected to be updated, of which the manually determined values are denoted by $\boldsymbol{p}_{\textrm{ref}}$. These updating parameters (among which are damping ($d$), stiffness ($k$), inertia ($m$ and $I$), motor force constant ($K$), and dimensional ($L$) variables) are listed in Table 1, where the subscript denotes to which body these parameters refer and, if applicable, in which direction. This table also lists the lower and upper bounds per parameter that define the allowed parameter value space $\mathbb{P}\subset \mathbb{R}^{n_{p}}$ in which these parameters are expected to lie or evolve in over time in the physical system. These bounds have been determined by using engineering knowledge and experience with the physical machine, as well as by performing a brief parameter study to evaluate the influence of the parameters on the output signals. For confidentiality reasons, all signals and parameter values shown in this paper are normalized and information on controllers is not provided.

Table 1 Updating parameters and their lower and upper bound for ℙ, expressed as a factor of their reference value. The subscripts of the parameters denote which body each parameter refers to, or in case of damping and stiffness parameters, between which two bodies (separated by a ‘2’) and in which direction (after the comma). Furthermore, $L_{\textrm{CoM}_{Z},z}$ denotes the distance, in the $z$-direction, between the center of mass (CoM) of the Z-stage and the pivot point of the Z-stage

4.2 Offline data generation and training

This section describes the offline aspects of the IMPU method. Firstly, in Sect. 4.2.1, data generation to be used to train the ANN is discussed. Subsequently, the results of FS, which are based on the training data, are analyzed in Sect. 4.2.2. Finally, ANN training and HPT is discussed and evaluated for various sets of selected features in Sect. 4.2.3.

4.2.1 Data generation

The dataset used to train the ANNs in Sect. 4.2.3 consists of $n_{s}=10{,}000$ training samples. For each training sample, a set of parameter values $\boldsymbol{p}_{s}$ is sampled from ℙ using Latin Hyper Cube sampling. By employing Latin Hyper Cube sampling, the training parameters are sampled consistently and with sufficient uniformity (see [34] for a detailed explanation). Then, the Simscape model is parameterized and simulated for each training sample for a simulated experiment defined by reference trajectories $r_{X}(t)$, $r_{Y}(t)$, and $r_{Z}(t)$ over some period of time. The simulated signals are sampled with a sampling frequency identical to the sampling frequency of the encoders on the physical setup. The reference trajectories, together with the feedback and feedforward controllers, take over the role of $u(t)$ in Figs. 1 and 3 and (1), where (1) represents the closed-loop dynamics. The experiment used to train the IMM in the offline phase and provide inputs to the ANN based on (simulated) measurements in the online phase is referred to as ‘experiment 1’. In this work, we employ alternating smoothed forward and backward trajectories (closely resembling steps in the reference trajectories used in practice) for all stages, see the lines in Fig. 4. As initial conditions, the system is at rest at the origin (achieved using a homing procedure on the physical system in Sect. 4.4).

Fig. 4

Reference trajectories (setpoint profiles) per stage used for experiment 1 (, used to train IMM and update the parameter values) and experiment 2 (, used to test generalization of the updated model) (see Sect. 4.4.2)

The set of potential features (from which specific features can be selected) is extracted from the discretized tracking errors ${\overline{\mathbf{\text{e}}}}_X$, ${\overline{\mathbf{\text{e}}}}_Y$, and ${\overline{\mathbf{\text{e}}}}_Z$ of the X-, Y-, and Z-stage, respectively, where (the • can be substituted by $X$, $Y$, or $Z$). Here, ${\overline{\mathbf{\text{y}}}}_{•}$ represents a discretized measured output signal (similar to a row in (4)) in either the X-, Y-, or Z-direction. Similarly, the discretized setpoint profile is determined from $r_{\bullet}(t)$. Note that the length of ${\overline{\mathbf{\text{e}}}}_{•}$, $N=7600$, generally exceeds the number of features to be extracted. In this work, different feature types are extracted: (1) time sample (TS) features, i.e., samples of ${\overline{\mathbf{\text{e}}}}_{•}$ at equidistant moments in time (less than $N$), (2) time extrema (TE) features, i.e., (local) maxima and minima in ${\overline{\mathbf{\text{e}}}}_{•}(t)$ and timestamps of when these occur (the latter in contrast to TS features), and (3) real and imaginary (RI) values of the fast Fourier transform of the discretized ${\overline{\mathbf{\text{e}}}}_{•}(t)$ within a range of frequency bins of interest (FBoIs). For a detailed definition of these feature types, the reader is referred to [1]. For each feature type, a different number of features is extracted: $n_{\psi ,\textrm{TS}}=2250$, $n_{\psi ,\textrm{TE}}=50$, and $n_{\psi ,\textrm{RI}}=2253$. This results in a total of $n_{\psi}=4553$ features to select from.³ After feature extraction, all training parameters and features are normalized between 0 and 1 to improve the conditioning of the training process, see [1] for more information.

Besides training data, 500 validation samples (used during HPT and ANN training for early stopping, see Sect. 4.2.3 for more details) and 500 test samples (used in Sect. 4.3) are generated similarly to the training data. For validation and test samples, parameter values are, however, randomly sampled from ℙ (of which the boundaries are defined, per parameter, in Table 1) using a uniform distribution.

4.2.2 Feature selection results

Feature selection is performed using the training data as described in Sect. 4.2.1 and, for MRMR and JMI, in Algorithm 1, where for each parameter $k$ ($k=1, \dots , 10$) $n_{\psi ,\textrm{sel},k}=30$ features are selected. In Table 2, several FS results are listed per FS strategy.

Table 2 Total number of selected features $n_{\psi ,\textrm{sel}}$ and selected features per feature type $n_{\psi ,\textrm{sel},\bullet}$ for the three FS strategies. Furthermore, computation time⁴ and the number of dissimilar features with respect to the other FS strategies are listed

When using MIM, there is an overlap between features selected for different parameters, causing the total number of selected features to be smaller than 300, i.e., $n_{\psi , \textrm{sel}, \textrm{MIM}}< n_{\psi , \textrm{sel}, \textrm{MRMR}} = n_{\psi , \textrm{sel}, \textrm{JMI}}=300$. Furthermore, we observe that only the MIM method selects a single TE feature. Consequently, we can conclude that TE features are relatively uninformative for this particular use case (possibly due to the lack of dominant transient behavior). In contrast, RI features are relatively informative. This corroborates a similar observation made in [1]. Additionally, a clear difference in computation times⁴ between the strategies is noticed. For example, MIM is relatively cheap (since it is a noniterative method), whereas JMI is comparatively expensive (due to the costly computation of CMI for the set of already selected features). The final three columns of Table 2 confirm that the strategies select different features, yet also share features that are identified as relevant by multiple strategies.

4.2.3 ANN training and HPT

Selected sets of features, together with their corresponding training parameter values, are employed to train ANNs. In this work, the ANNs are implemented using the Keras application programming interface for the Tensorflow library in the Python programming language [35]. Furthermore, the Adams optimizer is used to train the ANNs. Each ANN employed in this work is a fully connected direct feed-through network [20] and has Sigmoid activation functions in the output layer. Furthermore, early stopping with a patience of 40 epochs is employed, i.e., if the validation loss does not decrease for 40 consecutive epochs, the training process is terminated [36]. After training, the ANN that achieved the lowest validation loss is saved.

As a benchmark, one ANN is trained on the training data without FS, i.e., $n_{\psi}=4553$ features are used, with manually tuned hyperparameter values. Here, manual HPT is mostly based on general experience in neural network training, i.e., understanding the effects of hyperparameters on, among others, training/inference time and inference accuracy (see [22] for some general insights). The hyperparameter values used for this ‘manual’ ANN that are related to the training settings are listed in the first row of Table 3. Regarding the ANN structure, a network with three hidden layers is used with $n^{(1)}_{z}=1000$, $n^{(2)}_{z}=400$, and $n^{(3)}_{z}=100$ neurons in the first, second, and third hidden layer, respectively.

Table 3 Training settings and results of ANN obtained using manually tuned hyperparameters (first row) and results of HPT phase 1, i.e., without FS (second row). Note that the validation loss was defined in Remark 1

Manually tuning hyperparameters is suboptimal and time consuming for the (data) engineer. Therefore, HPT is performed using the Weights & Biases platform [37]. Since HPT requires extensive searches within the multidimensional hyperparameter space, we suffer from the curse of dimensionality. To limit the effect of this curse, the HPT procedure is split in two phases in which two distinct sets of hyperparameters are tuned. First, hyperparameters related to the training settings are tuned in phase 1. Then, using training settings that are based on the results of phase 1, the structure of the ANN is tuned in phase 2. In both phases, Bayesian searches are applied.

For phase 1, an HPT search of 250 hyperparameter configurations is performed for the data without FS. Here, the number of neurons in the hidden layers is kept equal to those of the manual ANN. The training-related hyperparameters (and their search ranges) that are tuned are: the activation functions for all hidden layers (either ‘ReLU’ or ‘Sigmoid’), the batch size (range: $[20,320]$), the number of epochs (range: $[50,600]$), and the learning rate (sampled logarithmically in the range $[10^{\textrm{-}4}, 10^{\textrm{-}1}]$). The found hyperparameter values and validation loss of the best ANN, i.e., with the lowest validation loss, are listed in Table 3. Here, it is shown that HPT indeed is able to improve the validation loss. Note that the objective of HPT is to decrease the validation loss; the training time is thus not optimized and its significant increase is tolerated.

In HPT phase 2, the goal is to further improve the validation loss by tuning the number of neurons per hidden layer in 200 hyperparameter configurations. Here, $n^{(1)}_{z}\in [10, 1000]$, $n^{(2)}_{z}\in [10, 400]$, and $n^{(3)}_{z}\in [10,100]$. Based on the results of phase 1, the ‘ReLU’ activation function is used for the hidden layers, $\textrm{learning rate}=1.5\times 10^{\textrm{-}4}$, batch size⁵$=50$, and number of $\textrm{epochs} = 350$.

Now, separate searches are performed for the data without FS and with the three FS strategies. In Table 4, $n^{(1)}_{z}$, $n^{(2)}_{z}$, and $n^{(3)}_{z}$ are given for one selected ANN for each search. Here, the ANN is selected by first ordering all ANNs in a search based on their validation loss. Then, from the top ten ANNs with the lowest validation losses (which typically are comparable), the ANN that most accurately reproduces the measured response for experiment 1, based on some simulation error metrics, (see Sect. 4.4) is selected and analyzed in Sects. 4.3 and 4.4. The learning curves for the ANNs using no FS and JMI FS are shown in Fig. 11 in Appendix B. Additionally, Table 4 lists the search time and total number of trainable weights per ANN (which is indicative of the training and inference complexity and hence computation times). Clearly, due to the considerably lower number of trainable weights when using FS (a result of the smaller input dimension of the ANN), the search time is significantly reduced when FS is employed. For the current study, the difference in search times between the FS strategies is considered negligible. Most importantly, the validation losses in Table 4 show that FS also improves the accuracy of the ANN. Here, the JMI FS strategy performs best since it incorporates both relevance and conditional redundancy of features. Note that the JMI FS strategy comes at the cost of increased computation time, however (see Table 2).

Table 4 Results of HPT phase 2 (i.e., the number of neurons per hidden layer and the number of weights and validation losses following from those) for various FS strategies. The first row shows the results for the ANN with manually tuned hyperparameters

Finally, it is remarked that the tuned hyperparameters likely do not constitute the global optimum. In practice, it is impractical to search the entire highly nonconvex (continuous) hyperparameter space for the optimum. However, by using an HPT methodology that searches a sufficiently large space, the user gains confidence that the performance (i.e., validation loss) of the resulting ANN is relatively close to the global optimum.

4.3 Online inference using simulated measurements

In this section, inference results obtained using $n_{\bar{s}}=500$ simulated test samples are evaluated. Since we know the true parameter values $\boldsymbol{\bar{p}}_{\bar{s}}$ for each test sample $\bar{s}$, the accuracy of the inferred parameter values can be determined. For confidentiality reasons, the (true) parameter values are first normalized using

$$ \boldsymbol{\bar{p}}^{\textrm{nor}}_{\bar{s}} = \boldsymbol{\bar{p}}_{ \bar{s}} \oslash \boldsymbol{p}_{\textrm{ref}} , $$

(12)

where ⊘ denotes the element-wise division operator. The normalized inferred parameter values $\boldsymbol{\hat{p}}_{\bar{s}}^{ \textrm{nor}}$ are obtained similarly as in (12). The mean (over all test samples) absolute error of the (normalized) inferred parameter values, $\boldsymbol{\varepsilon}^{\textrm{nor}}\in \mathbb{P}$, is defined⁶ as

$$ \boldsymbol{\varepsilon}^{\textrm{nor}} = \frac{1}{n_{\bar{s}}} \sum _{ \bar{s}=1}^{n_{\bar{s}}} \left | \boldsymbol{\hat{p}}^{\textrm{nor}}_{ \bar{s}} - \boldsymbol{\bar{p}}_{\bar{s}}^{\textrm{nor}} \right |. $$

(13)

For conciseness, the average of $\boldsymbol{\varepsilon}^{\textrm{nor}}$ over all parameters, i.e., $\boldsymbol{\varepsilon}^{\textrm{nor}}_{\textrm{av}} = \frac{1}{n_{p}}\left \| \boldsymbol{\varepsilon}^{\textrm{nor}} \right \|_{1}$, is listed in Table 5 for ANNs obtained using the various FS strategies. Here, we see that, as may be expected, a low validation loss results in a low inferred parameter error⁷$\boldsymbol{\varepsilon}^{\textrm{nor}}_{\textrm{av}}$. Consequently, and also as expected, employing HPT and FS reduces $\boldsymbol{\varepsilon}^{\textrm{nor}}_{\textrm{av}}$. Specifically, it is observed that, based on parameter estimation accuracy as listed in the fourth column of Table 5, the JMI strategy is again the most favorable FS strategy. Finally, although the inference computation time for one test sample is negligible for all five cases (in the order of milli/microseconds), the fifth column in Table 5 clearly shows that HPT of the ANN structure and especially FS decrease inference times substantially. Please note that the (average) inference time is strongly correlated with the number of trainable weights given in the second last column of Table 4, and thus with the number of (selected) features and the number of neurons in the hidden layers. In general, as the number of neurons in the hidden layers is a result of HPT phase 2 (i.e., ANN structure), it is nontrivial to give a preference, prior to the HPT, to any of the FS strategies with respect to their inference time. The number of selected features (with $n_{\psi , \textrm{sel}, \textrm{MIM}}\leq n_{\psi , \textrm{sel}, \textrm{MRMR}} = n_{\psi , \textrm{sel}, \textrm{JMI}}$) may, however, give an indication. Overall, we advise to primarily select an FS method based on its resulting validation loss and the computation time required to select the features, see Table 2.

Table 5 Results for inference using simulated data for updated models obtained using ANNs obtained by employing various FS strategies. The average RMSE and peak error (e.g., $\textrm{RMSE}_{\textrm{av},\bullet}$ and $\texttt{e}^{\textrm{max}}_{\textrm{av},\bullet}$) are obtained by calculating their mean value over the $n_{\bar{s}}$ test samples, i.e., $\textrm{RMSE}_{\textrm{av},\bullet} =\frac{1}{n_{\bar{s}}}\sum _{ \bar{s}=1}^{n_{\bar{s}}}\textrm{RMSE}_{\bar{s},\bullet}$ and $\texttt{e}^{\textrm{max}}_{\textrm{av},\bullet} =\frac{1}{n_{\bar{s}}} \sum _{\bar{s}=1}^{n_{\bar{s}}}\texttt{e}^{\textrm{max}}_{\bar{s}, \bullet}$. Inference is performed on a singe core 2.60 GHz CPU and the average inference time over all $n_{\bar{s}}$ test samples is listed

Next, since the goal of model parameter updating is to obtain a more accurate model, the simulation error of the updated model is evaluated. To illustrate this, the simulated measurements of the tracking error signals for all three stages (corresponding to an arbitrarily chosen test sample) are indicated by the solid black lines in Fig. 5. Additionally, the tracking errors obtained by simulating an updated model are indicated by the orange lines. The corresponding simulation errors (of the tracking errors) are shown in Fig. 6. This model is updated using parameter values inferred using the ANN specified in row 5 of Table 5 that has a set of JMI-selected features which are extracted from the simulated X-, Y-, and Z-measurements, i.e., the black lines, as input. Visually comparing both sets of signals, we conclude that the updated model reproduces the simulated measurement accurately, thereby demonstrating the mapping accuracy of the ANN.

Fig. 5

Comparison between simulated measurement of tracking error () and simulated tracking error obtained using the updated model () (the latter is acquired using JMI-based FS and Bayesian HPT, i.e., corresponding to the last row of Table 5). These results are obtained using the lines in Fig. 4 as setpoint profiles

Fig. 6

Simulation errors of normalized tracking errors, i.e., ${\widehat{\mathbf{\text{e}}}}_{•}-{\overline{\mathbf{\text{e}}}}_{•}$, related to Fig. 5 for the updated X- (), Y- (), and Z-signal ()

To quantify the errors between responses obtained with real parameter values and inferred parameter values, two metrics are defined. Firstly, the root mean squared error ($\textrm{RMSE}$) is defined as

where $N$ is the total number of measured/simulated time samples, and ${\widehat{\mathbf{\text{e}}}}_{\overline{s},•}$ and ${\overline{\mathbf{\text{e}}}}_{\overline{s},•}$ are the tracking errors for test sample $\bar{s}$ (with the • indicating the X-, Y-, or Z-direction) obtained from the simulated updated model and (simulated) measurement with the true parameter values, respectively. As a second metric, the peak absolute error of the tracking error in the •-direction is defined as

Note that, for confidentiality reasons, the $\textrm{RMSE}$ and $\texttt{e}^{\textrm{max}}$ values shown in this paper are calculated using normalized tracking errors (which have also been plotted in Fig. 5). The normalized tracking error in •-direction is calculated using

where the original (updated) tracking error is denoted by ${\widehat{\mathbf{\text{e}}}}_{\overline{s},•}^{\text{orig}}$. To enable comparison between different simulations/measurements shown in this work, all signals are normalized with respect to a single measurement on the real wire bonder machine denoted by ${\overline{\mathbf{\text{e}}}}_{•,\text{exp,upd}}^{\text{orig}}$ (shown in Fig. 7 in Sect. 4.4). Note that all signals with respect to the X-direction, i.e., updated, measured, and reference (see Sect. 4.4), are normalized with the same scaling factor, i.e., ${\parallel {\overline{\mathbf{\text{e}}}}_{X,\text{exp, upd}}^{\text{orig}}\parallel }_{\mathrm{\infty }}$, obtained from the aforementioned real measurement. Similarly, ${\widehat{\mathbf{\text{e}}}}_{\overline{s},Y}$ and ${\widehat{\mathbf{\text{e}}}}_{\overline{s},Z}$, i.e., the normalized tracking error in Y-, and Z-direction, respectively, are calculated.

Fig. 7

Comparison between physical measurement of tracking error () and simulated tracking error obtained using the reference () and updated model () (the latter is acquired using JMI-based FS and Bayesian HPT, i.e., corresponding to the last row of Table 6). These results are obtained using experiment 1, i.e., the lines in Fig. 4 are used as setpoint profiles. The black lines indicate ${\overline{\mathbf{\text{e}}}}_{•,\text{exp,upd}}^{\text{orig}}$

In the last six columns of Table 5, the average (over all test samples) $\textrm{RMSE}$ and $\texttt{e}^{\textrm{max}}$ are listed per motion direction for the evaluated ANNs. In general, it is observed that all ANNs yield small simulation errors compared to the magnitude of the (normalized) signals. This indicates that the updated models accurately reproduce the true (simulated) system. Furthermore, we observe that employing HPT yields slightly better results compared to the benchmark ANN. Choosing different FS strategies, however, has a less pronounced effect on the simulation error. Some ANNs perform relatively well for specific output signals, whereas they perform comparatively poorly for other output signals. This is attributed to the fact that the ANN is trained to minimize the parameter error rather than the simulation error, where each updating parameter influences the output signals to a different extent due to the dynamic coupling. Furthermore, features are selected using FS strategies that aim to approximate the optimal set of features for which, however, no guarantee can be given. Finally, due to the black box nature of the ANN, it is nontrivial to predict which features yield accurate updating parameter estimates. As a consequence, the effect of the FS strategy on the accuracy of the individual output signals would require a practically infeasible sensitivity analysis that spans the MI-based FS, ANN mapping, and nonlinear time-domain simulation. However, if the user would like to be relatively more accurate for some output signal (or signals), a parameter sensitivity study can be performed to identify the most relevant updating parameters for that signal. Then, the user may select more features for these parameters (by varying $n_{\psi , \textrm{sel}, k}$ for each parameter indexed by $k$). Additionally or alternatively, the ANN training/validation loss can be weighted such that these parameters are estimated with a comparatively high accuracy.

4.4 Online parameter inference using measurements on physical system

In practice, model parameters will be updated (in real-time) based on measurements on a physical machine. Therefore, in this section, the ANNs are fed with (selected) sets of features that are extracted from measurements performed on a physical ASMPT wire bonder system. Note that in the IMPU method, ANNs are always trained on simulated data because supervisory learning requires known parameter values that are assumed to be unknown for a physical system. Consequently, the ANNs employed here are the same ANNs as evaluated in Sects. 4.2.3 and 4.3.

In Fig. 7, measured tracking errors and their simulated counterparts are compared. Here, the responses of two simulated models are shown, one reference model (i.e., the Simscape model parameterized with $\boldsymbol{p}_{\textrm{ref}}$ as determined by engineers of the commercial company, see Sect. 4.1) and one model updated using IMPU (JMI FS and Bayesian HPT) on the basis of the measured tracking errors. Note that in contrast to the simulated results, for the measured system, JMI features result in slightly more accurate simulated responses than the other FS methods, see Table 6. The accompanying Fig. 8 shows the corresponding simulation errors for clarity. As observed in Figs. 7 and 8, the reference model suboptimally simulates the physical measurement. Comparing the responses obtained using the model updated using the IMPU method to those obtained using the reference model, a significant increase in accuracy is observed for the updated model. The above observations are also apparent when comparing simulation error metrics ($\textrm{RMSE}$ and ^max, as defined in (14) and (15)) in rows 1 and 6 of Table 6. Furthermore, it is concluded from the inference times in Table 6 once more that with the IMPU method this model can be updated again with negligible computational effort whenever the physical system has changed under the influence of, e.g., wear. Note that the inference times shown here are not averaged over a large number of test samples (as was the case in Table 5) and are thus subject to variability due to background processes on the computing hardware. Nevertheless, a clear improvement in inference time is observed when employing FS compared to retaining all features.

Fig. 8

Simulation errors of normalized tracking errors, i.e., ${\widehat{\mathbf{\text{e}}}}_{•}-{\overline{\mathbf{\text{e}}}}_{•}$, related to Fig. 7 for the updated X- (), Y- (), and Z-signal (), and the reference X- (), Y- (), and Z-signal ()

Table 6 Simulation errors for experiment 1 (i.e., setpoint profiles are the lines in Fig. 4) for models that are updated based on measurements using selected ANNs that employ various FS strategies and Bayesian HPT. Simulation errors of the reference model and model updated using the benchmark ANN, i.e., without FS (all features retained) and with manual HPT, are given for comparison

Overall, the simulation obtained using the updated model resembles the measurement. However, this resemblance is not as close as was observed for the simulated test data analyzed in Sect. 4.3. This is mainly caused by the fact that the physical system will obviously not completely be captured by the model class (i.e., the Simscape multibody model) that we estimate parameters for. Recall that the IMPU method assumes that the EoMs of the model contain all relevant dynamics of the true system. For example, dynamic phenomena such as dry friction and flexible body dynamics might be present in the physical system, but are missing in the model. Moreover, the rigid body system model has been simplified to 10 DoFs, while a rigid four-body system actually has 24 DoFs. Additionally, just as for the simulated experiments in Sect. 4.3, see Table 5, for the measured experiments, it is observed in Table 6 that some ANNs might perform relatively well for some motion directions and relatively poorly for others. For example, JMI performs relatively well for the $X$ and $Y$ motions, but is outperformed by MIM and MRMR for the $Z$ motion. As a consequence, no definitive conclusion about the efficacy with respect to the accuracy of the various FS strategies for measured data can be given.

Overall, Table 6 shows that, again, Bayesian HPT is able to improve results (although not drastically) with respect to manual tuning. In contrast to the simulated experiment case in Sect. 4.3, there is a pronounced advantage to using FS for the measurement data. This is most likely caused by the fact that the selected features have the highest sensitivity with respect to the parameter values for the simulated model. Even though the real system is not (completely) in the model class, the features selected based on the simulated data are still highly sensitive towards parameter changes for the real system. Other, non-selected, features that were less informative for the simulated case, might however be (somewhat) relevant for the measured system. Since the ANN does not expect this, however, these non-selected measured features can confuse the ANN leading to less accurately updated models. Consequently, when using FS, the ANN is less perturbed by measured features that are significantly dissimilar from their simulated (relatively uninformative) counterparts. As a result, any of the FS strategies improves all error metrics with respect to the cases that use all features.

It should be noted that each ANN used in the last four rows of Table 6 is selected to have the best performance on the measured data from the top ten ANNs (in terms of validation loss) as obtained during a (Bayesian) HPT search. Other ANNs may perform significantly worse on the measured data. In other words, there is limited correlation between the validation loss and updated simulation error (metrics) if the ANN is used to infer on measured data that is obtained from a plant that is not part of the model class. This is caused by the stochastic nature of the training process, which utilizes simulated training data. Consequently, some ANNs might be trained such that they generalize relatively well to accommodate for the (partly) different set of measured features, whereas others are trained such that they adapt relatively poorly to these features. It is therefore wise to check the simulation error of multiple trained ANNs in preliminary experiments. The trained ANN with the lowest error should then be used for the actual implementation.

Summarizing, we observe clear potential for the IMPU method to be used on measured data. Particularly when combined with FS and (Bayesian) HPT, significant improvement in simulation error metrics over the reference model is observed. Moreover, the IMPU method can be made much more efficient in this way, both in terms of training and in terms of inferring parameter values. Since the current model does, however, not yet contain all relevant dynamics, nonrobust ANNs (in terms of the simulation error of the updated model) can be obtained and the simulation error can still be improved significantly. As a solution, the EoMS of the model to be updated could be enhanced. It is expected that results will then behave more similarly to the simulated experiment (Sect. 4.3) in which more robust ANNs and lower simulation errors are obtained.

4.4.1 Inferred parameter accuracy

Next, although we do not know all parameter values of the model describing the true system with high certainty, the (normalized) inferred parameter values can be compared to those of the reference model, see Table 7. Here, we again focus on the results obtained using JMI FS and (Bayesian) HPT. Some parameters, e.g., $m_{X}$, $m_{Y}$, and $L_{\textrm{CoM}_{Z},z}$ of which the reference values are known with high confidence, are inferred close to their reference value. This gives confidence in the ability of the IMPU method to correctly estimate parameter values based on measured data. Other parameters, e.g., $d_{BF2X,x}$, $d_{X2Y,y}$, and $k_{Y2Z}$, have significantly different values, suggesting that the original reference parameter values might be poorly estimated by the engineers of the commercial company (note that it is notoriously difficult to accurately estimate damping parameter values manually). For $m_{Z}$ (of which the reference value is known with high confidence), $K_{Z}$, and $I_{Z,xx}$, the inferred parameters are at their edges of ℙ. This indicates that the ANN struggles to find proper values for these parameters based on the features it is provided with. Note, however, that, according to Newton’s second law, an equal relative change in forcing and mass does not affect the acceleration. Therefore, ${\overline{\mathbf{\text{e}}}}_Z$ is largely unaffected, making it a more difficult task to estimate these three parameter values simultaneously. Nevertheless, the simulation error is still clearly improved as has been shown in the last row of Table 6.

Table 7 Normalized parameter values for reference case (manually determined by engineers) and parameter values inferred from measured data using IMPU with JMI FS and Bayesian HPT for artificially changed $K_{Z}$ values

By changing the feedback and feedforward gains, the motor force constant $K_{Z}$ can be artificially changed on the physical system (from 1 to 0.8). Here, we again see that this is captured poorly in terms of inferred parameter values (last row of Table 7). Nonetheless, as shown in Table 8, the simulation error is (drastically) decreased using the IMPU method (both using the benchmark and using JMI FS with Bayesian HPT) compared to the reference model.

Table 8 Simulation errors for experiment 1 (i.e., setpoint profiles are the lines in Fig. 4) with ANN (JMI with Bayesian HPT) updated using measurements with artificially changed $K_{Z}$ ($80\%$ of reference value). Simulation errors of the reference model and model updated using the benchmark ANN, i.e., without FS (all features retained) and with manual HPT, are given for comparison

4.4.2 Generalization on different setpoint profile

A model updated on the basis of some dedicated experiment 1 should preferably generalize well to other experiments, e.g., when using different setpoint profiles. Therefore, simulations using experiment 2 (i.e., the lines in Fig. 4 are used as setpoint profiles) using the updated and the reference model are compared to a measurement of experiment 2 in Fig. 9. Here, the updated model is obtained using the experimental data shown by the black lines in Fig. 7, which were obtained using experiment 1 (for which the setpoint profiles are given by the lines in Fig. 4). Again, the corresponding simulation errors are plotted in Fig. 10. The absolute values of the extrema in this figure correspond to the values for $\mathbf{\texttt{e}}^{\textrm{max}}$ in the first and last row of Table 9). From Figs. 9 and 10 and Table 9 it is evident that the model updated using the IMPU method (again, JMI FS and Bayesian HPT) gives an improvement over the reference model and thus generalizes well. Note that the JMI based ANN performs best for the $X$ and $Y$ signals, as was also the case in Table 6.

Fig. 9

Comparison between physical measurement of tracking error () and simulated tracking error obtained using the reference () and updated model () (the latter is acquired using JMI-based FS and Bayesian HPT, i.e., corresponding to the third row of Table 9). These results are obtained using experiment 2, i.e., the lines in Fig. 4 are used as setpoint profiles

Fig. 10

Simulation errors of normalized tracking errors, i.e., ${\widehat{\mathbf{\text{e}}}}_{•}-{\overline{\mathbf{\text{e}}}}_{•}$, related to Fig. 9 for the updated X- (), Y- (), and Z-signal (), and the reference X- (), Y- (), and Z-signal ()

Table 9 Simulation errors for experiment 2 (i.e., setpoint profiles are the lines in Fig. 4) for the model updated based on the measured black lines, ${\overline{\mathbf{\text{e}}}}_{•,\text{exp,upd}}^{\text{orig}}$, in Fig. 7 which are obtained using experiment 1. Simulation errors of the reference model and model updated using the benchmark ANN, i.e., without FS (all features retained) and with manual HPT, are given for comparison

5 Conclusions and recommendations

The IMPU method is used to update, within microseconds, (nonlinear) multi-body dynamics models by inferring parameter values from specific features that are extracted from measured response data. To do so, an inverse mapping model (IMM) is utilized that is constituted by an artificial neural network (ANN), which is trained on simulated data using supervised learning. In the current paper, the IMPU method, introduced in [1], is extended to incorporate three mutual information-based feature selection (FS) strategies: MIM, MRMR, and JMI. These FS strategies leverage training data to determine which response features are informative with respect to the updating parameters.

In this paper, the IMPU method is applied to an industrial use case (a wire bonder machine). An analysis based on simulated data has demonstrated that the IMPU method results in accurately inferred parameter values. This also results in accurate updated models that are capable to generate responses that closely resemble the response of the actual plant. It is shown that employing FS increases the accuracy of the inferred parameter values since uninformative, yet noisy, features are omitted. Moreover, training time and inference time are decreased since less trainable weights are required due to the smaller input space. Comparing the different FS strategies, approximately equivalent offline training times and online inference times are observed. The resulting validation losses and parameter errors are also comparable, although taking into account redundancy between features (using the JMI strategy) results in a slight decrease in validation loss and increase in parameter estimation accuracy. This comes, however, at the cost of the more expensive (offline) process to select the features using the JMI strategy. With respect to the accuracy of the simulated response signals, no clear preference for any of the FS strategies is recognized.

Furthermore, hyperparameter values (related to the training settings and structure of the ANN) are tuned in two separate Bayesian searches. Hyper parameter tuning (HPT) is shown to improve accuracy of the estimated parameters and response signals obtained using the updated models. Moreover, employing HPT gives more confidence in the (approximate optimality of the) employed ANN.

The IMPU method is also applied on measured data of the industrial wire bonder. The model updated using the IMPU method yields more accurate response signals than a reference model with parameter values based on engineering knowledge. Here, the use of FS (especially the JMI strategy) yields a significant increase in the accuracy of the response signals that are obtained with the updated models. Generalization capabilities of the updated model are also successfully demonstrated by evaluating the simulation error for an experiment unrelated to the updating experiment (employed to generate the data used to infer the parameter values from). Although the signals simulated using the updated models resemble the measured signals, some of the inferred parameter values do not agree with their true physical values. This occurs because the physical plant is not in the model class.

Consequently, the IMPU method would highly benefit from a model structure of higher fidelity. Therefore, for future work, it is recommended to extend the equations of motion of the model by adding terms or even states on the basis of measured data prior to using the IMPU method to update model parameters online. Additionally, as observed for the measured data, some parameter values are relatively difficult to infer accurately. Methods that quantify the uncertainty in the inferred parameter values will therefore be investigated in further research. Finally, the possibility to use the IMPU methodology for different updating experiments (e.g., different excitations or reference signals) should be explored. This could be achieved by, next to the response features, providing the IMM with a set of ‘input parameters’ that, for the training data, are sampled from a range of potential values. These input parameters may describe settings used to define the updating experiment (e.g., controller values, excitation signals, and generic system settings).

Appendices

Appendix A: Discretized probability functions

In this appendix, the probability, joint probability, and joint conditional probability functions, approximated by discretizing a finite dataset containing $n_{s}$ samples, are defined. The discretization of the collection of training features and parameters is discussed in Sect. 3.1 (directly below (6)). These functions are used to calculate the (conditional) mutual information in (6) and (7).

1.1 A.1 Probability

The probability that a discretized feature equals $\boldsymbol{\check{\Psi}}_{i}^{(a)}$ is given as a fraction:

$$ \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}\right ) = \frac{ \left |\left \{x\in \boldsymbol{\check{\Psi}}_{i} \left | x=\boldsymbol{\check{\Psi}}_{i}^{(a)} \right . \right \}\right | }{n_{s}}, $$

(A1)

where the numerator indicates the number of observations over the $n_{s}$ training samples for which the discretized feature value of feature $i$ equals $\boldsymbol{\check{\Psi}}_{i}^{(a)}$.

1.2 A.2 Joint probability

The joint probability of having a feature and parameter equal to $\boldsymbol{\check{\Psi}}_{i}^{(a)}$ and $\boldsymbol{\check{P}}_{k}^{(c)}$, respectively, is given by

$$ \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{P}}_{k}^{(c)}\right ) = \frac{ \left |\left \{x\in \boldsymbol{\check{\Psi}}_{i}\times \boldsymbol{\check{P}}_{k} \left |\ x=\left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{P}}_{k}^{(c)}\right ) \right . \right \}\right | }{n_{s}}, $$

(A2)

where the numerator indicates the number of observations over the $n_{s}$ training samples for which the discretized feature value of feature $i$ equals $\boldsymbol{\check{\Psi}}_{i}^{(a)}$ while, simultaneously, the discretized parameter value for parameter $k$ equals $\boldsymbol{\check{P}}_{k}^{(c)}$.

1.3 A.3 Joint conditional probability

The joint conditional probability of having one feature equal to $\boldsymbol{\check{\Psi}}_{i}^{(a)}$ and another feature equal to $\boldsymbol{\check{\Psi}}_{j}^{(b)}$, while knowing that the parameter value is $\boldsymbol{\check{P}}_{k}^{(c)}$, is given by

$$ \phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{\Psi}}_{j}^{(b)} \left | \boldsymbol{\check{P}}_{k}^{(c)} \right .\right ) = \frac{\phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{\Psi}}_{j}^{(b)}, \boldsymbol{\check{P}}_{k}^{(c)}\right )}{\phi \left (\boldsymbol{\check{P}}_{k}^{(c)}\right )}, $$

(A3)

where $\phi \left (\boldsymbol{\check{\Psi}}_{i}^{(a)}, \boldsymbol{\check{\Psi}}_{j}^{(b)}, \boldsymbol{\check{P}}_{k}^{(c)} \right )$ is obtained using a trivial extension of (A2).

Appendix B: Learning curves

In Fig. 11, the training and validation losses for ANNs, trained with tuned hyperparameters, without FS and with FS (JMI) are plotted. As shown in the figure, typical ANN training behavior is observed for both cases. However, it is observed that the ANN with FS is able to achieve lower validation losses than when no FS is employed (as is also observed in Table 4). In contrast, a lower training loss is achieved for the ANN without FS. As a result, the gap between the validation and training loss is larger without employing FS, hinting at a form of overfitting. Moreover, for the ANN without FS, training is prematurely stopped due to early stopping. Consequently, we conclude that including FS may reduce the chance on overfitting. Regularization of the weights of the ANN may prevent overfitting as well. However, since the trend of the validation loss (towards the final epochs) is nonincreasing, the accuracy of the ANN might improve still. For that reason, regularization has not been applied here.

Fig. 11

Learning curves with training loss () and validation loss () for the ANNs without FS () and with JMI FS (). These ANNs are trained with tuned hyperparameters (e.g., the number of neurons per hidden layer are listed in Table 4)