1 Introduction

Multibody dynamics support important computational tools to study the dynamic behaviour of road vehicles. It allows us to characterize vehicle behaviour [5], support the vehicle design process [6], develop and test control methods [7], study vehicle ride [8], or develop digital twins [9]. In all cases, tire–road contact models are required to realistically describe the excitation arising from the tire–road interaction. Thus the numerical stability and smoothness of the tire and road models are of fundamental importance for the numerical efficiency of the time integration algorithms whose variable time-step becomes too small in the presence of discontinuities or abrupt changes in the system dynamic response.

There are two main steps in the implementation of tire–road contact models in a multibody framework: (1) solving the contact detection problem, which means determining the tire–road contact conditions and deriving the motion parameters required to calculate the contact forces, and (2) calculation of the contact forces obtained using a tire model that relates the tire–d motion with the forces developed at the contact patch. Not only both steps are instrumental to the realism of the simulations, but also they impact negatively the efficiency of the time integration methods when the dynamic response is not smooth.

A wide variety of tire models can be found the literature. In multibody applications, empirical or physical models are most often used. The empirical models resort to nonlinear mathematical approximations to fit experimentally obtained data, of which the Pacejka magic tire formula is a good example [10]. Empirical models can be very accurate but require extensive and expensive testing for tuning the many parameters. In contrast, physical models try to establish a physically based relationship between the tire–road kinematics and the contact forces by studying the physics at the contact patch. The physical tire models often require less extensive testing, when compared to the empirical tire models, but fail to reach the degree of accuracy of the empirical models. A relevant benchmark to validate and compare tire models can be found in [11, 12], which resulted in a series of papers describing the tire models involved [13–19]. A distinction between low-mid-frequency and high-frequency tire models is made, where high-frequency tire models should be able to handle obstacles smaller than the contact patch, whereas low-mid-frequency tire modes are dedicated to vehicle handling applications. This work does not intend to discuss or compare different tire models but simply to address the numerical smoothness of a selected low-mid-frequency tire model, the UA tire model [2–4], to overcome the negative impact on time-integration due to the lack of smoothness inherent to the tire model itself.

To use the tire models within multibody simulations, the motion parameters and slip ratios must be evaluated at each time step. A suitable contact detection method is required to derive such quantities from the tire and road relative motion and geometric properties. The first step is to detect if there is contact and to evaluate the radial deformation of the tire. This requires solving a contact detection problem. Later, based on the motion of the tire and road, the tire deformation, the motion parameters, and slip ratios, which serve as input for the tire models, are derived. Since the contact problem is three-dimensional, the description and solution of the contact problem are not straightforward. Rill [1] provides a detailed description of a contact calculation approach for handling tire models. When dealing with higher-frequency vibrations, generated from obstacles that are shorter than the contact patch, it requires a different approach. Schmeitz et al. [20] describe an enveloping model for such cases using a tandem model with elliptical cams, which is also discussed by Pacejka [21].

Given that the tire model and the contact detection method are implemented in the multibody framework, the tire–road contact forces obtained can be applied to the bodies to which the tire is attached. Besides providing realistic forces, the tire-road contact implementation should provide smooth forces that contribute for the simulation efficiency and stability. In a general multibody framework, the forces are incorporated in the equations of motion of the multibody system, which are solved to obtain the velocities and accelerations of the bodies. These velocities and accelerations are then integrated in the time to obtain the positions and velocities at the subsequent time-step [22]. When the forces are continuous, the solution is, generally, non-stiff [23]. However, when the forces change rapidly, the solution becomes stiff, and it may require to reduce the time-step of integration to minimize the integration error. This happens if variable time step integration schemes, such as the Gear algorithm [24], are used to control and adapt the time step to boost convergence. Therefore the effect of rapid changes in forces, or even discontinuities, significantly affects the simulation efficiency, by decreasing the time-step, as well as the simulation stability, by hampering the integration convergence. These issues are frequent in impact multibody simulations, which deal with rapid changes in the normal and tangential contact forces [25]; however, it is seldom discussed in the context of tire–road contact modelling.

The present work provides a thorough description of the tire–road contact modelling for multibody simulations, aimed at vehicle handling applications. The incorporation of the tire–road contact methodology within the multibody framework is explained in detail. The idea of the simple but sophisticated approach proposed by Rill [1], to handle the orientation of the road plane, is used to smooth the transition between the triangular patches that describe the road surface, in the methodology proposed in this work. Emphasis is put on the methods for solving the contact detection problem and their impact on the simulation efficiency and stability as a result of the smoothness of the geometric contact and the tire models.

2 Tire–road contact modelling

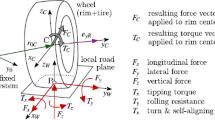
The characterisation of the contact between the tire and road and the identification of the contact forces generally require the definition of a tire coordinate system with the origin centred in the geometric centre of the tire contact patch. Let the wheel and tire assembly be in contact with the road, as in Fig. 1, where the centre of the tire patch contact in the ground is denoted by \(G\), whereas the undeformed tire point of contact is denoted by \(B\).

Fig. 1
figure 1

Contact between the tire and ground and the tire coordinate system

Full size image

The complete tire contact problem can be divided into four steps, illustrated in Fig. 2 as implemented in the in-house code MUBODyn [26]: (1) the contact detection problem in which the coordinates of point \(G\) and the normal to the contact surface are identified and expressed in the inertia referential XYZ, and the tire coordinate system (XYZ)plane, represented in Fig. 1, is defined; (2) the calculation of the slip ratios, the camber and slip angles, and several other kinematic quantities in the tire-ground coordinate system; (3) the calculation of the tire contact forces and resisting moments using an appropriate tire model; (4) the transformation of the tire contact forces and moment vectors to the appropriate coordinate systems and the application to the wheel body of the vehicle multibody system which the tire belongs to.

Fig. 2
figure 2

Tire–road contact algorithm of MUBODyn [26]

Full size image

2.1 Wheel kinematic data available from a multibody program

Let a wheel with a tire be a body of the multi-body system, as shown in Fig. 3. At any given time of the simulation, the kinematics of the wheel is known, with its position, orientation, and velocity, in particular, denoted in Fig. 3. Therefore, in what follows, the following quantities are known:

Fig. 3
figure 3

Position, orientation, and velocity of a wheel fitted with a tire

Full size image

\(\mathbf{r}_{\mathrm{w}}\) – Position of the wheel centre of mass,

\(\dot{\mathbf{r}}_{\mathrm{w}}\) – Velocity of the wheel centre of mass,

\(\boldsymbol{\omega}_{\mathrm{w}}\) – Angular velocity of the wheel,

\(\mathbf{A}_{\mathrm{w}}\) – Transformation matrix from the wheel coordinate frame to the inertia frame.

Due to its importance, in what follows, i.e., in the definition of the tire coordinate system and in the calculations of the tire–ground interaction, the normal vector to the wheel plane, \(\mathbf{u}_{\mathrm{w}}\), is evaluated as the unit vector in the direction of \(\upeta \)wheel expressed in global coordinates as

$$ \mathbf{u}_{\mathrm{w}} = \mathbf{A}_{\mathrm{w}}\mathbf{u}\boldsymbol{'}_{\upeta} \equiv \left \{ \textstyle\begin{array}{c} a_{12} \\ a_{22} \\ a_{32} \end{array}\displaystyle \right \} $$
(1)

with \(\mathbf{u}\boldsymbol{'}_{\upeta} = \left [ \begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0 \end{array} \right ]^{T}\). Note that the components of the vector \(\mathbf{u}_{\mathrm{w}}\) are simply those of the second column of the wheel transformation matrix, that is, the unit vector along \(\upeta \) expressed in the XYZ coordinate system.

2.2 Contact detection

The tire contact search strategy depends on the way the road is described. In what follows, for any point \(G\) in the ground surface, the \(z^{G}\) coordinate of the ground is a function of the (\(x^{G}\), \(y^{G}\)) coordinates, i.e., to each pair (\(x\), \(y\)), there is a unique point belonging to the ground surface,

$$ z^{G} =f \left ( x^{G}, y^{G} \right ). $$
(2)

In the applications foreseen here, the ground geometry is described by a mesh of triangles, as depicted in Fig. 4 (a). In each triangle, the nodes are numbered counterclockwise with respect to the normal to the surface, as seen in Fig. 4 (b). A set of friction coefficients is associated with each triangle. The present implementation includes dynamic and friction coefficients for each triangular patch, \(\upmu _{0}\) and \(\upmu _{1}\), respectively. The use of the triangular mesh is particularly useful since the triangular geometry of any given surface can be extracted directly from any CAD program, which, in turn, can be directly used for the tire–ground contact modelling method proposed here.

Fig. 4
figure 4

Representation of the ground: (a) mesh of triangles; (b) definition of a triangular patch

Full size image

For a flat surface, i.e., a bilinear surface as that of a triangle, Equation (2) is written explicitly as

$$ z^{G} = a + bx^{G} + cy^{G}, $$
(3)

where the coefficients are obtained by solving the system of equations

$$ \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & x_{1} & y_{1} \\ 1 & x_{2} & y_{2} \\ 1 & x_{3} & y_{3} \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} a \\ b \\ c \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} z_{1} \\ z_{2} \\ z_{3} \end{array}\displaystyle \right \}, $$
(4)

and in which the coordinates of the three nodes that describe the triangle are used to form the leading matrix and right-hand-side vector. The unit normal vector is obtained as

$$ \mathbf{u}_{\mathrm{normal}} = \frac{\tilde{\mathbf{s}}_{12}\mathbf{s}_{23}}{\left \| \tilde{\mathbf{s}}_{12}\mathbf{s}_{23} \right \|} \equiv \frac{1}{\sqrt{b^{2} + c^{2} + 1}} \left \{ \textstyle\begin{array}{c} - b \\ - c \\ 1 \end{array}\displaystyle \right \}. $$
(5)

To describe all kinematic and kinetic quantities related to the tire contact, not only the contact detection is necessary, in which the tire deformation is evaluated, but also a tire coordinate system, represented in Fig. 1 as (XYZ)plane with its origin at point \(G\), is required. For this purpose, it is necessary to identify in which triangle contact occurs if there is contact between the tire and road. The generic algorithm for tire–road contact detection is illustrated in Fig. 5, where the main tasks are identified and are overviewed in detail in the following sub-sections.

Fig. 5
figure 5

Contact detection algorithm

Full size image

2.2.1 Preliminary contact evaluation assuming horizontal ground

To start the ground contact search, let us first assume that the triangular patch in which contact occurs is parallel to XY with its normal parallel to Z, i.e., that the patch is horizontal, as shown in Fig. 6. Note that in this strategy the gravity acts downwards along Z.

Fig. 6
figure 6

Tire contact with a triangle ground patch, point \(G\) being the centre of the tire contact patch: (a) horizontal triangle patch; (b) view of the tire with reference to the relative orientation between the tire and inertia frames

Full size image

Assuming that the ground is horizontal, the position of the undeformed tire contact point \(B\) in closest proximity, or even penetration, with the ground is shown in Fig. 6 (b). Its position in the inertia frame (XYZ) is

$$ \mathbf{r}^{B} = \mathbf{r}_{\mathrm{w}} + \mathbf{s}_{1} + \mathbf{s}_{2}. $$
(6)

The unit vector along the Xplane direction is perpendicular to both \(\mathbf{u}_{\mathrm{Z}}=\mathbf{u}_{\mathrm{Zplane}}=[0, 0, 1]^{T}\) and \(\mathbf{u}_{\mathrm{w}}\), which is obtained as

$$ \mathbf{u}_{\mathrm{X}_{\mathrm{plane}}} = \frac{\tilde{\mathbf{u}}_{\mathrm{w}}\mathbf{u}_{\mathrm{Z}}}{\left \| \tilde{\mathbf{u}}_{\mathrm{w}}\mathbf{u}_{\mathrm{Z}} \right \|}, $$
(7)

where \(\tilde{\mathbf{u}}_{\mathrm{w}}\) is the skew-symmetric matrix of \(\mathbf{u}_{\mathrm{w}}\), used to compute the cross-product of \(\mathbf{u}_{\mathrm{Z}}\) and \(\mathbf{u}_{\mathrm{w}}\), which is given by

$$ \tilde{\mathbf{u}}_{\mathrm{w}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & - a_{32} & a_{22} \\ a_{32} & 0 & - a_{12} \\ - a_{22} & a_{12} & 0 \end{array}\displaystyle \right ]. $$
(8)

Then the vector \(\mathbf{s}_{1}\) is obtained as

$$ \mathbf{s}_{1} = \mathrm{R}_{3} \tilde{\mathbf{u}}_{\mathrm{w}} \mathbf{u}_{\mathrm{X}_{\mathrm{plane}}}, $$
(9)

which by substituting the definitions of \(\mathbf{u}_{\mathrm{Z}}=[0, 0, 1]^{T}\) and \(\mathbf{u}_{\mathrm{w}}\) given by Equation (1) into Equations (7) and (9) and rearranging leads to

$$ \mathbf{s}_{1} = \mathrm{R}_{3} \left \{ \textstyle\begin{array}{c} a_{12}a_{32} \\ a_{22}a_{32} \\ - \left ( 1 - a_{32}^{2} \right ) \end{array}\displaystyle \right \}\frac{1}{\sqrt{1 - a_{32}^{2}}}. $$
(10)

The vector \(\mathbf{s}_{2}\) is obtained, by inspection of Fig. 6 (b), as

$$ \mathbf{s}_{2} = - \mathrm{R}_{2} \left \{ \textstyle\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\displaystyle \right \}. $$
(11)

The undeformed tire contact point \(B\) being either in close proximity with the ground or penetrating it, the next step in the procedure is identifying the triangle patch in which contact occurs. Because the number of triangle patches that is used to describe the ground geometry may be large, the search must be efficient. With reference to Fig. 6 (a), the position of the projection of point B in the horizontal plane must be inside the box that contains the triangle patch, i.e.,

$$ \textstyle\begin{array}{l} X_{\min} \leq x^{B} \leq X_{\max},\\ Y_{\min} \leq y^{B} \leq Y_{\max}. \end{array} $$
(12)

The use of these conditions allows us to carry a faster and more efficient identification of the triangle patch in which the contact occurs by reducing the number of triangles in which the final contact conditions are evaluated.

Provided that for a particular triangle, all conditions in Equation (12) are met, the candidate to contact point B is inside the triangle if all angles \(\alpha _{1}\), \(\alpha _{2}\), and \(\alpha _{3}\), defined in Fig. 7, are positive. Due to the definition of the function of the ground geometry given by Equation (3), i.e., to each pair (\(x\), \(y\)), there is one and only one \(z\), these three conditions are expressed using the projection of all vectors in the horizontal plane as

$$ \textstyle\begin{array}{l} \sin \alpha _{1} = s_{1B(y)} s_{12(x)} - s_{1B \left ( x \right )} s_{12 \left ( y \right )} \geq 0,\\ \sin \alpha _{2} = s_{2B(y)} s_{23(x)} - s_{2B \left ( x \right )} s_{23 \left ( y \right )} \geq 0,\\ \sin \alpha _{3} = s_{3B(y)} s_{31(x)} - s_{3B \left ( x \right )} s_{31 \left ( y \right )} \geq 0, \end{array} $$
(13)

In which the components of vectors \(\mathbf{s}_{iB} = \mathbf{r}^{B} - \mathbf{r}_{\text{node } i}\), \(i=1,2,3\), are used. The tire is in contact or close to a particular road triangle if all conditions in Equations (13) are met.

Fig. 7
figure 7

Conditions for a potential contact point \(B\), projected over point \(G\), to be inside a triangle are that the angles \(\alpha _{1}\), \(\alpha _{2}\), and \(\alpha _{3}\) are positive

Full size image

A preliminary normal unit vector,\(\mathbf{u}\)normal, corresponding to the normal of the triangular patch, now takes the role of the Zplane vector \(\mathbf{u}\)Zp of the tire coordinate system represented in Fig. 9 for a general contact patch orientation, i.e.,

$$ \mathbf{u}_{\mathrm{Zp}} = \mathbf{u}_{\mathrm{normal}}. $$
(14)

According to Fig. 1, the Xplane vector \(\mathbf{u}\)Xp of the tire coordinate system is in the tire plane, whose normal is \(\mathbf{u}_{\mathrm{w}}\), and perpendicular to \(\mathbf{u}\)Zp:

$$ \mathbf{u}_{\mathrm{Xp}} = \frac{\tilde{\mathbf{u}}_{\mathrm{w}}\mathbf{u}_{\mathrm{Zp}}}{\left \| \tilde{\mathbf{u}}_{\mathrm{w}}\mathbf{u}_{\mathrm{Zp}} \right \|}. $$
(15)

Finally, the Yplane vector \(\mathbf{u}\)Yp of the tire coordinate system is obtained as

$$ \mathbf{u}_{\mathrm{Yp}} = \tilde{\mathbf{u}}_{\mathrm{Zp}}\mathbf{u}_{\mathrm{Xp}}. $$
(16)

To fully define the contact plane, it is required to obtain the centre of the tire patch contact in the ground, i.e., point \(G \) shown in Fig. 6. In the case of horizontal ground, the position of point \(G\) is defined as

$$ \mathbf{r}^{G} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} x^{B} & y^{B} & z^{G} \end{array}\displaystyle \right ]^{T}, $$
(17)

where \(x^{B}\) and \(y^{B}\) are obtained using Equation (6), and \(z^{G}\) is calculated using Equation (3), for the triangular patch identified with \(x^{G}=x^{B}\) and \(y^{G}=y^{B}\).

The undeformed tire point of contact \(B\), the centre of the tire patch contact in the ground, point \(G\), and the tire coordinate system are preliminarily defined. Since this comes from the assumption that the ground is horizontal, which may not be the case when non-horizontal ground is considered, it requires further re-evaluation, as discussed in the next sections.

2.2.2 Calculation of auxiliary points

When the contact point \(B\) transitions from one triangular patch to another, there is a rapid change in the surface normal, which leads to discontinuities in the tire–ground interaction forces. These discontinuities are not only unrealistic but also highly undesirable in dynamic simulations. To avoid or minimize this effect, a set of auxiliary points is used to regularise the transitions between the triangular patches. This strategy proposed by Rill [1] is implemented in this work to obtain a smooth transition between triangular patches describing the road geometry.

After determining the preliminary centre of the tire patch contact in the ground, point \(G\), and the preliminary tire coordinate system, a set of four auxiliary points \(A_{i}\) is computed, which are illustrated in Fig. 8 (b). To obtain these four auxiliary points, four intermediate points \(A'_{i}\), shown in Fig. 8 (a), are determined in the lateral and longitudinal directions of the tire from the preliminary undeformed tire point of contact \(G\):

$$\begin{aligned} & \mathbf{r}^{A'_{1,2}} = \mathbf{r}^{G} \pm \Delta x\mathbf{u}_{\mathrm{Xp}}, \end{aligned}$$
(18)
$$\begin{aligned} & \mathbf{r}^{A'_{3,4}} = \mathbf{r}^{G} \pm \Delta y\mathbf{u}_{\mathrm{Yp}}, \end{aligned}$$
(19)

where \(\Delta x\) and \(\Delta y\) are a priori set constant values. The selection of these parameters is discussed in Sect. 3, which focusses on the analysis of simulation results associated with the road model mesh refinement.

Fig. 8
figure 8

Tire contact patch in the transition between triangular patches: (a) intermediate points used for the calculation of the auxiliary points and auxiliary contact plane; (b) intermediate and auxiliary points and respective vectors to compute auxiliary contact plane

Full size image

The intermediate points \(A'_{i}\) are co-planar and are not necessarily in the surface of any triangular patch. Therefore, to obtain the auxiliary points \(A_{i}\), the triangular patch in which each of the intermediate points is projected is identified using Equations (12) and (13). After identifying the triangle and assuming that \(x^{A_{i}} = x^{A'_{i}}\) and \(y^{A_{i}} = y^{A'_{i}}\), Equation (3) may be used to determine the position of the auxiliary points in the triangular patches, \(x^{G}=x^{Ai}\) and \(y^{G}=y^{Ai}\), \(i=1\),2,3,4. The normal unit vectors \(\mathbf{u}_{\mathrm{n},i}\), i = 1,2,3,4, can be obtained through Equation (5), which will be further used to compute an auxiliary plane if the contact patch is in the transition between two or more triangular patches.

2.2.3 Contact re-evaluation

After the preliminary assessment of points \(B\) and \(G\), assuming horizontal ground, and the calculation of auxiliary points \(A_{i}\), we may need to re-evaluate the contact in the case of non-horizontal ground. At this point, one out of three situations may occur: (a) all normal unit vectors, corresponding to each auxiliary point, are vertical, i.e., \(\mathbf{u}_{\mathrm{n},1}= \mathbf{u}_{\mathrm{n},2}= \mathbf{u}_{\mathrm{n},3}= \mathbf{u}_{\mathrm{n},4}=\mathbf{u}_{\mathrm{Z}}\), and the preliminarily obtained points and coordinate system are used without requiring further contact re-evaluation; (b) all normal unit vectors are equal but are non-vertical, i.e., \(\mathbf{u}_{\mathrm{n},1}= \mathbf{u}_{\mathrm{n},2}= \mathbf{u}_{\mathrm{n},3}= \mathbf{u}\)n,4\(\neq \mathbf{u}_{\mathrm{Z}}\), and the normal vector is defined as \(\mathbf{u}_{\mathrm{normal}}=\mathbf{u}\)n,1, or (c) at least one of the normal unit vectors is different from the others, requiring to calculate an auxiliary contact plane to regularise the transition between the triangular patches. In cases (b) and (c), points \(B\) and \(G\) and the tire coordinate system must be re-evaluated using the non-vertical normal unit vector \(\mathbf{u}\)normal. In case (c), the normal unit vector is calculated using the auxiliary points. It requires to compute two auxiliary vectors, shown in Fig. 8 (b), as follows:

$$\begin{aligned} & \mathbf{u}_{1} = \mathbf{r}^{A1} - \mathbf{r}^{A2}, \end{aligned}$$
(20)
$$\begin{aligned} & \mathbf{u}_{2} = \mathbf{r}^{A3} - \mathbf{r}^{A4}. \end{aligned}$$
(21)

Then the normal unit vector of the contact surface is defined by a vector that is simultaneously perpendicular to \(\mathbf{u}_{1}\) and \(\mathbf{u}_{2}\):

$$ \mathbf{u}_{\mathrm{normal}} = \frac{\mathbf{u}_{1} \times \mathbf{u}_{2}}{\left \| \mathbf{u}_{1} \times \mathbf{u}_{2} \right \|}. $$
(22)

This newly calculated normal unit vector is used to update the tire coordinate system using Equations (14)–(16).

Regardless of whether the ground is horizontal or not, the tire contact formulation uses the tire coordinate system to represent all vector quantities necessary for the calculation of the contact forces and the location of the contact points. Therefore it requires to calculate the transformation matrix from the tire coordinate system (XYZ)plane to the global coordinate system (XYZ), which is given as

$$ \mathbf{A}_{r} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{u}_{\mathrm{Xp}} & \mathbf{u}_{\mathrm{Yp}} & \mathbf{u}_{\mathrm{Zp}} \end{array}\displaystyle \right ]. $$
(23)

If the contact plane is non-horizontal, then the position of the undeformed tire contact point \(B\) is re-evaluated. Due to the construction of the tire coordinate system, described by Equations (14)–(16), all quantities required for the evaluation of the contact are described in the plane (YZ)plane. Following the procedure proposed by Gim and Nikravesh [2–4], the tire is described as a toroidal surface in which the torus radius is R1 and the carcass radius, equal to half of the carcass width, is R2, as shown in Fig. 9. Therefore, let the wheel plane normal vector be obtained as

$$ \mathbf{u}\boldsymbol{'}_{\mathrm{w}} = \mathbf{A}_{r}^{T}\mathbf{u}_{\mathrm{w}} \equiv \left \{ \textstyle\begin{array}{c} u_{\mathrm{w}(\mathrm{xp})} \\ u_{\mathrm{w}(\mathrm{yp})} \\ u_{\mathrm{w}(\mathrm{zp})} \end{array}\displaystyle \right \}, $$
(24)

where the components of the normal vector in the tire coordinate system are written as \(e_{1}\), \(e_{2}\), and \(e_{3}\) for convenience. Note that due to the method of construction of the tire coordinate system, \(e_{1}=0\). The position of the undeformed tire point of contact \(B\) is given in the tire coordinate system as

$$ \mathbf{r}\boldsymbol{'}^{B} = \mathbf{A}_{r}^{T}\mathbf{r}_{\mathrm{w}} + \mathbf{s}\boldsymbol{'}_{1} + \mathbf{s}\boldsymbol{'}_{2}, $$
(25)

where the vectors \(\mathbf{s}\boldsymbol{'}_{1}\) and \(\mathbf{s}\boldsymbol{'}_{2}\) are obtained by inspection of Fig. 9 as

$$\begin{aligned} & \mathbf{s}\boldsymbol{'}_{1} = \mathrm{R}_{3} \mathbf{R}_{\mathrm{X} = - 90^{\circ}}\mathbf{u}\boldsymbol{'}_{\mathrm{w}} \equiv \mathrm{R}_{3} \left \{ \textstyle\begin{array}{c} 0 \\ u_{\mathrm{w}(\mathrm{zp})} \\ - u_{\mathrm{w}(\mathrm{yp})} \end{array}\displaystyle \right \}, \end{aligned}$$
(26)
$$\begin{aligned} & \mathbf{s}\boldsymbol{'}_{2} = - \mathrm{R}_{2} \left \{ \textstyle\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\displaystyle \right \}. \end{aligned}$$
(27)

Note that the rotation matrix \(\mathbf{R}_{\mathrm{X} = - 90^{\circ}}\) means a rotation of −90° about \(\mathrm{Xp}\). Since the problem is planar in the coordinate system used, the construction of the point \(B\) position vector does not involve any particular time-consuming calculations and is given as

$$ \mathbf{r}^{B} = \mathbf{A}_{r}\mathbf{r}\boldsymbol{'}^{B}. $$
(28)
Fig. 9
figure 9

View of the tire with reference to the relative orientation between the tire and inertia frames for non-horizontal ground

Full size image

Now the position of the origin of the tire reference frame, point \(G\), is defined as the projection of point \(B\) in the plane of the contact patch:

$$ \mathbf{r}^{G} = \mathbf{r}^{B} - \left ( \frac{\left ( \mathbf{r}^{B} - \mathbf{r}^{C} \right )\mathbf{u}_{\mathrm{normal}}}{\left \| \mathbf{u}_{\mathrm{normal}} \right \|^{2}} \right )\mathbf{u}_{\mathrm{normal}}, $$
(29)

where \(C\) is a point in the plane of the contact patch defined as the mean value of the four auxiliary points, as shown in Fig. 8 (b):

$$ \mathbf{r}^{C} = \frac{1}{4}\left ( \mathbf{r}^{A1} + \mathbf{r}^{A2} + \mathbf{r}^{A3} + \mathbf{r}^{A4} \right ). $$
(30)

2.2.4 Tire deformation

Knowing the undeformed tire point of contact \(B\) and the origin of the tire reference frame \(G\) allows us to determine the tire deformation, which is required to further obtain the normal contact force of the tire. In what follows, the term tire deformation is used; however, the terms indentation or penetration could also be used since the wheel is considered a rigid body, and therefore it is the tire indentation that is measured and approximates the tire deformation. The apparent deformation of the tire, shown in Fig. 10, is evaluated as

$$ \delta ' = z^{G} - z^{B}. $$
(31)

By observing the similarity between triangles in Fig. 10 we obtain the relation between the effective and apparent deformation:

$$ \delta = \frac{\left \| \mathbf{u}_{\mathrm{normal}} \right \|\delta '}{u_{\mathrm{n}(\mathrm{z})}}. $$
(32)

If the tire deformation \(\delta \) is positive, i.e., \(\delta >0\), then there is tire–road contact. Otherwise, if \(\delta \ \leq \)0, then there is no contact, and the contact forces are, obviously, null, and the process stops here.

Fig. 10
figure 10

Apparent tire deformation and real tire deformation

Full size image

2.3 Motion parameters and slip ratios

From the moment that contact is detected between the tire and ground it is necessary to calculate several kinematic parameters associated with tire orientation and velocity, on which the tire forces depend. For this purpose, consider the position of the contact point \(G\) with respect to the wheel centre of mass, depicted in Fig. 11, which is calculated as

$$ \mathbf{s}_{\mathrm{w}}^{G} = \mathbf{r}^{G} - \mathbf{r}_{\mathrm{w}}. $$
(33)

Notice that the magnitude of this position vector is in fact the loaded radius of the tire. Furthermore, it is important to retain that when applying the tire contact forces, to be calculated, to the wheel, the position vector \(\mathbf{s}^{G}\) is required to evaluate the transport moments of the forces from point \(G\) to the wheel centre of mass.

Fig. 11
figure 11

Position of the ground contact and undeformed wheel points with respect to the wheel

Full size image

The velocity of point \(G\) in the tire is obtained as

$$ \dot{\mathbf{r}}^{G} = \dot{\mathbf{r}}_{\mathrm{w}} + {\tilde{\omega}}_{\mathrm{w}}\mathbf{s}_{\mathrm{w}}^{G}. $$
(34)

Due to their role in the definition of the longitudinal slip and slip angle, it is important to retain the components of velocity of point \(G\) vector expressed in the tire coordinate frame given by

$$ \dot{\mathbf{r}}_{\mathrm{r}}^{G \prime} = \mathbf{A}_{r}^{T}\dot{\mathbf{r}}^{G} = \left \{ \textstyle\begin{array}{c} v_{\mathrm{xp}} \\ v_{\mathrm{yp}} \\ v_{\mathrm{zp}} \end{array}\displaystyle \right \} \equiv \left \{ \textstyle\begin{array}{c} v_{\mathrm{xp}} \\ v_{\mathrm{y}} \\ \dot{\rho} \end{array}\displaystyle \right \}, $$
(35)

where \(v_{\mathrm{xp}}\) is the longitudinal velocity, \(v_{\mathrm{yp}}\) is the lateral velocity, denoted hereafter as \(v_{\mathrm{y}}=v_{\mathrm{yp}}\), and \(v_{\mathrm{zp}}\) is the ground penetration velocity, denoted hereafter as \(\dot{\rho} = v_{\mathrm{zp}}\), which is used to calculate the damping force of the tire radial deformation.

A quantity that plays a pivotal role in the calculation of the tire forces is the effective rolling radius \(R_{\mathrm{eff}}\), depicted in Fig. 12. Various authors have alternative definitions for the effective rolling radius, which lead to more or less important implications on the quantification of the slip quantities [21]. In this work, we use the definition by Gim and Nikravesh [2–4]:

$$ R_{\mathrm{eff}} = \mathrm{R}_{0} - \delta . $$
(36)

Note that other definitions of the effective rolling radius may be used with the present methodology.

Fig. 12
figure 12

Nominal (\(\mathrm{R}_{0}\)), deformed (\(R_{\mathrm{f}}\)), and effective (\(R_{\mathrm{eff}}\)) radius of a loaded tire

Full size image

Due to the use of the toroidal tire to evaluate the tire contact, we now define the point \(E\), as depicted in Fig. 13, to enable the calculation of \(R_{\mathrm{eff}}\) for a general case.

Fig. 13
figure 13

Position of the ground contact \(G\) and point \(E\) at which the effective radius of the tire is measured with respect to the wheel referential frame

Full size image

The position of point \(E\) with respect to the wheel referential frame origin, expressed in the tire coordinate frame, is evaluated as

$$ \mathbf{s}_{\mathrm{w}}^{E} = \mathbf{s}_{\mathrm{w}}^{G} + \left ( \delta - \delta _{E} \right )\mathbf{u}_{\mathrm{zp}}, $$
(37)

where

$$ \delta _{E} = \mathrm{R}_{0} - R_{\mathrm{eff}}. $$
(38)

Therefore the effective radius for a general orientation of the tire is evaluated as the length of the position vector of point \(E\):

$$ R_{\mathrm{eff}} = \sqrt{\left ( \mathbf{s}_{\mathrm{w}}^{E} \right )^{T}\mathbf{s}_{\mathrm{w}}^{E}}. $$
(39)

Note that the definition for the effective rolling radius by Gim and Nikravesh [2–4] implies that points \(G\) and \(E\) coincide with \(\delta _{E}=\delta \), and we can directly use Equation (39) with \(\mathbf{s}_{\mathrm{w}}^{E} = \mathbf{s}_{\mathrm{w}}^{G}\).

The evaluation of the longitudinal slip requires the velocity of the wheel, \(V_{\mathrm{x}}\), along \(X_{\mathrm{p}}\), which is evaluated as

$$ \dot{\mathbf{r}}_{\mathrm{w}}^{\prime} = \mathbf{A}_{\mathrm{r}}^{T}\dot{\mathbf{r}}_{\mathrm{w}} = \left \{ \textstyle\begin{array}{c} v_{\mathrm{wx}} \\ v_{\mathrm{wy}} \\ v_{\mathrm{wz}} \end{array}\displaystyle \right \} \equiv \left \{ \textstyle\begin{array}{c} v_{\mathrm{x}} \\ v_{\mathrm{wy}} \\ v_{\mathrm{wz}} \end{array}\displaystyle \right \}. $$
(40)

Note that Equation (40) is used with the single intent to calculate \(V_{\mathrm{x}}\), which due to the definition of the wheel transformation matrix in Equation (23) is simply \(V_{\mathrm{x}} = \mathbf{u}_{\mathrm{Xp}}^{T} \dot{\mathbf{r}}_{\mathrm{w}}\).

Now let the angular velocity of the wheel be decomposed into the sum of angular velocities about the wheel normal and \(\mathrm{z}_{\mathrm{p}}\) and \(\mathrm{x}_{\mathrm{p}}\) axes as

$$ {\omega '}_{\mathrm{wp}} = \mathbf{A}_{t}^{T} {\omega}_{\mathrm{w}} = \left \{ \textstyle\begin{array}{c} \omega _{\mathrm{w}(\mathrm{xp})} \\ \omega _{\mathrm{w}(\mathrm{yp})} \\ \omega _{\mathrm{w}(\mathrm{zp})} \end{array}\displaystyle \right \} = \dot{\alpha} \mathbf{u}\boldsymbol{'}_{\mathrm{Zp}} + \dot{\gamma} \mathbf{u}\boldsymbol{'}_{\mathrm{Xp}} + \dot{\varphi} \mathbf{u}\boldsymbol{'}_{\mathrm{w}}, $$
(41)

Where \(\dot{\alpha} \) is the slip angular velocity, \(\dot{\gamma} \) is the camber angular velocity, and \(\dot{\varphi} \) is the wheel spin angular velocity. By performing the dot product of both sides of Equation (41) with the unit vector \(\mathbf{u}\boldsymbol{'}_{\mathrm{Yp}}\) and rearranging we have

$$ \dot{\varphi} = \frac{\omega _{\textup{w}(\textup{yp})}}{u_{\textup{w}(\textup{yp})}}. $$
(42)

The circumferential velocity of the wheel, relative to its centre of mass, along the \(x_{\textup{p}}\) direction is

$$ v_{\textup{c}} = \dot{\varphi} \left ( \tilde{\mathbf{u}}_{\textup{w}}\mathbf{s}_{\textup{w}}^{G} \right )^{T}\mathbf{u}_{\textup{Xp}}. $$
(43)

The actual longitudinal velocity of the contact point \(G\), ignoring the wheel rotation, is defined as

$$ v_{\textup{x}} = v_{\textup{xc}} - v_{\textup{c}}, $$
(44)

which can be understood as the imaginary velocity of the point in the ground that follows the contact patch.

The slip ratio is now defined as

$$ s= \left \{ \textstyle\begin{array}{c@{\quad}c} \frac{v_{\textup{xc}}}{\left \vert v_{\textup{x}} \right \vert} >0, & \mathrm{braking},\\ \frac{v_{\textup{xc}}}{\left \vert v_{\textup{c}} \right \vert} < 0, & \mathrm{traction}. \end{array}\displaystyle \right . $$
(45)

The slip angle \(\alpha \), depicted in Fig. 1, is obtained as

$$ \alpha = \arctan \left ( \frac{v_{\textup{y}}}{v_{\textup{x}}} \right ), $$
(46)

whereas the camber angle \(\gamma \), also presented in Fig. 1, is obtained as

$$ \gamma = \frac{\pi}{2} - \arccos \left ( \mathbf{u}_{\textup{w}}^{T} \mathbf{u}_{\textup{Zp}} \right ). $$
(47)

The absolute value for the longitudinal slip ratio is defined as

$$ S_{s} = \left | s \right |. $$
(48)

The absolute value for the lateral slip ratio, due to the slip angle, is defined as

$$ S_{\alpha} = \left \{ \textstyle\begin{array}{c@{\quad}c} \left \vert \tan \alpha \right \vert , & \mathrm{braking},\\ \left ( 1- S_{s} \right ) \left \vert \tan \alpha \right \vert , & \mathrm{traction}. \end{array}\displaystyle \right . $$
(49)

The absolute value for the lateral slip ratio, due to the camber angle, is defined as

$$ S_{\gamma} = \left | \sin \gamma \right |. $$
(50)

In the case of combined slip, other two slip ratios need to be defined, which are the combined lateral slip due to the slip and camber angles, written as

$$ S_{\alpha \gamma} = \left \{ \textstyle\begin{array}{c@{\quad}c} \left \vert \tan \alpha + \frac{l \sin \gamma}{2 \mathrm{R}_{1}} \right \vert , & \mathrm{braking},\\ \left ( 1- S_{s} \right ) \left \vert \tan \alpha + \frac{l \sin \gamma}{2 \mathrm{R}_{1}} \right \vert , & \mathrm{traction}, \end{array}\displaystyle \right . $$
(51)

in which the length of the tire contact patch is given by \(l \approx \sqrt{8\delta \mathrm{R}_{1}}\) [3]. The resultant slip ratio due to a combination of the slip ratio, slip angle, and camber angle is given by

$$ S_{s\alpha \gamma} = \sqrt{S_{s}^{2} + S_{\alpha \gamma}^{2}}. $$
(52)

Not all the slip ratios defined in this section are necessary to be defined for all tire models available in the literature. However, because different tire models use these slip ratios in different forms, they are defined to be available if necessary.

2.4 Contact forces

The tire models relate the relative motion between the tire and ground with the contact forces and moments developed at the contact patch. In this work, the UA tire model is employed. The original UA tire model was developed by Gim and Nikravesh at The (U)niversity of (A)rizona and published in a three-part paper in 1991 [2–4]. The UA tire model is an analytical model for vehicle dynamic simulations that uses explicit formulations to obtain the tire–road contact forces and moments based on the tire characteristics, the tire–terrain condition, and the tire travelling conditions, allowing calculation of the contact forces for both pure and combined slips. The main advantages of the model are the small number of input parameters required, obtained via simple and inexpensive measurements, and its ability to incorporate them to deal with riding and handling dynamic simulations.

The UA tire model, implemented in this work, results from an enhancement of the original model to improve the computational efficiency of the original UA tire model without affecting the realism of the results [27]. The input parameters required for the UA tire model, which are used to calculate the forces developed at the contact patch, can be divided into two main groups, represented in Fig. 14: the tire characteristics, including the tire geometry, stiffness, damping, and friction parameters; and the tire travelling condition, composed by the motion parameters and slip ratios. Depending on the motion parameters and slip ratios, various formulas are employed to obtain the contact forces from the corresponding inputs, to handle pure and combined slip conditions. As a consequence, the variation of the tire orientation and motion may imply a change in the explicit formulas used to obtain the contact forces. Such transitions in the explicit formulas may lead to discontinuities in the forces and moments. These discontinuities are undesirable as it may compromise the computational efficiency and simulation stability. The enhanced UA tire model, employed in this work, regularises the force discontinuities that may result from the transitions in the explicit formulas employed. The enhanced UA tire model, described in detail in [27], addresses the conditions that may lead to force discontinuities and provides the corresponding methodology to avoid them. In short, the enhanced UA tire model proposes the use of cubic smoothing functions to ensure first-order continuity between the explicit formulas employed to calculate the variation of the contact forces as a function of the tire–road relative kinematics.

Fig. 14
figure 14

Inputs and outputs of the UA tire model

Full size image

Note that the aim of this section is only to review the UA tire model rather than discuss in detail its formulas and parameters, which are presented in Appendix A and discussed in the original work by Gim and Nikravesh [2–4] and in the work by the authors [27]. The force discontinuities in the transition between particular kinematic conditions of the original UA tire model [2–4] are avoided in the enhanced UA tire model [27] by making such transitions smooth, thus allowing the more stable numerical integration and using larger time integration steps. Appendix A provides all the formulas required for the implementation of the UA tire model according to Gim and Nikravesh [2–4] and highlights the changes that correspond to the use of the enhanced version, employed in this work and described in [27]. To use the enhanced UA tire model, the formulas identified with (*) in Tables A.7 and A.8 of Appendix A should be updated by the respective formulas in Table A.9. In addition, the use of the enhanced UA tire model requires the selection of the input parameters for the smoothing ranges, which are listed as model inputs in Table A.1. As a default, the smoothing ranges employed in this work, described in Table B.1 in Appendix B, should be used when using the enhanced UA tire model.

The forces and moments developed at the tire–road contact using the UA tire model include the normal \(f_{\mathrm{z}}\), lateral \(f_{\mathrm{y}}\), and longitudinal \(f_{\mathrm{x}}\) forces and the self-aligning moment \(m_{z}\). The rolling resistance moment, \(m_{\mathrm{y}}\) and the overturning moment \(m_{\mathrm{x}}\) are neglected. For any tire model that provides forces and moments in the tire coordinate system (XYZ)plane, the vector of the forces is written as

$$ \mathbf{f}_{\mathrm{tc}} = \left \{ \textstyle\begin{array}{c} f_{\mathrm{x}} \\ f_{\mathrm{y}} \\ f_{\mathrm{z}} \end{array}\displaystyle \right \}, $$
(53)

whereas the vector of the moments, also in the tire coordinate system, is written as

$$ \mathbf{m}_{\mathrm{tc}} = \left \{ \textstyle\begin{array}{c} m_{\mathrm{x}} \\ m_{\mathrm{y}} \\ m_{\mathrm{z}} \end{array}\displaystyle \right \}. $$
(54)

2.5 Application of forces in the wheel body

The final step, to integrate the tire contact modelling approach in the multibody methodology, is to transform the tire contact forces and moments obtained in the tire coordinate system (XYZ)plane to the global coordinate system (XYZ) and to transport them to the centre of mass of the wheel body. The forces are directly transported to the centre of gravity of the wheel, requiring only to transform them to the global coordinate system. Using the transformation matrix \(\mathbf{A}_{\mathrm{r}}\) given in Equation (23), the forces expressed in the global coordinate system and applied in the wheel body are written as

$$ \mathbf{f}_{\mathrm{wc}} = \mathbf{A}_{\mathrm{r}}^{T}\mathbf{f}_{\mathrm{tc}}. $$
(55)

The moments to apply in the wheel body, in the global coordinate system, are written as

$$ \mathbf{m}_{\mathrm{wc}} = \mathbf{A}_{\mathrm{r}}^{T}\mathbf{m}_{\mathrm{tc}} + \tilde{\mathbf{s}}_{\mathrm{w}}^{E}\mathbf{f}_{\mathrm{wc}} + \mathbf{u}_{\mathrm{w}}m_{\mathrm{rr}}, $$
(56)

where \(m\)rr is the rolling resistance moment defined as a function of the vertical load \(f_{z}\) and the radial damping coefficient \(\zeta _{\mathrm{d}}\) as

$$ m_{\mathrm{rr}} = f_{\mathrm{z}}\zeta _{\mathrm{d}}. $$
(57)

The forces and moments obtained at the centre of mass of the wheel are added to any other force in the same body. The equations of motion of the multibody system and the tire–road contact are re-evaluated for the same wheel for any subsequent time step evaluation.

3 Demonstration scenarios

This section overviews a set of simulation scenarios, with a vehicle travelling over various types of roads, to verify the implementation of the tire–road contact methodology, identify the influence of selected modelling parameters, and highlight its capabilities. One of the important issues is on how the definition of the auxiliary points and the discretization of the road mesh affect the results obtained and how these affect the efficiency of the simulations.

3.1 Vehicle model

In this work, we consider a multibody model of a Lancia Stratos to verify the tire–road contact methodology proposed. The vehicle model considered has been studied and described in the works by Gonçalves and Ambrósio [28–31]. The use of a car, instead of a more simplistic one-wheeled mechanism, allows to test the tire–road contact methodology in its intended use, road vehicle dynamics applications. It is not the aim of the present work to provide a detailed discussion on the vehicle model, but rather to employ it to analyse the tire–road contact modelling approach. The multibody model of the Lancia Stratos comprises seventeen rigid bodies, including the vehicle body, the four wheels, and twelve other bodies that comprise the front and rear suspension system. The rigid bodies are connected by kinematic joints, which allow us to represent the suspension kinematics and by linear force elements to model the springs and dampers of the suspension, as well as the anti-roll bars. For a detailed description of the model, including all data used, the reader is referred to the work by Ambrósio and Gonçalves [28]. The tire model inputs used in the simulations are presented in Appendix B and include the tire geometry and stiffness parameters.

3.2 Bump road scenarios

The first simulation scenario considered is an asymmetric bump under the right side of the vehicle while it travels at 40 km/h. The geometry of the bump, illustrated in Fig. 15, corresponds to a slightly tilted protrusion on the road that excites the wheels and the vehicle vertically and laterally and promotes tire—road camber as the wheel goes through the bump. This road geometry allows us to understand how the tire–road contact methodology deals with the transition from the flat road to a localized element that has a significantly different mesh size.

Fig. 15
figure 15

Lancia Stratos going through bump: (a) original bump mesh; (b) refined bump mesh

Full size image

The results discussed hereafter correspond to simulations with a sample rate and maximum time step of 0.001 s. Note that the MUBODyn code uses a variable time step integrator to accommodate rapid changes in the motion of the system. Therefore, when there are sudden changes in the velocities or accelerations of the system, provoked by rapid changes or even discontinuities in the tire–road contact forces, the time step is reduced to minimize the integration error. The reduction of the time step will, in turn, penalise the simulation efficiency by increasing the total number of integration steps. In extreme cases, the reduction of the time-step size can be such that the integration stalls and no solution is obtained.

3.2.1 Road model: auxiliary points

The tire–road contact methodology proposed in this work includes the use of a set of auxiliary points that support the regularisation of the transition between triangular patches with different orientations. The regularisation, or smoothing, of the transition between triangular patches is done to avoid peaks in the tire–road contact forces due to the rapid transitions in road geometries. However, it is not clear how the use of these auxiliary points affects the results and the simulation efficiency and how to parametrize the parameters \(\Delta \)x and \(\Delta \)y shown in Fig. 8 (a).

Figure 16 shows the tire–road contact forces and moments at the right front tire of the cars while it goes through the bump for three different definitions of the auxiliary points: (1) auxiliary points are not used, meaning that not only the transition between triangle patches is not smooth but also only one contact point is evaluated for each wheel at each time step, instead of the five points evaluated when using auxiliary points; (2) auxiliary points are used with \(\Delta \)x = 1 cm and \(\Delta \)y = 1.3 cm in Equations (18) and (19) and; (3) auxiliary points are used with \(\Delta \)x = 6 cm and \(\Delta \)y = 8 cm. Note that the dimensions for case (3) are approximate to the size of the contact patch of a tire, whereas the dimensions for case (2) do not have any physical meaning/interpretation.

Fig. 16
figure 16

Longitudinal force (fx), vertical force (fz), lateral force (fy), and self-aligning moment (mz), measured at the right front tire for various auxiliary points parameters

Full size image

Figure 16 shows that there is an overall match between the different cases considered; however, slight differences are observed. By observing the zoom boxes in Fig. 16 the differences become evident. Not only is there a smoother transition between the flat road and the bump (∼1.7 s) for the case with larger \(\Delta \)x and \(\Delta \)y, but the variations of the forces developed as the tire travels in the middle of the bump are also much smoother. The rapid changes or discontinuities in the vertical forces are a consequence of the rapid change in the tire–road penetration when the tire goes from one triangular patch to the subsequent one. This also holds for the slip and camber angles, since an immediate change in the orientation of the contact patch will impose an immediate change in the motion parameters. It becomes evident that the use of auxiliary points contributes significantly to the regularisation of the forces.

3.2.2 Road model: mesh refinement

A given road geometry or obstacle can be discretised with a more or less refined triangular mesh. Figure 17 shows the vertical force developed at the right front tire of the car for two levels of mesh refinement of the bump geometry depicted in Fig. 15. The results correspond to the use of auxiliary points with \(\Delta \)x = 6 cm and \(\Delta \)y = 8 cm. The results in Fig. 17 show a good match between the two cases. However, when observing in detail the zoomed area of the plot, it becomes evident that there are some oscillations or even peaks of the tire contact forces for the original mesh, in contrast to a smooth force transition in the case of the refined mesh.

Fig. 17
figure 17

Vertical force (fz) measured at the right front tire, for two different bump surface discretizations

Full size image

3.2.3 Numerical efficiency and simulation stability

The considerations in terms of the auxiliary points and road mesh refinement suggest that the use of larger \(\Delta \)x and \(\Delta \)y together with the use of a more refined mesh leads to smoother tire–road contact forces. However, to better understand how it affects the efficiency of the simulations, it is relevant to analyse the computational cost and the number of iterations required to run each simulation. It is important to note that the integration method used to obtain the results further analysed is a multistep integrator based on the Gear BDF (Backward Differentiation Formulae) algorithm as implemented in the subroutine DIVPAG of the IMSL library [32]. Even though the results can slightly differ based on the use of different integration methods, the development of the smooth tire–road contact forces always contributes to the simulation efficiency and stability. Thus the current results represent the effects of the different modelling decisions. Table 1 summarizes the processing time and the total number of integration steps required to run each simulation, highlighting the relative cost between different parameters, shown as normalized CPU time and number of iterations with respect to the fastest simulation case.

Table 1 Processing time in seconds (CPU) and the number of integration steps required (ITER) to solve the simulation of the car going through the bump. Values inside brackets correspond to quantities normalised to the lowest value
Full size table

The results in Table 1 highlight a significant increase of the computational time with the refinement of the mesh geometry, i.e., the use of a more refined road mesh increases the computational cost of the simulation by a factor of 2–4, depending on the use or not of auxiliary points. This is caused because of the number of operations required to identify a triangular patch corresponding to a given point. The greater the number of triangles, the longer the time for the algorithm to find the triangular patch in which a given point is lying. In terms of the use of auxiliary points, it becomes evident that the number of integration time steps is reduced when auxiliary points are employed. This is due to the smoother forces that develop when auxiliary points are used. Nonetheless, it becomes evident from the results in Table 1 that the reduction of the number of integration steps when using auxiliary points does not compensate, in terms of simulation efficiency, for the cost associated with the evaluation of the four auxiliary points for each tire at each time step.

It is important to note, again, that the use of the variable time step integrator results in a decrease of the time step or an increase in the number of integration steps, to deal with rapid changes in the motion of the system. These rapid changes may be due to non-smooth transitions on the road geometric model or to transitions between different states of the tire model in the case of the original UA tire model [2–4]. Also note that when no auxiliary points are used, there is a reduction in the number of evaluations required to identify the triangular patches because the number of points used to define the contact patch decreases from five to one, but, in turn, the tire forces exhibit now physical abrupt variations, shown in Fig. 16.

3.2.4 Windy road scenario

To better understand the capability of the tire-contact methodology and to explore the effect of the auxiliary points on the tire–road contact detection, a simulation of the Lancia Stratos running over the windy road depicted in Fig. 18 is analysed. Two simulations are carried out; in the first the auxiliary points are not considered, whereas in the second the auxiliary points are used with \(\Delta \)x = 6 cm and \(\Delta \)y = 8 cm. Figure 19 shows the vertical and lateral force developed at the right front tire when the vehicle travels at 60 km/h in the windy road. The results show that for the case where auxiliary points are not used, there are significant peaks in the forces, which are associated with the transitions between triangular patches, which is physically unrealistic. In contrast, the forces corresponding to the case where the auxiliary points are employed show a smooth and continuous profile. In terms of the number of integration steps required to run the simulations, the case using auxiliary points outperforms the case without auxiliary points, with 118,203 vs 194,990 integration steps, respectively. However, in terms of processing time required to run the simulation, the case without auxiliary points is significantly faster, with 12,037 s vs 19,328 s. This suggests that the necessity of performing more evaluations of triangular patches, required when using auxiliary points, has a stronger contribution to the processing time than the reduction of integration steps.

Fig. 18
figure 18

Triangular mesh of a section of windy road

Full size image
Fig. 19
figure 19

Vertical force (fz) and lateral force (fy) at the left front tire of the Lancia Stratos while travelling over the windy road, with the number of integration steps required to run the simulation (ITER) and processing time in seconds (CPU)

Full size image

3.2.5 Jump road scenario

The final simulation scenario considered is the Lancia Stratos going over a ramp at 60 km/h, as depicted in Fig. 20 (a). The simulation is performed considering the use of auxiliary points with \(\Delta \)x = 6 cm and \(\Delta \)y = 8 cm. During the maneuver, all tires lose contact with the road, which is regained as the car lands. The simulation allows us to evaluate the capability of the contact algorithm to handle contact discontinuities in which the tires lose and regain contact. Figure 20 (b) shows the vertical force measured at each tire during the maneuver. The leading tires are the first to lose contact as they leave the ramp and are also the first to regain contact after landing. The simulation runs smoothly with large time steps during normal tire–road contact but requires a drastic reduction of the time step during the landing of the tires due to the strong impact between the road and the tires. This scenario demonstrates the capability of the contact algorithm to deal with tire–road contact loss and geometric discontinuities.

Fig. 20
figure 20

Lancia Stratos travelling over a ramp with 25 cm: (a) three frames of the Lancia Stratos during the maneuver: (1) before front wheels leave the ramp; (2) all wheels in the air; (3) immediatelly after rear wheels land; (b) vertical force in each tire during the maneuver

Full size image

4 Conclusions

This work provides a thorough description of a methodology to model the tire–road contact interaction in multibody simulations. In both the contact detection algorithm and the tire model, it is necessary to ensure that the methods lead to smooth dynamic responses, thus mitigating discontinuities. The numerical integrators for ordinary differential equations (ode) perceive such discontinuities as high-frequency perturbations and decrease the size of the integration time steps to a point in which, eventually, the process may stall. Particular emphasis is put on the tire–road contact detection method for which a numerical procedure is proposed to overcome the discontinuities that occur when the contact patch transits from one triangular patch to the next one. The different orientations of their normal vectors are smoothed by using a set of auxiliary points to regularise the transition between the triangular patches. The tire model considered is an enhanced UA tire model, which overcomes the discontinuities between kinematic states of the original model, to ensure smooth tire–road contact force variations. The methodology proposed is verified by simulating a road vehicle running over different road topographies. The impact of the parameters associated with the road model smoothness characteristics, i.e., the auxiliary points and the level of refinement of the road profiles, in the results and efficiency of the simulations, are explored.

Simulation results obtained for a multibody model of a Lancia Stratos show the capability of the tire–road contact methodology to deal with different road topographies: (1) a speed bump under the right wheels of the vehicle; (2) a long windy road defined by a sinusoidal input, and (3) driving over a ramp, requiring the loss and restitution of contact. The results also show, for the scenarios considered, that the tire–road contact methodology provides the necessary level of smoothness, both in the contact parameters and tire–contact model to obtain efficient numerical integrations.

The use of the auxiliary points to smooth the tire–road contact forces when the tire travels through irregular tracks allows us to significantly reduce the total number of integration time steps when compared to the case in which no auxiliary points are used. Without the smoothing, the transitions between triangular patches lead to rapid changes in the tire–road contact forces, which in turn require the reduction of the time step to reduce the time integration error. However, the use of auxiliary points comes with a cost. When using auxiliary points, it requires a larger number of evaluations of the triangular patch associated with each auxiliary point. When the road mesh is composed of a large number of triangles, the triangular patch search is time-consuming. In the simulation cases considered, even though the use of auxiliary points allows us to reduce the total number of integration steps, the total processing time increases due to the greater number of triangular patch evaluations. The use of a more refined road mesh to minimize the peaks associated with the changes between triangular patches is also explored. The refinement of the road mesh smooths the tire–road contact forces but increases the time spent on each triangular patch identification, emphasising that a balance between accuracy and efficiency needs to be achieved.