Autonomous unicycle: modeling, dynamics, and control

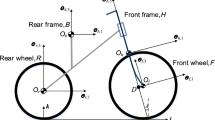
Abstract

This article focuses on modeling and analyzing the dynamics of an autonomous unicycle. The equations of motion of the nonholonomic multibody system are derived using the Appellian approach, which enables the use of a minimum number of state variables and results in a system of low complexity. The final equations of motion consist of 8 first-order kinematic differential equations and 6 first-order dynamic differential equations. The stability of the open-loop dynamics is investigated and a PD-type controller with 3 input torques is proposed that enables the unicycle to stabilize its upright position and travel along a straight path. The performance of the closed-loop system is demonstrated via numerical simulations.

Appendices

Appendix A: Detailed expressions of accelerations

The components of the acceleration of the center of mass B and the angular acceleration of the body in (32) are

$$ \begin{aligned} a_{{\mathrm{B}}x}= & \dot{\sigma}_{2} R \cos \gamma + \dot{\sigma}_{4} h + \sigma _{1}^{2} \big( R \sin \gamma + h \cos \gamma \sin \gamma \big) - \sigma _{3}^{2} h \cos \gamma \sin \gamma \\ & + \sigma _{1} \sigma _{3} \Big( R \cos \gamma + h \big( \cos ^{2} \gamma - \sin ^{2}\gamma \big) \Big) + \sigma _{2} \sigma _{3} R \tan \theta \sin \gamma \,, \\ a_{{\mathrm{B}}y}= & - \dot{\sigma}_{1} (R + h \cos \gamma ) + \dot{\sigma}_{3} h \sin \gamma - \sigma _{3}^{2} h \tan \theta \cos \gamma \\ &- \sigma _{1} \sigma _{3} h \tan \theta \sin \gamma + \sigma _{2} \sigma _{3} R + 2 \sigma _{1} \sigma _{4} h \sin \gamma + 2 \sigma _{3} \sigma _{4} h \cos \gamma \,, \\ a_{{\mathrm{B}}z}= & \dot{\sigma}_{2} R \sin \gamma - \sigma _{1}^{2} \big( R \cos \gamma + h \cos ^{2}\gamma \big) - \sigma _{3}^{2} h \sin ^{2}\gamma - \sigma _{4}^{2} h \\ &+ \sigma _{1} \sigma _{3} \big( R \sin \gamma + 2 h \cos \gamma \sin \gamma \big) - \sigma _{2} \sigma _{3} R \tan \theta \cos \gamma \, \end{aligned} $$

(A1)

and

$$ \begin{aligned} \alpha _{x}= &\dot{\sigma}_{1} \cos \gamma -\dot{\sigma}_{3} \sin \gamma +\sigma _{3} ^{2} \tan \theta \cos \gamma \\ &+ \sigma _{1} \sigma _{3} \tan \theta \sin \gamma - \sigma _{1} \sigma _{4} \sin \gamma - \sigma _{3} \sigma _{4} \cos \gamma \,, \\ \alpha _{y}=& \dot{\sigma}_{4}\,, \\ \alpha _{z}= &\dot{\sigma}_{1} \sin \gamma + \dot{\sigma}_{3} \cos \gamma +\sigma _{3} ^{2} \tan \theta \sin \gamma \\ &- \sigma _{1} \sigma _{3} \tan \theta \cos \gamma + \sigma _{1} \sigma _{4} \cos \gamma - \sigma _{3} \sigma _{4} \sin \gamma \,. \end{aligned} $$

(A2)

The components of the angular accelerations of the flywheels in (36) are

$$ \begin{aligned} \alpha _{{\mathrm{b}}x} = & \dot{\sigma}_{5}\,, \\ \alpha _{{\mathrm{b}}y} = & \dot{\sigma}_{4} - \sigma _{1}^{2} \cos \gamma \sin \gamma + \sigma _{3}^{2} \cos \gamma \sin \gamma \\ & - \sigma _{1} \sigma _{3} \big(\cos ^{2}\gamma -\sin ^{2}\gamma \big) + \sigma _{1} \sigma _{5} \sin \gamma + \sigma _{3} \sigma _{5} \cos \gamma \,, \\ \alpha _{{\mathrm{b}}z}= & \dot{\sigma}_{1} \sin \gamma + \dot{\sigma}_{3} \cos \gamma + \sigma _{3}^{2} \tan \theta \sin \gamma \\ &- \sigma _{1} \sigma _{3} \tan \theta \cos \gamma + 2 \sigma _{1} \sigma _{4} \cos \gamma - 2 \sigma _{3} \sigma _{4} \sin \gamma - \sigma _{4} \sigma _{5} \, \end{aligned} $$

(A3)

and

$$ \begin{aligned} \alpha _{{\mathrm{s}}x}= & \dot{\sigma}_{1} \cos \gamma - \dot{\sigma}_{3} \sin \gamma + \sigma _{3}^{2} \tan \theta \cos \gamma \\ & + \sigma _{1} \sigma _{3} \tan \theta \sin \gamma - 2 \sigma _{1} \sigma _{4} \sin \gamma - 2 \sigma _{3} \sigma _{4} \cos \gamma + \sigma _{4} \sigma _{6} \,, \\ \alpha _{{\mathrm{s}}y}= & \dot{\sigma}_{4} + \sigma _{1}^{2} \cos \gamma \sin \gamma - \sigma _{3}^{2} \cos \gamma \sin \gamma \\ &+ \sigma _{1} \sigma _{3} \big( \cos ^{2}\gamma - \sin ^{2}\gamma \big) - \sigma _{1} \sigma _{6} \cos \gamma + \sigma _{3} \sigma _{6} \sin \gamma \,, \\ \alpha _{{\mathrm{s}}z}=&{\dot{\sigma} }_{6}\,. \end{aligned} $$

(A4)

Appendix B: Elements of matrices in the linearized systems

The components of matrix $A$ in (61) are:

$$ \begin{aligned} A_{13}&= \frac{2\big( 3 m_{\mathrm{w}} R + 2 \widehat{m} (R+h) \big)v^{*}}{Q_{1}}, \quad A_{14}=- \frac{2 m_{\mathrm{s}} r_{\mathrm{s}}^{2} \omega _{\mathrm{s}}^{*}}{Q_{1}}, \\ A_{17}&=\frac{4\big( m_{\mathrm{w}} R + \widehat{m} (R+h) \big)g}{Q_{1}}, \\ A_{21}&=- \frac{4 \widehat{m} m_{\mathrm{s}} h r_{\mathrm{s}}^{2} \omega _{\mathrm{s}}^{*}}{R Q_{2}}, \quad A_{23}= \frac{4 \widehat{m} m_{\mathrm{b}} h r_{\mathrm{b}}^{2} \omega _{\mathrm{b}}^{*}}{R Q_{2}}, \quad A_{28} = - \frac{8 \widehat{m}^{2} h^{2} g}{R Q_{2}}, \\ A_{31} &= - \frac{2 m_{\mathrm{w}} R v^{*} }{Q_{3}}, \qquad \,\,\, A_{34}= \frac{2 m_{\mathrm{b}} r_{\mathrm{b}}^{2} \omega _{\mathrm{b}}^{*} }{Q_{3}}, \\ A_{41} &= \frac{2 \big(3 m_{\mathrm{w}} + 2 \widehat{m} \big) m_{\mathrm{s}} r_{\mathrm{s}}^{2} \omega _{\mathrm{s}}^{*}}{Q_{2}}, \quad A_{43} = - \frac{2 \big(3 m_{\mathrm{w}} + 2 \widehat{m} \big) m_{\mathrm{b}} r_{\mathrm{b}}^{2} \omega _{\mathrm{b}}^{*}}{Q_{2}} \\ A_{48}&= \frac{4 \big(3 m_{\mathrm{w}} + 2 \widehat{m} \big) \widehat{m} h g}{Q_{2}}, \end{aligned} $$

(B1)

the components of matrix $B$ in (61) are:

$$ \begin{aligned} B_{12}&=-\frac{4}{Q_{1}}, \quad B_{21}= \frac{ 2 \big( 4 \widehat{m} (R+h) h + m_{\mathrm{b}} r_{\mathrm{b}}^{2} + m_{\mathrm{s}} r_{\mathrm{s}}^{2} + 4J_{y} \big)}{R^{2} Q_{2}}, \\ B_{33}&=-\frac{4}{Q_{3}}, \quad B_{41}=- \frac{4 \big(3 m_{\mathrm{w}} R + 2 \widehat{m} (R+h) \big)}{R Q_{2}}, \end{aligned} $$

(B2)

the components of matrix $\bar{A}$ in (70) are:

$$\begin{aligned} \bar{A}_{11}&=-\frac{4 d_{\mathrm{b}} }{Q_{1}}, \quad \bar{A}_{17}= \frac{4\big( m_{\mathrm{w}} R + \widehat{m} (R+h) \big) g - 4 p_{\mathrm{b}} }{Q_{1}}, \\ \bar{A}_{24}&= \frac{ 2 \big( 4 \widehat{m} (R+h) h + m_{\mathrm{b}} r_{\mathrm{b}}^{2} + m_{\mathrm{s}} r_{\mathrm{s}}^{2} + 4J_{y} \big) d_{\mathrm{w}}}{R^{2} Q_{2}}, \\ \begin{aligned} \bar{A}_{28}&=- \frac{8 \widehat{m}^{2} R h^{2} g - 2 \big( 4 \widehat{m} (R+h) h + m_{\mathrm{b}} r_{\mathrm{b}}^{2} + m_{\mathrm{s}} r_{\mathrm{s}}^{2} + 4J_{y} \big) p_{\mathrm{w}}}{R^{2} Q_{2}}, \\ \bar{A}_{33}&=-\frac{4 d_{\mathrm{s}} }{Q_{3}}, \quad \bar{A}_{39}=- \frac{4 p_{\mathrm{s}} }{Q_{3}}, \end{aligned} \\ \bar{A}_{44}&=- \frac{4 \big(3 m_{\mathrm{w}} R + 2 \widehat{m} (R+h) \big) d_{\mathrm{w}}}{R Q_{2}}, \\ \bar{A}_{48}&= \frac{4 \widehat{m} \big(3 m_{\mathrm{w}} + 2 \widehat{m} \big) R h g - 4 \big( 3 m_{\mathrm{w}} R + 2 \widehat{m} (R+h) \big) p_{\mathrm{w}}}{R Q_{2}}, \end{aligned}$$

(B3)

where

$$ \begin{aligned} \widehat{m} = & m + m_{\mathrm{b}} + m_{\mathrm{s}} , \\ Q_{1} = & 5 m_{\mathrm{w}} R^{2} + 4 \widehat{m} (R+h)^{2} + m_{\mathrm{s}} r_{ \mathrm{s}}^{2} + 4 J_{x} , \\ Q_{2} = & \big( 3 m_{\mathrm{w}} + 2 \widehat{m} \big) \big( m_{\mathrm{b}} r_{ \mathrm{b}}^{2} + m_{\mathrm{s}} r_{\mathrm{s}}^{2} + 4 J_{y} \big) + 12 \widehat{m} m_{ \mathrm{w}} h^{2} , \\ Q_{3} = & m_{\mathrm{w}} R^{2} + m_{\mathrm{b}} r_{\mathrm{b}}^{2} + 4 J_{z} . \end{aligned} $$

(B4)

The polynomial in (71) is:

$$\begin{aligned} p(\lambda ) ={}& \lambda ^{6} - ( \bar{A}_{11} + \bar{A}_{33} + \bar{A}_{44} )\lambda ^{5} + (\bar{A}_{11} \bar{A}_{33} + \bar{A}_{11} \bar{A}_{44} - A_{13} A_{31} - A_{14} A_{41} \\ &{} + \bar{A}_{33} \bar{A}_{44} - A_{34} A_{43} - \bar{A}_{17} - \bar{A}_{39} - \bar{A}_{48}) \lambda ^{4} \\ &{}+ (-\bar{A}_{11} \bar{A}_{33} \bar{A}_{44} + \bar{A}_{11} A_{34} A_{43} + A_{13} A_{31} \bar{A}_{44}- A_{13} A_{34} A_{41} \\ &{}- A_{14} A_{31} A_{43} + A_{14} \bar{A}_{33} A_{41} + \bar{A}_{11} \bar{A}_{39} + \bar{A}_{11} \bar{A}_{48} + \bar{A}_{17} \bar{A}_{33} \\ &{}+ \bar{A}_{17} \bar{A}_{44} + \bar{A}_{33} \bar{A}_{48} + \bar{A}_{39} \bar{A}_{44})\lambda ^{3} + (-\bar{A}_{11} \bar{A}_{33} \bar{A}_{48} - \bar{A}_{11} \bar{A}_{39} \bar{A}_{44} + A_{13} A_{31} \bar{A}_{48} \\ &{}+ A_{14} \bar{A}_{39} A_{41} - \bar{A}_{17} \bar{A}_{33} \bar{A}_{44} + \bar{A}_{17} A_{34} A_{43} + \bar{A}_{17} \bar{A}_{39} + \bar{A}_{17} \bar{A}_{48} + \bar{A}_{39} \bar{A}_{48})\lambda ^{2} \\ &{}- (\bar{A}_{11} \bar{A}_{39} \bar{A}_{48} + \bar{A}_{17} \bar{A}_{33} \bar{A}_{48} + \bar{A}_{17} \bar{A}_{39} \bar{A}_{44})\lambda - \bar{A}_{17} \bar{A}_{39} \bar{A}_{48}\,. \end{aligned}$$

(B5)

Appendix C: Eigenvectors of the open-loop system

When ${\omega _{\mathrm{b}}^{*}=\omega _{\mathrm{s}}^{*}=0}$, the eigenvectors corresponding to the nonzero eigenvalues (63) are

$$ v_{1,2} = \begin{bmatrix} 0 \\ \pm \sqrt{A_{48}} \\ 0 \\ \frac{\pm (\sqrt{A_{48}})^{3}}{A_{28}} \\ 0 \\ 0 \\ 0 \\ \frac{A_{48}}{A_{28}} \\ 0 \\ R \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \,, \quad v_{3,4} = \begin{bmatrix} -\frac{A_{13} A_{31} + A_{17}}{A_{31}} \\ 0 \\ \mp \sqrt{A_{13} A_{31} + A_{17}} \\ 0 \\ 0 \\ 0 \\ \frac{\mp \sqrt{A_{13} A_{31} + A_{17}}}{A_{31}} \\ 0 \\ -1 \\ 0 \\ \pm \big(\frac{R\sqrt{A_{13} A_{31} + A_{17}}}{A_{31}} - \frac{v^{*}}{\sqrt{A_{13} A_{31} + A_{17}}} \big) \\ 0 \\ \frac{\pm \sqrt{A_{13} A_{31} + A_{17}}}{A_{31}} \\ 1 \end{bmatrix} \,, $$

(C1)

where $A_{ij}, B_{ij}$ are defined in Appendix B.

Appendix D: Transfer functions for the open-loop system

When ${\omega _{\mathrm{b}}^{*}=\omega _{\mathrm{s}}^{*}=0}$, the transfer function from input torques $M_{\mathrm{w}}$, $M_{\mathrm{b}}$, and $M_{\mathrm{s}}$ to angles $\gamma$, $\theta$, and $\psi$ are:

$$ \begin{aligned} T_{M_{\mathrm{w}} \rightarrow \gamma}(\lambda ) &= \frac{B_{41}}{\lambda ^{2}-A_{48}}\, , \\ T_{M_{\mathrm{b}} \rightarrow \theta}(\lambda ) &= \frac{B_{12}}{\lambda ^{2}-(A_{13} A_{31} + A_{17})}\, , \\ T_{M_{\mathrm{s}} \rightarrow \psi}(\lambda ) &= \frac{B_{33}(\lambda ^{2}-A_{17})}{\lambda ^{2}\big(\lambda ^{2}-(A_{13} A_{31} + A_{17})\big)} \, , \\ T_{M_{\mathrm{b}} \rightarrow \psi}(\lambda ) &= \frac{A_{31}B_{12}}{\lambda \big(\lambda ^{2}-(A_{13} A_{31} + A_{17})\big)} \, , \\ T_{M_{\mathrm{s}} \rightarrow \theta}(\lambda ) &= \frac{A_{13}B_{33}}{\lambda \big(\lambda ^{2}-(A_{13} A_{31} + A_{17})\big)} \, , \\ T_{M_{\mathrm{w}} \rightarrow \theta}(\lambda ) &= T_{M_{\mathrm{b}} \rightarrow \gamma}(\lambda ) = T_{M_{\mathrm{s}} \rightarrow \gamma}( \lambda ) = T_{M_{\mathrm{w}} \rightarrow \psi}(\lambda ) = 0\, , \end{aligned} $$

(D1)

where $A_{ij}, B_{ij}$ can be found in Appendix B.

Appendix E: MATLAB code for the EoM derivation