Absolute coordinate formulation and generalized component mode synthesis with rigid body coordinates

Abstract

The dynamics of linearly-elastic multibody (MB) systems is conventionally modeled via the floating frame of reference formulation (FFRF); however, its equations of motion (EOMs) involve significantly more nonlinear terms and quantities than alternative formulations, such as the absolute coordinate formulation (ACF) and generalized component mode synthesis (GCMS). This large number of operations required makes computer implementations of the FFRF laborious as well as error-prone and introduces more complexity in general. These issues associated with the FFRF, and the fact that the formulations are mathematically equivalent as shown by the authors, render the ACF and its relatives appealing alternatives due to their simplistic equation structures. To make these alternatives even more appealing, this contribution proposes an improved ACF and GCMS, which (i) reduces the nonlinearity in the EOMs compared to their standard versions and (ii) eliminates the necessity to calculate the rigid body (RB) motion from the global nodal displacement field to obtain the flexible part of the degrees of freedom (DOFs) and the rotation matrix. The proposed EOMs feature a constant mass matrix, a corotated stiffness matrix in the flexible part, and a “small” nonlinear stiffness matrix in the RB rotation part. Moreover, attaching the moving reference frame to the center of mass of the underlying rigid body and employing linearized Tisserand and rotation matrix constraints eliminates coupling terms within the mass matrix and yields implementation-friendly EOMs to analyze the dynamics of linear-elastic flexible MB systems.

1 Objectives in a nutshell

Before going into details, the objectives of this research should be explained and highlighted for the reader in a nutshell as follows:

These aspects are elaborated on in the following sections.

2 Introduction and detailed problem statement

Flexible MB dynamics refers to the computational strategies used to determine time histories of motion, deformation, strain, and stress of interconnected components undergoing large overall motion due to applied forces, constraints, contact, and initial conditions.

The so-called, linearly-elastic flexible MB simulations are oftentimes sufficient for engineering systems, and are usually based on a corotational approach, where a moving frame per body follows the corresponding body’s rigid body motion and the deformation is analyzed within this local coordinate system; this description is subjected to the following assumptions:

$\square$:

Large rigid body translations and rotations are present.

$\square$:

Flexible deformations and strains of each body are small with respect to (w.r.t.) each body’s moving frame.

$\square$:

The bodies obey a linear constitutive law.

Recently it has been proposed [12–14] and even more recently shown more rigorously [16] that such linearly-elastic MB systems discretized via isoparametric finite elements (FEs) may be described fully by the constant mass matrix $\overline {\boldsymbol {M}} \in \mathbb{R}^{3n_{\mathrm{n}} \times 3n_{\mathrm{n}} }$ and stiffness matrix $\overline {\boldsymbol {K}} \in \mathbb{R}^{3n_{\mathrm{n}} \times 3n_{\mathrm{n}} }$ from the underlying linear FE model, as well as the corresponding nodal quantities.¹ Hence, the kinetic energy $T$ and the strain energy $U$ may be expressed as

$$\begin{aligned} {T} &=\frac{1}{2} \dot{\boldsymbol{r}}^{\mathrm{T}} \overline {\boldsymbol {M}} \dot{\boldsymbol{r}} , \end{aligned}$$

(1)

$$\begin{aligned} {U} &=\frac{1}{2} \boldsymbol {\overline {c}}_{\mathrm {f}}^{\mathrm {T}} \overline {\boldsymbol {K}} \boldsymbol {\overline {c}}_{\mathrm {f}}^{\mathrm {}} , \end{aligned}$$

(2)

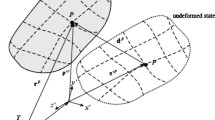
where the nodal quantities used in this work are illustrated and described in Fig. 1 and Sect. 3.1. Note that in Eqs. (1) to (2) and throughout the paper lower-case nodal quantities are arranged in the standard FE manner (stacked format), e.g.,

$$\mathit{c}=\left[\begin{array}{c}{\mathit{c}}^{(1)}\\ ⋮\\ {\mathit{c}}^{(n_{\mathrm{n}})}\end{array}\right]\in {\mathbb{R}}^{3n_{\mathrm{n}}\times 1},$$

(3)

and the corresponding upper-case nodal quantities in list format, where each row corresponds to one node, e.g.,

$$\mathit{C}=\left[\begin{array}{c}{\mathit{c}}^{{(1)}^{\mathrm{T}}}\\ ⋮\\ {\mathit{c}}^{{(n_{\mathrm{n}})}^{\mathrm{T}}}\end{array}\right]\in {\mathbb{R}}^{n_{\mathrm{n}}\times 3},$$

(4)

where $n_{\mathrm{n}}$ denotes the number of FE nodes of the body under consideration.

Fig. 1

FE-discretized body $\Omega$ ($\Omega _{e}$ depicts a representative element of the FE mesh) with global inertial ℱ $(x,y,z)$ and local moving $\overline{\mathcal{F}}$ $(\overline {x},\overline {y},\overline {z})$ frame; the translation between the frames is given by $\boldsymbol {\tau} \in \mathbb{R}^{3 \times 1}$ and the orientations are related by the rotation matrix $\boldsymbol {A} \in \mathbb{R}^{3 \times 3}$. The position vector $\boldsymbol {r}^{(i)} \in \mathbb{R}^{3 \times 1}$ defines the current position of representative node $(i)$. The flexible nodal displacement and deformed nodal position of node $(i)$, with reference position $\overline {\boldsymbol {x}}^{(i)} \in \mathbb{R}^{3 \times 1}$, relative to the moving frame are given by $\overline {\boldsymbol {c}}_{\mathrm {f}}^{(i)} \in \mathbb{R}^{3 \times 1}$ and $\overline {\boldsymbol {r}}_{\mathrm {f}}^{(i)} \in \mathbb{R}^{3 \times 1}$, respectively. Note that overlined quantities are expressed in the moving frame in contrast to global quantities expressed in the inertial frame. The illustration is adapted from [14].

In [16] the authors also showed that the EOMs of one body of the aforementioned linearly-elastic MB systems may be described by formulation-independent EOMs given by

$$ \boldsymbol {L}^{\mathrm {T}} \overline {\boldsymbol {M}} \boldsymbol {L} \ddot{\boldsymbol {q}} + \boldsymbol {L}^{\mathrm {T}} \overline {\boldsymbol {M}} \dot{\boldsymbol {L}} \dot{\boldsymbol {q}} + \boldsymbol {P}_{\mathrm {}}^{\mathrm {T}} \overline {\boldsymbol {K}} \overline {\boldsymbol {c}}_{\mathrm {f}} \left ( \boldsymbol {q} \right ) + \boldsymbol {J}^{\mathrm {T}} \boldsymbol {\lambda} = \boldsymbol {L}^{\mathrm {T}} \boldsymbol {f} ,$$

(5)

where

$$\begin{aligned} \boldsymbol {L} &= \frac{\partial {\boldsymbol {r}} }{\partial \boldsymbol {q}} , \end{aligned}$$

(6)

$$\begin{aligned} \boldsymbol {P} &= \frac{\partial \overline {\boldsymbol {c}}_{\mathrm {f}}}{\partial \boldsymbol {q}} , \end{aligned}$$

(7)

$$\begin{aligned} \boldsymbol {J} &= \frac{\partial \boldsymbol {g}}{\partial \boldsymbol {q}} \end{aligned}$$

(8)

are Jacobian matrices given by the partial derivatives of the global nodal positions $\boldsymbol {r}\in \mathbb{R}^{3n_{\mathrm{n}} \times 1 }$, the local flexible nodal displacements $\overline {\boldsymbol {c}}_{\mathrm {f}} \in \mathbb{R}^{3n_{\mathrm{n}} \times 1}$, and the constraint equations $\boldsymbol {g} \left ( \boldsymbol {q}, t\right ) = \boldsymbol {0} \in \mathbb{R}^{n_{ \mathrm{c}} \times 1}$ w.r.t. the generalized DOFs $\boldsymbol {q} \in \mathbb{R}^{n_{q} \times 1}$. Note that $n_{\mathrm{c}}$ and $n_{q}$ denote the number of constraints and DOFs, respectively. Furthermore, $\boldsymbol {f} \in \mathbb{R}^{3n_{\mathrm{n}} \times 1}$ and $\boldsymbol {\lambda} \in \mathbb{R}^{n_{\mathrm{c}} \times 1}$ represent the applied nodal forces and Lagrange multipliers, respectively, and $\dot{\bullet}$ denotes the time derivative. Hence, to define a linearly-elastic MB formulation the following steps are sufficient [16]:

• 1. Choose the DOFs $\boldsymbol {q}$ – this choice defines the formulation.

• 2. Define the coordinate mappings $\boldsymbol {r}=\boldsymbol {r} \left ( \boldsymbol {q} \right )$ and $\overline {\boldsymbol {c}}_{\mathrm {f}}=\overline {\boldsymbol {c}}_{\mathrm {f}} \left ( \boldsymbol {q} \right )$.

• 3. Calculate the Jacobians of the coordinate mappings, i.e., $\boldsymbol {L}$ and $\boldsymbol {P}$.

• 4. Calculate the time derivative of $\boldsymbol {L}$, i.e., $\dot{\boldsymbol {L}}$.

• 5. Perform the matrix multiplications to obtain the final EOMs.

These steps were outlined in [16] to derive the conventional inertia-shape-integral/ lumped-mass FFRF with and without modal reduction [9], the nodal-based FFRF with [15] and without [14] modal reduction, the ACF [4, 12] (not to be mixed up with the absolute nodal coordinate formulation (ANCF), see, e.g., [5]), the GCMS [8, 13], and the flexible natural coordinate formulation (FNCF) [10].

The advantage of the FFRF – the formulation implemented in virtually all commercial flexible MB dynamics software packages such as Recurdyn (FunctionBay, Inc.) [2] and Adams (MSC Software Corporation) [7] – is that within the body-fixed moving frame the local flexible coordinates may be easily reduced using well-established modal reduction methods, see, e.g., [1]. Extensions are available to employ modal reduction also with absolute coordinates as DOFs leading to the already mentioned GCMS or FNCF (which is a straightforward extension of GCMS), however, realized at the expense of a nine- or tenfold increase of the flexible modal coordinates, respectively, which is why the FFRF prevailed in the MB community, despite the linear relationship between nodal positions and DOFs associated with formulations based on absolute coordinates, which yields a constant mass matrix and no quadratic velocity “vector,” and the fact that the efficient factorization of the Jacobian leads to an increased performance of GCMS for larger number of boundary nodes [3]. Nevertheless, ACF is popular within the FE community because it is a tailor-made FE formulation for the efficient high-fidelity simulation of systems undergoing large RB motions – the efficiency stems from the fact the Jacobi matrix may be prefactorized once and for all times [4]; a feature that may be also employed for the formulations presented in this paper.

Looking at the EOMs of the ACF [12], we have

$$ \overline {\boldsymbol {M}} \ddot{\boldsymbol {c}} + \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \overline{\boldsymbol {K}} \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} + \boldsymbol {c}_{\mathrm {f}}^{\mathrm {T}} \frac{\partial \boldsymbol {A}_{\mathrm {bd}}^{\mathrm {}}}{\partial \boldsymbol {c}_{\mathrm {}}^{\mathrm {T}}} \overline{\boldsymbol {K}} \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} + \boldsymbol {J}^{\mathrm {T}} \boldsymbol {\lambda} = \boldsymbol {f} ,$$

(9)

subjected to

$$ \boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}} = \boldsymbol {0} ,$$

(10)

where $\boldsymbol {c} \in \mathbb{R}^{3 n_{\mathrm {n}} \times 1}$ denotes the global nodal displacements, $\boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} \in \mathbb{R}^{3 n_{\mathrm {n}} \times 1}$ denotes the flexible part of $\boldsymbol {c}$, and

$$ \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} =\mathrm {{diag}}(\boldsymbol {A},\dots ,\boldsymbol {A}) \in \mathbb{R}^{3 n_{ \mathrm{n}} \times 3n_{\mathrm{n}}} .$$

(11)

Note that no reference constraints are required for the ACF, hence, $\boldsymbol {g} =\boldsymbol {0} \Rightarrow \boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}}= \boldsymbol {0}$.

In comparison to the ACF, the FFRF EOMs read [14]

$$\begin{array}{rl}\left[\begin{array}{ccc}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\mathbf{1}\otimes \mathit{I})& -\mathit{A}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& \mathit{A}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\bar{\mathit{M}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\bar{\mathit{M}}\\ \text{sym.}& & \bar{\mathit{M}}\end{array}\right]\left[\begin{array}{c}\ddot{\mathit{\tau }}\\ \ddot{\mathit{\theta }}\\ {\ddot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]+& \\ \left[\begin{array}{c}\mathit{A}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\bar{\mathit{M}}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ \bar{\mathit{M}}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\end{array}\right]+& \\ \left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ & \mathbf{0}& \mathbf{0}\\ \mathrm{s}\mathrm{y}\mathrm{m}.& & \bar{\mathit{K}}\end{array}\right]\left[\begin{array}{c}\mathit{\tau }\\ \mathit{\theta }\\ {\bar{\mathit{c}}}_{\mathrm{f}}\end{array}\right]+\left[\begin{array}{c}{\mathit{J}}_{\mathit{\tau }}^{\mathrm{T}}\\ {\mathit{J}}_{\mathit{\theta }}^{\mathrm{T}}\\ {\mathit{J}}_{{\bar{\mathit{c}}}_{\mathrm{f}}}^{\mathrm{T}}\end{array}\right]\mathit{\lambda }=\left[\begin{array}{c}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\\ -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\\ {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\mathit{f}& ,\end{array}$$

(12)

subjected to

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{ref}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(13)

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(14)

with the rigid body translation modes

$$\mathbf{1}\otimes \mathit{I}=\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right]\otimes \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{c}\mathit{I}\\ ⋮\\ \mathit{I}\end{array}\right]\in {\mathbb{R}}^{3n_{\mathrm{n}}\times 3},$$

(15)

where ⊗ denotes Kronecker’s product,² and the matrix $\overline {\boldsymbol {G}} \in \mathbb{R}^{3 \times n_{\mathrm {r}}}$ which is implicitly defined by the local angular velocity $\overline {\boldsymbol {\omega}} \in \mathbb{R}^{3 \times 1}$ and the rotational parameters $\boldsymbol {\theta}$ as

$$ \overline {\boldsymbol {\omega}}=\overline {\boldsymbol {G}}\dot{\boldsymbol {\theta}} .$$

(17)

Furthermore,

$$ \widetilde {\overline {\boldsymbol {\omega }}}_{\mathrm {bd}}=\mathrm{diag}(\widetilde{\overline{\boldsymbol {\omega}}},\dots , \widetilde{\overline{\boldsymbol {\omega}}}) \in \mathbb{R}^{3 n_{\mathrm{n}} \times 3 n_{\mathrm{n}}} $$

(18)

denotes a block-diagonal matrix with the skew-symmetric³ local angular velocity matrix on its diagonal. Additional kinematic quantities used in Eq. (12) are explained in more detail in Fig. 1 and Sect. 3.1. Note that the FFRF requires in addition to joint constraints $\boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}} = \boldsymbol {0}$ between different system bodies also reference constraints $\boldsymbol {g}_{\mathrm {{ref}}}^{\mathrm {}} = \boldsymbol {0}$ to eliminate the RB motion from the flexible displacement field and enforce potential orthogonality conditions on the rotation parameters, see also Sect. 3.4.

It should be emphasized that the EOMs structures of the modally-reduced FFRF and ACF, i.e., GCMS, are equal to their nonreduced companions, respectively.

It is clear from Eqs. (9) and (12) that we have highly nonlinear stiffness terms but linear inertia forces when choosing the global total nodal displacements as DOFs, or highly nonlinear inertia terms but linear-elastic forces when decomposing the DOFs into RB motion and local elastic deformation. However, what is more striking – given that [12, 16] showed that the formulations are equivalent – is the fact that the FFRF EOMs involve significantly more nonlinear terms and quantities than the EOMs of the ACF; this large number of operations required in the former method makes computer implementations of the FFRF laborious as well as error-prone,⁴ and introduces more complexity in general, which is why significant ongoing effort is directed towards, e.g., the investigation of the importance of different inertia terms of the FFRF EOMs, see, e.g., [11].

These issues associated with the FFRF, and the fact that the formulations are mathematically equivalent [12, 16], render the ACF an appealing alternative due to the simplistic equation structure, see Eq. (9). However, Eq. (9) does not emphasize the full complexity of the formulation since the ACF DOFs are $\boldsymbol {c}$, and hence

$$\begin{aligned} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} &= \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} (\boldsymbol {c}) , \end{aligned}$$

(20)

$$\begin{aligned} \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} &= \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \left ( \boldsymbol {A}(\boldsymbol {c}) \right ) . \end{aligned}$$

(21)

This contribution, therefore, employs absolute flexible DOFs in combination with explicit RB DOFs to obtain an improved ACF (and GCMS), which not only eliminates the necessity to calculate the RB motion from the global total nodal displacement field⁵ to obtain $\boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} = \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} (\boldsymbol {c})$ and $\boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} = \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \left ( \boldsymbol {A}(\boldsymbol {c}) \right )$ during time integration but also reduces the non-linearity present in the EOMs.

3 Derivation of the proposed formulations

3.1 Kinematics

Let us consider a representative FE-discretized body of a MB system with $n_{\mathrm {n}}$ nodes and an attached moving frame $\overline {\mathcal{F}}$; the origin of $\overline {\mathcal{F}}$ is translated by $\boldsymbol {\tau} \in \mathbb{R}^{3 \times 1}$ w.r.t. the origin of the global inertial frame ℱ and their orientations are related by the rotation matrix $\boldsymbol {A} \in \mathbb{R}^{3 \times 3}$, see Fig. 1. The current position of the FE nodes is given by

$$ \boldsymbol {r} =\boldsymbol {x}_{\mathrm {{ref}}}^{\mathrm {}} + \boldsymbol {c} ,$$

(22)

where $\boldsymbol {x}_{\mathrm {{ref}}}^{\mathrm {}} = \mathrm {{const}.}$ is the reference position of all FE nodes w.r.t. the global frame. The global nodal displacements $\boldsymbol {c}$ account for rigid body translation $\boldsymbol {c}_{\mathrm {t}}^{\mathrm {}} \in \mathbb{R}^{3 n_{\mathrm {n}} \times 1}$, rigid body rotation $\boldsymbol {c}_{\mathrm {r}}^{\mathrm {}} \in \mathbb{R}^{3 n_{\mathrm {n}} \times 1}$, and flexible deformation $\boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} \in \mathbb{R}^{3 n_{\mathrm {n}} \times 1}$, i.e.,

$$ \boldsymbol {c}=\boldsymbol {c}_{\mathrm {t}}^{\mathrm {}}+\boldsymbol {c}_{\mathrm {r}}^{\mathrm {}}+\boldsymbol {c}_{\mathrm {f}}^{\mathrm {}}. $$

(23)

Assuming without loss of generality that the coordinate systems ℱ and $\overline {\mathcal{F}}$ coincide in the reference configuration, i.e.,

$$ \boldsymbol {\tau}_{\mathrm {{ref}}}^{\mathrm {}} =\boldsymbol {0} \quad \text{and} \quad \boldsymbol {A}_{\mathrm {{ref}}}^{\mathrm {}}=\boldsymbol {I} \quad \Rightarrow \quad {\boldsymbol {x}}_{\mathrm {{ref}}}^{(i)}=\overline {\boldsymbol {x}}^{(i)} ,$$

(24)

yields (Fig. 1) [12, 16]

$$ \boldsymbol {r} = \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right ) \boldsymbol {\tau} + \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \boldsymbol {\overline {x}}_{\mathrm {}}^{\mathrm {}} + {\boldsymbol {c}}_{\mathrm{f}} .$$

(25)

3.2 Improved ACF

Equation (25) reveals that the configuration of the flexible body is fully described by the translation of the floating frame, the rotation matrix and the flexible deformation. Hence, these quantities are a suitable choice for the DOFs, i.e.,

$$\mathit{q}=\left[\begin{array}{c}{\mathit{\tau }}_{}^{}\\ {\mathit{a}}_{}^{}\\ {\mathit{c}}_{\mathrm{f}}^{}\end{array}\right],$$

(26)

with $\boldsymbol {a} = \mathrm {{vec}}\left (\boldsymbol {A}_{\mathrm {}}^{\mathrm {}} \right )$, i.e.,

$$\mathit{a}=\left[\begin{array}{c}{A}_{11}\\ A_{21}\\ A_{31}\\ A_{12}\\ A_{22}\\ A_{32}\\ A_{13}\\ A_{23}\\ A_{33}\end{array}\right].$$

(27)

This specific choice leads to a linear mapping between the nodal positions and the DOFs, since

$$\begin{aligned} \boldsymbol {r} &= \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right ) \boldsymbol {\tau} + \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \boldsymbol {\overline {x}}_{\mathrm {}}^{\mathrm {}} + {\boldsymbol {c}}_{\mathrm{f}} \end{aligned}$$

(28)

$$=\left[\begin{array}{ccc}(\mathbf{1}\otimes \mathit{I})& (\bar{\mathit{X}}\otimes \mathit{I})& {\mathit{I}}_{\mathrm{bd}}^{}\end{array}\right]\mathit{q}$$

(29)

$$\begin{aligned} &= \boldsymbol {L} \boldsymbol {q} , \end{aligned}$$

(30)

where⁶

$$\bar{\mathit{X}}=\left[\begin{array}{c}{\bar{\mathit{x}}}^{{(1)}^{\mathrm{T}}}\\ ⋮\\ {\bar{\mathit{x}}}^{{(n_{\mathrm{n}})}^{\mathrm{T}}}\end{array}\right]\in {\mathbb{R}}^{n_{\mathrm{n}}\times 3}$$

(32)

and

$$ \boldsymbol {I}_{\mathrm {{bd}}}^{\mathrm {}} =\mathrm {{diag}}(\boldsymbol {I},\dots ,\boldsymbol {I}) \in \mathbb{R}^{3 n_{ \mathrm{n}} \times 3n_{\mathrm{n}}} .$$

(33)

Hence, the coordinate Jacobian $\boldsymbol {L}_{\mathrm {}}^{\mathrm {}}$ is constant, and furthermore

$$ \dot{\boldsymbol {L}} = \boldsymbol {0}.$$

(34)

The inertia forces take a simple form due to the specific choice of the DOFs as in the conventional ACF. In addition, due to the employment of explicit RB DOFs, the coordinate mapping between local flexible nodal coordinates and the DOFs (see Eq. (5)) is simpler, i.e.,

$$\begin{aligned} \overline {\boldsymbol {c}}_{\mathrm {f}} &=\boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} \end{aligned}$$

(35)

$$\begin{aligned} &= \left ( \boldsymbol {C}_{\mathrm {f}}^{\mathrm {}} \otimes \boldsymbol {I} \right ) \boldsymbol {B} \boldsymbol {a} , \end{aligned}$$

(36)

where, again,

$${\mathit{C}}_{\mathrm{f}}^{}=\left[\begin{array}{c}{\mathit{c}}_{\mathrm{f}}^{{(1)}^{\mathrm{T}}}\\ ⋮\\ {\mathit{c}}_{\mathrm{f}}^{{(n_{\mathrm{n}})}^{\mathrm{T}}}\end{array}\right]\in {\mathbb{R}}^{n_{\mathrm{n}}\times 3},$$

(37)

and $\boldsymbol {B}$ is a constant, symmetric, and orthogonal permutation matrix such that

$$ \mathrm {{vec}}(\boldsymbol {A}_{\mathrm {}}^{\mathrm {T}}) = \boldsymbol {B} \mathrm {{vec}}(\boldsymbol {A}_{\mathrm {}}^{\mathrm {}}) ,$$

(38)

i.e.,

$$ \boldsymbol {B}= \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} .$$

(39)

Hence, see Eqs. (35) to (36),

$$\begin{aligned} \boldsymbol {P} &= \begin{bmatrix} \dfrac{\partial \overline {\boldsymbol {c}}_{\mathrm {f}} }{\partial \boldsymbol {\tau}} & \dfrac{\partial \overline {\boldsymbol {c}}_{\mathrm {f}} }{\partial \boldsymbol {a}_{\mathrm {}}^{\mathrm {}}} & \dfrac{\partial \overline {\boldsymbol {c}}_{\mathrm {f}} }{\partial \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}}} \end{bmatrix} \end{aligned}$$

(40)

$$\begin{aligned} &= \begin{bmatrix} \boldsymbol {0} & \left ( \boldsymbol {C}_{\mathrm {f}}^{\mathrm {}} \otimes \boldsymbol {I} \right ) \boldsymbol {B} & \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \end{bmatrix}. \end{aligned}$$

(41)

Finally, according to Eq. (5) with Eqs. (26), (29), (30), (34), (35), (36), and (41), we have

$$\begin{array}{r}\left[\begin{array}{ccc}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\mathbf{1}\otimes \mathit{I})& {(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathit{X}}\otimes \mathit{I})& {(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}\\ & {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathit{X}}\otimes \mathit{I})& {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}\\ \mathrm{s}\mathrm{y}\mathrm{m}.& & \bar{\mathit{M}}\end{array}\right]\left[\begin{array}{c}\ddot{\mathit{\tau }}\\ \ddot{\mathit{a}}\\ {\ddot{\mathit{c}}}_{\mathrm{f}}\end{array}\right]+\\ \left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ & {\mathit{B}}_{}^{\mathrm{T}}{({\mathit{C}}_{\mathrm{f}}^{}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{K}}({\mathit{C}}_{\mathrm{f}}^{}\otimes \mathit{I})\mathit{B}& \mathbf{0}\\ \mathrm{s}\mathrm{y}\mathrm{m}.& & {\mathit{A}}_{\mathrm{bd}}^{}\bar{\mathit{K}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{c}\mathit{\tau }\\ \mathit{a}\\ {\mathit{c}}_{\mathrm{f}}^{}\end{array}\right]+\left[\begin{array}{c}{\mathit{J}}_{\mathit{\tau }}^{\mathrm{T}}\\ {\mathit{J}}_{\mathit{a}}^{\mathrm{T}}\\ {\mathit{J}}_{{\mathit{c}}_{\mathrm{f}}}^{\mathrm{T}}\end{array}\right]\mathit{\lambda }=\\ \left[\begin{array}{c}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\\ {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\\ {\mathit{I}}_{\mathrm{bd}}^{}\end{array}\right]\mathit{f},\end{array}$$

(42)

subjected to

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{ref}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(43)

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(44)

see Sect. 3.4 for the treatment of reference constraints.

Note that all the submatrices of the generalized mass matrix in Eq. (42) are constant and can be precomputed from the FE mass matrix $\overline {\boldsymbol {M}}$ and the FE reference nodal coordinates $\overline {\boldsymbol {x}}$.

3.3 Improved GCMS

It is usually required to reduce the number of flexible DOFs due to limited computation resources or efficiency reasons. However, the fact that global flexible displacements are employed as DOFs, see Eq. (26), precludes “standard” structural dynamics modal reduction techniques, see [1], inapplicable. However, it is known that generalizing these “standard” reduction modes enables their use with absolute coordinates, since the flexible so-called generalized component modes can represent “standard” deformation modes in any possible orientation of the body, see [13] for further explanations and illustrated generalized component modes.

“Standard” reduction methods approximate the local flexible deformation by a linear combination of $n_{\mathrm {m}}$ component modes, such as vibration eigenmodes, static modes, etc., i.e.,

$$ \overline {\boldsymbol {c}}_{\mathrm {f}} \approx \sum _{m=1}^{n_{\mathrm {m}}} \overline {\boldsymbol {\psi}}_{m} {\zeta}_{m}=\overline {\boldsymbol {\Psi}} \boldsymbol {\zeta} \quad \text{with} \quad n_{ \mathrm {m}}=\mathrm{dim}(\boldsymbol {\zeta}) \ll \mathrm{dim}(\overline {\boldsymbol {c}}_{\mathrm {f}} )=3 n_{\mathrm {n}} ,$$

(45)

where $\overline {\boldsymbol {\Psi}} \in \mathbb{R}^{3n_{\mathrm {n}} \times n_{\mathrm {m}}}$ contains column-wise the modes included in the reduction basis, i.e., a low-dimensional solution subspace, and $\boldsymbol {\zeta} \in \mathbb{R}^{n_{\mathrm {m}} \times 1}$ are the associated modal coordinates.⁷

The GCMS framework generalizes any type of modes included in the reduction basis as follows [16], see also Eqs. (31) and (45):

$$\begin{aligned} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} &= \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \overline {\boldsymbol {c}}_{\mathrm {f}} \end{aligned}$$

(46)

$$\begin{aligned} &= \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {}} \overline {\boldsymbol {\Psi}} \boldsymbol {\zeta} \end{aligned}$$

(47)

$$\begin{aligned} &= \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \left ( \boldsymbol {\zeta} \otimes \boldsymbol {a} \right ) , \end{aligned}$$

(48)

where

$$\bar{\mathbf{\Upsilon }}=\left[\begin{array}{ccc}{\bar{\mathit{\psi }}}_1^{{(1)}^{\mathrm{T}}}& \dots & {\bar{\mathit{\psi }}}_{n_{\mathrm{m}}}^{{(1)}^{\mathrm{T}}}\\ ⋮& \ddots & ⋮\\ {\bar{\mathit{\psi }}}_1^{{(n_{\mathrm{n}})}^{\mathrm{T}}}& \dots & {\bar{\mathit{\psi }}}_{n_{\mathrm{m}}}^{{(n_{\mathrm{n}})}^{\mathrm{T}}}\end{array}\right]\in {\mathbb{R}}^{n_{\mathrm{n}}\times 3n_{\mathrm{m}}}$$

(49)

simply contains all modes included in the reduction basis arranged according to Eq. (4). Hence, it follows from Eqs. (35) and (48) that

$$ \overline {\boldsymbol {c}}_{\mathrm {f}} = \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \left ( \boldsymbol {\zeta} \otimes \boldsymbol {a} \right ) .$$

(50)

Furthermore, Eqs. (37), (45), and (49) imply that

$$ \overline {\boldsymbol {C}}_{\mathrm {f}} = \overline {\boldsymbol {\Upsilon}} \left ( \boldsymbol {\zeta} \otimes \boldsymbol {I} \right ) ,$$

(51)

and Eq. (37) gives

$$ {\boldsymbol {C}}_{\mathrm {f}} = \overline {\boldsymbol {C}}_{\mathrm {f}} \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}} .$$

(52)

Hence, combining the previous two equations,

$$ {\boldsymbol {C}}_{\mathrm {f}} = \overline {\boldsymbol {\Upsilon}} \left ( \boldsymbol {\zeta} \otimes \boldsymbol {I} \right ) \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}} ,$$

(53)

and furthermore,⁸

$$\begin{aligned} {\boldsymbol {C}}_{\mathrm {f}} \otimes \boldsymbol {I} &= \left [ \overline {\boldsymbol {\Upsilon}} \left ( \boldsymbol {\zeta} \otimes \boldsymbol {I} \right ) \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}}\right ] \otimes \boldsymbol {I} \end{aligned}$$

(55)

$$\begin{aligned} &= \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \left ( \boldsymbol {\zeta} \otimes \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}} \otimes \boldsymbol {I} \right ) . \end{aligned}$$

(56)

Therefore, from Eqs. (36) and (56) we also have

$$ \overline {\boldsymbol {c}}_{\mathrm {f}} = \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \left ( \boldsymbol {\zeta} \otimes \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}} \otimes \boldsymbol {I} \right ) \boldsymbol {B} \boldsymbol {a} ,$$

(57)

where we would like to introduce the term

$$ \boldsymbol {\Xi}= \left ( \boldsymbol {\zeta} \otimes \boldsymbol {A}_{\mathrm {}}^{\mathrm {T}} \otimes \boldsymbol {I} \right ) \boldsymbol {B} ,$$

(58)

which contains simply the components of the newly introduced flexible GCMS DOFs

$$ \boldsymbol {\xi}= \boldsymbol {\zeta} \otimes \boldsymbol {a} $$

(59)

in a rearranged manner.

In summary, for GCMS (see Eqs. (26), (48), and (59)),

$$\mathit{q}=\left[\begin{array}{c}{\mathit{\tau }}_{}^{}\\ {\mathit{a}}_{}^{}\\ \mathit{\xi }\end{array}\right],$$

(60)

and (see, in addition, Eqs. (28) to (30))

$$\mathit{r}=\left[\begin{array}{ccc}(\mathbf{1}\otimes \mathit{I})& (\bar{\mathit{X}}\otimes \mathit{I})& (\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\end{array}\right]\mathit{q},$$

(61)

as well as (see Eqs. (50) and (57)–(59))

$$\begin{aligned} \overline {\boldsymbol {c}}_{\mathrm {f}} &=\boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\xi} \end{aligned}$$

(62)

$$\begin{aligned} &= \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\Xi} \boldsymbol {a} . \end{aligned}$$

(63)

Following now the same procedure as outlined for ACF in Sect. 3.2, we have

$$\mathit{L}=\left[\begin{array}{ccc}(\mathbf{1}\otimes \mathit{I})& (\bar{\mathit{X}}\otimes \mathit{I})& (\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\end{array}\right]\Rightarrow \dot{\mathit{L}}=\mathbf{0},$$

(64)

and

$$ \boldsymbol {P} = \begin{bmatrix} \boldsymbol {0} & \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\Xi} & \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \end{bmatrix} .$$

(65)

Finally, the reduced EOMs read

$$\begin{array}{rl}\left[\begin{array}{ccc}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\mathbf{1}\otimes \mathit{I})& {(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathit{X}}\otimes \mathit{I})& {(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\\ & {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathit{X}}\otimes \mathit{I})& {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\\ \mathrm{s}\mathrm{y}\mathrm{m}.& & {(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{M}}(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\end{array}\right]\left[\begin{array}{c}\ddot{\mathit{\tau }}\\ \ddot{\mathit{a}}\\ \ddot{\mathit{\xi }}\end{array}\right]+& \\ \left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ & {\mathbf{\Xi }}^{\mathrm{T}}{(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{K}}(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})\mathbf{\Xi }& \mathbf{0}\\ \mathrm{s}\mathrm{y}\mathrm{m}.& & {\hat{\mathit{A}}}_{\mathrm{bd}}^{}{(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})}^{\mathrm{T}}\bar{\mathit{K}}(\bar{\mathbf{\Upsilon }}\otimes \mathit{I}){\hat{\mathit{A}}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{c}\mathit{\tau }\\ \mathit{a}\\ \mathit{\xi }\end{array}\right]+& \\ \left[\begin{array}{c}{\mathit{J}}_{\mathit{\tau }}^{\mathrm{T}}\\ {\mathit{J}}_{\mathit{a}}^{\mathrm{T}}\\ {\mathit{J}}_{\mathit{\xi }}^{\mathrm{T}}\end{array}\right]\mathit{\lambda }=\left[\begin{array}{c}{(\mathbf{1}\otimes \mathit{I})}^{\mathrm{T}}\\ {(\bar{\mathit{X}}\otimes \mathit{I})}^{\mathrm{T}}\\ {(\bar{\mathbf{\Upsilon }}\otimes \mathit{I})}^{\mathrm{T}}\end{array}\right]\mathit{f}& ,\end{array}$$

(66)

subjected to⁹

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{ref}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(67)

$$\begin{aligned} \boldsymbol {g}_{\mathrm {{joint}}}^{\mathrm {}} &= \boldsymbol {0} , \end{aligned}$$

(68)

since

$$ \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \boldsymbol {{A}}_{\mathrm {{bd}}}^{\mathrm {}} = \boldsymbol {\hat{A}}_{\mathrm {{bd}}}^{\mathrm {}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} .$$

(69)

The matrices commute¹⁰, since the GCMS modal matrix consists of blocks that are multiples of the identity matrix $\boldsymbol {I}$.

Note that, as for the unreduced EOMs, all the submatrices of the generalized mass matrix in Eq. (66) are constant and can be precomputed from the FE mass matrix $\overline {\boldsymbol {M}}$, the FE reference nodal coordinates $\overline {\boldsymbol {x}}$, and the reduction modes $\overline {\boldsymbol {\Psi}}$.

3.4 Moving frame position and reference constraints

Positioning the moving frame in the center of mass yields

$$ \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right ) = \boldsymbol {0} ,$$

(70)

since [15]

$$ \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \overline {\boldsymbol {x}} =m \overline {\boldsymbol {\chi}}_{\mathrm {u}} ,$$

(71)

where $\overline {\boldsymbol {\chi}}_{\mathrm {u}}$ is the position of the center of mass of the undeformed body w.r.t. the moving frame and $m$ is the total mass.

The linearized Tisserand reference conditions may be written directly with the nodal-based quantities as¹¹ [15]

$$\begin{aligned} \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \overline {\boldsymbol {c}}_{\mathrm {f}} &= \boldsymbol {0} , \end{aligned}$$

(73)

$$\begin{aligned} \widetilde {\overline {\boldsymbol {x}}}^{\mathrm {T}} \overline {\boldsymbol {M}} \overline {\boldsymbol {c}}_{\mathrm {f}} &= \boldsymbol {0} , \end{aligned}$$

(74)

which may be written in terms of ACF DOFs as

$$ \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} {\boldsymbol {c}}_{ \mathrm {f}} = \boldsymbol {0} ,$$

(75)

since the block-diagonal rotation matrix commutes with the FE mass matrix and the rigid body translation modes, and

$$ \widetilde {\overline {\boldsymbol {x}}}^{\mathrm {T}} \overline {\boldsymbol {M}} \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \boldsymbol {c}_{\mathrm {f}}^{\mathrm {}} = \widetilde {\overline {\boldsymbol {x}}}^{\mathrm {T}} \overline {\boldsymbol {M}} \left ( \boldsymbol {C}_{\mathrm {f}}^{\mathrm {}} \otimes \boldsymbol {I} \right ) \boldsymbol {B} \boldsymbol {a} = \boldsymbol {0} ,$$

(76)

see Eqs. (35) to (36).

Likewise, the linearized Tisserand reference conditions may be written in terms of GCMS DOFs as

$$ \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\xi} = \boldsymbol {0} ,$$

(77)

see Eq. (48) as well as Eq. (59), and

$$ \widetilde {\overline {\boldsymbol {x}}}^{\mathrm {T}} \overline {\boldsymbol {M}} \boldsymbol {A}_{\mathrm {{bd}}}^{\mathrm {T}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\xi} = \widetilde {\overline {\boldsymbol {x}}}^{\mathrm {T}} \overline {\boldsymbol {M}} \left (\overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \boldsymbol {\Xi} \boldsymbol {a} = \boldsymbol {0} ,$$

(78)

see Eqs. (62) to (63).

In addition, six (due to symmetry) orthogonality conditions of the rotation matrix $\boldsymbol {A}= \begin{bmatrix} \boldsymbol {a}_{1} & \boldsymbol {a}_{2} & \boldsymbol {a}_{3} \end{bmatrix}$, i.e.,

$$ \boldsymbol {a}_{i}^{\mathrm {T}} \boldsymbol {a}_{j} - \delta _{\mathit{ij}} = 0 \quad \forall \; i ,j \in \left \{ 1 ,2 ,3\right \} \; \vert \; i \leq j ,$$

(79)

where $\delta _{\mathit{ij}}$ denotes Kronecker’s delta, are to be enforced to obtain a proper set of reference conditions.

Hence, the improved ACF proposed in this paper reads

and its reduced version, i.e., the improved GCMS

with the translational mass matrix

$$ m \boldsymbol {I} = \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right ) ,$$

(90)

the resultant force vector

$$ \boldsymbol {f}_{\mathrm {{res}}}^{\mathrm {}} = \left ( \boldsymbol {1} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \boldsymbol {f} ,$$

(91)

the inertia tensor projected into the space of $\boldsymbol {a}$, i.e.,

$$ \mathrm {{proj}}_{\boldsymbol {a}} \! \left ( \boldsymbol {\Theta} \right ) = \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right ) ,$$

(92)

the resultant moment (including the moment due to nodal accelerations) projected into the space of $\boldsymbol {a}$, i.e.,

$$\begin{aligned} \mathrm {{proj}}_{\boldsymbol {a}}^{\ast}\! \left ( \boldsymbol {m}_{\mathrm {{res}}}^{\mathrm {}} \right )&= \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \left [\boldsymbol {f} - \overline {\boldsymbol {M}} \ddot{\boldsymbol {c}}_{\mathrm {f}} \right ] \end{aligned}$$

(93)

$$\begin{aligned} &= \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \left [\boldsymbol {f} - \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) \ddot{\boldsymbol {\xi}} \right ], \end{aligned}$$

(94)

and the reduced flexible GCMS system matrices and applied nodal forces, i.e.,

$$\begin{aligned} \boldsymbol {\hat{M}} &= \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right )^{ \mathrm {T}} \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) , \end{aligned}$$

(95)

$$\begin{aligned} \boldsymbol {\hat{K}} &= \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right )^{ \mathrm {T}} \overline {\boldsymbol {K}} \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right ) , \end{aligned}$$

(96)

$$\begin{aligned} \boldsymbol {\hat{f}}^{\ast} &= \left ( \overline {\boldsymbol {\Upsilon}} \otimes \boldsymbol {I} \right )^{\mathrm {T}} \boldsymbol {f}_{\mathrm {}}^{\mathrm {\ast}} , \end{aligned}$$

(97)

with the modified nodal force due to rotational acceleration, i.e.,

$$ \boldsymbol {f}_{\mathrm {}}^{\mathrm {\ast}} = \boldsymbol {f} - \overline {\boldsymbol {M}} \left ( \overline {\boldsymbol {X}} \otimes \boldsymbol {I} \right ) \ddot{\boldsymbol {a}} .$$

(98)

Note that it is hypothesized that the additional force contributions in Eqs. (93) to (94) and Eq. (98), as well as the stiffness matrices in Eqs. (81) and (86) should vanish since the effect of the flexibility on a pure rigid body rotation, and vice versa, must be null.

4 Conclusions

This contribution proposes an improved absolute coordinate formulation and generalized component mode synthesis based on explicit rigid body coordinates, which (i) reduces the nonlinearity in the equations of motion compared to their standard versions and (ii) eliminates the necessity to calculate the rigid body motion from the global total nodal displacement field to obtain the flexible part of the degrees of freedom and the rotation matrix. This, however, entails the necessity to enforce reference conditions, i.e., the orthogonality the of rotation matrix and the uniqueness of deformation field (e.g., linearized Tisserand), as in the floating frame of reference formulation. Reference constraints are enforced with existing “infrastructure” in multibody codes, i.e., via Lagrange multipliers.

The proposed equations of motion feature a constant mass matrix, no quadratic velocity “vector”, a corotated stiffness matrix in the flexible part, and a “small” nonlinear stiffness matrix in the rigid body rotation part, i.e., a lower order nonlinearity compared to the standard absolute coordinate formulations and less nonlinear terms compared to the floating frame of reference formulation.

Attaching the moving reference frame to the center of mass of the underlying rigid body and employing linearized Tisserand and rotation matrix constraints eliminates coupling terms within the mass matrix and yields implementation-friendly equations of motion to analyze the dynamics of linear-elastic flexible multibody systems.

Future research shall be directed to numerical experiments – analyzing a variety of benchmark problems in order to draw meaningful conclusions on the evaluation of the efficiency of the formulations that fit within the unified framework shown in Eq. (5), i.e., the floating frame of reference formulation, absolute coordinate formulation, generalized component mode synthesis, flexible natural coordinate formulation, and the formulations presented in this paper.