Abstract
A new method, which is an extension of a finite-element formulation, introduces generalized strains related to nodal coordinates by implicit equations, which can be treated as constraints. This formulation allows a larger freedom in developing elements, so it eases the building of elements with a higher accuracy. In many cases, this enables modelling flexible multibody systems with fewer elements and fewer degrees of freedom for a given accuracy or using more accurate models. Because the systems are modelled with coordinates and constraints, all familiar analysis techniques can be applied, such as simulation, calculation of static solutions, linearization and an input–output description. The method is tested for planar and spatial beam elements based on assumed strains. Some examples of large static deflection and dynamics are presented, which show the advantage over some existing element formulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last decades, the modelling of flexible bodies in multibody dynamic systems has gone far, as shown in books [1–4]. Still, the need for more efficient models remains, especially in the design stage in which many models have to be analysed during optimizations. A higher efficiency can be obtained if models with fewer degrees of freedom keeping the same accuracy will be developed. Moreover, an increased ease of setting up models and introducing new modelling elements is desirable. In this article, we propose a new way of modelling flexible multibody systems and formulating the equations of motion to achieve these goals.
This study starts from the finite element approach developed by van der Werff and Jonker [5–7]. In this approach, a finite number of coordinates that describe the state of deformation of an element, called the generalized strains, are defined as explicit functions of the nodal coordinates of the element. The generalized strains are invariant under rigid-body motions and can therefore be considered relative coordinates. They can also be used as relative coordinates in the description of joints as special elements, whereas rigid bodies are located at the nodal points. The elements can be made rigid by giving the generalized strains fixed values as constraints. Kinematic transfer functions describe the relations between all coordinates and the degrees of freedom of a system and similar relations between their time derivatives, which are also called velocity transformation matrices. The equations of motion are formulated as a minimal system in the degrees of freedom.
The existing beam element [8, 9] is quite satisfactory, but to get accurate results, still a fairly large number of elements are needed. A shortcoming is that the order of convergence is two instead of four as could be expected for a cubic interpolation of lateral displacements. Especially for problems involving torsion, the convergence is slow, and many elements are needed to model one physical beam. An improvement has recently been proposed [10], which fits within the original framework. It is difficult to extend the approach in its present form to elements with a higher accuracy.
Here we propose an extension of the original approach, in which generalized strains are defined implicitly, that is, the relations between the generalized strains and the nodal coordinates are given by implicit functions that are set equal to zero. The explicit definition is a special case of this more general approach, so existing elements can still be used. The implicit relations can be seen as constraints, which brings the presented approach within the realm of most existing multibody formalisms. Constraints that do not contain generalized strains can be defined, and there can be more generalized strains than constraints for an element, so internal degrees of freedom unrelated to nodal coordinates can be used.
For modelling flexible beam elements, we follow an assumed strain approach, where the generalized strains represent assumed strain distributions. We obtain the implicit relations with the nodal coordinates by integrating the position gradients over the length of the beam. In the classical assumed-strain approach, the relations are inverted to get explicit expressions in terms of the nodal coordinates [11–15], but we do not need this here. By adding more generalized strains with their strain distributions, elements of a high-order accuracy can be easily derived.
We present examples with a planar beam element with the usual linearly varying curvature in static large-deflection bending and in a dynamic problem of a pendulum with an extremely small flexural rigidity. We use a spatial curved beam with a more accurate description for the torsional deformation in static and dynamic high-deflection cases.
2 An extended theory with generalized strains
In this section, we explain an extended theory involving generalized strains for the description of flexible multibody systems and show that it leads to equations having the structure of differential-algebraic equations in a familiar form, so the development of solution methods does not introduce new difficulties. We show some specific solution techniques.
2.1 Implicit relations for generalized strains
In a finite element description of a mechanical system, there are nodes whose kinematic configuration is given by nodal coordinates, \(\boldsymbol{x}^{p}\) for a node \(p\), and possibly some parameters. The nodal coordinates can be position coordinates, orientation coordinates and other coordinates. Several types of nodes can be defined with different kinds of nodal coordinates. Furthermore, there are elements that are essentially finite sequences of nodes and may have internal coordinates that describe their configuration together with the nodal coordinates of their nodes. The properties of elements are determined by their type and their parameters. A way to characterize the state of deformation is to define generalized strains \(\boldsymbol{\varepsilon}^{e}\) of an element \(e\) as explicit functions of the element nodal coordinates \(\boldsymbol{x}^{e}\), which are the coordinates of the nodes belonging to the element, as
where \(\boldsymbol{D}^{e}\) is the element deformation function. The deformation function is invariant under rigid-body motions of the nodes, so subjecting a deformed element to a rigid-body motion does not change the generalized strains.
Instead of defining the generalized strains of an element as explicit functions of the nodal coordinates, these relations can be maintained in an implicit form as
The functions \(\boldsymbol{C}^{e}\) are called constraint functions. Under rigid-body motion, they no longer need to be invariant, but they must define equivalent relations. The explicit definition is a special case of this formulation with
One advantage of this modification of the formulation is that it may sometimes be easier to keep the relations in an implicit form instead of performing extensive manipulations of the equations to rewrite them, exactly or approximately, in an explicit form. Another advantage is that the number of generalized element strains no longer needs to be equal to the number of constraint functions. There can be additional generalized strains, so internal deformations of elements can be described that are not coupled to nodal displacements. An example of these is fixed-interface vibration modes in the Craig–Bampton component mode synthesis method [16]. In many cases, the number of constraint functions is equal to the dimension of the element nodal coordinate vector minus the number of rigid-body modes of the element. More constraint functions can be defined if there are alternative definitions of generalized deformations, some of which have to be chosen to define the element properties, and others are dependent and not needed to define the element properties; a way to handle this case efficiently will be explained in the next subsection. The constraint on the four Euler parameters \(\boldsymbol{\lambda}^{p}= (\lambda _{0}^{p},\lambda _{1}^{p},\lambda _{2}^{p}, \lambda _{3}^{p})^{\mathrm{T}}\), used to describe a spatial rotation, can be directly written in the form \(C^{p}(\boldsymbol{\lambda}^{p}) = \boldsymbol{\lambda}^{p\mathrm{T}}\boldsymbol{\lambda}^{p}-1 = 0\) without having to introduce a generalized strain as was done in [6].
The constraint relations for the elements can be assembled in a global vector constraint equation as a direct sum as
where \(\boldsymbol{x}\) contains the nodal coordinates of the system, and \(\boldsymbol{\varepsilon}\) are the system generalized strains obtained as a direct sum of the element generalized strains.
2.2 Partitioning of the coordinates and the generalized strains
The coordinates \(\boldsymbol{x}\) can be partitioned, first, in prescribed ones \(\boldsymbol{x}^{\mathrm{p}}\) and free ones \(\boldsymbol{x}^{\mathrm{f}}\). The prescribed coordinates can be partitioned into fixed ones \(\boldsymbol{x}^{\mathrm{o}}\) and ones with a prescribed motion, \(\boldsymbol{x}^{\mathrm{m}}\). The free coordinates can be partitioned into degrees of freedom \(\boldsymbol{x}^{\mathrm{d}}\) and dependent coordinates \(\boldsymbol{x}^{\mathrm{c}}\). A special form of dependent coordinates are coordinates having the same values as some other coordinates. The generalized strains \(\boldsymbol{\varepsilon}\) can be partitioned in a similar way into prescribed ones \(\boldsymbol{\varepsilon}^{\mathrm{p}}\) and free ones \(\boldsymbol{\varepsilon}^{ \mathrm{f}}\), where the prescribed ones are subdivided into generalized strains with a fixed value \(\boldsymbol{\varepsilon}^{\mathrm{o}}\) and generalized strains with a prescribed motion, \(\boldsymbol{\varepsilon}^{\mathrm{m}}\). The free generalized strains can be subdivided into degrees of freedom \(\boldsymbol{\varepsilon}^{\mathrm{d}}\) and dependent generalized strains \(\boldsymbol{\varepsilon}^{\mathrm{c}}\). The system degrees of freedom are collected in a vector
Another distinction is in the coordinates and generalized strains that contribute to the description of the system or are of interest to the solution of the problem at hand and coordinates that are present, but whose values and associated forces are not needed, which will be called insignificant. The qualification of a coordinate or generalized strain as insignificant is not a property of the system, but a modelling decision depending on the problem at hand. A common case is the use of spatial elements in a planar analysis, so all out-of-plane coordinates can be ignored and are insignificant. These insignificant coordinates and generalized strains come from the ones with fixed values and the dependent ones. The generalized strain of the Euler parameter element (if present at all) can be seen as another instance, as can alternative definitions of generalized strains not actually used. The insignificant coordinates can only appear as parameters in the model.
2.3 Kinematic transfer functions
In a position analysis, the dependent nodal coordinates and generalized strains are determined at a given time for given values of the degrees of freedom. For this problem to be locally uniquely solvable, the number of dependent variables must be equal to the number of constraint equations in Eq. (4) and the constraint equations must be independent. From the given values of \(\boldsymbol{x}^{\mathrm{p}}\), \(\boldsymbol{x}^{\mathrm{d}}\), \(\boldsymbol{\varepsilon}^{\mathrm{p}}\) and \(\boldsymbol{\varepsilon}^{\mathrm{d}}\), and the estimated values of \(\boldsymbol{x}^{\mathrm{c}}\) and \(\boldsymbol{\varepsilon}^{\mathrm{c}}\), corrected values for the dependent variables can be obtained from a step in a Newton–Raphson iteration,
and the dependent variables are updated by adding the corrections \(\Delta \boldsymbol{x}^{\mathrm{c}}\) and \(\Delta \boldsymbol{\varepsilon}^{\mathrm{c}}\) to them. A subscript comma followed by variables indicates partial derivatives with respect to these variables, where the order of the derivative is equal to the number of subscript variables after the comma. The system is solvable if the matrix of coefficients is square and regular, which means that the sum of the number of dependent nodal coordinates and the number of dependent generalized strains must be equal to the number of constraints and the constraints must be independent. The iteration is repeated until the corrections become sufficiently small. The free variables can be formally written as functions of the degrees of freedom and the time \(t\) as
where the functions \(\boldsymbol{X}\) and \(\boldsymbol{E}\) are called the zeroth-order kinematic transfer functions. The parts related to the dependent variables are denoted by \(\boldsymbol{X}^{\mathrm{c}}\) and \(\boldsymbol{E}^{\mathrm{c}}\). The relations for the degrees of freedom are trivial. Successive derivatives of these functions can be obtained by substituting the kinematic transfer functions into the constraint equations (4) and taking partial derivatives with respect to the degrees of freedom and then solving the linear system for the derivatives of the dependent variables. For the first-order kinematic transfer functions, we obtain
Higher-order derivatives can be obtained in a similar way. These derivatives are useful in several calculations, such as in the derivation of linearized equations of motion or in cases that there are few degrees of freedom and many more dependent coordinates. In addition, the higher-order kinematic transfer functions can be useful for a purely kinematic analysis.
A velocity analysis determines the rates of the dependent variables for a given time and configuration when the rates of the degrees of freedom are known. The rates of the prescribed nodal coordinates and generalized strains are obtained by taking the time derivatives of the functions that prescribe them. The other unknown rates can now directly be obtained by taking the time derivative of the constraint equations, which yields the system of linear equations
where the dot over a variable denotes the time derivative. This system of equations can be readily solved for the time derivatives of the dependent nodal coordinates and dependent generalized strains.
Another time derivative of the constraint equations yields a relation between the accelerations of the dependent variables and the accelerations of the degrees of freedom together with the velocities as
This equation can be used to express the dependent accelerations as linear functions of the independent accelerations, which are not yet known and follow from the equations of motion discussed in the following subsection. Formally, the velocities and accelerations can be written as
2.4 Equations of motion
Two sets of dual quantities are defined for each element \(e\): generalized stresses \(\boldsymbol{\sigma}^{e}\), which are the energetically dual quantities to the generalized strains, and Lagrangian multipliers \(\boldsymbol{\mu}^{e}\) to enforce the constraints (2), which are the energetically dual quantities of the constraint functions. The inner product of the generalized stresses and variations of the generalized strains represents the negative virtual work of the internal forces in the element, \(\updelta W_{\mathrm{int}}^{e} = - \boldsymbol{\sigma}^{e\mathrm{T}} \updelta \boldsymbol{\varepsilon}^{e}\), where a prefixed \(\updelta \) denotes a virtual variation. If these strains are not prescribed either as constant values or as functions of the time, then the associated generalized stresses are given by constitutive relations, which in many cases are assumed to be linear, so they can be specified by a stiffness matrix \(\boldsymbol{S}^{e}\), a damping matrix \(\boldsymbol{S}_{\mathrm{d}}^{e}\) and an initial stress (pre-stress) \(\boldsymbol{\sigma}_{\mathrm{i}}^{e}\) as
More complicated constitutive relations could be introduced if needed. For prescribed generalized strains, the corresponding generalized stresses are reactions, denoted by \(\boldsymbol{\sigma}_{0}^{e}\), which have no direct influence on the dynamics. In addition, applied stresses can come from gravity, depending on the way mass is modelled. The contribution to the virtual work can be written as \(-\updelta \boldsymbol{\varepsilon}^{e\mathrm{T}}(\boldsymbol{\sigma}^{e} + \boldsymbol{\sigma}_{0}^{e})\). The dynamic properties are described by a symmetric positive semidefinite mass matrix \(\boldsymbol{M}^{e}(\boldsymbol{x}^{e},\boldsymbol{\varepsilon}^{e})\) and velocity-dependent inertia terms \(\boldsymbol{h}^{e}(\dot{\boldsymbol{x}}^{e},\dot{\boldsymbol{\varepsilon}}^{e},\boldsymbol{x}^{e}, \boldsymbol{\varepsilon}^{e})\), so the virtual work of the inertia force of the element written in a partitioned form is given by
For tube elements with a prescribed mass flow rate [17], the inertia terms due to the fluid flow are included in the vector \(\boldsymbol{h}^{e}\).
Each node \(p\) can have applied forces \(\boldsymbol{f}^{p}\) and also reaction forces \(\boldsymbol{f}_{0}^{p}\) for nodal points with prescribed coordinates, such as supports, which give a contribution of \(\updelta \boldsymbol{x}^{p\mathrm{T}}(\boldsymbol{f}^{p} +\boldsymbol{f}_{0}^{p})\) to the virtual work, so these forces are the energetically dual quantities to the nodal coordinates. For point masses and bodies attached to nodes and parts of element masses directly lumped to nodes and not included in the inertia forces of the element, the virtual work of the inertia forces of each node is
where \(\boldsymbol{M}^{p}\) is the mass matrix of the node, and \(\boldsymbol{h}^{p}\) is the vector of velocity-dependent inertia terms of the node.
A system can be modelled by a number of elements of several kinds, which are connected by sharing nodal coordinates. The equations of motion for the system are obtained from the application of the principle of virtual work. The expression for the virtual work of the system can be written as
where \(e\) ranges over all elements and \(p\) over all nodes.
The equations for the complete system can be obtained by the familiar finite-element assembly process. Collecting terms in the virtual work expression (17) and equating the total virtual work to zero yields, with a change of sign,
Here, \(\boldsymbol{x}\), \(\boldsymbol{\varepsilon}\) and \(\boldsymbol{C}\) are as in Eq. (4), \(\boldsymbol{M}\) is the system mass matrix (which has been partitioned), \(\boldsymbol{h}\) is the system vector of velocity-dependent inertia terms, \(\boldsymbol{\sigma}\) are the applied generalized stresses, \(\boldsymbol{\sigma}_{0}\) are the reaction stresses, \(\boldsymbol{\mu}\) are the Lagrangian multipliers, \(\boldsymbol{f}\) are the applied forces, and \(\boldsymbol{f}_{0}\) are reaction forces. The applied forces dual to the nodal coordinates are partitioned in the same way as these coordinates into \(\boldsymbol{f}^{\mathrm{p}}\) and \(\boldsymbol{f}^{\mathrm{f}}\), but the reaction forces have only a part \(\boldsymbol{f}^{\mathrm{p}}_{0}\). Similarly, the applied generalized stresses are partitioned in the same way as their dual generalized strains into \(\boldsymbol{\sigma}^{\mathrm{p}}\) and \(\boldsymbol{\sigma}^{\mathrm{f}}\), and the reaction stresses have only a part \(\boldsymbol{\sigma}_{0}^{\mathrm{p}}\). The partitioned resulting equations of motion and the corresponding constraint equations following from the virtual work equation (18) can be written as
Here \(\boldsymbol{M}\) and \(\boldsymbol{h}\) are partitioned in the same way as the nodal coordinates and the generalized strains. Equation (23) can be differentiated twice with respect to time to obtain the constraint equations for the accelerations as in Eq. (12), which yields
Equations (20), (22) and (24) can be written as
From the solution of these equations we obtain the accelerations and Lagrangian multipliers. On the other hand, we can eliminate the Lagrangian multipliers with the aid of the first-order kinematic transfer functions. The kinematically admissible virtual variations of the free nodal coordinates and generalized strains are
The kinematically admissible virtual variations of the prescribed nodal coordinates, the prescribed generalized strains and the constraint functions are zero. Substituting these virtual variations and expressions (13) into Eq. (18) yields the equations of motion in the degrees of freedom as
After all accelerations are known, the reaction forces can be obtained from Eq. (19) and the reaction stresses from Eq. (21).
An acceleration of gravity \(\boldsymbol{g}\) can be seen as an acceleration of the reference frame with the same magnitude, but in the opposite direction. This means that all coordinates representing positions can be thought to have an acceleration corresponding to this opposite direction, and all other types of coordinates are unaffected. If all the accelerations of gravity are collected in a vector denoted by \(\boldsymbol{a}_{g}\), then the forces of gravity \(\boldsymbol{f}_{g}\) and the generalized stresses of gravity \(\boldsymbol{\sigma}_{g}\) are given by
Note that also the gravity forces at nodal points that are fixed or have prescribed displacements and the gravity generalized stresses dual to prescribed generalized strains have to be taken into account to obtain the correct reaction forces and stresses.
If we introduce inertia forces \(\boldsymbol{f}_{\mathrm{inertia}}\) and inertia stresses \(\boldsymbol{\sigma}_{\mathrm{inertia}}\) as
then equations (19), (20), (21) and (22) can be written as
For the case of Eq. (3), the equations for the Lagrangian multipliers become
This shows that for the case in with the inertia stresses are zero, the Lagrangian multipliers are equal to the generalized stresses. In the present formulation, the distinction between Lagrangian multipliers and generalized stresses is clearly shown.
2.5 Static solutions
Static solutions can be calculated in a way similar to the procedure described in [18]. For static solutions, the system of equations (20), (22) and (23) becomes
where the unknowns are \(\boldsymbol{x}^{\mathrm{f}}\), \(\boldsymbol{\varepsilon}^{\mathrm{f}}\) and \(\boldsymbol{\mu}\). The Jacobian matrix \(\boldsymbol{J}_{\mathrm{NR}}\) and the residual \(\boldsymbol{r}_{\mathrm{NR}}\) for the Newton–Raphson iteration become
The terms with \(\boldsymbol{\mu}\) in the Jacobian matrix are the traditional geometric stiffness terms, and \(\boldsymbol{S}^{\mathrm{ff}} = \boldsymbol{\sigma}^{\mathrm{f}}_{,\boldsymbol{\varepsilon}^{ \mathrm{f}}}\) is the physical stiffness matrix, which is usually constant. Normally, the forces do not depend on the generalized strains, and the generalized stresses do not depend on the coordinates, so the terms \(-\boldsymbol{f}_{,\boldsymbol{\varepsilon}^{\mathrm{f}}}^{\mathrm{f}}\) and \(\boldsymbol{\sigma}_{,\boldsymbol{x}^{\mathrm{f}}}^{\mathrm{f}}\) are not present. After a converged iteration has yielded a static solution, the reaction forces and reaction generalized stresses are found from Eqs. (19) and (21) as
The compliance can be easily calculated with the same matrix of coefficients from
where \(\Delta \boldsymbol{f}^{\mathrm{f}}\) is chosen as a unit load on a free nodal coordinate, and the compliances for this load are found in \(\Delta \boldsymbol{x}^{\mathrm{f}}\).
2.6 Linearized equations of motion
The linearized equations can be obtained by taking small perturbations of the state variables \(\boldsymbol{x}^{\mathrm{d}}\), \(\boldsymbol{\varepsilon}^{\mathrm{d}}\), \(\dot{\boldsymbol{x}}^{\mathrm{d}}\) and \(\dot{\boldsymbol{\varepsilon}}^{\mathrm{d}}\). If a perturbation is denoted by a prefixed \(\Delta \), then the perturbations of the free nodal coordinates and generalized strains and their first time derivatives are related to perturbations of the degrees of freedom and their time derivatives by the first- and second-order kinematic transfer functions as
as follows from Eqs. (7), (8) and (13). Initially, the case of linearizing the equations of motion around a static equilibrium position is shown, where all accelerations and velocities are zero, and time-dependent prescribed motions are absent. Equations (25) then result in
Again, in most cases, the forces do not depend on the generalized strains, and the generalized stresses do not depend on the nodal coordinates. The system of equations can be solved for the perturbations of the free accelerations and the Lagrangian multipliers, which are expressed as linear functions of the perturbations of the state variables. Restricting to the degrees of freedom gives the linearized state-space description for the case without inputs and outputs; that is, we obtain the system matrix \(\boldsymbol{A}_{\mathrm{ss}}\) defined in the next subsection. Also the perturbations of the dependent coordinates and the perturbations of the Lagrangian multipliers are given as linear functions of the perturbations of the state variables. We now derive the perturbations of the reaction forces and reaction generalized stresses from the linearization of Eqs. (19) and (21) as
The products of matrices on the right-hand side of Eq. (38) need not be determined in full. The perturbations of the degrees of freedom and their time derivatives can be taken one by one, so only a single column of the first-order kinematic transfer functions and the right-hand sides are needed at a time, which may save computer time and memory space.
For the general case, some additional terms have to be included in Eq. (38), which yields
The accelerations are treated as independent variables in the calculation of the partial derivatives. Third-order derivatives of the constraint functions are needed in this general case. The linearized reaction equations are
2.7 Linearized input–output description
A procedure to calculate linearized input–output relations for multibody systems was introduced by Jonker et al. [19]. The input–output relations can be determined in a way similar to the linearization procedure. The most important kinds of input and output are forces, generalized stresses, coordinates, velocities, accelerations, and generalized strains with their first and second time derivatives. The states, denoted by \(\boldsymbol{x}_{\mathrm{ss}}\), are perturbations in the degrees of freedom and their rates,
The inputs are denoted by \(\boldsymbol{u}_{\mathrm{ss}}\), and the outputs by \(\boldsymbol{y}_{\mathrm{ss}}\). The state-space equations can be written as
where \(\boldsymbol{A}_{\mathrm{ss}}\) is the system matrix obtained from the linearized equations, \(\boldsymbol{B}_{\mathrm{ss}}\) is the input matrix, \(\boldsymbol{C}_{\mathrm{ss}}\) is the output matrix, and \(\boldsymbol{D}_{\mathrm{ss}}\) is the throughput matrix. The linearization can be performed at an arbitrary nominal motion, which leads to a linear time-varying system. The equations will be given for the more specific case of linearization about an equilibrium point, which yields a time-invariant system.
Inputs in the applied forces and generalized stresses give the equations for the perturbations of the accelerations, analogous to Eq. (38),
By giving the inputs one by one a unit value and solving this equation we obtain the perturbations of the accelerations and the Lagrangian multipliers. The columns of the input matrix \(\boldsymbol{B}_{\mathrm{ss}}\) have zero values for the upper half, and the lower half contains the calculated perturbations of accelerations of the degrees of freedom.
If prescribed motions are the input, then the position, velocity and acceleration are treated as three separate inputs whose values are related by differentiations with respect to time. In analogy with Eq. (9), the perturbations of the dependent nodal coordinates and generalized strains due to perturbations of the prescribed motions become
In the case of a nominal static solution, similar relations for the velocities are
The perturbations of the accelerations due to perturbations of the prescribed motions can now be calculated from
The perturbations of the dependent quantities \(\Delta \boldsymbol{x}^{\mathrm{c}}\), \(\Delta \boldsymbol{\varepsilon}^{\mathrm{c}}\), \(\Delta \dot{\boldsymbol{x}}^{\mathrm{c}}\) and \(\Delta \dot{\boldsymbol{\varepsilon}}^{\mathrm{c}}\) are expressed in the perturbations of the prescribed motion by means of Eqs. (45) and (46). The prescribed nodal coordinates and generalized strains and their first and second time derivatives are considered as independent inputs for a given time. The upper half of the corresponding column of the input matrix \(\boldsymbol{B}_{\mathrm{ss}}\) is zero, and the lower half is extracted from the accelerations if one input at a time is given a unit value.
The output equations for the state variables \(\Delta \boldsymbol{q}\) and \(\Delta \dot{\boldsymbol{q}}\) can be directly obtained by extracting the relevant state variable; the output equations for the accelerations of the degrees of freedom are found from the corresponding rows of the state matrix and the input matrix. The output equations for the dependent nodal coordinates and generalized strains and their rates can be found with the aid of the transfer functions and from Eqs. (45) and (46). Output equations for stresses dual to free generalized strains are found from constitutive relations such as Eq. (14). The output equation involves some additional calculations if reaction forces or reaction generalized stresses are chosen as outputs. In analogy with Eqs. (39), the perturbations in these reactions are
The perturbations of the dependent quantities and Lagrangian multipliers are obtained from the solution of Eq. (44) or Eq. (47). There could be other kinds of input and output, most of which can be treated in a similar way.
3 Large deflections of beams: some examples
3.1 Planar beam element
We propose a planar beam element with a constant axial strain and linearly varying curvature. The element has two nodes at its ends, indicated by the node numbers \(p\) and \(q\), with as the nodal coordinates the position, given by two coordinates \(x\) and \(y\), and the rotation angle of the cross-section \(\phi \), as shown in Fig. 1, so the element coordinate vector is \(\boldsymbol{x}^{e}=(x^{p}, y^{p}, \phi ^{p}, x^{q}, y^{q}, \phi ^{q})^{ \mathrm{T}}\). The undeformed length of the element is \(l_{0}\), the area of its cross-section is \(A\), the second area moment of its cross-section with respect to the centroid is \(I\), the material properties are Young’s modulus \(E\), the shear modulus \(G\) and the mass density, \(\rho \). The position of a point of the beam is given by the coordinate \(s\) measured from the nodal point \(p\) along the line of centroids in the undeformed straight configuration.
The element has the following strains: a constant axial strain \(\varepsilon =\varepsilon _{1}\) and a linearly varying curvature \(\kappa = \varepsilon _{2}(1-\xi )/l_{0} + \varepsilon _{3}\xi /l_{0}\), where \(\xi = s/l_{0}\) is the normalized coordinate along the centre line of the beam. Therefore the element generalized strains are \(\boldsymbol{\varepsilon}^{e} = (\varepsilon _{1}, \varepsilon _{2}, \varepsilon _{3})^{ \mathrm{T}}\). Furthermore, the shear strain is approximated by \(\gamma = (\varepsilon _{2} - \varepsilon _{3})EI/(l_{0}^{2} GAk) = ( \varepsilon _{2} - \varepsilon _{3})\Phi /12\), where \(k\) is the shear factor, and \(\Phi = 12EI/(l_{0}^{2} GAk)\) is a dimensionless parameter. If the strains remain small, then we can assume a linear constitutive relation, which has the form \(\boldsymbol{\sigma}^{e} = \boldsymbol{S}^{e} \boldsymbol{\varepsilon}^{e}\) with the element stiffness matrix
This relation is most simply derived by considering the strain energy of the beam element, which can be written as \(\boldsymbol{\varepsilon}^{e\mathrm{T}} \boldsymbol{S}^{e} \boldsymbol{\varepsilon}^{e}/2\). A damping matrix as in Eq. (14) proportional to the stiffness matrix, \(\boldsymbol{S}^{e}_{\mathrm{d}} = d \boldsymbol{S}^{e}\), can be added.
The differential equations for the shape of the centre line of the beam are
where a prime denotes the derivative with respect to length parameter \(s\). From the assumed strain distribution we can find relations among the nodal coordinates by integrating these differential equations over the length of the beam, which give the constraint equations formally written as
where \(\phi (\xi ) = \phi ^{p} + (2\xi -\xi ^{2})\varepsilon _{2}/2 + \xi ^{2} \varepsilon _{3}/2\). The integral for the angle is exactly determined, and the integrals for the position are approximated by Simpson’s rule, although they can be evaluated exactly in terms of Fresnel integrals.
For the mass description, a uniform mass per unit of length is assumed to be concentrated at the centre of the cross-sections. The position is obtained from a cubic interpolation based on the positions and orientations of the two nodes, as in [8]. The mass matrix and the velocity-dependent inertia terms are the two-dimensional reductions of the expression for the spatial beam. The moment of inertia of the cross-section is neglected.
As an example, a planar cantilever beam loaded by a large transverse tip force used in previous publications [9, 20] is analysed. The beam has a length of \(L=2\text{ m}\), a square cross-section with sides of 0.1 m and Young’s modulus \(E=207\) GPa. The force is \(3EI/L^{2}\), so the deflection according to linear beam theory would be equal to the length of the beam. The generalized strains of the elements are chosen as degrees of freedom. Figure 2 shows the final configuration and the decrease of the error with an increased number of elements. Initially, the order of convergence is four, but for larger numbers of elements used, the order of convergence drops to two. This drop can be explained to result from the low-order approximation of the axial strain and the shear deformation: by artificially increasing the normal stiffness \(EA\) and shear stiffness \(GA\), the order of convergence is four over a larger range. For the standard beam element, the order of convergence is two over the whole range of meshes [9]. For a small number of elements, the present element gives more accurate results than the element in [20], which is based on the absolute nodal coordinate formulation (ANCF). However, the ANCF-element has an order of convergence equal to four over the whole range, which is due to the higher-order approximation of the axial displacement. The present element can easily include the effect of transverse shear, which is more complicated for ANCF-elements. The convergence results for the case with shear are also shown in Fig. 2.
The first four eigenfrequencies of the linearized equations in the deflected equilibrium state are shown in Table 1 if the beam is modelled with 4 and with 32 elements, together with the analytically obtained eigenfrequencies for the straight unloaded beam. The first three modes are bending modes, and the fourth mode is an axial mode for the straight beam, whereas a coupling is present in the deflected configuration. The first eigenfrequency is increased by the load, which is mainly due to the positive axial force in the deformed configuration.
The compliance matrix at the tip in the deformed configuration for a model with four elements in the deflected equilibrium configuration if no shear is taken into account is given by
This matrix relates the displacement of the tip and the rotation at the tip multiplied by the length of the beam to the increments of the forces at the tip and the bending moment at the tip divided by the length of the beam.
The input–output description with a transverse base displacement as input and the transverse tip displacement as output is examined. The three inputs are the base displacement, the base velocity and the base acceleration, which are correlated. The matrix \(\boldsymbol{A}_{\mathrm{ss}}\) is as in the linearization. The input matrix \(\boldsymbol{B}_{\mathrm{ss}}\) contains only non-zero elements for the acceleration input, which expresses the fact that the beam deformation is directly influenced only by the base acceleration. The output matrix \(\boldsymbol{C}_{\mathrm{ss}}\) contains the row of the first-order transfer function corresponding to the transverse tip displacement. The throughput matrix \(\boldsymbol{D}_{\mathrm{ss}}\) has a one for the base displacement input and zeros for the velocity and acceleration input. A damping factor \(d=0.001\sqrt{\rho AL^{4}/(EI)}\) has been introduced. The amplitude response for a model with four elements with sinusoidal transverse base displacement and corresponding velocity and acceleration is shown in Fig. 3, where the resonance peaks at the first four eigenfrequencies are seen. The first resonance peak is lower than it would have been in the unloaded undeflected configuration. Also, the axial mode is excited by a transverse base displacement in the deflected configuration. The response does not approach zero for high excitation frequencies, which is caused by the discretization: in a model with 32 elements, the amplitude ratio becomes very small for high frequencies.
3.2 Spatial beam element
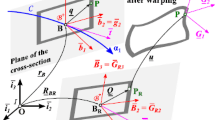
The spatial beam element has two nodes, as the planar beam element has, with as nodal variables the position coordinates \(\boldsymbol{x}=(x,y,z)^{\mathrm{T}}\) and four Euler parameters \(\boldsymbol{\lambda}=(\lambda _{0},\lambda _{1},\lambda _{2},\lambda _{3})^{ \mathrm{T}}\) for the orientation: \(\boldsymbol{x}^{e}=\big(\boldsymbol{x}^{p\mathrm{T}}, \boldsymbol{\lambda}^{p\mathrm{T}}, \boldsymbol{x}^{q\mathrm{T}}, \boldsymbol{\lambda}^{q\mathrm{T}}\big)^{\mathrm{T}}\). Seven generalized strains are introduced as follows. The axial strain is assumed to be constant, \(\varepsilon _{x} = \varepsilon _{1}\). The torsion angle per unit of undeformed beam length and the two curvatures are assumed to vary linearly over the length of the beam as
The case of a constant torsional strain is obtained by putting \(\varepsilon _{2} = \varepsilon _{3}\), which can be used to compare the element with the standard spatial beam element. The axial stiffness is \(EA\), the flexural rigidities are \(EI_{y}\) about the local central \(y\)-axis and \(EI_{z}\) about the local central \(z\)-axis, Saint-Venant’s torsion constant is \(S_{\mathrm{t}}\), and the shear rigidities are \(GAk_{y}\) in the local \(y\)-direction and \(GAk_{z}\) in the local \(z\)-direction. The transverse shears are constant and related to the curvatures as
The element stiffness matrix now follows from the expression for the strain energy, \(\boldsymbol{\varepsilon}^{e\mathrm{T}} \boldsymbol{S}^{e} \boldsymbol{\varepsilon}^{e}/2\), as
The rotation matrix describing the orientation of a cross-section is denoted by \(\boldsymbol{R}(\boldsymbol{\lambda})\), where the Euler parameters describe the orientation of the cross-section with respect to an orientation aligned with the global coordinate axes. The nodes may have an independent description of their orientations, so a transformation may be needed from the nodal coordinates used to describe the system and the specific Euler parameters at the end points of an element. In the examples, no transformation is needed. The differential equations relating the position to the strain measures are
The six constraints are expressed as
The strain measures have to be expressed in the generalized strains according to the chosen interpolations and substituted into Eqs. (56) and (57), after which the derivatives have to be substituted into Eq. (58). The constraint equations express that at the node \(q\), the position and orientation are continuous. The condition for the Euler parameters reduces the four dependent continuity conditions, which may be inconsistent due to the truncation error of the numerically determined integrals, to three independent conditions. In addition to this, there are the constraints of the Euler parameters at the nodes, \(\boldsymbol{\lambda}^{p\mathrm{T}} \boldsymbol{\lambda}^{p} - 1 = 0\) and \(\boldsymbol{\lambda}^{q\mathrm{T}} \boldsymbol{\lambda}^{q} - 1 = 0\).
The integrals are evaluated by an implicit numerical integration method for ordinary differential equations, the three-stage Lobatto-IIIA scheme [21], which is the equivalent of Simpson’s rule for evaluating integrals. The coefficients \(\boldsymbol{A}\), \(\boldsymbol{b}\) and \(\boldsymbol{c}\) for his method are given by the Butcher array
This method is symmetric, that is, integrating in the forward direction and then integrating in the backward direction returns the initial values, so no asymmetry between the nodes is introduced by the method. As the differential equations for the Euler parameters are linear, a single iteration to obtain the values at the stages is sufficient, after which the evaluation for the positions is a simple numerical integration. Furthermore, the first stage is explicit, so one system of eight equations has to be solved once. The same matrix of coefficients appears in the calculation of the derivatives of the constraint functions.
The mass description is analogous to the case of the planar beam element and taken from [8]. In addition, to model the moments of inertia of the cross-section, three solid discs, which are massless, but have moments of inertia, are used: two discs are placed on the nodes, each having moments of inertia equal to the area moments of inertia multiplied by the mass density and one sixth of the length of the element; the third disc is placed in the centre of the element and has moments of inertia that are four times as large. The orientation of the central disc is taken from the second stage of the integration method.
The theory is applied to the problem of large deflections of a curved beam [22]. The beam as shown in Fig. 4 is curved over 45∘ with a radius of \(R=100\text{ m}\) and has a square cross-section of \(1~\mathrm{m} \times 1~\mathrm{m}\). The elastic properties of the beam are \(EA=10\times 10^{6}\) N, \(GAk_{y}=GAk_{z}=5\times 10^{6}\) N and \(S_{\mathrm{t}}=EI_{y}=EI_{z}=1\times 10^{7}/12\) Nm2.
Due to the initial curvature, the initial values of the generalized strains for an element of length \(l_{0}\) are \(\boldsymbol{\varepsilon}_{0}^{e} = (0, 0, 0, -l_{0}/R, -l_{0}/R, 0, 0)^{ \mathrm{T}}\), and the constitutive relation becomes \(\boldsymbol{\sigma}^{e}=\boldsymbol{S}^{e} (\boldsymbol{\varepsilon}^{e}-\boldsymbol{\varepsilon}_{0}^{e})\).
Figure 5 shows the relative error in the tip displacement in the \(y\)-direction for a tip force of 600 N and several types of elements as a function of the number of elements used. The standard Spacar element is the least accurate, whereas the element with a constant torsional strain performs better with, initially, an order of convergence equal to four. The element with a linearly varying torsional strain gives the least error for a given number of elements; two of these elements give about the same error as eight standard elements. The reduction of the order of convergence for a large number of elements used is due to the constant approximation of the axial strain and shear, which is confirmed by artificially increasing the axial and shear stiffness values in the model giving a larger range with an order of convergence equal to four.
3.3 Motion of a very flexible pendulum
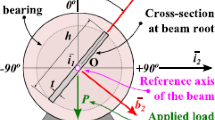
As a dynamic example, the motion of a flexible beam hinged at one end and subjected to gravity is simulated; see Fig. 6. If the beam were rigid, then the system would be a classical physical pendulum. The flexural rigidity of the beam is very small, so a large number of elements are needed to obtain accurate results. The parameters used for the model are: the acceleration of gravity \(g=9.81\text{ m}/\text{s}^{2}\); the length of the beam \(L=1.2\text{ m}\); Young’s modulus \(E=0.7\times 10^{6}\text{ Pa}\); Poisson’s ratio \(\nu =0.3\); the area of the cross-section \(A=0.0018\text{ m}^{2}\); the second area moment of inertia of the cross-section \(I=12.15 \times 10^{-9}\text{ m}^{4}\); and the mass density \(\rho =5540\text{ kg}/\text{m}^{3}\). The shear factor is chosen as \(k_{\mathrm{s}}=10(1+\nu )/(12+11\nu )\). For this slender beam, the influence of shear is negligible. This example was originally proposed in [23].
A characteristic length scale can be found as
which is directly related to the length of a beam that buckles due to the total gravity load. It is expected that for accurate results, the element length should be smaller than this length. For a simulation of 2 seconds, 400 elements are sufficient, which corresponds to an element length of \(0.003\text{ m}\). Fewer elements give a qualitative impression of the motion, but there are differences in the details. At the initial time, the beam is released from a horizontal orientation without any initial deformation and velocity. The configuration at intervals of \(0.1\text{ s}\) is shown in Fig. 7, and the tip position and orientation are shown in Fig. 8 as functions of the time.
The deformed shapes of the pendulum resemble the results reported in [23, 24], but both differ in some details. In [25], the vertical tip displacement for their large stretching model is quite close to the solution in Fig. 8.
3.4 Motion of a curved cantilever beam
The example of the curved cantilever spatial beam is reconsidered for a dynamic calculation. The mass per unit of length is taken as \(\rho A=2.6\times 10^{-4}\text{ kg}/\text{m}\), and the transverse moment of inertia per unit of length is taken as \(\rho I=2.1667\times 10^{-5}\text{ kg}\) m. Two kinds of damping are added: an internal material damping modelled by a damping matrix proportional to the stiffness matrix, \(\boldsymbol{S}_{\mathrm{d}}^{e} = d\boldsymbol{S}^{e}\) with \(d=5\times 10^{-6}\text{ s}\), and an external isotropic damping at the nodes of 0.05 Ns/m. The internal damping is most effective in reducing high-frequency vibrations, whereas the external damping acts mostly on the low-frequency motion. The beam is modelled with eight elements.
At the initial time, the beam is unstressed, and the tip force of 600 N is applied. Figure 9 shows the resulting motion of the tip. The motion approaches the static solution calculated before. If the results are compared with those obtained with 16 original elements, then the differences in tip displacement are below \(0.4\text{ m}\), and the final static deflection differs by \(0.05\text{ m}\).
4 Conclusions
A method for modelling flexible multibody systems has been presented in which generalized strains describing the state of deformation of an element are related to nodal coordinates by implicit equations. The relations are seen as constraint equations as in more traditional modelling techniques, so many available analysis techniques can be applied. The modelling technique allows a systematic development of higher-order elements, for instance, by making use of assumed strains, and hence modelling systems with fewer elements and degrees of freedom for the same accuracy, which can give a more efficient model and reduce computation time.
Some examples for planar and spatial beams have shown that the accuracy is increased with respect to some elements from the literature and the calculations do not break down if individual elements undergo large deflections or deformations.
The ultimate usefulness of the modelling technique has to be proved in more challenging kinds of structural elements, such as leaf springs with a large aspect ratio, beams with open thin-walled asymmetric cross-sections, plates and shells, which are subjects of further studies.
References
Schwertassek, R., Wallrapp, O.: Dynamik flexibeler Mehrkörpersysteme, Methoden der Mechanik zum rechnergestützten Entwurf und zur Analyse mechatronischer Systeme. Friedr. Vieweg & Sohn, Braunschweig/Wiesbaden (1999)
Géradin, M., Cardona, A.: Flexible Multibody Dynamics, a Finite Element Approach. Wiley, Chichester (2001)
Bauchau, O.A.: Flexible Multibody Dynamics. Springer, Dordrecht (2011)
Shabana, A.A.: Dynamics of Multibody Systems, 4th edn. Cambridge University Press, New York (2013)
van der Werff, K.: Kinematic and Dynamic Analysis of Mechanisms, a Finite Element Approach. Dissertation, Delft University Press, Delft (1977)
van der Werff, K., Jonker, J.B.: Dynamics of flexible mechanisms. In: Haug, E.J. (ed.) Computer Aided Analysis and Optimization of Mechanical System Dynamics, pp. 381–400. Springer, Berlin (1984)
Jonker, J.B.: A finite element dynamic analysis of spatial mechanisms with flexible links. Comput. Methods Appl. Mech. Eng. 76, 17–40 (1989)
Meijaard, J.P.: Validation of flexible beam elements in dynamics programs. Nonlinear Dyn. 9, 21–36 (1996)
Jonker, J.B., Meijaard, J.P.: A geometrically non-linear formulation of a three-dimensional beam element for solving large deflection multibody system problems. Int. J. Non-Linear Mech. 53, 63–74 (2013)
Jonker, J.B.: Three-dimensional beam element for pre- and post-buckling analysis of thin-walled beams in multibody systems. Multibody Syst. Dyn. 52, 59–93 (2021)
Turner, M.J., Clough, R.W., Martin, H.C., Topp, L.J.: Stiffness and deflection analysis of complex structures. J. Aeronaut. Sci. 23, 805–823, 854 (1956).
Ashwell, D.G., Sabir, A.B., Roberts, T.M.: Further studies in the application of curved finite elements to circular arches. Int. J. Mech. Sci. 13, 507–517 (1971)
Dawe, D.J.: A finite-deflection analysis of shallow arches by the discrete element method. Int. J. Numer. Methods Eng. 3, 519–552 (1971)
Dawe, D.J.: Curved finite elements for the analysis of shallow and deep arches. Comput. Struct. 4, 559–580 (1974)
MacNeal, R.H.: Derivation of element stiffness matrices by assumed strain distributions. Nucl. Eng. Des. 70, 3–12 (1982)
Craig, R.R. Jr, Bampton, M.C.C.: Coupling of substructures for dynamic analyses. AIAA J. 6, 1313–1319 (1968)
Meijaard, J.P.: Fluid-conveying flexible pipes modeled by large-deflection finite elements in multibody systems. ASME J. Comput. Nonlinear Dyn. 9, 011008 (2014)
Meijaard, J.P.: A method for calculating and continuing static solutions for flexible multibody systems. ASME J. Comput. Nonlinear Dyn. 13, 071002 (2018)
Jonker, J.B., Aarts, R.G.K.M., van Dijk, J.: A linearized input-output representation of flexible multibody systems for control synthesis. Multibody Syst. Dyn. 21, 99–122 (2009)
Gerstmayr, J., Irschik, H.: On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line approach. J. Sound Vib. 318, 461–487 (2008)
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I, Nonstiff Problems (second revised edition), Springer, Berlin (1993)
Bathe, K.J., Bolourchi, S.: Large displacement analysis of three-dimensional beam structures. Int. J. Numer. Methods Eng. 14, 961–986 (1979)
Shabana, A.A., Hussien, H.A., Escalona, J.L.: Application of the absolute nodal coordinate formulation to large rotation and large deformation problems. ASME J. Mech. Des. 120, 188–195 (1998)
Campanelli, M., Berzeri, M., Shabana, A.A.: Performance of the incremental and non-incremental finite element formulations in flexible multibody problems. ASME J. Mech. Des. 122, 498–507 (2000)
Sheng, F., Zhong, Z., Wang, K.-H.: Theory and model implementation for analyzing line structures subject to dynamic motions of large deformation and elongation using the absolute nodal coordinate formulation (ANCF) approach. Nonlinear Dyn. 101, 333–359 (2020)
Acknowledgements
Dr. M. Nijenhuis made some useful comments on a draft version.
Funding
This publication was financially supported by the Netherlands Organisation for Scientific Research (Nederlandse organisatie voor wetenschappelijk onderzoek, NWO, projects 15146 and 16210).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meijaard, J.P. An extended modelling technique with generalized strains for flexible multibody systems. Multibody Syst Dyn 57, 133–155 (2023). https://doi.org/10.1007/s11044-022-09854-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-022-09854-9