Abstract
A new methodology for constructing stability maps (phase-plane analysis) is presented and validated for application to complex multibody vehicle models implemented in Multibody Dynamics simulation software (Adams®). Traditional methodologies are developed to be applied to explicit mathematical models. Given the complexity of some special multibody systems, particularly in vehicle dynamics, simplifications are needed to apply this stability analysis technique. The main limitation when using simplified models is the need to neglect components which could have a significant influence on the dynamic behavior of the system and therefore on its stability. In the proposed methodology it is not necessary to have access to explicit mathematical models of multibody systems. Thus, the stability map of a vehicle model can be constructed by considering highly nonlinear dynamic elements, such as tires and silent-blocks components, modeled using the nonlinear finite element technique.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Following a multibody dynamics approach, the equations of a mechanical system are a set of nonlinear differential-algebraic equations. This form of the equations allows the accurate systematic analysis of complex mechanical systems in different scenarios. However, for the stability analyses of the system it is necessary to have access to the linearized system dynamics [1].
The linearization of the dynamics equations can be performed in different ways, depending on the strategy selected to formulate the Differential Algebraic Equations (coordinate selection and kinematic constraints formulation) [1]. Several methods for the linearization of multibody dynamics have been published in the literature [2–6].
The stability analysis of a dynamic system about an equilibrium point involves the eigenvalue analysis of the corresponding linearized equations of motion. In the literature, several methods, such as the Lyapunov second method, are applied for analyzing the stability of dynamic systems [7], including both linear and nonlinear systems. The main difficulty in applying these methods is that the dynamic systems may need to be explicitly expressed [8].
Escalona [9] proposed a stability analysis method based on two coordinate projections and a special eigenvalue analysis of differential algebraic equations. It is applied to the stability analysis of steady motions of a vehicle in order to improve the computational cost, because applying Floquet’s theory to large multibody systems involves very high computational costs.
For some applications, it is fundamental to have suitable stability maps available, which are typically constituted by curves in a phase plane (phase portrait). These methodologies allow comprehensive characterization of the dynamic response of a nonlinear system, which often has multiple steady-state solutions, providing an easy way to analyze the steady-state solution that a set of initial conditions will converge to.
For example, the stability analysis of vehicles, using stability maps (phase-plane analysis), is applied to improve the designs or to the development of control systems strategies [10–12].
Due to the necessity that the dynamic systems are explicitly expressed to construct these maps, several authors proposed methods based on extremely simplified vehicle models [10–19]. Therefore, instead of a complex multibody vehicle model with nonlinear components (bushing, dampers, structural behavior, etc.), the most frequently used simplified vehicle model is a two-state vehicle dynamics model. This model is known as the bicycle model or the two-wheel model (single-track model). To incorporate the nonlinearities of the tires, these models use the brush tire model [10–12, 17] or the Magic Formula (Pacejka) tire model [13–16, 18, 19].
Flavio Farroni [20] proposed an improved model, a quadricycle planar model, characterized by two states referring to in-plane vehicle body motions (lateral and yaw motions). The model implements a nonlinear tire model for lateral behavior and two different analytical methods, the phase plane and the handling diagram, are applied to better analyze the in-curve vehicle lateral stability. With the same vehicle and tire model, Wencai Sun [21] analyzed the stability region of the vehicle, using the phase plane, employing the GA (Genetic Algorithm) method to solve for the bifurcation points.
Craig [22] extended the phase portrait to three states in order to include the longitudinal vehicle dynamics (drive/braking control inputs). Craig used a four-wheel vehicle model with a Brush tire model.
One recent application of phase plane analysis, using a single-track bicycle model, is to develop the path-tracking controller for autonomous vehicles [23, 24].
The main problem with using simplified models for the stability analysis of complex multibody models is the fact that they neglect components which could have a significant influence on the dynamic behavior of the system and therefore on its stability.
A full vehicle model contains an important number of bodies connected not only by kinetic joints, but also by nonlinear springs, shock absorbers, silent-blocks (bushings), elastic bodies (anti-roll bars, etc.) and highly nonlinear tires [25]. In addition, tire behavior is affected by variables such as temperature, internal pressure and wear, with a significant impact on the vehicle performance [26, 27].
As the extensive bibliography reveals [10–25], the simplified models neglect these elements or the highly nonlinear dependence of the tires with combined slip (longitudinal/lateral), temperature, or internal pressure. A local linear model can be accurate enough to analyze the behavior of the vehicle in the vicinity of the equilibrium point and at low lateral acceleration, but it is not suitable if the distance between the different equilibrium points is large or the lateral accelerations are medium or high [21]. It means that the accuracy of the stability analysis of these models is clearly compromised.
For future improvements to vehicle control systems, it will be necessary to know and monitor the nonlinear dynamics of the vehicle, taking into account simultaneous inputs [22].
In order to improve the understanding of the nonlinear dynamics of the vehicle, in this paper a new methodology is presented to build stability maps (phase-plane) of multibody vehicle models implemented in a commercial software. The main advantage of the proposed methodology is that it is not necessary to have access to the explicit mathematical models of the multibody systems (the mathematical model does exist inside the simulation software, but the equations are not visible) and that it can be applied to any type of vehicle modeled in Multibody Dynamics (MBD) simulation software.
The existing MBD simulation software (e.g., the one used in this work, Adams®) is a simulation, analysis, and optimization tool, with high accuracy in modeling complex systems. This type of software allows the user to implement complex multibody models, avoiding mathematical formulation but including all dynamic properties [25].
Therefore, the proposed methodology allows taking advantage of the capabilities of this type of software, such as the possibility of including flexible bodies (linear or nonlinear), nonlinear elements (bushings, dampers, etc.), complex tire models, or to perform co-simulation with other software (FEM, real-time data, etc.).
Furthermore, the methodology easily allows the implementation of simultaneous driver inputs (steering, drive/brake forces, etc.) or control inputs (individual control of wheel torques, etc.).
This paper does not aim to improve the traditional theories on the dynamics of nonlinear systems (Poincaré–Bendixson, etc.), but an advance in the construction of stability maps (phase-plane analysis) of complex multibody vehicle models.
The methodology was applied and validated with a complete three-dimensional model of a vehicle implemented in Adams® (Fig. 2). This multibody system is easily implemented and simulated in a Multibody System Dynamics simulation software. In addition, it can be easily modified to analyze its sensitivity to design variables.
2 Methodology
The phase-plane plot is applied to two-state variable systems in order to analyze their stability. A complex multibody model has more than two state variables but, for many systems, its stability can be analyzed using only two state variables of one body. This is the case of ground vehicles where the phase portrait describes vehicle sideslip angle (\(\beta ^{V}\)) and vehicle yaw rate (\(\omega _{z}^{V}\)) or vehicle body side slip angle (\(\beta ^{V}\)) and its changing rate (\(\dot{\beta}^{V}\)) in a planar diagram [10–24].
The sideslip angle is defined as follows:
with \(v_{x}^{V}\) and \(v_{y}^{V}\) being the longitudinal and lateral velocities (Fig. 1) in a noninertial vehicle-fixed reference (\(x^{V}\), \(y^{V}\)).
A phase-plane plot for these two-state variables consists of curves of one state variable versus the other (\(\omega _{z}^{V} (t)\) vs. \(\beta ^{V} (t)\)), where each curve is based on a different initial condition (\(\beta ^{V} (0)\), \(\omega _{z}^{V} (0)\)).
At each point in this phase-plane, a corresponding vector (\(\dot{\beta}^{V}\), \(\dot{\omega}_{z}^{V}\)) is associated. By repeating this for sufficiently many points (grid) in the state space, a vector field plot is obtained. From the field plot, a phase trajectory can be sketched out for any initial condition.
The points on the phase-plane plot where \(\left ( \dot{\beta}^{V} =0 \wedge \dot{\omega}_{z}^{V} =0 \right )\) the system is considered to be in equilibrium. For a vehicle traveling along a curve at constant speed, this is equivalent to steady state motion. An analysis of the phase plane around that point would allow an assessment of whether the equilibrium is stable, unstable, or indifferent.
For the other points in the phase-plane plot, the system is not in equilibrium, which implies that the vehicle is moving in a transient mode. This movement is characterized both by its kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)), and by its movement tendency, which is analyzed as a function of the values of \(\dot{\beta}^{V}\) and \(\dot{\omega}_{z}^{V}\).
Both obtaining and characterization of the equilibrium points, as well as the study of the motion tendencies at any other point (\(\beta ^{V}\), \(\omega _{z}^{V}\)), have been widely analyzed in the state-of-the-art investigations, as discussed above, but always requiring the explicit formulation of the equations of the system. In general, if the equations of the system \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right ) =f \left ( \beta ^{V}, \omega _{z}^{V} \right )\) can be derived, from an initial kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)), the values \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\) can be obtained.
When a dynamic system (e.g., a road vehicle) is implemented in MBD simulation software, a “black box” (this term is used under the consideration that the equations of the system are not explicitly known) is available, which can perfectly characterize the dynamic response of the system to defined inputs. If the inputs are time invariant, the system will reach, after a transient process, a steady state regime characterized by a kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)) in which the energy of the system is minimal.
Taking all this into account, obtaining the equilibrium points (steady state circulation) of a vehicle is quite straightforward using an MBD simulation software by setting initial (and time invariant) conditions for the speed and the steering wheel angle. When the simulation is performed, after a transient period, a steady state regime characterized by its kinematics \(\left ( \beta ^{V}, \omega _{z}^{V} \right )\) is reached. This implies that the system is free, i.e., in “unforced” conditions. That is, there are no additional external forces or torques (\(\mathbf{F}^{\mathbf{V}}\), \(\mathbf{T}^{\mathbf{V}}\)). In case of applying external actions (forces or torques), the kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)) obtained in the steady state will be different and will be a function \(( \mathrm{f}' )\) of the input (\(\mathbf{F}^{\mathbf{V}}\), \(\mathbf{T}^{\mathbf{V}} \)),
Taking all of the above into account, what is proposed in the methodology developed in this work is a modification of the original system (vehicle driving at constant speed with a fixed steering wheel angle) by including external forces and torques. These forces and torques will be called “virtual” (\(\mathbf{F}_{\mathbf{v}}^{\mathbf{V}}\), \(\ \mathbf{T}_{\mathbf{v}}^{\mathbf{V}} \)), since they do not exist in the real system (vehicle), but they allow (force) the system to be taken to a certain kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)). In the real system, this condition represents a point where the vehicle is not in equilibrium. However, in the modified system (virtual system), this kinematic condition is reached in a steady state, forced by the added external forces and torques, after a transient period.
As will be demonstrated in Sect. 2.2, these virtual forces and torques, which force the virtual system to reach a certain kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)), are related to the response \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\) of the real system if it were in this initial condition.
So, the presented method proposes that the vector field be obtained by the introduction of a virtual force and torque (in the multibody model of the vehicle) in order to impose each kinematic (initial) condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)).
For a multibody vehicle model traveling at a constant longitudinal velocity and keeping the tires in contact with the road, the application of an external lateral force at ground level and an external yaw moment allow reaching a condition that could occur while driving.
The longitudinal movement of the vehicle is controlled by the traction forces (longitudinal tire forces) that allow maintaining a constant longitudinal velocity. In the virtual system, the vertical forces on the vehicle body and the pitch and roll torques are balanced by the ground reactions (tire forces, linked to the vehicle body through the steering and suspension mechanisms). Any situation other than equilibrium is impossible or would mean an accident (e.g., rollover) and is not the subject of this methodology. Therefore, it is not necessary to introduce a force to reach equilibrium in this direction.
Therefore, the vehicle sideslip angle and yaw rate (kinematic condition) depend on the virtual force and moment and the lateral forces and self-aligning torques of the tires. Thus, the stability of a vehicle traveling at constant longitudinal velocity can be analyzed using these two state variables (\(\omega _{z}^{V} \ \mathrm{vs}. \beta ^{V}\)).
As detailed in the following sections, this virtual force and torque allows the calculation of the corresponding vector (\(\dot{\beta}^{V}\), \(\dot{\omega}_{z}^{V}\)) for each (\(\beta ^{V}\), \(\omega _{z}^{V}\)) point.
2.1 Constrained multibody systems
The differential-algebraic equations of motion for multibody systems, such as a vehicle, can be expressed as follows [28]:
where \(\mathbf{q}\) is the composite set of generalized coordinates for the system, \(\mathbf{Q} \) is the vector of generalized forces (applied forces and torques), \(\boldsymbol{\Phi}_{\mathbf{q}}\) is the Jacobian matrix of the vector of constraints, \(\lambda \) is the vector of Lagrange multipliers associated with the constraints present in the system, \(\mathbf{M}\) is the system mass matrix, and \(\gamma \) is the vector obtained by the following acceleration equation:
For \(k\) bodies in the system, \(\mathbf{q}\) takes the following expression (where \(k\) is the number of bodies in the system):
where \(\mathbf{q}_{i}\) is the generalized coordinate vector associated with the rigid body \(i\) in a system.
For a 3D vehicle model, the differential-algebraic equations of motion can be expressed as follows [28]:
where \(\mathbf{r} \) is the composite set of generalized coordinates, defined by three Cartesian coordinates for each body of the vehicle (origin of the body-fixed coordinate system with respect to the global inertial frame XYZ), \(\boldsymbol{\omega} '\) is the body angular velocity expressed in the body-fixed coordinate system (centroidal frame xyz), \(\mathbf{M}\) is the mass matrix, \(\mathbf{J} '\) is the inertia tensor with respect to the centroidal frame; and \(\mathbf{F}^{A} \mathbf{T}^{\prime\,A}\) are the applied forces and torques.
Considering a vehicle model formed by \(k\) bodies, the components in the equation are:
The Lagrange multipliers, obtained along with \(\ddot{\mathbf{r}}\) and \(\dot{\boldsymbol{\omega}} '\) as the solution of system (6), are related to the reaction forces and torques produced by the constraints of the system.
2.2 Phase plot of the multibody vehicle model
Considering as state variables the vector (\(\dot{r}_{i}^{m}\), \(\omega_{i}^{\prime\, n}\)), corresponding to the velocity variables of the body \(i\) coordinates \(m\) and \(n\), of a body-fixed reference frame, the phase portrait can be generated using the method of building the vector field diagram. As mentioned above, in the case of analyzing the stability of a road vehicle, the variables to be considered are the vehicle body sideslip angle (\(\beta ^{V}\)) and vehicle yaw rate (\(\omega _{z}^{V}\)).
In the traditional approach, simplified models are used to provide an explicit formulation of the equations of the system. This allows the algebraic solution of the system of equations
where the values of \(\beta ^{V}\) and \(\omega _{z}^{V}\) are delimited in a predefined interval with maximum and minimum values, which define the state space under study.
Solving system (8) for enough points in the state space, a vector field diagram can be obtained. Thus, setting a pair of values (\(\beta ^{V}\), \(\omega _{z}^{V}\)) that identify the kinematics of the vehicle body, a pair of values \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\) are obtained that allow assessing the dynamic response and the trend of the handling response of the vehicle.
In the case of a detailed approximation to the dynamics of the system, by means of a mathematical model based on MBD software, an explicit formulation of the equations is not available. To solve this issue, a methodology based on the introduction of a virtual force and torque (applied force and torque external to the system) that provide the system with the desired kinematic response (\(\beta ^{V}\), \(\omega _{z}^{V}\)) is proposed. This virtual force and torque are introduced into the complete highly nonlinear model, without simplifications, to obtain the characterization of its dynamic response \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\) by solving with an MBD software.
So, the methodology proposed to obtain the vector field is based on the introduction of a virtual force and torque vectors \(\left ( \mathbf{F}_{\mathbf{v}},\ \mathbf{T}_{\mathbf{v}} \right )\) in the system (6) in order to impose each kinematic condition \(\left ( \beta ^{V}, \omega _{z}^{V} \right )\), with the virtual system in dynamic equilibrium (steady state response).
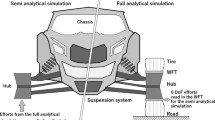
Assuming the road is flat, for a local-level reference frame with the origin at ground level (Fig. 2), the virtual force \(\left ( \mathbf{F}_{\mathbf{v}}^{\mathbf{ll}} \right )\) and torque \(\left ( \mathbf{T}_{\mathbf{v}}^{\mathbf{ll}} \right )\) are:
Solving the system of Eqs. (6) at a constant longitudinal velocity \(v_{x}^{V}\), when the vehicle reaches dynamic equilibrium, the kinematic condition (\(\beta ^{V}\), \(\omega _{z}^{V}\)) is obtained. In this condition, the tire forces and moments (longitudinal, vertical, lateral, etc.), other external forces (e.g., aerodynamic) or the vehicle body angles (pitch and roll) are the same as if the condition is kinematically imposed.
The numerical integration of the differential-algebraic equations of motion is carried out in an MBD software.
For each point \(\left ( \beta ^{V}, \omega _{z}^{V} \right )\) of the state space, the vector field associated is a function of the virtual force/torque imposed to reach that point, so
This vector \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\), as a function of the force and virtual torque, must be obtained. For this purpose, the whole vehicle is considered as an unconstrained system. The Newton–Euler equations of motion in the vehicle body frame are:
The force equation in lateral direction is
After the introduction of a virtual force and torque, the system reaches the dynamic equilibrium for each initial condition, so \(\dot{v}_{y}^{V} = \omega _{x}^{V} = v_{z}^{V} =0\). Equation (12) can be simplified as follows:
where \(F_{v_{y}}^{V}\) is the component of the virtual force in the \(y\) axis of the vehicle body frame.
With the system in dynamic equilibrium, if the virtual force disappears, the equation in a lateral direction will be
Therefore, the virtual force (\(F_{v_{y}}^{V}\)) is related to the inertia effect and \(\dot{\beta}^{V}\) can be obtained as follows:
The virtual torque is applied in the vertical axis. It is assumed that the axes of the vehicle’s reference system are the principal axes of inertia, so the equation in this direction is
The system of Eq. (6) was solved to reach the dynamic equilibrium for each initial condition, so \(\dot{\omega}_{z}^{V} = \omega _{x}^{V} = \omega _{y}^{V} =0\). Equation (16) can be simplified as follows:
where \(T_{v_{y}}^{V}\) is the component of the virtual torque in the \(z\) axis of the vehicle body frame. The virtual torque (\(T_{v_{y}}^{V}\)) is related to the inertia effect, so if this torque disappears, the equation will be
Therefore, \(\dot{\omega}_{z}^{V}\) is evaluated as
Once the values of \(\left ( \dot{\beta}^{V}, \dot{\omega}_{z}^{V} \right )\) have been obtained, by means of Eq. (15) and (19), for each of the points defined in the state space the phase plot can be drawn.
The application of a virtual force and torque to achieve a dynamic equilibrium is valid for conditions far from the equilibrium points. It is a methodology applied to multibody vehicle models, so these situations must be possible to achieve during real driving, and the multibody model is able to simulate them.
The main limitation of the methodology is in those situations where the vehicle reaches the rollover situation. In such cases the virtual forces and torques do not allow an equilibrium condition to be reached. These situations are not the subject of the methodology. Its development is intended to be applied to the development of stability controls in a sliding situation and not in a rollover situation.
3 Results
In order to apply the proposed methodology, a multibody vehicle model is implemented and its simulation is performed in Adams® commercial software developed by MSC Software Corporation, as shown in Fig. 2.
The vehicle model implemented in Adams® has 65 moving parts, 3 flexible bodies, 26 nonlinear bushings, and 59 joints, which gives a model with 144 independent degrees of freedom.
A detailed model of the front and rear suspension system has been implemented. The front suspension is McPherson type with a lower control arm and an antiroll bar, modeled as a flexible body (Fig. 3).
The rear suspension is a compound crank axle suspension mechanism, with a twistable cross-member (V shape) and an antiroll bar, both modeled as flexible bodies (Fig. 4).
For tires, the Pacejka PAC2002 tire model is used, with cornering and longitudinal slip considered simultaneously with combined slip and transient behavior.
Inputs required for simulating the model are the steering-wheel angle and drive torque. The first is constant and the drive torque is applied to maintain the longitudinal velocity constant. To properly define it, a PID (Proportional Integral Derivative) controller is used.
Several simulations were carried out at constant speeds and for different steering angles. The methodology described in point 2 has been applied in order to obtain the phase-plane. Figure 5 shows the phase-plane at 30 km/h for four steering angles (mean front wheels steering angles 0, 0.1, 0.2, and 0.3 rad).
As can be seen, there is one stable equilibrium point and a saddle equilibrium point for each steering angle. In the case of 0.3 rad of steering, the stable equilibrium point and the saddle equilibrium point are close together.
In order to verify the identification of the phase-plane stable equilibrium points, an open-loop step steer maneuver of the vehicle model has been carried out (Fig. 6). At a constant velocity (30 km/h), the input steer angle is as shown in Fig. 6.
As a result, the equilibrium points for each steering angle are shown in the following Table 1:
The equilibrium points are the same as those identified in the phase-plane (Fig. 5).
The main advantage of the new methodology is that it allows the phase-plane to be defined whilst taking into consideration all the nonlinearities of the model. This is especially important when the vehicle is close to its limits, i.e., when one or more tires are saturated or close to saturation. This is the test case with a 0.3 rad steering angle. As can be seen in Fig. 7, the response of the vehicle is not the same as in the previous steps. The vehicle slip angle passes through a maximum value, stabilizing at a lower value.
To analyze why this vehicle slip reduction occurs, the lateral forces of each tire are checked. As can be seen in Figs. 7 and 8, the inner rear tire of the curve (rear left) is saturated. It reaches a maximum value of lateral force because it exceeds its slip limit (Fig. 9), as a consequence of a reduction in the vertical load.
This phenomenon is only identifiable if the nonlinearity of its rear axle is considered, in addition to the tires themselves. The twistable cross-member affects the kinematic and dynamic behavior of the compound crank axle suspension [29]. Due to this and other nonlinear elements (bushings, etc.), it shows a nonlinear relationship between the wheel angles (toe-in and camber) and the wheel displacement [30]. This nonlinear relationship significantly influences tire response.
Simplified models, such as those currently used, neglect these nonlinearities and do not consider the influence of each tire individually. Therefore, they would not be able to take these effects into consideration when determining the phase plot.
Therefore, this limitation of traditional methods conditions the validity of the phase-plot in the vicinity of the vehicle limits. Furthermore, this questions the validity of the phase-plot at points far from the equilibrium point, even when this equilibrium point is far from the vehicle limits.
Obviously these traditional methods have a lower computational cost. In any case, the application for which the methodology is developed does not require the simulation to run in real time.
4 Conclusions
The stability maps are a tool that allows the stability of complex systems to be analyzed. The traditional methods for their construction, curves in a phase plane (phase portrait), require that the dynamic systems be explicitly expressed. Therefore, in the traditional approach, simplified models are used that ignore components which could have a significant influence on the dynamic behavior of the system and, therefore, on its stability.
Road vehicles are among the complex systems to which stability maps are applied, for example, for the development of control systems. Simplified vehicle models are used that do not take nonlinear components into consideration. Examples are nonlinear bushing, antiroll bars, twistable cross members, tires, etc., which are linearized or neglected.
This paper proposes a methodology for the construction of stability maps, that does not need explicit equations and that considers all the nonlinearities of the model. The methodology is based on the introduction of virtual forces, in the multibody model, that allow a dynamic equilibrium of the system to be reached under different conditions.
The methodology is applied to a passenger car. A complex virtual model was created using Adams® commercial software. The model includes different nonlinear components: antiroll bars, coil springs, dampers, tires, and a twistable cross-member in the rear axle.
Several simulations were carried out at constant speeds and for different steering angles. The phase-planes for each steering angle have been obtained. To validate the identification of the phase-plane stable equilibrium points, an open-loop step steer maneuver of the vehicle model has been carried out. The correlation has been proven.
The open-loop maneuver shows the influence of the nonlinearities at high lateral acceleration, when one or more tires are saturated or close to saturation. With a simplified model, the behavior of the system would be different, and it would not allow the real behavior to be reproduced.
Therefore, this limitation of traditional methods conditions the validity of the phase-plot in the vicinity of the vehicle limits. That is, when the point of stability is very close to non-equilibrium points. Furthermore, this questions the validity of the phase-plot at points that are far from the equilibrium point, even when this equilibrium point is far from the vehicle limits.
Three-dimensional multibody vehicle models are usually completely modeled in Multibody Dynamics simulation software, such as Adams® from MSC Software, for simulation, analysis, and optimization, including highly nonlinear dynamic elements, such as tires and silent-blocks. Therefore, applying the phase-plane to these non-explicit models is needed so as to be able to continue improving the designs and control systems on these models.
Data Availability
Not applicable
Materials Availability
Not applicable
Code Availability
Not applicable
Abbreviations
- \(\beta ^{V}\) :
-
Vehicle sideslip angle measured in the vehicle-fixed reference frame
- \(\omega _{x}^{V}\), \(\omega _{y}^{V}\), \(\omega _{z}^{V}\) :
-
Components of vehicle angular velocity (vehicle-fixed reference frame)
- \(x^{V}\), \(y^{V}\), \(z^{V}\) :
-
Axis of the vehicle-fixed reference frame
- \(v_{x}^{V}\), \(v_{y}^{V}\), \(v_{y}^{V}\) :
-
Components of vehicle velocity in the vehicle-fixed reference frame
- \(\mathbf{F}^{\mathbf{V}}\), \(\mathbf{T}^{\mathbf{V}}\) :
-
Applied force and torque (vehicle-fixed reference frame)
- \(\mathbf{F}_{\mathbf{v}}^{\mathbf{V}}\), \(\mathbf{T}_{\mathbf{v}}^{\mathbf{V}}\) :
-
Virtual force and torque (vehicle-fixed reference frame)
- \(\mathbf{F}_{\mathbf{v}}^{\mathbf{ll}}\), \(\mathbf{T}_{\mathbf{v}}^{\mathbf{ll}}\) :
-
Virtual force and torque (local-level reference frame at ground level)
- \(\mathbf{M}\) :
-
System mass matrix
- \(\boldsymbol{\Phi}_{\mathbf{q}}\) :
-
Constraint Jacobian
- \(\mathbf{q}\) :
-
Vector of generalized coordinates
- \(\lambda \) :
-
Lagrange multiplier vector
- \(\mathbf{Q}\) :
-
Generalized forces (applied forces and torques)
- \(\gamma \) :
-
Right side of acceleration equation
- \(\mathbf{F}^{A}\) :
-
Applied force on body
- \(\mathbf{T}^{\prime\,A}\) :
-
Applied torque on body (body-fixed coordinate system)
- \(\mathbf{J}'\) :
-
Inertia matrix of body
- \(\boldsymbol{\omega} '\) :
-
Angular velocity in a body-fixed coordinate system
- \(\mathbf{r}\) :
-
Composite set of generalized coordinates
- \(\boldsymbol{\omega}^{\mathbf{V}}\) :
-
Angular velocity in the vehicle body coordinate system
- \(m\) :
-
Vehicle mass
- \(F_{y\ tires}^{V}\) :
-
Component of tire forces in the \(y\) axis of the vehicle body reference frame
- \(T_{z\ tires}^{V}\) :
-
Resultant torque of tire forces and moments in the \(z\) axis of the vehicle body reference frame
References
González, F., Masarati, P., Cuadrado, J., Naya, M.A.: Assessment of linearization approaches for multibody dynamics formulations. J. Comput. Nonlinear Dyn. 12, 4–5 (2017). https://doi.org/10.1115/1.4035410
Negrut, D., Ortiz, J.L.: A practical approach for the linearization of the constrained multibody dynamics equations. J. Comput. Nonlinear Dyn. 1, 230–239 (2006). https://doi.org/10.1115/1.2198876
Ge, X.-S., Zhao, W.-J., Chen, L.-Q., Liu, Y.-Z.: Symbolic linearization of differential/algebraic equations based on Cartesian coordinates. Tech. Mech. 25, 230–240 (2005)
Wallrapp, O.: Linearized flexible multibody dynamics including geometric stiffening effects. Mech. Struct. Mach. 19, 385–409 (1991)
Lin, T.C., Yae, K.H.: Recursive linearization of multibody dynamics and application to control design. J. Mech. Des. 116, 445–451 (1994)
Ni, Ch-Sh., Hong, J.-Zh., He, Q.-Y.: Symbolic linearization of nonlinear coupled differential and algebraic dynamic equation. Acta Mech. Sin. 29, 491–496 (1997)
Samsundar, J., Huston, J.C.: Estimating lateral stability region of a nonlinear 2 degree-of-freedom vehicle. In: SAE Technical Paper. SAE International (1998)
Huang, Y., Chen, Y.: Estimation and analysis of vehicle lateral stability region with both front and rear wheel steering. In: ASME 2017 Dyn. Syst. Control Conf. DSCC 2017. 3, 4303–4308 (2017). https://doi.org/10.1115/DSCC2017-5154
Escalona, J.L., Chamorro, R.: Stability analysis of vehicles on circular motions using multibody dynamics. Nonlinear Dyn. 53, 237–250 (2008). https://doi.org/10.1007/s11071-007-9311-5
Beal, C.E., Gerdes, J.C.: Model predictive control for vehicle stabilization at the limits of handling. IEEE Trans. Control Syst. Technol. 21, 1258–1269 (2013). https://doi.org/10.1109/TCST.2012.2200826
Bobier, C.G.: A phase portrait approach to vehicle stabilization and envelope control (2012)
Bobier, C.G., Gerdes, J.C.: Staying within the nullcline boundary for vehicle envelope control using a sliding surface. Veh. Syst. Dyn. 51, 199–217 (2013). https://doi.org/10.1080/00423114.2012.720377
Rossa, F. Della, Mastinu, G., Piccardi, C.: Bifurcation analysis of an automobile model negotiating a curve. Veh. Syst. Dyn. 50, 1539–1562 (2012). https://doi.org/10.1080/00423114.2012.679621
Della Rossa, F., Mastinu, G.: Analysis of the lateral dynamics of a vehicle and driver model running straight ahead. Nonlinear Dyn. 92, 97–106 (2018). https://doi.org/10.1007/s11071-017-3478-1
Ko, Y.E., Song, C.K.: Vehicle modeling with nonlinear tires for vehicle stability analysis. Int. J. Automot. Technol. 11, 339–344 (2010)
Ono, E., Hosoe, S., Tuan, Hoang D., Doi, S.: Bifurcation in vehicle dynamics and robust front wheel steering control. IEEE Trans. Control Syst. Technol. 6, 412–420 (1998)
Catino, B., Santini, S., Di Bernardo, M.: MCS adaptive control of vehicle dynamics: an application of bifurcation techniques to control system design. In: Proc. IEEE Conf. Decis. Control, vol. 3, pp. 2252–2257 (2003)
Lu, Q., Gentile, P., Tota, A., Sorniotti, A., Gruber, P., Costamagna, F., De Smet, J.: Enhancing vehicle cornering limit through sideslip and yaw rate control. Mech. Syst. Signal Process. 75, 455–472 (2016). https://doi.org/10.1016/j.ymssp.2015.11.028
Chung, T., Yi Kyongsu, K.: Design and evaluation of side slip angle-based vehicle stability control scheme on a virtual test track. IEEE Trans. Control Syst. Technol. 14, 224–234 (2006). https://doi.org/10.1109/TCST.2005.863649
Farroni, F., Russo, M., Russo, R., Terzo, M., Timpone, F.: A combined use of phase plane and handling diagram method to study the influence of tyre and vehicle characteristics on stability. Veh. Syst. Dyn. 51, 1265–1285 (2013). https://doi.org/10.1080/00423114.2013.797590
Sun, W., Tian, J., Li, S., Yang, Z., Ma, Z.: Stability analysis of vehicle negotiating a curve in the plane. Adv. Mech. Eng. 2013 (2013). https://doi.org/10.1155/2013/893835
Beal, C.E., Boyd, C.: Coupled lateral-longitudinal vehicle dynamics and control design with three-dimensional state portraits. Veh. Syst. Dyn. 57, 286–313 (2019). https://doi.org/10.1080/00423114.2018.1467019
Li, S.E., Chen, H., Li, R., Liu, Z., Wang, Z., Xin, Z.: Predictive lateral control to stabilise highly automated vehicles at tire-road friction limits. Veh. Syst. Dyn. 58, 768–786 (2020). https://doi.org/10.1080/00423114.2020.1717553
Cui, Q., Ding, R., Wei, C., Zhou, B.: Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope. Veh. Syst. Dyn. 59(11), 1–25 (2020). https://doi.org/10.1080/00423114.2020.1776344
Cuesta, C., Luque, P., Mántaras, D.A.: State estimation applied to non-explicit multibody models. Nonlinear Dyn. 86, 1673–1686 (2016). https://doi.org/10.1007/s11071-016-2985-9
Damiano, C., Flavio, F., Aleksandr, S., Gianluca, S., Antonio, S., Francesco, T.: On the implementation of an innovative temperature-sensitive version of pacejka’s mf in vehicle dynamics simulations. In: Lecture Notes in Mechanical Engineering, pp. 1084–1092. Springer, Berlin (2020)
Durand-Gasselin, B., Dailliez, T., Mossner-Beigel, M., Knorr, S., Rauh, J.: Assessing the thermo-mechanical TaMeTirE model in offline vehicle simulation and driving simulator tests. In: Vehicle System Dynamics, pp. 211–229 (2010)
Haug Edward, J.: Computer Aided Kinematic and Dynamics in Mechanical Systems. Ed. Allyn and Bacon, Massachusetts (1998).
Mántaras, D.A., Luque, P., Vera, C.: A three-dimensional kinematic model for compound Crank axle suspension mechanism. Proc. Inst. Mech. Eng., Part D, J. Automob. Eng. 217(2), 115–123 (2003). https://doi.org/10.1177/095440700321700205
Lee, D., Yang, C.: An analytical approach for design and performance evaluation of torsion beam rear suspension. Finite Elem. Anal. Des. 63, 98–106 (2013). https://doi.org/10.1016/j.finel.2012.09.002
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mantaras, D.A., Luque, P. & Alonso, M. Phase plane analysis applied to non-explicit multibody vehicle models. Multibody Syst Dyn 56, 173–188 (2022). https://doi.org/10.1007/s11044-022-09846-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-022-09846-9









 stable equilibrium point
stable equilibrium point  saddle equilibrium point
saddle equilibrium point


