Abstract
This paper presents a formulation for frictionless beam-to-beam contact using the mortar method. The beams are modelled using the geometrically exact theory. A similar approach has been proposed very recently, with respect to which we offer a formulation based on a Lagrange-multiplier method and a simpler algorithm to cover the static interaction within the contact zone and analyse the performance of the method for different orders of interpolation for the Lagrange multiplier and in the presence of self-contact. Appropriate contact kinematics is developed from which the residual vector and the tangent stiffness matrix are obtained from a suitable contact potential and its variation and consistent linearisation for implementation in the finite element method. The algorithm describing the fulfilment of the contact kinematics is described in detail. The mortar method is found out to be suitable for modelling beam-to-beam contact and self-contact. The geometrically exact beam theory assumes full rigidity of the cross-sections and as such is naturally prone to higher oscillations in the contact force near the boundaries of the contact zone. For sufficiently small load steps, however, a stable solution is obtained, making it appropriate for future research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Finite element analysis with geometrically exact beam elements is widely used in modern industry with applications ranging from dynamical analysis of umbilical cables, offshore risers and mooring dynamics in maritime engineering [11, 21, 29], bridge columns and rope-way systems in civil engineering [12, 41], composites and fibre materials in material engineering [10, 25], wind turbine blades and multi-body dynamics in mechanical engineering [17, 36], DNA molecules in biological engineering [9] and more. Treating a mechanical system as a one-dimensional can provide a variety of advantages. Generally it results in a smaller model, reducing the computational effort in a solution procedure, and modified boundary conditions, specifically in the rotational degrees of freedom.
There has been a lot of research on efficient, robust and precise finite elements. The watershed moment in this field was the development of geometrically exact beam theory by Simo [31] and its finite-element implementation by Simo & Vu-Quoc [32, 33]. Since then, many variants have been proposed for interpolating kinematic fields, with some more notable improvements proposed in [5, 6, 8, 16, 34] and investigated in detail in [1, 2, 30]. However, the original element is still highly revered and widely used in practice.
Modern contact mechanics extensively utilises mortar method [3, 4, 15, 22, 26–28, 37]. It is a Lagrange multipliers based method with contact conditions imposed in a weak sense. There are additional variables introduced into the system compared to the penalty approach, however, such method is proved to comply with Ladyzhenskaya–Babuška–Brezzi (LBB) condition stating that there exists a unique solution to the underlying saddle-point type problem [3]. Contact analysis in beam models is lagging behind these developments and it was not until very recently that the first paper has been published presenting a mortar formulation for frictionless beam-to-beam contact [7]. A lot of research in beam contact mechanics is focused on a point-to-point contact where a point force is applied at the closest point between two beams [18–20, 40]. Although this theory is attractive from the numerical-efficiency point of view, it cannot properly describe distributed contacts. To account for this, some researchers have introduced a line-to-line type contact in the beam contact problems, mainly by means of the so-called Gauss-point-to-segment method based on the penalty approach [9, 23]. Some attempts to combine the two methods also exist [24], where one or the other is chosen depending on the size of an angle formed by the two beams at a contact point. The attractiveness of the mortar method is in the efficient handling of both point-like and distributed contacts.
The first application of the mortar method in static frictionless beam-to-beam contact was proposed in [7]. The authors show that such a continuous non-smooth formulation is appropriate also for thin beam-like structures where the assumption of rigid cross-sections is in place. This assumption has deterred some authors, [23], from non-smooth contact mechanics, as it is somehow contradictory to the nature of contact, where some deformation is expected, and thus has directed the focus of research on the penalty method. Nevertheless, the authors in [7] adopt an augmented-Lagrangian approach and validate the method with an adapted version of the patch test and a twisting example for the distributed contact. The point-to-point contact was validated using a cantilever bending test. These tests demonstrate that the method is stable and convergent and yields results comparable to the penalty method.
This paper presents an alternative mortar method formulation for the analysis of a static frictionless beam-to-beam contact based on the Lagrange-multipliers method. The term beam-to-beam contact is meant here in the broadest sense possible, as it includes beam-to-rigid-surface and self contacts, both of which are tested in numerical examples.
Section 2 outlines the geometrically exact beam theory. Section 3 discusses contact geometry, kinematics and contact potential. In Sect. 4 we present contact virtual work and linearization and give details of a numerical implementation. Finally, verification tests from literature are considered in Sect. 5.
2 Geometrically exact beam theory
As mentioned in the introduction, the geometrically exact beam theory is used to model beams. A beam is represented through a centreline which connects cross-sections. The representation, chosen in [31], delegates the centreline to \(\mathbb{R}^{3}\) space and the cross-section orientation to the Lie group \(SO(3)\). As illustrated in Fig. 1, centreline position is denoted by vector \(\boldsymbol{x}\). The rotation matrix \(\mathbf{R}\) denoting the orientation of the cross-section is assembled from the spatial orthogonal basis \(\mathbf{R} = \begin{bmatrix} \boldsymbol{e}_{1} &\boldsymbol{e}_{2} &\boldsymbol{e}_{3} \end{bmatrix} \). Both \(\boldsymbol{x}\) and \(\mathbf{R}\) are parametrised by the arc-length coordinate \(s\) and so the entire configuration can be expressed as a single coordinate function.
The geometrically exact beam theory can account for shear deformation as the cross-section need not be aligned with a tangent at the centreline. However, the cross-section itself is considered to be rigid. Within this setup, the strain measures for position and rotation are defined as the difference between the current and the initial deformation
where \((\cdot )_{0}\) denotes a quantity in the initial configuration and a hat denotes a skew-symmetric matrix which is an element of the Lie algebra \(\mathfrak{so}(3)\). The strains are in combination with a linear elastic material law related to the internal forces via material properties matrix
where \(\mathbf{K} = \operatorname{diag}(EA, GA_{1}, GA_{2}, G J_{t}, EI_{1}, EI_{2})\). Balance equations in the weak form are finally defined as
where vector \(\boldsymbol{f}_{\text{ext}}\) represents a vector of external distributed forces and moments.
Following the Simo & Vu-Quoc formulation [32], a finite element is obtained through a discretization of the configuration which is an element of the \(\mathbb{R}^{3}\times SO(3)\) manifold. A parametric centreline function is obtained simply by interpolating the nodal positions. The rotations are not directly interpolated and are updated through interpolated iterative rotation changes. An element’s order defines the order of the Lagrange polynomial shape functions. Further details on interpolation are described in Sect. 4.3.
Other discretizations are possible. For comparison, in [7] the authors implement the mortar method on an element based on the first-order Lie group \(SE(3)\) interpolation, which requires quantities expressed in the local frame of reference.
3 Contact geometry and potential
A beam-to-beam contact describes an interaction between two bodies, which can be represented by the beam theory. In a more general case, these two bodies can be viewed as segments of one or more beams and in this way refer to both the contact between the two beams as well as self-contact in either of them. In what follows, these two segments will be simply referred to as beam \((1)\) and beam \((2)\).
This paper is considering segment-to-segment contacts between beams. These include (i) point-to-point type contact where the two beams in contact form a large-enough angle whereby due to the rigid nature of the cross-sections contact-region appears to be a point, and (ii) a line-to-line type where the contact force is distributed along a larger region which appears to be a line. The latter case occurs when beams either lean on or twist around each other. Although there exist specific models for point-to-point contacts only, e.g. [20], the strength of the mortar method rests in its capacity to model both contact types with the same algorithm. Some limitations, naturally, exist and they are discussed further in Sect. 5.
Beam geometry follows the geometrically exact beam theory described in Sect. 2. This is the preferred choice in the literature, [7, 9, 10], although some researchers, e.g. [24], prefer to use the Kirchhoff theory for thin beams instead, which simplifies the beam formulation by neglecting the shear deformation. Although the choice influences the numerical results for thicker beams, it does not usually affect the contact formulation itself because of the introduced assumptions. A centreline position in the deformed configuration is for each beam denoted as \(\boldsymbol{x}^{(i)}( s^{(i)} )\) for \(i=1,2\). For more information on the geometrical layout see Fig. 2.
A contact problem may be defined by the well-known Karush–Kuhn–Tucker (KKT) conditions through \(\lambda = -F_{N}\):
where \(g\) and \(\lambda \) denote the gap and the Lagrange multiplier, respectively, and \(F_{N}\) denotes a contact force. The non-penetration condition (5a) states that there should be no penetration between the bodies. It is prevented by the appearance of a pair of opposite contact forces at the point of contact, which results in a positive pressure on each beam (5b). The zero-work condition (5c) ensures that a contact force appears only if there is a contact and the gap is zero. These conditions apply to each individual point on the beam’s surface.
In the contact-geometry definition, the shear deformation is neglected, i.e. the cross-section is assumed to remain perpendicular to the centreline. This assumption, together with the assumption of circular cross-sections, simplifies the gap function as it now depends solely on the position of the two centrelines. It is justified by the fact that the shear deformation only marginally changes the distance between the two beams and holds true for reasonably thin beams. The same assumptions are considered also in most other publications [7, 10, 23] etc. Some point-to-point models are also extended to the rectangular cross-section shapes [20]. Line-to-line models also allow such generalization, but have so far not been implemented due to the added complexity.
Successful measurement of the gap between beams in a line-to-line model requires a continuous evaluation of the distance between the centrelines. Such a measurement is most often interpreted as an orthogonal projection from one beam to the other [7, 9, 23]. The alternative is proposed in [10], where the distance is measured perpendicularly from the intermediate geometry constructed as the average of the two centrelines. Geometry in the mortar contact formulation (Fig. 2) is based on the distinction between the non-mortar (assigned to beam \((1)\)) and the mortar side (beam \((2)\)). The two centrelines are connected by the projection vector \(\boldsymbol{v}(s^{(1)},s^{(2)})\), where, for a given \(s^{(1)}\), \(s^{(2)}\) is found so that the magnitude of the projection vector is the shortest. This is performed using the nearest point projection algorithm, and the solution is thus denoted as \(s^{(2)}(s^{(1)})\) emphasizing the dependence on \(s^{(1)}\) coordinate,Footnote 1 which in general cannot be explicitly expressed. The projection is defined by the following pair of vector equations that needs to be solved for \(s^{(2)}\)
where the prime \((\cdot )'\) here and throughout the paper denotes the derivative with respect to the curvilinear coordinate that is referring to the particular beam: \(\boldsymbol{x}^{\prime (i)} = \mathrm{d}\boldsymbol{x}^{(i)} / \mathrm{d}s^{(i)}\) for \(i = 1,2\). For additional details on nearest point projection, see Appendix A.
The non-frictional component of the contact force appears in the direction of the unit normal vector \(\boldsymbol{n}(s^{(1)})\) which is aligned with the projection vector. The definition of the normal vector as in the literature [7, 9, 18, 23] is
The gap function is now defined as the distance between the two beam centrelines (6) in the direction of the normal vector (8), from which the combined beam thickness is subtracted
where \(\rho ^{(1)}\) and \(\rho ^{(2)}\) the are cross-section radii of each beam, respectively. Since we assume cross-section to be circular, the radii are constants. We acknowledge that subtracting the thicknesses directly from the orthogonal distance between centrelines induces some geometrical error, but this is commonly accepted in the literature [7, 9, 10, 23]. This error stems from the fact that the projection vector is not perpendicular to the non-mortar centreline. Decreasing the angle between the centreline and the projection vector would increase the error in the computation, reaching its maximum when the two beams would be oriented perpendicularly (one piercing the other). Still, we set this issue aside and leave it to future research.
Contribution of the frictionless contact to the total energy of the system can be defined by the contact potential [39]
in which the true integration domain of the contact potential is the actual contact segment \(\Gamma _{c}\), where the two surfaces intersect. The distributed normal contact force is acting on both beams as an interaction force pair, making it equal and opposite on both sides. As such, it can be fully defined by the Lagrange-multiplier field \(\lambda \) on the non-mortar-side beam. So we approximate it by the centreline of the non-mortar-side beam \(\Gamma ^{(1)}\). The contact potential allows an elegant transition into the virtual work, which is the usual starting point of formulations [7, 9, 23]. In these references, the integration domain varies slightly. In [7], the authors compute the actual boundaries of the contact to determine the integration domain. This is not strictly necessary, since the contribution of virtual contact work outside the contact domain can be dismissed according to the contact constraints. The numerical implications of this choice are further discussed in Sect. 4.1.
4 Contact element
4.1 Weak form of contact potential
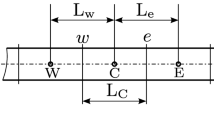
The contact potential integral (10) is approximated by an existing discretization of the non-mortar-side beam \((1)\) into non-mortar-side beam-elements (non-mortar elements) and contact elements, see Fig. 3. A contact element can be regarded as a parasitic finite element, attached to a non-mortar element and sharing its displacement field. It features its own Lagrange-multiplier field. The integral needs not include all non-mortar elements, but an appropriately large subset \(Q\) must be selected. All non-mortar elements prone to contact must be included in this subset. The discretized contact potential is
where \(L^{e}\) is the initial length of the non-mortar element \(e\). To simplify the notation, the index \(e\), denoting a particular non-mortar element, will from now on be omitted on the right-hand side. This agrees with the interpretation in which, after discretization, each beam element may be viewed as an individual beam in terms of the contact. It allows to reduce the number of contact elements if the contact location can be predicted in advance. It is also a simpler alternative to the computation of integration boundaries in [7] and integration segments in [23]. The drawback is that the contact discretization depends on the beam discretization, which may be unsuitable for very long beam elements relative to their contact-region size.
Contact discretization: Non-mortar elements are denoted as \(n_{i}\) and mortar elements as \(m_{i}\). The integration point \(A\) has two candidates for a mortar element partners as a result of the orthogonal projection of mortar elements \(m_{1}\) and \(m_{3}\). Among these, \(m_{3}\) is selected based on the projection vector magnitude \(||\boldsymbol{v}||\). Integration point \(B\) has a different mortar element as a partner although it belongs to the same contact element
Remark 1
As the non-mortar subset \(Q\) can change between load steps, advanced algorithms can be employed to include the optimal number of elements. For the simple numerical examples presented in this paper, an initial guess with a constant subset suffices.
Remark 2
Although it is not explicitly denoted, the integration is performed numerically using the Gauss-quadrature rule. Integrating over the entire element therefore might slightly increase the numerical integration error, however, we argue that it greatly simplifies the algorithm, as there is no need to compute boundaries and the Jacobian, as in [7], but simply integrate over the initial length of the beam. In [23] in penalty potential, the authors introduce integration segments to decouple beam discretization from contact discretization. Our argument is that with the Lagrange-multiplier method this is not strictly necessary as the large number of integration points is not essential. The number of integration points indeed depends on the shape of the gap function, which is further discussed in Sect. 5.
The variation of the contact potential (12) is
where the first and the second terms are associated with the virtual contact work and the weak form of the non-penetration condition, respectively. The enforcement of the non-penetration condition is described in Sect. 4.6.
The variation of the projection vector is obtained from (6)
Remark 3
Variation of the displacement field on the mortar side is affected by varying the field itself, but also by varying displacement field on the non-mortar side. This is because the corresponding mortar side point is determined through the orthogonal projection. Its variation is thus in total written as \(\delta \boldsymbol{x}^{(2)}(s^{(1)}) = \delta \boldsymbol{x}^{(2)}(s^{(2)}) + \boldsymbol{x}^{\prime (2)} \delta s^{(1)}\).
The variation of the normal vector follows from (8)
where the hat on a vector denotes a skew-symmetric matrix representing a cross-product operator (\(\widehat{\boldsymbol{a}}\boldsymbol{b} = \boldsymbol{a}\times \boldsymbol{b}\) for \(\boldsymbol{a},~\boldsymbol{b}\in \mathbb{R}^{3}\)). The variation of the gap function required in (13) is obtained by varying (9) which with the help of (14) and (15) yields
Using the result of the gap variation (16), the variation of the contact potential (13) can be finally written as
4.2 Consistent linearization
We start the linearization from equation (13) rather than the expanded form (17). For a consistent linearization, both the virtual work and the weak non-penetration condition must be considered
Linearization of the projection vector (6) and the normal vector (8) is the same as in (14) and (15)
The linearization of the gap function (9) then takes the same form as its variation (16)
The term \(\Delta s^{(1)}\) from (19) is obtained by linearizing the orthogonality condition (7)
from where \(\Delta s^{(1)}\) can be extracted as
where
The variation of the gap function (16) can now be linearized using the previously obtained results for the linearization of the projection vector (19) and the normal (20) as
The final expression for the linearization of the virtual contact work is presented in Appendix B.
4.3 Interpolation
The interpolation on the elements follows the standard finite-element approach using the shape functions. The additional degrees of freedom for the Lagrange-multiplier field need not to be attached to the existing beam nodes. This allows for a different interpolation order of the displacement and the Lagrange-multiplier field. In the following, however, we assume for the sake of simplicity of notation in the equations that the nodes do actually coincide. A general case with a reduced order of interpolation has also been implemented, analysed and discussed in Sect. 5.
In [7], the augmented-Lagrangian method is used in which the Lagrange multipliers are treated as a linear combination of their current value and the gap. This introduces new numerical constants (augmentation parameters) which influence the rate of convergence of the required iterative process to determine the equilibrium solution. Although the Lagrange-multiplier method and augmented-Lagrangian method are expected to acquire similar results, each method follows its own convergence path. Studies on solid elements [13] have found that both require a comparable computation cost.
Nodes connected to the selected elements are then supplied with an additional degree of freedom for the Lagrange multiplier. The nodal values of the displacement and the Lagrange-multiplier field are then assembled in a common matrix
where \(i \in \left \{ 1,2\right \} \) denotes a beam, while the element number is, again, omitted.
The Lagrange-multiplier field is chosen to be interpolated using the Lagrange polynomials \(\boldsymbol{\Phi }^{(1)} (s^{(1)}) = \begin{Bmatrix} \Phi _{1}(s^{(1)}) & \Phi _{2}(s^{(1)}) & \ldots \end{Bmatrix} ^{\mathrm{T}}\), while the centreline position interpolation \(\boldsymbol{N}^{(i)}(s^{(i)}) = \begin{Bmatrix} N_{1}(s^{(i)}) & N_{2}(s^{(1)}) & \ldots \end{Bmatrix} ^{\mathrm{T}}\) is inherited from the beam element
where \(i \in \left \{ 1,2\right \} \) again denotes a beam. In the case of the Simo & Vu-Quoc element [32] used in the present study, the shape functions \(\boldsymbol{N}^{(i)}\) are also Lagrange polynomials. Some studies concerning with point-to-point friction implement the Hermitian interpolation [19], which is \(C^{1}\) continuous. In [7], the \(SE(3)\) interpolation developed by [34] is used.
Inserting the interpolation (26a), (26b) into the variation of the contact potential (17) results in the residual force vector contribution from the contact for both beams. The integrals in the formulation are computed using the Gauss quadrature rule so that all integrated quantities are evaluated only at the integration points \(s^{(1)}_{g_{j}}\) for \(j \in \left \{ 1, 2, \ldots N_{\mathrm{Gauss}}\right \} \). Note that quantities like shape functions \(\boldsymbol{N}^{(2)}\), which are parametrised on the mortar side must be evaluated at the position obtained from the solution of the nearest point projection, i.e. \(s^{(2)}(s^{(1)}_{g_{j}})\).
Because of discretization, an appropriate mortar element must be selected for each integration point for the evaluation of the contact geometry, see Fig. 3. Maintaining the same mortar element during the Newton–Raphson algorithm is a prerequisite for its second-order convergence rate due to the piece-wise definition of the centreline across different elements. Mortar elements are selected for each integration point on the contact element at the beginning of each Newton–Raphson loop. For a particular integration point, a mortar element is chosen from a set of potential mortar elements. This set must in general include all mortar elements and can prove to be quite numerically demanding. For specific cases, a subset only in the neighbourhood of the contact element in question can be considered. In the present study, this subset was selected manually for each example depending on the possible contact positions. Generally, advanced algorithms for contact detection exist to select an optimal number of mortar elements, e.g. [38]. For all selected mortar elements, the nearest point projection must be computed at the beginning of each contact loop (see Sect. 4.6). From this, the closest mortar element with the projection point \(s^{(2)}\) value within its domain is selected as the mortar-element partner for the particular contact element integration point.
A contribution from an integration point without a converged projection is neglected, which is discussed in more detail in Sect. 4.7.
4.4 Residual vector
Combining equations (16) and (17) with (26a), (26b) leads to the discrete form of the variation of the contact potential. It can be written in vector notation for each node \(i\) on a non-mortar element as
from which the residual force vector contribution from contact follows as
where \(\boldsymbol{n}\) and \(g\) are the contact unit normal defined in (8) and the gap function defined in (9), respectively. All quantities with index \(i\) refer to the node for which the residual vector is computed. \(N_{i}\) thus refers to the appropriate shape function from (26a), (26b). The Lagrange-multiplier field \(\lambda \) is evaluated using equations (26a), (26b).
Similarly, for each node \(i\) on a mortar element it can be written as
from which the residual force vector contribution from contact follows as
All integrated quantities are functions of the non-mortar side parameter \(s^{(1)}\), except for the shape functions \(\boldsymbol{N}^{(2)}\) on the mortar side, which need to be mapped using
4.5 Tangent matrix
The tangent matrix is obtained from (16), (18), (21) and (23) along with (26a), (26b). The contributions consist of combinations of mortar and non-mortar element nodes, resulting in four different pairings. A pair of nodes \(i\) and \(j\) on the non-mortar element results in
from where the tangent matrix contribution follows as
where
Pairing a node \(i\) on the non-mortar element and a node \(j\) on the mortar element results in
from where the tangent matrix contribution follows as
where
Pairing a node \(i\) on the mortar element and a node \(j\) on the non-mortar element results in
from where the tangent matrix contribution follows as
Finally, a pair of nodes \(i\) and \(j\) on the mortar element results in
from where the tangent matrix contribution follows as
where
4.6 Enforcing contact condition
Non-smooth contact methods also require an appropriate algorithm for determining the status of each Lagrange multiplier, since only some multipliers actively participate in the contact and contribute to the contact force. In this paper, the active-set strategy is used, which requires a secondary iterative loop. It separates all Lagrange-multipliers into an active and an inactive set. The inactive nodes have the Lagrange multiplier set to zero and its respected degree of freedom disabled, while the active nodes can have the Lagrange multiplier with any real value and its respected degree of freedom enabled. Based on the configuration of beams after the Newton–Raphson loop, the sets are re-evaluated using the contact constraints below to reflect the current configuration. A new contact iteration is started if the sets change. Since this process is non-smooth and cannot be linearized, it represents a bottleneck in the overall convergence rate of the method. The inner Newton–Raphson iterative loop, solving the balance equations, has a second-order convergence rate provided that the full tangent matrix is used as described. The outer contact loop only experiences a first-order convergence rate. The overall convergence rate of the method is thus reduced due to the contact non-linearities in the system.
To avoid the secondary loop for determination of the contact conditions, the authors in [7] utilise a semi-smooth Newton scheme, akin to [14]. As emphasised by the authors in [14], such an alternative algorithm does not change the convergence rate and is expected to be equivalent to the method employed here. Nevertheless, a comparison in convergence of the two methods is undertaken in Sect. 5, Examples 2 and 4.
A more detailed description of the active-set strategy follows. All non-mortar nodes in the initial configuration are inactive. At the beginning of each Newton–Raphson loop, the contact conditions are checked for each non-mortar node thus determining the status of each node.
For an inactive node \(p\) to become active, the non-penetration condition must fail. The idea behind the mortar method is to transform a strong, point-wise non-penetration condition (5a) into a weak form and integrate it along the non-mortar elements by taking into consideration all (both) elements \(e\) that are connected to node \(p\)
For an active node \(p\) to become inactive, the positive pressure condition (5b) must fail. It is enforced point-wise by checking the nodal values of the Lagrange multipliers against the condition
The zero-work condition (5c) is guaranteed by the use of the active and inactive sets of nodes.
4.7 Integration points without projection
As already mentioned in Sect. 3, the integrals are evaluated only in the region of contact. This region is approximated by the non-mortar element centreline. The boundaries are enforced by the active-set strategy discussed in the previous Sect. 4.6. However, this approximation fails if the gap function cannot be evaluated, for example, when an element is partially extended beyond the mortar side. In this case, the projection of an integration point on a non-mortar element to a mortar side does not converge or it is not within the domain of any of the mortar elements. The contribution of such an integration point is neglected as it is reasonable to expect that it does not contribute to the virtual contact work.
5 Numerical examples
The presented numerical examples are run using the research code developed in Python, which is available online [35]. The geometrically exact beam theory [32] is used for the beam elements. The examples are selected to test different aspects of the contact formulation and demonstrate a broad field of possible applications. The tests are compared to the study of Meier et al. [23], where they implement a penalty method for a line-to-line contact, and Bosten et al. [7], where a mortar method with augmented-Lagrangian approach is used. Both studies are interesting for comparison because, together with the present study, they present the three main versions of the numerical algorithm for solving a line-to-line contact problem.
Example 1
Patch test
This test was proposed by Meier et al. [23] and is shown in Fig. 4. A static analysis of two beams of different lengths in contact is conducted. Both beams have the same Young’s modulus \(E_{1}=E_{2}=10^{9}\), Poisson’s ratio \(\nu _{1}=\nu _{2}=0.3\) and cross-section radius \(\rho ^{(1)}=\rho ^{(2)}=0.005\). The top beam is designated to be non-mortar and consists of two linear elements. Each element of the top beam has a length of 0.4. The bottom beam consists of three elements of length 0.9, 0.3 and 0.8. In the initial configuration, the beams are not in contact. The top beam has its left end controlled via a displacement along the \(x\) axis, while all of the bottom beam’s degrees of freedom are fixed, making it completely rigid. Then, in a single time step, the top beam is pressed against the bottom one by a distributed line force \(p=1.0\). Afterwards, in 100 equal load steps, the top beam is moved rightwards for a total displacement of \(U_{0} = 1.001\).
The exact solution of this problem is trivial, i.e. the gap must remain equal to zero throughout the analysis. The numerical solution of the problem is presented in Fig. 5. The gap error is computed as the norm of all computed values of the gap in a converged solution and is constant with value \(3.47\times 10^{-18}\). The non-penetration condition is thus fulfilled within the numerical machine precision and the validity of the method is thus established. Due to the weak fulfilment of the non-penetration condition, sliding over the elements does not lead to any loss of convergence. All Newton–Raphson loops require a single iteration to converge. The number of contact integration points used in the test is 2, however, larger values have been tested as well yielding the same result.
Compared to [23], where the penalty method is used, this presents a considerable improvement. With the penalty method, some penetration proportional to the chosen parameters is expected. Secondly, the numerical results in the original study are dependent on the number of integration points. Even with increasing the number of the integration points, the solution does not converge to the expected solution of −0.002 (a solution expected for the chosen penalty parameters). Furthermore, the gap varies with load steps due to sliding. Both problems were averted with the mortar method. We can see in Fig. 5 that the gap is stable and constant, with load steps and sliding appearing to have no effect on the result. The exact solution is reached with full integration, that is with 2 Gauss points.
In [7] a simplified version of this test was studied. Two beams of equal length but different discretization are pressed together. They arrive to the same conclusion that the gap equals to zero within the machine precision and that the system converges in a single Newton–Raphson iteration. The effects of the discontinuities due to sliding were not tested in [7].
Example 2
Cantilever
This is an example proposed by Bosten et al. in [7]. A cantilever beam of the length 0.3 with a circular cross-section with the radius \(\rho =0.001\) is positioned above a rigid body. Between them is a gap \(H = 0.0005\). The beam has the following material properties: axial stiffness \(EA = 6.28 \times 10^{5}\), shear stiffness \(GA = 0.242 \times 10^{5}\), torsional stiffness \(GI_{t} = 0.12\) and bending stiffness \(EI = 0.16\). The beam is pressed towards the rigid body by a distributed load \(p=10\). The elements used in this example use the same order of interpolation for displacement and the Lagrange multipliers.
In Fig. 6 we can see how the results for the final contact force distribution from [7] compare to the present study. The beam is discretized using 64 linear or quadratic elements and the full load is applied in 240 steps. The main difference originates from the selection of the beam element. In [7] the authors use \(SE(3)\) beam elements. Our first-order elements have a significantly different distribution of the Lagrange-multiplier field, while our second-order elements produce comparable results to the reference \(SE(3)\) solution. It is also interesting to compare how the second-order interpolation of the Lagrange multipliers affects the oscillations at the boundary of the contact region. In [7], the authors test only the first-order interpolation of the Lagrange multipliers, which leads to smaller oscillations compared to the second-order interpolation. Also an interesting artefact of the second-order interpolation is a partially negative Lagrange-multiplier field, which is permitted by the constraint enforcement, since only the nodal values are checked. The differences are not attributed to the difference in solution technique (augmented-Lagrangian vs Lagrange-multipliers method), but to the difference in elements and interpolation of the Lagrange-multiplier field.
In Fig. 7, spatial convergence of both elements compared to the reference solution is presented. Convergence speed is attributed to the interpolation order of the Lagrange-multiplier field. The present linear and \(SE(3)\) elements both exhibit slower convergence than does the present quadratic element with the second-order Lagrange-multiplier interpolation.
Figure 8 shows on a logarithmic scale how the gap is distributed for both orders of elements. The differences between them are small, but one can observe that the value of the gap function is consistently closer to zero in the contact region with the second-order interpolation.
The energy evolution for the example with 64 linear elements is shown in Fig. 9. The energy difference \(W_{ext} - E_{P}\) is relatively small for the entire duration of the simulation. In Fig. 10 we can observe more closely the first 10 steps. The contact happens after step 2 which is visible in the change of \(W_{ext} - E_{P}\) which is now different from zero. This behaviour is expected in non-smooth mechanics. The energy difference changes for the entire duration of the contact, as is visible in Fig. 11. There we can also see, that the second-order interpolation has a smaller difference in \(W_{ext} - E_{P}\).
Median convergence in two iterations is observed as in [7]. The average number of Newton–Raphson iterations is 1.3, but there are also 1.6 secondary contact loop iterations which brings to a total of 2.1 iterations per time step.
Example 3
Rotating beams
Two cantilever beams are placed one above the other at a certain angle. The bottom beam is collinear with the \(x\)-axis and completely fixed. The top beam lays initially in the plane \(x\)-\(y\) at an angle \(\alpha \) around the \(z\) axis like shown in Fig. 12. The beams are initially touching, so if the position of the top beam on \(z\)-axis is at \(H\), the contact radius of each beam is \(\rho =H/2\). The displacement of the free end of the top beam is free only in the \(z\)-axis. The rotations of the free end are not constrained. The free end is loaded with a point force in the \(z\)-axis. The appropriate size of the point force is such that if the contact were not considered, the two centrelines would intersect in the middle as shown in Fig. 13. The size of the force is computed using the same setup only without contact constraints. This ensures the maximum possible penetration for a given setup. The material parameters are: \(EA=GA=1\) and \(GI = EI = 10\).
Each beam consists of only a single linear element with 3 integration points, which reduces the total number of degrees of freedom to 5 (4 for the movement of the only free node and 1 for its Lagrange multiplier). The contact radius is varied in order to determine the smallest possible ratio between the thickness of an element and its length, at which contact is still detectable by the mortar method.
The test was first analysed analytically. Evaluating equation (9) for the deformed configuration without contact detection, as shown in Fig. 13, yields the following gap function
This gap is integrated according to (44) for the free node giving the following expression
When this expression equals zero, the condition is just before switching the Lagrange-multiplier degree of freedom. Solved for \(H\), it defines the limit at which contact is detected for a given configuration, which is
The test was also conducted numerically for values of \(\alpha \) from 0 to \(\pi \) with a step \(\pi /60\) and \(H\) for values from 0.06 to 1.99 with a step 0.06. This produces a matrix of results which can be seen in Fig. 14. A unified measure \((\rho ^{(1)} + \rho ^{(2)}) / L^{(1)}\) is introduced, where index \((1)\) is associated with the non-mortar element (blue in Fig. 12) and \((2)\) with the mortar element (orange in the same figure). Successfully converged results with a contact detected are coloured green, while the rest remains white. Some results can converge to an unphysical solution, but this can be averted by introducing the load in several load steps and is as such not a concern of this test case. The contour is cross-plotted with the analytical solution for the minimal detectable radius (48). Numerical and analytical results match as expected.
In a general situation, contact can happen anywhere on the element. However, if all nodes can become active, having the contact point exactly in the middle of the element is weighted by the shape functions the least and moving it towards some node would result in a quicker detection of a contact. So, in some special cases, the contact can be detected even with a smaller ratio of \((\rho ^{(1)} + \rho ^{(2)}) / L^{(1)}\). In general, the worst case scenario must govern the choice for the size of the elements, which is predicted by this example.
Finally, the convergence of the mortar method for \(\alpha =\pi /2\) and \(H=1\) was tested. The load size is computed as above, but now added in 4 equal steps. Only the meshes with an odd number of first-order elements were tested to avoid direct nodal contact. The final deformed configuration for the example using 81 elements is shown in Fig. 15. Lagrange-multiplier field convergence is presented in Fig. 16. The force distribution converges towards a step function with some boundary effects. A silhouette of the bottom-beam’s cross section is overlaid to better illustrate the effective width of the contact. The corresponding gap functions can be seen in Fig. 17. The gap flattens to the same width as observed for the force. Some penetration is present for coarser meshes.
Example 4
Twisting of two cantilever beams
Two beams are positioned one above the other, fixed at one end and rotated around axis \(x_{1}\) at the other using a displacement control (see Fig. 18) to form a helix-like shape. This test was originally proposed by Meier et al. [23], where Kirchhoff–Love theory was used to describe the beam element. Here Simo–Reissner beam elements were used and in order to maintain convergence due to large twisting strains, slightly different material parameters are used compared to the original test.
Both beams are equal in terms of material, geometry and finite element discretization. The material is linear elastic with Young’s modulus \(E=10^{9}\) and Poisson’s ratio \(\nu =0.3\). The geometry is shown in Fig. 18. The length of each beam is 5 and they are initially touching, making the distance between their centrelines \(H=0.02\). The cross-sections are circular with radius \(\rho =0.01\). These beams are effectively very long and thin, as can be properly seen in Fig. 19. The angular increments are such that a full circle is completed in 8 load steps. Before the twisting is applied, the beams are pre-tensioned in a separate load step with an axial displacement of 0.049647. Second-order elements are used in both beams. They are discretised with 8, 16, 32 and 64 elements, each with a varying number of contact integration points.
The convergence of the final contact force distribution is shown in Fig. 20. An alternating solution can be identified with the overall amplitude becoming smaller as the number of elements increases. The contact force is converging towards a constant value of around −50 with the clear boundary effects explained later. The integration error has been tested using 8 elements in combination with 2, 3 and 8 contact integration points on each element. While all solutions successfully converge, it is necessary to use at least the number of nodes on an element for the number of contact integration points to eliminate significant integration error (see Fig. 21). Higher order integration might also be necessary if strong \(C^{1}\) discontinuities are present on the mortar side. This, however, has not been encountered in this example.
Finally, the reduced-order interpolation of the Lagrange-multiplier field has been also tested. A comparison has been made between the linear and the quadratic interpolation, both in combination with 16 quadratic beam elements. The results are given in Figs. 22 and 23. Interestingly, it can be seen that the fluctuations in the contact force have been significantly reduced while the error in the gap approximation has reciprocally increased. These fluctuations are actually the same as the ones observed in Fig. 6 and are a consequence of the relatively high curvature present at the boundary of the contact. In order to reduce the internal bending forces, the radius of curvature of the beam is increased and thus presses harder on the other beam in contact. Due to the rigid nature of the cross-section it results in unphysical oscillations in the contact force. As such, these fluctuation are inherent to the beam theory independent on the type of formulation that is used. In [23], the authors argue that the penalty approach is more appropriate for such cases, as it numerically allows for some penetration, simulating the deformability of the cross-section. However, the introduced penalty parameter affects the solution, while not being a mechanical property of the system and is as such problematic to determine appropriately. Also, a similar boundary effect is present in their formulation with the penalty method, although, the distribution of the contact force is significantly smoother. Clearly, there is a trade-off between the penetration and the oscillations of the force. These oscillations do not seem to affect the convergence of the method, which is the same observation as in [7], where a similar study has been undertaken.
A comparative simulation with the definition of this example from [7] was also conducted. Four full turns are applied using 64 quadratic elements. The final integrated gap comparison can be seen in Fig. 24. As expected, the mortar method fulfils the weighted gap constraint (44) in both cases. The difference shows in the Lagrange-multiplier field illustrated in Fig. 25, which has a lot less oscillations in [7]. This is attributed to the \(SE(3)\) element, which can interpolate helix-like shape of the centreline much better than the polynomial interpolation used in our elements. Stable oscillations of the force in the most part of the beam show that this is indeed the converged solution, which is required to force the beams into the helix-like shape.
Twisting: integrated gap using second-order elements compared to \(SE(3)\) elements [7]
Twisting: Lagrange-multipliers using second-order elements compared to \(SE(3)\) elements [7]
Example 5
Twisting of a ring
A single beam in a shape of a ring is clamped at one end, as shown in Fig. 26. Diametrically across, it is being twisted by a concentrated moment around \(x_{1}\) axis. The test is similar to the one proposed by Chamekh et al. [9]. The ring radius is \(R= 1\), while the circular cross-section radius is \(\rho = 0.04 \pi \). The material parameters are selected in a way to avoid any bifurcation phenomena. The axial stiffness is \(E A = 2.76461 \times 10^{3}\), the shear stiffness is \(G A = 1.03924 \times 10^{3}\), the bending stiffness is \(E I = 2764.52\) and the torsional stiffness is \(G I_{t} = 2078.5\). The moment is applied in 14 load steps. The first 9 load steps increase the moment magnitude by 700, after which the contact is expected and thus in the following steps the moment increase is reduced to 70. The total moment load accumulates to 6650. The final deformed shape with 32 second-order elements is presented in Fig. 27.
First, the ring has been discretised with 8 second-order beam elements. Two cases have been analysed – test case A, where all 8 beam elements are also non-mortar and test case B, where only the first half of the elements (4 elements between the fixing point and the concentrated moment) are non-mortar. No issues arise in any of the two cases and the resulting gap function in Fig. 28 is matching completely in both cases. In test case A, the contact force in Fig. 29 gets distributed equally between the non-mortar elements on both sides of the contact and is therefore half the size of the one in test case B.
Second, the convergence of the solution is tested by refining the mesh using 8 and 32 quadratic elements. The gap function evaluated at the integration points can be seen in Fig. 30. It can be observed that in the case with 8 elements the curve is not defined in the entire domain, specifically where the gap should be larger. This is due to the divergence in the nearest point projection algorithm. As the contribution of these integration points is small, it does not affect the overall solution. Close to the contact, where the gap is smaller, the results almost match those from the finer mesh. The position of the contact is slightly shifted, probably due to the larger approximation error of the geometry itself. The contact force forms a spike that is higher and narrower with increasing number of elements (Fig. 31). The nature of the beam theory with rigid cross-section would suggest that the expected result is exactly a point force in the shape of the Dirac delta function. However, due to the weak character of the non-penetration condition, it is approximated by a distributed force.
Also, due to the weak non-penetration condition employed in the mortar method, it has been expected from the start that if the ratio between cross-section radius and element length \((\rho ^{(1)} + \rho ^{(2)})/L^{(1)}\) is too large, it may pose a problem for contact detection when two beams intersect perpendicularly. This example has been used to test this property and it is determined that at least 7 elements are required for contact to be detected, in which case, the ratio is \((\rho ^{(1)} + \rho ^{(2)})/L^{(1)}=0.28\). This value agrees with Example 3, Fig. 14 for an angle close to \(\pi /4\).
6 Conclusion
An alternative formulation to [7] is proposed for static analysis of beam-to-beam and self contacts without friction. It is
-
based on the Lagrange-multipliers method,
-
performs no computation of the integration boundaries,
-
may have an arbitrary order of interpolation for Lagrange multipliers field.
While well-known and widely used by the contact-mechanics community when dealing with solid finite elements, the mortar method has proven to be well suited also for beam applications, as already shown in [7]. No significant difference was detected in the performance between the augmented-Lagrangian and Lagrange-multiplier method. The present study further shows the applicability of the method to regular \(\mathbb{R}^{3}\times SO(3)\) manifold by the usage of the Simo & Vu-Quoc beam element [32], yielding consistent results in terms of contact. Inferior results can be expected when twisting compared to \(SE(3)\) due to the helicoidal interpolation used in those elements. Compared to [7], we have additionally investigated some properties of the mortar method, specifically the ability to handle a side-to-side contact. It has been shown analytically and confirmed numerically what are the limits to the contact radius vs. element length ratio. A different integration scheme compared to [7] is used which is shown to simplify the formulation while not deteriorating the results. A full tangent matrix is derived which consistently leads to a second-order convergence in the Newton–Raphson loop. Additional comparisons to the penalty method from [23] are made, specifically we analysed the sliding, which has been shown to be more stable than in the penalty method and twisting, which is more precise in terms of the gap function but has higher oscillations in the force. The latter do not lead to any loss of convergence, as already discussed in [7].
Additional application with self-contact has shown that the formulation is very robust in terms of selecting the correct set for the non-mortar elements. Even by selecting all beam elements, the system does not become over-constrained but instead successfully converges to the same solution. This might prove useful in cases where the specific nature of contact cannot be predicted.
Because of the weak fulfilment of the non-penetration condition and a distributed contact force, a high resemblance with the physical phenomenon of contact is achieved, resulting in a robust and precise method. For parallel contact cases, the mortar method provides a solution with evenly distributed contact force that is not influenced by sliding, while the perpendicular contact cases require an appropriately small ratio between the cross-section radii and the non-mortar element length. Surprisingly, the mortar method, in contrast to the penalty method, proves to be rather independent of the number of integration points. Only a few of them per element are sufficient for all test cases.
These tests prove that the mortar method is not only an effective formulation for beam-to-beam contact but also provides a lot of space for improvement and future research. In the future, our research will focus on making the formulation independent of the choice of mortar/non-mortar side.
Notes
While having similar notation, note that explicit \(s^{(2)}(s^{(1)})\) denotes the solution to the nearest point projection problem, while the independent natural coordinate on beam \((2)\) is denoted by \(s^{(2)}\).
References
Bauchau, O.A., Han, S.: Interpolation of rotation and motion. Multibody Syst. Dyn. 31(3), 339–370 (2014). https://doi.org/10.1007/s11044-013-9365-8
Bauchau, O.A., Epple, A., Heo, S.: Interpolation of finite rotations in flexible multi-body dynamics simulations. Proc. Inst. Mech. Eng., Proc., Part K, J. Multi-Body Dyn. 222(4), 353–366 (2008). https://doi.org/10.1243/14644193JMBD155
Belgacem, F.B.: The Mortar finite element method with Lagrange multipliers. Numer. Math. 84(2), 173–197 (1999). https://doi.org/10.1007/s002119900100
Belgacem, F.B., Hild, P., Patrick, L.: Approximation du problème de contact unilatéral par la méthode des éléments finis avec joints. C. R. Acad. Sci., Ser. 1 Math. 324(1), 123–127 (1997). https://doi.org/10.1016/s0764-4442(97)80115-2
Borri, M., Bottasso, C.: An intrinsic beam model based on a helicoidal approximation – Part I: formulation. Int. J. Numer. Methods Eng. 37(13), 2267–2289 (1994). https://doi.org/10.1002/nme.1620371308
Borri, M., Bottasso, C.: An intrinsic beam model based on a helicoidal approximation – Part II: linearization and finite element implementation. Int. J. Numer. Methods Eng. 37(13), 2291–2309 (1994). https://doi.org/10.1002/nme.1620371309
Bosten, A., Cosimo, A., Linn, J., Brüls, O.: A mortar formulation for frictionless line-to-line beam contact. Multibody Syst. Dyn. (2021). https://doi.org/10.1007/s11044-021-09799-5
Bottasso, C.L., Borri, M.: Integrating finite rotations. Comput. Methods Appl. Mech. Eng. 164(3–4), 307–331 (1998). https://doi.org/10.1016/S0045-7825(98)00031-0
Chamekh, M., Mani-Aouadi, S., Moakher, M.: Modeling and numerical treatment of elastic rods with frictionless self-contact. Comput. Methods Appl. Mech. Eng. 198(47), 3751–3764 (2009). https://doi.org/10.1016/j.cma.2009.08.005
Durville, D.: Contact-friction modeling within elastic beam assemblies: an application to knot tightening. Comput. Mech. 49(6), 687–707 (2012). https://doi.org/10.1007/s00466-012-0683-0
Gay Neto, A.: Dynamics of offshore risers using a geometrically-exact beam model with hydrodynamic loads and contact with the seabed. Eng. Struct. 125, 438–454 (2016). https://doi.org/10.1016/j.engstruct.2016.07.005
Gonçalves, R., Carvalho, J.: An efficient geometrically exact beam element for composite columns and its application to concrete encased steel I-sections. Eng. Struct. 75, 213–224 (2014). https://doi.org/10.1016/j.engstruct.2014.05.042
Hiermeier, M., Wall, W.A., Popp, A.: A truly variationally consistent and symmetric mortar-based contact formulation for finite deformation solid mechanics. Comput. Methods Appl. Mech. Eng. 342, 532–560 (2018). https://doi.org/10.1016/j.cma.2018.07.020
Hintermüller, M., Ito, K., Kunisch, K.: The primal-dual active set strategy as a semismooth Newton method. SIAM J. Optim. 13(3), 865–888 (2003). https://doi.org/10.1137/S1052623401383558
Hüeber, S., Wohlmuth, B.I.: A primal-dual active set strategy for non-linear multibody contact problems. Comput. Methods Appl. Mech. Eng. 194(27–29), 3147–3166 (2005). https://doi.org/10.1016/j.cma.2004.08.006
Jelenić, G., Crisfield, M.A.: Geometrically exact 3D beam theory: implementation of a strain-invariant finite element for statics and dynamics. Comput. Methods Appl. Mech. Eng. 171(1–2), 141–171 (1999). https://doi.org/10.1016/S0045-7825(98)00249-7
Lang, H., Linn, J., Arnold, M.: Multi-body dynamics simulation of geometrically exact Cosserat rods. Multibody Syst. Dyn. 25(3), 285–312 (2011). https://doi.org/10.1007/s11044-010-9223-x
Litewka, P.: The penalty and Lagrange multiplier methods in the frictional 3d beam-to-beam contact problem. Civ. Environ. Eng. Rep. 1(1), 189–207 (2005)
Litewka, P.: Hermite polynomial smoothing in beam-to-beam frictional contact. Comput. Mech. 40(5), 815–826 (2007). https://doi.org/10.1007/s00466-006-0143-9
Litewka, P., Wriggers, P.: Contact between 3D beams with rectangular cross-sections. Int. J. Numer. Methods Eng. 53(9), 2019–2041 (2002). https://doi.org/10.1002/nme.371
Martin, T., Bihs, H.: A numerical solution for modelling mooring dynamics, including bending and shearing effects, using a geometrically exact beam model. J. Mar. Sci. Eng. 9(5), 486 (2021). https://doi.org/10.3390/jmse9050486
McDevitt, T.W., Laursen, T.A.: A mortar-finite element formulation for frictional contact problems. Int. J. Numer. Methods Eng. 48(10), 1525–1547 (2000). https://doi.org/10.1002/1097-0207(20000810)48:10<1525::AID-NME953>3.0.CO;2-Y
Meier, C., Popp, A., Wall, W.A.: A finite element approach for the line-to-line contact interaction of thin beams with arbitrary orientation. Comput. Methods Appl. Mech. Eng. 308, 377–413 (2016). https://doi.org/10.1016/j.cma.2016.05.012
Meier, C., Wall, W.A., Popp, A.: A unified approach for beam-to-beam contact. Comput. Methods Appl. Mech. Eng. 315, 972–1010 (2017). https://doi.org/10.1016/j.cma.2016.11.028
Meier, C., Grill, M.J., Wall, W.A., Popp, A.: Geometrically exact beam elements and smooth contact schemes for the modeling of fiber-based materials and structures. Int. J. Solids Struct. 154, 124–146 (2018). https://doi.org/10.1016/j.ijsolstr.2017.07.020
Popp, A., Gitterle, M., Gee, M.W., Wall, W.A.: A dual mortar approach for 3D finite deformation contact with consistent linearization. Int. J. Numer. Methods Eng. 83(11), 1428–1465 (2010). https://doi.org/10.1002/nme.2866
Puso, M.A.: A 3D mortar method for solid mechanics. Int. J. Numer. Methods Eng. 59(3), 315–336 (2004). https://doi.org/10.1002/nme.865
Puso, M.A., Solberg, J.M.: A dual pass mortar approach for unbiased constraints and self-contact. Comput. Methods Appl. Mech. Eng. 367, 113092 (2020). https://doi.org/10.1016/j.cma.2020.113092
Quan, W.C., Zhang, Z.Y., Zhang, A.Q., Zhang, Q.F., Tian, Y.: A geometrically exact formulation for three-dimensional numerical simulation of the umbilical cable in a deep-sea ROV system. China Ocean Eng. 29(2), 223–240 (2015). https://doi.org/10.1007/s13344-015-0016-0
Romero, I.: The interpolation of rotations and its application to finite element models of geometrically exact rods. Comput. Mech. 34(2), 121–133 (2004). https://doi.org/10.1007/s00466-004-0559-z
Simo, J.C.: A finite strain beam formulation. The three-dimensional dynamic problem. Part I. Comput. Methods Appl. Mech. Eng. 49(1), 55–70 (1985). https://doi.org/10.1016/0045-7825(85)90050-7
Simo, J.C., Vu-Quoc, L.: A three-dimensional finite-strain rod model. Part II: computational aspects. Comput. Methods Appl. Mech. Eng. 58(1), 79–116 (1986). https://doi.org/10.1016/0045-7825(86)90079-4
Simo, J.C., Vu-Quoc, L.: On the dynamics in space of rods undergoing large motions – a geometrically exact approach. Comput. Methods Appl. Mech. Eng. 66(2), 125–161 (1988). https://doi.org/10.1016/0045-7825(88)90073-4
Sonneville, V., Cardona, A., Brüls, O.: Geometrically exact beam finite element formulated on the special Euclidean group SE(3). Comput. Methods Appl. Mech. Eng. 268, 451–474 (2014). https://doi.org/10.1016/j.cma.2013.10.008
Tomec, J.: tomecj/beam. https://github.com/tomecj/beam
Wang, L., Liu, X., Renevier, N., Stables, M., Hall, G.M.: Nonlinear aeroelastic modelling for wind turbine blades based on blade element momentum theory and geometrically exact beam theory. Energy 76, 487–501 (2014). https://doi.org/10.1016/j.energy.2014.08.046
Wohlmuth, B.I.: A mortar finite element method using dual spaces for the Lagrange multiplier. SIAM J. Numer. Anal. 38(3), 989–1012 (2001). https://doi.org/10.1137/S0036142999350929
Wriggers, P.: Computational Contact Mechanics (2006). https://doi.org/10.1007/978-3-540-32609-0
Wriggers, P., Simo, J.C.: Note on tangent stiffness for fully nonlinear contact problems. Commun. Numer. Methods Eng. 1(5), 199–203 (1985). https://doi.org/10.1002/cnm.1630010503
Wriggers, P., Zavarise, G.: On contact between three-dimensional beams undergoing large deflections. Commun. Numer. Methods Eng. 13(6), 429–438 (1997). https://doi.org/10.1002/(SICI)1099-0887(199706)13:6<429::AID-CNM70>3.0.CO;2-X
Xiao, X., Xue, H., Chen, B.: Nonlinear model for the dynamic analysis of a time-dependent vehicle-cableway bridge system. Appl. Math. Model. 90, 1049–1068 (2021). https://doi.org/10.1016/j.apm.2020.09.053
Funding
This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 860124. The present paper only reflects the authors’ views. The European Commission and its Research Executive Agency are not responsible for any use that may be made of the information it contains.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Nearest point projection
The shortest distance from a curve \(\mathcal{C}\) to a point \(P\) (Fig. 32) is the magnitude of the vector perpendicular to the curve. The curve could potentially have multiple points \(\boldsymbol{r}_{i}\), where the normal is going through \(P\), however, this algorithm is restricted to finding the local minimum close to the initial guess. The curve is defined parametrically by the coordinate \(s\) and its position is denoted by \(\boldsymbol{r}\). The point \(P\) has the position vector denoted by \(\boldsymbol{r}_{P}\). The following set of equations needs to be solved
where \(\boldsymbol{x}\) denotes the combined vector of unknowns and \(\boldsymbol{x}_{n}\) its converged value satisfying the equation (50). Since the system is nonlinear for non-straight curves \(\mathcal{C}\), Newton–Raphson iterative algorithm is employed
with the residual vector
and the tangent matrix
where \(\mathbf{I}\) is the identity matrix of rank 3.
Appendix B: Tangent matrix
Final expression for the linearization of the virtual contact work following from (16), (18), (21) and (23)
This expression can be condensed by using the following substitutions
resulting in
Each row describes the interaction of a different combination of nodes belonging to beam 1 and beam 2. Inserting interpolation functions (26a), (26b) for individual node leads to
Rewriting this in the matrix form finally reveals Eqs. (33)–(43)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tomec, J., Jelenić, G. Analysis of static frictionless beam-to-beam contact using mortar method. Multibody Syst Dyn 55, 293–322 (2022). https://doi.org/10.1007/s11044-022-09823-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-022-09823-2