1 Introduction

Rigid body dynamics algorithms for evaluating the equations of motion (EOM) and their derivatives find numerous applications in the design optimization and control of modern robotic systems. The equations of motion can be differentiated with respect to state variables, control output (generalized forces), time and physical parameters of the robot (see [8] for an overview). These derivatives can be computed with several methods: 1) approximation by finite differences, 2) automatic differentiation [31], i.e. by applying the chain rule formula in an automatic way knowing the derivatives of basic functions (cos, sin or exp), 3) closed-form derivatives of the EOM and 4) recursive and analytical formulations exploiting the structure of the closed-form equations of motion. While the first two methods are generic and numerical in nature, the latter two are analytical in nature and exploit the structure of the EOM. Analytical and recursive partial derivatives of the EOM of rigid body systems with respect to state variables and generalized forces have been reported in the literature [3, 17]. These are useful in optimal control of legged robots (e.g. differential dynamic programming [19]) and their computational design and optimization [12]. Time derivatives of EOM are required for the model-based control and motion planning of robots with higher-order continuity [27], since for highly dynamic applications not only the actuation forces but also their derivatives must be bounded in order to ensure feasibility. Flatness-based control of robots with flexible joints, and of robots equipped with series elastic actuators (SEA) or variable stiffness actuators (VSA), necessitate the first and second time derivatives of the EOM of the robot [6, 9, 26]. Therefore, recursive \(O\left ( n\right ) \)-algorithms for the evaluation of the time derivatives were developed [1, 2, 10, 11, 21, 24] extending existing \(O\left ( n\right ) \)-formulations for the evaluation of EOM. While \(O\left ( n\right ) \)-formulations are deemed computationally advantageous when dealing with large systems, formulating and evaluating the EOM in closed form remains an efficient alternative for many robotic systems and provides insights into the structure of the problem. Yet, such closed-form formulations were not reported in the literature, with the exception of [13] where first-order time derivatives of the EOM were presented within the so-called spatial operator framework. A relatively recent research topic, where higher-order derivatives of the EOM are required, is the dynamic balancing of articulated mechanisms [4, 30, 32]. In [5], the time derivatives of the spatial momentum were used to derive global balancing conditions. Recently, we also proposed \(n\)th order time derivatives of EOM in both recursive and closed forms [15].

In this paper, the first and second time derivatives of the EOM are presented. For the subsequent treatment, the EOM are written in the form suitable for solving the inverse dynamics problem

$$ \mathbf{Q}=\mathbf{M}\left ( \mathbf{q}\right ) \ddot{\mathbf{q}}+ \mathbf{C}\left ( \dot{\mathbf{q}},\mathbf{q}\right ) \dot{\mathbf{q}}+ \mathbf{Q}_{\mathrm{grav}}\left ( \mathbf{q}\right ) +\mathbf{Q}_{\mathrm{ext}} \left ( \mathbf{q},t\right ) $$
(1)

where the vector of generalized coordinates \(\mathbf{q}=\left ( q_{1},\ldots ,q_{n}\right ) ^{T}\) comprises the \(n\) joint variables, \(\mathbf{M}\) and \(\mathbf{C}\) is the generalized mass and Coriolis matrix, respectively, and \(\mathbf{Q}_{\mathrm{grav}}\) represents generalized gravity forces. The generalized forces due to external loads (e.g. interaction/contact forces and torques) are summarized in \(\mathbf{Q}_{\mathrm{ext}}\). Finally, \(\mathbf{Q}\) are the generalized forces (drive forces/torques) required for a prescribed motion \(\mathbf{q}\left ( t\right ) \).

In the following, the derivatives of (1) are derived using the Lie group formalism reported in [23], which is equivalent to those presented in [18] and [25]. A salient feature of the Lie group formulation is that it admits model description in terms of readily available data without compromising computational efficiency (of closed-form expressions as well as \(O\left ( n\right ) \) algorithms). As a side contribution, we also prove the structural properties of EOM from a closed-form perspective. For the sake of simplicity, and without loss of generality a single serial kinematic chain, comprising 1-DOF joints, mounted at the ground is considered. The generalizations to systems with arbitrary tree-topologies is straightforward, but will not be considered here in order to simplify notation and make the paper easily accessible.

Organization:

Section 2 presents the equations of motion of serial kinematic chain in closed form using the body–fixed representation of the twists. Section 3 and Sect. 4 presents the first- and second-order time derivatives of the equations of motion in closed form, respectively. Section 5 proves the structural properties of the EOM using the closed-form formulations. Section 6 presents the application of the proposed derivatives in evaluating second-order inverse dynamics of two exemplary robot manipulators and a discussion on its computational performance. Section 7 concludes the paper.

2 Equations of motion in closed form

2.1 Kinematics in terms of joint screws

In the following, the notation and formulation of the EOM are adopted from [23]. The configuration (pose, posture) of body \(i=1,\ldots ,n\) is denoted \(\mathbf{C}_{i}\in SE\left ( 3\right ) \), which describes the frame transformation from a body-fixed frame (arbitrarily located at the body) to the inertial frame. Bodies and joints are numbered increasing order starting from the ground, so that joint \(i\) links body \(i\) to its predecessor \(i-1\), while the ground is indexed with 0, and by convention \(\mathbf{C}_{0}=\mathbf{I}\). The relative configuration of body \(j\) with respect to body \(i\) is then

$$\begin{aligned} \mathbf{C}_{i,j} =&\mathbf{C}_{i}^{-1}\mathbf{C}_{j} \\ =&\left ( \textstyle\begin{array}{c@{\quad }c} \mathbf{R}_{ij} & {^{i}}\mathbf{r}_{i,j} \\ \mathbf{0} & 1\end{array}\displaystyle \right ) \end{aligned}$$
(2)

where \(\mathbf{R}_{ij}\in SO\left ( 3\right ) \) is the rotation matrix transforming coordinates expressed in the reference frame on body \(j\) to their expression in the reference frame on body \(i\), and \({^{i}}\mathbf{r}_{i,j}\in {\mathbb{R}}^{3}\) is the position vector from the origin of frame \(i\) to the origin of frame \(j\) expressed in frame \(i\). Without loss of generality, all joints are assumed to have 1-DOF. Denote with \(q_{i}\) the joint variable (rotation angle, translation) of joint \(i\). The configuration of body \(i\) is determined by the product of exponential (POE) as

$$ \mathbf{C}_{i}\left ( \mathbf{q}\right ) =\mathbf{B}_{1}\exp ({^{1} \mathbf{X}}_{1}q_{1})\mathbf{B}_{2}\exp ({^{2}\mathbf{X}}_{2}q_{2})\cdot \ldots \cdot \mathbf{B}_{i}\exp ({^{i}\mathbf{X}}_{i}q_{i}) $$
(3)

where \({\mathbf{B}}_{i}:=\mathbf{C}_{i-1,i}\left ( \mathbf{0}\right ) \in SE \left ( 3\right ) \) is the configuration of body \(i\) relative to its predecessor \(i-1\), in the reference configuration \(\mathbf{q}=\mathbf{0}\), and \({^{i}\mathbf{X}}_{i}\) is the screw coordinate vector associated to joint \(i\) represented in the body-frame of body \(i\) [22]. The vectors \({^{i}\mathbf{X}}_{i}\) are constant due to the body-fixed representation. For 1-DOF lower-pair joints they are given as

X i i = ( e i i i x i × i e i + i e i h i ) =: ( ξ i i η i i )
(4)

where \({^{i}}\mathbf{e}_{i}\in {\mathbb{R}}^{3}\) is a unit vector along the joint axis, \({^{i}}\mathbf{x}_{i}\in {\mathbb{R}}^{3}\) is the vector to a point on this axis, and \(h_{i}\in {\mathbb{R}}\) is the pitch of the joint. In particular, for a revolute and prismatic joint, the screw coordinate vector is, respectively,

$$ \mathrm{Revolute:\ }{^{i}\mathbf{X}}_{i}=\left ( \textstyle\begin{array}{c} {^{i}}\mathbf{e}_{i} \\ \ {^{i}}\mathbf{x}_{i}\times {^{i}}\mathbf{e}_{i}\end{array}\displaystyle \right ) ,\ \ \ \mathrm{Prismatic:\ }{^{i}\mathbf{X}}_{i}=\left ( \textstyle\begin{array}{c} \mathbf{0} \\ {^{i}}\mathbf{e}_{i}\end{array}\displaystyle \right ) . $$
(5)

In terms of these screw coordinates \({\mathbf{X}}\), the exponential map attains the explicit form [18, 20]

$$\begin{aligned} \exp (\varphi \mathbf{X}) =&\left ( \textstyle\begin{array}{c@{\quad }c} \exp (\varphi \widetilde{\mathbf{e}}) & \ \ \ (\mathbf{I}-\exp ( \varphi \widetilde{\mathbf{e}}))\mathbf{x}+\varphi h\mathbf{e} \\ \mathbf{0} & 1\end{array}\displaystyle \right ) ,\ \mathrm{for\ \ }h\neq \infty \\ =&\left ( \textstyle\begin{array}{c@{\quad }c} \mathbf{I} & \ \varphi \mathbf{e} \\ \mathbf{0} & 1\end{array}\displaystyle \right ) ,\ \mathrm{for\ \ }h=\infty \end{aligned}$$
(6)

where the rotation matrix is determined by the Euler–Rodrigues formula

$$ \exp (\varphi \widetilde{\mathbf{e}})=\mathbf{I}+\sin \varphi \widetilde{\mathbf{e}}+\left ( 1-\cos \varphi \right ) \,\widetilde{\mathbf{e}}^{2}. $$
(7)

Denote with \(\mathbf{V}_{i}^{{\mathsf{b}}}=(\boldsymbol{\omega }_{i}^{ {\mathsf{b}}},\mathbf{v}_{i}^{{\mathsf{b}}})^{T}\) the twist of body \(i\) represented in the body-fixed frame. The superscript b is used to indicate the body-fixed representation [23, 25]. An alternative representation is so-called spatial representation of twist, which would be indicated by a superscript s. A recursive \(O\left ( n\right ) \)-algorithm for evaluating the EOM and their higher-order derivatives using the spatial representation was reported in [24]. In [14] the EOM were presented in closed form in terms of the spatial representation of twists. The potential advantage of using the spatial representation to express the EOM in closed form remains to be explored, however. In this paper the (classical) body-fixed representation is used.

The individual twists of all bodies are summarized in the vector \(\mathsf{V}\in {\mathbb{R}}^{6n}\), which is referred to as the system twist in body-fixed representation. It is determined as

$$ \mathsf{V}=\mathsf{J}\dot{\mathbf{q}} $$
(8)

with the system Jacobian \(\mathsf{J}\left ( \mathbf{q}\right ) \). The latter admits the factorization

$$ \mathsf{J}=\mathsf{AX} $$
(9)

in terms of the block-triangular and block-diagonal matrices

$$ \mathsf{A}\left ( \mathbf{q}\right ) =\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf{I} & \mathbf{0} & \mathbf{0} & & \mathbf{0} \\ \mathbf{Ad}_{\mathbf{C}_{2,1}} & \mathbf{I} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{Ad}_{\mathbf{C}_{3,1}} & \mathbf{Ad}_{\mathbf{C}_{3,2}} & \mathbf{I} & & \mathbf{0} \\ \vdots & \vdots & \ddots & \ddots & \\ \mathbf{Ad}_{\mathbf{C}_{n,1}} & \mathbf{Ad}_{\mathbf{C}_{n,2}} & \cdots & \mathbf{Ad}_{\mathbf{C}_{n,n-1}} & \mathbf{I}\end{array}\displaystyle \right ) ,\mathsf{X}=\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {^{1}\mathbf{X}}_{1} & \mathbf{0} & \mathbf{0} & & \mathbf{0} \\ \mathbf{0} & {^{2}\mathbf{X}}_{2} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & {^{3}\mathbf{X}}_{3} & & \mathbf{0} \\ \vdots & \vdots & \ddots & \ddots & \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} & {^{n}}\mathbf{X}_{n}\end{array}\displaystyle \right ) . $$
(10)

The matrix \(\mathbf{Ad}_{\mathbf{C}_{i,j}}\) transforms screw coordinates represented in the reference frame at body \(j\) to those represented in the frame on body \(i\) [18, 25, 28]. With the relative configuration (2) this matrix is

$$ \mathbf{Ad}_{\mathbf{C}_{i,j}}=\left ( \textstyle\begin{array}{c@{\quad }c} \mathbf{R}_{ij} & \mathbf{0} \\ {^{i}}\tilde{\mathbf{r}}_{i,j}\mathbf{R}_{ij} & \mathbf{R}_{ij}\end{array}\displaystyle \right ) $$
(11)

where \(\tilde{\mathbf{x}}\in so\left ( 3\right ) \) is the skew-symmetric matrix associated to vector \(\mathbf{x}\in {\mathbb{R}}^{3}\) so that \(\tilde{\mathbf{x}}\mathbf{y}=\mathbf{x}\times \mathbf{y}\). A central relation for deriving the EOM in closed form is the following expression for the time derivative of the matrix \(\mathsf{A}\) and thus of the system Jacobian [23]:

$$ \dot{\mathsf{J}}\left ( \mathbf{q},\dot{\mathbf{q}}\right ) =- \mathsf{A}\left ( \mathbf{q}\right ) \mathsf{a}\left ( \dot{\mathbf{q}}\right ) \mathsf{J}\left ( \mathbf{q}\right ) $$
(12)

where

$$ \mathsf{a}\left ( \dot{\mathbf{q}}\right ) :=\mathrm{diag}~(\dot{q}_{1} \mathbf{ad}_{{{^{1}}\mathbf{X}_{1}}},\ldots ,\dot{q}_{n}\mathbf{ad}_{{{^{n}} \mathbf{X}_{n}}}). $$
(13)

Therein, the matrix \(\mathbf{ad}_{{{^{i}}\mathbf{X}_{i}}}\) (also called as spatial cross product by Featherstone [7]) is given in terms of the joint screw coordinate vector (4) as

$$ \mathbf{ad}_{{^{i}\mathbf{X}}_{i}}=\left ( \textstyle\begin{array}{c@{\quad }c} {^{i}}\tilde{\boldsymbol{\xi }}_{i} & \ \mathbf{0} \\ {^{i}}\tilde{\boldsymbol{\eta }}_{i} & {^{i}}\tilde{\boldsymbol{\xi }}_{i}\end{array}\displaystyle \right ) . $$
(14)

This gives rise to the closed-form expressions for the system acceleration

$$ \dot{\mathsf{V}}=\mathsf{J}\ddot{\mathbf{q}}-\mathsf{AaJ} \dot{\mathbf{q}}=\mathsf{J}\ddot{\mathbf{q}}-\mathsf{AaV}. $$
(15)

For calculating the derivatives, the time derivative of matrix \(\mathsf{A}\) will be needed. To this end, the expression

$$ \mathsf{A}=\left ( \mathbf{I}-\mathsf{D}\right ) ^{-1} $$
(16)

is used [23], with the matrix

$$ \mathsf{D}\left ( \mathbf{q}\right ) =\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf{0} & \mathbf{0} & \mathbf{0} & & \mathbf{0} \\ \mathbf{Ad}_{\mathbf{C}_{2,1}} & \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{Ad}_{\mathbf{C}_{3,2}} & \mathbf{0} & & \mathbf{0} \\ \vdots & \vdots & \ddots & \ddots & \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{Ad}_{\mathbf{C}_{n,n-1}} & \mathbf{0}\end{array}\displaystyle \right ) . $$
(17)

With (16), the derivative of \(\mathsf{A}\) is then

$$ \dot{\mathsf{A}}=\left ( \mathbf{I}-\mathsf{D}\right ) ^{-1} \dot{\mathsf{D}}\left ( \mathbf{I}-\mathsf{D}\right ) ^{-1}=\mathsf{A} \dot{\mathsf{D}}\mathsf{A}. $$
(18)

Using the relation \(\dot{\mathbf{Ad}}_{\mathbf{C}_{i,j}}=-\dot{q}_{i}\mathbf{ad}_{{^{i}\mathbf{X}}_{i}}\mathbf{Ad}_{\mathbf{C}_{i,-1}}\) [23], the derivative of \(\mathsf{D}\) attains the closed form \(\dot{\mathsf{D}}=-\mathsf{aD}\). Finally, with \(\mathsf{D}=\mathbf{I}-\mathsf{A}^{-1}\), it follows

$$ \dot{\mathsf{A}}\left ( \mathbf{q},\dot{\mathbf{q}}\right ) = \mathsf{A}\left ( \mathbf{q}\right ) \mathsf{a}-\mathsf{A}\left ( \mathbf{q}\right ) \mathsf{a}\left ( \dot{\mathbf{q}}\right ) \mathsf{A}\left ( \mathbf{q}\right ) . $$
(19)

Clearly, the derivative (12) of the system Jacobian is recovered as \(\dot{\mathsf{J}}=\dot{\mathsf{A}}\mathsf{X}\) noting that \(\mathsf{aX}\equiv \mathbf{0}\).

2.2 Equations of motion

The generalized mass and Coriolis matrix in the EOM (1) of a simple kinematic chain mounted at the ground are found via Jourdain’s principle of virtual power as (or likewise as the Lagrange equations) [23]

$$ \mathbf{M}\left ( \mathbf{q}\right ) =\mathsf{J}^{T} \mathsf{MJ,\ \ \ \ }\mathbf{C}\left ( \mathbf{q},\dot{\mathbf{q}}\right ) =\mathsf{J}^{T} \mathsf{CJ} ,$$
(20)

where

$$\begin{aligned} \mathsf{M} :&=\mathrm{diag}\,(\mathbf{M}_{1},\ldots ,\mathbf{M}_{n}) , \end{aligned}$$
(21)
$$\begin{aligned} \mathsf{C}(\mathbf{q},\dot{\mathbf{q}},\mathsf{V}\left ( \dot{\mathbf{q}}\right ) ) :&=-\mathsf{MAa}-\mathsf{b}^{T}\mathsf{M}, \end{aligned}$$
(22)

and

$$ \mathsf{b}\left ( \mathsf{V}\right ) :=\mathrm{diag}~(\mathbf{ad}_{ \mathbf{V}_{1}},\ldots ,\mathbf{ad}_{\mathbf{V}_{n}}). $$
(23)

Therein, the (constant) \(6\times 6\) inertia matrix of body \(i\) expressed in the body-frame is defined as

$$ \mathbf{M}_{i}=\left ( \textstyle\begin{array}{c@{\quad }c} {\boldsymbol{\varTheta }_{i}^{\mathsf{b}}} & {^{i}}\widetilde{\mathbf{c}}_{i}m_{i} \\ -{^{i}}\widetilde{\mathbf{c}}_{i}m_{i}\ \ \ & m_{i}\mathbf{I}\end{array}\displaystyle \right ) $$
(24)

where \(m_{i}\) is the body mass, \({^{i}}\mathbf{c}_{i}\) is the position vector to the COM of body \(i\) measured in the reference frame at body \(i\), and \({\boldsymbol{\varTheta }_{i}^{\mathsf{b}}}\) is the inertia tensor with respect to the body-fixed frame. The latter is related to the inertia tensor with respect to the COM, denoted \({\boldsymbol{\varTheta }_{i}^{\mathsf{c}}}\), via Steiner’s (parallel axis) theorem \(\boldsymbol{\varTheta }_{i}^{\mathsf{b}}=\mathbf{R}_{\mathsf{b},\mathsf{c}}\boldsymbol{\varTheta }_{i}^{\mathsf{c}}\mathbf{R}_{\mathsf{b}, \mathsf{c}}^{T}-m_{i}{^{i}}\widetilde{\mathbf{c}}_{i}{^{i}} \widetilde{\mathbf{c}}_{i}\) where \(\mathbf{R}_{\mathsf{b},\mathsf{c}}\) denotes the rotation matrix of the COM frame to the body frame.

A closed form of the EOM is obtained after replacing the system twist by (8). Alternatively, first the kinematic relation (8) and then the coefficient matrices in (22) are evaluated for a given state \(\mathbf{q},\dot{\mathbf{q}}\). The generalized gravity forces are given as

$$ \mathbf{Q}_{\mathrm{grav}}\left ( \mathbf{q}\right ) =\mathsf{J}^{T} \mathsf{MU}\mathbf{G} $$
(25)

with

$$ \mathbf{G}:=-\left ( \textstyle\begin{array}{c} \mathbf{0} \\ ^{0}\mathbf{g}\end{array}\displaystyle \right ) ,\ \ \mathsf{U}\left ( \mathbf{q}\right ) :=\mathsf{A}\left ( \textstyle\begin{array}{c} \mathbf{Ad}_{\mathbf{C}_{1}}^{-1} \\ \mathbf{0} \\ \vdots \\ \mathbf{0}\end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c} \mathbf{Ad}_{\mathbf{C}_{1}}^{-1} \\ \mathbf{Ad}_{\mathbf{C}_{2}}^{-1} \\ \vdots \\ \mathbf{Ad}_{\mathbf{C}_{n}}^{-1}\end{array}\displaystyle \right ) . $$
(26)

Here, \(^{0}\mathbf{g}\) is the vector of gravitational acceleration expressed in the inertial frame, which is transformed to the individual bodies by \(\mathsf{U}\). The effect of contact or external wrenches acting on the bodies is given by the generalized forces

$$ \mathbf{Q}_{\mathrm{ext}}\left ( \mathbf{q},t\right ) =\mathsf{J}^{T} \left ( \mathbf{q}\right ) \mathsf{W}_{\mathrm{EE}}\left ( t\right ) \quad \text{where}\quad \mathsf{W}_{\mathrm{ext}}\left ( t\right ) =\left ( \textstyle\begin{array}{c} \mathbf{W}_{\mathrm{ext},1}\left ( t\right ) \\ \mathbf{W}_{\mathrm{ext},2}\left ( t\right ) \\ \vdots \\ \mathbf{W}_{\mathrm{ext},n}\left ( t\right )\end{array}\displaystyle \right ) . $$
(27)

The vector \(\mathsf{W}_{\mathrm{ext},i}\) accounts for applied load at body \(i \). For instance, \(\mathbf{W}_{\mathrm{ext},n}\) can be used to describe the wrench at the end-effector of a robotic arm. More generally, \(\mathsf{W}_{\mathrm{ext}}\) and thus \(\mathbf{Q}_{\mathrm{ext}}\), may account for arbitrary (time and velocity dependent) loads at the system.

3 First time derivative of the equations of motion

The first time derivative of the generalized forces is

$$ \dot{\mathbf{Q}}=\mathbf{M}\dddot{\mathbf{q}}+(\dot{\mathbf{M}}+ \mathbf{C})\ddot{\mathbf{q}}+\dot{\mathbf{C}}\dot{\mathbf{q}}+\dot{\mathbf{Q}}_{ \mathrm{grav}}+\dot{\mathbf{Q}}_{\mathrm{ext}}. $$
(28)

The time derivative of the generalized mass matrix \(\mathbf{M}\) in (20) follows with \(\dot{\mathsf{J}}\) in (12) as

$$\begin{aligned} \dot{\mathbf{M}}\left ( \mathbf{q},\dot{\mathbf{q}}\right ) =&\mathsf{J}^{T}\mathsf{M}\dot{\mathsf{J}}+\dot{\mathsf{J}}^{T}\mathsf{MJ} \\ =&\mathsf{J}^{T}\mathsf{M}^{\left ( 1\right ) }\mathsf{J} \end{aligned}$$
(29)

with

$$ \mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q},\dot{\mathbf{q}} \right ) :=-\mathsf{MAa}-\left ( \mathsf{MAa}\right ) ^{T} $$
(30)

where \(\mathsf{A}=\mathsf{A}\left ( \mathbf{q}\right ) \) and \(\mathsf{a}=\mathsf{a}\left ( \dot{\mathbf{q}}\right ) \). By the same token, the time derivative of the generalized Coriolis matrix \(\mathbf{C}\) is

$$\begin{aligned} \dot{\mathbf{C}}\left ( \mathbf{q},\dot{\mathbf{q}},\ddot{\mathbf{q}} \right ) =&\mathsf{J}^{T}\mathsf{C}\dot{\mathsf{J}}+\dot{\mathsf{J}}^{T} \mathsf{CJ}+\mathsf{J}^{T}\dot{\mathsf{C}}\mathsf{J} \\ =&\mathsf{J}^{T}\mathsf{C}^{\left ( 1\right ) }\mathsf{J} \end{aligned}$$
(31)

where now

$$ \mathsf{C}^{\left ( 1\right ) }:=\dot{\mathsf{C}}-\mathsf{CAa}- \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C}. $$
(32)

The expression for \(\mathsf{C}\) in (22) together with (12) yields

$$ \dot{\mathsf{C}}(\mathbf{q},\dot{\mathbf{q}},\ddot{\mathbf{q}}, \mathsf{\dot{\mathsf{V}}})=\mathsf{C}(\mathbf{q},\ddot{\mathbf{q}}, \mathsf{\dot{\mathsf{V}}})+\mathsf{MAaAa}-\mathsf{MAaa}=\mathsf{MAaAa}-\mathsf{MAaa}- \mathsf{MA\dot{\mathsf{a}}-\dot{\mathsf{b}}}^{T}\mathsf{M}, $$
(33)

with \(\dot{\mathsf{a}}=\dot{\mathsf{a}}\left ( \ddot{\mathbf{q}}\right ) , \dot{\mathsf{b}}=\mathsf{\dot{\mathsf{b}}}(\mathsf{\dot{\mathsf{V}}})\), and thus

$$\begin{aligned} \mathsf{C}^{\left ( 1\right ) } =&\mathsf{C}(\mathbf{q}, \ddot{\mathbf{q}},\mathsf{\dot{\mathsf{V}}})+\mathsf{MAaAa}-\mathsf{MAaa}-\mathsf{CAa}- \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C} \end{aligned}$$
(34)
$$\begin{aligned} =&-\mathsf{MA\dot{\mathsf{a}}-\dot{\mathsf{b}}}^{T}\mathsf{M}+ \mathsf{b}^{T}\mathsf{MAa}+\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{b}^{T}\mathsf{M}+ \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{MAa}+2\mathsf{MAaAa}- \\ &\mathsf{MAaa}. \end{aligned}$$
(35)

The form (34) allows for reusing expression (22) for the matrix \(\mathsf{C}\), where (22) is evaluated with \(\ddot{\mathbf{q}},\mathsf{\dot{\mathsf{V}}}\) instead with the velocities. Also in the second form (35), terms like \(\mathsf{Aa}\), \(\mathsf{MAa}\), and \(\mathsf{b}^{T}\mathsf{M}\) can be reused. A direct calculation yields

$$ \dot{\mathbf{Q}}_{\mathrm{grav}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) =\mathsf{J}^{T}\mathsf{M}^{\left ( 1\right ) }\mathsf{U}\mathbf{G} $$
(36)

where the relation \(\dot{\mathsf{U}}=-\mathsf{AaU}\) (obtained by time differentiation of (26) and using the identity in (19)) and the fact that \(\mathbf{G}\) is constant has been used. The time derivative of (27) along with (12) yields the expression for calculating first-order derivative of generalized forces due to external wrenches

$$ \dot{\mathbf{Q}}_{\mathrm{ext}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) =\mathsf{J}^{T}(\dot{\mathsf{W}}_{\mathrm{EE}}-(\mathsf{A}\mathsf{a})^{T}\mathsf{W}_{\mathrm{EE}}). $$
(37)

4 Second time derivative of the equations of motion

The second time derivative of the generalized motor forces (1) is determined by

$$ \ddot{\mathbf{Q}}=\mathbf{M}\ddot{\ddot{\mathbf{q}}}+(2 \dot{\mathbf{M}}+\mathbf{C})\dddot{\mathbf{q}}+(\ddot{\mathbf{M}}+2\dot{\mathbf{C}}) \ddot{\mathbf{q}}+\ddot{\mathbf{C}}\dot{\mathbf{q}}+\ddot{\mathbf{Q}}_{ \text{grav}}+\ddot{\mathbf{Q}}_{\mathrm{ext}}. $$
(38)

The second time derivative of the generalized mass matrix is

$$\begin{aligned} \ddot{\mathbf{M}}\left ( \mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}}\right ) =&\mathsf{J}^{T}(\dot{\mathsf{M}}^{\left ( 1 \right ) }-\mathsf{M}^{\left ( 1\right ) }\mathsf{Aa}-\mathsf{a}^{T} \mathsf{A}^{T}\mathsf{M}^{\left ( 1\right ) })\mathsf{J} \end{aligned}$$
(39)
$$\begin{aligned} =&\mathsf{J}^{T}\mathsf{M}^{\left ( 2\right ) }\mathsf{J} \end{aligned}$$
(40)

with \(\mathsf{M}^{\left ( 2\right ) }:=\dot{\mathsf{M}}^{\left ( 1\right ) }-\mathsf{M}^{\left ( 1\right ) }\mathsf{Aa}-\mathsf{a}^{T}\mathsf{A}^{T} \mathsf{M}^{\left ( 1\right ) }\). Inserting relation (19) in the differentiation of (30) yields

$$\begin{aligned} \dot{\mathsf{M}}^{\left ( 1\right ) }\left ( \mathbf{q}, \dot{\mathbf{q}},\ddot{\mathbf{q}}\right ) =&\mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q},\ddot{\mathbf{q}}\right ) +\mathsf{M(AaA-Aa)a}+\left ( \mathsf{M(AaA-Aa)a} \right ) ^{T} \end{aligned}$$
(41)
$$\begin{aligned} =&\mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q}, \ddot{\mathbf{q}}\right ) -\mathsf{MAaa}+\mathsf{MAaAa}-\left ( \mathsf{MAaa}\right ) ^{T}+ \left ( \mathsf{MAaAa}\right ) ^{T} \end{aligned}$$
(42)

which leads immediately to the explicit form

$$\begin{aligned} \mathsf{M}^{\left ( 2\right ) } =&\mathsf{M}^{\left ( 1\right ) } \left ( \mathbf{q},\dot{\mathbf{q}}\right ) +\mathsf{M(AaA-Aa)a}+\left ( \mathsf{M(AaA-Aa)a}\right ) ^{T} \\ &-\mathsf{M}^{\left ( 1\right )}\left ( \mathbf{q},\dot{\mathbf{q}}\right )\mathsf{\mathsf{Aa}}-(\mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q},\dot{\mathbf{q}}\right )\mathsf{\mathsf{Aa}})^{T} \end{aligned}$$
(43)
$$\begin{aligned} =&-\mathsf{MA\mathsf{\dot{\mathsf{a}}}}-\left ( \mathsf{MA\mathsf{\dot{\mathsf{a}}}}\right ) ^{T}+2\mathsf{\mathsf{MAaAa}}+2\left ( \mathsf{\mathsf{\mathsf{MAaAa}}}\right ) ^{T}+2\mathsf{\mathsf{a}}^{T} \mathsf{\mathsf{A}}^{T}\mathsf{\mathsf{MAa}} \\ &-\mathsf{MAaa}-\left ( \mathsf{MAaa}\right ) ^{T}. \end{aligned}$$
(44)

Equation (43) allows for reusing \(\mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \). It should be observed that the term \(\mathsf{M}^{\left ( 1\right ) }\left ( \mathbf{q}, \ddot{\mathbf{q}}\right ) \) is the relation (30) evaluated with \(\ddot{\mathbf{q}}\) instead of \(\dot{\mathbf{q}}\).

Repeated time derivative of the generalized Coriolis matrix yields

$$ \ddot{\mathbf{C}}\left ( \mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}},\dddot{\mathbf{q}}\right ) =\mathsf{J}^{T}\mathsf{C}^{\left ( 2\right ) } \mathsf{J} $$
(45)

with

$$ \mathsf{C}^{\left ( 2\right ) }\left ( \mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}},\dddot{\mathbf{q}}\right ) =\dot{\mathsf{C}}^{\left ( 1 \right ) }-\mathsf{C}^{\left ( 1\right ) }\mathsf{Aa}-\mathsf{a}^{T}\mathsf{A}^{T} \mathsf{C}^{\left ( 1\right ) } .$$
(46)

Taking the derivative of (32) yields \(\dot{\mathsf{C}}^{\left ( 1\right ) }(\mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}},\dddot{\mathbf{q}},\mathsf{\dot{\mathsf{V}}},\ddot{\mathsf{V}})\) in closed form as

$$\begin{aligned} \dot{\mathsf{C}}^{\left ( 1\right ) } =&\ddot{\mathsf{C}}- \dot{\mathsf{C}}\mathsf{Aa}-\mathsf{a}^{T}\mathsf{A}^{T}\dot{\mathsf{C}}-\mathsf{CA} \dot{\mathsf{a}}-\dot{\mathsf{a}}^{T}\mathsf{A}^{T}\mathsf{C}+ \mathsf{CAaAa}+\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C} \\ &-\mathsf{CAaa}-\mathsf{a}^{T}\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C} \\ =&\ddot{\mathsf{C}}-(\mathsf{C}^{\left ( 1\right ) }+\mathsf{a}^{T} \mathsf{A}^{T}\mathsf{C})\mathsf{Aa}-\mathsf{a}^{T}\mathsf{A}^{T}(\mathsf{C}^{ \left ( 1\right ) }+\mathsf{CAa})-\mathsf{CA}\dot{\mathsf{a}}- \dot{\mathsf{a}}^{T}\mathsf{A}^{T}\mathsf{C} \\ &-\mathsf{CAaa}-\mathsf{a}^{T}\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C}. \ \ \ \ \ \ \ \end{aligned}$$
(47)

This requires the derivative of (33), which are found to be

$$\begin{aligned} \ddot{\mathsf{C}} =&\mathsf{C}(\mathbf{q},\dddot{\mathbf{q}}, \mathsf{\ddot{\mathsf{V}}})+\mathsf{MA\dot{\mathsf{a}}Aa}+2 \mathsf{MAaA\dot{\mathsf{a}}-2MAaAaAa}+\mathsf{2MAaAaa}-\mathsf{3MAa}\dot{\mathsf{a}} \end{aligned}$$
(48)
$$\begin{aligned} &-\mathsf{MAaaa}+\mathsf{MAaaAa} \\ =&-\mathsf{MA\ddot{\mathsf{a}}-\ddot{\mathsf{b}}}^{T}\mathsf{M}+ \mathsf{MA\dot{\mathsf{a}}Aa}+2\mathsf{MAaA\dot{\mathsf{a}}-2MAaAaAa}+ \mathsf{2MAaAaa} \\ &-\mathsf{3MAa}\dot{\mathsf{a}}-\mathsf{MAaaa}+\mathsf{MAaaAa}. \end{aligned}$$
(49)

Also here it should be observed that the matrix \(\mathsf{C}(\mathbf{q},\dddot{\mathbf{q}},\mathsf{\ddot{\mathsf{V}}})\) is the expression for \(\mathsf{C}\) in (22) evaluated with \(\dddot{\mathbf{q}},\mathsf{\ddot{\mathsf{V}}}\). Inserting (48) along with (49) into (46) yields \(\mathsf{C}^{\left ( 2\right ) }\left ( \mathbf{q},\dot{\mathbf{q}},\ddot{\mathbf{q}},\dddot{\mathbf{q}}\right ) \) in the explicit form

$$\begin{aligned} \mathsf{C}^{\left ( 2\right ) } =&\mathsf{C}(\mathbf{q}, \dddot{\mathbf{q}},\mathsf{\ddot{\mathsf{V}}})-2\mathsf{C}^{\left ( 1\right ) } \mathsf{Aa}-2\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C}^{\left ( 1\right ) }- \mathsf{CA}\dot{\mathsf{a}}-\dot{\mathsf{a}}^{T}\mathsf{A}^{T}\mathsf{C}-2\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{CAa} \\ &-\mathsf{CAaa}-\mathsf{a}^{T}\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C}+\mathsf{MA\dot{\mathsf{a}}Aa}+2\mathsf{MAaA}\dot{\mathsf{a}}-2 \mathsf{MAaAaAa} \end{aligned}$$
(50)
$$\begin{aligned} &+\mathsf{2MAaAaa}-\mathsf{3MAa}\dot{\mathsf{a}}-\mathsf{MAaaa}+ \mathsf{MAaaAa} \\ =&-\mathsf{MA}\ddot{\mathsf{a}}-\ddot{\mathsf{b}}^{T}\mathsf{M}+2 \dot{\mathsf{b}}^{T}\mathsf{MAa}+2\mathsf{a}^{T}\mathsf{A}^{T} \dot{\mathsf{b}}^{T}\mathsf{M} \\ &+3\mathsf{MA}\dot{\mathsf{a}}\mathsf{Aa}+2\mathsf{MAaA} \dot{\mathsf{a}}+2\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{MA}\dot{\mathsf{a}}-\mathsf{CA} \dot{\mathsf{a}}-\dot{\mathsf{a}}^{T}\mathsf{A}^{T}\mathsf{C} \\ &+2\mathsf{CAaAa}+2\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{CAa}+2 \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{C}-4 \mathsf{MAaAaAa} \\ &-2\mathsf{a}^{T}\mathsf{A}^{T}\mathsf{MAaAa}+\mathsf{2MAaaAa}+2 \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{MAaa} \\ &+\mathsf{2MAaAaa}-\mathsf{3MAa}\dot{\mathsf{a}}-\mathsf{MAaaa}+ \mathsf{MAaaAa}-\mathsf{CAaa}-\mathsf{a}^{T}\mathsf{a}^{T}\mathsf{A}^{T} \mathsf{C} \end{aligned}$$
(51)

with \(\ddot{\mathsf{a}}=\ddot{\mathsf{a}}\left ( \dddot{\mathbf{q}}\right ) \) and \(\ddot{\mathsf{b}}=\ddot{\mathsf{b}}(\ddot{\mathsf{V}})\) in (13) and (23) evaluated with \(\dddot{\mathbf{q}}\) and \(\ddot{\mathsf{V}}\), respectively. The first form (51) may be beneficial since it involves \(\mathsf{C}\) and \(\mathsf{C}^{\left ( 1\right ) }\), which are already available from (22) and (34).

Taking the derivative of (36) yields the second time derivative of the generalized gravity forces

$$ \ddot{\mathbf{Q}}_{\text{grav}}(\mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}})=\mathsf{J}^{T}\mathsf{M}^{\left ( 2\right ) }\mathsf{U}\mathbf{G}. $$
(52)

The second time derivative of the generalized forces (27) due to end-effector loads is readily found to be

$$\begin{aligned} \ddot{\mathbf{Q}}_{\mathrm{ext}}\left ( \mathbf{q},\dot{\mathbf{q}}, \ddot{\mathbf{q}}\right ) =&\mathsf{J}^{T}(\ddot{\mathsf{W}}_{\mathrm{EE}}-2(\mathsf{A}\mathsf{a})^{T}\dot{\mathsf{W}}_{\mathrm{EE}}+(2(\mathsf{A} \mathsf{a}\mathsf{A}\mathsf{a)}^{T}-(\mathsf{A}\dot{\mathsf{a}})^{T} \\ &-\left ( \mathsf{Aaa}\right ) ^{T})\mathsf{W}_{\mathrm{EE}}). \end{aligned}$$
(53)

5 Structural properties of the EOM

There are two important and well-known structural properties of EOM:

  1. 1.

    The generalized mass matrix \(\mathbf{M}\) is symmetric and positive definite.

  2. 2.

    \(\dot{\mathbf{q}}^{T}\left ( \dot{\mathbf{M}}\left ( \mathbf{q}, \dot{\mathbf{q}}\right ) -2\mathbf{C}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \right ) \dot{\mathbf{q}}\equiv 0\) for any \(\dot{\mathbf{q}}\)

Positive definiteness and the symmetric properties of the generalized mass matrix follows directly from its definition in (20). The symmetry property indeed applies to all higher derivatives, which is also evident from (29) and (40). An important property of the EOM (1), which is crucial for proving stability of passivity-based control schemes, is that the Coriolis matrix can be formulated as

$$ \bar{\mathbf{C}}:=-\mathsf{J}^{T}(\mathsf{MAa}+\mathsf{b}^{T} \mathsf{M}-\mathsf{Mb})\mathsf{J} $$
(54)

so that \(\dot{\mathbf{M}}-2\bar{\mathbf{C}}\) is skew symmetric. To show this property, notice that \(\mathsf{bJ}\dot{\mathbf{q}}=\mathsf{bV}=\mathrm{diag}\left ( \mathbf{ad}_{\mathbf{V}_{1}}\mathbf{V}_{1},\ldots , \mathbf{ad}_{\mathbf{V}_{n}}\mathbf{V}_{n}\right ) \equiv \mathbf{0}\), so that \(\mathbf{C}\dot{\mathbf{q}}\) can be rewritten as

$$ \mathbf{C}\dot{\mathbf{q}}=-\mathsf{J}^{T}(\mathsf{MAa}+\mathsf{b}^{T}\mathsf{M})\mathsf{J}\dot{\mathbf{q}}=-\mathsf{J}^{T}(\mathsf{MAa}+ \mathsf{b}^{T}\mathsf{M}-\mathsf{Mb})\mathsf{J}\dot{\mathbf{q}}= \bar{\mathbf{C}}\dot{\mathbf{q}} .$$
(55)

In view of the time derivative (29) of \(\mathbf{M}\), the so defined Coriolis matrix \(\bar{\mathbf{C}}\) satisfies the relation

$$ \bar{\mathbf{C}}+\bar{\mathbf{C}}^{T}=-\mathsf{J}^{T}(\mathsf{MAa}+ \mathsf{a}^{T}\mathsf{A}^{T}\mathsf{M})\mathsf{J}=\dot{\mathbf{M}}. $$
(56)

With (54), it hence follows

$$ \dot{\mathbf{M}}-2\bar{\mathbf{C}}=\bar{\mathbf{C}}^{T}- \bar{\mathbf{C}}=-(\bar{\mathbf{C}}^{T}-\bar{\mathbf{C}})^{T}=-(\dot{\mathbf{M}}-2 \bar{\mathbf{C}})^{T}. $$
(57)

It should be remarked that the Coriolis matrix is not unique, and the property 2) holds true for the particular arrangement as in (22). It may not hold if the equations are arranged differently. The skew symmetry of \(\dot{\mathbf{M}}-2\bar{\mathbf{C}}\) is indeed carried over to its derivatives.

6 Examples

The higher-order closed-form inverse dynamics formulation presented in Sect. 3 and Sect. 4 were implemented in MATLAB.Footnote 1 This MATLAB implementation can also be used for efficient symbolic code generation in MATLAB and C languages. This section presents the application of this work to the computation of higher-order inverse dynamics of two robot manipulators and presents a discussion on its computational efficiency.

6.1 Planar 2R robot

A 2R serial chain consists of a base, two links, and two revolute joints. A simple 2R chain is shown in Fig. 1. First link of length \(L_{1}\) is connected to the base or ground through a revolute joint. The second link of length \(L_{2}\) is connected to first link through a revolute joint. The center of mass is shown with a red circle on the links and lies at the end of each link. The mass of first and second links are \(m_{1}\) and \(m_{2}\) respectively. The gravity acting on the system is shown as \(g\) in the figure.

Fig. 1
figure 1

Planar 2R robot schematic

Full size image

Kinematic model The \(z\)-axes represent the joint axes, and thus the joint screw coordinates in body-fixed representation for the two revolute joints are

$$\begin{aligned} {^{1}\mathbf{X}}_{1} =&\left ( 0,0,1,0,0,0\right ) ^{T} \\ {^{2}\mathbf{X}}_{2} =&\left ( 0,0,1,0,0,0\right ) ^{T}. \end{aligned}$$

The relative reference configurations for the two bodies are

$$ \mathbf{B}_{1}=\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\displaystyle \right ) ,\quad \mathbf{B}_{2}=\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 & 0 & 0 & L_{1} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\displaystyle \right ) . $$

The mass matrices of the two bodies in the body-fixed configuration according to (24) are

$$\begin{aligned} \mathbf{M}_{1} =&\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {L_{1}}^{2}\,m_{1} & 0 & 0 & 0 & 0 & 0 \\ 0 & {L_{1}}^{2}\,m_{1} & 0 & 0 & 0 & -L_{1}\,m_{1} \\ 0 & 0 & {L_{1}}^{2}\,m_{1} & 0 & L_{1}\,m_{1} & 0 \\ 0 & 0 & 0 & m_{1} & 0 & 0 \\ 0 & 0 & L_{1}\,m_{1} & 0 & m_{1} & 0 \\ 0 & -L_{1}\,m_{1} & 0 & 0 & 0 & m_{1}\end{array}\displaystyle \right ) , \\ \mathbf{M}_{2} =&\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {L_{2}}^{2}\,m_{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & {L_{2}}^{2}\,m_{2} & 0 & 0 & 0 & -L_{2}\,m_{2} \\ 0 & 0 & {L_{2}}^{2}\,m_{2} & 0 & L_{2}\,m_{2} & 0 \\ 0 & 0 & 0 & m_{2} & 0 & 0 \\ 0 & 0 & L_{2}\,m_{2} & 0 & m_{2} & 0 \\ 0 & -L_{2}\,m_{2} & 0 & 0 & 0 & m_{2}\end{array}\displaystyle \right ) . \end{aligned}$$

Second-order inverse dynamics With the above information about the robot, using the closed-form expressions of \(\mathbf{M}(\mathbf{q}), \mathbf{C}(\mathbf{q},\mathbf{\dot{q}})\) and \(\mathbf{Q}_{\text{grav}}(\mathbf{q})\) provided in Sect. 2.2 in (1), one can arrive at the analytical expression for generalized forces \((\tau _{1},\tau _{2})\) which solves inverse dynamics problem as follows:

$$\begin{aligned} \tau _{1} =&{L_{1}}^{2}\,\ddot{q}_{1}\,m_{1}+{L_{1}}^{2}\,\ddot{q}_{1}\,m_{2}+{L_{2}}^{2}\,\ddot{q}_{1}\,m_{2}+{L_{2}}^{2}\,\ddot{q}_{2}\,m_{2}+L_{2}\,g\,m_{2}\,\cos \left ( q_{1}+q_{2}\right ) \\ &+L_{1}\,g\,m_{1}\,\cos \left ( q_{1}\right ) +L_{1}\,g\,m_{2}\, \cos \left ( q_{1}\right ) -L_{1}\,L_{2}\,{\dot{q}_{2}}^{2}\,m_{2}\, \sin \left ( q_{2}\right ) \\ &+2\,L_{1}\,L_{2}\,\ddot{q}_{1}\,m_{2}\,\cos \left ( q_{2}\right ) +L_{1} \,L_{2}\,\ddot{q}_{2}\,m_{2}\,\cos \left ( q_{2}\right ) -2\,L_{1}\,L_{2} \,\dot{q}_{1}\,\dot{q}_{2}\,m_{2}\,\sin \left ( q_{2}\right ), \\ \tau _{2} =&L_{2}\,m_{2}\,\left ( L_{1}\,\sin \left ( q_{2}\right ) \,{\dot{q}_{1}}^{2}+L_{2}\,\ddot{q}_{1}+L_{2}\,\ddot{q}_{2}+g\,\cos \left ( q_{1}+q_{2} \right ) +L_{1}\,\ddot{q}_{1}\,\cos \left ( q_{2}\right ) \right ) . \end{aligned}$$

These expressions are indeed identical to those reported in [18] for instance.

Using the closed-form expressions of \(\dot{\mathbf{M}}(\mathbf{q,\dot{q}}),\dot{\mathbf{C}}(\mathbf{q},\mathbf{\dot{q}},\mathbf{\ddot{q}})\) and \(\dot{\mathbf{Q}}_{\text{grav}}(\mathbf{q},\mathbf{\dot{q}})\) provided in Sect. 3 in (28), one obtains the analytical expression for first-order time derivatives \((\dot{\tau }_{1},\dot{\tau }_{2})\) of the generalized forces, which solves the first-order inverse dynamics problem, as follows:

$$\begin{aligned} \dot{\tau }_{1} =&{L_{1}}^{2}\,\dddot{q}_{1}\,m_{1}+{L_{1}}^{2}\, \dddot{q}_{1}\,m_{2}+{L_{2}}^{2}\,\dddot{q}_{1}\,m_{2}+{L_{2}}^{2}\, \dddot{q}_{2}\,m_{2}-L_{2}\,\dot{q}_{1}\,g\,m_{2}\,\sin \left ( q_{1}+q_{2} \right ) \\ &-L_{2}\,\dot{q}_{2}\,g\,m_{2}\,\sin \left ( q_{1}+q_{2}\right ) +2 \,L_{1}\,L_{2}\,\dddot{q}_{1}\,m_{2}\,\cos \left ( q_{2}\right ) +L_{1} \,L_{2}\,\dddot{q}_{2}\,m_{2}\,\cos \left ( q_{2}\right ) \\ &-L_{1}\,\dot{q}_{1}\,g\,m_{1}\,\sin \left ( q_{1}\right ) -L_{1}\, \dot{q}_{1}\,g\,m_{2}\,\sin \left ( q_{1}\right ) -L_{1}\,L_{2}\,{\dot{q}_{2}}^{3}\,m_{2}\,\cos \left ( q_{2}\right ) \\ &-4\,L_{1}\,L_{2}\,\ddot{q}_{1}\,\dot{q}_{2}\,m_{2}\,\sin \left ( q_{2} \right ) -2\,L_{1}\,L_{2}\,\ddot{q}_{2}\,\dot{q}_{1}\,m_{2}\,\sin \left ( q_{2}\right ) \\ &-3\,L_{1}\,L_{2}\,\ddot{q}_{2}\,\dot{q}_{2}\,m_{2}\,\sin \left ( q_{2} \right ) -2\,L_{1}\,L_{2}\,\dot{q}_{1}\,{\dot{q}_{2}}^{2}\,m_{2}\, \cos \left ( q_{2}\right ), \\ \dot{\tau }_{2} =&L_{2}\,m_{2}\,(L_{2}\,\dddot{q}_{1}+L_{2}\, \dddot{q}_{2}-\dot{q}_{1}\,g\,\sin \left ( q_{1}+q_{2}\right ) -\dot{q}_{2}\,g\, \sin \left ( q_{1}+q_{2}\right ) \\ &+L_{1}\,\dddot{q}_{1}\,\cos \left ( q_{2}\right ) +2\,L_{1}\, \ddot{q}_{1}\,\dot{q}_{1}\,\sin \left ( q_{2}\right ) -L_{1}\,\ddot{q}_{1}\, \dot{q}_{2}\,\sin \left ( q_{2}\right ) +L_{1}\,{\dot{q}_{1}}^{2}\,\dot{q}_{2} \,\cos \left ( q_{2}\right ) ). \end{aligned}$$

The correctness can be easily checked taking the analytical time derivative of \((\tau _{1},\tau _{2})\) above.

Using the closed-form expressions of \(\ddot{\mathbf{M}}(\mathbf{q,\dot{q}, \ddot{q}}),\ddot{\mathbf{C}}(\mathbf{q},\mathbf{\dot{q}}, \mathbf{\ddot{q}},\mathbf{\dddot{q}})\) and \(\ddot{\mathbf{Q}}_{\text{grav}}(\mathbf{q},\mathbf{\dot{q}},\mathbf{\ddot{q}})\) provided in Sect. 4 in (38), one obtains the analytical expression for second-order time derivatives of generalized forces \((\ddot{\tau }_{1},\ddot{\tau }_{2})\), solving the second-order inverse dynamics problem:

$$\begin{aligned} \ddot{\tau }_{1} =&{L_{1}}^{2}\,\ddot{\ddot{q}}_{1}\,m_{1}+{L_{1}}^{2} \,\ddot{\ddot{q}}_{1}\,m_{2}+{L_{2}}^{2}\,\ddot{\ddot{q}}_{1}\,m_{2}+{L_{2}}^{2}\,\ddot{\ddot{q}}_{2}\,m_{2}-3\,L_{1}\,L_{2}\,{\ddot{q}_{2}}^{2}\,m_{2}\,\sin \left ( q_{2}\right ) \\ &+L_{1}\,L_{2}\,{\dot{q}_{2}}^{4}\,m_{2}\,\sin \left ( q_{2}\right ) -L_{1} \,{\dot{q}_{1}}^{2}\,g\,m_{1}\,\cos \left ( q_{1}\right ) -L_{1}\,{ \dot{q}_{1}}^{2}\,g\,m_{2}\,\cos \left ( q_{1}\right ) \\ &-L_{2}\,\ddot{q}_{1}\,g\,m_{2}\,\sin \left ( q_{1}+q_{2}\right ) -L_{2} \,\ddot{q}_{2}\,g\,m_{2}\,\sin \left ( q_{1}+q_{2}\right ) +2\,L_{1}\,L_{2} \,\ddot{\ddot{q}}_{1}\,m_{2}\,\cos \left ( q_{2}\right ) \\ &+L_{1}\,L_{2}\,\ddot{\ddot{q}}_{2}\,m_{2}\,\cos \left ( q_{2} \right ) -L_{1}\,\ddot{q}_{1}\,g\,m_{1}\,\sin \left ( q_{1}\right ) -L_{1} \,\ddot{q}_{1}\,g\,m_{2}\,\sin \left ( q_{1}\right ) \\ &-L_{2}\,{\dot{q}_{1}}^{2}\,g\,m_{2}\,\cos \left ( q_{1}+q_{2} \right ) -L_{2}\,{\dot{q}_{2}}^{2}\,g\,m_{2}\,\cos \left ( q_{1}+q_{2} \right ) -6\,L_{1}\,L_{2}\,\ddot{q}_{1}\,\ddot{q}_{2}\,m_{2}\,\sin \left ( q_{2}\right ) \\ &-6\,L_{1}\,L_{2}\,\dddot{q}_{1}\,\dot{q}_{2}\,m_{2}\,\sin \left ( q_{2} \right ) -2\,L_{1}\,L_{2}\,\dddot{q}_{2}\,\dot{q}_{1}\,m_{2}\,\sin \left ( q_{2}\right ) -4\,L_{1}\,L_{2}\,\dddot{q}_{2}\,\dot{q}_{2}\,m_{2}\,\sin \left ( q_{2}\right ) \\ &-6\,L_{1}\,L_{2}\,\ddot{q}_{1}\,{\dot{q}_{2}}^{2}\,m_{2}\,\cos \left ( q_{2}\right ) -6\,L_{1}\,L_{2}\,\ddot{q}_{2}\,{\dot{q}_{2}}^{2} \,m_{2}\,\cos \left ( q_{2}\right ) +2\,L_{1}\,L_{2}\,\dot{q}_{1}\,{ \dot{q}_{2}}^{3}\,m_{2}\,\sin \left ( q_{2}\right ) \\ &-2\,L_{2}\,\dot{q}_{1}\,\dot{q}_{2}\,g\,m_{2}\,\cos \left ( q_{1}+q_{2} \right ) -6\,L_{1}\,L_{2}\,\ddot{q}_{2}\,\dot{q}_{1}\,\dot{q}_{2}\,m_{2}\,\cos \left ( q_{2}\right ), \\ \ddot{\tau }_{2} =&-L_{2}\,m_{2}\,({\dot{q}_{1}}^{2}\,g\,\cos \left ( q_{1}+q_{2} \right ) -L_{2}\,\ddot{\ddot{q}}_{2}-L_{2}\,\ddot{\ddot{q}}_{1}+{\dot{q}_{2}}^{2}\,g\,\cos \left ( q_{1}+q_{2}\right ) \\ &-2\,L_{1}\,{\ddot{q}_{1}}^{2}\,\sin \left ( q_{2}\right ) + \ddot{q}_{1}\,g\,\sin \left ( q_{1}+q_{2}\right ) +\ddot{q}_{2}\,g\,\sin \left ( q_{1}+q_{2}\right ) -L_{1}\,\ddot{\ddot{q}}_{1}\,\cos \left ( q_{2} \right ) \\ &+L_{1}\,{\dot{q}_{1}}^{2}\,{\dot{q}_{2}}^{2}\,\sin \left ( q_{2} \right ) +2\,\dot{q}_{1}\,\dot{q}_{2}\,g\,\cos \left ( q_{1}+q_{2}\right ) +L_{1} \,\ddot{q}_{1}\,\ddot{q}_{2}\,\sin \left ( q_{2}\right ) -2\,L_{1}\,\dddot{q}_{1} \,\dot{q}_{1}\,\sin \left ( q_{2}\right ) \\ &+2\,L_{1}\,\dddot{q}_{1}\,\dot{q}_{2}\,\sin \left ( q_{2}\right ) +L_{1} \,\ddot{q}_{1}\,{\dot{q}_{2}}^{2}\,\cos \left ( q_{2}\right ) -L_{1}\, \ddot{q}_{2}\,{\dot{q}_{1}}^{2}\,\cos \left ( q_{2}\right ) -4\,L_{1}\, \ddot{q}_{1}\,\dot{q}_{1}\,\dot{q}_{2}\,\cos \left ( q_{2}\right ) ). \end{aligned}$$

They can again be verified by taking analytic derivatives of the above \((\dot{\tau }_{1},\dot{\tau }_{2})\).

6.2 KUKA LBR iiwa manipulator

The closed-form formulation presented in this paper are used to compute the second-order inverse dynamics of the 7 degrees of freedom KUKA LBR iiwa robot.

Kinematic model The body-fixed frames are introduced according to [29], which follow the modified Denavit–Hartenberg (DH) convention. As the \(z\)-axis represents the joint axis in this convention, the joint screw coordinates in body-fixed representation are

$$ {^{i}\mathbf{X}}_{i}=\left ( 0,0,1,0,0,0\right ) ^{T},i=1,\ldots ,7. $$
(58)

The relative reference configurations \({\mathbf{B}}_{i}\) in (3) have the form (2), with the relative rotation matrix \(\mathbf{R}_{i-1,i}\) and the position vector \({^{i-1}}\mathbf{r}_{i-1,i}\) from the origin of the reference of body \(i-1\) to that of its successor body \(i\). According to the zero reference configuration shown in Fig. 2 in [29], the body-fixed displacement vectors are

$$\begin{aligned} {^{i-1}}\mathbf{r}_{i-1,i} =&\mathbf{0},\quad i=1,2,4,6,7 \\ {^{2}}\mathbf{r}_{2,3} =&\left ( 0,r_{3},0\right ) ^{T},{^{4}} \mathbf{r}_{4,5}=\left ( 0,-r_{5},0\right ) ^{T} \end{aligned}$$

and the relative rotation matrices are

$$\begin{aligned} \mathbf{R}_{0,1} =&\mathbf{I} , \\ \mathbf{R}_{i-1,i} =&\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0\end{array}\displaystyle \right ) ,\quad i=2,5,6, \\ \mathbf{R}_{i-1,i} =&\left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0\end{array}\displaystyle \right ) ,\quad i=3,4,7. \end{aligned}$$
Fig. 2
figure 2

Link frames of the KUKA LBR iiwa 14 R820 robot [29]

Full size image

Dynamic model parameters The mass and inertia data used in this example is taken from the identified model of KUKA LBR iiwa robot reported in [29] as listed in Table 1. The COM position vector \({}^{i}\mathbf{c}_{i}=({^{i}}c_{i,x},{^{i}}c_{i,y},{^{i}}c_{i,z})^{T}\in \mathbb{R}^{3}\) of link \(i\) is measured with respect to the link \(i\) frame. The parameters in the symmetric inertia tensor of link \(i\) are defined relative to the COM of link \(i\) in the \(i\)th link frame.

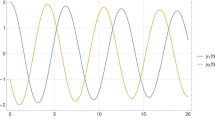
Table 1 Inertia data of different bodies in the KUKA robot as identified in [29]
Full size table

Second-order inverse dynamics The joint trajectory is described by means of cos-function as shown in Fig. 3a, and used for the inverse dynamics computation of the robotic manipulator (see Fig. 3b). Figure 4a and Fig. 4b show first- and second-order time derivatives of the generalized forces. The results computed from the closed-form expressions are compared against the numerical differentiation. As apparent from Fig. 4, the closed-form derivatives match the numerical time differentiation of generalized forces in both cases which attests the correctness of the formulation presented in this paper.

Fig. 3
figure 3

Joint trajectories and corresponding joint torques of the KUKA LBR iiwa 14 R820 robot

Full size image
Fig. 4
figure 4

Results for the higher-order inverse dynamics

Full size image

Computational performance The computational performance of the closed-form algorithm was evaluated by measuring the total CPU time spent in 10000 evaluations of second-order inverse dynamics on a standard laptop with Intel Core i9-7960X CPU clocked at 2.80 GHz and 128 GB RAM. It was found that the closed-form implementation takes 16.34 seconds leading to the average computational time of 1.6 milliseconds per evaluation, which is sufficient for many real-time control applications.

7 Conclusion and outlook

This paper presents closed-form expressions for the first and second time derivative of the EOM of a kinematic chain. Building upon the Lie group formulation of the EOM, the formulations are advantageous as they are expressed in terms of joint screw coordinates, and thus facilitate parameterization in terms of vector quantities that can be easily obtained. The computationally efficiency of these closed-form relations compared to recursive algorithms and their efficient implementation will be a topic of further research. It is already obvious from the presented expressions that they involve many repeated terms that can be precomputed and reused. Future research will also address the time derivatives of general mechanisms with kinematic loops and an efficient C++ based implementation in Hybrid Robot Dynamics (HyRoDyn) software framework [16].