Inverse dynamics of underactuated planar manipulators without inertial coupling singularities

Abstract

In this paper, we present a model for the inverse dynamics of underactuated manipulators that is free from inertial coupling singularities. The framework’s main idea is to include a small-amplitude wave on the trajectory of the rotating active joints. First, we derive the modified nonlinear dynamics for the multijoint manipulators with multiple degrees-of-freedom (DoF). Next, a 4-DoF mass-rotating underactuated manipulator with two passive and two active joints is chosen. Then, a condition assuming the positive definiteness of the inertia matrix is developed to have the singularity-free inverse dynamics. Finally, we analytically study how singularities can be avoided and show an example simulation with a feed-forward control at the singular configuration.

Appendix A: Dynamics of the 4-DoF manipulator

We show the 4-DoF nonlinear dynamics of a manipulator by the derived general formulation in Sect. 3.

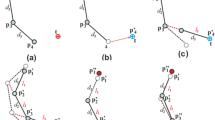
In our study, we consider our system with two passive and two active joints. The active joints on the second and forth links have the wavy trajectory with variables $\{a_{2},n_{2},\varepsilon _{2}\}$ and $\{a_{4},n_{4},\varepsilon _{4}\}$. The passive joints in the first and third links do not have the wave functions $a_{1}=n_{1}=\varepsilon _{1}=0$ and $a_{3}=n_{3}=\varepsilon _{3}=0$. So for the considered system, the Lagrangian function in (10) becomes

$$\begin{aligned} &L= \frac{1}{2} ( m_{1}+m_{2}+m_{3}+m_{4}) l^{2}_{1} \dot{q}^{2}_{1}+ \frac{1}{2} (m_{3}+m_{4}) l^{2}_{3} \dot{q}^{2}_{3} \\ &+\frac{1}{2} (m_{2}+m_{3}+m_{4})\dot{q}_{2}^{2} \big[ a^{2}_{2} n^{2}_{2} \cos ^{2}(n_{2} q_{2}+\varepsilon _{2}) +(l_{2}+a_{2} \sin (n_{2} q_{2} +\varepsilon _{2} ))^{2} \big] \\ &+\frac{1}{2}m_{4} \dot{q}_{4}^{2} \big[ a^{2}_{4} n^{2}_{4} \cos ^{2}(n_{4} q_{4}+\varepsilon _{4}) +(l_{4}+a_{4} \sin (n_{4} q_{4} +\varepsilon _{4}))^{2} \big] \\ &+(m_{2}+m_{3}+m_{4})\dot{q}_{1} \dot{q}_{2} \big[ l_{1} (l_{2}+a_{2} \sin (n_{2} q_{2}+\varepsilon _{2}))\cos (q_{1}-q_{2}) \\ &+ a_{2} n_{2} l_{1} \cos (n_{2} q_{2} +\varepsilon _{2})\sin (q_{2}-q_{1}) \big] +(m_{3}+m_{4}) \dot{q}_{1} \dot{q}_{3} l_{1}l_{3}\cos (q_{1}-q_{3}) \\ &+ (m_{3}+m_{4}) \dot{q}_{2} \dot{q}_{3} \big[ l_{3} (l_{2} +a_{2} \sin (n_{2} q_{2}+\varepsilon _{2}))\cos (q_{2}-q_{3}) \\ &+ a_{2} n_{2} l_{3} \cos (n_{2} q_{2} +\varepsilon _{2})\sin (q_{2}-q_{3}) \big] \\ &+ m_{4} \dot{q}_{1} \dot{q}_{4} \big[ l_{1}(l_{4}+a_{4}\sin (n_{4}q_{4}+ \varepsilon _{4}))\cos (q_{1}-q_{4}) +a_{4}n_{4}l_{1} \cos (n_{4}q_{4}+ \varepsilon _{4}) \sin (q_{4}-q_{1}) \big] \\ &+m_{4} \dot{q}_{2} \dot{q}_{4} \big[ (l_{2}+ a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2}))(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \cos (q_{2}-q_{4}) \\ & + a_{2}n_{2}a_{4} n_{4} \cos (n_{2}q_{2}+\varepsilon _{2})\cos (n_{4}q_{4}+ \varepsilon _{4}) \cos (q_{2}-q_{4}) \\ &+ a_{2}n_{2}(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \cos (n_{2}q_{2}+ \varepsilon _{2}) \sin (q_{2}-q_{4}) \\ &+a_{4}n_{4}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2})) \cos (n_{4}q_{4}+ \varepsilon _{4}) \sin (q_{4}-q_{2}) \big] \\ &+ m_{4} \dot{q}_{3} \dot{q}_{4} \big[ l_{3}(l_{4}+a_{4}\sin (n_{4}q_{4}+ \varepsilon _{4}))\cos (q_{3}-q_{4}) +a_{4}n_{4}l_{3} \cos (n_{4}q_{4}+ \varepsilon _{4}) \sin (q_{4}-q_{3}) \big] \\ & +\frac{1}{2} \sum ^{4}_{k=1} I_{k} \left ( \sum ^{k}_{i=1} \dot{q}_{k} \right )^{2}+\sum ^{4}_{k=1} \sum _{i=1}^{k} m_{k} g \left (l_{i}+a_{i} \sin \left ( n_{i} q_{i} +\varepsilon _{i}\right )\right ) \cos q_{i} . \end{aligned}$$

(28)

Furthermore, by using equation (28) and the Lagrangian equations (11), the motion equation terms of (12) become

$$\begin{aligned} & \mathbf {M}^{*}= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {M}_{11} & {M}_{12}& {M}_{13} &{M}_{14} \\ {M}_{21} & {M}_{22}& {M}_{23} &{M}_{24} \\ {M}_{31} & {M}_{32} & {M}_{33} &{M}_{34} \\ {M}_{41}& {M}_{42}& {M}_{43} & {M}_{44} \\ \end{array}\displaystyle \right ], \ \mathbf {h}^{*}= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {h}_{1}& {h}_{2} & {h}_{3} & {h}_{4} \end{array}\displaystyle \right ]^{T},\ \mathbf {u}^{*}=\left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0& {\tau }_{2}& 0 &{\tau }_{4} \end{array}\displaystyle \right ]^{T}, \end{aligned}$$

(29)

where

$$\begin{aligned} &M_{11}=I_{1}+I_{2}+I_{3}+I_{4} + (m_{1}+m_{2}+m_{3}+m_{4})l^{2}_{1}, \\ &M_{22}=I_{2}+I_{3}+I_{4}+(m_{2}+m_{3}+m_{4})\big[a_{2}^{2}n^{2}_{2} \cos ^{2}(n_{2}q_{2}+\varepsilon _{2}) +(l_{2}+a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2}))^{2}\big], \\ &M_{33}=I_{3}+I_{4}+(m_{3}+m_{4})l^{2}_{3},\; \\ &M_{44}=I_{4}+m_{4}\big[a_{4}^{2}n^{2}_{4}\cos ^{2}(n_{4}q_{4}+ \varepsilon _{4})+(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4}))^{2} \big], \\ &M_{12} = M_{21}=I_{2}+I_{3}+I_{4} +(m_{2}+m_{3}+m_{4})\big[l_{1}(l_{2}+a_{2} \sin (n_{1}q_{1}+\varepsilon _{1}))\cos (q_{1}-q_{2}) \\ &+a_{2} n_{2} l_{1} \cos (n_{2}q_{2}+\varepsilon _{2})\sin (q_{2}-q_{1}) \big], \\ &M_{13} =M_{31}=I_{3}+I_{4}+ (m_{3}+m_{4})l_{1}l_{3}\cos (q_{1}-q_{3}), \\ & M_{23} =M_{32}= I_{3}+I_{4}+ (m_{3}+m_{4}) \big[ l_{3}(l_{2} +a_{2} \sin (n_{2} q_{2} +\varepsilon _{2}))\cos (q_{2}-q_{3}) \\ &+a_{2}n_{2}l_{3}\cos (n_{2} q_{2}+\varepsilon _{2})\sin (q_{2}-q_{3}) \big], \\ &M_{34} = M_{43}=I_{4}+ m_{4} \big[ l_{3} (l_{4}+a_{4}\sin (n_{4} q_{4} + \varepsilon _{4}))\cos (q_{3}-q_{4}) \\ &+a_{4} n_{4} l_{3} \cos (n_{4} q_{4} +\varepsilon _{4})\sin (q_{4}-q_{3}) \big], \\ &M_{14} =M_{41}=I_{4}+m_{4}\big[ l_{1}(l_{4}+a_{4}\sin (n_{4}q_{4}+ \varepsilon _{4}))\cos (q_{1}-q_{4}) \\ &+a_{4}n_{4}l_{1}\cos (n_{4}q_{4}+\varepsilon _{4})\sin (q_{4}-q_{1}) \big], \\ &M_{24} =M_{42}=I_{4}+m_{4} \big[ (l_{2}+a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2})) (l_{4} +a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \cos (q_{2}-q_{4}) \\ &+a_{2}n_{2}a_{4} n_{4} \cos (n_{2}q_{2}+\varepsilon _{2})\cos (n_{4}q_{4}+ \varepsilon _{4}) \cos (q_{2}-q_{4}) \\ &+ a_{2}n_{2}(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \cos (n_{2}q_{2}+ \varepsilon _{2}) \sin (q_{2}-q_{4}) \\ &+a_{4}n_{4}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2})) \cos (n_{4}q_{4}+ \varepsilon _{4}) \sin (q_{4}-q_{2}) \big]. \end{aligned}$$

(30)

Additionally, the velocity dependencies and gravitational terms $h_{k}$ in each link are obtained by using (13) as

$$\begin{aligned} h_{1}&=(m_{2}+m_{3}+m_{4})\dot{q}^{2}_{2} \big[2a_{2} n_{2} l_{1} \cos (n_{2} q_{2} +\varepsilon _{2}) \cos (q_{1}-q_{2}) \\ +&l_{1}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2}))\sin (q_{1}-q_{2})-a_{2} n^{2}_{2} l_{1} \sin (n_{2} q_{2}+\varepsilon _{2}) \sin (q_{2}-q_{1}) \big] \\ +& (m_{3}+m_{4}) \dot{q}^{2}_{3} \big[ l_{1} l_{3} \sin (q_{1}-q_{3}) \big] \\ +&m_{4} \dot{q}^{2}_{4} \big[2a_{4} n_{4} l_{1} \cos (n_{4} q_{4} + \varepsilon _{4}) \cos (q_{1}-q_{4}) \\ +&l_{1}(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4}))\sin (q_{1}-q_{4})-a_{4} n^{2}_{4} l_{1} \sin (n_{4} q_{4}+\varepsilon _{4}) \sin (q_{4}-q_{1}) \big] \\ +&(m_{1}+m_{2}+m_{3}+m_{4})g \big[ (l_{1}+a_{1}\sin (n_{1}q_{1}+ \varepsilon _{1}))\sin q_{1} -a_{1}n_{1}\cos (n_{1}q_{1}+\varepsilon _{1}) \cos q_{1} \big], \\ h_{2}&=(m_{2}+m_{3}+m_{4})\dot{q}^{2}_{1} \big[2a_{2} n_{2} l_{1} \cos (n_{2} q_{2} +\varepsilon _{2}) \cos (q_{1}-q_{2}) \\ +&l_{1}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2}))\sin (q_{1}-q_{2})-a_{2} n^{2}_{2} l_{1} \sin (n_{2} q_{2}+\varepsilon _{2}) \sin (q_{2}-q_{1}) \big] \\ +&(m_{2}+m_{3}+m_{4})\dot{q}^{2}_{2} \big[ a_{2} n_{2} \cos (n_{2} q_{2} + \varepsilon _{2}) (l_{2}+a_{2}\sin (n_{2} q_{2}+\varepsilon _{2})) \\ -&a^{2} n^{3}_{2} \sin (n_{2} q_{2} +\varepsilon _{2}) \cos (n_{2} q_{2} +\varepsilon _{2}) \big] \\ +&(m_{3}+m_{4})\dot{q}^{2}_{3} \big[l_{3}(l_{2}+a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2}))\sin (q_{2}-q_{3})-a_{2}n_{2}l_{3}\cos (n_{2}q_{2} \\ +& \varepsilon _{2})\cos (q_{2}-q_{3})\big] \\ +&m_{4}\dot{q}^{2}_{4}\big[ 2a_{4} n_{4} \cos (n_{4} q_{4} + \varepsilon _{4}) (l_{2}+a_{2}\sin (n_{2} q_{2}+ \varepsilon _{2})) \cos (q_{2}-q_{4}) \\ +&2a_{2} n_{2} a_{4}n_{4}\cos (n_{2} q_{2}+\varepsilon _{2}) \cos (n_{4} q_{4}+\varepsilon _{4})\sin (q_{2}-q_{4}) \\ +&(l_{2}+a_{2}\sin (n_{2} q_{2}+\varepsilon _{2})) (l_{4}+a_{4}\sin (n_{4} q_{4} +\varepsilon _{4}))\sin (q_{2}-q_{4}) \\ -&a_{2} n_{2} a_{4} n^{2}_{4}\sin (n_{4}q_{4}+\varepsilon _{4}) \cos (n_{2} q_{2} +\varepsilon _{2})\cos (q_{2}-q_{4}) \\ -&a_{2}n_{2}(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4}))\cos (n_{2}q_{2}+ \varepsilon _{2})\cos (q_{2}-q_{4}) \\ -&a_{4}n^{2}_{4}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2}))\sin (n_{4}q_{4}+ \varepsilon _{4})\sin (q_{4}-q_{2})\big] \\ +&(m_{2}+m_{3}+m_{4})g \big[ (l_{2}+a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2}))\sin q_{2}-a_{2}n_{2}\cos (n_{2}q_{2}+\varepsilon _{2}) \cos q_{2} \big], \end{aligned}$$

and

$$\begin{aligned} h_{3}& =(m_{3}+m_{4}) \dot{q}^{2}_{1} \big[ l_{1} l_{3} \sin (q_{1}-q_{3}) \big] \hfill \\ +& (m_{3}+m_{4})\dot{q}^{2}_{2} \big[l_{3}(l_{2}+a_{2}\sin (n_{2}q_{2}+ \varepsilon _{2}))\sin (q_{2}-q_{3}) \\ -& a_{2}n_{2}l_{3}\cos (n_{2}q_{2} + \varepsilon _{2})\cos (q_{2}-q_{3})\big] \\ +&m_{4}\dot{q}^{2}_{4} \big[ 2a_{4}n_{4} l_{3} \cos (n_{4}q_{4}+ \varepsilon _{4}) \cos (q_{3}-q_{4}) \\ +& l_{3} (l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4}))\sin (q_{3}-q_{4})- a_{4}n^{2}_{4}l_{3} \sin (n_{4}q_{4}+\varepsilon _{4})\sin (q_{4}-q_{3}) \big] \\ +& (m_{3}+m_{4})g \big[ (l_{3}+a_{3}\sin (n_{3}q_{3}+\varepsilon _{3})) \sin q_{3}-a_{3}n_{3}\cos (n_{3}q_{3}+\varepsilon _{3})\cos q_{3} \big] , \\ h_{4}& = m_{4} \dot{q}^{2}_{1} \big[2a_{4} n_{4} l_{1} \cos (n_{4} q_{4} +\varepsilon _{4}) \cos (q_{1}-q_{4})+l_{1}(l_{4}+a_{4}\sin (n_{4}q_{4}+ \varepsilon _{4}))\sin (q_{1}-q_{4}) \\ -& a_{4} n^{2}_{4} l_{1} \sin (n_{4} q_{4}+\varepsilon _{4}) \sin (q_{4}-q_{1}) \big] \\ +& m_{4}\dot{q}^{2}_{2}\big[ 2a_{4} n_{4} \cos (n_{4} q_{4} + \varepsilon _{4})(l_{2}+a_{2}\sin (n_{2} q_{2}+ \varepsilon _{2})) \cos (q_{2}-q_{4}) \\ + &2a_{2} n_{2} a_{4}n_{4}\cos (n_{2} q_{2}+\varepsilon _{2})\cos (n_{4} q_{4}+\varepsilon _{4})\sin (q_{2}-q_{4}) \\ +&(l_{2}+a_{2}\sin (n_{2} q_{2}+\varepsilon _{2})) (l_{4}+a_{4}\sin (n_{4} q_{4} +\varepsilon _{4}))\sin (q_{2}-q_{4}) \\ -& a_{2} n_{2} a_{4} n^{2}_{4}\sin (n_{4}q_{4}+\varepsilon _{4}) \cos (n_{2} q_{2} +\varepsilon _{2})\cos (q_{2}-q_{4}) \\ -&a_{2}n_{2}(l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \cos (n_{2}q_{2}+ \varepsilon _{2})\cos (q_{2}-q_{4}) \\ -&a_{4}n^{2}_{4}(l_{2}+a_{2}\sin (n_{2}q_{2}+\varepsilon _{2})) \sin (n_{4}q_{4}+\varepsilon _{4})\sin (q_{4}-q_{2})\big] \\ +& m_{4}\dot{q}^{2}_{3} \big[ 2a_{4}n_{4} l_{3} \cos (n_{4}q_{4}+ \varepsilon _{4}) \cos (q_{3}-q_{4}) \\ +& l_{3} (l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4}))\sin (q_{3}-q_{4})- a_{4}n^{2}_{4}l_{3} \sin (n_{4}q_{4}+\varepsilon _{4})\sin (q_{4}-q_{3}) \big] \\ +& m_{4}\dot{q}^{2}_{4}[a_{4} n_{4} \cos (n_{4} q_{4} + \varepsilon _{4})(l_{4}+a_{4} \sin (n_{4} q_{4}+\varepsilon _{4}))-a^{2}_{4} n^{3}_{4} \sin (n_{4} q_{4} +\varepsilon _{4}) \cos (n_{4} q_{4} +\varepsilon _{4})] \\ +& m_{4} g \big[ (l_{4}+a_{4}\sin (n_{4}q_{4}+\varepsilon _{4})) \sin (q_{4})-a_{4}n_{4}\cos (n_{4}q_{4}+\varepsilon _{4})\cos (q_{4}) \big]. \end{aligned}$$

(31)