Abstract
Three rotation parameters are commonly used in multibody dynamics or in spacecraft attitude determination to represent large spatial rotations. It is well known, however, that the direct time integration of kinematic equations with three rotation parameters is not possible in singular points. In standard formulations based on three rotation parameters, singular points are avoided, for example, by applying reparametrization strategies during the time integration of the kinematic equations. As an alternative, Euler parameters are commonly used to avoid singular points. State-of-the-art approaches use Lie group methods, specifically integrators, to model large rigid body rotations. However, the former methods are based on additional information, e.g. the rotation matrix, which must be computed in each time step. Thus, the latter method is difficult to incorporate into existing codes that are based on three rotation parameters. In this contribution, a novel approach for solving rotational kinematics in terms of three rotation parameters is presented. The proposed approach is illustrated by the example of the rotation vector and the Euler angles. In the proposed approach, Lie group time integration methods are used to compute consistent updates for the rotation vector or the Euler angles in each time step and therefore singular points can be surmounted and the accuracy is higher as compared to the direct time integration of rotation parameters. The proposed update formulas can be easily integrated into existing codes that use either the rotation vector or Euler angles. The advantages of the proposed approach are demonstrated with two numerical examples.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The parametrization of spatial rotations is an important issue in many fields such as multibody dynamics (MBD) or in spacecraft attitude determination, for example, since the efficiency of non-linear computations involving large rotations depends largely upon the adequacy of the set of parameters adopted [16]. A commonly used type of rotation parameters in multibody systems dealing with the orientation of rigid or flexible bodies are Euler angles [41], whereas in spacecraft attitude determination, the rotation vector components are often used as rotation parameters [39, 52]. It is well known, however, that the direct time integration of kinematic equations with three rotation parameters is not possible in singular points. For a detailed discussion of singular points, see [49]. Hence, the rotational motion cannot be reconstructed by direct integration of the kinematic equations.
This contribution provides a novel numerical solution for the problem of direct time integration of Euler angles and, alternatively, the rotation vector as well as a novel implementation strategy for Lie group time integration methods.
1.1 The problem with the direct time integration of rotation parameters
To illustrate the problem of direct time integration of rotation parameters, we consider Euler’s equations of motion (EOM) for a single rigid body expressed in a local frame [35, 40]
that provides the angular velocity \(\boldsymbol {\omega }\in \mathbb {R}^{3}\), defined by
where \(\mathbf {R}\) is the rotation matrix transforming the body fixed coordinates of a point to the spatial coordinates. In Eq. (2), \(\widetilde {\boldsymbol {\omega }}\) is the skew-symmetric matrix such that \(\boldsymbol {\omega }\times \mathbf{x}=\widetilde {\boldsymbol {\omega }}\mathbf{x}\) for \(\boldsymbol {\omega },\mathbf{x}\in \mathbb {R}^{3}\) [30]. Solving Eq. (1) for angular velocity does not reveal the rotational motion of the rigid body. Therefore, Euler’s EOMs (1) must be complemented with the kinematic-reconstruction equation
which relates the angular velocity \(\boldsymbol {\omega }\) expressed in a local frame with the time derivative of the rotation matrix [51]. In order to determine \(\mathbf {R}\) and thus obtain the orientation of the body, it is required to solve Eq. (3), which is an ordinary differential equation (ODE) on the rotation group \(SO(3)\) [30, 51].
In many applications, however, e.g. rotor dynamics [38], the direct time integration in the rotation group is avoided by the introduction of a parametrization with generalized coordinatesFootnote 1\(\mathbf {q}\in \mathbb {R}^{3}\), e.g. Euler angles, such that their time derivatives \(\dot{\mathbf {q}}\) are related via
to the angular velocity \(\boldsymbol {\omega }\) [30]. When solving the kinematic equations (4) numerically, it is important to note that for each choice of rotation parameters \(\mathbf {q}\), regardless of the transformation itself, the transformation (4) depends on the configuration. For any three rotation parameters (e.g. Euler angles, Rodrigues parameter, rotation vector, etc.), \(\mathbf {G}\) becomes singular at certain configurations, leading to discontinuities in \(\mathbf {q}\). If such points are passed, the direct time integration of Eq. (4) is no longer possible. Therefore, a reconstruction of the rotational motion is no longer possible, although the discontinuities in \(\mathbf {q}\) are finite.
1.2 State-of-the-art solutions for direct integration of rotation parameters
In spacecraft attitude determination, switching algorithms are often used as a reparametrization strategy to avoid singular points when using three rotation parameters. For example, the singular points of the rotation vector are often avoided by considering only small rotations (thus the rotation vector represents a locally non-singular three-dimensional rotation parametrization) and by accumulating the incremental attitude in a unit quaternion or direction cosine matrix (DCM) such that the rotation angle corresponding to a rotation vector never gets large [39]. However, the storage in a unit quaternion or a DCM increases the amount of memory required as compared to three rotation parameters. In [48] a switching algorithm is proposed to switch between different Euler angle sets to avoid the singular points while integrating the kinematic equations (4). In [29] a reparametrization strategy based on Shuster’s idea of artificial rotation [45] is presented, which shifts the rotation angles associated with singular points of the rotation vector in such a way that either the Rodrigues parameters or the rotation axis and rotation angle can be used without running into a singular point. However, applying a switching algorithm during the integration of Eq. (4) increases the computational complexity as well as the implementation complexity compared to the direct integration of Eq. (4).
Three rotation parameters can be used in simulation if a reparametrization strategy such as, for example, the updated Lagrangian point of view [9, 16] is implemented to avoid singular points [8]. In the updated Lagrangian point of view, rotations are treated in an updated incremental form. In each step of the solution process, the rotation increment required for moving from the known reference configuration to the current configuration is determined by means of the rotation vector, which is used as a local but not as a global parametrization of the rotation group [9]. Using the rotation vector as well as the rotation matrix from the previous time step, the rotation matrix is updated in the updated Lagrangian point of view in each time step. As in the updated Lagrangian point of view the rotation matrix is used as rotation variable instead of three rotation parameters, it may be difficult to implement the updated Lagrangian point of view approach in existing codes that are based on three rotation parameters.
A common approach in MBD and spacecraft attitude determination to avoid singular points is to use Euler parameters (also known as unit quaternions) [38], as they have only four components – just one more parameter than the dimension of the space of rotations. However, the extra component is bothersome, it requires extra storage as well as extra work to manage the redundancy, e.g. renormalization to unit length [17], or requires solving differential–algebraic equations (DAEs) [5, 51]. The need of solving DAEs, however, can be eliminated as shown in [51]. However, it is important to note that if the quaternion integration scheme proposed in [51] is implemented correctly, redundancy will not appear at any time.
The rest of the paper is organized as follows: In Sect. 2, we introduce the standard approach to integrating the kinematic-reconstruction equation (3) using Lie group methods. This section presents the fundamentals on which the proposed approach builds. Subsequently, in Sect. 3, we present our approach independently of a specific choice of rotation parameters. In Sect. 4 (resp. Sect. 5), we apply the proposed approach to the rotation vector (resp. Euler angles). The implementation of the proposed approach is discussed in Sect. 6. In Sect. 7, numerical examples are discussed which illustrate the benefits of the proposed approach. Finally, Sect. 8 draws conclusions from the study.
2 Standard Lie group approach
The singular points in formulations based on three rotation parameters can be circumvented by using the so-called Lie group integrators [3]. In MBD (see, e.g. the integrators proposed in [7, 9]), one seeks, similarly as in the Munthe–Kaas methods [18, 25, 34] for solving ODEs on Lie groups, a solution to the kinematic-reconstruction equation (3) in the form
where \(\widetilde {\mathbf {\Omega }}\in \mathfrak {so}(3)\) is the new unknown and the solution of
In Eq. (5), \(\mathbf {R}_{0}\) is the initial attitude, and \(\mathfrak {so}(3)\) is the Lie algebra of the Lie group \(SO(3)\). Note that \(\mathbf {\Omega }_{0}\) in Eq. (6) is an initial condition and that \(\mathfrak {so}(3)\) is isomorphic to \(\mathbb {R}^{3}\); see, e.g. [3]. The smooth coordinate map \(\boldsymbol {\phi }\) takes \(\mathfrak {so}(3)\) to \(SO(3)\) [22, 24]. The most important coordinate map is the matrix exponentialFootnote 2\(\textrm {exp}(\cdot )\), which may be evaluated on \(SO(3)\) efficiently by Rodrigues’ formula [3, 24]. In Eq. (6), \(\mathbf {T}_{\boldsymbol {\phi }}^{-1}\) is the inverse tangent operator associated with the coordinate mapFootnote 3\(\boldsymbol {\phi }\). In case \(\boldsymbol {\phi }(\mathbf {\Omega })=\textrm {exp}(\mathbf {\Omega })\), \(\mathbf {\Omega }\) is termed instantaneous or incremental rotation vector in the context of Lie group methods on \(SO(3)\) [32, 47, 51]. To ensure a consistent notation in the following, the term incremental rotation vector is associated with \(\mathbf {\Omega }\) regardless of the choice of a coordinate map.
The crucial feature of Eq. (5) is that no global parametrization is required. In contrast to Eq. (4), Eq. (6) can be integrated without running into a singular point. This is because \(\mathbf {\Omega }\) serves as a coordinate vector that locally parametrizes the configuration increment from time step \(i\) to time step \(i+1\) and is assumed to describe small rotations [32].
As shown in [7], \(\mathbf {R}_{0}\) is updated in Eq. (5) in each integration step. Therefore, the rotation matrix \(\mathbf {R}_{0}\) represents a kind of history variable that needs to be available in each integration step during the simulation.Footnote 4 Handling the history variable \(\mathbf {R}_{0}\) during time integration is cumbersome and requires additional memory compared to three rotation parameters. The latter procedure may therefore be difficult to implement in existing codes. Specifically on embedded systems, additional history variables might be difficult to be integrated.
3 Proposed approach (independent of specific rotation parameters)
In this section we present the proposed approach for computing consistent updates for a general set of three rotation parameters, which is subsequently applied to the rotation vector as well as Euler angles.
In the proposed approach, the rotation matrix \(\mathbf {R}\) that is reconstructed with Eq. (5) using the incremental rotation vector \(\mathbf {\Omega }\) is parametrized by three rotation parametersFootnote 5\(\mathbf {q}\in \mathbb {R}^{3}\), and therefore Eq. (5) may be represented in the form
where \(\mathbf {q}_{0}\) represents initial attitude such that \(\mathbf {R}(\mathbf {q}_{0})=\mathbf {R}_{0}\).
The idea of the proposed approach is to consider Eq. (7) as that rotation, which is equivalent to a rotation \(\mathbf {R}(\mathbf {q}_{0} \circ \Delta \mathbf {q})\) due to an incremental change of the rotation parameters \(\Delta \mathbf {q}\in \mathbb {R}^{3}\) such that
applies and therefore to consider
as the solution of Eq. (3) instead of Eq. (5). In Eqs. (8)–(9), the symbol ‘∘’ represents the composition rule for the selected rotation parameters \(\mathbf {q}\). Note that the explicit form of the composition rule ‘∘’ for rotation parameters depends on the selected rotation parameters. Note also that the symbol ‘∘’ is used here to indicate that the rotation parameters \(\mathbf {q}\) are determined from the rotation parameters \(\mathbf {q}_{0}\) and \(\Delta \mathbf {q}\) using the appropriateFootnote 6composition rule. In Eq. (9), we assume that
and that \(\Delta \mathbf {q}\) does not need to be small. Furthermore, we consider the incremental change of the rotation parameters \(\Delta \mathbf {q}\) as a finite increment of rotation. To be able to compute the rotation parameter update with Eq. (9), \(\Delta \mathbf {q}(\mathbf {q}_{0},\mathbf {\Omega })\) must be determined for the selected rotation parameters depending on the incremental rotation vector \(\mathbf {\Omega }\), where the incremental rotation vector is determined in each time step by solving Eq. (6) numerically.
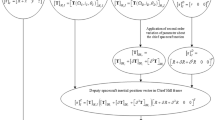
The rotation parameters \(\mathbf {q}\) can, of course, also be extracted from the rotation matrix as shown in [19, 27, 43], which is a detour compared to the method proposed in this paper. In the proposed approach, the rotation parameters \(\mathbf {q}\) are computed directly using the incremental rotation vector without having to evaluate in advance the rotation matrix, see Fig. 1, last line.
As shown in Fig. 1, in the proposed approach the rotation parameters are not determined by integrating the corresponding kinematic equations (4), but by using the incremental rotation vector. Thus, we do not need to deal with the singular points occurring in the kinematic equations (4). Of course, there is no three-parametric description of spatial rotations that is free of singular points [49]. Consequently, singular points are also present in the proposed approach. However, Eq. (9) allows dealing with singular points at the coordinate level. At the coordinate level, singular points can be embedded within the composition rule of rotations that applies to the selected rotation parameters using case distinctions, for example, such that the time integration scheme reconstructs the rotation parameters associated with a singular point without failing.
We would like to note, however, that the idea of computing rotation updates based on the incremental rotation vector is not new at all, see the references in Sect. 1.2 and Sect. 2. However, the authors are not aware that an approach similar to the presented one has already been discussed for the time integration of three rotation parameters.
As a final remark, we would like to note that the reason why we consider different parametrizations for the map \(\boldsymbol {\phi }\) in Eq. (7) is that the choice of the parametrization of the map \(\boldsymbol {\phi }\) has a significant influence on the computational effort required to compute \(\Delta \mathbf {q}\) and thus on the computational effort required to determine a rotation parameter update.
The advantages of the proposed approach are shown in the following by the example of the rotation vector, as well as by the example of Euler angles.
4 Proposed approach for the time integration of rotation vector
In this section, we apply the general approach to integrating rotation parameters presented in Sect. 3 to the rotation vector parametrization, i.e. \(\mathbf {q}=\mathbf {v}\).
4.1 Definition of the rotation vector
If \(\mathbf {n}\in \mathbb {R}^{3}\) is a unit vector along the rotation axis and \(\varphi \in \mathbb {R}\) is the rotation angle, then the corresponding rotation vector \(\mathbf {v}\in \mathbb {R}^{3}\) is given by [4, 28, 32, 43] (see also Fig. 2)
where the rotation angle \(\varphi \) and rotation axis \(\mathbf {n}\) can be recovered from rotation vector \(\mathbf {v}\) by
Body-fixed vector in positions \(\mathbf{r}\) before and \(\mathbf{r}^{*}\) after the rotation (\(\varphi \), \(\mathbf {n}\)), see also [53]
4.2 Rotation vector update
To be able to compute an update of the rotation vector in the form of Eq. (9), we need to find the composition rule for rotation vectors depending on the incremental rotation vectorFootnote 7\(\mathbf {\Omega }\).
The relation between the incremental rotation vector \(\mathbf {\Omega }\) and the rotation vector increment \(\Delta \mathbf {v}\) when \(\boldsymbol {\phi }=\textrm {exp}\) isFootnote 8
The composition rule of two successive rotations with rotation vectors
and
with \(\mathbf {v}\) being the resultant rotation vector, is determined by using Eq. (11) as
In Eq. (16), \(\varphi (\varphi _{0},\Delta \varphi , \mathbf {n}_{0},\Delta \mathbf {n})\) and \(\mathbf {n}(\varphi _{0},\Delta \varphi , \mathbf {n}_{0},\Delta \mathbf {n})\) are given by
after elementary transformations of the equations given in [1, 37, 39, 54] where \(\mathbf {I}\) is a 3×3-identity matrix. In Eqs. (17)–(18), we have used the relationships
and
In Eqs. (17)–(18), \(\varphi _{0} \circ \Delta \varphi \) represents the composition rule for rotation angles and \(\mathbf {n}_{0} \circ \Delta \mathbf {n}\) represents the composition rule for rotation axes. It should be noted, however, that Eqs. (17)–(18) can only be evaluated for \(\Vert \mathbf {\Omega }\Vert \neq 0\) and \(\varphi \notin S_{v}\) where
4.3 Improved rotation vector update
The case \(\Vert \mathbf {\Omega }\Vert =0\) can be covered using the cardinal sine function
which is continuous and computable at \(x=0\) [32]. Therefore, we replace Eqs. (17)–(18) with
To cover the case \(\varphi \in S_{v}\), we introduce the rotation axis \(\bar {\mathbf {n}}\) using the case distinctionFootnote 9
By using Eqs. (23) and (25), the composition rule for rotation vectors reads
which can be evaluated for all \(\varphi \in \mathbb {R}\) without restrictions.
The improvements of Eqs. (23) and (24) (resp. Eq. (25)) compared to Eqs. (17)–(18) are shown with the following considerations:
-
Case 1. In the case that \(\varphi _{0} \neq 0\) and \(\mathbf {\Omega }=\mathbf {0}\), after a few steps of calculation, it follows from Eqs. (23) and (25) that
$$ \varphi (\varphi _{0} \neq 0,\,\mathbf {\Omega }=\mathbf {0}) = \varphi _{0} $$(27)and
$$ \bar {\mathbf {n}}(\varphi _{0} \neq 0,\,\mathbf {\Omega }= \mathbf {0}) = \mathbf {n}_{0}. $$(28)For this case, Eq. (26) therefore gives
$$ \mathbf {v}(\varphi _{0} \neq 0,\,\mathbf {\Omega }=\mathbf {0}) = \mathbf {v}_{0}. $$(29) -
Case 2. In the case that \(\varphi _{0} = 0\) and \(\mathbf {\Omega }\neq \mathbf {0}\), after a few steps of calculation it follows from Eqs. (23) and (25) that
$$ \varphi (\varphi _{0} = 0,\,\mathbf {\Omega }\neq \mathbf {0}) = \Vert \mathbf {\Omega }\Vert $$(30)and
$$ \bar {\mathbf {n}}(\varphi _{0} = 0,\,\mathbf {\Omega }\neq \mathbf {0}) =\frac{\mathbf {\Omega }}{\Vert \mathbf {\Omega }\Vert }. $$(31)For this case, Eq. (26) therefore gives
$$ \mathbf {v}(\varphi _{0} = 0,\,\mathbf {\Omega }\neq \mathbf {0}) = \mathbf {\Omega }. $$(32) -
Case 3. Of course, for the trivial case \(\varphi _{0} = 0\) and \(\mathbf {\Omega }=\mathbf {0}\), Eq. (26) yields
$$ \mathbf {v}(\varphi _{0} = 0,\,\mathbf {\Omega }=\mathbf {0}) = \mathbf {0}. $$(33)
Note that the rotation vector exhibits a redundancy at the rotation angles \(\varphi \in S_{v}\) [20]. However, the Rodrigues’ formula
resolves the redundancy \(\varphi \in S_{v}\),
Note that the redundancy of the rotation vector at \(\varphi \in S_{v}\) can be bypassed by scaling the rotation vector such that its magnitude always belongs to an interval \(\varphi \in \left [-\pi ,\,\pi \right ]\) as shown in [20].
Since we use the exponential map Eq. (77) in Eq. (13) to establish a relation between \(\mathbf {\Omega }\) and \(\Delta \mathbf {v}\), the inverse tangent operator corresponding to the exponential map \(\mathbf {T}_{\textrm {exp}}^{-1}\) in Eq. (82) needs to used in Eq. (6). Therefore, Eq. (6) takes the form
The incremental rotation vector \(\mathbf {\Omega }\) is then determined in each time step by solving Eq. (36) numerically.
As a final remark, we would like to note that Engø [14] presented a closed form of the Baker–Campbell–Hausdorff formula on \(\mathfrak {so}(3)\) and has interpreted it as a composition of two rotations, which was extended in [12] for \(\mathit{SE}(3)\) and dual quaternions. However, the formula presented in [14] cannot be applied directly for the time integration of the rotation vector, since it only provides correct answers for rotation angles smaller than \(\pi \)/2 as noted in the paper.
5 Proposed approach for the time integration of Euler angles
In this section, we apply the general approach to the Euler angle parametrization, i.e. \(\mathbf {q}=\boldsymbol {\alpha }\).
To be able to compute an update for Euler angles in the form of Eq. (9), we need to find the composition rule as well as the Euler angle increment depending on the incremental rotation vector \(\mathbf {\Omega }\). Since there are 12 possible sets of Euler angles [13, 19, 44], we present a general procedure to determine the Euler angle increment for an arbitrary set of Euler angles. In Appx. B we apply the general procedure shown in this section to determine the Euler angle increment for Cardan/Tait–Bryan angles, which has been omitted here for reasons of space and clarity.
Any combination of three elementary rotations is given as
with \(\mathbf {e}_{i}\) being a constant unit vector [32, 48] and \(\textrm {exp}\) being the exponential map Eq. (77). For the Cardan/Tait–Bryan angle parametrization, these are the unit vectors
whereas for 313-Euler angles these are unit vectors [32]
In the proposed approach, the composition rule of two successive rotations with Euler angles \(\alpha _{0,1}\), \(\alpha _{0,2}\), \(\alpha _{0,3}\) and \(\Delta \alpha _{1}\), \(\Delta \alpha _{2}\), \(\Delta \alpha _{3}\) where \(\alpha _{1}\), \(\alpha _{2}\), \(\alpha _{3}\) are the resulting Euler angles is applied asFootnote 10
where \(\Delta \alpha _{i}\) is implicitly defined by the standard Lie group method Eq. (5) and explicitly computed in our approach.
By using Eq. (40), the elementary rotation \(\textrm {exp}(\alpha _{i}\widetilde {\mathbf {e}}_{i})\) associated with the \(i\)th Euler angle \(\alpha _{i}\) is written as
By multiplying Eq. (41) with \(\textrm {exp}^{T}(\alpha _{0,i}\widetilde {\mathbf {e}}_{i})\) from the left, the elementary rotation \(\textrm {exp}(\Delta \alpha _{i}\widetilde {\mathbf {e}}_{i})\) associated with the Euler angle increment \(\Delta \alpha _{i}\) is given by
From Eq. (42) two equations are obtained for \(\Delta \alpha _{i}\), one equation for the sine and one equation for the cosine of an incremental angle, which readFootnote 11
From Eqs. (43)–(44), the Euler angle increment \(\Delta \alpha _{i}\) is computed using the proper four-quadrant inverse tangent function atan2Footnote 12
In order to be able to compute \(\Delta \alpha _{i}\) with Eq. (45), \(\sin \alpha _{i}\) and \(\cos \alpha _{i}\) in Eqs. (43)–(44) need to be expressed depending on the incremental rotation vector. However, the equations that provide this connection assume different forms for each of the 12 possible Euler angle combinations. The procedure for establishing a relationship between \(\sin \alpha _{i}\) and \(\cos \alpha _{i}\) and \(\mathbf {\Omega }\) is illustrated in Appx. B using the Cardan/Tait–Bryan angles as an example.
By combining the Euler angles \(\alpha _{0,i}\) in vector
and the Euler angle increments \(\Delta \alpha _{i}\) obtained with Eq. (45) in vector
and the Euler angles \(\alpha _{i}\) in vector
the composition rule of two successive rotations in vector form for Euler angles is
6 Time integration scheme for the proposed approach
In the proposed approach, the rotational update within the \(i\)th integration step is based on Eq. (9), where the incremental rotation vector updates a rotation of \(\mathbf {q}_{i}\) to \(\mathbf {q}_{i+1}\). Therefore we express the update for the step \(i+1\) in the form
where \(\mathbf {\Omega }_{i}\) is the incremental rotation vector of step \(i\) and \(\mathbf {q}_{i}\) represents the rotation parameters at the \(i\)th step; see, e.g. [3, 8]. In order to obtain \(\mathbf {\Omega }_{i}\), we write Eq. (6) as
where \(\mathbf {\Omega }_{0}\) is the initial condition for the integration of Eq. (51) in the \(i\)th integration step and \(\boldsymbol {\omega }_{i+1}\) is the angular velocity of step \(i+1\). The equations (51) should be integrated within each integration step together with the dynamical equations of motion, which determine the angular velocity field \(\boldsymbol {\omega }\) from the angular acceleration field
by using Euler’s EOMs (1); see, for example, [51].
6.1 Explicit Euler (RK1)
Using the time step size \(h\), the explicit Euler method takes the following form for the proposed approach:
which differs from the standard explicit Euler Lie group method presented in [26] by the fact the no history variables are required. The conventional explicit Euler method for the direct time integration of rotation parameters would have the form
The comparison of Eqs. (56)–(57) with Eqs. (53)–(55) shows that the proposed approach can be integrated into existing applications that use three rotation parameters by simply replacingFootnote 13Eq. (57) with Eqs. (54)–(55).
Using the rotation vector, i.e. \(\mathbf {q}=\mathbf {v}\), for Euler’s EOMs (1)
for the proposed approach, the explicit Euler method takes the form
At this point, we would like to give a brief interpretation of the RK1 method with regard to its functionality in a singular point: Since \(\dot{\boldsymbol {\omega }}\) is bounded (due to the physical limitation of torque), \(\boldsymbol {\omega }\) is also bounded, and thus also \(\mathbf {\Omega }\). Consequently, \(\mathbf {v}\) is also bounded due to the definition of the composition rule for rotation vectors defined in Sect. 4. However, if one would consider the direct integration of the kinematic equations of the rotation vector Eq. (87) (Appx. A.3), \(\dot{\mathbf {v}}\) would not be bounded at a singular point.
Note that, according to the explicit Euler method, Eqs. (53)–(55) are only first-order accurate and have a numerical stability limit for the step size \(h\) in case of stiff differential equations.
6.2 Explicit Runge–Kutta method of fourth-order (RK4)
To achieve a higher accuracy with larger step sizes \(h\), we consider the explicit fourth-order Runge–Kutta method presented for time integration of Euler parameters by Terze et al. in [51] in all presented numerical examples, which we have written here in accordance with the proposed approach. Starting with values at the previous step \(\mathbf {q}_{i}\), \(\boldsymbol {\omega }_{i}\), the slope estimations are obtained by
The four coefficients \(\mathbf{K}_{1},\ldots ,\mathbf{K}_{4}\) represent the slopes within one time step \((i \rightarrow i+1)\) in the solution process of Eq. (51) and the four coefficients \(\mathbf{k}_{1},\ldots ,\mathbf{k}_{4}\) contain the slopes within one time step in the solution process of the dynamic equations of motion. The equations
update the angular velocity vector \(\boldsymbol {\omega }\) and the rotation parameter vector \(\mathbf {q}\) to \((\mathbf {q}_{i+1},\, \boldsymbol {\omega }_{i+1})\) based on the current state \((\mathbf {q}_{i},\, \boldsymbol {\omega }_{i})\).
Since the composition rule of two successive rotations can be expressed in a closed form for the rotation vector and the Euler angles, the order of accuracy of the overall algorithm depends only on the accuracy of the ODE integrator used to solve Eq. (51). The main paradigm of the Lie group methods is the reformulation of the underlying equation on the Lie group as an algebra action, and since the Lie algebra is a linear space, all reasonable discretization methods can be expected to respect its structure [23, 24]. Therefore the user can influence the accuracy of the overall algorithm by choosing the ODE integrator to solve Eq. (51).
7 Numerical examples
7.1 Behaviour in singular configurations
As a first numerical example, we investigate the behaviour of the proposed rotation vector and Euler angle approach near and in a singular point where \(\mathbf {G}(\mathbf {q})\) in Eq. (4) becomes singular. For this purpose, we consider a parameter study for the torque-free, free rotation of a rigid body with parametrized initial conditions, which are changed such that the orientation approaches the singular point and finally reaches it. Since there are a total of 12 possible Euler angle sets, we limit ourselves to Cardan/Tait–Bryan angles for the proposed Euler angle approach in all following numerical examples. The rigid body is considered to be a box with inertia tensor \(\mathbf{J}\) given in standard units equal to \(\mathbf{J} = \mathrm{diag}(5.2988, 1.1775, 4.3568)\). The rotation vector parametrization has a singular points at the rotation angles \(\varphi \in S_{v}\), see Eq. (87) in Appx. A.3, whereas the Cardan/Tait–Bryan angles exhibit a singular point at \(\alpha _{2}=\pm n\frac{\pi }{2}\) with \(n\in \mathbb {N}\), see Eq. (88) in Appx. A.4. In order to determine \(\boldsymbol {\omega }(t)\), \(\mathbf {\Omega }(t)\) and thus also \(\mathbf {v}(t)\) and \(\boldsymbol {\alpha }(t)\), Euler’s equations of motion (1) as well as the incremental rotation vector differential equation (36) are integrated using the RK4 algorithm presented in Sect. 6.2, whereby in the proposed Cardan/Tait–Bryan approach we use the exponential map Eq. (78) as a coordinate map. Similar results for Cardan/Tait–Bryan angles can be obtained by choosing the Cayley transform Eq. (83) as a coordinate map. The whole algorithm has been implemented in MATLAB R2018b.
7.1.1 Numerical tests for the proposed rotation vector approach
In this subsection we investigate the behaviour of the rotation vector approach proposed in this paper near and in the singular point at \(\varphi =0\). Similar results can be obtained for other singular points of the rotation vector. In order to reach the singular point at \(\varphi =0\) step by step, we change the initial condition for angular velocity according to
gradually increasing the factor \(\epsilon \in \left \{ 0,\,\textrm{1e--7},\,\textrm{1e--5},\, 1\right \} \) whereby the initial orientation of the rigid body is kept constant at \(\mathbf {v}_{0}= \begin{bmatrix} 0, & -\frac{\pi }{2}, & 0\end{bmatrix} ^{T}\text{ rad}\). Thus, the singular point is reached after \(t=0.5\text{ s}\).
As can be seen in Fig. 3(a), in the case of \(\varphi =0\), the rotation vector \(\mathbf {v}_{\mathrm{StdAppr}}\) can no longer be determined by integrating Eq. (87) at \(t=0.5\text{ s}\) due to the division by zero. In contrast, as can be seen in Fig. 3(b), the proposed approach for computing a rotation vector update \(\mathbf {v}_{\mathrm{PropAppr}}\) is able to pass through the singular point without failing.
Time history of the rotating rigid body’s rotation angle \(\Vert \mathbf {v}\Vert _{2}\) using different initial conditions, see Eq. (71). (a) shows the time history of the rotation angle \(\Vert \mathbf {v}_{\mathrm{StdAppr}}\Vert _{2}\) computed by direct time integration of Eq. (87). (b) shows the time history of the rotation angle \(\Vert \mathbf {v}_{\mathrm{PropAppr}}\Vert _{2}\) computed with the proposed approach
Figure 4 illustrates convergence in the norm of the rotation error \(\Vert \mathbf {v}_{\mathrm{Ref}} - \mathbf {v}_{ \mathrm{converged}}\Vert \) for decreasing values of the integration step \(h_{n} = (2^{(1-n)})_{n=2,3,\ldots,15}\), where the rotation vector \(\mathbf {v}_{\mathrm{StdAppr}}\) is obtained by directly integrating (87). The converged reference solution \(\mathbf {v}_{\mathrm{Ref}}\) is obtained with \(h=1/32768\text{ s}\) using the proposed approach. As can be seen in Fig. 4(a), the rotation vector \(\mathbf {v}_{\mathrm{StdAppr}}\) converges slower the closer the rotation angle comes to the singular point at \(\varphi =0\) and it even fails as the rotation angle reaches \(\varphi =0\). The failure of the standard method corresponds to the expectation, since in the kinematic Eq. (87) a division by zero occurs at \(\varphi =0\). In contrast, the rotation vector \(\mathbf {v}_{\mathrm{PropAppr}}\) computed with the proposed approach exhibits the expected fourth-order convergence characteristics for all considered values of \(\epsilon \), as can be seen in Fig. 4(b). Furthermore, as can be seen in Fig. 4(b), the rotation angle \(\Vert \mathbf {v}_{\mathrm{PropAppr}}\Vert _{2}\) for \(\epsilon =0\) is already converged at larger time steps, such that \(\Vert \mathbf {v}_{\mathrm{Ref}} - \mathbf {v}_{ \mathrm{converged}}\Vert =0\), except at \(h=1/2048\) where a deviation of approximately \(1\textrm{e--}13\) is observed. To illustrate the situation \(\Vert \mathbf {v}_{\mathrm{Ref}} - \mathbf {v}_{ \mathrm{converged}}\Vert =0\) in a better way, \(\Vert \mathbf {v}_{\mathrm{Ref}} - \mathbf {v}_{ \mathrm{converged}}\Vert =1\textrm{e--}14\) was set in Fig. 4(b) for \(\epsilon =0\).
7.1.2 Numerical tests for the proposed Cardan/Tait–Bryan angle approach
In this subsection we investigate the behaviour of the proposed Cardan/Tait–Bryan angle approach near and in the singular point at \(\alpha _{2}=\frac{\pi }{2}\). In order to reach the singular point at \(\alpha _{2}=\frac{\pi }{2}\) step by step, we change the initial condition for angular velocity according to
gradually increasing the factor \(\epsilon \in \left \{ 0,\,\textrm{1e--5},\,\textrm{1e--2},\, \textrm{1e--1}\right \} \) whereby the initial orientation of the rigid body is kept constant at \(\boldsymbol {\alpha }_{0}= \begin{bmatrix} 0, & 0, & 0\end{bmatrix} ^{T}\text{ rad}\). Thus, the singular point is reached after \(t=0.5\text{ s}\).
As can be seen in Fig. 5(a), as \(\Vert \boldsymbol {\alpha }_{\mathrm{StdAppr}}\Vert _{2}\) (which is dominated by the rotation angle \(\alpha _{2}\)) comes to the singular point at \(\alpha _{2}=\frac{\pi }{2}\), \(\Vert \boldsymbol {\alpha }_{\mathrm{StdAppr}}\Vert _{2}\) can no longer be determined at \(t=0.5\text{ s}\) by integrating the kinematic equation (88). This corresponds to the expectation, since in Eq. (88) a division by zero occurs at \(\alpha _{2}=\frac{\pi }{2}\). In contrast, as can be seen in Fig. 5(b), the proposed approach is able to pass through the singular point at \(\alpha _{2}=\frac{\pi }{2}\) without failing.
Time history of the rotating rigid body’s norm of Cardan/Tait–Bryan angles for different initial conditions, see Eq. (72)
In the case that \(\epsilon =0\), the rigid body performs a pure rotation around the middle axis of rotation. For this simple case an analytical solution of Eq. (88) for the rotation angle \(\alpha _{2}\) can be given, which is
However, as can be seen in Fig. 6(b), the Cardan/Tait–Bryan angles determined with the proposed approach show finite jumps compared to the analytical solution (Fig. 6(a)) at angle values for \(\alpha _{2}= n\frac{\pi }{2}\) with \(n\in \mathbb {N}\) (these are the angle values where the Cardan/Tait–Bryan angle parametrization has singular points). However, the Cardan/Tait–Bryan angles determined with the proposed approach can, if desired, be converted in the course of post-processing, see Fig. 7(a). The conversion can be done by evaluating the rotation matrix and extracting the angles as shown for example in [19]. However, we would like to emphasize that this conversion is not necessary in order to uniquely represent the rotational attitude of a rigid body using the proposed approach. Figure 7(b) shows the deviation of the converted angle \(\alpha _{2}\) from the analytic solution for a time interval of 100 s, whereby the angles determined with the proposed approach were determined with a time step size of \(h=1\textrm{e--}3\text{ s}\).
Figure 8 illustrates convergence in the norm of the rotation error \(\Vert \boldsymbol {\alpha }_{\mathrm{Ref}} - \boldsymbol {\alpha }_{\mathrm{converged}} \Vert \) for decreasing values of the integration step \(h_{n} = (2^{(1-n)})_{n=1,2,\ldots,14}\), where the rotation vector \(\boldsymbol {\alpha }_{\mathrm{StdAppr}}\) is obtained by integrating the kinematic equation (88). The converged reference solution \(\boldsymbol {\alpha }_{\mathrm{Ref}} \) is obtained with \(h=1/16384\text{ s}\) using the proposed approach. As can be seen in Fig. 8(a), \(\boldsymbol {\alpha }_{\mathrm{StdAppr}}\) converges slower the closer \(\alpha _{2}\) comes to the singular point at \(\alpha _{2}=\frac{\pi }{2}\) and it even fails as the rotation angle \(\alpha _{2}\) reaches \(\alpha _{2}=\frac{\pi }{2}\). The failure of the standard method corresponds to the expectation, since in the kinematic Eq. (88) a division by zero occurs at \(\alpha _{2}=\frac{\pi }{2}\). In contrast, the proposed Cardan/Tait–Bryan angle approach exhibits the expected fourth-order convergence characteristics for all considered values of \(\epsilon \), as can be seen in Fig. 8(b). Furthermore, as can be seen in Fig. 8(b), \(\Vert \boldsymbol {\alpha }_{\mathrm{PropAppr}}\Vert _{2}\) is in case that \(\alpha _{2}=\frac{\pi }{2}\) already converged at larger time steps. For the convergence investigations in Fig. 8, the Cardan/Tait–Bryan angles determined with the proposed approach were converted as described above in the case of \(\epsilon =0\).
7.1.3 Influence of the used ODE integrator for solving Eq. (51)
To illustrate how the accuracy of the proposed approach depends on the order of the ODE integrator used to integrate Eq. (51), we compare in Fig. 9 the rotation vector error when the integration of Eq. (51) (resp. Eq. (36)) was performed using the two methods RK1 (see Sect. 6.1) and RK4 (see Sect. 6.2). As model problem we consider here the rotation of a torque-free rigid body about an axis close to its unstable axis of rotation. The rigid body is considered to be a box with inertia tensor equal to \(\mathbf{J} = \mathrm{diag}(5.2988, 1.1775, 4.3568)\). Since \(J_{11} > J_{33} > J_{22}\), an unstable rotation about the third axis is expected. The initial conditions are set as \(\mathbf {v}_{0} = \begin{bmatrix} 0, & 0, & 0\end{bmatrix} ^{T}\) and \(\boldsymbol {\omega }_{0}= \begin{bmatrix} 0.01, & 0, & 100 \end{bmatrix} ^{T}\).
Figure 9 illustrates convergence in the norm of the rotation error \(\Vert \mathbf {v}_{\mathrm{Ref}} - \mathbf {v}_{\mathrm{converged}}\Vert \) for decreasing values of the integration step \(h_{n} = (\frac{1}{2}\cdot 10^{(1-n)})_{n=2,3,\ldots,6}\), where the converged reference solution \(\mathbf {v}_{\mathrm{Ref}}\) is obtained with \(h=1/2000000\text{ s}\). Convergence is investigated at \(t=0.5\text{ s}\). As can be seen in Fig. 9, the overall integration results show first and fourth order convergence characteristics as expected. This demonstrates the fact that the order of accuracy of the proposed approach can be selected by the user and that it depends only on the accuracy of the ODE integrator used for the integration of Eq. (51). The versatility of the proposed approach in terms of the possibility of arbitrarily selecting the order of accuracy according to the field of application should contribute positively to its use in the various fields of application, including those requiring higher-order integration schemes. The same behaviour is observed in the Euler angle integration scheme presented in this paper. However, due to space reasons we do not present the corresponding figure here. We would like to note that the latter behaviour is also observed for the Euler parameter integration scheme presented in [51].
7.1.4 Convergence comparison with the standard Lie group method
To illustrate how the proposed approach compares to the standard Lie group method in terms of accuracy, we compare in Fig. 10 the position error of a point \(\mathbf{p}= \begin{bmatrix} 1, & 1, & 1\end{bmatrix} ^{T}\) that is located on a rotating rigid body. In the standard Lie group method, the point \(\mathbf{p}\) is rotated with the rotation matrix obtained from Eq. (5). In the proposed approach for the integration of the rotation vector the point \(\mathbf{p}\) is rotated with the rotation matrix Eq. (86), which is computed from the rotation vector obtained from Eq. (26). In the proposed approach for the integration of the Cardan/Tait–Bryan (CTB) angles, the point \(\mathbf{p}\) is rotated using the rotation matrix Eq. (77), which is computed based on the Cardan/Tait–Bryan angles obtained from Eq. (49). As coordinate map \(\boldsymbol {\phi }\) the exponential map Eq. (77) is used. The time integration of Eq. (51) is performed with the RK4 method shown in Sect. 6.2.
The rigid body is considered to be a box with inertia tensor equal to \(\mathbf{J} = \mathrm{diag}(5.2988, 1.1775, 4.3568)\) that rotates about an axis close to its unstable axis of rotation. No external torques are acting on the rigid body. Since \(J_{11} > J_{33} > J_{22}\), an unstable rotation about the third axis is expected. The initial conditions are set as \(\mathbf {R}_{0} = \mathbf {I}\), \(\mathbf {v}_{0} = \boldsymbol {\alpha }_{0} = \begin{bmatrix} 0, & 0, & 0\end{bmatrix} ^{T}\) and \(\boldsymbol {\omega }_{0}= \begin{bmatrix} 0.01, & 0, & 100 \end{bmatrix} ^{T}\).
Figure 10 illustrates convergence in the norm of the position error \(\Vert \mathbf{p}_{\mathrm{Ref}} - \mathbf{p}_{\mathrm{converged}} \Vert \) for decreasing values of the time step \(h_{n} = (10^{-2}\cdot 2^{(1-n)})_{n=1,2,\ldots,7}\). Convergence is investigated at \(t=1\text{ s}\). The converged reference solution \(\mathbf{p}_{\mathrm{Ref}}\) is obtained with \(h=1/12800\text{ s}\) using the standard Lie group method. Table 1 shows the position error \(\Vert \mathbf{p}_{\mathrm{Ref}} - \mathbf{p}_{\mathrm{converged}} \Vert \) of the three methods considered.
As can be seen in Fig. 10 and Table 1, the proposed approach exhibits almost the same convergence behaviour as the standard Lie group method. The difference between the standard Lie group method and the proposed approach that can be observed in Table 1 is due to round-off errors. From this observation we conclude that the proposed method is equivalent to a Lie group method. As the proposed approach is equivalent to a Lie group method, we will not further compare the proposed approach with the standard Lie group method in the following accuracy comparisons. For further investigations and results on Lie group methods, we would like to refer to the corresponding literature; see, e.g. [2, 3, 18, 26].
7.2 Heavy top
As a second example, we present the integration of the dynamics of a heavy top to illustrate the performance of the proposed approach. The heavy top is a kind of benchmark problem in the context of geometric integration methods, which is, for example, also discussed in [3, 8, 15, 33, 50, 51]. Following [51], the configuration space of the heavy top is set as \(SO(3)\) and the dynamical model is formulated in the classical ODE form on the basis of Euler’s rotational equation
In Eq. (74), \(\boldsymbol {\omega }\) and \(\dot{\boldsymbol {\omega }}\) are the body angular velocity and angular acceleration, \(\mathbf{J}_{\textrm{FP}}\) is the tensor of inertia with respect to the top’s fixed point, which is computed from the mass center inertia tensor \(\mathbf{J}\) using the parallel-axis theorem
In Eq. (75), \(m\) is body mass and \(\mathbf{r}_{b}\) is the body mass center position expressed in the body fixed frame with respect to the top’s fixed point. The gravity torque \(\boldsymbol{\tau }_{\textrm{FP}}\) with respect to the fixed point is computed as
where \(\mathbf{g}=\left [0, \,\, 0, \,\, -9.81 \right ]^{T}\) represents gravity and \(\mathbf {R}\) is a rotation matrix.Footnote 14
In standard units, the mass center inertia tensor is defined as
the mass \(m\) is given by \(m = 15\), and the center of the mass is positioned in the body-fixed frame at \(\mathbf{r}_{b} = \left [0, \,\, 1, \,\, 0 \right ]^{T}\). The initial conditions are set as \(\mathbf {q}_{0} = \left [0, \,\,\, 0, \,\, 0 \right ]^{T}\) and \(\boldsymbol {\omega }_{0}=\left [0, \,\, 150, \,\, -4.61538 \right ]^{T}\).
In order to determine \(\boldsymbol {\omega }(t)\), \(\mathbf {\Omega }(t)\) and thus also the rotation vector \(\mathbf {v}(t)\) as well as the Cardan/Tait–Bryan angles \(\boldsymbol {\alpha }(t)\), the equations of motion (74) as well as the incremental rotation vector ODE (36) are integrated using the RK4 algorithm shown in Sect. 6.2. In the proposed Cardan/Tait–Bryan angle approach, we use the exponential map as a coordinate map. Similar results can be obtained by choosing the Cayley transform as a coordinate map. The whole algorithm has been implemented in MATLAB R2018b. The integration results, obtained using a fixed time step size of \(h = 1e-3 s\), are shown in Figs. 11–17.
The variables \(\boldsymbol {\omega }(t)\), \(\mathbf {v}(t)\) and \(\boldsymbol {\alpha }(t)\) shown in Figs. 14 and 15–16 are basic results that result from the integration of the equations of motion and from the selected rotation parameters, while the results shown in Figs. 11, 12, 13 and 17 are computed on the basis of \(\mathbf {v}(t)\) and \(\boldsymbol {\omega }(t)\) using basic kinematic relationships. The results shown in Figs. 11–13 and 17 can, of course, also be achieved with the proposed Cardan/Tait–Bryan angle approach, which is why we do not present them explicitly here.
The time evolution of the rotation vector components as well as the time evolution of the Cardan/Tait–Bryan angle components, obtained by the proposed approach, are illustrated in Figs. 15–16.
The deviation of the orthogonality constraint of the rotation matrix is shown in Fig. 17(a). As can be seen in Fig. 17(a), the proposed approach does not introduce any drift in the integration results during the whole simulation time domain of 1000 s. In comparison, Fig. 17(a) shows the deviation of the orthogonality condition of the rotation matrix in the case where Euler parameters are used as rotation parameters, whereby the Euler parameters were computed using the method presented by Terze et al. in [51]. As illustrated in Fig. 17(b), the maximum error of the orthogonality constraint of the rotation matrix is for the simulation time domain of 1000 s in the range of machine precision.
Figure 18 illustrates the convergence in norm of the rotation error \(\Vert \mathbf {v}-\mathbf {v}_{\mathrm{converged}}\Vert \) as well as the convergence in norm of the rotation error \(\Vert \boldsymbol {\alpha }- \boldsymbol {\alpha }_{\mathrm{converged}}\Vert _{2}\) for decreasing values of the time step \(h_{n} = (10^{-2}\cdot 2^{(1-n)})_{n=1,2,\ldots,11}\). The reference solution for the rotation vector \(\mathbf {v}_{\mathrm{converged}} = \mathbf {v}(t = 1)\) as well as the reference solution for the Cardan/Tait–Bryan angles \(\boldsymbol {\alpha }_{\mathrm{converged}} = \boldsymbol {\alpha }(t = 1)\) were computed using the proposed approach and a integration step of \(h = 1/204800\). In order to be able to compare the convergence behaviour of the proposed approach with the convergence behaviour of the standard approach (direct integration of the kinematic equations of the rotation vector and the Cardan/Tait–Bryan angles), the initial orientation of the heavy top may not be defined by \(\mathbf {v}_{0} = \mathbf {0}\), since the kinematic equations (87) of the rotation vector cannot be evaluated at \(\mathbf {v}_{0} = \mathbf {0}\) (because of the division by zero). Therefore, the initial conditions for the convergence considerations are set as \(\mathbf {q}_{0} = \mathbf {v}_{0} = \boldsymbol {\alpha }_{0} = \left [0, \,\, 0.52359877, \,\, 0 \right ]^{T}\text{ rad}\).
As can be seen in Fig. 18(a) as well as in Fig. 18(b), the proposed approach for computing a rotation vector update and a Cardan/Tait–Bryan angle update exhibit smaller errors (of about the order of \(1\textrm{e--}2\)) in norm of the rotation error for each time step \(h\) in comparison to the rotation updates computed by directly integrating the corresponding kinematic equations. Especially the newly introduced rotation vector formulation shows a much smaller error at larger time steps than the direct integration of the corresponding kinematic equations, as can be seen in Fig. 18(a).
7.3 Computational costs
Finally, we compare in Tables 2–3 the number of arithmetic operations required by the proposed approach Eq. (9) with those required by the standard Lie group method Eq. (5) and by the Euler parameter integration scheme presented in [51] to determine an update for the rotation vector or Euler angles. For the comparison of the standard Lie group method and the Euler parameter integration scheme with the proposed approach, three rotation parameters are computed from the rotation matrix Eq. (5), respectively the Euler parameters computed with Eq. (12) in [51]. The rotation matrix \(\mathbf {R}_{0}\) in Eq. (5) and the Euler parameters \(\boldsymbol{\theta }_{0}\) are reconstructed from the rotation vector \(\mathbf {v}_{0}\) and the Cardan/Tait–Bryan angles \(\boldsymbol {\alpha }_{0}\), respectively. The cost of the integration of the incremental rotation vector differential equation (6) is left out in the following considerations, since the computational cost depends on the chosen integration scheme. As the three rotation parameters determined by direct integration of the kinematic equations (4) cannot be determined in singular points, we do not consider the computational costs of this methods any further here. The columns in Tables 2–3 show the respective number of additions, subtractions, multiplications, divisions, trigonometric functions and roots and the results of adding all these together. While the rows of Tables 2–3 show the method considered in each case.
As shown in Table 2, the proposed rotation vector approach requires fewer operations to determine a rotation vector update as compared to determining the rotation vector update from the rotation matrix computed with the standard Lie group method. In contrast, the method which computes an update for the rotation vector from the Euler parameters requires fewer operations than the proposed approach. As shown in Table 3, the proposed Cardan/Tait–Bryan angle approach requires fewer operations to determine a Cardan/Tait–Bryan angle update as compared to determining the Cardan/Tait–Bryan angle update from the rotation matrix. In contrast, the method which computes an update for the Cardan/Tait–Bryan angles from the Euler parameters requires fewer operations as the proposed approach.
8 Conclusions
A novel numerical solution for solving rotational kinematics by using three rotation parameters is presented in this paper. The proposed approach is illustrated by the example of the rotation vector and the Euler angles. In contrast to standard formulations based on three rotation parameters, in which singular points are avoided, for example, by applying reparametrization strategies, singular points can be passed through in the proposed approach by computation of finite increments of rotation. On the contrary to standard formulations based on three rotation parameters, the proposed approach is based on the numerical integration of the kinematic relations in the form of the so-called incremental rotation vector. The kinematic relations of the incremental rotation vector form a system of ODEs on the Lie algebra \(\mathfrak {so}(3)\) of the rotation group \(SO(3)\) that can be solved singularity-free by any standard ODE integration scheme. In the proposed approach, after the incremental rotation vector has been determined for the current step, the rotation parameter update for the current step is determined with the composition rule of rotations that applies to the particular rotation parameters using the finite increments of rotation (which are expressed in dependence of the incremental rotation vector), and the rotation parameters of the previous integration step.
By taking this route, the proposed approach is able to reconstruct the rotation parameters even in singular configurations. As shown in the paper, the proposed approach exhibits the same accuracy as the standard Lie group method and the accuracy is higher as compared to the direct time integration of rotation parameters. As the presented results show, the order of accuracy of the presented integration scheme depends only on the accuracy of the ODE integrator used for solving Eq. (51). Therefore the user can influence the accuracy of the overall algorithm by choosing the ODE integrator to solve Eq. (51).
The new methods proposed in this paper are more favourable compared to the standard Lie group method in terms of their computational effort. However, the newly proposed methods are less favourable in terms of the required computational effort as compared to reconstructing the rotation vector or Cardan/Tait–Bryan angles from the Euler parameter integration scheme proposed in [51]. Therefore, the improvement of the proposed approach regarding its computational efficiency will be the subject of future research.
For solving stiff problems, the use of an implicit time integration scheme is advantageous [18]. Therefore, embedding the proposed approach in an implicit time integration scheme will be the content of future work.
In summary, the current paper provides a novel numerical solution for the long-standing problem of direct time integration of Euler angles and, alternatively, the rotation vector. The paper provides ready to implement update formulas that allow to compute consistent updates for the rotation vector and the Euler angles. The provided update formulas can be easily integrated into existing codes that uses either the rotation vector or Euler angles and provide a novel implementation strategy of Lie group methods.
Notes
By introducing a global rotation parametrization with the rotation parameters \(\mathbf {q}\), \(\mathbf {R}=\mathbf {R}(\mathbf {q})\) applies.
Note that only the matrix \(\mathbf {R}_{0}\) belonging to the previous time step must be stored.
Note that, in contrast to the standard Lie group integration approach presented in Sect. 2, our approach reintroduces a global parametrization of the rotation matrix.
Note that although the incremental rotation vector in the case that \(\boldsymbol {\phi }=\textrm {exp}\) is a rotation vector, it is assumed that the incremental rotation vector describes small rotations, in contrast to the classical rotation vector parametrization.
Equation (13) can be verified with \(\mathbf {R}(\mathbf {v}) = \mathbf {R}(\mathbf {v}_{0})\,\textrm {exp}( \mathbf {\Omega }) \,\,\widehat {=}\,\,\mathbf {R}(\mathbf {v}_{0})\,\mathbf {R}( \Delta \mathbf {v})\) from which it follows that \(\mathbf {R}(\Delta \mathbf {v}) = \textrm {exp}(\mathbf {\Omega })\) and thus \(\Delta \mathbf {v}= \mathbf {\Omega }\). To find a relation between \(\Delta \mathbf {v}\) and \(\mathbf {\Omega }\), a Cayley transform could also be used as a coordinate map in Eq. (13) instead of the exponential map. However, the relationship between \(\Delta \mathbf {v}\) and \(\mathbf {\Omega }\) would be more complicated since \(\mathbf {R}(\mathbf {v}) \neq \textrm {cay}(\mathbf {v})\).
Note that the Euler angle composition rule shown in Eq. (40) is written for a single elementary rotation whose axis of rotation is given by one of the unit vectors from Eq. (38) (resp. Eq. (39)). Note also that \(\Delta \alpha _{i}\) is associated with the \(i\)th Euler angle increment and that \(\Delta \alpha _{i}\) is non-linear in \(\alpha _{0,1}\), \(\alpha _{0,2}\), \(\alpha _{0,3}\) and \(\mathbf {\Omega }\), see Eq. (45).
In the numerical examples shown in Sect. 7, we have used the atan2 function implemented by default in Matlab2018b. We would like to point out that compared to the implementation of the atan2 function proposed in IEEE [21], the Matlab2018b implementation of the atan2 differs by having the property atan2(0,0)=0. This property is essential for the correct implementation of the proposed Euler angle integration scheme.
Note that these considerations also apply to other time integration schemes such as the fourth-order Runge–Kutta method discussed in Sect. 6.2.
Note that Eq. (76) includes the rotation matrix. Since the rotation matrix is not directly available in the proposed approach, the rotation matrix has to be computed from the rotation parameters. In contrast, when implementing the standard Lie group approach, see Sect. 2, the rotation matrix is directly available.
References
Altmann, S.L.: Hamilton, Rodrigues, and the Quaternion Scandal. Math. Mag. 62(5), 291–308 (1989)
Arnold, M., Brüls, O., Cardona, A.: Convergence analysis of generalized-alpha Lie group integrators for constrained systems. In: Proceedings of Multibody Dynamics ECCOMAS Conference, pp. 4–7 (2011)
Arnold, M., Cardona, A., Brüls, O.: A Lie algebra approach to Lie group time integration of constrained systems. In: Betsch, P. (ed.) Structure-Preserving Integrators in Nonlinear Structural Dynamics and Flexible Multibody Dynamics, pp. 91–158. Springer, Berlin (2016)
Bauchau, O.A.: Flexible Multibody Dynamics. Springer, Berlin (2010)
Betsch, P., Siebert, R.: Rigid body dynamics in terms of quaternions: Hamiltonian formulation and conserving numerical integration. Int. J. Numer. Methods Eng. 79, 444–473 (2009)
Bortz, J.E.: A new mathematical formulation for strapdown inertial navigation. IEEE Trans. Aerosp. Electron. Syst. 7(1), 61–66 (1971)
Brüls, O., Cardona, A.: On the use of Lie group time integrators in multibody dynamics. J. Comput. Nonlinear Dyn. 5(3), 1–13 (2010)
Brüls, O., Arnold, M., Cardona, A.: Two Lie group formulations for dynamic multibody systems with large rotations. In: Proceedings of IDETC/MSNDC 2011, ASME 2011 International Design Engineering Technical Conferences, Washington, USA (2011)
Cardona, A., Géradin, M.: Time integration of the equations of motion in mechanism analysis. Comput. Struct. 33, 801–820 (1989)
Celledoni, E., Owren, B.: Lie group methods for rigid body dynamics and time integration on manifolds. Comput. Methods Appl. Mech. Eng. 192, 421–438 (2003)
Chevallier, D.P., Lerbet, J.: Multi-Body Kinematics and Dynamics with Lie Groups, 1st edn. ISTE Press – Elsevier, London (2018)
Condurache, D.: Closed form of the Baker–Campbell–Hausdorff formula for the Lie algebra of rigid body displacements. In: ECCOMAS Thematic Conference on Multibody Dynamics, January, Duisburg, Germany (2019)
Davenport, P.B.: Rotations about non orthogonal axes. AIAA J. 11(6), 853–857 (1973)
Engø, K.: On the BCH-formula in \(\mathit{so}(3)\). BIT Numer. Math. 41(3), 629–632 (2001)
Engø, K., Marthinsen, A.: Modeling and solution of some mechanical problems on Lie groups. Multibody Syst. Dyn. 2, 71–88 (1998)
Géradin, M., Cardona, A.: Flexible Multibody Dynamics: A Finite Element Approach. John Wiley & Sons, New York (2001)
Goldstein, N.J.: Nonsingular efficient modeling of rotations in 3-space using three components. In: Proceedings of the 7th International Congress on Industrial and Applied Mathematics ICIAM 2011, Vancouver, BC, pp. 1–5 (2011)
Hairer, E., Wanner, G., Lubich, C.: Geometric Numerical Integration, 2nd edn. Springer, Berlin (2010)
Henderson, D.M.: Euler angles, quaternions, and transformation matrices for space shuttle analysis. Tech. Rep., NASA (1977)
Ibrahimbegović, A., Frey, F., Kožar, I.: Computational aspects of vector-like parametrization of three-dimensional finite rotations. Int. J. Numer. Methods Eng. 38, 3653–3673 (1995)
IEEE: 754-2008 – IEEE Standard for Floating-Point Arithmetic. IEEE, New York (2008). https://doi.org/10.1109/IEEESTD.2008.4610935
Iserles, A.: Numerical analysis in Lie groups. In: DeVore, R.A., Iserles, A., Süli, E. (eds.) Foundations of Computational Mathematics, pp. 105–124. Cambridge University Press, Cambridge (2001)
Iserles, A.: On Cayley-transform methods for the discretization of Lie-group equations. Found. Comput. Math. 1, 129–160 (2001)
Iserles, A.: Magnus expansions and beyond. In: Contemporary Maths, vol. 539, pp. 171–186 (2008)
Iserles, A., Munthe-Kaas, H.Z., Nørsett, S.P., Zanna, A.: Lie-group methods. Acta Numer. 9, 215–365 (2000)
Kobilarov, M.: Solvability of geometric integrators for multi-body systems. In: Zdravko, T. (ed.) Multibody Dynamics – Computational Methods and Applications. Computational Methods in Applied Sciences, pp. 145–174. Springer, Berlin (2014)
Lesk, A.M.: On the calculation of Euler angles from a rotation matrix. Int. J. Math. Educ. Sci. Technol. 17(3), 335–337 (1986)
Markley, F.L., Crassidis, J.L.: Fundamentals of Spacecraft Attitude Determination and Control, 1st edn. Springer, New York (2014)
Mortari, D., Angelucci, M., Markley, F.L.: Singularity and attitude estimation. In: Paper No. AAS 00-130 of the 10th Annual AIAA/AAS Space Flight Mechanics Meeting, Clearwater, Florida (2000).
Müller, A.: Approximation of finite rigid body motions from velocity fields. Z. Angew. Math. Mech. 90(6), 514–521 (2010)
Müller, A.: Group theoretical approaches to vector parametrization of rotations. J. Geom. Symmetry Phys. 19, 43–72 (2010)
Müller, A.: Coordinate mappings for rigid body motions. J. Comput. Nonlinear Dyn. 12(2), 10 (2017)
Müller, A., Terze, Z.: On the choice of configuration space for numerical Lie group integration of constrained rigid body systems. J. Comput. Appl. Math. 262, 3–13 (2014)
Munthe-Kaas, H.: Runge–Kutta methods on Lie groups. BIT 381(1), 92–111 (1998)
Nikravesh, P.E.: Computer-Aided Analysis of Mechanical Systems. Prentice Hall, New York (1988)
Owren, B., Marthinsen, A.: Integration methods based on canonical coordinates of the second kind. Numer. Math. 87(4), 763–790 (2001)
Paul, B.: On the composition of finite rotations. Am. Math. Mon. 70(8), 859–862 (1963)
Pechstein, A., Reischl, D., Gerstmayr, J.: The applicability of the floating-frame based component mode synthesis to high-speed rotors. In: Proceedings of the ASME 2011 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference DETC/CIE 2011, Washington, DC, USA (2011)
Pittelkau, M.E.: Rotation vector in attitude estimation. J. Guid. Control Dyn. 26(6), 855–860 (2003)
Shabana, A.A.: Dynamics of Multibody Systems, 4th edn. Cambridge University Press, Cambridge (2013)
Sherif, K., Nachbagauer, K., Steiner, W.: On the rotational equations of motion in rigid body dynamics when using Euler parameters. Nonlinear Dyn. 81, 343–352 (2015)
Shuster, M.D.: A survey of attitude representations. J. Astronaut. Sci. 41(4), 439–517 (1993)
Shuster, M.D.: The kinematic equation for the rotation vector. IEEE Trans. Aerosp. Electron. Syst. 29(1), 263–267 (1993)
Shuster, M.D., Markley, F.L.: Generalization of the Euler angles. J. Astronaut. Sci. 51(2), 123–132 (2003)
Shuster, M.D., Oh, S.D.: Three-axis attitude determination from vector observations. J. Guid. Control 4(1), 70–77 (1981)
Siciliano, B., Sciavicco, L., Luigi, V., Oriolo, G.: Robotics: Modelling, Planning and Control. Springer, Berlin (2008)
Simo, J.C., Wong, K.K.: Unconditionally stable algorithms for rigid body dynamics that exactly preserve energy and momentum. Int. J. Numer. Methods Eng. 31, 19–52 (1991)
Singla, P., Mortari, D., Junkins, J.L.: How to avoid singularity when using Euler angles? Adv. Astronaut. Sci. 119, 1409–1426 (2005)
Stuelpnagel, J.: On the parametrization of the three-dimensional rotation group. SIAM Rev. 6(4), 422–430 (1964)
Terze, Z., Müller, A., Zlatar, D.: Lie-group integration method for constrained multibody systems in state space. Multibody Syst. Dyn. 34(3), 275–305 (2015)
Terze, Z., Müller, A., Zlatar, D.: Singularity-free time integration of rotational quaternions using non-redundant ordinary differential equations. Multibody Syst. Dyn. 38(3), 201–225 (2016)
Verbin, D., Lappas, V.J., Ben-Asher, J.Z.: Time efficient angular steering laws for rigid satellites. J. Guid. Control Dyn. 34(3), 878–892 (2011)
Wittenburg, J.: Kinematics – Theory and Applications, 1st edn. Springer, Berlin (2016)
Zanetti, R.: Rotations, transformations, left quaternions, right quaternions? J. Astronaut. Sci. 66(3), 1–21 (2019)
Acknowledgements
We would like to thank Prof. Martin Arnold for his valuable comments on this work.
Funding
Open Access funding provided by University of Innsbruck and Medical University of Innsbruck.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Basic expressions for exponential map, Cayley transform, rotation vector and Euler angles
1.1 A.1 The exponential map on \(SO(3)\)
According to [3, 26, 32], the matrix exponential map \(\textrm {exp}\,\, : \,\, \mathbb {R}^{3}\,\, \rightarrow \,\, SO(3)\) may be evaluated in \(SO(3)\) by
Since \(\mathbf {\Omega }\) represents a rotation vector, the exponential map also exhibits a singular point. The singular point at \(\Vert \mathbf {\Omega }\Vert =0\) is crucial for the evaluation of the exponential map. However, the singular point in case that \(\Vert \mathbf {\Omega }\Vert =0\) is removable using the cardinal sine function sinc(\(x\)) Eq. (22). Thus, the form
allows an evaluation of the exponential map for the case that \(\Vert \mathbf {\Omega }\Vert =0\) as shown in [32].
An alternative to implementing the exponential map in the form of Eq. (78) is to remove the singular point of the exponential map at \(\Vert \mathbf {\Omega }\Vert =0\) using the case distinction
which is used in [11, 26], for example.
The inverse tangent operator \(\mathbf {T}_{\textrm {exp}}^{-1}\) corresponding to the exponential map on \(SO(3)\) is given by [51]
which exhibits singular points at \(\Vert \mathbf {\Omega }\Vert =\pm 2 \pi k\), \(k=0,1,2,\ldots \) Decisive for the evaluation of Eq. (80) is the situation \(\Vert \mathbf {\Omega }\Vert =0\), because \(\mathbf {T}_{\textrm {exp}}^{-1}\) has a discontinuity there, which is removable due to
as shown in [32]. In the implementation, the singular point at \(\mathbf {\Omega }=\mathbf {0}\) in Eq. (80) is according to Eq. (81) removed by using the case distinction
which allows a singular-point-free integration of the angular kinematics in the range \(\Vert \mathbf {\Omega }\Vert \in (-2\pi ,2\pi )\), i.e. for a full double turn [32].
1.2 A.2 The Cayley transform on \(SO(3)\)
The Cayley transform can be used as coordinate map \(\boldsymbol {\phi }(\widetilde {\mathbf {\Omega }})=\textrm {cay}(\widetilde {\mathbf {\Omega }})\) as well. This is due the fact that the Cayley transform also maps algebra elements to group elements, which is well know on \(SO(3)\) [31].
The Cayley transform \(\textrm {cay}\,\, : \,\, \mathbb {R}^{3}\,\, \rightarrow \,\, SO(3)\) is defined by [10, 26]
while the corresponding inverse tangent operator is given by
1.3 A.3 Rotation vector
The rotation matrix is represented in the form [16]
Note that \(\mathbf {R}(\mathbf {v})=\textrm {exp}(\mathbf {v})\) holds. The kinematic equation of the rotation vector is according to [6] given by
An equivalent form of Eq. (87) can be found in [43], for example.
1.4 A.4 Cardan/Tait–Bryan angles
The kinematic equation of Cardan/Tait–Bryan angles is according to [35] given by
Appendix B: Proposed approach with Cardan/Tait–Bryan angles
This section is an extension of Sect. 5. In the following we show how \(\sin \alpha _{i}\) and \(\cos \alpha _{i}\) for Cardan/Tait–Bryan angles are determined depending on the incremental rotation vector \(\mathbf {\Omega }\). The relation between \(\sin \alpha _{i}\) and \(\cos \alpha _{i}\) and \(\mathbf {\Omega }\) is needed to be able to compute the Cardan/Tait–Bryan angle increments \(\Delta \alpha _{i}\) with Eq. (45). The procedure shown in the following can be applied analogously to the derivation of \(\sin \alpha _{i}\) and \(\cos \alpha _{i}\) for 313-Euler angles, for example.
When writing down the components of the rotation matrix for Cardan/Tait–Bryan angles,
it is observed that there are six entries \(R_{\mathit{ij}}\in \mathbb {R}\) in Eq. (77), such that the relations
are valid.Footnote 15 In Eq. (77), we used the abbreviation \(\mathrm {c}_{\alpha _{i}}=\cos \alpha _{i}\) and \(\mathrm {s}_{\alpha _{i}}=\sin \alpha _{i}\). To establish a relation between the incremental rotation vector \(\mathbf {\Omega }\) and the Cardan/Tait–Bryan angle increments \(\Delta \alpha _{i}\), we consider Eq. (7) in the form
Using Eq. (81), each entry \(R_{\mathit{ij}}\) in Eq. (77) may be computed by
where the vectors \(\mathbf{u}_{i}\) and \(\mathbf{v}_{j}\) are defined as
In Eq. (82) (resp. Eq. (83), the unit vectors shown in Eq. (38) are used. The vectors \(\mathbf{u}_{i}\) and \(\mathbf{v}_{i}\) can be specified explicitly for the selected coordinate map \(\boldsymbol {\phi }(\cdot )\). Due to the vast number of possible coordinate maps and space reasons, we do not explicitly state them here. However, the interested reader may determine the explicit form of \(\mathbf{u}_{i}\) and \(\mathbf{v}_{i}\) for the coordinate map of interest using Eq. (83). By considering Eqs. (78)–(80) and Eq. (82), \(R_{13}\), \(R_{23}\), \(R_{33}\), \(R_{12}\) and \(R_{11}\) are expressed in dependence of the incremental rotation vector as
Inserting Eqs. (78)–(80) into Eqs. (43)–(44) taking into account Eqs. (84)–(88) results in
It should be noted, that Eqs. (89)–(90) and (93)–(94) can only be evaluated for \(\alpha _{2}\notin S_{\alpha }\) where
To cover the case \(\alpha _{2}\in S_{\alpha }\), we replace
in Eqs. (89)–(90) and (93)–(94) byFootnote 16
By using Eq. (97), Eqs. (89)–(94) take the form
From Eqs. (98)–(103), the Cardan/Tait–Bryan angle increments \(\Delta \alpha _{i}\) can be computed without restrictions using the atan2 function
Note that it is not necessary to select a specific coordinate map \(\boldsymbol {\phi }(\mathbf {\Omega })\) in Eq. (82) when deriving the general expression for the angle increments depending on the incremental rotation vector. Therefore, it is possible to implement the proposed approach for any choice of Euler angles in such a way that it is easy to switch between different coordinate maps. This allows influencing the computational efficiency of the proposed approach in a specific way. Note also that, in general, the coordinate map and the inverse tangent operator must match, i.e. \(\mathbf {T}_{\boldsymbol {\phi }}^{-1}=\mathbf {T}_{\textrm {exp}}^{-1}\) if \(\boldsymbol {\phi }=\textrm {exp}\) or \(\mathbf {T}_{\boldsymbol {\phi }}^{-1}=\mathbf {T}_{\textrm {cay}}^{-1}\) if \(\boldsymbol {\phi }=\textrm {cay}\). However, note that switching between different coordinate maps is not necessary in the proposed approach. As a final remark, we would like to note that for an efficient implementation of the proposed Cardan/Tait–Bryan angle approach, it is advantageous to optimize the implementation for a specific coordinate map by computing and implementing \(\mathbf{u}_{i}\) and \(\mathbf{v}_{i}\) explicitly.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Holzinger, S., Gerstmayr, J. Time integration of rigid bodies modelled with three rotation parameters. Multibody Syst Dyn 53, 345–378 (2021). https://doi.org/10.1007/s11044-021-09778-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-021-09778-w