Dynamic advantages of singular configurations in moving heavy object by a two-link mechanism

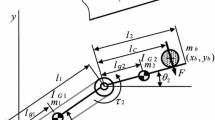
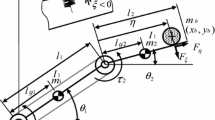
Abstract

This paper demonstrates dynamic advantages of singular configurations for a two-link mechanism by theoretical analysis and numerical simulations. The advantages can be utilized in moving a heavy object by the mechanism. The theoretical analysis reveals that the configurations of the mechanism near the singular ones are advantageous in generating large acceleration of the object through the joint torques and the kinetic energy of the mechanism. We illustrate the advantages by numerical simulations for two typical motions, that is, a lifting motion of a two-link manipulator and a jumping motion of a two-link legged robot. It is shown that the joint torques necessary to achieve these motions are reduced to a large extent by using the advantages.

Appendices

Appendix A

The acceleration ${\boldsymbol{a}}_{t}$ corresponds to the dynamic manipulability ellipsoid with $\dot{\boldsymbol{q}}=0$ and no gravity effect. In [14], the ellipsoid is defined by

$$ {\boldsymbol{a}}_{t}^{T}\bigl(\boldsymbol{M} \boldsymbol{J}^{-1}\bigr)^{T} \boldsymbol{M} \boldsymbol{J}^{-1}{\boldsymbol{a}}_{t}= \boldsymbol{\tau }^{T}\boldsymbol{\tau }\leq 1 , $$

(33)

and illustrates the relation between bounded joint torques and the end-effector acceleration caused from the torques. Fig. 17 shows the dynamic manipulability ellipsoids with different postures by using the physical parameters in Table 1.

Fig. 17

Dynamic manipulability ellipsoid (Color figure online)

In Fig. 17, the shape of the ellipsoid changes rapidly as the robot approaches its singular configurations. The maximum possible acceleration in $y$-axis firstly increases as the manipulator extends, and reaches the peak when the manipulator is almost extended. From then on, it intensely decreases to 0 in $C_{0}$. A similar behavior of the maximum acceleration in $x$-axis can also be found near $C_{\pi }$.

Appendix B

If (15) holds but $\ddot{\theta }_{2}\neq -2\ddot{\theta } _{1}$ on the $y$-axis, the horizontal component of $\boldsymbol{a}$ does not equal zero. Under the same assumptions as in Sect. 3, the horizontal components of ${\boldsymbol{a}}_{t}$, ${\boldsymbol{a}} _{g}$, and ${\boldsymbol{a}}_{v}$, that is, $a_{tx}$, $a_{gx}$, and $a_{vx}$, are investigated.

2.1 B.1 Torque-dependent acceleration

When $\theta_{1}\in [O(1/\sqrt{m_{w}}), \pi /2]$, $a_{tx}$ is approximately calculated as

$$\begin{aligned} {a}_{tx}\approx \frac{2lc(1-c^{2})\tau_{1}}{4m_{w}l^{2}c^{2}(1-c^{2})+ K_{1}} . \end{aligned}$$

(34)

The absolute value of $a_{tx}$, $\vert a_{tx} \vert$, has a peak value at $c=c^{*}$, where $c=\cos (\theta_{1})$ and $c^{*}=\sqrt{K_{1}}/(2l\sqrt{m _{w}})\ll 1$. According to (34), joint torques should satisfy the following relation to generate the maximum value of $a_{tx}$:

$$ \frac{\tau_{2}}{\tau_{1}}=\frac{0}{1} . $$

(35)

We chose the joint torques that satisfy $\Vert \boldsymbol{\tau } \Vert =15$ and (35), and drew the profiles of the actual value of $a_{tx}$ from (18) and the approximate value of $a_{tx}$ from (34) as shown in Fig. 18 with the physical parameters in Table 1. The drastic variation of $a_{tx}$ near $C_{\pi }$ corresponds to the drastic change in the shape of the dynamic manipulability ellipsoid.

Fig. 18

Variation of $a_{tx}$ with respect to $\theta_{1}$ (Color figure online)

2.2 B.2 Gravity-dependent acceleration

Substituting (25) into (19), $a_{gx}$ can be approximately obtained for $\theta_{1}\in [0,\pi /2]$ as

$$ {a}_{gx}\approx \frac{ -\sqrt{1-s^{2}}sg\{2ls^{2}(m_{1}l_{g1}+m _{2}(l-l_{g2}))-K_{3}\}}{4m_{w}l^{2}s^{2}(1-s^{2})+K_{1}} , $$

(36)

where $K_{3}=m_{1}l_{g1}^{2}+m_{2}(l^{2}-l_{g2}^{2})+I_{1}-I_{2}=O(1)$. The acceleration ${a}_{gx}$ has one local maximum and one local minimum of $O(1/\sqrt{m_{w}})$ near the singular configurations. Fig. 19 shows the profiles of the actual value of $a_{gx}$ from (19) and the approximate value of $a_{gx}$ from (36).

Fig. 19

Variation of $a_{gx}$ with respect to $\theta_{1}$ (Color figure online)

2.3 B.3 Velocity-dependent acceleration

Substituting (27) into (20), $a_{vx}$ is approximated for $\theta_{1}\in [0,\pi /2]$ as

$$ a_{vx}\approx \frac{2K_{3}ls(1-s^{2})\dot{\theta }_{1}^{2}}{4m_{w}l ^{2}s^{2}(1-s^{2})+K_{1}} . $$

(37)

The acceleration $a_{vx}$ has a peak value of $O(1/\sqrt{m_{w}})$ at $s=\sqrt{K_{1}}/(2l\sqrt{2m_{w}})$. Fig. 20 shows the profiles of the actual value of $a_{vx}$ from (20) and the approximate value of $a_{vx}$ from (37).

Fig. 20

Variation of $a_{vx}$ with respect to $\theta_{1}$ (Color figure online)

It should be noted that, when $l_{1} \neq l_{2}$, the approximate solution of $a_{vx}$ is quite different from (37). A large $a_{vx}$ of $(l_{1}-l_{2})O(1)$ is caused from the energy of $O(1)$ in the singular configuration $C_{\pi }$.

2.4 B.4 Total acceleration

From (17), (18), (19), and (20), we drew the profiles of the actual values of $a_{tx}$, $a_{gx}$, $a_{vx}$, and $a_{x}$ in Fig. 21 with the same physical parameters used for drawing Fig. 7. Comparing Figs. 7 and 21, we found that the maximum value of $a_{vx}$ are much smaller than the one of $a_{vy}$. When $\Vert \boldsymbol{\tau } \Vert =O(1)$, the maximum value of $a_{tx}$ near $C_{\pi }$ is also smaller than the one of $a_{ty}$ near $C_{0}$. The peak value of $\vert a_{gx} \vert$ is also small by comparing to the one of $\vert a_{gy} \vert$.

Fig. 21

Total acceleration $a_{x}$ with respect to $\theta_{1}$ (Color figure online)