Abstract
Flexible multibody dynamics (FMD) has found many applications in control, analysis and design of mechanical systems. FMD together with the theory of structural optimization can be used for designing multibody systems with bodies which are lighter, but stronger. Topology optimization of static structures is an active research topic in structural mechanics. However, the extension to the dynamic case is less investigated as one has to face serious numerical difficulties. One way of extending static structural topology optimization to topology optimization of dynamic flexible multibody system with large rotational and transitional motion is investigated in this paper. The optimization can be performed simultaneously on all flexible bodies. The simulation part of optimization is based on an FEM approach together with modal reduction. The resulting nonlinear differential-algebraic systems are solved with the error controlled integrator IDA (Sundials) wrapped into Python environment by Assimulo (Andersson et al. in Math. Comput. Simul. 116(0):26–43, 2015). A modified formulation of solid isotropic material with penalization (SIMP) method is suggested to avoid numerical instabilities and convergence failures of the optimizer. Sensitivity analysis is central in structural optimization. The sensitivities are approximated to circumvent the expensive calculations. The provided examples show that the method is indeed suitable for optimizing a wide range of multibody systems. Standard SIMP method in structural topology optimization suggests stiffness penalization. To overcome the problem of instabilities and mesh distortion in the dynamic case we consider here additionally element mass penalization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When designing a mechanical system where the main task is carrying or transferring a load, an economical product is obtained if the same functionality can be achieved by using a lighter structure. It can be accomplished by minimizing or maximizing an objective function which represents the quality of the system in the limits of given constraints. Structural optimization is about finding the best design where the main task is carrying a load. In particular, topology optimization (TO), a branch of structural optimization, is a part of conceptual design of a product. In TO, optimization starts from an initial model which is mostly a box called design space. A design is characterized by the material distribution in the design space. The design space is discretized by finite elements. Each finite element represents a design variable. The design variable ranges between a given upper bound exhibiting the material state and a lower bound exhibiting a hole. The optimization algorithm changes iteratively the design variable to reach an optimized hole-material state. The design variable is selected to be the normalized density in case of a spatial structure and the normalized thickness in case of a planar structure. In many TO problems the goal is to minimize the deformation of the structure as a response to a prescribed load. In this case the objective function can be defined as the strain energy stored in the structure (compliance) which must be minimized within the limiting constraints – the total amount of the material [2, 3].
Topology optimization of static structures was subject of extensive research on methods. However, the extension to the dynamic case is less investigated. One strategy for topology optimization on a single body under transient loads is called component-based approach [11]. In the component-based approach multiple static loads are selected from the transient loads acting on the isolated body. Thus, it is assumed that there is enough time for the body to settle before the load changes. This assumption is not realistic in case when the bodies encounter high accelerations. On the other hand, the shape and the weight of the body change in every optimization step, if the transient loads depend on the design. For instance, in a multibody system (MBS), the dynamic behavior and forces at joints change accordingly, hence the selected load cases are not valid anymore, cf. [16].
Another strategy for dynamic response structural optimization is the equivalent static loads method (ESLM) [8, 9]. In this approach the body is isolated from the rest of the system where all forces including the inertia forces are accounted for. A set of equivalent quasi-static load cases in every time step must be defined which produces the same displacement field as the one caused by dynamic loads. Then it would be possible to use the theory of the static structural optimization directly. However, original ESLM is mostly developed for size and shape optimization. Using this method for topology optimization causes instability and failure of the optimization algorithm. In [8] this problem is attenuated by removing some of elements and updating the grid data in every optimization process. This approach has to restrict the design area and later revival of removed elements cannot be treated. Moreover, the element removal needs post processing of the data which is not unique for different problems. In addition, since the body is isolated from the rest of the system, constraints and the objective function cannot be defined based on the overall system response [16].
We present here an alternative approach treating topology optimization of all flexible bodies simultaneously while they are operating in an MBS based on the system overall response considering all transient reaction and inertia forces. In this paper this approach is called topology optimization of a multibody system (TOMBS). In [7] a related approach is used with two different regimes of stiffness penalization. The switching criteria between two regimes might differ between problems, so that this formulation is not always applicable. Here it is argued that the origin of the numerical difficulties and mesh distortion which result in non-convergence of the optimization algorithm suggested by SIMP [2] is an effect of what we call flying elements. To reduce this effect, we suggest element mass penalization in addition to stiffness penalization, see also [12].
The suggested method in dynamic response topology optimization is demonstrated by two simple planar MBS. Sensitivity expressions are approximated by eliminating terms which are assumed to have low order of magnitude but are numerically expensive to calculate. These approximations make the sensitivity analysis comparable to ESLM. Achieving convergence of the optimization algorithm in a reasonable computation time in problems with large number of design variables proves that the above assumption is valid for a wide range of multibody systems. The approach is applicable for designing vehicle components, high-speed robotic manipulators, airplanes and space structures.
2 Optimization problem
The optimization problem for a multibody system consisting of \(n_{b}\) rigid or flexible bodies is mathematically described as
where \(J\) is the index set of the flexible bodies which will be optimized and \(C^{j}\) denote their compliances. \(\boldsymbol{X}^{i}\) is the vector of the \(n_{i}\) design variables of body \(i\), \(t\) is time, and \(t_{s}\) is the simulation final time. Equation (2) states the equality constraint which is a system of nonlinear differential algebraic equations describing the motion of the flexible multibody system. Here, \(\boldsymbol{q}= \large (\boldsymbol{q}^{i})_{i=1}^{n_{b}}\) is the state vector of coordinates including elastic coordinates \(\boldsymbol{q}_{f}\), \(\boldsymbol{M}\) is the mass matrix, \(\boldsymbol{K}\) is the global stiffness matrix associated with rigid and elastic coordinates, \(\boldsymbol{f}\) is the vector of generalized reaction and external forces including Coriolis and centrifugal terms, \(\boldsymbol{\lambda}\) is the vector of Lagrange multipliers, \(\boldsymbol{C}(\boldsymbol{q},t)\) is the vector of kinematic algebraic constraint equations describing joints and prescribed trajectories.
In Eqs. (3), \(g\) denotes the inequality constraints, \(A^{j}\) is the total area of body \(j\) and \(V_{\max}^{j}\) is the maximum of its allowable normalized volume, \(\boldsymbol{X}^{j,\min}\) and \(\boldsymbol{X} ^{j,\max}\) are the lower and upper bounds of the design variable also called a box constraint.
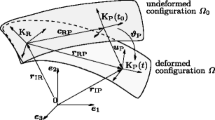
According to the floating frame of reference approach [13], the mass matrix is composed of submatrices corresponding to rigid coordinates, elastic coordinates and coupling terms; in planar mechanism, three first rows and columns of the body stiffness matrix are entirely zero. The nonzero submatrix, \(\boldsymbol{K} _{ff}\), corresponds to the elastic coordinates which are a function of the design variable. A detailed derivation of the mass matrix and the stiffness matrix can be found in [4, 13].
We consider, for notational simplicity, a non-weighted time integration of the compliance as the objective function. In practice a weight function has to be introduced in Eq. (1) to give small but relevant peaks in the objective function a higher influence in the minimization process [8, 10].
The relation between the design variables \(\boldsymbol{X}\) and the displacement vector \(\boldsymbol{q}\) is given by equality constraints in Eq. (2). Having solved the dynamic equation of motion and replacing the integration by a summation, the objective function has the following form when scaled by the step size, \(t_{s}/s\),
where \(C_{l}^{j}\) is the compliance at time step \(l\) and \(s\) is the total number of time steps. The compliance is given by
where \(\boldsymbol{q}_{f,l}^{j}\) is the elastic displacement vector of body \(j\) at time step \(l\), \(\boldsymbol{K}_{ff}^{j}\) is the stiffness matrix associated to the elastic coordinates which is obtained by finite element analysis.
The solid isotropic material with penalization approach (SIMP) is widely used for topology optimization problems. SIMP is based on the convex linearization method (CONLIN) or the optimality criteria (OC) method which are gradient based methods [2, 3]. The big advantage of CONLIN and OC methods is that they make an explicit approximation of the objective and constraint functions. More importantly, the result of the approximation is a separable function with respect to the design variable. These properties make it possible to find a local minimum in an efficient way when the number of design variables is large.
CONLIN and OC introduce an intervening variable, \(\boldsymbol{Y}(\boldsymbol{X})= \large(Y_{e}(X_{e}))_{e=1}^{nj}\). The idea is to linearize the objective and constraint functions at the intervening variable \(\boldsymbol{Y}(\boldsymbol{X}^{j,k})\) by writing the two first terms of their Taylor expansion at \(\boldsymbol{Y}(\boldsymbol{X}^{j,k})\), where \(\boldsymbol{X}^{j,k}\) is the design variable at iteration \(k\) which is a constant vector; then, to solve the optimization subproblem in the vicinity of \(\boldsymbol{X}^{j,k}\) with Lagrangian duality method. The intervening variable is chosen such that the objective or constraint functions become closer to a linear function; thus the linearization at iteration step \(k\) introduces a smaller approximation error; see Sect. 2.2. The solution of the subproblem, \(\boldsymbol{X}^{j,(k+1)}\), is then assigned to \(\boldsymbol{X}^{j,k}\) and the method is repeated until convergence is achieved. The convergence criterion can be the change of the objective function from one iteration to the next or the change in the norm of the design variable, \(\|\boldsymbol{X}^{j,(k+1)}-\boldsymbol{X}^{j,k}\|< \epsilon\), where, \(\epsilon\) is a given small threshold.
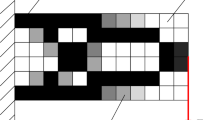
Filters are also important in topology optimization to avoid so-called checkerboard patterns [14]. More or less the same filters as in the static response topology optimization are applicable in the dynamic case also. In particular, the mean sensitivity filter is used for the examples in a later section. In Fig. 1, the general steps of TOMBS are illustrated.
2.1 Solving the differential algebraic equation of motion
An independent code was developed by the authors for building and simulating a planar flexible multibody system with the purpose of implementing and conceptional testing TOMBS. The simulation is based on a floating frame of reference approach and finite element formalism together with modal reduction and static condensation, Craig–Bampton method [13, 15]. The resulting nonlinear differential-algebraic system is solved with the error controlled integrator IDA (Sundials) wrapped into a Python environment by Assimulo [1]. The code is also interfaced to Dymola to allow its verification.
Due to the large number of degrees of freedom occurring in topology optimization problems, the simulation would not be possible without the use of a model reducing method, e.g., modal reduction. Moreover, the simulation must be repeated with the updated thickness in every optimization iteration, thus it is important to reduce the simulation time. On the other hand, for modal reduction, an eigenvalue problem has to be solved, and full coordinates must be retained for the entire system in every iteration step.
2.2 Sensitivity approximations and optimization subproblem
CONLIN or OC approximation of the objective and constraint functions can be done as follows. At time step \(l\) and iteration \(k\) taking the first two terms of the Taylor expansion of the objective function and linearizing the intervening variable, \(\boldsymbol{Y}(\boldsymbol{X}^{j,k})\), about \(\boldsymbol{X}^{j,k}\) gives
Subscript \(e\) denotes the element index. The choice of the intervening variable \(\boldsymbol{Y}(\boldsymbol{X}^{k})\) depends on the function to be linearized, \(C_{l}^{j}(\boldsymbol{X}^{j})\). A good choice of \(\boldsymbol{Y}(\boldsymbol{X}^{k})\) results in a fast convergence of the optimization algorithm. Similar to static response topology optimization when the strain energy is the objective function [2, 3], we select the intervening variable for a design variable according to OC method as
where, in this paper, \(\alpha=3\) since this choice gives higher convergence rate.
In order to evaluate Eq. (5), it is necessary to compute the sensitivity of the objective function with respect to the design variable at iteration \(k\) and time \(t_{l}\). Calculating the sensitivity numerically by direct methods is very expensive. The approach used here for minimization is a gradient based method based on Newton’s method. Its convergence properties depend on the quality of the approximation of the sensitivity matrices. Rough approximations might cause convergence failures but if convergence is achieved the result is as correct as if accurate sensitivity matrices were taken.
The idea here is to speed up the process drastically by introducing simplifying assumptions when approximating sensitivity expressions. Here, we assumed that for the derivatives
holds. Omitting these terms leads to a simplified computation of the sensitivity of the dynamic response problem which becomes comparable to that in the static response problem. In our computations, the above made simplifying assumptions were justified by the convergence of the algorithm. However reaching convergence would not be possible without mass penalization introduced in Sect. 2.3. Note that alternatively the adjoint method [5, 6] can be used. So far its efficient use needs more investigations for the dynamic multibody case.
The sensitivity of the compliance can be calculated as follows:
where \(\frac{\partial{\boldsymbol{q}}_{f,l}^{j}(\boldsymbol{X}^{j})}{\partial{X} _{e}^{j}}\) can be found by differentiating the equilibrium constraint with respect to the design variable. The differential part of the differential-algebraic equation (2), when decoupled for each body, is
Differentiating Eq. (9) with respect to \(X_{e}^{j}\) gives
Differential equation Eq. (10), together with the constraint equations \(\boldsymbol{c}(\boldsymbol{q},t)=\mathbf{0}\), has the same form as the equations of motion (2) which have to be solved numerically. However, Eq. (10) needs to be solved for all times \((s+1)\) and for every element of the body. For topology optimization the number of design variables often is large. Many design variables and time steps make finding the sensitivity very expensive. To circumvent this problem, we eliminate terms (7) and also assume that the sensitivity of the coordinates of a body, for instance body \(j\), does not depend on other bodies, \(\frac{\partial{\boldsymbol{q}}^{i}}{\partial {X}_{e}^{j}}=0\) if \(i\neq j\), then Eq. (10) simplifies to
where \(\boldsymbol{K}_{ff}^{j}\) is the global stiffness matrix of body \(j\) associated with the elastic coordinates. Solving Eq. (11) for \(\frac{\partial{\boldsymbol{q}}_{f}^{j}}{\partial{X}_{e}^{j}}\) gives
Substituting Eq. (12) into Eq. (8) gives an expression for the sensitivity of the objective function, compliance, with respect to the design variable.
where \(\frac{\partial{\boldsymbol{K}}_{ff}^{j}}{\partial{X}_{e}^{j}}\) is a known constant positive definite matrix.
Algebraic manipulation on Eqs. (5), (6) and (13) and eliminating the constant terms give the objective function at iteration \(k\) in the form
where superscript OC stands for optimality criteria method and \(b_{e}^{j,k}\) is a constant at iteration \(k\) defined as
Objective function (14) is an approximation of the one in Eq. (1) for body \(j\) which is separated for each design variable, \(X_{e}^{j}\). The objective function in the form shown in Eq. (14) is similar to the one in static response optimization which, together with constraints Eq. (3), forms the optimization subproblem at iteration \(k\). Thus, the subproblem for body \(j\) can be written as
where \(a_{e}\) is the area of a finite element in planar case. Lagrangian duality method is used for solving the subproblem, see [2, 3]. The implementation of the method is summarized as follows. Using the given design, \(\boldsymbol{X}^{j,k}\), the displacement field i.e., elastic coordinates of body \(j\), \(\boldsymbol{q}_{f}^{j}\), over time is calculated using a numerical integration of Eq. (2). Then, having found the value of \(b_{e}^{j,k}\) in Eq. (15), the updated design variables for \(e=1,\ldots,n_{j}\) can be calculated by solving the following system of equations:
Optimization iteration must be continued until a convergence criterion is satisfied individually for each body, e.g., \(\|\boldsymbol{X}^{j,(k+1)}- \boldsymbol{X}^{j,k}\|< \epsilon\).
The number of iterations has a direct influence on the computational effort of solving the optimization problem. The quality of convergence depends on the initial guess of design variables, sensitivity matrix, filters and OC intervening variable. Similar to the case of static response topology optimization a change of any of these parameters may result in a different local optimum.
The computational effort of solving a subproblem is mainly caused by solving the nonlinear system of equations describing the flexible multibody system. The major effort is done on solving the eigenvalue problem, numerical integration of the reduced model, and then retaining all elastic coordinates for each body to be optimized in every optimization iteration. Thus, the number of degrees of freedom of the system as well as number of design variables has a direct influence on the overall computational effort.
2.3 Solid isotropic material with penalization approach in TOMBS
In topology optimization, the desired value of the design variable after convergence is either \(X_{e}^{\max}=1\) or \(X_{e}^{\min}=\epsilon\), where \(\epsilon\) is a given small threshold. Other values need to be avoided in order to get an acceptable so-called material-hole state. However, these values are obtained. The solid isotropic material with penalization (SIMP) approach penalizes these values such that more numbers of design variables reach the box limits after convergence. Penalizing is done by introducing an effective Young’s modulus \((X_{e})^{q} E\); see [2, 4].
This approach works for static response topology optimization where there is no mass in the system; however, this kind of penalization is the reason of instability, mesh distortion, and non-convergence of the optimization algorithm in the dynamic case regardless of the sensitivity analysis approach.
Element stiffnesses are proportional to Young’s modulus. Further, scaling the Young’s modulus is large when the design variable reaches small values in the optimization iteration steps. In a flexible multibody model a uniform mass distribution is converted to a lumped mass distribution. The lumped masses are located in nodal points of the finite element mesh. Schematically the lumped masses are connected with springs shown in Fig. 2. By reducing the stiffness of the elements around a lumped mass, it will be no longer strongly attached to the body. Thus when the body experiences acceleration the mass does not follow the body’s trajectory. This is what is happening in TOMBS when the element stiffness is penalized in SIMP. In this case, the stiffness of an element might be different from the neighboring elements where the mass is the same. Hence, due to inertia force, elements with small design variable experience higher displacement than others. Here, such an element with high displacement is called a flying element, see Fig. 3. Consequently, the objective function shows a peak at the position of flying elements and in the next iteration step larger thickness is assigned to them giving raise to convergence failure of the process.
A simple modification of traditional SIMP reduces the effect of flying elements considerably. Here, in addition to scaling Young’s modulus it is suggested to scale element mass by scaling element’s density:
where \(E^{j}\) is the Young’s modulus of the body material, \(E_{e}^{j}\) is the penalized Young’s modulus of an element, \(\rho^{j}\) is the density of the body, \(\rho_{e}^{j}\) is the penalized element density, and \(q\) is the penalization factor. However, according to the nonlinear differential algebraic equation of motion of a flexible MBS, Eq. (2), the relation between the lumped (or element) masses and element stiffness is not linear, thus, scaling of the mass and stiffness is subject to further investigation; nevertheless, modification (19) helps convergence of the optimization algorithm with no need of element removal. Penalization (19) directly affects the calculation of the mass matrix in Eq. (2) and also the body stiffness matrix through constitutive relation. Thus, \(b_{e}^{j,k}\) in (15) is altered accordingly.
3 Examples
In a flexible multibody system, rigid bodies can also be present. However, the optimization is done only on flexible bodies. One or several flexible bodies can be optimized simultaneously. Thus, the overall system behavior is accounted for during optimization process. A design space is assigned to the flexible bodies which are to be optimized. Then, design variables of bodies are updated iteratively by the optimizer. We present here two examples to illustrate the pros and cons of the method. In both examples, the penalization factor is chosen to be \(q=3\), and the volume change is constrained by \(40 \%\) of the initial volume. Also, four-node rectangular linear elements are used for finite element mesh of all flexible bodies here. It should be noted that smaller strain energy is achieved if more material is used. Selecting the volume constraint is an engineering judgment. Small values give a weak design, i.e., high stresses as a response to a force, or might result in removal of material between joints which needs to be avoided.
3.1 Slider–crank
The first example is a simple slider–crank mechanism. First, the crank is driven with a constant angular velocity from zero angle, the initial position of the crank, to \(120^{\circ}\) as shown in Fig. 4. TO is applied on both bodies simultaneously, cf. Fig. 5 (left). The objective function and volume constraint history of both bodies, as well as the elastic deformation of the upper center node of the connecting rod, for a non-optimized design and the optimized one are illustrated in Fig. 6. The non-optimized design is similar to Fig. 4 but the thickness is changed such that the overall weight equals to the optimized design. The crank’s angular velocity is \(2~\mbox{rad}/\mbox{s}\) and the mass of the slider is 2 kg. The boundary conditions are clamped-free and simply-supported for crank and connecting rod, respectively. The reason of selecting such a boundary condition is that we would like to have full freedom at one end of the crank. The modulus of elasticity, density, thickness for both bodies are \(70~\mbox{GPa}\), \(2700~\mbox{kg}/\mbox{m}^{3}\) and 0.02 m, respectively. A mass proportional damping with constant 10 is introduced to the system. The convergence criterion is \(\|\boldsymbol{X}^{(k+1)}-\boldsymbol{X}^{k}\|< 0.085\). Other TOMBS input data is provided in Table 1.
The average of the time dependent displacement field and similarly the average of the compliance vary with the time integration interval. Thus, the optimal design also depends on the time integration. To illustrate such a dependence, the same slider–crank mechanism is optimized when the crank makes a complete revolution, see Fig. 5 (right). However, in this example, since the behavior of the system can be completely determined by only simulating one loop, it is possible to eliminate the dependency of the final topology on the integration interval.
The convergence criterion is checked individually for each body. If it is satisfied for one body, but not for another, its thickness is not updated at the next iteration step while the optimization process continues for the other bodies.
The reason for having a peak in the objective function history is that we do a constraint optimization. The optimizer tries to satisfy the volume constraint during the first iterations where there is a jump in the objective function history. If the initial state satisfies the constraints, no peak is observed.
3.2 Seven-body mechanism
The second example is a seven-body mechanism [17] with a constant driving angular velocity. A schematic is shown in Fig. 7, where a design space is assigned to each body which is exposed to topology optimization. First, we let body 3 be the only flexible body in the system. The result of topology optimization is shown in Fig. 8 (left). The time history of the displacement field is here the only input to the optimizer. If more bodies in the system are considered to be flexible, the time history of the displacement field of body 3 changes, and thus the optimized design changes accordingly. This argument demonstrates the significance of the overall system behavior on the optimization process. Figure 8 (right) shows the optimal design of the system where topology optimization is applied on three bodies simultaneously. The objective function history for all three bodies is shown in Fig. 9. The driver rotates with the speed of \(1000~\mbox{rad}/\mbox{s}\). The integration covers one complete loop of the driver. Simply-supported boundary conditions are used for all flexible bodies. The modulus of elasticity, density, thickness of flexible bodies are \(70~\mbox{GPa}\), \(2700~\mbox{kg}/\mbox{m}^{3}\) and \(5\times 10^{-3}~\mbox{m}\). The convergence criterion is \(\|f^{(k+1)}-f^{k}\|< 5 \times 10^{-6}\), where \(f\) is the objective function of each body. Other TOMBS data can be found in Table 2.
The example above uses ten modes for modal reduction with Kraig–Bampton method for body 3. However, we observed that considering a smaller number of modes down to three or a larger number of modes does not have a considerable effect either on the optimal topology or on the iteration history of the objective function, see Fig. 10. The reason for obtaining a different optimal topology than that is shown in Fig. 8 (left) is the difference in mesh size (\(40 \times70\)) as well as a larger filter size.
3.3 Remarks
-
The choice of the boundary condition of bodies influences the optimization result significantly.
-
Static response topology optimization as well as TOMBS is sensitive to optimization parameters such as filters, number of design variables, and SIMP parameters. In addition, TOMBS is sensitive to MBS simulation parameters which might alter the displacement field such as number of considered modes below a threshold, simulation interval and also some parameters that influence the differential algebraic equations solver performance such as absolute and relative tolerances.
-
The time integration intervals must be chosen appropriately to include all major deflections of bodies during the operation. If the MBS behaves periodically, at least one period can be enough. Weighted integration is an alternative.
4 Conclusions
We presented an implementation of topology optimization based on the dynamic behavior of an entire multibody system. We discussed simplifying assumptions on the sensitivity matrices, which enabled us to achieve convergence of the optimization algorithm within reasonable computational time. Besides, achieving convergence would not be possible without mass penalization in addition to stiffness penalization to avoid flying elements in dynamic planar bodies.
Furthermore, we demonstrated the influence of the number of modes and the simulation time horizon on the optimization results.
References
Andersson, C., Führer, C., Åkesson, J.: Assimulo: A unified framework for ODE solvers. Math. Comput. Simul. 116(0), 26–43 (2015). doi:10.1016/j.matcom.2015.04.007
Bendsoe, M.P., Sigmund, O.: Topology Optimization: Theory, Methods and Applications. Springer, Berlin (2003)
Christensen, P.W., Klarbring, A.: An Introduction to Structural Optimization, vol. 153. Springer, Berlin (2008)
Ghandriz, T.: An algorithm for structural topology optimization of multibody systems. Master’s thesis, Lund University (2014)
Ghandriz, T., Führer, C.: Topology optimization of dynamic structures and multibody systems based on reduced model adjoint sensitivity analysis. In: Berezovski, A., Tamm, K., Peets, T. (eds.) Proceedings of the 28th Nordic Seminar on Computational Mechanics, pp. 55–58 (2015)
Held, A., Knüfer, S., Seifried, R.: Topology optimization of members of dynamically loaded flexible multibody systems using integral type objective functions and exact gradients. In: Li, Q., Steven, G.P., Zhang, Z.L. (eds.) Proceedings of the 11th World Congress on Structural and Multidisciplinary Optimization, Sydney, Australia pp. 500–505. International Society for Structural and Multidisciplinary Optimization (ISSMO), Sydney (2015)
Held, A., Seifried, R.: Topology optimization of members of elastic multibody systems. PAMM 12(1), 67–68 (2012)
Jang, H., Lee, H., Lee, J., Park, G.: Dynamic response topology optimization in the time domain using equivalent static loads. AIAA J. 50(1), 226–234 (2012)
Kang, B.S., Park, G.J., Arora, J.S.: Optimization of flexible multibody dynamic systems using the equivalent static load method. AIAA J. 43(4), 846–852 (2005)
Kang, B.S., Park, G.J., Arora, J.S.: A review of optimization of structures subjected to transient loads. Struct. Multidiscip. Optim. 31(2), 81–95 (2006)
Saravanos, D., Lamancusa, J.: Optimum structural design of robotic manipulators with fiber reinforced composite materials. Comput. Struct. 36(1), 119–132 (1990)
Seifried, R., Moghadasi, A., Held, A.: Analysis of design uncertainties in structurally optimized lightweight machines. Proc. IUTAM 13, 71–81 (2015)
Shabana, A.A.: Dynamics of Multibody Systems. Cambridge University Press, Cambridge (2013)
Sigmund, O.: Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 33(4–5), 401–424 (2007)
Simeon, B.: Computational Flexible Multibody Dynamics: A Differential-Algebraic Approach. Springer, Berlin (2013)
Tromme, E., Brüls, O., Virlez, G., Duysinx, P.: Structural optimization of flexible components under dynamic loading within a multibody system approach: A comparative evaluation of optimization methods based on a 2-dof robot application. In: 10th World Congress on Structural and Multidisciplinary Optimization (2013)
Wanner, G., Hairer, E.: Solving Ordinary Differential Equations II, vol. 1. Springer, Berlin (1991)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ghandriz, T., Führer, C. & Elmqvist, H. Structural topology optimization of multibody systems. Multibody Syst Dyn 39, 135–148 (2017). https://doi.org/10.1007/s11044-016-9542-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-016-9542-7