Load assessment and analysis of impacts in multibody systems

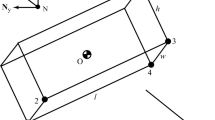
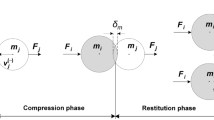
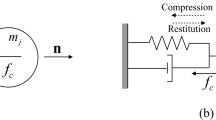Abstract

The evaluation of contact forces during an impact requires the use of continuous force-based methods. An accurate prediction of the impact force demands the identification of the contact parameters on a case-by-case basis. In this paper, the preimpact effective kinetic energy $T_{c}^{-}$ is put forward as an indicator of the intensity of the impact force along the contact normal direction. This represents a part of the total kinetic energy of the system that is associated with the subspace of constrained motion defined by the impact constraints at the moment of contact onset. Its value depends only on the mechanical parameters and the configuration of the system. We illustrate in this paper that this indicator can be used to characterize the impact force intensity. The suitability of this indicator is confirmed by numerical simulations and experiments.

Appendix: Coordinate transformation

The dynamics of the two circular objects selected as an example in Sect. 2.1 can be expressed in terms of the set of absolute velocities $\dot{\mathbf{q}} = [ \dot{x}_{1} \ \dot{x}_{2} ]^{\mathrm{T}}$ with Eq. (2)

$$ \mathbf{M} \ddot{\mathbf{q}} = \mathbf{A} ^{\mathrm{T}} \lambda $$

(28)

where

$$ \mathbf{M} = \left [ \textstyle\begin{array}{c@{\quad}c} m_{1} & 0\\ 0 & m_{2} \end{array}\displaystyle \right ]; \qquad\ddot{\mathbf{q}} = \left [ \textstyle\begin{array}{c} \ddot{x}_{1} \\ \ddot{x}_{2} \end{array}\displaystyle \right ]; \qquad\mathbf{A} ^{\mathrm{T}} \lambda= \left [ \textstyle\begin{array}{c} -f_{c} \\ f_{c} \end{array}\displaystyle \right ] $$

(29)

The system motion can also be described in terms of a new set of velocities $\dot{\mathbf{d}} = [ \dot{d}_{c}\ \ \dot{d}_{a} ]^{\mathrm{T}}$, where $\dot{d}_{c}=\dot{x}_{2}-\dot{x}_{1}$ and $\dot {d}_{a}=\frac {m_{1}}{m_{2}}\dot{x}_{1}+\dot{x}_{2}$. The relation between the two velocity sets is given by

$$ \dot{\mathbf{d}} = \left [ \textstyle\begin{array}{c} \dot{d}_{c} \\ \dot{d}_{a} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} {\mathbf{A}} \\ \mathbf{B} \end{array}\displaystyle \right ] \dot{ \mathbf{q}} $$

(30)

where

$$ {\mathbf{A}} = \left [ \textstyle\begin{array}{c@{\quad}c} -1 & 1 \end{array}\displaystyle \right ]; \qquad \mathbf{B} = \left [ \textstyle\begin{array}{c@{\quad}c} m_{1}/m_{2} & 1 \end{array}\displaystyle \right ] $$

(31)

The matrix $\mathbf{B}$ has been selected to verify the decoupling condition $\mathbf{A}\mathbf{M} ^{-1}{\mathbf{B}}^{\mathrm{T}} = 0$.

The dynamics can be expressed in terms of the new set of velocities $\dot{\mathbf{d}}$ via the velocity transformation

$$ \dot{\mathbf{q}} = \mathbf{R} \dot{\mathbf{d}} $$

(32)

where R is the constant matrix

$$ {\mathbf{R}} = \frac{1}{m_{1} + m_{2}}\left [ \textstyle\begin{array}{c@{\quad}c} -m_{2} &m_{2} \\ m_{1} &m_{2} \end{array}\displaystyle \right ] $$

(33)

and so differentiation of Eq. (32) with respect to time gives

$$ \ddot{\mathbf{q}} = \mathbf{R} \ddot{\mathbf{d}} $$

(34)

Premultiplying Eq. (28) with $\mathbf {R}^{\mathrm{T}}$ and substituting in it the expression of $\ddot{\mathbf{q}}$ from Eq. (34) allows us to obtain the dynamics equations in terms of the set of velocities $\dot{\mathbf{d}}$, as expressed in Eq. (4)

$$ {\mathbf{R}}^{\mathrm{T}} \mathbf{M} {\mathbf{R}} \ddot{\mathbf{d}} = \mathbf{R}^{\mathrm{T}} \mathbf{A} ^{\mathrm{T}} \lambda $$

(35)

where

$$ {\mathbf{R}}^{\mathrm{T}} \mathbf{M} {\mathbf{R}} = \frac{1}{m_{1} + m_{2}} \left [ \textstyle\begin{array}{c@{\quad}c} m_{1} m_{2} & 0\\ 0 & m_{2}^{2} \end{array}\displaystyle \right ]; \qquad \mathbf{R}^{\mathrm{T}} \mathbf{A} ^{\mathrm{T}} \lambda= \left [ \textstyle\begin{array}{c} f_{c} \\ 0 \end{array}\displaystyle \right ] $$

(36)