1 Introduction

The complex anatomy of the human neck allows for high flexibility in rotation and translation through seven cervical vertebrae controlled by over 70 muscles. This high level of complexity has made it difficult for scientists to understand load distributions occurring in the cervical spine. Although in vitro research has made properties available related to the anatomy and passive loading of the neck, it has proven difficult to obtain in vivo data of the deep cervical tissues from experiments. Computer models have been successful at combining anatomical knowledge with volunteer data to estimate internal loads acting on the cervical system. Available biomechanical head and neck models vary widely in complexity. Simple models using one or two pivots (inverted pendulum models) are helpful to gain insight into the overall dynamics of the head and neck system [1–3], but to mimic internal tissue deformation [4–6] detailed three-dimensional models become necessary.

Detailed models with passive musculature have been used extensively to evaluate injury risks during high impact loading [7–13]. Recently developed automotive systems in active safety [14, 15] and driving comfort [16] involve the occupant response to (autonomous) braking and evasive maneuvers prior to crash, which has pushed the demand towards simulations with active muscles. This requires proper validation of the modeled muscular responses in pre-crash conditions, as well as during impact. In several active neck models the joint centers of rotation are fixed [17–21], even though intervertebral motion can only be fully captured when both joint translations and rotations are possible [4, 22, 23]. The placement of fixed joint locations greatly influences the model’s behavior, particularly because of its effect on muscle moment arms [17, 18]. To model intervertebral motion correctly joints should ideally have full freedom of motion in rotation, shear, and compression/elongation. Of the active neck models with sufficient detail to accurately model tissue dynamics between vertebral joints [4, 7, 11, 13, 24–28], none have provided a validation of muscle activation patterns in isometric conditions. It is important to evaluate the model’s isometric response first to properly assess cervical muscle strength in different loading directions, and secondly to verify the directional activity of the muscles. In a number of models, isometric validation is performed by evaluating moments at the lowest joint (T1–C7) while equilibrium at other joints is disregarded [17, 18]. For proper isometric validation, the equilibrium of the entire spine should be taken into account when evaluating cervical strength and muscular responses.

Our objectives were (1) to enhance a dynamic nonlinear musculoskeletal neck model with 48 degrees of freedom [9, 29], (2) to validate passive properties and muscle moment arms, and (3) to validate isometric strength and muscular activity of healthy volunteers, taking into account the equilibrium of all vertebral joints.

2 Methods

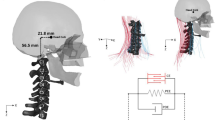
A dynamic nonlinear neck model (Fig. 1), previously validated for automotive impact [9, 11, 29, 30], was extensively revised and validated using biomechanical data summarized in Tables 1, 2, 3. The model contains nonlinear intervertebral disc compliance in rotation and translation, ligaments and facet joint contact dynamics, and was extended with 34 muscle pairs (129 bilateral segments) with discrete lines of action using via points.

Fig. 1
figure 1

Lateral (sliced) and anterior view of the nonlinear dynamic model depicting muscles, vertebral geometry, and skull. Joint centers of rotation of the linear static model are illustrated by green balls

Full size image
Table 1 Intervertebral disc stiffness and damping used in the model at each joint except for C2–C1 and C1–C0. Disc stiffness was obtained from cadaveric segments tests. Damping was adjusted manually to improve the model’s response during impact loading
Full size table
Table 2 Model parameters for active and passive muscle behavior (largely adapted from van der Horst [29])
Full size table
Table 3 Biomechanical sources for modeling and verification (see also Tables 1 and 2)
Full size table

2.1 Simulation

The dynamic nonlinear neck model was written in the graphics-based simulation software MADYMO 7.5 [31] and was called by Matlab R2012b (Matlab/Simulink, The Mathworks Inc., Natick, USA) through Simulink to control muscle actuation. A time step of 2×10−5 s was applied with a fixed-step 4th order Runge–Kutta ordinary differential equation solver. Execution time was roughly 240 times real-time on a 2.8 GHz processor.

A “static model” was derived by linearization of the dynamic model in the neutral position (Fig. 1). The static model was implemented in Matlab and was used to estimate maximum isometric horizontal head forces and head twist moments. Muscle activations, derived with the static model, were subsequently applied to the dynamic model for verification.

2.2 Passive properties

2.2.1 Skeletal geometry

The dynamic model comprised nine rigid bodies; the skull (C0), seven cervical vertebrae (C1–C7), and the first thoracic vertebra (T1) as a fixed base, allowing for a total of 48 DOF. The outer surface of bony structures was modeled using three-dimensional finite-element (FE) surfaces attached to rigid bodies. The geometry of the vertebrae and skull was based on data from the Human Model for Safety project (HUMOS) of a 78 year old male post mortem human subject (PMHS) with a weight of 80 kg and height of 1.73 m [33]. The relative positions and orientations of the lower cervical vertebrae in the neutral posture were estimated based on lateral X-rays of standing young males [9, 34]. Inertial and geometric data of the model are supplied in [9, 29].

2.2.2 Intervertebral joint compliance

Disc compliance was captured with nonlinear six degrees-of-freedom (DOF) translational and rotational spring-dampers, allowing for movement in all directions [29, 32]. Intervertebral discs were given a nonlinear stiffness curve and a damping coefficient in six loading directions derived from cadaveric segment tests (Table 1) between all thoracic (T1) and lower cervical vertebrae (C7–C2), but not between the axis (C2), atlas (C1), and occiput (C0—base of the skull) [29]. Linear stiffness parameters for shear [35] and tension [8] were obtained from isolated discs, and compression was defined by a nonlinear curve [9, 36] ranging between 822 and 1490 N/mm. Stiffness estimates for disc flexion and extension [8], and lateral bending and axial rotation [37] were derived from disc data including ligaments. Following an estimate by Moroney [35], it was assumed that half of the stiffness in [8] and [37] was due to the disc and the other half due to ligaments. Stiffness in lateral bending and axial rotation was nonlinear up to 1 N m [37] and was modeled linearly for loads exceeding 1 N m [35]. Linear damping coefficients were adjusted manually to improve the model’s response in impact loading conditions [9], resulting in 1000 N s/m and 1.5 N m s/rad as linear and rotational damping coefficients, respectively.

Spinous process contact (which is relevant only in extreme bending) and facet joint compliance were modeled with a contact stiffness chosen to be twice the disc compression stiffness as specific biomechanical data was lacking [29].

Ligaments were implemented with insertions and origins based on anatomical landmarks of the vertebral geometry [29]. Line elements were defined with nonlinear unidirectional force-strain curves, only producing force when in tension [38]. All ligaments received specific nonlinear force–strain curves [29] based on cadaver testing [29, 39, 40]. When ligaments were assumed to be at their rest length (not slack or taut) in the model’s neutral position, the model proved overly stiff at small bending angles. It was therefore chosen to adapt the initial slack length of ligaments while fitting the model’s passive stiffness to experimental data [37].

The combined passive spine stiffness including ligaments, but excluding passive muscle stiffness, was verified at low loads (up to 1 N m) using experimental data from Panjabi [37]. Similar to the experiment, consecutive moments of 0.33, 0.66, and 1 N m were applied to the skull of the model in flexion/extension, lateral bending, and axial rotation. These were followed by a zero load to quantify the remaining deformation due to hysteresis. Local angular displacements were measured in the respective loading direction at all joints. The origin was defined in the mid sagittal plane at the inferior-most point on the posterior wall of the vertebral body. All joints were validated, except for the lowest (T1–C7). Kinematic validation at high loads (high speed impact) has previously been published [29, 30].

2.2.3 Muscle geometry

A recently published extensive muscle geometry set of one PMHS (86 year old, 75 kg, 1.71 m height) was implemented, with 34 muscle pairs divided into 129 segments per body side [41]. The data set contained muscle physical cross-sectional area (PCSA), mass, pennation angles, and geometrical data including bony landmarks and muscle attachment sites, which were digitized using an Optotrak system [42]. To correctly transfer the attachment sites, the PMHS muscle geometry was reoriented and scaled to match the HUMOS skeletal geometry. A linear least-squares optimization was used to reorient and scale the PMHS skull to minimize the error of eleven bony landmarks between both skulls [41, 43]. The resulting scaling factor of 0.95 was applied to all bones and attachment sites of [41]. The PMHS vertebral posture and the origin of the coordinate system differed from the HUMOS subject. The origin of the muscle geometry coordinate system (located at the suprasternal notch of the thorax) was reoriented to the HUMOS model origin located at the geometric center of the T1. Each scaled bone (skull and seven cervical vertebrae) was then individually reoriented with the same optimization algorithm [43] using five (C3 to C6), four (C1), and three (C7 and C2) bony landmarks. The hyoid bone was not modeled, requiring a solution for the attachment of the hyoid muscles (sternohyoid, omohyoid, sternothyroid, and thyrohyoid). The contribution of these muscles in the generation of flexion moment in the upper spine (C2–C0) is considerable [17]. It was chosen to attach the hyoid muscles to the skull, as its movement has the highest correlation with the hyoid bone movement of the available bony structures [44]. Intermediate ‘via points’ which connected the muscles to adjacent vertebrae were implemented to ensure the muscle took on a curved path with large displacements [45]. Muscle paths were determined by visually fitting transversal slices of the model to MRI data of the Visible Human project (Ecole Polytechnique Fédérale de Lausanne) available online [46]. The muscles not visible in the MRI data were given curvatures based on the paper [47] and anatomy books [48, 49].

Muscle force (F m ) was modeled using a nonlinear Hill-type model [38, 50], where a contractile element described the muscle’s active dynamic force–length–velocity response and a parallel elastic element described passive muscle force. A description of all active and passive muscle parameters is given in Table 2. The contractile element and parallel elastic elements are described as follows:

$$\begin{aligned} F_m=F_\mathrm{CE}+F_\mathrm{PE} & \end{aligned}$$
(1)
$$\begin{aligned} F_\mathrm{CE}=x\cdot\sigma_{\max}\cdot \mathit{PCSA}\cdot f_{H} (v_{r})\cdot f_{L}(l_{r}), & \end{aligned}$$
(2)
$$\begin{aligned} F_\mathrm{PE}=\mathit{PCSA}\cdot f_{p}(l_{r}), & \end{aligned}$$
(3)

where the contractile force depends on muscle PCSA, maximal isometric stress σ max, and muscle activation x. The relative muscle length l r and velocity v r were defined by dividing respectively muscle length and muscle lengthening velocity by the optimum muscle length l opt and maximum shortening velocity v max. The force–velocity function f H (v r ) is defined as

$$ f_{H}(v_{r})=\left\{\begin{array}{l@{\quad }l} 0 & \mbox{for}\ v_{r}< -1 \\ \frac{1+v_{r}}{1-v_{r}/\mathit{CE}_\mathrm{sh}} & \mbox{for}\ -1< v_{r}\leq 0 \\ \frac{1+v_{r}\mathit{CE}_\mathrm{ml}/\mathit{CE}_\mathrm{shl}}{1+v_{r}/\mathit{CE}_\mathrm{shl}} & \mbox{for}\ v_{r}>0 \end{array} \right. $$
(4)

where parameters CE sh and CE shl define the force–velocity curve shape (the implemented force–velocity function (Eq. (4)) is irrelevant in the isometric analysis presented in this paper).

The active force–length function f L (l r ) is defined as

$$ f_{L}(l_{r})=e^{-( \frac{l_r-1}{S_{k}})} $$
(5)

with the shaping curve parameter S k [38]. The passive force–length curve f p (l r ) is defined as

$$ f_{p}(l_{r})= \frac{k\cdot \epsilon}{1-\frac{\epsilon}{a}} $$
(6)
$$ \epsilon=l_{r}-1 $$
(7)

where k [29, 51] and a [51] are respectively stiffness and asymptote parameters. Passive force is generated when muscle length exceeds l opt (defined by muscle strain ϵ), and was selected 5 % larger than the initial muscle length [9, 52]. Pennation angle and sarcomere length were accounted for in the muscle PCSA obtained from the new muscle data set [41]. The maximal isometric stress (σ max) was set to the rather high value of 70 N/cm2 to correct for the age of the PMHS [53–55]. The PCSA data of the flexor muscles in the upper spine (in particular the hyoid muscles) in [41] were on average 40 % weaker than other estimates from the literature [24]. Therefore, the longus capitis, omohyoid, sternohyoid, thyrohyoid, and sternocleidomastoid PCSA was enlarged with 60 %.

2.2.4 Instantaneous joint centers of rotation

The dynamic model used in this study allows for full rotational and translational intervertebral joint motion and does not fix joint centers of rotation. To determine the instantaneous joint centers of rotation (ICR), a sinusoidal flexion and extension moment was applied on the skull large enough to generate a total angular displacement of at least eight degrees at each joint. The flexion–extension axis of rotation was estimated over two degree increments using the helical axis method [56]. The ICR were placed at the median of these estimates along the mid sagittal plane (y=0). ICR estimates were compared with experimental data by Anderst et al. [57] for the lower spine (C7–C2) and Chancey et al. [58] for the upper spine (C1–C0). The axis (C2–C1) ICR was not evaluated as its motion is primarily in twist. Instead, the ICR of combined C2–C0 motion was estimated. In the experiment by Anderst, cervical motion between C2 and C7 of 20 healthy subjects was tracked using biplane radiographs and ICR were estimated using the helical axis method. Chancey used 3D visual tracking to estimate centers of rotation of ten upper cervical spine specimens including the skull.

2.3 Isometric strength

Maximum voluntary contraction (MVC) strength and muscle activation were evaluated by simulation of horizontal head force and head axial rotation (twist) tasks. An isometric solution could theoretically be derived directly for the nonlinear dynamic model but this would require extensive computational efforts to optimize the 258 muscle activations, where dynamic analysis would be needed allowing the joints to settle in compression and shear. Hence the isometric analysis was performed using a linearized static model, and verified using the nonlinear dynamic model.

2.3.1 Static model

For the neutral position, a linearized “static model” was derived with 3D rotational joints located at the instantaneous centers of rotation (ICR) shown in Fig. 1 which were estimated by simulation of the dynamic model as described above. Combined upper neck motion between C2–C0 was captured with one spherical joint, which represented the combined C1–C0 and C2–C1 motion in the static model. Thus the static model has 21 degrees of freedom representing 3D rotation in 7 joints. Thereby we assumed that the translational intervertebral joint degrees of freedom do not need active muscular stabilization, even while performing MVC tasks.

The static model consists of the system equilibrium Eq. (8) and the load sharing Eq. (9) equations:

$$ M_\mathrm{des} = N\left( \begin{array}{c} F_\mathrm{head}\\ M_\mathrm{head}\end{array} \right), $$
(8)
$$ M_\mathrm{des} = F_\mathrm{CE}\cdot R + M_\mathrm{pas} $$
(9)

with active muscle forces F CE according to Eqs. (2), (5)–(7). The desired neck joint torques M des are calculated based on the forces F head and moments M head applied on the environment at the head center of gravity and the neck moment arm matrix N derived from the location of the neck joints with respect to the head center of gravity.

M des is generated by the 258 active muscle forces F CE multiplied by the muscle moment arm matrix R plus the passive moments M pas exerted at the joints by the intrinsic spine stiffness (i.e., moments generated without muscle activation, and including passive muscle forces F PE).

2.3.2 Moment arm matrix

The moment arm matrix R and the passive moments M pas were derived by simulation of the dynamic model. All joints were locked in the neutral position. Each muscle was individually activated to 1 N and the three-dimensional moments were measured at the ICR of all joints simultaneously to obtain the moment arm matrix R of the 258 muscle segments at the seven joints in the three moment directions. Similarly, M pas was derived without muscle activation.

The moment arms of nine muscles were validated with a study in which moment arms were determined using the tendon excursion method on the neck of five fresh-frozen cadavers [59]. In this study, individual joints were rotated via a head clamp (visually assessed motion between 2.9 and 8.9 degrees) and the slope of a least-squares fit between joint motion and tendon excursion defined the moment arm in the neutral position. Muscle segment moment arms (23 segments) were compared for the semispinalis capitis, semispinalis cervicis, splenius capitis, splenius cervicis, sternocleidomastoidus, levator scapulae, scalenus (anterior and middle), trapezius (superior, middle, and inferior), rectus capitis (major and minor), and obliquus capitis (inferior and superior).

2.3.3 Load sharing

As in most musculoskeletal models, the number of muscle segments (258) exceeds the number of degrees of freedom (21). Thus the load sharing equation Eq. (9) will generally have an infinite number of solutions F CE. A common approach is to define a cost function representing the metabolic cost of muscle contraction, and to solve the load sharing equation while minimizing this cost function. It shall be noted that the maximum (MVC) head forces and moments do not depend on this cost function. The cost function only affects the individual muscle contributions.

We adopted a metabolic energy-related cost function [60] based on the detachment of cross bridges (\(\dot{E}_{f}\)) and the re-uptake of calcium (\(\dot{E}_{a}\)). For isometric conditions and assuming a 1:2 ratio between the linear and nonlinear components at maximal activation [60], we minimized the cost function J summing the efforts over N muscle segments:

$$ \min J=\sum_{k=1}^{N} \dot{E}_{f}^{k}+\dot{E}^{k}_a= 0.5m^{k}\frac{F_\mathrm{CE} ^{k}}{\mathit{PCSA}^{k}} +0.5m^{k} \biggl(\frac{F_\mathrm{CE}^{k}}{ \mathit{PCSA}^{k}\cdot\sigma_{\max}} \biggr), $$
(10)

where F PE follows from Eq. (2) with muscle activation x constrained between zero and one, and m represents muscle segment mass. For the generated muscle moments M des a 1 % deviation was allowed to obtain a realistic numerical solution (results were marginally sensitive when varying this tolerance between 0.5 and 2.0 %).

2.3.4 Maximum voluntary contraction

The model’s MVC was determined for eight equidistant transversal head force directions and in axial rotation (head twist). To obtain MVC the desired load was incrementally increased (increments of 1 N in transversal head force F head and 0.1 N m in axial moment M head), until Eqs. (8) and (9) could no longer be solved under the applicable constraints.

Once the optimal muscle activation patterns were determined using the linear static model, it was necessary to verify the accuracy using the nonlinear dynamic model. Constant muscle activations were fed into the nonlinear model which was simulated for one second to let the joints settle in translation and rotation. The skull was rigidly fixed at the head center-of-gravity where the generated isometric loads were measured and compared with loads derived from the static model.

Our method results in full spinal equilibrium across all seven joints in three moment directions. A number of model studies assessed maximum cervical strength by evaluating moments only at a single joint (generally T1–C7), thereby disregarding spinal equilibrium at other joints [17, 18]. However, an imbalance in moments across the other joints will cause intervertebral motion and buckling of the spine. Arguably, in experiments subjects keep their cervical joints balanced during isometric contractions to avoid bending the vertebrae to their physiological limits. To test the hypothesis that cervical strength of the model under a full spinal equilibrium provided more realistic results, a simplified MVC analysis was performed similar to [17, 18], where joint equilibrium and load sharing (Eq. (9)) were evaluated and constrained only at the T1–C7 joint.

The MVC moments generated by the linear and the nonlinear model were compared with three studies in which peak moment generating capacities of healthy males were evaluated at T1–C7 [61–63]. In addition, the maximum transversal forces were compared with three studies in which peak transversal forces of young healthy males were measured [64–66]. The muscle activations were compared with a similar study by Siegmund et al. [67] reporting isometric maximum voluntary contractions in eight head force directions in three subjects. Muscle activation patterns of the sternocleidomastoidus, levator scapulae, trapezius, splenius capitis, semispinalis capitis, semispinalis cervicis, and multifidus were measured using fine wire electrodes. The sternohyoid was measured using surface electromyography.

3 Results

3.1 Passive properties

The passive stiffness properties of the ligamentous spine were in general agreement with the study by Panjabi et al. [37] in flexion–extension (Fig. 2), lateral bending (Fig. 3), and in axial rotation (Fig. 4). The lower spine (C7 to C3) with ligaments showed similar levels of stiffness compared to the experimental data. All differences observed at 1 N m were within one standard deviation of the experimental data, with the exception of C2–C1 during axial rotation and C2–C3 during extension. The displacements at zero load describe the settling range of the joint after unloading. In the experimental data, most joints showed a considerable hysteresis referred by the experimenters as the neutral zone [37]. Joints would settle in an angle depending on its previous state (e.g., if the joint was previously in left bending it would likely settle in the lowest point of the neutral zone). The model returned predominantly towards a single neutral joint position when no moments were applied, specifically during lateral bending, resulting in increased stiffness up to approximately 0.33 N m. In the neutral zone, four joints (between C6 to C2) during lateral bending and three joints (C6–C5, C4–C3, and C2–C1) during axial rotation were outside two standard deviations of the experimental data. The largest model discrepancy was found in the C2–C1 joint during axial rotation, where the model had a considerably smaller neutral zone (a 10 degrees range compared to 50 degrees in the experiment) and was unable to perform the expected large axial rotation.

Fig. 2
figure 2

Stiffness of the passive ligamentous spine in flexion and extension. Individual joint excursions were measured simultaneously when a pure moment was applied to the skull. The model is compared to the mean of sixteen neck specimens [37]

Full size image
Fig. 3
figure 3

Stiffness of the passive ligamentous spine in lateral bending. Individual joint excursions were measured simultaneously when a pure moment was applied to the skull. The model is compared to the mean of sixteen neck specimens [37]

Full size image
Fig. 4
figure 4

Stiffness of the passive ligamentous spine in axial rotation (twist). Individual joint excursions were measured simultaneously when a pure moment was applied to the skull. The model is compared to the mean of sixteen neck specimens [37]

Full size image

3.1.1 Instantaneous joint centers of rotation

The joint ICR are depicted as green balls in Fig. 1. The posterior–anterior position of the model ICR between C7 and C3 were within 1.6 mm of the in vivo experiments performed by Anderst et al. [57] (Table 4). Larger deviations were found for vertical ICR position, where all model ICR were superior to the data, except for C7–C6. The C1–C0 ICR was at a similar location as estimated by Chancey [58]. The model estimate was slightly posterior (6 mm) and inferior (3.4 mm) to Chancey’s estimate and respectively just outside and well within one standard deviation (SD) of the experimental data (posterior SD 5.8 mm, superior SD 8.6 mm).

Table 4 Comparison between the instantaneous joint center of rotation (ICR) of the dynamic model in the neutral position and experimental data [57]. As in the experiment, the mean and confidence interval (CI) ICR locations are expressed in anatomic coordinate systems with an origin at the geometric center of the lower vertebral body. Positive coordinates are in the anterior and superior direction
Full size table

3.2 Isometric strength

3.2.1 Moment arm matrix

The muscle moment arms (Table 5) of nine muscles (23 muscle segments) were for the most part consistent with data from Ackland [59] in the frontal and midsagittal plane. The superior and middle trapezius had considerably larger lateral and extension moment arms in the model, with the largest difference at the C7–C6 joint of approximately 38 mm. This may have been caused by the broadness of the trapezius and the different way this muscle can be segmented in dissection studies [41]. The semispinalis capitis, sternocleidomastoid, and obliquus capitis superior showed smaller extension moment arms at the C1–C0 joint than expected. Part of this difference can be explained by the more posterior model ICR position at C1–C0 compared to the experimental ICR found by Chancey et al. [58].

Table 5 Experimental moment arm measurements of nine muscles (23 muscle segments) [59] compared to the dynamic model. The mean and standard deviation of experimental cadaver data (exp.) and the model are shown in mm. The rectus capitis posterior major and minor and the obliquus capitis superior muscles are attached to the OC bone and respectively the C2, C1, and C1
Full size table

3.2.2 Maximum voluntary contraction

The head transversal MVC force generated by the nonlinear dynamic model agreed reasonably well with the linear static model (red and green lines Fig. 5(A)). In all directions the deviation was below 11 %. This confirmed the applicability of isometric analysis using the linearized static model in conjunction with the nonlinear dynamic model.

Fig. 5
figure 5

MVC validation with transversal forces (A) at the head center-of-gravity and moments (B) at the T1–C7 joint. See Table 6 for details and axial rotation. Bars represent standard deviations of experimental studies. Axes were scaled by a moment arm of 0.15 m such that the left and right figures were equivalent. The nonlinear dynamic model (red) produced very similar forces compared to the linear static model (A). Model strength exceeds experimental MVC in extension (A, B). The linear static model predicted considerably more strength particularly in flexion when spinal equilibrium was only required at T1–C7 (B)

Full size image

The model was somewhat weak in flexion, fell within the range of experimental studies for lateral flexion, and was stronger than the experimental studies in extension (Figs. 5(A), 5(B) and Table 6).

Table 6 MVC validation, see also Fig. 5. All studies tested healthy males, while the authors of [65] also tested femalesa
Full size table

Isometric bending strength was strongly reduced with full spinal equilibrium, particularly in flexion and axial rotation. With full spinal in equilibrium (green line) moments had to be balanced between T1 and C0, resulting in reduced flexion (47 %), lateral bending (20 %), and extension (4 %) moments compared to balancing joint moments around just the T1–C7 joint (dashed line). In axial rotation the model showed excessive strength when balancing moments around T1–C7 alone, which was reduced by 81 % under full neck equilibrium, being weaker than experimental data [62, 68] (Table 6).

The predicted muscle activity during MVC (red lines Fig. 6) was very similar to findings of Siegmund et al. [67] although there was a discrepancy in the splenius capitis muscle. The model primarily showed activation during ipsilateral extension, while Siegmund and colleagues found this muscle to be especially active during ipsilateral bending and flexion. The sternohyoid had a larger range of activation in the model, where it was also active in ipsilateral extension. Muscle patterns during 50 % MVC (green lines Fig. 6) show a somewhat reduced range of activation presumably due to the linear term in the cost criterion (Eq. (10)).

Fig. 6
figure 6

Muscle activation of left muscles in eight transversal head force directions. Activation was estimated with the static linear model and compared with data MVC from Siegmund et al. [67]. The effect of the metabolic energy criterion on muscle activation is illustrated by responses during 50 % MVC. The model was in general agreement with the experimental data, except for the splenius capitis. The sternohyoid in the model showed activation in a broader range, specifically during ipsilateral extension

Full size image

4 Discussion

The purpose of our study was to validate passive properties and muscle moment arms of a nonlinear dynamic neck model allowing full joint motion, and to validate maximum isometric cervical strength and muscle activation when the spine was under full equilibrium. In general, the model results agreed well with experimental data. However, a number of limitations apply to the model which will now be discussed in detail.

4.1 Passive properties

Some model parameters could not be derived directly from biomechanical data. For instance, the rest length of the ligaments was chosen such that the ligamentous spine matched the experimental passive stiffness. The origin and insertion of ligaments were based on anatomical landmarks obtained through cadaver studies. As the vertebral surface was built up of a finite element mesh, landmark locations were not necessarily exactly defined in the model. Nevertheless, the passive stiffness of the ligamentous spine was similar to experimental data. The upper spine was stiffer than the cadaver data, where the C1–C0 joint was slightly stiffer in extension and the C2–C1 joint was much stiffer in axial rotation. As the upper spine does not have intervertebral discs, its passive properties were regulated entirely by facet joint contact interactions and ligaments. The nearly flat facet articulations are in reality very smooth [37] and it is possible that the course mesh surfaces of the modeled vertebral bodies were unable to provide smooth motion, contributing to the mismatch at C2–C1.

4.1.1 Muscle geometry

In this model muscle paths were determined by using via points fixed to vertebral bodies. The assumed fixation of via points will strongly affect the accuracy of the muscle path in extreme postures [21]. Most via points are hardly relevant for this study as the model is analyzed in its neutral position, where most muscles follow a nearly straight line. Another limitation was that the hyoid bone was not modeled and the hyoid muscles were attached to the skull. While the movement of the hyoid bone is nearly linearly related to the skull [44], dynamics involving the hyoid bone were neglected and in future studies a separate hyoid bone could be included.

4.1.2 Instantaneous joint centers of rotation

There was a relevant discrepancy between the ICR estimated using the dynamic model and the biomechanical data of Anderst et al. [57]. Each model ICR was outside the experimental 95 % confidence interval in either the superior–inferior or anterior–posterior direction. However, the offset in the anterior–posterior direction was on average only 1.3 mm and at most 2.1 mm. Considering that Baillargeon and Anderst found the accuracy of their measurements to be between 1.1 and 3.1 mm [69], their confidence intervals seem very narrow. Our C5–C4 and C3–C2 ICR were located respectively 4.7 and 6.1 mm superior to the experimental mean. It is possible that the mesh of the zygapophysial joint contacts was not modeled with sufficient detail, which could have resulted in the upward deviation of the ICR [70]. Nevertheless, the model ICRs bear close resemblance to those estimated in a different study [22]. Additionally, while the muscle moment arm estimates depend heavily on the ICR they agreed largely with experimental results [59], thereby implying that the ICR estimates should also be reasonably accurate.

4.2 Isometric strength

4.2.1 Moment arm matrix

The muscle moment arms showed some deviations from experimental data particularly for the trapezius. The C1–C0 extension moment arms were consistently approximately 1 cm shorter than data of Ackland et al. [59]. This can partly be explained by the more posterior location of the C1–C0 ICR in the model. However, the authors also warn for overestimation of moment arms of some muscles with concave paths due to their measurement technique, although they do not mention which muscles were problematic. Additionally, insertion points of a number of muscles (among others the trapezius and levator scapulae) in the study of Ackland were based on anatomical atlases, which may have caused discrepancies. Furthermore, joint excursions to establish the ICR differed between specimens and joints, which could have influenced the moment arm estimates. Unfortunately, differences in joint ICR’s between Ackland’s and this study could not be established as the ICRs were not reported. Moment arm discrepancies could also be due to a difference in choices made between Borst et al. [41] (muscle data used in the model) and Ackland et al. [59] when dissecting the muscles. The attachment points have been described in both articles on the basis of anatomical landmarks, but some of these are quite large and could have been interpreted differently. For instance, in both studies the insertion of the middle trapezius is at the scapular spine, even though this landmark stretches across a significant part of the back. The lateral moment arms were considerably larger for the superior and middle trapezius, and the levator scapula segment attached to C1. It seems that in Ackland’s experiments the insertion of the trapezius was defined at a more proximal point on the scapular spine than the modeled trapezius. As the trapezius curves away from the spine sharply, small changes in the point of insertion have a large effect on the moment arm.

4.2.2 Maximum voluntary contraction

The isometric analysis was performed using a linearized static model in which fixed rotation points were assumed and translational joint motions were omitted. Verification using the nonlinear dynamic model showed that this resulted in acceptable predictions of maximal voluntary contraction. The maximum transversal head forces and moments generated by the model were in line with experimental data, although forces in extension were higher. Two likely causes are at the basis of this excessive strength. First, the model results are a depiction of the absolute maximum cervical force and are, in contrast to human subjects, not susceptible to fatigue or lack of motivation. Second, the model did not account for vertebral dynamics below T1 and assumed all joints below T1 to be rigidly connected. With this assumption stabilizing contributions below T1 of muscles spanning thoracic joints are not considered and their contribution to cervical strength is exaggerated. While a few flexor muscles also extended below the T1, this was primarily true for muscles providing extension and lateroflexion. In particular, scapular muscles have a primary function in fixing the scapula [71] along with generating neck strength. The trapezius, levator scapulae, and rhomboid minor likely provided excessive extension and lateral moment. With these scapular muscles disabled, the model produced reduced extension (338N) and lateral bending (194N) forces close to the experiments (flexion force did not change).

A few muscle segments were not used in any of the eight transversal and two axial directions. A number of choices were made that were influential to the outcome. The linear static model assumed a single upper spine center of rotation for C2–C0. Three bilateral muscle segments spanning only the C2–C1 joint (intertransversarii cervicis anterior, posterior, and obliquus capitis inferior) were therefore not used in any loading direction. Two bilateral muscle segments (interspinalis cervicis C7–C6 and semispinalis capitis C6–C0) were only used when scapular muscle forces were limited to 30 %. This confirms that scapular muscle activation should be limited during cervical contractions. The inactivity of two other segments (interspinalis cervicis C5–C4 and multifidus cervicis C5–C2) cannot fully be explained. It is possible that these segments are primarily active in off-diagonal loading directions or when the head is out of its neutral position.

The linear static model assumed constant values for the muscle moment arm matrix R, the neck moment arm matrix N, and the passive joint moments M pas in Eqs. (8), (9). These were derived from the nonlinear dynamic model in the neutral position. For larger motions these could be adapted using methods such as gain scheduling.

Overall, the model predicted EMG of the muscles well during MVC, although a discrepancy was present at the splenius capitis where all six muscle segments in the model were primarily active in extension. Siegmund et al. [67] mentioned that this muscle showed the largest variability in activation patterns between subjects and they suggested that this might be due to differences in the insertion points of the measuring electrodes, as the splenius has a broad attachment along the superior nuchal line. Indeed, other studies [65, 72] found splenius capitis activity, primarily in ipsilateral extension in congruence with the model.

4.2.3 Sensitivity

Model variations performed while developing the model disclosed that the passive stiffness primarily depended on ligament stiffness and slack and on the rotational stiffness of the intervertebral discs. Maximum voluntary contraction forces and moments were proportional to the assumed muscle maximum isometric stress of 70 N/m2 and to the muscle moment arms. Model variations disclosed that MVC depends in particular on the anterior–posterior location of the instantaneous joint centers of rotation, and obviously depends on all muscle attachments and PCSA values.

4.3 Spinal equilibrium

The requirement to balance moments across the entire cervical spine had the largest effect in flexion strength and axial rotation, to a smaller degree in lateral bending, and nearly no effect in extension. The effects in flexion could be explained by the curvature of the spine, where its convex surface is oriented anteriorly (middle vertebrae positioned anteriorly to the upper and lower vertebrae). Spinal compression caused by contracting muscles tends to increase the convex spinal bend. Active flexor muscles further contribute to this bending. To counter spinal buckling opposing extension moments must be produced. In contrast, muscles active in extension tend to straighten the spine, while their contraction simultaneously causes spinal compression. Stability is therefore more inherent during extension. The effects of stabilizing the entire spine in axial rotation could relate to buckling in a similar fashion as the effects in flexion. With regard to modeling, this study shows that a moment balance over the entire spine must be considered when calculating muscle activation and cervical strength. Bending moments were in better agreement with experiments under full spinal equilibrium, supporting the hypothesis that the model estimates with balanced joint moments are more realistic.

With this study muscle synergies are derived that generate transversal head loads and these loads are accurately predicted. In a future study the model will be extended with reflexive feedback loops to investigate and predict stabilization in dynamic loading conditions.

5 Conclusions

The nonlinear musculoskeletal neck model provides passive properties, muscle moment arms, MVC strength, and muscle activation patterns in congruence with experimental results during maximal isometric contractions. When moments are balanced over all joints, spinal strength is reduced particularly in flexion and axial rotation compared to considering a joint equilibrium only at the lowest joint T1–C7. Model strength can therefore be severely overestimated in calculations that do not consider full spinal equilibrium. The method in this study is useful in deriving muscle synergies that produce transversal head loads for detailed neck models without a fixed joint center of rotation. The accurate biomechanics and muscle contributions of the model are of importance when simulating active human behavior and can help in understanding cervical muscle contributions during dynamic loading.