Skip to main content
SpringerLink
Log in

Nonminimal Kane's Equations of Motion for Multibody Dynamical Systems Subject to Nonlinear Nonholonomic Constraints

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

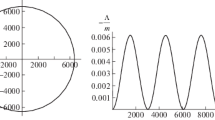
Abstract

Nonholonomic constraint equations that are nonlinear in velocities are incorporated with Kane's dynamical equations by utilizing the acceleration form of constraints, resulting in Kane's nonminimal equations of motion, i.e. the equations that involve the full set of generalized accelerations. Together with the kinematical differential equations, these equations form a state-space model that is full-order, separated in the derivatives of the states, and involves no Lagrange multipliers. The method is illustrated by using it to obtain nonminimal equations of motion for the classical Appell–Hamel problem when the constraints are modeled as nonlinear in the velocities. It is shown that this fictitious nonlinearity has a predominant effect on the numerical stability of the dynamical equations, and hence it is possible to use it for improving the accuracy of simulations. Another issue is the dynamics of constraint violations caused by integration errors due to enforcing a differentiated form of the constraint equations. To solve this problem, the acceleration form of the constraint equations is augmented with constraint stabilization terms before using it with the dynamical equations. The procedure is illustrated by stabilizing the constraint equations for a holonomically constrained particle in the gravitational field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Roberson, R.E. and Schwertassek, R., Dynamics of Multibody Systems, Springer-Verlag, Berlin, 1988.

    Google Scholar 

  2. Appell, P., ‘Exemple de mouvement d'un point assujetti à une liaison exprimée par une relation non linéaire entre les composantes de la vitesse’, Rend. Circular Mat. Palermo 32, 1911, 48–50.

    Google Scholar 

  3. Hamel, G., Theoretische Mechanik, Spring-Verlag, Berlin, 1949.

    Google Scholar 

  4. Neimark, J.I. and Fufaev, N.A., Dynamics of Nonholonomic Systems, American Mathematical Society, Providence, RI, 1972.

    Google Scholar 

  5. Saletan, E. and Cromer, A., ‘A variational principle for non-holonomic systems’, American Journal of Physics 38(7), 1970, 892–897.

    Article  Google Scholar 

  6. Xu, M., Liu, C. and Huston, R.L., ‘Analysis of nonlinearly constrained non-holonomic multibody systems’, International Journal of Non-Linear Mechanics 25(5), 1990, 511–519.

    Article  Google Scholar 

  7. Kitzka, F., ‘An example for the application of nonholonomic constraint of second order in particle mechanics’, Zeitschrift Fur Angewandte Mathematik und Mechanik 66, 1986, 312–314.

    Google Scholar 

  8. Fufaev, N.S., ‘About an example of a system with a non-holonomic constraint of a second order’, Zeitschrift Fur Angewandte Mathematik und Mechanik 70, 1990, 593–594.

    Google Scholar 

  9. Blajer, W., ‘Dynamics and control of mechanical systems in partly specified motion’, Journal of the Franklin Institute-Engineering and Applied Mechanics 334B(3), 1997, 407–426.

    Article  Google Scholar 

  10. Huston, R.L. and Passerello, C.E., ‘Nonholonomic systems with non-linear constraint equations’, International Journal of Nonlinear Mechanics 11, 1976, 331–336.

    Article  Google Scholar 

  11. Wang, J.T. and Huston, R.L., ‘Kane's equations with undetermined multipiers-application to constrained multibody systems’, ASME Journal of Applied Mechanics 54, 1987, 424–429.

    Google Scholar 

  12. Wang, J.T. and Huston, R.L., ‘Computational methods in constrained multibody dynamics: Matrix formalisms’, Computers and Structures 29, 1988, 331–338.

    Article  Google Scholar 

  13. Kane, T.R. and Levinson, D.A., ‘Multibody dynamics’, ASME Journal of Applied Mechanics 50, 1983, 1071–1078.

    Google Scholar 

  14. Anderson, K., Recursive Derivation of Explicit Equations of Motion for the Efficient Dynamic/Control Simulation of Large Multibody Systems, Ph.D. Thesis, {S}tanford {U}niversity, {D}epartment of {M}echanical {E}ngineering, {S}tanford, CA, 1990.

  15. Rosenthal, D., ‘An order n formulation for robotic systems’, Journal of Astronautical Sciences 38(4), 1990, 511–529.

    Google Scholar 

  16. Banerjee, A., ‘Block-diagonal equations for multibody elastodynamics with geometric stiffness and constraints’, Journal of Guidance, Control, and Dynamics 16(6), 1993, 1092–1100.

    Google Scholar 

  17. Blajer, W., ‘A geometric unification of constrained system dynamics’, Multibody System Dynamics 1, 1997, 3–21.

    Article  Google Scholar 

  18. Blajer, W., ‘A geometrical interpretation and uniform matrix formulation of multibody system dynamics’, Zeitschrift Für Angewandte Mathematik und Mechanik 81, 2001, 247–259.

    Article  Google Scholar 

  19. Anderson, K. and Critchley, J., ‘Improved ‘order-N’ performance algorithm for the simulation of constrained multi-rigid-body dynamic systems’, Multibody System Dynamics 9(2), 2003, 185–212.

    Article  Google Scholar 

  20. Bajodah, A.H., Hodges, D.H. and Chen, Y.H., ‘New form of K'ane's equations of motion for constrained systems’, Journal of Guidance, Control, and Dynamics 26(1), 2003, 79–88.

    Google Scholar 

  21. Wampler, C., Buffinton, K. and Shu-hui, J., ‘Formulation of equations of motion for systems subject to constraints’, Journal of Applied Mechanics 52, 1985, 465–470.

    Google Scholar 

  22. Huston, R.L., ‘Constraint forces and undetermined multipliers in constrained multibody systems’, Multibody System Dynamics 3, 1999, 381–389.

    Article  Google Scholar 

  23. Kane, T.R. and Levinson, D.A., Dynamics: Theory and Applications, 1st edn., McGraw-Hill Series in Mechanical Engineering, 1985.

  24. Baumgarte, J., ‘Stabilization of constraints and integrals of motion in dynamical systems’, Computer Methods in Applied Mechanics and Engineering 1, 1972, 1–16.

    Article  Google Scholar 

  25. Wehage, R.A. and Haug, E.J., ‘Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems’, Journal of Mechanical Design 104, 1982, 247–255.

    Google Scholar 

  26. Blajer, W., Schiehlen, W. and Schirm, W., ‘A projective criterion to the coordinate partitioning method for multibody dynamics’, Archive of Applied Mechanics 64, 1994, 86–98.

    Google Scholar 

  27. Lesser, M., ‘A geometrical interpretation of K'ane's equations’, Proceedings of the Royal Society of London. Series A, Mathematical Physical and Engineering Sciences 436, 1992, 69–87.

    Google Scholar 

  28. Chang, C.O. and E., N.P., ‘An adaptive constraint violation stabilization method for dynamic analysis of mechanical systems’, Journal of Mechanisms, Transmissions, and Automation in Design 107, December 1985, 488–492.

    Google Scholar 

  29. Blajer, W., ‘Elimination of constraint violation and accuracy aspects in numerical simulation of multibody systems’, Multibody Sysems Dynamics 7, 2002, 265–284.

    Article  Google Scholar 

  30. Yoon, S., Howe, R. and Greenwood, D., ‘Geometric elimination of constraint violations in numerical simulation of Lagrangean equations’, Journal of Mechanical Design 116, 1994, 1058–1064.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Aeronautical Engineering Department, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    Abdulrahman H. Bajodah

  2. School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, Georgia, 30332, U.S.A.

    Dewey H. Hodges

  3. School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia, 30332, U.S.A.

    Ye-Hwa Chen

Authors
  1. Abdulrahman H. Bajodah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dewey H. Hodges
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ye-Hwa Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bajodah, A.H., Hodges, D.H. & Chen, YH. Nonminimal Kane's Equations of Motion for Multibody Dynamical Systems Subject to Nonlinear Nonholonomic Constraints. Multibody Syst Dyn 14, 155–187 (2005). https://doi.org/10.1007/s11044-005-5968-z

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-005-5968-z

Keywords

Search

Navigation