1 Introduction

For the last few decades, fractional calculus (FC) has drawn increasing attention in various scientific disciplines involving attenuation and dispersion in complex viscoelastic media, nanoprecipitate growth in solids, heat transfer, diffusion and wave propagation, electrical spectroscopy impedance, chaos and fractals, biology, environmental science, signal and image processing, robotics, system identification, traffic systems, genetic algorithms, percolation, modeling and identification, telecommunications, chemistry, physics, control systems, as well as economy and finance (Hilfer 2000; Gutierrez et al. 2010). Any researcher citing review/survey papers on the applications of FC has the risk of forgetting some because the list is long, as proved by the increasing number of articles, congresses, and treaties involving FC. Many experimental and laboratory results have shown that new fractional-order models are more adequate than previously used integer-order models (Sun et al. 2018; Machado et al. 2011).

Previous FC models have historical challenges in capturing real-world description of properties of various real materials, in particular the description of memory and hereditary properties of various materials and processes. The advantages of using FC have produced a successful revolution to modify many existing models of physical processes, e.g., the description of rheological properties of rocks, as well as mechanical modeling of engineering materials such as polymers over extended ranges of time and frequency (Caputo and Mainardi 1971; Mainardi 2022). Fractional-order models often work well, particularly in heat transfer and electrochemistry, for example, the half-order fractional integral is the natural integral operator connecting the applied gradients (thermal or material) with the diffusion of ions of heat (Gorenflo et al. 2007), which motivated researchers to introduce more mathematical models in both thermo-elasticity and hereditary thermo-elasticity (thermo-viscoelasticity) theory.

In the theory of thermo-elasticity, a quasistatic uncoupled theory based on the fractional heat conduction equation with the Caputo time-fractional derivative was put forward by Povstenko (2004, 2010). Sherief et al. (2010) introduced a new model of thermoelasticity using fractional calculus, proved a uniqueness theorem, and derived a reciprocity relation together with a variational principle. During the last years, a new trend of using FC in thermo-elastic applications has been observed. Ezzat and Fayik (2011) constructed a model in generalized thermos-elastic diffusion by using fractional time-derivatives. Ezzat et al. (2012b) introduced a new model of fractional thermo-elasticity associated with three-phase lag. During the last years, a trend has been observed in thermo-elasticity application research employing tools from FC (Yu et al. 2014; Sur and Kanoria 2014; Hamza et al. 2015; Ezzat et al. 2012a; Povstenko 2015; Abouelregal and Zenkour 2013; Awad 2012, 2019). On the other hand, linear viscoelasticity is certainly the field of the most extensive applications of fractional calculus since the appearance of FC in 1974. Caputo (1969) and Mainardi (1997) employed the tools of FC to describe the behavior of viscoelastic materials. Their model was successful in producing results in accordance with physical observations. Adolfsson et al. (2005) constructed a newer fractional-order model of viscoelasticity. In the framework of the thermo-viscoelasticity, Sherief et al. (2011) derived a new mathematical model of thermo-viscoelasticity associated with one relaxation time in integer-order derivatives’ domain, proved a uniqueness theorem, as well as a reciprocity relation. Ezzat et al. (2013) derived a new model of thermo-viscoelasticity associated with singular Caputo relaxation kernel using the methodology of FC. The previous models in thermo-viscoelasticity are widely used by many authors in their applications (Ezzat et al. 2015; Zenkour and Abouelregal 2015; Ezzat and El-Bary 2014, 2016; Awad et al. 2022). Elhagary (2010) solved a two-dimensional problem for the generalized thermoelasticity theory with one relaxation time in the absence of the internal heat source. The authors of (Sherief et al. 2022) established a new theory of generalized fractional hereditary thermo-elasticity associated with Mittag-Leffler relaxation function and solved a two-dimensional thick plate problem under axisymmetric boundary conditions.

The main objective of our work is to construct a new generalized fractional thermo-viscoelasticity theory associated with a nonsingular relaxation kernel “Mittag-Leffler relaxation function”. Atangana and Baleanu (2016) wrote: “The non-singular kernel in integral operator will be helpful to discuss real world problems and it also will have a great advantage when using the Laplace transform to solve some physical problems with initial conditions and good for describing the dynamics of systems with memory effect for small and large times”. The main advantage of using this model is that it predicts finite speeds (Sherief et al. 2022) of propagation for thermal and mechanical waves while the thermal wave speed in all previous fractional models in both fields of thermo-elasticity and thermo-viscoelasticity (Ezzat et al. 2013, 2015; Ezzat and El-Bary 2016) is infinite, contrary to physical observations. In order to illustrate the obtained results, the authors have solved a 2D thermo-viscoelastic problem. With help of a Laplace–Fourier transform, the governing equations of our new model are solved analytically. After acquiring the solution in the transformed domain, the inversion of the Laplace–Fourier transform is computed numerically using a method based on Fourier expansion technique (Honig and Hirdes 1984; Foutsitzi et al. 1997; Fayik et al. 2023) such that we have chosen PMMA as viscoelastic material and copper as the elastic material. Finally, according to the numerical results and their graphs, conclusion about the new model of thermo-viscoelasticity has been provided, which provides a good motivation to investigate thermo-viscoelastic materials as a new class of applicable materials.

2 Derivation of the mathematical model for generalized fractional thermo-viscoelasticity

We consider a continuous viscoelastic medium contained within a volume \(V\) and bounded by a closed surface \(S\) (cf. Sherief et al. 2022). Let the position vector of a point be denoted by \(\boldsymbol{x} ( x_{1}, x_{2,} x_{3} )\). It is subject to a body force \(F_{i}\) per unit mass and a heat source of strength \(Q\) per unit mass. Let \(e_{ij}\) be the strain tensor components defined at every point \(\boldsymbol{x}\) of the body and given by

$$ e_{ij} = \frac{1}{2} \left ( u_{i,j} + u_{j,i} \right ), $$
(1)

where \(u_{i},i=1,2,3\) are the components of the displacement vector. A comma indicates a material derivative.

Now, we define a linear thermo-viscoelastic material to be one for which the stress tensor components \(\sigma _{ij} ( \boldsymbol{x},t)\) are related to \(e_{ij} ( \boldsymbol{x},t)\) by a convolution integral as follows:

$$ \sigma _{ij} \left ( \boldsymbol{x},t \right ) = \int _{0}^{t} \mathcal{R}_{ijkl} (t-\nu ) \frac{\partial e_{kl} \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu - \alpha _{T} \int _{0}^{t} \gamma _{ij} \left ( t-\nu \right ) \frac{\partial \theta \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu , $$
(2)

where \(\mathcal{R}_{ijkl}\) and \(\gamma _{ij}\) are fourth- and second-order tensorial relaxation functions of the material, respectively. In addition, it is assumed that the following symmetry relations hold: \(\left ( \mathcal{R}_{ijkl} = \mathcal{R}_{klij} = \mathcal{R}_{ikjl} = \mathcal{R}_{jlik},\ \gamma _{ij} = \gamma _{ji} \right )\), \(\theta =T- \vartheta _{0},\ T\) is the absolute temperature, \(\vartheta _{0}\) is a reference temperature such that \(\left \vert \frac{T- \vartheta _{0}}{\vartheta _{0}} \right \vert \ll 1\), and \(\alpha _{T}\) is the coefficient of linear thermal expansion.

Substituting from Eq. (2) into the equation of motion which has the form

$$ \sigma _{ji,j} +\rho F_{i} =\rho \ddot{u}_{i}, $$
(3)

where \(\rho \) is the density, we obtain

$$ \rho \ddot{u}_{i} =\rho F_{i} + \int _{0}^{t} \mathcal{R}_{ijkl} \left ( t-\nu \right ) \frac{\partial e_{kl,j} \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu - \alpha _{T} \int _{0}^{t} \gamma _{ij} \left ( t-\nu \right ) \frac{\partial \theta _{,j} \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu . $$
(4)

The dot denotes differentiation with respect to time.

For an isotropic body, the tensorial relaxation functions can be written as follows (Fung 1965):

$$\begin{aligned} & \mathcal{R}_{ijkl} = \mathcal{R}_{1} \delta _{ij} \delta _{kl} + \mathcal{R}_{2} \left ( \delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk} \right ), \end{aligned}$$
(5)
$$\begin{aligned} & \gamma _{ij} = \left ( 3 \mathcal{R}_{1} +2 \mathcal{R}_{2} \right ) \delta _{ij}, k_{ij} =k \delta _{ij}, \end{aligned}$$
(6)

where \(\mathcal{R}_{i} \left ( t;\beta \right )\), \((i=1, 2 )\) are assumed to be a causal relaxation functions of time.

For the present purposes, we take these relaxation functions as a variation of the Mittag-Leffler relaxation function which arises in the description of complex relaxation processes. There has been much recent interest in the Mittag-Leffler and related functions in connection with the description of relaxation phenomena in complex physical and biophysical systems (Weron and Kotulski 1996; Hilfer and Anton 1995).

The relaxation functions \(\mathcal{R}_{i} \left ( t;\beta \right )\), \((i=1, 2 )\) are taken of the form:

$$ \mathcal{R}_{i} \left ( t;\beta \right ) = R_{i} \tau ^{\beta} E_{\beta} \left ( -\beta \frac{t^{\beta}}{1-\beta} \right ), t>0, $$
(7)

where \(R_{1}\), \(R_{2}\) are the viscoelastic material constants, \(\tau \) is a positive constant for the ratio of the shear viscosity to Young’s modulus, and \(\beta \) is an arbitrary parameter which represents the order of the time derivative, \(\beta \in \left ( 0,1 \right )\).

Equations (5) and (6) can be written as follows:

$$\begin{gathered} \mathcal{R}_{ijkl} \left ( t;\beta \right ) = \left [ R_{1} \delta _{ij} \delta _{kl} + R_{2} \left ( \delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk} \right ) \right ] \tau ^{\beta} E_{\beta} \left ( -\beta \frac{t^{\beta}}{1-\beta} \right ), \end{gathered}$$
(8)
$$\begin{gathered} \gamma _{ij} \left ( t;\beta \right ) =R \delta _{ij} \tau ^{\beta} E_{\beta} \left ( -\beta \frac{t^{\beta}}{1-\beta} \right ), \end{gathered}$$
(9)

where \(R= \left ( 3 R_{1} +2 R_{2} \right )\).

By substituting from Eqs. (8) and (9) into Eq. (2), we obtain

$$ \begin{aligned} \sigma _{ij} \left ( \boldsymbol{x},t \right ) ={}&2 R_{2} \tau ^{\beta} \int _{0}^{t} E_{\beta} \left ( -\beta \frac{\left ( t- \nu \right )^{\beta}}{1-\beta} \right ) \frac{\partial e_{ij} \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu \\ &{}+ \tau ^{\beta} \delta _{ij} \left [ R_{1} \int _{0}^{t} E_{\beta} \left ( -\beta \frac{\left ( t- \nu \right )^{\beta}}{1-\beta} \right ) \frac{\partial e \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu\right. \\ &\left.{}- \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{T} \int _{0}^{t} E_{\beta} \left ( -\beta \frac{\left ( t- \nu \right )^{\beta}}{1-\beta} \right ) \frac{\partial \theta \left ( \boldsymbol{x}, \nu \right )}{\partial \nu} d\nu \right ]. \end{aligned} $$
(10)

The integral terms on the right-hand side of Eq. (10) represent a new fractional derivative with nonlocal and nonsingular kernel which was suggested by Atangana and Baleanu (2016).

After some manipulations, we can rewrite Eq. (10) in the form

$$ \sigma _{ij} = \hat{\boldsymbol{R}}_{\beta} \left ( 2 R_{2} e_{ij} + \delta _{ij} \left [ R_{1} e - \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{T} \theta \right ] \right ), $$
(11)

where \(e\) is the cubical dilatation given by \(e = e_{kk}\), and the operator \(\hat{\boldsymbol{R}}_{\beta} \left ( \boldsymbol{\cdot} \right )\) is defined for any function \(g ( \boldsymbol{x}, t )\) of class \(C_{1}\) as

$$ \hat{\boldsymbol{R}}_{\beta} \left [ g ( \boldsymbol{x}, t ) \right ] = \tau ^{\beta} \int _{0}^{t} E_{\beta} \left ( - \beta \frac{( t - v )^{\beta}}{1- \beta} \right ) \frac{\partial g ( \boldsymbol{x}, v )}{\partial v} dv. $$
(12)

Hence, the equation of motion (3) can be written as follows:

$$ \rho \hat{u}_{i} = \hat{\boldsymbol{R}}_{\beta} \left ( 2 R_{2} e_{ij, j} + R_{1} e_{, i} - \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{T} \theta _{, i} \right ) + \rho F_{i}. $$
(13)

To derive the equation of heat conduction, we start by assuming that for a thermally conducting viscoelastic solid subjected to small strain and small temperature changes, we have (Foutsitzi et al. 1997)

$$ \rho \vartheta _{0} \eta = \rho c_{E} \theta + \alpha _{T} \vartheta _{0} \int _{0}^{t} \gamma _{ij} \left ( t - v \right ) \frac{\partial e_{ij} \left ( \boldsymbol{x}, v \right )}{\partial v} dv, $$
(14)

where \(\eta \) is the entropy per unit mass and \(\vartheta _{0}\) is a reference temperature for which the medium is in equilibrium free of strain. By the same manner, Eq. (14) can be written in the form

$$ \begin{aligned} \rho \vartheta _{0} \eta &= \rho c_{E} \theta + \left ( 3 R_{1} +2 R_{2} \right ) \tau ^{\beta} \alpha _{T} \vartheta _{0} \delta _{ij} \int _{0}^{t} E_{\beta} \left ( - \beta \frac{( t - v )^{\beta}}{1- \beta} \right ) \frac{\partial e_{ij} \left ( \boldsymbol{x}, v \right )}{\partial v} dv\\ &= \rho c_{E} \theta + \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{T} \vartheta _{0} \hat{\boldsymbol{R}}_{\beta} \left ( e \right ). \end{aligned} $$
(15)

We shall use the linearized entropy balance equation, namely

$$ \rho \vartheta _{0} \dot{\eta} =- q_{i, i} + \rho Q, $$
(16)

where \(q_{j}\) is the heat flux vector and \(Q\) is the internal heat source per unit mass. Using Eq. (15), the previous Eq. (16) reduces to

$$ q_{i, i} =- \frac{\partial}{\partial t} \left ( \rho c_{E} \theta + \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{t} \vartheta _{0} \hat{\boldsymbol{R}}_{\beta} \left ( e \right ) \right ) + \rho Q. $$
(17)

The non-Fourier formula of heat conduction is given by

$$ \left ( 1+ \tau _{0} \frac{\partial}{\partial t} \right ) q_{i} =- k_{ij} \theta _{, j}, $$
(18)

where \(\tau _{0} \ll 1\) is the thermal relaxation time and \(k_{ij}\) is a thermal conductivity tensor. Now, taking divergence of both sides of Eq. (18) and using Eq. (17), we arrive at

$$ \left ( k_{ij} \theta _{, j} \right )_{, i} = \left ( 1+ \tau _{0} \frac{\partial}{\partial t} \right ) \left ( \frac{\partial}{\partial t} \left [ \rho c_{E} \theta + \left ( 3 R_{1} +2 R_{2} \right ) \alpha _{T} \vartheta _{0} \hat{\boldsymbol{R}}_{\beta} \left ( e \right ) \right ] -\rho Q \right ). $$
(19)

Here, all consider functions depend on (\(\boldsymbol{x}\), \(t \)). The summation notation is used and we ignore the microrotations.

3 Application of the constitutive model

3.1 Formulation of the problem

The structure of our problem (trilayered thermo-elastic materials) has been widely used in many applications like Micro-Electro-Mechanical System (MEMS) (Battal and Okyay 2013; Kim et al. 2011; Zuo et al. 2019). In smart structure design, when thermo-elasticity is assumed, it is important to understand the influence of an internal variable heat sources on manufacturing processes (Abouelregal et al. 2023).

The region under consideration in rectangular Cartesian coordinates (\(x\), \(y\), \(z\)) consists of three thick layers with finite thickness and infinite extent placed in perfect contact one on top of another. They occupy the region \(L_{1} \cup L_{2} \cup L_{3}\), where

$$ L_{1} = \left \{ \left ( x, y \right ):-\infty < x < \infty , h_{1} \leq y \leq h_{2} \right \}, $$
$$ L_{2} = \left \{ ( x, y ):-\infty < x < \infty ,- h_{1} \leq y \leq h_{1} \right \}, $$
$$ L_{3} = \left \{ ( x, y ):-\infty < x < \infty ,- h_{2} \leq y \leq - h_{1} \right \}. $$

The \(y\)-axis is perpendicular to the surfaces of the layers while the \(x\)-axis is parallel to them (see Fig. 1). The material constants can be taken as (\(R_{1} =\lambda \), \(R_{2} =\mu \)) such that \(\lambda \), \(\mu \) are Lame’s constants.

Fig. 1
figure 1

Schematic for the physical problem

Full size image

We shall consider two cases. In case (I), the middle layer \(L_{2}\) is made of a homogenous isotropic thermo-viscoelastic material acting as a heat source of intensity \(Q(x,y,t)\) per unit mass. The other two layers are composed of the same thermo-elastic material. On the other hand, in case (II), the middle layer \(L_{2}\) is the thermo-elastic one with the heat source while the other two layers are thermo-viscoelastic. We assume that the initial state of the medium is quiescent. The outer surfaces of layers \(L_{1}\) and \(L_{3}\) are rigidly fixed and thermally isolated. In what follows, we shall denote functions in layer \(L_{m}\) by the subscript \(m\), \(m =1,2,3\).

From the physics of the problem, all functions will depend on \(x\), \(y\), \(t\), and will be independent of \(z\). In layer \(L_{m}\), the displacement vectors thus have components

$$ \mathbf{u}_{m} = \left ( u_{m}, v_{m},0 \right ),m=1,2,3. $$
(20)

The cubical dilatations \(e_{m}\) are given by

$$ e_{m} = \operatorname{div} \left ( \mathbf{u}_{m} \right ) = \frac{\partial u_{m}}{\partial x} + \frac{\partial v_{m}}{\partial y}, m=1,2,3. $$
(21)

The equations of motion in vector form in the absence of body forces are

$$ \rho _{m} \frac{\partial ^{2} \mathbf{u}_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} + \mu _{m} \right ) \operatorname{grad} e_{m} + \mu _{m} \nabla ^{2} \mathbf{u}_{m} - \gamma _{m} \operatorname{grad} \theta _{m} \right ), m=1,2,3, $$
(22)

where \(\nabla ^{2} = \frac{\partial ^{2}}{\partial x^{2}} + \frac{\partial ^{2}}{\partial y^{2}}\) is Laplace operator in Cartesian coordinates and \(\left ( \lambda _{m},\ \mu _{m} \right )\) are Lame’s constants, \(\rho _{m}\) is the density, \(t\) is the time variable, \(\theta _{m} = T_{m} - \vartheta _{0}\), \(T_{m}\) is the absolute temperature of the \(m\)th medium, \(\gamma _{m} = \left ( 3 \lambda _{m} +2 \mu _{m} \right ) \alpha _{m}\), \(\alpha _{m}\) being the coefficients of linear thermal expansion.

The operator \(\hat{\boldsymbol{R}}_{\beta _{m}} \left [ g \left ( \boldsymbol{x},t \right ) \right ]\) is defined for any function of class \(C_{1}\) by

$$ \hat{\boldsymbol{R}}_{\beta _{m}} \left [ g \left ( \boldsymbol{x},t \right ) \right ] = \tau ^{\beta _{m}} \int _{0}^{t} E_{\beta _{m}} \left ( - \beta _{m} \frac{(t-v )^{\beta _{m}}}{1- \beta _{m}} \right ) \frac{\partial g \left ( \boldsymbol{x},v \right )}{\partial v} dv, {} \beta _{m} \in \left [ 0,1 \right ]. $$

We note that for the case of a thermo-viscoelastic material with no viscosity \(\left ( \beta _{m} = 0 \right )\), we have \(\hat{\boldsymbol{R}}_{\boldsymbol{\beta}_{m}} [ g ( \boldsymbol{x}, t )]= g ( \boldsymbol{x}, t )\).

Equation (22) can be written in Cartesian form

$$\begin{aligned} & \rho _{m} \frac{\partial ^{2} u_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} + \mu _{m} \right ) \frac{\partial e_{m}}{\partial x} + \mu _{m} \left ( \frac{\partial ^{2} u_{m}}{\partial x^{2}} + \frac{\partial ^{2} u_{m}}{\partial y^{2}} \right ) - \gamma _{m} \frac{\partial \theta _{m}}{\partial x} \right ),m=1,2,3, \end{aligned}$$
(23)
$$\begin{aligned} & \rho _{m} \frac{\partial ^{2} v_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} + \mu _{m} \right ) \frac{\partial e_{m}}{\partial y} + \mu _{m} \left ( \frac{\partial ^{2} v_{m}}{\partial x^{2}} + \frac{\partial ^{2} v_{m}}{\partial y^{2}} \right ) - \gamma _{m} \frac{\partial \theta _{m}}{\partial y} \right ), m=1,2,3. \end{aligned}$$
(24)

The generalized fractional equation of heat conduction has the form

$$ \begin{aligned} k_{m} \nabla ^{2} \theta _{m} ={}& \rho _{m} c_{Em} \left ( \frac{\partial}{\partial t} + \tau _{0 m} \frac{\partial ^{2}}{\partial t^{2}} \right ) \left ( \theta _{m} + \gamma _{m} \vartheta _{0} \hat{\boldsymbol{R}}_{\beta _{m}} e_{m} \right )\\ &{} - \left ( 1+ \tau _{0 m} \frac{\partial}{\partial t} \right ) Q, m=1,2,3. \end{aligned} $$
(25)

where \(k_{m}\) is the thermal conductivity of the \(m\)th layer, \(\tau _{0 m}\) are constants with the dimensions of time, \(\tau _{0 m}\) are relaxation times, \(c_{Em}\) is the specific heat at constant strain. Distributed variable heat sources are essential to many fields. These heat sources contribute to accurate temperature control and improve process quality and efficiency in manufacturing for metals and energy generation (Yang et al. 2023; Kiran et al. 2022).

The heat source is defined as

$$ Q ( x, y, t )= Q_{0} H ( t ) H \left ( h_{1} -\mid y \mid \right ) e^{-2 \pi \mid x \mid},-\infty < x < \infty , t \geq 0. $$
(26)

The selected heat source variable above is chosen to indicate symmetry with respect to the \(x\) and \(y\) axes. This particular form of applied heat source will lead to all function fields being dependent on the variables (\(x\), \(y\), \(t\)), hence modeling the problem into a two-dimensional (2D) problem.

Applying the \(\operatorname{div}\) operator to both sides of Eqs. (22), we obtain

$$ \rho _{m} \frac{\partial ^{2} e_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} +2 \mu _{m} \right ) \nabla ^{2} e_{m} - \gamma _{m} \nabla ^{2} \theta _{m} \right ),m=1,2,3. $$
(27)

These equations are supplemented by the constitutive equations

$$\begin{gathered} \sigma _{mxx} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} +2 \mu _{m} \right ) e_{m} -2 \mu _{m} \frac{\partial v_{m}}{\partial y} - \gamma _{m} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(28)
$$\begin{gathered} \sigma _{myy} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \left ( \lambda _{m} +2 \mu _{m} \right ) e_{m} -2 \mu _{m} \frac{\partial u_{m}}{\partial x} - \gamma _{m} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(29)
$$\begin{gathered} \sigma _{mzz} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \lambda _{m} e_{m} - \gamma _{m} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(30)
$$\begin{gathered} \sigma _{mxy} = \mu _{m} \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \frac{\partial u_{m}}{\partial y} + \frac{\partial v_{m}}{\partial x} \right ),m=1,2,3, \end{gathered}$$
(31)
$$\begin{gathered} \sigma _{mxz} = \sigma _{myz} =0, m=1,2,3, \end{gathered}$$
(32)

and by the generalized Fourier’s law (MCV) of heat conduction, namely

$$ \mathbf{q}_{m} + \tau _{0 m} \hat{\mathbf{q}}_{m} =- k_{m} \operatorname{grad} \theta _{m}, m=1,2,3, $$
(33)

where \(\mathbf{q}_{m}\) is the heat flux vector for layer \(L_{m}\).

The preceding governing equations can be put in nondimensional forms using the following dimensionless parameters (Elhagary 2010):

$$ \left ( x', y', u_{m}', v_{m}' \right ) = c_{2} \eta _{2} \left ( x, y, u_{m}, v_{m} \right ), $$
$$ \left ( t', \tau _{0 m}' \right ) = c_{2}^{2} \eta _{2} \left ( t, \tau _{0 m} \right ), $$
$$ \theta _{m}' = \frac{\gamma _{2} \left ( \theta _{m} - \vartheta _{0} \right )}{\left ( \lambda _{2} +2 \mu _{2} \right )}, \mathbf{q}_{m}' = \frac{\gamma _{2} \mathbf{q}_{m}}{k_{2} c_{2} \eta _{2} \left ( \lambda _{2} +2 \mu _{2} \right )}, \sigma _{mij}' = \frac{\sigma _{mij}}{\mu _{2}}, m =1,2,3, $$

where \(\eta _{m} = \frac{\rho _{m} c_{Em}}{k_{m}}\), and \(c_{m} = \sqrt{\frac{\left ( \lambda _{m} +2 \mu _{m} \right )}{\rho _{m}}}\) is the speed of propagation of isothermal elastic waves in the \(m \mathrm{th}\) layer. So, the governing Eqs. (23)–(33) in nondimensional form are simplified as (dropping the primes for convenience)

$$\begin{gathered} \xi _{m} \frac{\partial ^{2} u_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \psi _{m} \frac{\partial e_{m}}{\partial x} + \nabla ^{2} u_{m} - \delta _{m} \frac{\partial \theta _{m}}{\partial x} \right ),m=1,2,3, \end{gathered}$$
(34)
$$\begin{gathered} \xi _{m} \frac{\partial ^{2} v_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \psi _{m} \frac{\partial e_{m}}{\partial y} + \nabla ^{2} v_{m} - \delta _{m} \frac{\partial \theta _{m}}{\partial y} \right ),m=1,2,3, \end{gathered}$$
(35)
$$\begin{gathered} \nabla ^{2} \theta _{m} = \left ( \frac{\partial}{\partial t} + \tau _{0m} \frac{\partial ^{2}}{\partial t^{2}} \right ) \left ( \zeta _{m} \theta _{m} + \varepsilon _{m} \hat{\boldsymbol{R}}_{\beta _{m}} e_{m} \right ) - \left ( 1+ \tau _{0m} \frac{\partial}{\partial t} \right ) Q, m=1,2,3, \end{gathered}$$
(36)
$$\begin{gathered} \chi _{m} \frac{\partial ^{2} e_{m}}{\partial t^{2}} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \nabla ^{2} e_{m} - \phi _{m} \nabla ^{2} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(37)
$$\begin{gathered} \sigma _{mxx} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \Omega _{m1} e_{m} -2 \Omega _{m2} \frac{\partial v_{m}}{\partial y} - \Omega _{m3} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(38)
$$\begin{gathered} \sigma _{myy} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \Omega _{m1} e_{m} -2 \Omega _{m2} \frac{\partial u_{m}}{\partial x} - \Omega _{m3} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(39)
$$\begin{gathered} \sigma _{mzz} = \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \Omega _{m4} e_{m} - \Omega _{m3} \theta _{m} \right ),m=1,2,3, \end{gathered}$$
(40)
$$\begin{gathered} \sigma _{mxy} = \Omega _{m2} \hat{\boldsymbol{R}}_{\beta _{m}} \left ( \frac{\partial u_{m}}{\partial y} + \frac{\partial v_{m}}{\partial x} \right ),m=1,2,3, \end{gathered}$$
(41)
$$\begin{gathered} \mathbf{q}_{m} + \tau _{0m} \hat{\mathbf{q}}_{m} =- \Omega _{m5} \operatorname{grad} \left ( \theta _{m} \right ), m=1,2,3, \end{gathered}$$
(42)

where

$$\begin{gathered} \xi _{m} = \frac{\rho _{m} \left ( \lambda _{2} +2 \mu _{2} \right )}{\rho _{2} \mu _{m}}, \psi _{m} = \frac{\lambda _{m} + \mu _{m}}{\mu _{m}}, \delta _{m} = \frac{\gamma _{m}}{\gamma _{2}} \frac{\left ( \lambda _{2} +2 \mu _{2} \right )}{\mu _{m}}, \phi _{n} = \frac{\gamma _{m}}{\gamma _{2}} \frac{\left ( \lambda _{2} +2 \mu _{2} \right )}{\left ( \lambda _{m} +2 \mu _{m} \right )},\\ \zeta _{m} = \frac{\eta _{m}}{\eta _{2}}, \varepsilon _{m} = \frac{\gamma _{m} \gamma _{2} \vartheta _{0}}{\left ( \lambda _{2} +2 \mu _{2} \right ) k_{m} \eta _{2}}, \chi _{m} = \frac{c_{2}^{2}}{c_{m}^{2}}, \Omega _{m 1} = \frac{\lambda _{m} +2 \mu _{n}}{\mu _{2}}, \Omega _{m 2} = \frac{\mu _{m}}{\mu _{2}},\\ \Omega _{m 3} = \frac{\gamma _{m}}{\gamma _{2}} \frac{\left ( \lambda _{2} +2 \mu _{2} \right )}{\mu _{2}}, \Omega _{m 4} = \frac{\lambda _{m}}{\mu _{2}}, \Omega _{m 5} = \frac{k_{m}}{k_{2}}, m=1,2,3. \end{gathered}$$

Equation (42) can be written in Cartesian form as

$$\begin{aligned} & \left ( 1+ \tau _{0 m} \frac{\partial}{\partial t} \right ) q_{mx} =- \Omega _{m 5} \frac{\partial \theta _{m}}{\partial x}, m=1,2,3, \end{aligned}$$
(43)
$$\begin{aligned} & \left ( 1+ \tau _{0 m} \frac{\partial}{\partial t} \right ) q_{my} =- \Omega _{m 5} \frac{\partial \theta _{m}}{\partial y}, m=1,2,3. \end{aligned}$$
(44)

The previous equations are solved subject to the following boundary conditions: (i) Mechanical boundary conditions that the outer surfaces of layers \(L_{1}\) and \(L_{3}\) are rigidly fixed:

$$ \left . u_{m} \right \vert _{\left ( x,\pm h_{2}, t \right )} = \left . v_{m} \right \vert _{\left ( x,\pm h_{2}, t \right )} =0, {} m =1,3. $$
(45)

(ii) Thermal boundary conditions that the outer surfaces of layers \(L_{1}\) and \(L_{3}\) are thermally isolated:

$$ \left . \frac{\partial \theta _{m}}{\partial y} \right \vert _{\left ( x,\pm h_{2}, t \right )} =0, {} m =1,3. $$
(46)

The continuity conditions at the interfaces between the two media require that at \(y= h_{1}\), the following matching must hold:

$$ \left . \left ( \theta _{2}, u_{2}, v_{2}, q_{2 y}, \sigma _{2 yy}, \sigma _{2 xy} \right ) \right \vert _{\left ( x, h_{1}, t \right )} = \left . \left ( \theta _{1}, u_{1}, v_{1}, q_{1 y}, \sigma _{1 yy}, \sigma _{1 yy} \right ) \right \vert _{\left ( x, h_{1} t \right )}, $$
(47)

while at \(y =- h_{1}\)

$$ \left . \left ( \theta _{2}, u_{2}, v_{2}, q_{2 y}, \sigma _{2 yy}, \sigma _{2 xy} \right ) \right \vert _{\left ( x,- h_{1} t \right )} = \left . \left ( \theta _{3}, u_{3}, v_{3}, q_{3 y}, \sigma _{3 yy}, \sigma _{3 xy} \right ) \right \vert _{\left ( x,- h_{1}, t \right )}. $$
(48)

3.2 Solution in the transformed domain

We shall now define the Laplace transform with respect to a function \(f ( x, y, t )\) by the relation

$$ L [ f ( x, y, t )]= \hat{f} ( x, y, s )= \int _{0}^{\infty} \exp (- st)f ( x, y, t ) dt. $$
(49)

According to the homogenous initial conditions, applying the Laplace transform to both sides of Eqs. (34)–(44), we obtain the following set of equations:

$$\begin{gathered} \left ( \nabla ^{2} - \frac{\xi _{m} s^{2}}{\omega _{m}} \right ) \hat{u}_{m} = \frac{\partial}{\partial x} \left ( \delta _{m} \hat{\theta}_{m} - \psi _{m} \hat{e}_{m} \right ),m=1,2,3, \end{gathered}$$
(50)
$$\begin{gathered} \left ( \nabla ^{2} - \frac{\xi _{m} s^{2}}{\omega _{m}} \right ) \hat{\nu}_{m} = \frac{\partial}{\partial y} \left ( \delta _{m} \hat{\theta}_{m} - \psi _{m} \hat{e}_{m} \right ),m=1,2,3, \end{gathered}$$
(51)
$$\begin{gathered} \left ( \nabla ^{2} -s \zeta _{m} \left ( 1+ \tau _{0m} s \right ) \right ) \hat{\theta}_{m} = \varepsilon _{m} \varpi _{m} \left ( s+ \tau _{0m} s^{2} \right ) \hat{e}_{m} - \left ( 1+ \tau _{0m} s \right ) \hat{Q}, m=1,2,3, \end{gathered}$$
(52)
$$\begin{gathered} \left ( \nabla ^{2} - \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) \hat{e}_{m} = \phi _{m} \nabla ^{2} \hat{\theta}_{m}, m=1,2,3, \end{gathered}$$
(53)
$$\begin{gathered} \overline{\sigma}_{mxx} = \varpi _{m} \left ( \Omega _{m1} \hat{e}_{m} -2 \Omega _{m2} \frac{\partial \hat{\nu}_{m}}{\partial y} - \Omega _{m3} \hat{\theta}_{m} \right ),m=1,2,3, \end{gathered}$$
(54)
$$\begin{gathered} \overline{\sigma}_{myy} = \varpi _{m} \left ( \Omega _{m1} \hat{e}_{m} -2 \Omega _{m2} \frac{\partial \hat{u}_{m}}{\partial x} - \Omega _{m3} \hat{\theta}_{m} \right ),m=1,2,3, \end{gathered}$$
(55)
$$\begin{gathered} \hat{\sigma}_{mcz} = \varpi _{m} \left ( \Omega _{m4} \hat{e}_{m} - \Omega _{m3} \hat{\theta}_{m} \right ),m=1,2,3, \end{gathered}$$
(56)
$$\begin{gathered} \overline{\sigma}_{mxy} = \Omega _{m2} \varpi _{m} \left ( \frac{\partial \hat{u}_{m}}{\partial y} + \frac{\partial \hat{\nu}_{m}}{\partial x} \right ),m=1,2,3, \end{gathered}$$
(57)
$$\begin{gathered} \left ( 1+ \tau _{0m} s \right ) \overline{q}_{mx} =- \Omega _{m5} \frac{\partial \overline{\theta}_{m}}{\partial x}, m=1,2,3, \end{gathered}$$
(58)
$$\begin{gathered} \left ( 1+ \tau _{0m} s \right ) \overline{q}_{my} =- \Omega _{m5} \frac{\partial \overline{\theta}_{m}}{\partial y}, m=1,2,3, \end{gathered}$$
(59)

where \(\varpi _{m} ( s )= \frac{\left ( \tau _{m} s \right )^{\beta _{m}}}{\left ( s^{\beta _{m}} + \frac{\beta _{m}}{1- \beta _{m}} \right )}\).

The Laplace transform of the cubical dilatation (21) becomes

$$ \hat{e}_{m} = \frac{\partial \hat{u}_{m}}{\partial x} + \frac{\partial \hat{v}_{m}}{\partial y}, m=1,2,3. $$
(60)

Eliminating \(\hat{\theta}_{m}\) from (52) and (53), we obtain

$$ \begin{aligned} &\left ( \nabla ^{4} - \nabla ^{2} \left [ \left ( \zeta _{m} + \varepsilon _{m} \varpi _{m} \phi _{m} \right ) \left ( s + \tau _{0 m} s^{2} \right ) + \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ] \right.\\ &\left.\quad {}+ \frac{s^{3} \zeta _{m} \chi _{m} \left ( 1+ \tau _{0 m} s \right )}{\varpi _{m}} \right ) \hat{e}_{m} =- \left ( 1+ \tau _{0 m} s \right ) \nabla ^{2} Q. \end{aligned} $$
(61)

We use the Fourier exponential transform defined by the relation

$$ \hat{\hat{f}} \left ( q, y, s \right ) = \frac{1}{\sqrt{2 \pi}} \int _{-\infty}^{\infty} e^{- ixx} \hat{f} \left ( x, y, s \right ) dx, $$
(62)

with its corresponding inversion formula

$$ \hat{f} ( x, y, s )= \frac{1}{\sqrt{2 \pi}} \int _{-\infty}^{\infty} e^{iqx} \hat{\hat{f}} ( q, y, s ) dq, \ \text{where } i = \sqrt{-1}. $$
(63)

We assume that all the relevant functions (such as temperature and stress) are sufficiently smooth on the real line such that the Fourier transforms of these functions exist.

Applying the Fourier exponential transform to both sides of Eq. (61), we obtain

$$ \left ( D^{2} - h_{m 1}^{2} \right ) \left ( D^{2} - h_{m 2}^{2} \right ) \hat{\hat{e}}_{m} = \frac{Q_{0} q^{2} \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right )} H \left ( h_{1} -\mid y \mid \right ), $$
(64)

where \(h_{mn} = \sqrt{q^{2} + k_{mn}^{2}}\), \(( m =1,2,3, n =1,2)\) and \(\left ( k_{mn}^{2}, n =1,2 \right )\) are the roots of the characteristic equation

$$ k_{m}^{4} - k_{m}^{2} \left [ \left ( \zeta _{m} + \varepsilon _{m} \varpi _{m} \phi _{m} \right ) \left ( s + \tau _{0 m} s^{2} \right ) + \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ] + \frac{s^{3} \zeta _{m} \chi _{m} \left ( 1+ \tau _{0 m} s \right )}{\varpi _{m}} =0. $$
(65)

The general solution of equation (64) can be written as

$$ \begin{aligned} \hat{\hat{e}}_{m} ={}& \sum _{n =1}^{2} \phi _{m} k_{mn}^{2} \left [ A_{mn} \cosh \left ( h_{mn} y \right ) + B_{mn} \sinh \left ( h_{mn} y \right ) \right ]\\ &{} + \frac{Q_{0} q^{2} \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{m 1}^{2} h_{m 2}^{2}} H \left ( h_{1} -\mid y \mid \right ), \end{aligned} $$
(66)

where \(A_{mn}\) and \(B_{mn}\) are parameters depending on \(s\) and \(q\) for layer \(L_{m}\). Again, by eliminating \(\hat{e}_{m}\) from (52) and (53), we obtain

$$ \begin{aligned} &\left ( \nabla ^{4} - \left [ \left ( \zeta _{m} + \varepsilon _{m} \varpi _{m} \phi _{m} \right ) \left ( s + \tau _{0 m} s^{2} \right ) + \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ] \nabla ^{2} + \frac{\zeta _{m} \chi _{m} s^{3} \left ( 1+ \tau _{0 m} s \right )}{\varpi _{m}} \right ) \overline{\theta}_{m} \\ &\quad =- \left ( 1+ \tau _{0 m} s \right ) \left ( \nabla ^{2} - \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) \hat{Q}. \end{aligned} $$
(67)

Similarly, applying the Fourier exponential transform to both sides of Eq. (67), we get

$$ \left ( D^{2} - h_{m 1}^{2} \right ) \left ( D^{2} - h_{m 2}^{2} \right ) \hat{\hat{\theta}}_{m} = \frac{Q_{0} \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right )} \left ( q^{2} + \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) H \left ( h_{1} -\mid y \mid \right ). $$
(68)

The solution of Eq. (68) for layer \(L_{m}\) can be written as

$$ \begin{aligned} \hat{\hat{\theta}}_{m} = {}&\sum _{n =1}^{2} \left ( k_{mn}^{2} - \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) \left ( A_{mn} \cosh \left ( h_{mn} y \right ) \right ) \\ &{}+ \frac{Q_{0} \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{m 1}^{2} h_{m 2}^{2}} \left ( q^{2} + \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) H \left ( h_{1} -\mid y \mid \right ). \end{aligned} $$
(69)

Applying the Fourier exponential transform to both sides of Eqs. (50)–(59), we obtain the following set of equations:

$$\begin{gathered} \left ( D^{2} - \left ( q^{2} + \frac{\xi _{m} s^{2}}{\varpi _{m}} \right ) \right ) \hat{\hat{u}}_{m} =iq \left ( \delta _{m} \hat{\hat{\theta}}_{m} - \psi _{m} \hat{\hat{e}}_{m} \right ),m=1,2,3, \end{gathered}$$
(70)
$$\begin{gathered} \left ( D^{2} - \left ( q^{2} + \frac{\xi _{m} s^{2}}{\omega _{m}} \right ) \right ) \hat{\hat{v}}_{m} = \frac{\partial}{\partial y} \left ( \delta _{m} \hat{\hat{\theta}}_{m} - \psi _{m} \hat{\hat{e}}_{m} \right ),m=1,2,3, \end{gathered}$$
(71)
$$\begin{gathered} \hat{\overline{\sigma}}_{mxx} = \varpi _{m} \left ( \Omega _{m1} \hat{\hat{e}}_{m} -2 \Omega _{m2} \frac{\partial \hat{\hat{v}}_{m}}{\partial y} - \Omega _{m3} \hat{\hat{\theta}}_{m} \right ),m=1,2,3, \end{gathered}$$
(72)
$$\begin{gathered} \hat{\overline{\sigma}}_{myy} = \varpi _{m} \left ( \Omega _{m1} \hat{\hat{e}}_{m} -2iq \Omega _{m2} \hat{\hat{u}}_{m} - \Omega _{m3} \hat{\hat{\theta}}_{m} \right ),m=1,2,3, \end{gathered}$$
(73)
$$\begin{gathered} \hat{\overline{\sigma}}_{mzz} = \varpi _{m} \left ( \Omega _{m4} \hat{\hat{e}}_{m} - \Omega _{m3} \hat{\hat{\theta}}_{m} \right ),m=1,2,3, \end{gathered}$$
(74)
$$\begin{gathered} \left ( 1+ \tau _{0m} s \right ) \hat{\hat{q}}_{mx} =-iq \Omega _{m5} \hat{\hat{\theta}}_{m}, m=1,2,3, \end{gathered}$$
(75)
$$\begin{gathered} \left ( 1+ \tau _{0m} s \right ) \hat{\hat{q}}_{my} =- \Omega _{m5} \frac{\partial \hat{\hat{\theta}}_{m}}{\partial y}, m=1,2,3, \end{gathered}$$
(76)
$$\begin{gathered} \hat{\hat{e}}_{m} =iq \hat{\hat{u}}_{m} + \frac{\partial \hat{\hat{v}}_{m}}{\partial y}, m=1,2,3. \end{gathered}$$
(77)

Substituting from Eqs. (66) and (69) into the right-hand sides of Eqs. (70) and (71), we obtain

$$\begin{gathered} \left ( D^{2} - \left ( q^{2} + \frac{\xi _{m} s^{2}}{\varpi _{m}} \right ) \right ) \hat{\hat{u}}_{m} = iq \phi _{m} \left ( \textstyle\begin{array}{c} \sum _{n =1}^{2} A_{mn} \left ( k_{m}^{2} - \frac{\kappa _{m}^{2} s^{2}}{\omega _{m}} \right ) \cosh \left ( h_{mn} y \right )\\ + \frac{Q_{0} \left ( q^{2} + \frac{\kappa _{m}^{2} s^{2}}{\omega _{m}} \right ) \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{m 1}^{2} h_{m 2}^{2}} H \left ( h_{1} -\mid y \mid \right ) \end{array}\displaystyle \right ), \end{gathered}$$
(78)
$$\begin{gathered} \left ( D^{2} - \left ( q^{2} + \frac{\xi _{m} s^{2}}{\varpi _{m}} \right ) \right ) \hat{\hat{v}}_{m} =- \phi _{m} \left ( \sum _{n =1}^{2} A_{mn} h_{mn} \left ( k_{mn}^{2} - \frac{\kappa _{m}^{2} s^{2}}{\omega _{m}} \right ) \cosh \left ( h_{mn} y \right ) \right ), \end{gathered}$$
(79)

where \(\kappa _{m}^{2} = \frac{\chi _{m} \delta _{m}}{\varphi _{m}}\), \(m=1,2,3\). The general solutions of Eqs. (59) and (60) compatible with Eq. (38) are

$$\begin{gathered} \begin{aligned} \hat{\hat{u}}_{m} ={}& C_{m} \cosh \left ( d_{m} y \right )\\ &{} + iq \phi _{m} \left ( \sum _{n =1}^{2} \left ( A_{mn} \cosh \left ( h_{mn} y \right ) \right ) - \frac{Q_{0} \left ( 1+ \tau _{0 m} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{m 1}^{2} h_{m 2}^{2}} H \left ( h_{1} -\mid y \mid \right ) \right ), \end{aligned} \end{gathered}$$
(80)
$$\begin{gathered} \hat{\hat{v}}_{m} = \frac{iq}{d_{m}} C_{m} \sinh \left ( d_{m} y \right ) - \phi _{m} \sum _{n =1}^{2} A_{mn} h_{mn} \sinh \left ( h_{mn} y \right ), \end{gathered}$$
(81)

where \(d_{m} = \sqrt{q^{2} + \frac{\xi _{m} s^{2}}{\varpi _{m}}}\), \(m =1,2,3\).

Substituting from Eqs. (50), (53), and (61) into the right-hand sides of Eqs. (72)–(76), we get the solution for nonvanishing components of stress for layer \(L_{m}, m =1,2,3\).

$$\begin{gathered} \hat{\overline{\sigma}}_{mxx} = \Omega _{m 2} \varpi _{m} \left ( 2 iq C_{m} \sinh \left ( d_{m} y \right ) + \phi _{m} \sum _{n =1}^{2} A_{m} \left ( \frac{\kappa _{m}^{2} s^{2}}{\omega _{m}} -2 h_{mn}^{2} \right ) \sinh \left ( h_{mn} y \right ) \right ), \end{gathered}$$
(82)
$$\begin{gathered} \hat{\hat{\sigma}}_{mxy} =- \Omega _{m 2} \varpi _{m} \left ( \left ( \frac{d_{m}^{2} + q^{2}}{d_{m}} \right ) C_{m} \sinh \left ( d_{m} y \right ) +2 iq \phi _{m} \sum _{n =1}^{2} A_{mn} h_{mn} \sinh \left ( h_{mn} y \right ) \right ), \end{gathered}$$
(83)
$$\begin{gathered} \left ( 1+ \tau _{0 m} s \right ) \hat{\hat{q}}_{mx} =- iq \Omega _{m 5} \left ( \textstyle\begin{array}{c} \sum _{n =1}^{2} A_{mn} \left ( k_{mn}^{2} - \frac{\chi _{m} s^{2}}{\varpi _{m}} \right ) \cosh \left ( h_{mm} y \right )\\ + \frac{Q_{0} \left ( 1+ \tau _{m} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{m 1}^{2} h_{m 2}^{2}} \left ( q^{2} + \frac{\chi _{0 m} s^{2}}{\varpi _{m}} \right ) H \left ( h_{1} - \left \vert y \right \vert \right ) \end{array}\displaystyle \right ), \end{gathered}$$
(84)
$$\begin{gathered} \left ( 1+ \tau _{0 m} s \right ) \hat{\hat{q}}_{my} = \Omega _{m 5} \left ( \sum _{n =1}^{2} A_{mn} h_{mn} \left ( k_{mn}^{2} - \chi _{m} s^{2} \right ) \sinh \left ( h_{mn} y \right ) \right ) . \end{gathered}$$
(85)

Taking the Laplace and Fourier transforms of Eqs. (35), (36), and (37), respectively, we obtain the boundary conditions in the transformed domain as

$$\begin{gathered} \left . \hat{\hat{u}}_{m} \right \vert _{\left . (q, \pm h_{2},t \right )} = \left . \hat{\overline{v}}_{m} \right \vert _{\left . (q, \pm h_{2} t \right )} =0, {} m =2,3, \end{gathered}$$
(86)
$$\begin{gathered} \left . \frac{\partial \hat{\overline{\theta}}_{m}}{\partial y} \right \vert _{\left ( q, \pm h_{2}, t \right )} =0, {} m =2,3. \end{gathered}$$
(87)

The continuity conditions at the interfaces between the two media require that at \(y = h_{1}\) and \(y =- h_{1}\), the following matching must hold:

$$\begin{gathered} \left . \left ( \hat{\hat{\theta}}_{1}, \hat{\hat{u}}_{1}, \hat{\hat{v}}_{1}, \hat{\hat{q}}_{1 y}, \hat{\overline{\sigma}}_{1 yy}, \hat{\overline{\sigma}}_{1 xy} \right ) \right \vert _{\left ( x, h_{1}, t \right )} = \left . \left ( \hat{\hat{\theta}}_{2}, \hat{\hat{u}}_{2}, \hat{\hat{v}}_{1}, \hat{\hat{q}}_{2 y}, \hat{\overline{\sigma}}_{2 yy}, \hat{\overline{\sigma}}_{2 xy} \right ) \right \vert _{\left ( x, h_{1}, t \right )}, \end{gathered}$$
(88)
$$\begin{gathered} \left . \left ( \hat{\hat{\theta}}_{1}, \hat{\hat{u}}_{1}, \hat{v}_{1}, \hat{\hat{q}}_{1 y}, \hat{\overline{\sigma}}_{1 yy}, \hat{\overline{\sigma}}_{1 xy} \right ) \right \vert _{\left ( x,- h_{1}, t \right )} = \left . \left ( \hat{\hat{\theta}}_{3}, \hat{\hat{u}}_{3}, \hat{v}_{3}, \hat{\hat{q}}_{3 y}, \hat{\overline{\sigma}}_{3 yy}, \hat{\overline{\sigma}}_{3 xy} \right ) \right \vert _{\left ( x,- h_{1}, t \right )}. \end{gathered}$$
(89)

Due to the symmetry with respect to the \(x\)-axis, the boundary conditions at \(y = h_{2}\) and the continuity conditions between the two media at \(y = h_{1}\) are sufficient to determine the unknown parameters \(A_{mm}\) and \(C_{m}\), \(( m =1,2,3, n =1,2)\) by solving immediately the following system of linear equations:

$$\begin{gathered} C_{1} \cosh \left ( d_{1} h_{2} \right ) + iq \phi _{1} \sum _{n =1}^{2} \left ( A_{1 n} \cosh \left ( h_{1 n} h_{2} \right ) \right ) =0, \end{gathered}$$
(90)
$$\begin{gathered} \frac{iq}{d_{1}} C_{1} \sinh \left ( d_{1} h_{2} \right ) - \phi _{1} \sum _{n =1}^{2} A_{1 n} h_{1 n} \sinh \left ( h_{1 n} h_{2} \right ) =0, \end{gathered}$$
(91)
$$\begin{gathered} \sum _{n =1}^{2} \left ( k_{1 n}^{2} - \frac{\chi _{l} s^{2}}{\varpi _{1}} \right ) A_{1 n} h_{1 n} \cosh \left ( h_{1 n} h_{2} \right ) =0, \end{gathered}$$
(92)
$$\begin{gathered} \begin{aligned} & \sum _{l =1}^{2} \left ( \sum _{n =1}^{2} (-1 )^{l} A_{ln} \left ( k_{ln}^{2} - \frac{\chi _{l} s^{2}}{\varpi _{l}} \right ) \cosh \left ( h_{ln} h_{1} \right ) \right )\\ & \quad =- \frac{Q_{0} \left ( 1+ \tau _{02} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{21}^{2} h_{22}^{2}} \left ( q^{2} + \frac{\chi _{2} s^{2}}{\varpi _{2}} \right ), \end{aligned} \end{gathered}$$
(93)
$$\begin{gathered} \sum _{l =1}^{2} \left ( \sum _{n =1}^{2} (-1 )^{l} A_{ln} h_{ln} \left ( k_{ln}^{2} - \frac{\chi _{l} s^{2}}{\varpi _{l}} \right ) \cosh \left ( h_{ln} h_{1} \right ) \right ) =0, \end{gathered}$$
(94)
$$\begin{gathered} \sum _{l =1}^{2} iq \left ( (-1 )^{l} \left ( \sum _{n =1}^{2} A_{ln} \phi _{l} \cosh \left ( h_{ln} h_{1} \right ) + \frac{C_{l}}{iq} \cosh \left ( d_{l} h_{1} \right ) \right ) \right ) = \frac{iq Q_{0} \phi _{2} \left ( 1+ \tau _{02} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{21}^{2} h_{22}^{2}}, \end{gathered}$$
(95)
$$\begin{gathered} \sum _{l =1}^{2} (-1 )^{i} \left ( \frac{iq C_{l}}{d_{l}} \sinh \left ( d_{l} h_{1} \right ) - \sum _{n =1}^{2} \phi _{l} A_{ln} h_{ln} \sinh \left ( h_{ln} h_{1} \right ) \right ) =0, \end{gathered}$$
(96)
$$\begin{gathered} \begin{aligned} & \sum _{l =1}^{2} \Omega _{l 2} \varpi _{l} (-1 )^{l} \left ( - iq C_{l} \cosh \left ( d_{l} y \right ) + \phi _{l} \left ( \sum _{n =1}^{2} A_{ln} \left ( \frac{\kappa _{l}^{2} s^{2}}{\varpi _{1}} +2 q^{2} \right ) \cosh \left ( h_{ln} y \right ) \right ) \right )\\ & \quad = - \frac{2 \Omega _{22} \varpi _{2} \phi _{2} Q_{0} q^{2} \left ( 1+ \tau _{02} s \right )}{\pi s \left ( q^{2} +1 \right ) h_{21}^{2} h_{22}^{2}}, \end{aligned} \end{gathered}$$
(97)
$$\begin{gathered} \sum _{l =1}^{2} \Omega _{l 2} \varpi _{l} \left ( \left ( \frac{d_{l}^{2} + q^{2}}{d_{l}} \right ) C_{l} \sinh \left ( d_{l} y \right ) +2 iq \phi _{l} \sum _{n =1}^{2} A_{ln} h_{ln} \sinh \left ( h_{ln} y \right ) \right ) =0. \end{gathered}$$
(98)

The solution of the above system was carried out using the numerical methods, and this completes the solution of the problems in the transformed domain.

3.3 Numerical results

We have chosen copper as an elastic material and PMMA as a viscoelastic material. Their physical properties are listed in Table 1.

Table 1 Mechanical and thermal properties of copper and PMMA (Ezzat et al. 2015; Mahdy et al. 2021; Jahangir et al. 2021; Youssef and Al Thobaiti 2022))
Full size table

Numerical Laplace–Fourier inversion is performed to obtain the nondimensional temperature, displacement, and stress in a specific domain. The numerical code has been prepared using FORTRAN programming language. From an application point of view, the graphs have been displayed and divided into two categories for the two cases (I) and (II). In the figures, the shaded area refers to the viscoelastic region. Our main objective, in this connection, is to illustrate the shape memory effect (fractional time derivative parameter \(\beta \)) on the temperature, displacement, and stress distributions at a specific time \(t = 0.1\).

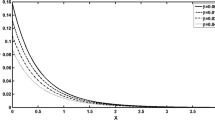
Figures 2(a) and 2(b) are plotted to show the variation of temperature \(\theta \) on the \(y\)-axis for different values of \(\beta \) for cases (I) and (II), respectively. In the middle layer, the temperature records its maximum value \(\theta _{\max} =\) (0.283725 for case (I), 0.31612 for case (II)) at the middle position \(y=0.0\), and drops gradually until it reaches the interfacial temperature \(\theta _{\mathrm{interfacial}} =\) (0.08233 for case (I), 0.240345 for case (II)) at the position \(\left ( \left \vert y \right \vert = h_{1} \right )\). In the upper and lower layers, the temperature gradually decays down until it falls to zero near the position (2.45 for case (I), 0.95 for case (II)).

Fig. 2
figure 2

(a) Temperature distribution against \(y\)-axis at different values of \(\beta \) for case (I). (b) Temperature distribution against \(y\)-axis at different values of \(\beta \) for case (II)

Full size image

By comparing Figs. 2(a) and 2(b), we note that

  • The temperature at the interface for case (I) is less than its counterpart for case (II).

  • The distance of propagation of the thermal wave in the regions \(\left ( L_{1}, L_{3} \right )\) for case (I) is greater than its counterpart for case (II).

The reason for these two phenomena is that the thermal conductivity of copper is much greater than that of PMMA (\(k_{copper} > k_{PMMA} \)). This produces two effects; first, the heat produced at the middle layer \(\left ( L_{2} \right )\) has some difficulty in reaching the interfaces. So, the accumulated temperature at the interface is less than that in case (II). Secondly, once the temperature wave leaves region \(\left ( L_{2} \right )\), it encounters a region where the conductivity is higher. This enables the wave to travel a greater distance.

Our calculations up to the specified accuracy (\(10^{ - 5}\)) show that the values of the temperature profile distribution are very closely for different values of \(\beta \).

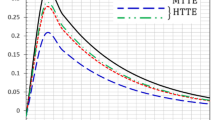
Figure 3(a) and 3(b) show the variations of the displacement component \(v\) on the \(y\)-axis for different values of fractional parameter \(\beta \) in cases (I) and (II), respectively. In both cases, we note that for any fixed value of \(\beta \), the magnitude of the displacement component increases from zero at \(\left ( y = 0 \right )\) to the maximum peak inside the middle layer and then decreases to the interfacial value. In the upper and lower layers, the magnitude of the displacement component increases from the interfacial value to a maximum peak near the interface and deceases gradually to zero at the position 3.00 for case (I), 0.8 for case (II). For case (I), the deformations in the middle layer (\(L_{2} \)) is smaller than that in layers (\(L_{1}\), \(L_{3} \)). In addition, the decrease of \(\beta \) for viscoelastic material induces a large deformation in the middle layer (\(L_{2} \)) and records the large interfacial values. In the upper and lower layers, the effects of \(\left ( \beta >0 \right )\) becomes insignificant. On the other side, for case (II), the deformations in the middle layer (\(L_{2} \)) is larger than that in the layers (\(L_{1}\), \(L_{3} \)). Also, the effect of time fractional derivative parameter \(\beta \) for viscoelastic materials in the layers (\(L_{1}\), \(L_{3} \)) is significant on the displacement component \(v\) in the middle elastic layer (\(L_{2} \)) such that a decrease in \(\beta \) leads to a decrease in \(v\), after crossing the interface, a decrease in \(\beta \) leads to an increase in \(v\) in the viscoelastic layers (\(L_{1}\), \(L_{3} \)).

Fig. 3
figure 3

(a) Displacement component \(v\) against \(y\)-axis at different values of \(\beta \) for case (I). (b) Displacement component \(v\) against \(y\)-axis at different values of \(\beta \) for case (II)

Full size image

By comparing Figs. 3(a) and 3(b), we observe that the different values of \(\beta \) which are related to the viscoelastic material lead to the different values for \(v\) in the elastic material also. The reason for this in Fig. 3(a) is that the fractional time parameter \(\beta \) changes the interfacial values (start values) of \(v \) for the layers (\(L_{1}\), \(L_{3} \)). In Fig. 3(b), the effects we see in the elastic region are due to the existence of the wave transmitted from the viscoelastic region to the elastic region.

Figure 4(a) and 4(b) depict the stress component \(\sigma _{yy}\) on the \(y\)-axis for different values of fractional parameter \(\beta \) for both cases (I) and (II). We note that for any fixed value of \(\beta \), the stress component records the positive value at \(y = 0\), it increases to a maximum peak in middle layer, and decreases sharply to the interfacial value. In the upper and lower layers, the stress component \(\sigma _{yy}\) still decreases from the interfacial value to a minimum peak near the interface and increases gradually to zero. For case (I), the magnitude of the stress component \(\sigma _{yy}\) increases in the middle layer as \(\beta \) decreases and, after crossing the interface planes, the effect is slightly observed for all values of \(\beta >0\). On the other hand, for case (II), the effect of \(\beta \) for viscoelastic material (\(L_{2} \)) is insignificant on the stress component \(\sigma _{yy}\) up to \(\left ( y=0.42 \right )\) in the middle elastic layer, but it is significant near the interface planes such that a decrease in \(\beta \) leads to a decrease in \(\sigma _{yy}\). After crossing the interface, the decrease of \(\beta \) leads to an increase the magnitude of the stress component \(\sigma _{yy}\) in the viscoelastic layers \((L_{1}, L_{3} )\).

Fig. 4
figure 4

(a) Stress component \(\sigma _{yy}\) against \(y\)-axis at different values of \(\beta \) for case (I). (b) Stress component \(\sigma _{yy}\) against \(y\)-axis at different values of \(\beta \) for case (II)

Full size image

Figure 5(a) and 5(b) represent the stress component \(\sigma _{xx}\) on the \(y\)-axis for different values of the fractional parameter \(\beta \). We note that the behavior of the stress component \(\sigma _{xx}\) and the effect of fractional order parameter are similar to those of \(\sigma _{yy}\).

Fig. 5
figure 5

(a) Stress component \(\sigma _{xx}\) against \(y\)-axis at different values of \(\beta \) for case (I). (b) Stress component \(\sigma _{xx}\) against \(y\)-axis at different values of \(\beta \) for case (II)

Full size image

Of course, on the plane \(\left ( x = 0 \right )\), the variations of the displacement component \(u\) and shear stress \(\sigma _{xy} \) are identically zero on the \(y\)-axis, which is in agreement with our theoretical results. We illustrated their variations against \(y\) for different \(\beta \) at the plane (\(x=0.05\), say) in Figs. 6 and 7. For any fixed value of \(\beta \), the displacement component \(u\) records a negative value at \(y=0\), it decreases to the minimum negative peak in the middle layer, and increases to the interfacial values. In the upper and lower layers, the magnitude of the displacement component still increases from the interfacial value to the maximum positive peak near the interface and deceases gradually to zero. Meanwhile, the magnitude of the shear stress \(\sigma _{xy}\) always begins at the zero value. It vibrates through the middle layer and records a maximum value for each \(\beta \) on the interfaces. In the upper and lower layers, it decreases sharply near the interfaces to a negative peak, and diminishes to zero.

Fig. 6
figure 6

(a) Displacement component \(u\) against distance \(y\) at different values of \(\beta \) in the plane (\(x=0.05\)) for case (I). (b) Displacement component \(u\) against distance \(y\) at different values of \(\beta \) in the plane (\(x=0.05\)) for case (II)

Full size image
Fig. 7
figure 7

(a) Stress component \(\sigma _{xy}\) against distance \(y\) at different values of \(\beta \) in the plane (\(x=0.05\)) for case (I). (b) Stress component \(\sigma _{xy}\) against distance \(y\) at different values of \(\beta \) in the plane (\(x=0.05\)) for case (II)

Full size image

4 Conclusion

The main goal of our paper was to introduce a new fractional mathematical model of generalized thermo-viscoelasticity associated with nonsingular fractional relaxation function. A simple physical explanation of using fractional derivatives over ordinary derivatives when constructing a physical model is the fact that the fractional model predicts that a retarded response is instantaneous. This is because the evaluation of the fractional derivatives is accomplished by integrating over a past period of time. Retarded response is observed in all physical situations, especially in thermo-viscoelasticity. This is why the early models of fractional viscoelasticity were so successful. Our new model is proven to be valid for analysis of wave propagation in sandwiched plates. Summing up the discussions through an application, we note that the fractional time parameter role was demonstrated to be a promising and powerful tool for precisely processing metals (i.e., the memory time effect is prominent on the thermal and mechanical nature).

Nowadays, the knowledge of generalized thermo-viscoelasticity theory associated with nonsingular fractional relaxation function can be utilized by engineers, in particular by mechanical and structural engineers for designing machine elements, e.g., when synthesizing metals, where temperature-induced viscoelastic deformation occurs.