Time domain homogenisation of elastic and viscoelastic metamaterials

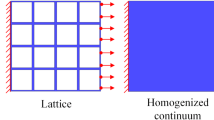
Abstract

The mechanical behaviour of metamaterials typically depends on their microstructural configuration and composition, in addition to their relative density. The design of these materials requires extensive experiments or complex finite element models which tend to be numerically demanding. In order to understand, control and optimise the macroscopic mechanical behaviour, in this paper numerical homogenisation is applied to a simple square unit cell with a single inclusion using a combination of elastic and viscoelastic responses on the micro level. Through a systematic analysis of unit cell behaviour with increasingly complex microstructural configurations, it is shown how certain macroscale constitutive laws can be obtained in a controlled and controllable manner.

1 Introduction

Modern manufacturing technologies have made it possible to specify and design microstructural properties to achieve desired macrostructural properties, which may be difficult to achieve with conventional or natural materials (Barchiesi et al. 2019). According to the literature, metamaterials’ applications in engineering roughly fall into three main fields, namely electromagnetic, acoustic and mechanical applications (Askari et al. 2020). In this paper, the focus will be on the mechanical behaviour of metamaterials with particular emphasis on elastic and viscoelastic properties. Mechanical metamaterials can be utilised in many real life applications, such as structural components of vehicles and aircraft, thermal insulators, wave filters, and blast and impact protective devices.

The general performance of metamaterials depends on the properties of the original material, relative density and the microstructural configuration of the unit cell, and they can be designed using different parent materials and manufacturing techniques. Typical lightweight geometries studied in the literature include lattice structures such as pyramids (Lee et al. 2006), octagons (Davami et al. 2019) and re-entrant cubes (Ozdemir et al. 2016, 2017). Furthermore, parent materials vary from metals such as titanium (Jamshidinia et al. 2013; Ozdemir et al. 2016, 2017; Lijun and Weidong 2018) and stainless steel (Lee et al. 2006; Smith et al. 2011; Winter et al. 2017; Gümrük et al. 2018) to polymers (Habib et al. 2019) and porous ceramics (Bruno et al. 2011).

Several studies have addressed the mechanical performance of metamaterials experimentally under static loading conditions, e.g. Bruno et al. (2011), Maskery et al. (2018). Sypeck and Wadley (2001) used an experimental procedure to compare open-cell periodic lattice metamaterials with stochastic cellular structures; they concluded that open-cell periodic lattice metamaterials provide higher mechanical properties (stiffness, energy absorption, and heat exchange) compared with stochastic cellular structures. Experimental approaches can be particularly useful to identify failure modes (Ozdemir et al. 2016). However, experimental approaches are not conclusive for optimisation of the metamaterial microstructure, since they are often costly, dependent on trial and error, and subject to limitations of the experimental setup (Kochmann et al. 2019).

To overcome the limitations of experimental procedures, analytical approaches can be utilised to design or determine the properties of metamaterials, for instance by using structural mechanics theories based on trusses or beams (Kochmann et al. 2019) or plates (Tancogne-Dejean et al. 2018). These methods can be used to identify the initial failure properties such as the yield strength, but they are feasible for relatively simple microstructural geometries and simple material models (Kochmann et al. 2019). To assess more general structural and material properties, analytical approaches can be combined with numerical simulations such as finite element (FE) computations. Bruno and coworkers studied the relationship between micro and macro properties on porous ceramic, closed-cell stochastic cellular materials under uniaxial loading (Bruno et al. 2011). Their results show a linear dependency between average microstress and applied macrostress through the porosity, void distribution and ratio, of the ceramic sample. Furthermore, it was found that the average microlevel strain depends on the macrolevel strain through the morphology factor, while the microscopic modulus did not depend on morphology and the Poisson ratio did not depend on porosity. Maskery and coworkers investigated a surface-based lattice numerically in terms of cell type, orientation and volume fraction, resulting in general design parameters and criteria (Maskery et al. 2018). The unit cell geometry was found to play an important role in determining the elastic modulus, while the effect of orientation on the elastic modulus was found to be less pronounced. In a related study, a Ti-6Al-4V titanium alloy lattice has been studied under cyclic and fatigue loading, which demonstrated the potential use of lattice metamaterials in dental fillings (Jamshidinia et al. 2013).

However, using conventional numerical modelling techniques, such as detailed FE models, to simulate the full metamaterial specimen usually requires high computational cost and time. A promising alternative is homogenisation, which depends on detailed modelling of a unit cell and using averaging techniques to homogenise the results to obtain mechanical properties of the full lattice specimen. This can lead to significant reductions in analysis time and computational cost. Kouznetsova et al. (2001) have provided an in-depth review of the various homogenisation schemes that are available to determine homogenised material properties. The first of these schemes focuses on homogenised moduli and follows the so-called rule of mixtures. This method is simple and straightforward and can provide upper and lower bounds of the relevant properties, however, it is only suitable for linear material behaviour (Kouznetsova et al. 2001).

The second approach is analytical homogenisation (Eshelby 1957; Hashin 1962; Hashin and Shtrikman 1963; Hill 1963). In this method, the homogenised material properties of the macrostructure are obtained from the analytical or semi-analytical solution of a boundary problem of one inclusion in an infinite matrix material. The method is self-consistent and it yields accurate results for regular geometries, however it cannot be used to model the behaviour of cluster structures nor high contrasts between phases (Kouznetsova et al. 2001).

A third method is asymptotic homogenisation theory (Toledano and Murakami 1987; Devries et al. 1989; Fish et al. 1999). This method is based on an expansion of displacement and stress fields utilising natural length parameters, such as the ratio of size and distribution of heterogeneities between microstructure to macrostructure. Effective homogenised properties can be obtained using this method as well as local stress and strain values. However, it is typically restricted to simple microstructural geometries, small strains and simple material behaviour (Kouznetsova et al. 2001).

Fourthly, unit cell numerical methods rely on fitting the results of detailed modelling of a microscale Representative Volume Element (RVE) to the macrostructural homogenised properties. The concept of an RVE was introduced by Hill (1963) and it is taken as a volume portion at microlevel such that the homogenised mechanical behaviour of the RVE is equivalent to the macrostructural mechanical behaviour. The RVE should typically be as small as possible, but large enough to contain sufficient detail about the microstructural heterogeneities (van der Sluis et al. 2001). A fundamental assumption in any numerical homogenisation scheme is that random heterogeneous material is statistically homogeneous – that is, the macrostructure behaves similarly, within user-defined levels of acceptable error, to duplicates of a single RVE. To predict the behaviour of heterogeneous materials using numerical homogenisation, an RVE should be defined and analysed; the results should be subsequently fitted in a postulated constitutive relation between micro and macro levels. Numerical homogenisation has been utilised and developed for many applications such as polymers (van der Sluis et al. 2001) and ceramics (Gourdin et al. 2017). This method allows simulation of complex microstructural behaviour and, hence, the study of the microstructural configuration effect on the overall macroscale properties and response. The main challenge in numerical homogenisation is establishing a robust and versatile constitutive connection between micro and macro levels (Kouznetsova et al. 2001).

Fifthly, multiscale computational homogenisation methods have been developed (Terada and Kikuchi 1995; Smit et al. 1998; Miehe et al. 1999; Feyel and Chaboche 2000; Kouznetsova et al. 2001). This method does not yield a closed-form expression for the macrostructural material behaviour, but instead estimates the macrostructural stress–strain relationship by solving, numerically, boundary value problems for RVEs assigned to every integration point of the macrostructural numerical model. Computational homogenisation consists of three main steps, which employ two levels of simulations and have to be applied iteratively for every time step. First, an arbitrary homogenised specimen (representing the macrolevel) is solved using the FEM. Next, the strains obtained at each integration point are applied as loading to a unique RVE corresponding to a given integration point. The last step is to solve the RVE response and translate the obtained microscale reaction forces into macroscale stresses for the full specimen (Kouznetsova et al. 2001). This method is suitable to model complex microstructures as it does not have a limitation on the number or configuration of RVEs. On the other hand, this method is less suitable for optimisation, design purposes and studying material behaviour due to microstructural effect, as it yields a phenomenological stress–strain behaviour for the macrostructure based on a microstructural solution, rather than a closed-form constitutive law.

Most of the methods discussed above have primarily been applied to static or quasi-static applications. However, the microstructural configuration of metamaterials also plays an important role in the dynamic mechanical response (Barchiesi et al. 2019; Askari et al. 2020). In this work, numerical homogenisation will be applied to time-dependent problems. Throughout this study, a unit cell with a single inclusion has been considered. Such a unit cell can be assumed to be an RVE as has been validated for periodic metamaterials by van der Sluis et al. (2000), Roca et al. (2018), Sridhar et al. (2018). In the case of aperiodic metamaterials, the same approach of numerical homogenisation can still be used, although an RVE size determination study should then be conducted beforehand such as those described in Gitman et al. (2007), Mirkhalaf et al. (2016). The effects of the inclusion’s size, aspect ratio and inclination angle with respect to the loading will be studied. An automated MATLAB code, interfacing with a commercial Finite Element software package, has been developed to study the effects of a range of microstructural configurations on macrostructural mechanical properties. Boundary conditions have been discussed and justified with emphasis on periodic boundary conditions. This work provides a baseline to optimise the macroscopic behaviour of a simple unit cell.

2 Principles of homogenisation

In this section a brief overview of the averaging concepts in homogenisation theories is presented, starting with a definition of the homogenised stress and strain, followed by the concepts of average stress and average strain theorems, and finalising with the Hill–Mandel macrohomogeneity condition (Hill 1984, 1963; Kouznetsova et al. 2001; van der Sluis et al. 2001; Yu 2016).

The volume average $\bar{\psi}$ of a generic quantity $\psi$ is defined as

$$ \bar{\psi}=\frac{1}{\Omega}\int _{\Omega} \psi (x,y) \,dV, \ $$

(1)

where $\Omega$ is the averaging volume at the microlevel. Within the context of homogenisation, $\Omega$ is taken to be the volume of the RVE and indicated here with $V_{R}$. The homogenised values, at the macrolevel, of stress ($\bar{\sigma}_{ij}$) and strain ($\bar{\varepsilon}_{ij}$) can thus be computed by the derivations that follow.

The strain is written as $\varepsilon _{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$, where $u$ is the displacement and an index following a comma indicates a partial derivative with respect to the relevant local spatial coordinate. Hence,

$$ \bar{\varepsilon}_{ij}=\frac{1}{V_{R}}\int _{V_{R}} \frac{1}{2}(u_{i,j}+u_{j,i}) \,dV=\frac{1}{2V_{R}}\oint \limits _{ \partial V_{R}}(u_{i}n_{j}+u_{j}n_{i})\,dS. $$

(2)

Here the Gauss divergence theorem has been employed and $n_{i}$ is the outward vector normal to the boundary $\partial V_{R}$ of the RVE. Substituting $u_{i}=x_{j}\bar{\varepsilon}_{ij}$ into Eq. (2) and transforming the result back into a volume integral then yields

$$ \frac{1}{2V_{R}}\oint \limits _{\partial V_{R}}(\bar{\varepsilon}_{ik}x_{k}n_{j}+ \bar{\varepsilon}_{jk}x_{k}n_{i}) \,dS = \frac{1}{2V_{R}}\int _{V_{R}}(\bar{\varepsilon}_{ik}\delta _{kj}+\bar{\varepsilon}_{jk} \delta _{ki})\,dV=\bar{\varepsilon}_{ij} .$$

(3)

This finding is called the average strain theorem and shows that the average strain, obtained from the displacement at the RVE boundaries, is equal to the homogenised strain $\bar{\varepsilon}_{ij}$ (Yu 2016).

Furthermore, the stress field can be written as follows:

$$ \sigma _{ij}=\sigma _{ik}\delta _{jk}=\sigma _{ik} \frac{\partial x_{j}}{\partial x_{k}}=(\sigma _{ik}x_{j})_{,k}- \sigma _{ik,k}x_{j} .$$

(4)

Assuming equilibrium and zero body forces, we have $\sigma _{ij,j}=0$. Therefore Eq. (4) reduces to

$$ \sigma _{ij}=(\sigma _{ik}x_{j})_{,k} .$$

(5)

Applying the averaging integral of Eq. (1) and employing the Gauss divergence theorem yields

$$ \bar{\sigma}_{ij}=\frac{1}{V_{R}}\int _{V_{R}} (\sigma _{ik}x_{j})_{,k} \,dV =\frac{1}{V_{R}}\oint \limits _{\partial V_{R}} \sigma _{ik}x_{j}n_{k} \,dS .$$

(6)

Using the equality $t^{0}_{i}=\sigma _{ik}n_{k}$, where $t^{0}_{i}$ is the traction on the boundary of the RVE, the homogenised stress can be written as

$$ \bar{\sigma}_{ij}=\frac{1}{V_{R}}\oint \limits _{\partial V_{R}} t^{0}_{i}x_{j} \,dS .$$

(7)

The so-called average stress theorem states that the averaged stress over the entire RVE is equal to the stress obtained from the boundary of the RVE (Yu 2016), as follows:

$$ \frac{1}{V_{R}}\int _{V_{R}} (\sigma _{ik}x_{j})_{,k} \,dV= \frac{1}{V_{R}}\oint \limits _{\partial V_{R}} t^{0}_{i}x_{j} \,dS= \bar{\sigma}_{ij} .$$

(8)

The transition from micro to macro properties satisfies the Hill–Mandel macrohomogeneity condition, which states that the homogenised, averaged strain energy density is equal to the strain energy density of the heterogeneous RVE (Hill 1984, 1963; Kouznetsova et al. 2001). Defining the strain energy density at the macrolevel $U$ as

$$ U=\frac{1}{2}\bar{\sigma}_{ij}\bar{\varepsilon}_{ij} ,$$

(9)

the following condition should be satisfied in order for the Hill–Mandel macrohomogeneity condition to hold:

$$ \bar{\sigma}_{ij}\bar{\varepsilon}_{ij}=\frac{1}{V_{R}}\int _{ V_{R}} \sigma _{ij}\varepsilon _{ij} \,dV .$$

(10)

It has been demonstrated that uniform traction, uniform displacement and periodic boundary conditions satisfy the Hill–Mandel macrohomogeneity condition (Yu 2016).

3 Finite element modelling

This section presents details of the numerical framework used for a parametric study to investigate the influence of microstructural geometry on macrostructural properties. Throughout, finite element modelling was conducted on the LS-DYNA software using 4-node quadrilateral plane stress elements.

3.1 Microstructural geometry of the unit cell

A simple 2D unit cell with a single elliptical inclusion (see Fig. 1) is considered. The major and minor diameters of the ellipse are represented with $A$ and $B$, respectively, by which the area $A_{r}$ and aspect ratio $AsR$ follow as $A_{r} = \frac{1}{4} \pi A B$ and $AsR=A/B$. The inclination angle of the inclusion, $\theta$, is measured anti-clockwise from the $x$-axis to the major axis of the ellipse. The size of the unit cell is taken to be 1 mm by 1 mm. First, a unit cell of linear elastic or linear viscoelastic material with an elliptical void is considered. Next, we study a viscoelastic inclusion in a linear elastic matrix material.

Fig. 1

Representative volume element

3.2 Periodic boundary conditions

To model the response of the microscale unit cells, four different types of boundary conditions can be considered, namely uniform kinematic, uniform static, mixed and periodic boundary conditions (van der Sluis et al. 2001, 2000). Uniform kinematic boundary conditions have an intuitive and direct link to the macroscopic strain tensor, but tend to overestimate the stiffness of the RVE. Conversely, uniform static boundary conditions have a clear link to the macroscopic stress tensor but tend to underestimate the stiffness of the RVE. To balance the two effects of over and underestimating the RVE stiffness, mixed boundary conditions can be used in which some edges have prescribed displacements and the remaining edges have prescribed tractions.

On the other hand, periodic boundary conditions provide a better representation of an infinite model. Through the coupling of the response of opposite edges, periodic boundary conditions also eliminate the effect of position of the inclusion within the unit cell. Therefore, this type of boundary conditions is considered to be the most accurate representation of the physical properties of a unit cell. Periodic boundary conditions can be imposed to study the mechanical response of any heterogeneous material with relatively small unit cells (van der Sluis et al. 2001). In the literature, periodic boundary conditions have been widely used for the homogenisation of heterogeneous materials (van der Sluis et al. 2001; Kouznetsova et al. 2001; Gitman et al. 2007).

Periodic boundary conditions can be used in conjunction with prescribed displacements or prescribed tractions. In a relaxation test, where the specimen is subjected to prescribed displacements, periodic boundary conditions are established straightforwardly as follows. Firstly, an average horizontal normal strain is realised by imposing horizontal displacements at the two corner nodes on the right edge of the unit cell (C2 and C3 in Fig. 2(a)), whereas an average shear strain can be achieved by imposing vertical displacements at these nodes. The translational degrees of freedom of the other two corner nodes (C1 and C4 in Fig. 2(a)) are fixed. Next, multipoint constraints are applied to the remaining edge nodes of the unit cell. In order to achieve this, the difference between displacements of the right edge nodes (RN1, RN2, RN3, …) and left edge nodes (LN1, LN2, LN3, …) are coupled with those of the corner node, that is,

$$\begin{aligned} u_{x}^{RNi}-u_{x}^{LNi} &= \bar{u}_{x}^{C2} , \end{aligned}$$

(11)

$$\begin{aligned} u_{y}^{RNi}-u_{y}^{LNi} &= \bar{u}_{y}^{C2}. \end{aligned}$$

(12)

Similarly, the displacements of the top edge nodes (TN1, TN2, TN3, …) are coupled to those of the bottom edge nodes (BN1, BN2, BN3, …):

$$\begin{aligned} u_{x}^{TNi}-u_{x}^{BNi} &= 0, \end{aligned}$$

(13)

$$\begin{aligned} u_{y}^{TNi}-u_{y}^{BNi} &= 0. \end{aligned}$$

(14)

Fig. 2

Periodic boundary conditions: (a) Relaxation, (b) Creep

On the other hand, in a creep test a constant force is imposed on an external node, while the difference between the horizontal displacements of the right edge nodes (RN1, RN2, RN3, …) and left edge nodes (LN1, LN2, LN3, …) are coupled with this externally loaded node’s horizontal displacement (Fig. 2(b)), i.e.

$$ u_{x}^{RNi}-u_{x}^{LNi}=u_{x}^{p} .$$

(15)

The degrees of freedom of the remaining nodes are coupled following a similar approach used for the relaxation case, that is, Eqs. (13) and (14). Periodic boundary conditions are implemented using the CONSTRAINED_MULTIPLE_GLOBAL command in the LS-DYNA software package.

4 Material models

This section summarises the relevant equations of linear elasticity, linear viscoelasticity and the Maxwell form of the Standard Solid Model for viscoelastic material behaviour. These constitutive equations will be employed in the numerical parametric studies in the following section.

4.1 Linear elasticity

A 2D linear elastic plane stress constitutive equation can be written, as usual, as

$$\begin{gathered} \begin{bmatrix} \sigma _{xx} \\ \sigma _{yy} \\ \sigma _{xy} \end{bmatrix} = \begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{21} & C_{22} & 0 \\ 0 & 0 & C_{33} \end{bmatrix} \begin{bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \end{bmatrix}, \end{gathered}$$

(16)

where $[\sigma _{xx}, \sigma _{yy}, \sigma _{xy}]^{T}$ and $[\varepsilon _{xx}, \varepsilon _{yy}, \gamma _{xy}]^{T}$ are the stress and strain vector, respectively. Depending on the particular loading case, homogenised values for Young’s moduli $\bar{E}$ and Poisson’s ratios $\bar{\nu}$ can be obtained, e.g. in the case of uniaxial tension

$$\begin{aligned} \bar{E}_{11}&=\bar{C}_{11}\left (1-\left ( \frac{\bar{C}_{21}}{\bar{C}_{11}}\right )^{2}\right ), \end{aligned}$$

(17)

$$\begin{aligned} \bar{\nu}_{12}&= \frac{\bar{C}_{21}}{\bar{C}_{11}}, \end{aligned}$$

(18)

and similarly for other elastic constants.

4.2 Linear viscoelasticity

The constitutive equation for a Maxwell-type material, composed of a linear spring and a linear dashpot connected in series as shown in Fig. 3(a), is written as

$$ \sigma +\frac{\eta}{E}\dot{\sigma}=\eta \dot{\varepsilon} ,$$

(19)

where $\eta$ is the dynamic viscosity of the dashpot and $E$ is the elastic modulus of the spring. In stress relaxation, $\varepsilon = \varepsilon _{0}$ is the imposed strain with $\dot{\varepsilon} = 0$. The solution of Eq. (19) can then be expressed as

$$ \sigma (t)=E \varepsilon _{0} e^{-E(t-\uptau ) / \eta} ,$$

(20)

where $\uptau$ is the load duration. On the other hand, in creep $\sigma = \sigma _{0}$ is the imposed stress with $\dot{\sigma} = 0$. The solution of Eq. (19) can then be written as

$$ \varepsilon (t)= \frac{\sigma _{0}}{\eta}(t-\uptau )+ \frac{\sigma _{0}}{E} .$$

(21)

The homogenised stress $\bar{\sigma}(t)$ and strain $\bar{\varepsilon}(t)$ can be constructed by evaluating Eqs. (2) and (7), respectively, at every time instant, while the macroscopic material properties $\bar{E}$ and $\bar{\eta}$ can be evaluated by fitting the curves of $\bar{\sigma}(t)$ and $\bar{\varepsilon}(t)$ to Eqs. (20) and (21). This homogenisation procedure is based on the assumption that the macro and micro constitutive models are expected to behave in a similar manner.

Fig. 3

(a) Maxwell viscoelastic model; (b) Maxwell form of the Standard Solid model

4.3 Maxwell form of the Standard Solid Model

The Standard Solid Model for viscoelasticity gives a better representation of both creep and stress relaxation phenomena. Here we consider the Maxwell form, constructed by connecting a linear spring element (elastic modulus $E_{1}$) in parallel with a Maxwell element (elastic modulus $E_{2}$ and dynamic viscosity $\eta$) as shown in Fig. 3(b). The stress–strain relationship for the standard solid model is thus given by

$$ \sigma +\frac{\eta}{E_{2}}\dot{\sigma}=E_{1}\varepsilon +\left (1+ \frac{E_{1}}{E_{2}}\right )\eta \dot{\varepsilon} .$$

(22)

For a relaxation test, the solution can be written as

$$ \sigma (t)=\left ( (E_{0}-E_{\infty}) e^{-(E_{0}-E_{\infty})(t- \uptau ) / \eta}+ E_{\infty }\right ) \varepsilon _{0} ,$$

(23)

where $E_{0} \equiv E_{1} + E_{2}$ is the initial elastic modulus and $E_{\infty }\equiv E_{1}$ is the final (long term) elastic modulus. On the other hand, a creep test results in

$$ \varepsilon (t)=\left ( \left (\frac{1}{E_{0}}-\frac{1}{E_{\infty}} \right )e^{\frac{-E_{\infty}(E_{0}-E_{\infty})}{E_{0}\eta}(t-\uptau )}+ \frac{1}{E_{\infty}} \right ) \sigma _{0} .$$

(24)

Fitting the homogenised stresses $\bar{\sigma}$ and strains $\bar{\varepsilon}$ to Eqs. (23) and (24) can again be used to obtain the material macroproperties $\bar{E}_{0}$, $\bar{E}_{\infty}$ and $\bar{\eta}$.

5 Parametric studies

A series of parametric FE analyses were performed on the RVE defined in Sect. 3.1 to investigate the effect of matrix and inclusion material properties, inclusion size and inclusion aspect ratio. In these simulations, the aspect ratio $AsR$ varies between 1 and 3 with increments of 0.5, the area $A_{r}$ ranges from 0.1 mm² to 0.175 mm² with 0.025 mm² increments, and the inclination angle $\theta$ varies between 0^∘ and 180^∘ with 10^∘ increments.

The nature of this research requires evaluating and optimising different unit cells with different microstructural configurations. To do so in a systematic manner, a MATLAB script was developed to perform the large number of FE simulations. The MATLAB script builds FE models of the microstructure under specific loading and boundary conditions using ABAQUS via a Python script, runs analyses on LS-DYNA and collects the required outputs using LS-PrePost. A mesh convergence study was conducted on the three types of RVE. Using approximately uniform mesh densities and taking 50 elements across each edge of the unit cell led to negligible variation in the homogenised properties compared to finer meshes. Therefore, the FE models in this study were considered to be sufficiently mesh independent.

5.1 Linear elastic RVE with void

By way of validation, first we consider a unit cell with a single elliptical void (Fig. 1) made of a linear elastic material to determine the homogenised elastic modulus $\bar{E}$. Three different values of the elastic modulus are assumed for the linear elastic matrix, namely $E = 105,\ 210$ and 420 GPa. Poisson’s ratio $\nu$ of the matrix material is set to zero. A convergence study (not reported) has been carried out to optimise the analysis duration. Figure 4 shows the variation of the homogenised elastic modulus $\bar{E}$ with the inclination angle $\theta$ for the unit cell made of linear elastic material with a single elliptical void shown in Fig. 1 with different aspect ratios (while $A_{r} = 0.175$ mm² and $E=210$ GPa). All simulations with different inclusion areas and elastic moduli followed the same pattern. It is noted that the macroscopic constitutive model is anisotropic linear elastic.

Fig. 4

Variation of homogenised elastic modulus $\bar{E}$ of linear elastic RVE with void inclination angle $\theta$ for different aspect ratios and constant area $A_{r}=0.175~\mbox{mm}^{2}$

An approximate closed-form expression can be obtained through fitting a trigonometric curve to represent the variation of homogenised elastic modulus $\bar{E}$ with inclination angle $\theta$ for the RVE. That is,

$$ \bar{E}(\theta )=E\left (x_{0}\cos (2\theta )+\sum _{i=1}^{n} x_{i} \cos \left (\frac{\pi -2\theta}{2^{i}}\right )+C\right ) ,$$

(25)

where $x_{0}$, $x_{i}$, $C$ are constants representing configurational parameters that depend on the microstructure of the unit cell. In this equation, a summation of higher-order trigonometric functions can be used to increase the degree of accuracy of the results. In the fundamental curve fit (i.e. neglecting the summation) approximation of Eq. (25), $C$ is inversely proportional to both the inclusion area $A_{r}$ and aspect ratio $AsR$; however, $x_{0}$ is directly proportional to the inclusion area $A_{r}$ and aspect ratio $AsR$. The values of $x_{0}$ and $C$ for different combinations of aspect ratios and inclusion area are summarised in the Appendix (Tables 2 and 3).

The fundamental curve fit prediction for the variation of homogenised elastic modulus $\bar{E}$ with inclination angle $\theta$ for the unit cell made of linear elastic material with single elliptical void is presented in Fig. 5 together with the FE results. As one can observe from this figure, the fundamental curve fit prediction yields accurate results. Higher-order terms in Eq. (25) slightly improve the prediction, but these results are not shown here.

Fig. 5

Comparison between the FE homogenised elastic modulus $\bar{E}$ of a linear elastic RVE and its prediction for different void inclination angles $\theta$ ($A_{r}=0.175$ mm²)

5.2 Viscoelastic RVE with void

Secondly, a series of FE analyses were conducted on a 2D unit cell with a single elliptical void made of a linear viscoelastic material with elastic modulus $E=210$ GPa, dynamic viscosity $\eta =190$ GN s/m² and Poisson’s ratio $\nu = 0$. The MAT_VISCOELASTIC material model of LS-DYNA is used to model the viscoelastic isotropic behaviour. This material model, which is based on Maxwell’s Standard Solid Model of viscoelasticity, is defined in LS-DYNA by initial shear modulus $G_{0} = E / 2(1+\nu ) = 105$ GPa, final shear modulus $G_{\infty }= 0$ GPa, decay constant $\beta = E / \eta = 1.1$ s⁻¹ and bulk modulus $k = E / 3(1-2\nu ) = 70$ GPa.

In the numerical simulations, two different loading conditions, namely creep and stress relaxation, are considered for the 2D unit cell with a single elliptical void. In these simulations, the variation of the homogenised elastic modulus $\bar{E}$ and homogenised dynamic viscosity $\bar{\eta}$ with inclination angle $\theta$ are evaluated. As one can observe from Figs. 6 and 7, the FE models for viscoelastic unit cells with creep and stress relaxation (using inclusion area $A_{r} = 0.175$ mm² and aspect ratio $AsR=3$) show good agreement; similar levels of correspondence were observed for all other values of inclusion area and aspect ratio. The macroscale material model again exhibits an anisotropic behaviour.

Fig. 6

Variation of homogenised elastic modulus $\bar{E}$ for viscoelastic RVE with void inclination angle $\theta$ using creep and relaxation tests ($A_{r}=0.175$ mm² and $AsR=3$)

Fig. 7

Variation of homogenised dynamic viscosity $\bar{\eta}$ for viscoelastic RVE with void inclination angle $\theta$ using creep and relaxation tests ($A_{r} =0.175$ mm² and $AsR=3$)

Similar to the linear elastic case, simple formulas are obtained through fitting the variation of homogenised elastic modulus $\bar{E}$ and homogenised dynamic viscosity $\bar{\eta}$ with inclination angle $\theta$ to a postulated trigonometric series:

$$\begin{aligned} \bar{E}(\theta )&=E\left (x_{0}\cos (2\theta )+\sum _{i=1}^{n} x_{i} \cos \left (\frac{\pi -2\theta}{2^{i}}\right )+C\right ) , \end{aligned}$$

(26)

$$\begin{aligned} \bar{\eta}(\theta )&=\eta \left (x_{0}\cos (2\theta )+\sum _{i=1}^{n} x_{i} \cos \left (\frac{\pi -2\theta}{2^{i}}\right )+C\right ). \end{aligned}$$

(27)

It is noted that the constants $C$, $x_{0}$ and $x_{i}$ in Eq. (26) are the same as those of the linear elastic RVE discussed in Sect. 5.1. However, Eq. (27) relates the homogenised dynamic viscosity $\bar{\eta}$ to the microscale dynamic viscosity $\eta$, whereby constants $C$, $x_{0}$ and $x_{i}$ are found that are different from those of Eq. (26) – see Tables 4 and 5 of the Appendix for details.

5.3 Linear elastic RVE with viscoelastic inclusion

Next, a composite unit cell consisting of a linear elastic matrix (Material 1) with a Maxwell viscoelastic inclusion (Material 2) is created as shown in Fig. 8. A parametric study is performed by varying the material properties of the inclusion, while the material properties of the matrix ($E = 210$ GPa and $\nu = 0$) are kept constant as shown in Table 1. Six different composite unit cells are considered. In composite unit cells 1 to 3, the elastic modulus of the viscoelastic inclusion ($E_{inc}$) is varied, while keeping the dynamic viscosity $\eta$ constant. On the other hand, in composite unit cells 4 to 6 the elastic modulus $E_{inc}$ and the dynamic viscosity $\eta$ of the viscoelastic inclusion are varied while keeping their ratio $\beta$ constant.

Fig. 8

Composite unit cell with viscoelastic inclusion

Table 1 Material properties of the composite unit cells

For the composite unit cells given in Table 1, richer behaviour is observed in the homogenised response that does not exist in either of the 2D linear elastic or viscoelastic unit cells with a single elliptical void presented in the previous sections. For instance, in a relaxation test, the final elastic modulus $\bar{E}_{\infty}$ is not null for the composite unit cells and the decay constant $\beta$ has a different definition on the macrolevel in comparison to its microlevel properties. Furthermore, the dependence of the homogenised dynamic viscosity on the inclination angle is opposite to that observed for a unit cell with a void. In a creep test, an exponential growth of the strain in time is observed, compared to a linear growth in material 2 and constant strain value in material 1 at the microlevel.

Figures 9, 10, 11 and 12 show the variation of the homogenised initial elastic modulus $\bar{E}_{0}$, the homogenised final elastic modulus $\bar{E}_{\infty}$ and the homogenised dynamic viscosity $\bar{\eta}$ with the inclination angle $\theta$ for the composite unit cells given in Table 1. FE analysis results show that the variation of the initial elastic modulus $\bar{E}_{0}$ with the inclination angle $\theta$ for composite unit cells 1 and 4, composite unit cells 2 and 5, and composite unit cells 3 and 6 are identical. On the other hand, the variation of the final elastic modulus $\bar{E}_{\infty}$ with the inclination angle $\theta$ are identical for all composite unit cells, since $\bar{E}_{\infty}$ depends only on the elastic matrix properties. The variation of the homogenised dynamic viscosity $\bar{\eta}$ with the inclination angle $\theta$ shows differences for composite unit cells 4 to 6. The dynamic viscosity is largest for a 90^∘ inclination angle, in which case the composite behaviour resembles most closely that of a series connection between elastic matrix and viscoelastic inclusion.

Fig. 9

Variation of homogenised initial elastic modulus $\bar{E}_{0}$ with the inclination angle $\theta$ for the composite unit cells 1 to 3 given in Table 1 ($A_{r}=0.175$ mm²)

Fig. 10

Variation of homogenised final elastic modulus $\bar{E}_{\infty}$ with the inclination angle $\theta$ for composite unit cells 1 to 3 given in Table 1 ($A_{r}=0.175$ mm²)

Fig. 11

Variation of homogenised dynamic viscosity $\bar{\eta}$ with the inclination angle $\theta$ for composite unit cells 1 to 3 given in Table 1 ($A_{r}=0.175$ mm²)

Fig. 12

Variation of homogenised dynamic viscosity $\bar{\eta}$ with the inclination angle $\theta$ for composite unit cells 4 to 6 given in Table 1 ($A_{r}=0.175$ mm²)

Simple approximate formulas are once again obtained through fitting the FE results to trigonometric series in order to represent the variation of homogenised final elastic modulus $\bar{E}_{\infty}$ and homogenised dynamic viscosity $\bar{\eta}$:

$$\begin{aligned} \bar{E}_{\infty}(\theta )&=E\left (x_{0}\cos (2\theta )+\sum _{i=1}^{n} x_{i}\cos \left (\frac{\pi -2\theta}{2^{i}}\right )+C\right ) , \end{aligned}$$

(28)

$$\begin{aligned} \bar{\eta}(\theta )&=\eta \left (x_{0}\cos (2\theta )+\sum _{i=1}^{n} x_{i} \cos \left (\frac{\pi -2\theta}{2^{i}}\right )+C\right ). \end{aligned}$$

(29)

As shown above, the homogenised final elastic modulus $\bar{E}_{\infty}$ depends on the elastic modulus of the matrix $E$. Again, the constants $C$, $x_{0}$ and $x_{i}$ in this equation are the same for linear elastic (Sect. 5.1) and Maxwell viscoelastic (Sect. 5.2) RVEs. However, Eq. (29) relates the macro dynamic viscosity $\bar{\eta}$ to the micro dynamic viscosity $\eta$: the constants $C$, $x_{0}$ and $x_{i}$ in this equation are different from those of the dynamic viscosity fit parameters of Sect. 5.2, and presented in Tables 6 and 7 in the Appendix.

6 Conclusions

Numerical homogenisation can be used to understand the material macroproperties of metamaterials with relatively low cost. Unit cells with a single void or with a viscous inclusion were modelled under periodic boundary conditions. Systematic parametric studies were conducted to investigate the effect of inclusion area, aspect ratio and inclination angle on the macroscopic material properties.

The macroscopic material properties of elastic unit cells studied in this paper can be captured with good accuracy using trigonometric functions, whereas the viscous unit cells show a multiplicative decomposition that consist of a linear elastic trigonometric function and a viscous exponential decay. Unit cells with voids show a macroscale constitutive model similar to the microscale one. On the other hand, the macroscale mechanical properties of the elastic unit cell with viscous inclusion show an enriched constitutive model at the macrolevel while using two simple models, linear elastic and Maxwell viscoelastic, for the microlevel. This enriched macroscale behaviour can be captured accurately with the Standard Solid Model of viscoelasticity. Consistent results were obtained for creep and relaxation tests using a nonlinear regression curve fitting tool to fit stresses and strains with time and obtain the macroscale properties.

The dependence of the homogenised properties on loading rate was checked; simulations show that homogenised properties tend to be constant for strain rates below 0.001 s⁻¹. Homogenised properties at higher strain rates, and in particular their frequency dependence, will be the scope for follow-up research.

Appendix

In this Appendix, we summarise the various values obtained for fitting the constants in the trigonometric expressions for the macroscopic material properties. Tables 2 and 3 contain the elastic modulus constants for a linear elastic RVE with a void, whereas Tables 4 and 5 contain the dynamic viscosity values for a viscoelastic RVE with a void. Finally, Tables 6 and 7 contain the dynamic viscosity values for a linear elastic RVE with a viscoelastic inclusion.

Table 2 Elastic modulus equation constant ($x_{0}$) values for different aspect ratio and area combinations for all types of RVEs

Table 3 Elastic modulus equation constant ($C$) values for different aspect ratio and area combinations for all types of RVEs

Table 4 Dynamic viscosity equation constant ($x_{0}$) values for different aspect ratio and area combinations for RVEs with viscoelastic matrix and void

Table 5 Dynamic viscosity equation constant ($C$) values for different aspect ratio and area combinations for RVEs with viscoelastic matrix and void

Table 6 Dynamic viscosity equation constant ($x_{0}$) values for different aspect ratio and area combinations for RVEs with elastic matrix and viscoelastic inclusion

Table 7 Dynamic viscosity equation constant ($C$) values for different aspect ratio and area combinations for RVEs with elastic matrix and viscoelastic inclusion