1 Introduction

The average kerb weight of passenger vehicles has been growing for the last four decades. The automotive industry has recently been committed to limiting this growth with the aim to reduce the damaging effect of vehicle emissions on the environment. One method to reduce the kerb weight is to apply a multi-material design strategy to the body structure (Cui et al. 2011; Sakundarini et al. 2013; Kim et al. 2014). Specific areas of the body structure pose different requirements on strength and stiffness; utilising appropriate materials in these areas can yield weight reduction, provided that the implications on the joining method do not overshadow the effect of the multi-material design (Seidlitz et al. 2015). Continuous fibre-reinforced polymers (CFRP) display favourable specific strength and stiffness properties (Lau et al. 2018). Hence, structural parts in the body structure are increasingly manufactured with CFRP (Machado et al. 2018). Automotive applications conventionally feature thermoset matrix systems. There are several findings on thermoset polymer composites in the literature that show the maturity of the relevant technologies in automobile and aerospace industries. Extensive performance items of thermoset composites are possible to predict. A recent paper by the author reviews the predictive models developed for such materials during manufacturing (Abouhamzeh et al. 2019). However, European legislation on increased recyclability requirements for newly produced vehicles from 2015 onwards led to the automotive industry investigating the use of thermoplastic matrix systems (European Parliament 2000). Additional merits of using a thermoplastic matrix include better damage tolerance, higher fatigue strength, and mass production capability (Gerstenberger et al. 2016; Sockol et al. 2017; Yao et al. 2018). Furthermore, specific thermoplastic matrix materials are shown to pass through the automotive paint shop without deterioration of relevant mechanical properties (Grätzl et al. 2019). Although CFRTP can offer short cycle times and weight-saving joining techniques over thermoset counterparts, their application in the body structure of existing vehicle models is challenged as they must pass through the automotive paint shop during the manufacturing chain. Significant thermal loads are imposed on structural CFRTP when passing through multiple paint-dryers. This engineering problem must be evaluated prior to successfully applying CFRTP in primary structures of the vehicle (Grätzl et al. 2016, 2018). From a manufacturing point of view, it needs less effort to introduce structural CFRTP into the body structure after the painting process. This is, however, obstructed by the high cost sensitivity of the automotive industry that prevents such measures to be taken for vehicles already in serial production (Mazumdar 2001). Therefore, a simulation approach that assesses the influence of the automotive painting process on the structural behaviour of CFRTP is desirable. The mechanical properties of thermoplastic polymers are significantly affected by thermal loading and viscoelastic behaviour is often observed (Goh et al. 2004; Starkova et al. 2007; Yilmaz and Sinmazcelik 2010; Soós and Goda 2011; Eftekhari et al. 2016). Constitutive equations for viscoelasticity can either be formulated in integral or derivative form (Sawant and Muliana 2008; Ding et al. 2015; Ropers et al. 2016; Dörr et al. 2017). Classical integration schemes can be adopted for the numerical representation of the constitutive equations in integral form. However, such integration schemes inherently result in exponentially larger computational expenses for longer simulations. Utilising a recursive formulation of the constitutive equations is a way of eliminating this disadvantage. Zocher provides a three-dimensional recursive formulation of anisotropic linear viscoelastic constitutive equations (Zocher et al. 1997). A prerequisite for obtaining accurate results with these constitutive equations is that the material is thermorheologically simple and the time–temperature superposition principle applies (Zeltmann et al. 2017). A generalisation to the recursive formulation of Zocher is presented by Ding et al., allowing thermorheologically complex materials to be modelled as well (Ding et al. 2015). Thermoplastic polymers exhibit thermal expansion and are often hydrophilic (Arhant et al. 2016; Sachs and Akkerman 2017; Yabu et al. 2017). These two phenomena must be taken into account to simulate the deformation behaviour accurately. In another work, Ding et al. present a three-dimensional thermo-viscoelastic model including chemical shrinkage without utilising a recursive formulation (Ding et al. 2015). Abouhamzeh et al. present a procedure to model thermo-viscoelasticity concerning materials with general orthotropy and geometry; a recursive formulation is adopted (Abouhamzeh et al. 2015). A recursive formulation has also been used by Abouhamzeh et al. to compute residual stresses in curing simulations (Abouhamzeh et al. 2016). Formerly, Jun et al. adopted a recursive formulation in a fully numerical model and include chemical shrinkage as well as hygrothermal expansion (Jun et al. 2010). The objective of the present study is to develop a simulation approach to numerically analyse the viscoelastic deformation behaviour of CFRTP subjected to the automotive painting process. The difference in the present study, compared to the work of Jun et al. (2010), lies in the semi-numerical procedure that determines the hygrothermal strains of the laminate. This allows to predict the deformation at relatively low computational costs. Validation experiments have been carried out with two levels of geometric complexity to compare the measured out-of-plane deformation of clamped specimens to the simulated ones. Multi-directional (MD) laminates were manufactured for validation purposes with Celstran® CFR-TP PA6-CF60-01 from Celanese Chemical Europe GmbH; a unidirectional (UD) tape of carbon-fibre reinforced polyamide 6. Material characterisation tests were carried out with this material. The results of the material characterisation is briefly displayed in the next section. Extensive details can be found in a previous work (van Dijk et al. 2018). The simulation approach accounts for hygrothermal expansion, polymer shrinkage, and features the orthotropic viscoelastic material behaviour. Examples of the mentioned polymeric phenomena are recrystallisation or change of polymer crystal form. It must be noted that the present study focuses solely on the cathodic dip painting-dryer, which imposes the most severe thermal loading (Streitberger and Dossel 2008).

2 Constitutive model

For the material behaviour of the CFRTP, the recursive integral form of the constitutive equations will be used. The constitutive equations are derived based on the procedure that was first documented by Zocher for orthotropic linear viscoelasticity (Zocher et al. 1997). The derivation of the recursive formulation starts with the Boltzmann integral,

$$\begin{aligned} \sigma _{ij}(\xi ) = \int _{0}^{\xi }C_{ij} (T_{0},\xi -\xi ') \dfrac{\delta \bar{\varepsilon _{kl}}(\xi ')}{\delta \tau} d\tau . \end{aligned}$$
(1)

The order of the elements in the stress tensor is chosen to be in agreement with the commercial finite element software ABAQUS (Dassault Systèmes 2014). The anisotropic time-dependent stiffness coefficients, valid for a chosen reference temperature \(T_{0}\), are denoted by \(C_{ij}(T_{0}, \xi -\xi ')\).

It is noted that the symbol \(\xi \) represents the reduced time as obtained by means of the principle of time–temperature superposition. The superposition principle is founded on the equivalence of increased temperature and accelerated time on the stress relaxation behaviour and is only valid for thermorheologically simple materials (Gutierrez-Lemini 2014). The reduced time is determined with temperature-dependent shift factors, \(a_{T}(T)\), as follows:

$$\begin{aligned} \xi (t) \equiv \int _{0}^{t} \dfrac{1}{a_{T}(T)} d\tau . \end{aligned}$$
(2)

The recursive formulation of the constitutive equations is obtained by introducing an incremental notation of the stress state and reduced time as demonstrated by

$$\begin{aligned} \begin{aligned} \sigma _{ij}(\xi _{n+1}) &= \sigma _{ij}(\xi _{n}) + \Delta \sigma _{ij}, \\ \xi _{n+1} &= \xi _{n} + \Delta \xi . \end{aligned} \end{aligned}$$
(3)

The incremental stress, indicated with \(\Delta \sigma _{ij}\), is defined as displayed by Eq. (4); a necessity that enables the recursive formulation is the definition of the stiffness coefficients by means of a Prony series:

$$ \Delta \sigma _{ij} = \int _{\xi _{n}}^{\xi _{n+1}} C_{ij}( \xi _{n+1}-\xi ') \dfrac{\delta \bar{\varepsilon}_{kl}(\xi ')}{\delta \xi '} d\xi ' + \int _{0}^{\xi _{n}} \Delta C_{ij} \dfrac{\delta \bar{\varepsilon}_{kl}(\xi ')}{\delta \xi '}d\xi ' .$$
(4)

Hence, the stiffness coefficients are defined analogously to a generalised stiffness Maxwell model with \(M\) Maxwell elements. Every non-zero stiffness coefficient can then be represented by a Prony series as

$$ C_{ij}(\xi _{n+1}-\xi ') = {C_{ij}}_{\infty }+ \sum _{m=1}^{M} {C_{ij}}_{m} e^{-(\xi _{n+1}-\xi ')/{\tau _{ij}}_{m}} .$$
(5)

The increment in stiffness coefficient, denoted by \(\Delta C_{ij}\) in Eq. (4), can be defined by making use of the Prony series shown in Eq. (5), to provide the expression

$$ \Delta {C_{ij}}_{m} = \sum ^{M}_{m=1} {C_{ij}}_{m} e^{-(\xi _{n+1} - \xi ')/{\tau _{ij}}_{m}} - \sum ^{M}_{m=1} {C_{ij}}_{m} e^{-( \xi _{n} - \xi ')/{\tau _{ij}}_{m}} .$$
(6)

By utilising the definition of the incremental reduced time and making use of mathematical manipulations on the exponential functions, the increment in stiffness coefficient shown in Eq. (6) can be rewritten as

$$ \Delta {C_{ij}}_{m} = - \sum ^{M}_{m=1} {C_{ij}}_{m} e^{(\xi _{n}- \xi ')/{\tau _{ij}}_{m}} \left (1-e^{-\Delta \xi /{\tau _{ij}}_{m}} \right ) .$$
(7)

Substituting the notation shown in Eq. (4) into the definition of the incremental stress that is depicted in Eq. (7) yields the desired incremental notation, namely

$$\begin{aligned} \begin{aligned} \Delta \sigma _{ij} &= \int \limits ^{\xi _{n+1}}_{\xi _{n}} \left ({C_{ij}}_{ \infty }+ \sum \limits ^{M}_{m=1} {C_{ij}}_{m} e^{-(\xi _{n+1}-\xi ')/{ \tau _{ij}}_{m}} \right ) \dfrac{\delta \bar{\varepsilon}_{kl}(\xi ')}{\delta \xi '} d\xi ' \\ & \quad - \int \limits ^{\xi _{n}}_{0} \sum \limits ^{M}_{m=1} {C_{ij}}_{m} e^{-(\xi _{n}-\xi ')/{\tau _{ij}}_{m}} \left (1-e^{-\Delta \xi /{ \tau _{ij}}_{m}} \right ) \dfrac{\delta \bar{\varepsilon}_{kl}(\xi ')}{\delta \xi '} d\xi '. \end{aligned} \end{aligned}$$
(8)

The reduced time derivative of the strain, shown in Eq. (8), is linearised to remove the differential from the integral. It is noted that this linearisation step introduces linearisation errors into the constitutive model based on the size of the reduced time step, represented with \(\Delta \xi \). The definition of the linearised reduced time derivative of the strain is

$$\begin{aligned} G_{\varepsilon }\equiv \dfrac{\Delta \bar{\varepsilon}_{kl}}{\Delta \xi '}. \end{aligned}$$
(9)

The linearisation step implies that the reduced time derivative of the strain is assumed to be constant across the region of linearisation. Hence, the dependency of the strain derivative on the reduced time disappears. This allows the introduced linearisation, shown in Eq. (9), to be substituted in the incremental notation of the stress, displayed in Eq. (8), and to be taken out of the integral. The result of these steps is

$$\begin{aligned} \begin{aligned} \Delta \sigma _{ij} &= G^{+}_{\varepsilon }\int \limits ^{\xi _{n+1}}_{ \xi _{n}} \left ({C_{ij}}_{\infty }+ \sum \limits ^{M_{m}}_{m=1} {C_{ij}}_{m} e^{-(\xi _{n+1}-\xi ')/{\tau _{ij}}_{m}} \right ) d\xi ' \\ & \quad - G^{-}_{\varepsilon }\left (1-e^{-\Delta \xi /{\tau _{ij}}_{m}} \right ) \int \limits ^{\xi _{n}}_{0} \sum \limits ^{M_{m}}_{m=1} {C_{ij}}_{m} e^{-(\xi _{n}-\xi ')/{\tau _{ij}}_{m}} d\xi '. \end{aligned} \end{aligned}$$
(10)

The symbols \(G^{+}_{\varepsilon}\) and \(G^{-}_{\varepsilon}\) in Eq. (10) denote the strain rate from \(\xi _{n+1}\) to \(\xi _{n}\) and \(\xi _{n}\) to \(\xi _{n-1}\), respectively, and are assumed to be constant as displayed in Eq. (9). The final recursive formulation of the constitutive equations is shown in Eq. (11). The intermediate steps to obtain Eq. (11) from Eq. (10) are omitted due to excessive size. The result is

$$\begin{aligned} \begin{aligned} \Delta \sigma _{ij} & = \Delta \bar{\varepsilon}_{kl} \left ({C_{ij}}_{ \infty }+ \dfrac{1}{\Delta \xi} \sum \limits ^{M_{m}}_{m=1} {\eta _{ij}}_{m} \left (1-e^{-\Delta \xi /{\tau _{ij}}_{m}} \right ) \right ) \\ & \quad - \left (1-e^{-\Delta \xi /{\tau _{ij}}_{m}} \right ) \left [e^{- \Delta \xi /{\tau _{ij}}_{m}} \cdot R(\xi _{n-1}) + G^{-}_{ \varepsilon }\sum \limits ^{M_{m}}_{m=1} {\eta _{ij}}_{m} \left (1-e^{- \Delta \xi /{\tau _{ij}}_{m}} \right ) \right ]. \end{aligned} \end{aligned}$$
(11)

The symbol \(R(\xi _{n-1})\) in Eq. (11) denotes the recursive part of the stress and is defined as depicted in Eq. (12). This recursive part must be calculated at the end of each solution step and stored as an internal variable for the next step:

$$\begin{aligned} R(\xi _{n}) = e^{-\Delta \xi /{\tau _{ij}}_{m}} R(\xi _{n-1}) + G^{-}_{ \varepsilon }\sum ^{M_{m}}_{m=1} {\eta _{ij}}_{m} \left (1-e^{- \Delta \xi /{\tau _{ij}}_{m}} \right ). \end{aligned}$$
(12)

3 Laminate properties and hygrothermal strains

A method is presented to obtain the hygrothermal strains of the MD laminates by means of classical laminate theory whilst taking into account the temperature-dependency of the mechanical properties. The first part of this procedure is a series of micromechanical calculations to obtain the longitudinal relaxation modulus and shear modulus of a UD layer. Moreover, an empirical relationship between the transverse stiffness and the Poisson’s ratio is adopted to implement temperature-dependency for the Poisson’s ratio. The second part of the presented procedure is used to calculate the hygrothermal strains of an MD laminate and to generate the stiffness coefficients that are laminate-dependent as input for the constitutive equations shown in Eq. (11).

The supplier of the UD tape does not provide information on the fibre type. Hence, based on quasi-static tensile tests of the UD tape, properties for high tenacity fibres were taken as input for the subsequent equations of the material model. The stiffness of the carbon fibre constituent is assumed to be constant within the temperature range. This assumption is supported by the degradation in stiffness of only 2.5% at a temperature of 1000 ∘C in comparison to room temperature for PAN-based fibres (Sauder et al. 2002). Thus, we can conclude that the properties of a unidirectional layer in fibre-direction are barely influenced by temperature (Melo and Radford 2005). However, the stress relaxation of the matrix material leads to the time-dependency of laminate properties.

The matrix stiffness is calculated from the measured (temperature-dependent) transverse stiffness of the UD tape using the classical rule-of-mixtures (Whitney 1967),

$$\begin{aligned} E_{m} = v_{m} \left (\dfrac{1}{\bar{E}_{22}} - \dfrac{v_{f}}{{E_{22}}_{f}} \right )^{-1}. \end{aligned}$$
(13)

The fibre volume content, denoted in Eq. (13) with \(v_{f}\), is 0.48 as provided by the supplier. The longitudinal relaxation modulus of the UD laminate is calculated by means of the rule-of-mixtures as

$$\begin{aligned} \bar{E}_{11} = v_{f} \cdot {E_{11}}_{f} + v_{m} \cdot E_{m}. \end{aligned}$$
(14)

Both the major and minor Poisson’s ratios are often reported in the literature to be assumed independent of temperature (Chen et al. 2014). However, this assumption is documented to lead to significant simulation inaccuracies (Pandini and Pegoretti 2011). Therefore, in this study, the major Poisson’s ratio is also counted to be dependent on temperature by adopting the empirical relationship as shown in Eq. (15) (Giencke and Meder 1981). The symbols \(\tilde{\nu}_{12}\) and \(\tilde{E}_{22}\) denote experimentally determined values of the major Poisson’s ratio and transverse stiffness under equal temperature conditions. The temperature-dependent major Poisson’s ratio, indicated with \(\bar{\nu}_{12}\), can then be determined with the temperature-dependent transverse stiffness, \(\bar{E}_{22}\). The latter is known from DMA experiments (van Dijk et al. 2018):

$$\begin{aligned} \bar{\nu}_{12} = 0.5 - \left (0.5 - {\tilde{\nu}_{12}} \right ) \dfrac{\bar{E}_{22}}{\tilde{E}_{22}}, \end{aligned}$$
(15)

which results in a temperature-dependent major Poisson’s ratio for the matrix that is calculated using

$$\begin{aligned} {\nu _{12}}_{m} =\dfrac{1}{v_{m}} \left (\bar{\nu}_{12} - v_{f} \cdot {\nu _{21}}_{f} \right ). \end{aligned}$$
(16)

The matrix shear modulus is calculated with the isotropic relation

$$\begin{aligned} {G_{12}}_{m} = \dfrac{E_{m}}{2 \left (1+{\nu _{12}}_{m} \right )}. \end{aligned}$$
(17)

The last step in obtaining the UD layer properties is to calculate the shear modulus of the UD laminate with the rule-of-mixtures

$$\begin{aligned} \bar{G}_{12} = \dfrac{{G_{12}}_{m} \cdot {G_{12}}_{f}}{v_{m}\cdot {G_{12}}_{f} + v_{f} \cdot {G_{12}}_{m}}. \end{aligned}$$
(18)

Hygrothermal strains and the stiffness coefficients of the MD laminate are determined based on classical laminate theory in an incremental manner. The stiffness matrix of an orthotropic individual ply in its local coordinate system is defined as (Kassapoglou 2013)

$$\begin{aligned} \mathbf{Q} = \begin{bmatrix} Q_{11} & Q_{12} & 0 \\ Q_{12} & Q_{22} & 0 \\ 0 & 0 & Q_{66} \end{bmatrix}. \end{aligned}$$
(19)

The entries of the stiffness values are computed with the expressions that are shown in Eq. (20), where all parameters are time- and temperature-dependent (Kassapoglou 2013):

$$\begin{aligned} \begin{aligned} Q_{11} &= \dfrac{E_{11}}{1-\nu _{12}\nu _{21}}, \\ Q_{12} &= \dfrac{\nu _{12}E_{22}}{1-\nu _{12}\nu _{21}}, \\ Q_{22} &= \dfrac{E_{22}}{1-\nu _{12}\nu _{21}}, \\ Q_{66} &= G_{12}. \end{aligned} \end{aligned}$$
(20)

A standard transformation is carried out to reduce the ply’s stiffness matrix from its local coordinate system to the global coordinate system (Kassapoglou 2013),

$$\begin{aligned} \bar{\mathbf{Q}}_{i} = \mathbf{T_{1}}^{-1}(\theta _{i}) \cdot \mathbf{Q} \cdot \mathbf{T_{2}}(\theta _{i}). \end{aligned}$$
(21)

The incremental hygrothermal resultants of the MD laminate are calculated with Eq. (22). The ply-level incremental thermal and hygroscopic resultants are indicated with \(\Delta {N_{T}}_{i}\) and \(\Delta {N_{M}}_{i}\), respectively. The symbol \(z\) represents the coordinates of the plies in thickness-direction:

$$\begin{aligned} \begin{aligned} \Delta {N_{T}}_{i} &= \left [z(i+1) - z(i) \right ] \Delta T \cdot \bar{\mathbf{Q}}_{i} \cdot \alpha _{T}(t,T), \\ \Delta {N_{M}}_{i} &= \left [z(i+1) - z(i) \right ]\Delta M \cdot \bar{\mathbf{Q}}_{i} \cdot \beta _{M}. \end{aligned} \end{aligned}$$
(22)

The total incremental hygrothermal resultant of the MD laminate is defined as the sum of the individual incremental hygroscopic and thermal resultants,

$$\begin{aligned} \Delta N = \sum _{i=1}^{I} {N_{T}}_{i} + \sum _{i=1}^{I} {N_{M}}_{i}. \end{aligned}$$
(23)

The laminate in-plane stiffness matrix, \(\mathbf{A}\), can be determined as

$$\begin{aligned} \mathbf{A} = \sum _{i=1}^{I} \bar{\mathbf{Q}}_{i} \cdot \left [ z(i+1) - z(i)\right ]. \end{aligned}$$
(24)

The incremental hygrothermal strain of the MD laminate is obtained with Eq. (25). It is noted that this inversion is allowed as the MD laminates are considered to be symmetric and balanced (Kassapoglou 2013):

$$\begin{aligned} \Delta \varepsilon (\Delta t) = \mathbf{A}^{-1} \cdot \Delta N. \end{aligned}$$
(25)

The final step is to generate the stiffness coefficients for the numerical model from the in-plane compliance matrix as

$$\begin{aligned} \mathbf{a} = \mathbf{A}^{-1} = \begin{bmatrix} a_{11} & a_{12} & 0 \\ a_{12} & a_{22} & 0 \\ 0 & 0 & a_{66} \end{bmatrix}, \qquad \text{where} \qquad \begin{aligned} C_{11} &= a_{11}, \\ C_{12} &= a_{12}, \\ C_{22} &= a_{22}, \\ C_{44} &= a_{66}. \end{aligned} \end{aligned}$$
(26)

4 Finite element implementation

In the present study, three sequential numerical simulations constitute the simulation approach, carried out in the commercial finite element software ABAQUS. A heat transfer simulation provides the temperature distribution throughout the specimen that is required for the follow-up mass diffusion simulation. Lastly, a general stress simulation is carried out to predict the deformation and stresses in the specimen due to the imposed thermal load by the cathodic dip painting-dryer. The heat transfer and mass diffusion are assumed to be uncoupled, making the sequential simulation approach valid. It is noted that the first two simulations share an identical mesh. The implementation of the constitutive equations shown in Eq. (11) is only required in the last simulation and was performed with a material user subroutine, or UMAT in ABAQUS. The second part of the procedure that is described in Sect. 3 is used between the mass diffusion simulation and the stress simulation to determine the hygrothermal strains based on the temperature distribution and time-dependent moisture content, resulting from the first two simulations. A full series of simulations was performed with the measured thermal conditions of every individual validation experiment to obtain complete numerical results.

4.1 Heat transfer simulation

The temperature distribution throughout the specimen is simulated by means of a heat transfer simulation with elements of type DC3D8. The heat transfer is assumed to be one-dimensional in thickness direction and convection is assumed to be the only mechanism of heat transfer from the environment into the specimen. The convection is implemented with the surface film condition interaction in ABAQUS. The governing expression for convection is displayed in Eq. (27). The symbols \(q\) and \(h\) in Eq. (27) represent the heat flux and convection coefficient, respectively. The air and surface temperatures are denoted with \(T_{air}\) and \(T_{sur}\), respectively:

$$\begin{aligned} q = h \cdot A \left (T_{air} - T_{sur}\right ). \end{aligned}$$
(27)

Both the maximum increment in time and in temperature were limited to 4 s and 1 ∘C, respectively, to restrain linearisation errors.

4.2 Mass diffusion simulation

The thermally-driven moisture diffusion out of the specimen is simulated by means of a mass diffusion simulation with corresponding elements of type DC3D8 and requires the nodal temperatures to be known as a function of time. The nodal temperatures are used from the heat transfer simulation and the simplicity of making use of equal meshes for both simulations is noted here. The mass diffusion is assumed to be one-dimensional in the thickness direction. The maximum increments in time and in concentration were chosen to be 4 s and 0.001. No mass diffusion simulation was carried out for dry specimens. The diffusion coefficients for the investigated material have been determined by means of thermogravimetric analysis, which is documented in our previous work (van Dijk et al. 2018).

4.3 Stress simulation

The resulting deformation of the specimen due to the hygrothermal strains is predicted by means of a general implicit stress simulation that accounts for geometric non-linearity. The used finite elements are fully integrated linear 3D solids, or C3D8. The two ends of each specimen were modelled to be clamped and the presence of symmetry was used to reduce computational costs. The constitutive equations in Eq. (11) were implemented through a UMAT. The calculations in the UMAT involve updating the recursive part of the stress, from the known solution to the incremental solution, and calculating the strain rate for the incremental solution. Convergence studies were carried out to determine required time step and element size of the mesh to obtain satisfactory accuracy for different specimens that were used for validation purposes. The results of this and the different specimens are described in Sect. 5. The required parameters for the stress simulation are the coefficients of the thermal and moisture expansion, the major Poisson’s ratio at room temperature, and the values to describe the generalised Maxwell model in the transverse stiffness direction of a UD ply. The latter is indicated by \(C_{22}\) in Eq. (1). The mentioned parameters have been experimentally determined through dilatometer experiments, digital image correlation, and dynamic mechanical analysis. For the presented model, a total of 233 material parameters are involved in the material model, from which a large number are entered into the Prony series. To find the input parameters for this model, experimental measurements are utilised. The details and results of these experiments are reported in a previous publication (van Dijk et al. 2018).

5 Numerical results and validation

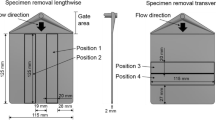
Clamped specimens have been subjected to a thermal loading profile that represents an exemplary thermal envelope of a cathodic dip painting-dryer. As long as the specimens are clamped at the edges, the produced thermal stresses will make them warp laterally. The out-of-plane displacements of the center of the clamped specimens are measured to compare with the numerical results. It is noted that these validation experiments have been carried out with two types of specimens. The first type of specimen is referred to as a coupon and features the geometry of a tensile test specimen; it measures \(250 \times 25 \) mm2. The geometry of the roof bow that is currently featured in the BMW 7 Series has been used for the second type of specimens and is referred as the component. All validation specimens are either completely dried in an oven at 80 ∘C or conditioned to moisture saturation in an environment chamber at 70 ∘C and 62% relative humidity to ensure repeatable conditions.

Measuring the displacement of the specimens has been carried out by means of digital image correlation (DIC) with the PONTOS optical measurement system, a photo of the experimental setup is shown in the left-hand side of Fig. 1. Samples are prepared by the second author at BMW Group. The specimens were clamped on both ends in the vertical direction. The small test setup has one bolt running through the specimen on each end. The large test setup has two bolts running through the specimen on each end. The optical system performs the measurement by the 12M sensor every minute. During the displacement measurement, the air circulation system inside the oven is temporarily deactivated to prevent distortion of the images. Two fixtures have been manufactured from graphite to limit the thermal expansion of the clamping areas for both specimen types during the experiment. The right-hand side of Fig. 1 displays the fixtures and the clamped specimens taken by the optical measurement system. A control measurement of the empty coupon fixture confirms the low thermal expansion of the fixture; the displacement in longitudinal direction between the two clamping areas is \(\approx 0.05\) mm at maximum temperature conditions, which is within the range of the measurement error of the DIC system. The convection coefficient, used for the heat transfer simulation, was empirically determined by measuring the air temperature and the surface temperature of a freely suspended specimen during the control measurement. The convection coefficient was then adjusted in the simulation until the numerical results of the surface temperature of the specimen were within 5% of the experimental values, yielding a convection coefficient of 25 Wm−2 ∘C−1.

Fig. 1
figure 1

Experimental setup used for measuring the center out-of-plane displacement for validation

Full size image

The numerical results and the validation measurements of the coupon level with a laminate of \([90^{\circ}_{14}]\) in dry and moisture-saturated states are shown in Fig. 2. Since there are no fibres along the specimen length, it is expected that the sample would deform laterally more than in the other directions. In another words, the laminate will have a higher thermal expansion along the length. The measured air temperature is also included in the graphs. The maximum time step and target element size of the mesh were set to 4 s and 2 mm, after conducting the convergence studies. From the figures, it can be observed that due to the diverse effects of moisture and temperature, i.e. opposite signs of the corresponding strains, the deflection of the moist specimens is less than that for the dry. A similar presentation for the component specimen with a lay-up of \([90^{\circ}_{14}]\) is provided in Fig. 3, although only results for the moisture-saturated specimen are shown as the dry specimen failed prematurely. The maximum time step and element size of the mesh for the component simulations were set to 0.25 s and 2 mm, respectively, after again checking for numerical convergence. Figure 4 displays the numerical result and measured out-of-plane displacement at the center of a dry component with a lay-up of \([(+60^{\circ}/-60^{\circ})_{3}/0^{\circ}]_{s}\). Correct clamping conditions were not in place for the moisture-saturated component during the application of the thermal load and the experimental results are therefore discarded. As it can be seen, the deformation is less than the previous lay-up, in which there was no fibre contribution along the specimen length. A comparison between the numerical results and the optical measurement is provided for both a dry and moisture-saturated component with a lay-up of \([0^{\circ}/+45^{\circ}/-45^{\circ}/0^{\circ}_{4}]_{s}\) in Fig. 5. The latter two lay-ups in the verification examples show the accuracy of the model, taking the coupling between the material stiffness components into account. It can be observed by qualitatively comparing the numerical results and the measured displacement values that an excellent agreement is obtained. Quantitative discrepancies between simulation and experiment at the last moment before cooling down are shown in Table 1. The large discrepancy for the moisture-saturated component with a lay-up of \([0^{\circ}/+45^{\circ}/-45^{\circ}/0^{\circ}_{4}]_{s}\) is attributed to the large degree of experimental scatter that was found in the coefficients of hygroscopic expansion in longitudinal direction of the UD material (van Dijk et al. 2018). Performing a large number of material characterisations to obtain more accurate coefficients of hygroscopic expansion can rule out a possible discrepancy due to material scatter. As another observation, the component with \([(+60^{\circ}/-60^{\circ})_{3}/0^{\circ}]_{s}\) lay-up resulted in much higher deflections compared to those with \([0^{\circ}/+45^{\circ}/-45^{\circ}/0^{\circ}_{4}]_{s}\), as a higher volume fraction of fibres in the specimen longitudinal direction limits the lateral deflection due to less induced expansion.

Fig. 2
figure 2

Numerical and experimental results of the measured coupon with a \([90^{\circ}_{14}]\) lay-up in dry and moisture-saturated state, including the temperature profile

Full size image
Fig. 3
figure 3

Numerical and experimental results of the measured component with a \([90^{\circ}_{14}]\) lay-up in moisture-saturated state, including the temperature profile

Full size image
Fig. 4
figure 4

Numerical and experimental results of the measured component with a \([(+60^{\circ}/-60^{\circ})_{3}/0^{\circ}]_{s}\) lay-up in dry state, including the temperature profile

Full size image
Fig. 5
figure 5

Numerical and experimental results of the measured component with a \([0^{\circ}/+45^{\circ}/-45^{\circ}/0^{\circ}_{4}]_{s}\) lay-up in dry and moisture-saturated state, including the temperature profile

Full size image
Table 1 Discrepancies between numerical results and validation measurements at the end of the maximum temperature condition
Full size table

6 Conclusion

A simulation approach was developed for the numerical analysis of the viscoelastic deformation behaviour of CFRTP for manufacturing processes of the automobile industry. The simulation approach was validated against experiments in which both dry and moisture-saturated specimens, manufactured with MD laminates, were subjected to a temperature profile representing an automotive cathodic dip painting-dryer. A recursive formulation of orthotropic linear viscoelastic constitutive equations was implemented to reduce computational costs and data volume. By a quantitative comparison of the numerical results with optical measurements from validation experiments, it was concluded that a good agreement exists between the two. The presented simulation approach allows analysing hygrothermal viscoelastic deformation behaviour of continuous fibre-reinforced thermoplastics. Including hygrothermal viscoelasticity is necessary to accurately simulate the structural response of CFRTP when passing through the automotive painting process, a standard process during the development of new series vehicles. As it can be seen from the results, the lateral defection changes considerably in case of moisture-saturated components which shows the noticeable effect of humidity in the predictions based on modelling simulation. Moreover, the presented simulation approach is valuable for numerically assessing the influence of different lay-ups in terms of the structural response of a body structure that passes through automotive drying ovens.