1 Introduction

For various research fields, i.e., machine learning, pattern recognition, network security, facial expression recognition, education, biology, psychology, medicine, many high-dimensional data are used to describe the complex subject [23, 33, 34, 48, 51].

The high-dimensional data are not easy to process due to the issues, such as “dimension disaster”, the cost of the hardware, and the execution times. Hence, the dimensionality reduction technology has attracted attentions which can remove noise data as well as find the valuable information by using the predefined rules or constructed models [4].

The main purpose of dimensionality reduction is to search a projection matrix in original high-dimensional data space, obtain the novel data with lower dimensions so that the data become divisible in the low-dimensional feature subspace and remove unnecessary outliers. Generally, the existing dimensionality reduction ways are broadly classified to feature extraction ways and feature selection ways [18, 29]. Feature extraction ways derive useful information from the original data to construct the novel data description, while feature selection ways exploit important information among original data with certain evaluation schemes, removing the influence of noise, outliers and redundant features and, at the same time, preserving the representative features [29].

For the number of obtaining labels in training procedure, feature selection ways contain supervised ways, semi-supervised ways, and unsupervised ways [40, 42]. In supervised ways, labels guide the selection of discriminant features according to certain criteria [21, 44]. Semi-supervised ways select important features using a particularly small percentage of labeled data and the numerous unlabeled data [22, 54]. For unsupervised ways, they employ various score evaluation metrics to exploit features through the uniqueness of features, such as variance [42, 47]. However, labels are difficult to mark by experts and the annotation cost is expensive. By this reason, unsupervised feature selection ways have become the important technology for the unseen and unknown data.

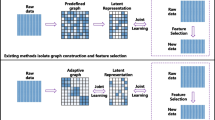
In unsupervised feature selection, many researchers usually embed the manifold regularization method into the feature selection model to find low-dimensional embedding, and apply smoothness to adjacent cluster labels for obtaining more compact data representation [17, 37]. For example, Cai et al. achieved good clustering performance by jointly learning the importance of each feature in different dimensions [7]. Liu et al. proposed a method by combining the global similarity with the local similarity to search the subset of features [26]. Feng et al. used automatic encoder to find the representative features subset, preserving the local correlations among data through the hidden layer [13]. Moreover, the common methods explore the representative features by the conducted model and utilize the selected features to connect with the task learning. In this way, it could easily lead to sub-optimal solution by these two steps, that is, the selected features are not suitable to task learning while task learning is not related to the model construction.

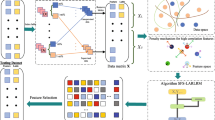
To solve the above issues, we design a novel unsupervised feature selection approach via taking the completed sample correlations and feature dependencies into account in a unified framework. Specifically, we consider sample importance to consider global structure among the samples by using a self-representation way, where each sample can be represented by all samples linearly, and a dynamic graph representation can be learned to consider local structure between the samples during the procedure. Besides, we take the dependencies between the features into account by mutual information, and then, a controllable sparse learning (i.e., ℓ2,p-norm) is utilized to remove the noisy and redundant features. Moreover, rank constraint and neighbors constraint is designed to conduct graph partition and to search the optimal number of neighbor, respectively, for clustering task and each sample. The final experiments on eight data sets with nine comparison methods test the clustering performance.

We summarize the contributions of the proposed method in the following.

  • The proposed method considers completed sample correlations and feature dependencies in a joint unsupervised model, it not only extends the novel method of unsupervised learning, but it also indicates the flexibility of embedded way which can embed different technologies to solve the issues (e.g., guarantee the optimization of model and task simultaneously in the framework of unsupervised learning) for various types of data. Moreover, experiments on eight data sets have verified the validity of the proposed method in comparison to other methods.

  • The proposed method provides a reliable unsupervised learning method and interpretable features for task learning. Besides, we design a new optimization algorithm to optimize our proposed method and obtain a global optimal solution.

The flow of the remaining parts is described as: information about related works is given in Section 2. The descriptions of proposed method is showed in Section 3. In Section 4, the optimization process, the convergence analysis, the complexity analysis, and deterministic parameter are discussed. Section 5 shows the experiments’ performance. Finally, a conclusion is given in Section 6.

2 Related work

Feature selection focuses on searching a small percentage of features to represent all data, and it is useful to help unseen data to obtain the reliable predict label for the task learning [3, 58]. Many feature selection algorithms have been developed including nature-inspired algorithms [5, 46]. However, since a great expense of obtaining labels in real world, unsupervised learning has become the mainstream way to conduct feature selection.

Generally, the existing unsupervised learning schemes regarding the strategies of feature selection contain three types of categories, i.e., filter-based, wrapper-based and embedded-based [1, 2, 20]. Specifically, the filter-based approaches select the informative feature subset by ranking the scores of features according to the predefined evaluation criteria [36, 38, 45]. For example, Cekik and Uysal proposed a filter-based unsupervised learning method to conduct shot text classification by the rough set theory [8]. Solorio et al. devised a filter-based learning method to recognize mixed features by considering information theory and spectral way [43]. He et al. conducted a graph Laplacian to preserve the local correlations among the data and select the subset of features with larger scores by decomposing the Laplacian matrix [17]. Yao et al. designed the locally linear embedding score to select the important features for the clustering task [52].

Compared with the filter-based schemes, the wrapper-based schemes construct the learner to search features so better features selection performance can be obtained [42]. Zhao et al. proposed a joint architecture considering both supervised and unsupervised, and utilized the graph Laplacian score by taking the correlation of features into account [55]. Chen et al. presented a framework by integrating a cosine measurement and support vector machine to select important features and obtain the classification performance [9]. Nouri-Moghaddam et al. proposed a wrapper feature selection method utilizing the forest optimization method which selects the informative features and extracts the non-dominated solution [32]. Feofanov et al. designed a wrapper feature selection method with partially labeled data, which distributes pseudo labels to unlabeled data and conducts a feature selection genetic method to guarantee sparsity and to remove unimportant features [14]. Hence, the wrapper-based methods can achieve the better classification results by conducting the feature selection method.

However, the filter-based method is heavily dependent on the selected score calculation, so the effect of the score method directly determines the final classification or clustering performance. Besides, the simple learning method in wrapper is hard to solve the data with high dimensions, leading to the consumption of heavy computational resources. Moreover, both the filter and the wrapper methods select the features independently, and it may lead to a sub-optimal solution to model construction for the tasks (e.g., classification or clustering). Consequently, the filter-based and the wrapper-based schemes may not solve the real issues in practice. In order to solve the above issues, the embedded-based method is proposed and show the potential ability for the tasks. This is because the embedded-based methods provides a joint model to combine feature selection with task learning, which have demonstrated better performance for a variety of tasks [28, 39, 42, 53]. For example, Zhu et al. conducted a feature selection combined with coupled dictionary learning, where dictionary learning is used to reconstruct the data and a coefficient matrix is learned to represent feature importance [56]. Zhu et al. [57] used subspace clustering to guide embedded-based unsupervised model via iteratively learning the clustering labels and important features. Zhu et al. proposed a robust unsupervised spectral feature selection which considers the local structure of samples and the global structure of features, and employs the sparse learning (i.e., ℓ2,1-norm) to remove the redundant features [58]. Liu et al. presented a robust neighborhood embedding method to select the important subset of features by minimizing the error of loss function and the regularization term [27]. Lim and Kim proposed a feature dependency-based unsupervised learning model to maintain the correlations between the features by using information theory [24]. Wu et al. developed an adaptive embedded-based way to search reliable and informative features subset in the intrinsic subspace [50]. Hence, the embedded-based methods demonstrate better learning ability and have easier operability for selecting a reliable subset of features.

3 Method

3.1 Notation

The used symbol markers in Table 1 and the scalar, vector, and matrix is defined by normal italic letter, boldface lower-case, and boldface upper-case letter, respectively, in this section.

Table 1 The used symbol markers
Full size table

3.2 Completed sample correlations

Given an original matrix \(\mathbf {X} \in \mathbb {R}^{d \times n}\), where n and d, respectively, denote the number of samples and features. The common supervised feature selection is

$$ \begin{array}{@{}rcl@{}} \underset{\mathbf{W}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{Y} \|_{F}^{2} + \gamma \|\mathbf{W}\|_{2,1}, \end{array} $$
(1)

where coefficient weight is \(\mathbf {W} \in \mathbb {R}^{d \times c}\), the reduced dimension is c, regularization term is ∥.∥2,1 and γ is the trade-off positive parameter. However, the labels are costly to obtain in practise due to the huge volume of data limitation as well as the expensive access to labels, so that (1) has a limitation to apply for numerous data in various research topics.

To keep the relations between the samples, sample self-representation is employed to search the global correlations of samples via assuming that each sample has the potential correlations with other parts of samples, that is, we can represent every sample by its important neighbor ones. It is an inherent property of one sample and has shown better performance in machine learning [19, 25]. Specifically, a linear combination way can be conducted to each sample x⋅,i in X and we have a sparse unsupervised feature selection model by

$$ \begin{array}{@{}rcl@{}} \underset{\mathbf{W}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \gamma \|\mathbf{W}\|_{2,1}, \end{array} $$
(2)

where \(\mathbf {S} \in \mathbb {R}^{n*n}\) is self-representation matrix, where each row is defined as \(\mathbf {W}^{T}\mathbf {x}_{\cdot ,i} \approx \) \({\sum }_{j=1}^{n} \mathbf {W}^{T}\mathbf {x}_{\cdot ,j} s_{i,j}\). Equation (2) can obtain dependable self-representation weight matrix and the reasons can be showed as follows, (1) there exist abundant noisy features in the original data set, but WTX can project the original data X into the low-dimensional subspace, obtaining the “clean” data. (2) It uses the inter-reconstruction representation and nearest neighbors to represent each sample that may cover the manifold structure among the original data set. Obviously, the larger value the si,j has, the more important the related neighbors are involved in the self-representation weight matrix.

Equation (2) has shown the global relations of samples, but the completed relationship is composed of global representation and local representation. Hence, we describe the local correlation consideration by

$$ \begin{array}{@{}rcl@{}} \underset{\mathbf{W}}{\min} {\sum}_{i,j}^{n} \|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}, \end{array} $$
(3)

where each element si,j represents the strength of similarity between two samples (i.e., x⋅,i and x⋅,j) in Euclidean space. That is, the value of si,j is larger while x⋅,j is close to x⋅,i, otherwise si,j is small. Besides, a Gaussian kernel is employed to calculate the distance between samples, such as \(d(\mathbf {x}_{\cdot ,i}, \mathbf {x}_{\cdot ,j}) = \exp (- \|\mathbf {x}_{\cdot ,i} - \mathbf {x}_{\cdot ,j}\|_{2}^{2} /2 \sigma )\) where σ is an adjustable parameter.

Although (2) or (3) are widely used in the existing unsupervised feature selection works [18, 35], there exist various aspects to improve the above models. (1) Both (2) and (3) have to select the important adjacent samples (i.e., the value of K) in advance since the size of K is essential parameter to model construction, but the predefined identify size K to each sample may lead to capturing inaccurate manifold information among data [11]. For example, if K takes the small value, it is hard to capture the important neighboring information of each sample. In contrast, the selected neighboring samples may contain uncorrelated ones while the vale of K is larger. (2) The parameter σ controls the size of edge weights between each samples and its neighbors in the Gaussian kernel function, but it is a time-consuming process. In this way, it increases the difficulty of model construction as well as rises the time complexity of dealing with big data. (3) As we examine this formula (3) carefully, we find the graph matrix is learned from the original data projection by WT in the intrinsic subspace. In other words, graph matrix is dependent on the weight matrix, the reverse is not true.

Motivated by the above discussions, we modify (3) by the following two aspects, (1) a joint model is conducted to learn graph matrix and weight matrix simultaneously, and each of them iteratively optimize itself by alternating mutual iterative optimisation until obtaining their optimal results; (2) the distribution of the samples in the intrinsic subspace are considered to search optimal graph representation, as well as constraints that are designed to find optimal number of neighbors for each sample, rather than employ both K and σ to conduct a fixed graph representation. Hence, we integrate (2) with (3) in a joint structure and design the new objective function as follows,

$$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W},\mathbf{S}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \gamma \|\mathbf{W}\|_{2,1} \\ && \quad + \alpha \left( {\sum}_{i,j}^{n} \left( \|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \|\mathbf{s}_{i,\cdot}\|_{2}^{2}\right)\right)\\ && s.t., \forall i, {\mathbf{s}}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \text{if } j \in \mathcal{N}(i), \text{otherwise } 0, \end{array} $$
(4)

where α and β are trade-off parameters, \(\|\mathbf {s}_{i,\cdot }\|_{2}^{2}\) is utilized to avoid trivial solution, \(\mathcal {N}(i)\) denotes the nearest neighbors set for i-th sample, and \(\mathbf {s}_{i}^{T} \mathbf {1} = 1\) achieves shift invariant similarity.

Different from the previous unsupervised feature selection approaches [19, 25, 31, 58], our (4) conducts a dynamic graph matrix via considering completed sample correlations (i.e., global message and local information) and an adaptive weight matrix in a joint framework. Obviously, each sample by our method can adaptively select the different number of nearest neighbors and can take global information and local information into account at the same time.

3.3 Feature dependency consideration

An optimal subset of features are learned through all features during feature selection and the corresponding common time complexity is O(2d). However, it may result in non-trivial problem. By this reason, we convert the combination way into an estimation way, that is, we employ mutual information [36] to consider the feature dependencies rather than use the iterative feature combination approach. Specifically, according to the definition of mutual information in information theory, the joint distribution and the marginal distribution are two basic variables. Then, mutual information is the relative entropy between joint distribution and marginal distribution. Hence, we consider mutual information between features that can be represented by

$$ \begin{array}{@{}rcl@{}} MI(\mathbf{x}_{\cdot,i};\mathbf{x}_{\cdot,j}) = F(\mathbf{x}_{\cdot,i}) + F(\mathbf{x}_{\cdot,j}) - F(\mathbf{x}_{\cdot,i},\mathbf{x}_{\cdot,j}), \end{array} $$
(5)

where \(F(\mathbf {x}_{\cdot ,i},\mathbf {x}_{\cdot ,j}) = - {\sum }_{i}^{d} {\sum }_{j}^{d} P(\mathbf {x}_{\cdot ,i},\mathbf {x}_{\cdot ,j})\log \frac {P(\mathbf {x}_{\cdot ,i},\mathbf {x}_{\cdot ,j})}{P(\mathbf {x}_{\cdot ,i}) P(\mathbf {x}_{\cdot ,j})}\) denotes the joint entropy, F(x⋅,i) and F(x⋅,j) denote the marginal entropy.

Due to the mutual information representing degree of interdependence between features, we calculate the dependence matrix Q to preserve the feature dependency and it can be described as

$$ \begin{array}{@{}rcl@{}} Q_{i,j} = MI(\mathbf{x}_{\cdot,i};\mathbf{x}_{\cdot,j}), ~~ if~~i \neq j; ~~ Q_{i,j} = {\sum}_{i \neq k} Q_{i,k}, otherwise. \end{array} $$
(6)

where Q denotes the dependencies between features and selects the independent features. It emphasizes the feature dependencies by its adjacent neighbor using mutual information i.e., i = j, otherwise, it only calculates mutual information between features. Furthermore, we conduct one regularization term tr(WTQW) embedding into the minimization problem in (4), since a positive semi-definite matrix Q which would be tractable in the optimization process and can be updated by the change of adjacent information.

3.4 Proposed method

The learned graph S comes from both sample self-representation and intrinsic space spanned by WTX. Moreover, graph matrix S guides weight matrix learning W and feature dependency matrix construction Q, but the three matrices are not known in advance. This paper integrates completed sample correlations in (4) with feature dependency consideration in a unified framework to solve this problem, and designs the objective function as

$$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W},\mathbf{S}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \beta tr(\mathbf{W}^{T}\mathbf{Q}\mathbf{W}) + \gamma \|\mathbf{W}\|_{2,1} \\ && \quad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \|\mathbf{s}_{i,\cdot}\|_{2}^{2}) \\ && s.t., \forall i, {\mathbf{s}}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \text{if } j \in \mathcal{N}(i), \text{otherwise } 0. \end{array} $$
(7)

Although sparsity-based term ∥W∥2,1 can select informative features by ranking the importance of features, it is not flexible to control the degree of features. Thus, we employ ℓ2,p-norm to select important features which may share more structures when p is small. Besides, low-rank constraint is embedded into graph S to preserve the connection with the task learning. Moreover, there are three parameters in (7) that need to be adjusted that increase the time complexity and decrease the model execution efficiency, so we employ a parameter-free way to release the parameters on regularization term tr(WTQW). As the main diagonal element in Q is connected with the graph matrix S, and other elements are not affected, so feature dependency matrix construction Q does not need to be updated as an independent variable in the optimization process. Therefore, we have

$$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W},\mathbf{S}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \beta tr(\mathbf{W}^{T}\mathbf{Q}\mathbf{W}) + \gamma \|\mathbf{W}\|_{2,p} \\ && \quad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \|\mathbf{s}_{i,\cdot}\|_{2}^{2}) \\ && s.t., \forall i, \mathbf{s}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \\ && \quad \text{if } j \in \mathcal{N}(i), \text{otherwise } 0,~~ rank(\mathbf{L}_{S})=n-c, \end{array} $$
(8)

where \(\beta = \sqrt {1/tr(\mathbf {W}^{T}\mathbf {Q}\mathbf {W})}\) can be automatic updated, p denotes a parameter for adjusting the sparsity of features, S learns both global and local information as well as extract c connected components for the final clustering task. rank(LS) denote the i-th smallest eigenvalues for LS and LS denote a positive semi-definite matrix and rank(LS) ≥ 0. Moreover, according to the theorem of Ky Fan [12] and the definition of rank(LS) in [30], we convert (8) into the following objective function

$$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W},\mathbf{S},\mathbf{F}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \beta tr(\mathbf{W}^{T}\mathbf{Q}\mathbf{W}) \\ && \quad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \|\mathbf{s}_{i,\cdot}\|_{2}^{2}) \\ && \quad + \gamma \|\mathbf{W}\|_{2,p} + \delta tr(\mathbf{F}\mathbf{L}_{S}\mathbf{F}^{T}) \\ && s.t., \forall i, \mathbf{s}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \text{if } j \in \mathcal{N}(i), \text{otherwise } 0, \end{array} $$
(9)

where the parameter δ controls the importance of regularization term. To decrease the number of parameters, we utilize the parameter-free way to release this parameter and set it to \(\delta = \sqrt {1/tr(\mathbf {F}L_{S}\mathbf {F}^{T})}\).

4 Model analysis

For model analysis, we give a detail discussion of the proposed method from four aspects, i.e., optimization, convergence analysis, complexity analysis, and deterministic parameter λ.

4.1 Optimization

Equation (9) is not jointly convex for all variables (i.e., W, S, and F), but is convex for each variable while fixing others. By observing this, the alternative optimization scheme is employed to optimize (9) until the proposed model converges. The pseudo description can be found in the Algorithm 1.

  1. (i)

    Optimize F via fixing W and S

    After fixing W and S, (9) can be converted into

    $$ \begin{array}{@{}rcl@{}} \underset{\mathbf{F}}{\min}~ \delta tr(\mathbf{F}\mathbf{L}_{S}\mathbf{F}^{T}). \end{array} $$
    (10)

    The optimal F can be obtained by conducting eigenvalue decomposition to LS and selecting all eigenvectors relating to the smallest c non-zero eigenvalues.

  2. (ii)

    Optimize W via fixing S and F

    While S and F are fixed, the optimization process of W is convex without non-smooth due to using ℓ2,p-norm. Thus, we use the Iteratively Reweighted Least Square (IRLS) [10] to optimize W until the convergence condition is satisfied.

    Then, the (9) about W can be changed to

    $$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \beta tr(\mathbf{W}^{T}\mathbf{Q}\mathbf{W}) \\ && \quad + \alpha {\sum}_{i,j}^{n} \|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \gamma \|\mathbf{W}\|_{2,p}. \end{array} $$
    (11)

    By utilizing the IRLS scheme, (11) is equal to

    $$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W}}{\min}~ tr(\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S})^{T} tr(\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S}) \\ && \quad + \beta tr(\mathbf{W}^{T}\mathbf{Q}\mathbf{W}) + \alpha tr(\mathbf{W}^{T}\mathbf{X} \mathbf{L}_{S} \mathbf{X}^{T}\mathbf{W}) \\ && \quad + \gamma tr(\mathbf{W}^{T} \mathbf{M} \mathbf{W}), \end{array} $$
    (12)

    where \(\mathbf {L}_{S} = \mathbf {D}_{S} - \mathbf {S} \in \mathbb {R}^{n \times n}\) denote a Laplacian matrix, DS denote a diagonal matrix \(\mathbf {D}_{S}{}_{i,i} = {\sum }_{j}^{n} s_{i,j}\), and then each element in diagonal matrix \(\mathbf {M} \in \mathbb {R}^{d \times d}\) is described as

    $$ \begin{array}{@{}rcl@{}} m_{i,i} = \frac{1}{(2/p)(\|\mathbf{m}_{i,\cdot}\|_{2})^{2-p}}. \end{array} $$
    (13)

    As each term in (12) is convex, and we change it to

    $$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{W}}{\min}~ tr(\mathbf{W}^{T} ((\mathbf{X} - \mathbf{X}\mathbf{S})(\mathbf{X} - \mathbf{X}\mathbf{S})^{T} \\ && \quad + \beta \mathbf{Q} + \alpha (\mathbf{X}\mathbf{L}_{S}\mathbf{X}) + \gamma \mathbf{M} ) \mathbf{W}). \end{array} $$
    (14)

    The optimal solution of W can be calculated to select c eigenvectors of \(((\mathbf {X} - \mathbf {X}\mathbf {S})(\mathbf {X} - \mathbf {X}\mathbf {S})^{T} + \beta \mathbf {Q} + \alpha (\mathbf {X}\mathbf {L}_{S}\mathbf {X}) + \gamma \mathbf {M})\) relating to c smallest non-zero eigenvalues.

  3. (iii)

    Optimize S via fixing W and F

    When W and F are fixed, we have a formula about S as follows,

    $$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{S}}{\min} \|\mathbf{W}^{T}\mathbf{X} - \mathbf{W}^{T}\mathbf{X}\mathbf{S} \|_{F}^{2} + \delta tr(\mathbf{F}\mathbf{L}_{S}\mathbf{F}^{T}) \\ && \quad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \|\mathbf{s}_{i,\cdot}\|_{2}^{2}) \\ && s.t., \forall i, \mathbf{s}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \text{if } j \in \mathcal{N}(i), \text{otherwise } 0. \end{array} $$
    (15)

    According to the definition of \(tr(\mathbf {F}\mathbf {L}_{S}\mathbf {F}^{T})\) in [30], and we have

    $$ \begin{array}{@{}rcl@{}} && \underset{\mathbf{S}}{\min} {\sum}_{i,j}^{n} \|\mathbf{B}_{\cdot,i} - \mathbf{BS}_{\cdot,j} \|_{2}^{2} + \delta \|\mathbf{f}_{\cdot,i} - \mathbf{f}_{\cdot,j}\|_{2}^{2} s_{i,j} \\ && \quad + \alpha (\|\mathbf{W}^{T}\mathbf{x}_{\cdot,i} - \mathbf{W}^{T}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j} + \lambda \mathbf{s}_{i,j}^{2}) \\ && s.t., \forall i, \mathbf{s}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0, \text{if } j \in \mathcal{N}(i), \text{otherwise } 0, \end{array} $$
    (16)

    where B = WTX.

    Note that each i in (16) is independent by each other, and we define \(e_{i,j} = \alpha \|\mathbf {W}^{T}\mathbf {x}_{\cdot ,i} - \mathbf {W}^{T}\mathbf {x}_{\cdot ,j}\|_{2}^{2} + \delta \|\mathbf {f}_{\cdot ,i} - \mathbf {f}_{\cdot ,j}\|_{2}^{2}\) so (16) is formulated as

    $$ \begin{array}{@{}rcl@{}} \underset{{\mathbf{s}}_{i}^{T} \mathbf{1} = 1, s_{i,i} = 0,s_{i,j} \geq 0}{\min} \|\mathbf{s}_{i,\cdot} - \mathbf{e}_{i,\cdot} \|_{2}^{2}. \end{array} $$
    (17)

    The Lagrangian function of (17) is

    $$ \begin{array}{@{}rcl@{}} \|\mathbf{s}_{i,\cdot} - \mathbf{e}_{i,\cdot} \|_{2}^{2} - {{\varDelta}}_{1} (\mathbf{s}_{i}^{T} \mathbf{1} - 1) - {{\varDelta}}_{2} s_{i,j}, \end{array} $$
    (18)

    where Δ1 and Δ2 denote the Lagrangian multipliers. By using the Karush-Kuhn-Tucker (KKT) conditions [6] and calculating the derivative on (18) regarding to si,j, we obtain the closed-form solution of \(\mathbf {s}_{i,j} = {\max \limits } (\mathbf {e}_{i,j} + {{\varDelta }}_{1}, 0)\). After ranking the element in ei,⋅ with descending order, we achieve the newly sorted vector \(\hat {\mathbf {e}}_{i,\cdot } = [\hat {e}_{i,1},...,\hat {e}_{i,n}]\). Moreover, due to the constraint \(\mathbf {s}_{i}^{T} \mathbf {1} = 1\) and each data point is represented by it K-nearest neighbors, the closed-form solution of si,j, j = 1,...,n is obtained as

    $$ \begin{array}{@{}rcl@{}} \mathbf{s}_{i,j} = \hat{\mathbf{e}}_{i,j} + \frac{1}{K} - \frac{1}{K} {\sum}_{j}^{K} \hat{\mathbf{e}}_{i,j},~~\text{if}~ j \in \mathcal{N}(i), ~otherwise~~0. \end{array} $$
    (19)
Algorithm 1
figure a

The pseudo of the proposed model in (9).

Full size image

4.2 Convergence analysis

We discuss the convergence of the proposed method in Algorithm 1, and we first employ the Lemma as follows,

Lemma 1

The inequality

$$ \begin{array}{@{}rcl@{}} \sqrt{v} - \frac{v}{2\sqrt{u}} \leq \sqrt{u} - \frac{u}{2\sqrt{u}} \end{array} $$
(20)

always hold for all positive real number of u and v [49].

Then, we design a new Theorem 1 to prove the convergence of Algorithm 1.

Theorem 1

The objective function value of (8) monotonically decreases until Algorithm 1 converges.

Proof

After the t-th iteration, we have obtained the current optimal F(t), W(t) and S(t) in (9). In the (t+ 1)-th iteration, we have need to optimize F(t+ 1) by fixing W(t+ 1) and S(t+ 1).

According to (10), F(t+ 1) has a closed-form solution, and thus we have the inequality as follows

$$ \begin{array}{@{}rcl@{}} && \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t+1)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t+1)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t+1)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t+1)}\mathbf{L}_{S}\mathbf{F}^{(t+1)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \end{array} $$
$$ \begin{array}{@{}rcl@{}} && \quad \leq \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t+1)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t+1)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t+1)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \end{array} $$
(21)

When fixing F(t) and W(t+ 1) to update S(t+ 1), \(s_{i,j}^{(t+1)}\) has a closed-form solution according to (19), i.e., global optimal solution, for all i,j = 1,...,n, and thus the following inequality we have is

$$ \begin{array}{@{}rcl@{}} && \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t+1)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t+1)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t+1)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \\ && \quad \leq \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \end{array} $$
(22)

When fixing F(t) and S(t) to update W(t+ 1), and according to (14), (22) can be rewritten by

$$ \begin{array}{@{}rcl@{}} && \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma {\sum\limits_{i}^{c}} \frac{(\|\mathbf{w}_{\cdot,i}^{(t+1)}\|_{2})^{2(2-p)}} {(2/p)(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{(2-p)}} \\ && \quad \leq \|\mathbf{W}^{(t)^{T}}\mathbf{X} - \mathbf{W}^{(t)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t)^{T}}\mathbf{Q}\mathbf{W}^{(t)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \sum\limits_{i}^{c} \frac{(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{2(2-p)}} {(2/p)(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{(2-p)}} \end{array} $$
(23)

According to Lemma 1 and for each i, we obtain

$$ (\|\mathbf{w}_{\cdot,i}^{(t+1)}\|_{2})^{(2-p)} - \frac{(\|\mathbf{w}_{\cdot,i}^{(t+1)}\|_{2})^{2(2-p)}}{(2/p)(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{(2-p)}} \leq (\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{(2-p)} - \frac{(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{2(2-p)}}{(2/p)(\|\mathbf{w}_{\cdot,i}^{(t)}\|_{2})^{(2-p)}} $$
(24)

By integrating (24) with (23) and for all c, we obtain

$$ \begin{array}{@{}rcl@{}} && \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \\ && \quad \leq \|\mathbf{W}^{(t)^{T}}\mathbf{X} - \mathbf{W}^{(t)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t)^{T}}\mathbf{Q}\mathbf{W}^{(t)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t)}\|_{2,p} \end{array} $$
(25)

After combining (21), (22) with (25), we finally have

$$ \begin{array}{@{}rcl@{}} && \|\mathbf{W}^{(t+1)^{T}}\mathbf{X} - \mathbf{W}^{(t+1)^{T}}\mathbf{X}\mathbf{S}^{(t+1)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t+1)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t+1)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t+1)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t+1)^{T}}\mathbf{Q}\mathbf{W}^{(t+1)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t+1)}\mathbf{L}_{S}\mathbf{F}^{(t+1)^{T}}) + \gamma \|\mathbf{W}^{(t+1)}\|_{2,p} \\ && \quad \leq \|\mathbf{W}^{(t)^{T}}\mathbf{X} - \mathbf{W}^{(t)^{T}}\mathbf{X}\mathbf{S}^{(t)} \|_{F}^{2} \\ && \qquad + \alpha {\sum}_{i,j}^{n} (\|\mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,i} - \mathbf{W}^{(t)^{T}}\mathbf{x}_{\cdot,j}\|_{2}^{2} s_{i,j}^{(t)} \\ && \qquad + \lambda \|\mathbf{s}_{i,\cdot}^{(t)}\|_{2}^{2}) + \beta tr(\mathbf{W}^{(t)^{T}}\mathbf{Q}\mathbf{W}^{(t)}) \\ && \qquad + \delta tr(\mathbf{F}^{(t)}\mathbf{L}_{S}\mathbf{F}^{(t)^{T}}) + \gamma \|\mathbf{W}^{(t)}\|_{2,p} \end{array} $$
(26)

According to (26), we prove that Algorithm 1 can converge to the optimal solutions. □

4.3 Complexity analysis

For every iteration, the time cost of Algorithm 1 focuses on the computation cost to LS, \(((\mathbf {X} - \mathbf {X}\mathbf {S})(\mathbf {X} - \mathbf {X}\mathbf {S})^{T} + \beta \mathbf {Q} + \alpha (\mathbf {X}\mathbf {L}_{S}\mathbf {X}) + \gamma \mathbf {M})\), the expression in (19), and the relating time complexity are O(cn2), O(cd2), and O(nd2) where n, d, and c, respectively, denote the number of the samples, the features, the clusters. Hence, the time complexity of Algorithm 1 is max{O(cn2),O(nd2)} where n,d > c.

4.4 Deterministic parameter λ

K-nearest neighbors (KNN) is the main way to guide the graph matrix construction, and this also determines the parameter λ value. In detail, we reorder \(\tilde {\mathbf {e}}_{i,\cdot }\) in (19) and obtain new vector \(\tilde {\mathbf {e}}^{\prime }_{i,\cdot } = [\tilde {e}^{\prime }_{i,1},...,\tilde {e}^{\prime }_{i,n}]\) after ranking all elements with descending order. By following the KNN way to reconstruct each sample, si,k+ 1 = 0 can be obtained. Therefore, we have

$$ \begin{array}{@{}rcl@{}} \mathbf{s}_{i,j} - \frac{\tilde{e}^{\prime}_{i,j}}{2 \lambda} + \frac{1}{K} - \frac{1}{K} {{\sum}_{j}^{K}} (\mathbf{s}_{i,j} - \frac{\tilde{e}^{\prime}_{i,j}}{2 \lambda}) = 0 \end{array} $$
(27)

and we obtain the optimal value of λ by

$$ \begin{array}{@{}rcl@{}} \lambda = \frac{K \tilde{e}^{\prime}_{i,j} - {{\sum}_{j}^{K}} \tilde{e}^{\prime}_{i,j}} {2 (1 + K \mathbf{s}_{i,j} - {{\sum}_{j}^{K}} \mathbf{s}_{i,j} )} \end{array} $$
(28)

5 Experiments

We introduce the source of eight data sets, and discuss nine comparison methods in detail. Then, the related experimental setting is provided to all methods. Moreover, experimental results on all data sets and the experimental analysis are discussed.

5.1 Data sets

Eight data sets are employed to conduct our experiments, including four benchmark data sets (i.e., Chess, Hillva, Vechile, and Newsgroup) from UCI Machine Learning Repository,Footnote 1 and image data sets (i.e., Coil,Footnote 2 Yaleb,Footnote 3 OrlFootnote 4) and one signal data set Isolet.Footnote 5 We give a detailed description about these data sets in Table 2.

Table 2 The description of the data sets
Full size table

5.2 Comparison methods

To test the performance of the proposed method, nine state-of-the-art are employed to be tested including the Baseline, two filter-based methods (i.e., LS LLES), two graph-based manifold methods (i.e., Ncut and Rcut), four embedded-based methods (i.e., CDLFS, SCUFS, RUSFS, and RNE). Besides, we introduce the comparison schemes as follows,

  • Baseline [16] uses K-means way to work on all features, and then, updates samples assignment and centroids computation iteratively until the clustering results are obtained.

  • Ratio cut (Rcut) [15] constructs a graph based on all samples, and utilizes normalized segmentation criterion to finish data division.

  • Normalized cut (Ncut) [41] converts clustering task into graph partitioning problem by extracting the global representation of all data.

  • Laplacian Score (LS) [17] belongs to a filter-based unsuperivsed learning model which keeps local relationships by graph Laplacian and selects the feature subset with larger scores.

  • Coupled Dictionary Learning Feature Selection (CDLFS) [56] uses dictionary learning to reconstruct the data and learns a coefficient matrix to represent feature importance.

  • Locally Linear Embedding Score (LLES) [52] measures relations of features and maintains the local structure between features in original data, as well as selects larger scores of features for the final clustering task.

  • Subspace Clustering guided Unsupervised Feature Selection (SCUFS) [57] employs self-representation and sparse subspace learning to search a robust graph representation and coefficient matrix.

  • Robust Unsupervised Spectral Feature Selection (RUSFS) [58] considers both local structure and global structure of samples and features separately, and employs ℓ2,1-norm to remove the unimportant features.

  • Robust Neighborhood Embedding (RNE) [27] selects the important features subset by minimizing reconstruction error with ℓ1-norm regularization constrain.

The employed comparison methods contain one Baseline method, two graph partition methods (i.e., Rcut and Ncut), two filter methods (LS and LLES), and four embedded methods (CDLFS, SCUFS, RUSFS, and RNE). Thereinto, graph partition-based methods use graph representation to consider samples’ local correlations combining with clustering task which can also guide the samples preservation among the data, but they do not consider the feature importance and select the representative features for the task learning. Filter-based methods employ the specific evaluation method (i.e., Laplacian score or locally linear embedding score) to select the informative features after ranking the scores of all features for the task learning. However, they do not take the importance of samples and features into account at the same time. Embedded-based methods employ different ways to the learning of important features where the coefficient weight is used to calculate the scores of features. But all of them consider either the part of samples importance using a self-representation way or feature importance using sparse learning, the considerations are insufficient.

5.3 Experimental setting

We repeated the K-means clustering process twenty times and obtained the final clustering results by calculating the average of all results, preserving the fair experimental environment and avoiding the problem of initialization for all methods. Additionally, we followed the parameters setting of each comparison method by the suggestion from the original paper. For our scheme, there are two variables (i.e., α and γ) that are setting to {10− 3,...,103}, and p is setting to [0.5,1.0,1.5,2.0], and we reported the best clustering performance by employing a heuristic search strategy. For simplicity, we let c to be equal to the number of classes for all methods.

We compared all methods using three evaluation metrics, i.e., clustering ACCuracy (ACC), Normalized Mutual Information (NMI), and Purity. All metrics were limited between 0 and 1, and the higher value the metric is, the better result the clustering task has. Moreover, we investigated the proposed method performance in two sides, such as the parameters’ sensitivity, convergence performance of the proposed method.

5.4 The results of clustering performance

Tables 3 and 4 indicated clustering results of all approaches we compared and all data sets we experimented with. Obviously, the proposed method obtained the best clustering performance in most of data sets, followed by RUSFS, RNE, SCUFS, LLES, CDLFS, LS, Rcut, Ncut, and Baseline. For instance, the proposed method improved averagely by 2.55%, 0.26%, and 1.63%, respectively, compared to the best comparison method (i.e., RUSFS) with regard to ACC, NMI, and Purity in all data sets. Hence, we obtain the observations as follows.

Table 3 The clustering results on four Benchmark data set
Full size table
Table 4 The clustering results on four common data sets
Full size table

First, the clustering performance of embedded-based methods are better than filter-based and graph-partition. For example, the proposed method averagely increased by 6.18% and 12.38% compared to the best filter-based method (i.e., LLES) and the best graph-partition method (i.e., Rcut), respectively, in terms of three evaluation metrics. This shows that the embedded method demonstrated the superior performance and the better model construction than the other two approaches.

Second, most of comparison methods are better than Baseline which utilizes K-means on the original data set. For example, the proposed method and the worst embedded-based method (i.e., CDLFS) improved on average by 14.46% and 6.86% in regards to ACC in all data sets, respectively. This demonstrates the effect of feature selection is necessary to explore the representative features and to be helpful for the clustering task.

5.5 Parameters’ sensitivity

We adjusted the parameter α and γ in {10− 3,...,103} and p in [0.5,1.0,1.5,2.0], and the results can be found in Figs. 1 and 2.

Fig. 1
figure 1

The sensitivity of α and γ of the proposed method on all data sets

Full size image
Fig. 2
figure 2

The sensitivity of p of the proposed method on all data sets

Full size image

In Fig. 1, the combination of parameters in the proposed method are sensitive to the parameters’ setting in the experiments. In other words, various parameters combination may output various clustering results. Therefore, it is essential to tune the parameters for the proposed method. For example, our method obtains the best clustering results on the data set Vechile and Isolet while setting α = 102, γ = 10− 3 and α = 10, γ = 10− 2, respectively.

In Fig. 2, diverse values of the parameter p relate to the clustering performance have been demonstrated, which is denoted by “Proposed-A”, and “Porpoosed-B” denotes the best clustering performance of our proposed method. For the most of data sets, as the value of p increases, the clustering result first rises and then falls. For example, our method obtains the best clustering results (i.e., 68.3%) when p = 1 and the worst clustering results (i.e., 62.5%) when p = 0.5 on the data set Chess. Similarly, our method obtains the best clustering results when the value of p is between 1 and 1.5 on the data set Coil.

5.6 Convergence analysis

In Fig. 3, the convergence performance of each data set can be found. Thereinto, the objective function value is monotonically reduced in (9) until Algorithm 1 obtains convergence. Moreover, by observing all figures, we found fifteen iterations may be the best times for most of the data sets which obtaining convergence results. Hence, the proposed Algorithm 1 is efficient for the most of data sets.

Fig. 3
figure 3

The Objective function value of the proposed method at different iterations on all data sets

Full size image

6 Conclusion

In this article, we have proposed a new unsupervised learning model to feature selection, via involving two components, including both global and local structure preservation to samples by self-representation way and graph representation, and local information and global information consideration to features by mutual information and sparse learning. Moreover, the better sample correlations and the reliable adjacent information are considered by dynamic graph learning and low-rank constraint, respectively, for clustering task. Experiments on eight data sets with nine comparison approaches have verified the validity of the proposed model.