PDE-based surface reconstruction in automotive styling design

Abstract

Surface reconstruction is an important part in automotive styling design. Existing reconstruction methods mainly rely on the proficiency of digital modelers who manually modify the surface shape to approximate the scanned data. Apart from manual modifications, the reconstructed surfaces cannot well reflect the design intent of designers since the feature curves of clay models have not been preserved accurately. In this paper, we propose a partial differential equation (PDE) based surface reconstruction method to analytically generate optimal surfaces with Cⁿ continuity under the constraint of the feature curves. The proposed method accurately preserves automotive feature curves and achieves automatic reconstruction of Class-A surfaces without time-consuming manual work. The effectiveness of the proposed method is demonstrated by a number of experiments that reconstruct main parts of automotive exteriors.

1 Introduction

Surface reconstruction is a fundamental problem in reverse engineering, computer aided design (CAD) and computer graphics. In the field of automotive styling design, the final stage is to scan a clay model of cars and reconstruct parametric surfaces of every part of the clay model, and then trim and stitch them to obtain a complete surface model [23]. The frequently-used parametric surfaces include Bézier, B-splines and NURBS surfaces because they can be modified by controlling a set of parameters such as control points and knot vectors.

In practice, there are two requirements in the automotive surface reconstruction: 1) high degree of similarity and 2) pleasing aesthetics [38].

To meet the first requirement, various optimization methods are involved in the surface fitting process where iterative steps were addressed to produce better results and fully approximate input data, as discussed in [27]. However, these methods of parametric surface reconstruction have several drawbacks such as long computing time and excessive control points [19, 20, 30, 32], which make them have limited applications in CAD system for real-time design. Digital modelers still need to create surfaces carefully by trial and error and spend much time repeatedly evaluating the quality of reconstructed surfaces. Therefore, the surface quality mainly relies on the proficiency of digital modelers.

The aesthetics, in the second requirement, have a key influence on a car’s desirability [34]. It is mainly reflected by the automotive feature curves and the smoothness of external surfaces. The feature curve plays a particularly important role in styling design because it determines the main shape of the automobile body and produces aesthetically pleasing forms [37]. Not only designers draw feature curves with a few strokes to indicate the main shape of a car at the sketching stage, but also clay modelers use tapes to mark the feature curves on automotive clay models, which helps them to communicate ideas with designers and improve modeling quality, as shown in Fig. 1. No matter what stage it is at in the styling design process, feature curves are the major contributor to the understanding of the automotive form [50].

Fig. 1

The feature curves in the styling design. The images taken from [24, 31] show automotive clay models with black tapes, which represent feature curves

At the reverse engineering stage, to generate the desired shapes as well as accord with the design intent of clay modelers, the boundary of reconstructed surfaces needs to strictly meet the feature curves [38, 39]. However, as mentioned above, digital modelers usually generate parametric surfaces by trial and error without the constraint of feature curves. For achieving smoothness, digital modelers struggle with aligning control points of two adjacent surfaces for generating high order continuities. However, a higher continuity level, such as Class-A surfaces, which are defined as freeform surfaces with high efficiency and quality and have G² even G³ continuity, needs more control points to be aligned manually.

In contrast, a PDE-based surface reconstruction method can perfectly meet the two requirements in automotive styling design due to the four advantages below: First, a PDE surface only has several control parameters (normally ≤ 4) such as a₁, a₂, and a₃ as shown in (1) below which can flexibly change the surface shape without changing boundary continuities and greatly reduce the computing time in optimization process. Second, a PDE surface is boundary-based, and it is capable to preserve the automotive feature curves in the surface reconstruction process. Third, since a PDE surface exactly satisfies boundary conditions, adjacent PDE surfaces naturally maintain position, tangent, or higher continuities and no manual operations are required to stitch different PDE surfaces together. Moreover, a PDE surface can achieve parametric continuity (C continuity) which is more stringent than geometric continuity (G continuity). Finally, PDE methods are physics-based [8], and have a potential to create more realistic surface shapes with natural aesthetics as shown in Fig. 2.

Fig. 2

Surface models generated by PDE methods. The left picture taken from [17] shows four simple PDE surfaces, and the right picture taken from [45] shows a PDE solid model

In this paper, we propose a PDE-based surface reconstruction method to generate optimal surfaces with Cⁿ continuity under the constraint of the feature curves for automotive styling design. We address this issue by first parameterizing the automotive feature curves to construct the boundary constraints of PDE surfaces, and then using a vector-valued fourth order PDE to analytically generate Cⁿ continuous surfaces from two opposite feature curves. By optimizing the three control parameters in PDE (1) in Section 3, the reconstructed surfaces achieve high precision in fitting the input data. Our contributions can be summarized as follows:

• A new surface reconstruction method based on an analytical vector-valued fourth order PDE combined with the Hausdorff distance and genetic algorithm (GA) optimization is proposed to generate optimal surface shapes in automotive styling design.

• Automotive feature curves are applied to constrain PDE surfaces and their geometric information is preserved to represent the designer’s intention in the reconstruction process.

• The Cⁿ continuity between adjacent surfaces is automatically guaranteed to generate high-quality surfaces with a natural curvature flow.

• The reconstructed surface first exactly satisfies the feature curves and the error between the surface and scanned data points is minimized through optimizing the values of three control parameters.

The remaining parts of this paper are organized as follows. The related work on surface reconstruction, PDE-based modeling methods and optimization and feature-based CAD/CAM is briefly reviewed in Section 2. Our method of PDE-based surface reconstruction is described in Section 3. The examples and experimental results are given in Section 4. The comparison with the existing methods is made in Section 5, and finally the conclusion is drawn in Section 6.

2 Related work

The work presented in this paper is related to surface reconstruction, PDE, styling design, Cⁿ continuity, feature-based design, Hausdorff distance and GA optimization. In this section, we briefly review the existing work on surface reconstruction techniques from 3D data points, PDE-based modeling, optimization and feature-based CAD/CAM.

2.1 Surface reconstruction from 3D data points

Surface reconstruction from 3D data points has been investigated intensively. Parametric surfaces [33], such as Bézier, B-splines and NURBS surfaces, are widely applied in CAD systems. Gálvez et al. [19] proposed a particle swarm optimization method to reconstruct a Bézier surface from a set of 3D data. With the similar scheme, they further proposed an evolutionary-based NURBS surface reconstruction method [18] and a GA-based B-spline surface reconstruction method [20] from clouds of 3D data points. Ma and Kruth [30] presented a parameterization method of randomly distributed points for performing least squares fitting of B-spline curves and surfaces. He and Qin [22] reconstructed a triangular B-spline surface with the user-specified n degree from a set of scanned 3D points. Park et al. [32] proposed a NURBS surface fitting technique from scattered and unorganized range data using hierarchical graph representation. These parametric surfaces, however, are free-from and their boundary curves cannot fully represent feature curves in the automotive styling design.

Since the feature information, such as boundaries and sharp features, plays an important role in high-quality surface reconstruction, feature-preserving surface reconstruction techniques are developed in recent years. Digne et al. [15] proposed a surface reconstruction and simplification method based on the decimation of a simplicial complex guided by an error metric, which preserves sharp features and boundaries. Dey et al. [14] developed a feature-preserving surface reconstruction algorithm from a set of discrete points by first reconstructing the features where singularities occur and then reconstructing surface patches containing these feature curves. Weber et al. [43] addressed the problem of sharp feature preserving surface reconstruction from point cloud data using the classic moving least squares method. These methods, however, can only generate non-parametric surfaces. In this work, we focus on the parametric surfaces reconstruction from feature curves rather than the detection of feature curves from data points.

The CAD-generated surfaces [11], such as loft and sweep surfaces, are popularly used in surface reconstruction. Lin et al. [28] proposed a surface lofting method for the reverse engineering of complex shapes from the measurement data. Ueng et al. [40] developed a sweep-surface reconstruction method from 3D measured data by using nonlinear least-squares minimization. Since the sweep surface shape depends on the profile curve and path curve, the sweeping method is similar to the practical claying process which is applied to automotive styling design [23]. Tsuchie [38] proposed a sweep-based method for reconstructing an underlying surface from scanned data of styling design objects with less torsion on the line of curvature. With the same scheme, the intersecting underlying surfaces with C⁰ continuity were further developed by applying a sweep-based method [39]. In automotive styling design, the feature curves are used as profile curves to reconstruct sweep or loft surfaces, which preserve feature curves and guarantee aesthetics. These methods, however, are essentially control point-based which involve excessive control points and long computing time in the reconstruction process, and low order of continuity between adjacent surfaces.

2.2 PDE-based modeling

PDE-based modeling is to define and create surfaces by the solution to a PDE subjected to exact satisfaction of boundary conditions, and automatically achieve parametric continuities on shared boundaries between adjacent PDE surfaces. Bloor and Wilson [7] introduced PDE in geometric modeling about three decades ago. They developed a vector-valued fourth order PDE with one control parameter to create surface shapes such as a propeller blade and a phone handset. Since then, this PDE form has been applied to a number of geometric modeling problems such as interactive surfaces design [41], surface manipulation [16], aircraft design [2] and human face design [36]. To diversify PDE surface shapes, Zhang and You [48] proposed a fourth order PDE with three shape control parameters for surface generation, which was applied in 3D vase model design, and they further developed a sixth-order PDE with four shape control parameters, which provides more degrees of freedom to manipulate surface shapes [49]. These PDE methods, however, normally generate a surface from two closed boundary curves and do not apply to our problem in which only open feature curves are available.

The solution of PDEs can be roughly classified into numerical and analytical solutions. Numerical methods are the most effective in solving PDEs. Popular numerical methods are the finite element method [9] and finite difference method [17, 42]. However, numerical solutions require expensive computing cost and are less ideal in real-time modeling applications. Conversely, analytical solutions are the most accurate and efficient, and exactly satisfy both PDEs and boundary conditions [5, 29, 48]. Since it is very difficult to obtain accurate analytical solutions of PDEs, which are only applicable to address some simple surface modeling problems, various approximate analytical solutions have been developed such as the collocation method [6], Fourier series method [7] and pseudo-spectral method [4]. These solutions can only deal with specific boundary conditions and none of them have a unified framework to achieve different order of continuities.

2.3 Optimization and feature-based CAD/CAM

In this work, we use the Hausdorff distance as an objective function, which needs to be minimized during the optimization process. Hausdorff distance is to measure the similarity between two arbitrary point sets, which has been widely used in surface reconstruction. Bartoň et al. [3] developed a computation algorithm for the Hausdorff distance between two polygonal meshes based on computing the lower envelope of curves. Kim et al. [26] presented an interactive-speed algorithm to calculate the Hausdorff distance between two NURBS surface models in close proximity. Zhang et al. [47] developed an efficient framework with two complementary algorithms, i. e., non-overlap Hausdorff distance and overlap Hausdorff distance, to calculate the exact Hausdorff distance for 3D point sets. Chen et al. [12] proposed a search algorithm called local start search to compute the exact Hausdorff distance for arbitrary point sets by using the spatial locality feature of point sets. Although existing studies develop different and efficient algorithms for the Hausdorff distance, this paper mainly focuses on reconstructing the PDE surface rather than developing new algorithms for the Hausdorff distance. How to improve the Hausdorff distance is not the key issue in this paper. Therefore, we directly adopt the classic and simple Hausdorff distance algorithm from [1].

Another related work is feature-based CAD/CAM. Feature-based CAD/CAM is to use features of geometric modeling such as functional features, assembly features, mating features and physical features to design products in CAD/CAM systems [35]. To share feature-based CAD models among heterogeneous CAD systems, Zhang et al. [46] proposed an asymmetric strategy to enrich the theory of feature-based interoperability, particularly when addressing a singular feature or singular sketch. Wu et al. [44] presented a service-oriented feature-based data exchange architecture for cloud-based design and manufacture and collaborative product development. The aim of feature-based CAD/CAM is to develop feature-based models which can be easily exchanged and edited in different CAD/CAM systems. In contrast, the purpose of our method is to preserve the main geometric features, i. e., feature curves, in different stages of styling design.

In summary, existing surface reconstruction methods have several limitations in automotive styling design, such as non-preservation of feature curves, long computing time, excessive control points and poor continuity between adjacent surfaces. Existing PDE methods have the potential to solve these problems but are not applicable to open boundary curves and arbitrary order of continuities. To tackle this problem, we will develop a unified framework of PDE-based modeling to achieve Cⁿ continuity surface reconstruction with high efficiency and accuracy in automotive styling design.

3 The proposed method

In this section, we propose a unified PDE mathematical model for surface modeling and obtain the first analytical Cⁿ continuous PDE surfaces with the constraint of two feature curves. In what follows, we first define the unified mathematical model of the PDE surface, which consists of a vector-valued fourth-order homogeneous PDE and the related boundary conditions in Section 3.1. Then, we investigate the general analytical solution of the unified PDE mathematical model in Section 3.2 and the Cⁿ continuous conditions in Section 3.3.

3.1 Unified PDE mathematical model

The PDE mathematical model usually choose an elliptic PDE to solve the surface generation problem because the elliptic PDE is regarded as an averaging process throughout the entire surface [10]. Due to the different order and the number of control parameters in PDE, the PDE mathematical model has several forms. In this paper, our target is to generate PDE surfaces with Cⁿ continuity. However, a higher order of continuity usually depends on a higher order PDE which is difficult to be solved. Since the continuity requirement of a Class-A surface can be G³ continuity and a fourth-order PDE is sufficient in achieving not only G³ continuity but also Cⁿ (n > 3) continuity as discussed below, the proposed unified mathematical model uses a vector-valued fourth-order PDE combined with three shape control parameters, which offers enough degrees of freedom to satisfy arbitrary order of continuity. The vector-valued fourth-order PDE is defined as

$$ (a_{1}\frac{\partial^{4}}{\partial u^{4}}+a_{2}\frac{\partial^{4}}{\partial u^{2}\partial v^{2}}+a_{3}\frac{\partial^{4}}{\partial v^{4}})\textbf{S}(u,v)=0 $$

(1)

where S(u,v) = [x(u,v),y(u,v),z(u,v)]^T is a vector-valued position function, which represents the generated parametric surface, a₁, a₂ and a₃ are three shape control parameters, and u and v are the parametric variables defined by u ∈ [0,1] and v ∈ [0,1].

As shown in Fig. 3, the PDE surface S is bounded by two feature curves C₁(v) and C₂(v) and controlled by the related boundary tangents T₁(v) and T₂(v) given in (2). We define the boundary tangent T_i(v) as a lerp function between two unit vectors T_Ai and T_Bi, which are tangents at the endpoints A and B of the feature curve C_i(v).

$$ \textbf{T}_{i}(v)={\textbf{T}}_{Ai}(1-v)+{\textbf{T}}_{Bi},\ (i=1, 2) $$

(2)

Usually, for generating free-from surfaces, the vectors T_Ai and T_Bi are user-defined. In this work, the surface shape near the boundary needs to be limited for a good reconstruction accuracy. Therefore, we define that T_Ai and T_Bi are along the unconstrained boundaries of scanned data as shown in Fig. 3. These constraints at the boundaries lead to the following boundary conditions

$$ \begin{array}{ll} u=0,\ \textbf{S}=\textbf{C}_{1}(v),\frac{\partial \textbf{S}}{\partial u}=\textbf{T}_{1}(v),\ v\in[0,1]\\ u=1,\ \textbf{S}=\textbf{C}_{2}(v),\frac{\partial \textbf{S}}{\partial u}=\textbf{T}_{2}(v),\ v\in[0,1] \end{array} $$

(3)

The boundary conditions in (3) can be decomposed into a linearly independent combination of some basic functions, such as exponential functions, trigonometric functions, power functions, logarithmic functions and the constant 1 [49]. We can rewrite boundary conditions in (3) as follows

$$ \begin{array}{ll} u=0,\ \textbf{S}=\sum\limits_{j=0}^{J} \textbf{b}_{1j}f_{j}(v),\frac{\partial \textbf{S}}{\partial u}=\sum\limits_{j=0}^{J} \textbf{b}_{2j}f_{j}(v),\ v\in[0,1]\\ u=1,\ \textbf{S}=\sum\limits_{j=0}^{J} \textbf{b}_{3j}f_{j}(v),\frac{\partial \textbf{S}}{\partial u}=\sum\limits_{j=0}^{J} \textbf{b}_{4j}f_{j}(v),\ v\in[0,1] \end{array} $$

(4)

where f_j(v) are the linearly independent basic functions, and b_1j, b_2j, b_3j and b_4j are known constants. J represents the number of the basic functions.

Fig. 3

The PDE surface S. Red curves, yellow arrows and green arrows represent feature curve C_i(v), boundary tangent T_i(v) and unit vectors T_Ai and T_Bi respectively where i = 1,2

3.2 Solution

Normally, it is extremely difficult to obtain the analytical solution of (1) subject to boundary conditions in (4). To effectively solve this PDE mathematical model, we develop a complementary solution with a composite form to represent the PDE surface S, which has the form of

$$ \textbf{S}(u,v)=\sum\limits_{j=0}^{J}\sum\limits_{m=0}^{M}\textbf{r}_{jm}u^{m}f_{j}(v) $$

(5)

where r_jm are the unknown constants to be determined, and M is the number of the terms of the power series.

The complementary solution combines the basic functions of variable v and the power functions of variable u. Substituting the complementary solution in (5) into the boundary constraints in (4) and solving for the unknown constants r_jm, the complementary solution is changed into

$$ \begin{array}{@{}rcl@{}} \textbf{S}(u,v)&=&\sum\limits\limits_{j=0}^{J}\{\textbf{b}_{1j}+\textbf{b}_{2j}u+[-3\textbf{b}_{1j}-2\textbf{b}_{2j}+3\textbf{b}_{3j}-\textbf{b}_{4j}+\sum\limits\limits_{m=4}^{M}(m-3)\textbf{r}_{jm}]u^{2}\\ &&+ [2\textbf{b}_{1j}+\textbf{b}_{2j}-2\textbf{b}_{3j}+\textbf{b}_{4j}-\sum\limits\limits_{m=4}^{M}(m-2)\textbf{r}_{jm}]u^{3}+\sum\limits\limits_{m=4}^{M}\textbf{r}_{jm}u^{m}\}f_{j}(v) \end{array} $$

(6)

By substituting (6) into (1), the PDE mathematical model can be effectively solved. When M = 3, all the unknown constants r_jm are obtained by (6). When M ≥ 4, the total number of the remaining unknown constants is (J + 1) × (M − 3), the least squares are used to minimize the error of the PDE (1), and the rest unknown constants are solved by

$$ \sum\limits_{j=0}^{J}\sum\limits_{m=4}^{M}\textbf{E}(u,v)\frac{\partial \textbf{E}(u,v)}{\partial \textbf{r}_{jm}}=0 $$

(7)

where

$$ \textbf{E}(u,v)=(a_{1}\frac{\partial^{4}}{\partial u^{4}}+a_{2}\frac{\partial^{4}}{\partial u^{2}\partial v^{2}}+a_{3}\frac{\partial^{4}}{\partial v^{4}})\textbf{S}(u,v) $$

(8)

3.3 C ⁿ continuity

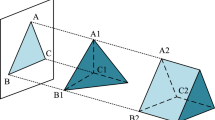
Since feature curves are regarded as the limit in the case of smooth surfaces [39], two adjacent surfaces sharing the same feature curve only have position continuity which is shown in Fig. 6c. As discussed above, the Cⁿ continuity such as C³ continuity needs to be satisfied when the feature curves of two adjacent surfaces are connected at same points. In order to meet the Cⁿ continuity requirement, the adjacent PDE surfaces S and $\bar {\textbf {S}}$ meeting at their common boundary curve $\widetilde {AB}$ as shown in Fig. 4, should satisfy the following (9) and (10).

Fig. 4

Two adjacent PDE surfaces

At the joint vertices A and B, the PDE surfaces S and $\bar {\textbf {S}}$ should satisfy up to Cⁿ continuity with respect to the parametric variable v which gives

$$ \sum\limits_{j=0}^{J}\textbf{b}_{ij}\frac{\partial^{k}f_{j}(v=1)}{\partial v^{k}}=\sum\limits_{j=0}^{\bar{J}}\bar{\textbf{b}}_{ij}\frac{\partial^{k}\bar{f}_{j}(v=0)}{\partial v^{k}}\ (k=0,1,2,...,n) $$

(9)

where b_ij and $\bar {\textbf {b}}_{ij}$ (i = 1,2,3,4) are the constants in the boundary conditions of the PDE surfaces S and $\bar {\textbf {S}}$, respectively, and k is the order of partial derivatives, which represents the order of continuities.

Except the joint vertices A and B, the PDE surfaces S and $\bar {\textbf {S}}$ on the boundary curve $\widetilde {AB}$ should also satisfy up to Cⁿ continuity. These up to Cⁿ continuities with respect to the parametric variable v at the boundary curve $\widetilde {AB}$ are found to be

$$ \sum\limits_{j=0}^{J}\textbf{r}_{jm}\frac{\partial^{k}f_{j}(v=1)}{\partial v^{k}}=\sum\limits_{j=0}^{\bar{J}}\bar{\textbf{r}}_{jm}\frac{\partial^{k}\bar{f}_{j}(v=0)}{\partial v^{k}}\ (m=4,5,...,M) $$

(10)

3.4 Optimization

Given a set of data points $\textbf {P}=\{\textbf {p}_{i}\}_{i=0}^{I_{p}}$, the reconstructed surface $\textbf {S}=\{\textbf {s}_{i}\}_{i=0}^{I_{s}}$ is usually compared to P according to some error measure methods, such as the point-wise Euclidean distance. However, for a set of scanned data, the distribution of point positions is irregular, and it is also difficult to make the number of the points in S exactly the same as P, i. e., I_s = I_p, even though I_p is known. In constrast, the Hausdorff distance provides a measure of dissimilarity between two arbitrary point sets without building the one-to-one correspondence between them [1]. We apply the classic Hausdorff distance as the objective function H, which needs to be minimized during the optimization process. It is defined by

$$ \min_{a_{1},a_{2},a_{3}}H=\max_{\textbf{s}\in \textbf{S}}(\min_{\textbf{p}\in \textbf{P}}\left \|\textbf{s}-\textbf{p} \right \|) $$

(11)

where a₁, a₂ and a₃ are shape control parameters in the PDE (1).

The surface reconstruction procedure contains the following steps:

• 1. Input. A set of scanned data points $\textbf {P}=\{\textbf {p}_{i}\}_{i=0}^{I_{p}}$ representing part of the automotive body and two opposite feature curves C_i(v) defined by scanning the tapes’ positions, or section curve from scanned data or discretized CAD curve, etc.

• 2. Setup of boundary conditions. The feature curves C_i(v) are regarded as the boundary curves, and the boundary tangents T_i(v) are obtained by (2). By decomposing C_i(v) and T_i(v) into linearly independent combinations of basic functions f_j(v), we can get the boundary conditions (4) of the PDE (1). Note that for achieving up to Cⁿ continuity between two adjacent surfaces S and $\bar {\textbf {S}}$, the known constants b_ij and $\bar {\textbf {b}}_{ij}$ and unknown constants r_jm and $\bar {\textbf {r}}_{jm}$ need satisfy (9) and (10), respectively.

• 3. Surface generation. After initializing the three shape control parameters a₁, a₂ and a₃ in (1), the unknown constants r_jm can be obtained by substituting (6) into (1) to obtain (7) and solving (7), and then the PDE surface S is generated using (5).

• 4. Optimization. We change the surface shape to find the optimal surface through minimizing the objective function H in (11) with respect to the three design variables, i. e., the shape control parameters a₁, a₂ and a₃.

• 5. Surface conversion. Since the optimized PDE surface cannot be directly used in CAD systems for downstream engineering and manufacturing operations, we convert the PDE surface into NURBS format by applying the optimal NURBS conversion method presented in [42].

4 Experiments

In our experiment, we apply power functions as the linearly independent basic functions to construct the boundary conditions, i. e., f_j(v) = v^j, and set the number of the basic functions J = 4 and the terms of the power series M = 4. To solve the nonlinear optimization problem, we use the classic GA [21] because it is a good solution to find a global minimum for highly nonlinear problems. We define that the range of input design variables a₁, a₂ and a₃ is [− 10,10], and the convergence criterion is that the change in H is less than the specified tolerance 10^− 6. We implemented the proposed method using MATLAB and run the results on a desktop computer with Intel/Xeon E5-1650 v3 (3.5 GHz) CPU.

For evaluating the quality of reconstructed surfaces with our method, we take the three visual surface analysis tools listed below, which are applied in the following figures.

• Color map of error: For evaluating the similarity between our results and input data, we measure surface error with respect to the bounding box diagonal which is evaluated with the Metro tool [13]. We use green and blue colors to represent the maximum and minimum errors, respectively.

• Zebra map: It is used to visualize curvature on surfaces and understand the shape and quality of surfaces especially for checking the C⁰, C¹, and C² continuities at the join of two adjacent surfaces.

• Curvature combs: Since C² and C³ continuities have a similar zebra map, the curvature comb can help us evaluate high order continuities because it displays the curvature value at a given point. A detailed algorithm of the curvature comb is provided in I.

4.1 Reconstruction of single surfaces

We conducted the single surface reconstruction experiments using two examples of input meshes, each of which represents a part of the hood of two automotive exteriors, respectively, and their feature curves are specified upfront by power functions. Figures 5 and 6 show the two resulting surfaces for Examples 1 and 2. For each example, we show the evaluation of the reconstruction accuracy by error analysis with a color map and zebra maps, which indicates the difference between the resulting surface and input mesh data.

Fig. 5

Reconstructed surface and surface analysis for Example 1. (a) Input mesh of a car hood. (b) The part used for reconstruction from (a) with two feature curves (red curve). (c) Reconstructed surface. (d) Color map of error. (e) The zebra map of (b). (f) The zebra map of (c)

Fig. 6

Reconstructed surface and surface analysis for Example 2. (a) Input mesh of a car hood. (b) The part used for reconstruction from (a) with three feature curves (red curve). (c) Reconstructed surface. (d) Color map of error. (e) The zebra map of (b). (f) The zebra map of (c)

Compared with the input data in Fig. 5b, the maximum error, mean error and root mean square error (RMSE) of the reconstructed surface in Fig. 5c are 1.25 × 10^− 2, 1.94 × 10^− 3 and 2.59 × 10^− 3, respectively. The maximum error, mean error and RMSE of the reconstructed surface in Fig. 6c are 2.90 × 10^− 3, 6.44 × 10^− 4 and 8.44 × 10^− 4, respectively. From these errors and Figs. 5 and 6, we observe: 1) The reconstructed surface, especially at the position of feature curves, has high quality and accuracy. 2) The zebra maps of the reconstructed surface and input mesh data are almost identical. Therefore, our method not only matches the requirement of feature curves’ preservation but also leads to reconstructed surfaces with a good curvature flow.

4.2 Reconstruction of adjacent surfaces with C ⁿ continuity

In order to demonstrate the effectiveness of our method in achieving Cⁿ continuity between two adjacent surfaces in styling design, we give two mesh examples (Examples 3 and 4) from two automotive exteriors as shown in Figs. 7a and 8a. Each example consists of two adjacent parts, i. e, two roof meshes in Example 3 as shown in Fig. 7a and a roof mesh and a rear window mesh in Example 4 as shown in Fig. 8a. We name the part in light grey with the yellow feature curves Part 1 and the part in dark grey with the red feature curves Part 2. In this experiment, we show the results with different orders of the continuity from C⁰ to C³ in Figs. 7b–e and 8b–e. Different from single surface reconstruction, we employ the curvature combs on each part to evaluate the continuity between two adjacent reconstructed surfaces besides the color map and zebra map. The values of three control parameters (CP) a₁, a₂ and a₃ in the PDE (1), computing time (CT), the maximum error (MaxE), mean error (MeanE) and RMSE of reconstructed C⁰, C¹, C² and C³ surfaces of Examples 3 and 4 are summarized in Table 1.

Fig. 7

Reconstructed surfaces with C⁰, C¹, C² and C³ continuities and their surface analysis for Example 3. (a) Input mesh data, two parts for reconstruction and original zebra map. (b) Reconstructed C⁰ surfaces with curvature combs, color map of error (the error range: 0 − 7.59 × 10^− 3) and zebra map. (c) Reconstructed C¹ surfaces with curvature combs, color map of error (the error range: 0 − 7.56 × 10^− 3) and zebra map. (d) Reconstructed C² surfaces with curvature combs, color map of error (the error range: 0 − 1.02 × 10^− 2) and zebra map. (e) Reconstructed C³ surfaces with curvature combs, color map of error (the error range: 0 − 1.35 × 10^− 3) and zebra map. (The detail of curvature combs is shown in the red circle in the first row, and the blue and green colors in the second row represent the minimum and maximum errors respectively)

Fig. 8

Reconstructed surfaces with C⁰, C¹, C² and C³ continuities and their surface analysis for Example 4. (a) Input mesh data, two parts for reconstruction and original zebra map. (b) Reconstructed C⁰ surfaces with curvature combs, color map of error (the error range: 0 − 2.15 × 10^− 2) and zebra map. (c) Reconstructed C¹ surfaces with curvature combs, color map of error (the error range: 0 − 2.32 × 10^− 2) and zebra map. (d) Reconstructed C² surfaces with curvature combs, color map of error (the error range: 0 − 1.91 × 10^− 2) and zebra map. (e) Reconstructed C³ surfaces with curvature combs, color map of error (the error range: 0 − 3.21 × 10^− 2) and zebra map. (The detail of curvature combs is shown in the red circle in the first row, and the blue and green colors in the second row represent the minimum and maximum errors respectively)

Table 1 Statistical data of C⁰, C¹, C² and C³ surfaces of Examples 3 and 4

In Table 1, the range of the computing time is from 20 to 29 seconds, and the order of magnitude of the maximum error is from 10^− 3 to 10^− 2 and the order of magnitude of the mean error and RMSE are both 10^− 3. These results indicate that our method can reconstruct surfaces with high precision in fitting the input data in a short time. From Figs. 7 and 8, we observe: 1) In Figs. 7b and 8b, the curvature combs of the two surfaces are at an angle without connection, and the zebra stripes do not line up due to C⁰ continuity. 2) In Figs. 7c and 8c, the curvature combs of the two surfaces are aligned but the curvature values are different at the join, and the zebra stripes line up but they turn sharply caused by C¹ continuity. 3) In Figs. 7d and 8d, the curvature combs of the two surfaces are aligned and the curvature values are the same at the join, and the zebra stripes line up and flow smoothly created by C² continuity. 4) In Figs. 7e and 8e, although the zebra stripes have no obvious difference compared with Figs. 7d and 8d at the join, the outline of curvature combs has tangential continuity at the join due to C³ continuity. These observations indicate that our method can achieve Cⁿ continuity at the join of two adjacent reconstructed surfaces.

5 Comparison with existing methods

The experiments made in Section 4 demonstrate that our method works well in reconstructing surfaces with Cⁿ continuity and strictly preserves feature curves for automotive styling design. In order to demonstrate the advantages of our method, we make several comparisons with the existing methods in this section.

Since traditional sweeping and lofting methods generate surfaces from profile curves, which can be regarded as feature curves, we first compare our method with sweeping and lofting methods. Figure 9 shows loft (b), sweep (c) and PDE (d) surfaces reconstructed from input mesh data (a) with feature curves. The values of the maximum error, mean error and RMSE are listed in Table 2.

Fig. 9

Reconstructed loft, sweep and PDE surfaces with error analysis. (a) Input mesh data. (b) The loft surface with two feature curves (red curve) and color map of error (the error range: 0 − 2.42 × 10^− 2). (c) The sweep surface with one feature curve (red curve) and a backbone curve (purple curve), and color map of error (the error range: 0 − 2.74 × 10^− 2). (d) The PDE surface with two feature curves (red curve) and color map of error (the error range: 0 − 8.21 × 10^− 3). (The blue and green colors in the second row represent the minimum and maximum errors, respectively)

Table 2 Statistical data of loft, sweep and PDE surfaces

In Fig. 9, the lofting method can preserve feature curves but cause big error in the middle of the reconstructed surface because there are no design variables to guarantee the surface quality. Although sweeping method can produce less error in the middle of the reconstructed surface, it can only preserve one feature curve and needs the extra help of a backbone curve. In contrast, our method can preserve two feature curves as well as guarantee the surface quality by using the shape control parameters in PDE. Moreover, from the data in Table 2, the reconstruction error of our method is small especially the maximum error which is one order of magnitude smaller than other methods. These results manifest that our method generates surfaces with higher accuracy than lofting and sweeping methods.

In addition, we compare our method with some state-of-the-art methods in surface reconstruction including two parametric methods, i. e., the NURBS fitting [33] and closed form PDE [51], and the non-parametric method, i. e., the screened poisson surface reconstruction [25]. We use Examples 1 and 2 as input mesh data and generate the reconstructed surfaces, zebra maps and color maps of errors by using the above different methods as shown in Fig. 10. We have the following observations from the comparison results. All reconstructed surfaces of different methods have small errors compared with the input mesh data. Although the reconstructed surfaces using our method have the largest errors, our method has two superiorities compared with other methods. First, since our method exactly satisfies the feature curves, the shapes of reconstructed surfaces are the same as the input meshes and there is no need to trim the surfaces. In contrast, all of the other methods need to trim their reconstructed surfaces to make them match the shape of the input meshes as shown by the trim regions encircled by the red lines. Second, the zebra maps of the reconstructed surfaces by using our method are most similar to the input meshes compared with other methods, which indicates our method can restore curvature information of original data as much as possible and generate a good curvature flow.

Fig. 10

Comparison of the proposed method with other surface reconstruction methods. The first, second and third rows represent the surface meshes, zebra maps and color maps of errors, respectively. The red lines indicate the trim regions. (a) Input mesh data. (b) Our method. (c) NURBS fitting. (d) Screened poisson surface reconstruction. (e) Closed form PDE

We also compare our method with the improved sweep-based method presented in [39] in automotive styling design. Since both methods use the data of external surfaces from real automobiles and focus on the reconstruction work of automotive hoods and roofs, the differences between both methods can be better demonstrated by comparing the statistical data of the reconstruction results from both methods, which are shown in Table 3. We apply the order of magnitude of maximum errors with respect to the bounding box diagonal for a fair comparison. From the results in Table 3, we observe that our method has obvious advantages such as a much smaller number of design variables, shorter computing time and higher order of surface continuity. Moreover, the reconstructed surfaces by using the improved sweep-based method need to be trimmed and remove redundant parts before stitching them together, whereas the surfaces generated by our method can directly applied in the next styling stage.

Table 3 Comparison of the proposed method with improved sweep-based method

All above experiments have demonstrated the effectiveness of our method. Our method is the first one which can reconstruct parametric surfaces with Cⁿ continuity as well as preserve feature curves. Furthermore, the shape of reconstructed surface is dependent on the three control parameters in PDE, which greatly reduces the number of design variables in the optimization process and shortens the calculation time. However, there are still some limitations. Since the reconstructed surface is constrained by only two opposite feature curves, the maximum error in a surface usually exist at or near unconstrained boundaries as shown in the error maps in Figs. 7 and 8. Moreover, since we primarily focus on developing a new PDE method for surface reconstruction in this paper, we only applied the existing classical GA method with default settings to minimize the objective function H in (11), which may increase the computing time. Therefore, we need to improve the GA method or consider another optimization method to minimize H within a shorter time.

6 Conclusion

We have presented a surface reconstruction method based on a vector-valued fourth order PDE in styling design. The proposed method automatically generates optimal Cⁿ continuous surfaces from scanned data with the constraint of two feature curves after optimizing three control parameters in the PDE. We have demonstrated the validity of our work by doing experiments on several examples of mesh data from automotive exteriors. Compared with existing surface reconstruction methods, our method is flexible to achieve arbitrary order of continuity, and has small reconstruction errors and pleasing aesthetics. In our following work, we wish to improve the optimization method and further decrease the computing time. We also plan to deal with more complicated situations such as a surface defined by four feature curves.

Appendix:: The curvature comb

A curvature comb consists of normal vectors with curvature value on the surface along u or v direction. We first define the unit tangent vector t(u,v), unit normal vector n(u,v) and curvature value κ(u,v) along v direction on the PDE surface S(u,v) in (5) as:

$$ \textbf{t}(u,v)=\frac{\frac{\partial \textbf{S}(u,v)}{\partial v}}{\left \| \frac{\partial \textbf{S}(u,v)}{\partial v} \right \|},\ \textbf{n}(u,v)=\frac{\frac{\partial \textbf{t}(u,v)}{\partial v}}{\left \| \frac{\partial \textbf{t}(u,v)}{\partial v} \right \|},\ \kappa(u,v)=\frac{\left \| \frac{\partial \textbf{t}(u,v)}{\partial v} \right \|}{\left \| \frac{\partial \textbf{S}(u,v)}{\partial v} \right \|} $$

(12)

Then, the curvature comb along v direction can be defined as:

$$ \textbf{c}(u,v)=\textbf{S}(u,v)-\omega\kappa(u,v)\textbf{n}(u,v) $$

(13)

where ω is the scaling factor which can control the size of the comb.