1 Introduction

Moment descriptors are widely used for the analysis, storage and transmission of signals and images. They are successfully used in different applications such as pattern recognition [3, 13], classification [16, 28], reconstruction [7, 21], compression [14, 34] and watermarking [12]. The moments are defined as the coefficients of projection of signals or images on often orthogonal basis. Based on this definition, we can distinguish two main categories of moments: continuous orthogonal moments (COMs) and discrete orthogonal moments (DOMs).

COMs are defined from continuous orthogonal polynomials such as Zernike [36], Legendre [17], Fourier-Mellin [25], pseudo-Zernike [4] and Gaussian-Hermite [18] polynomials. The use of this type of moments is limited by two types of errors: the errors of discretization of the continuous space of the polynomials towards the discrete space of the image and the errors of approximation of the continuous integrals by discrete sums. In order to overcome these problems, Mukundan [24] was the first to use Tchebichef’s discrete orthogonal moments for image reconstruction. Afterwards, the DOMs such as the moments of Tchebichef [6], Krawtchouk [35], Hahn [29], Dual Hahn [37], Racah [38], Charlier [8] and Meixner [9] received particular attention in the fields of images and signals because they can exactly represent signals and images [30] without information redundancy and without approximation and discretization errors. However, the calculation of DOMs is limited by the problems of fluctuation of numerical values and high calculation time, especially for high orders. To remedy these problems, the researchers use recursive computation of discrete orthogonal polynomials instead of direct computation from hypergeometric shapes. This type of calculation considerably reduces the complexity of calculation and the propagation of numerical errors. They also use the symmetry relations of certain discrete orthogonal polynomials such as Tchebichef [10], Krawtchouk [11] and Hahn [32] in order to further accelerate the computation time of DOMS. However, the computation of the values of discrete orthogonal polynomials in general remains unstable especially for high orders. In order to discover the sources of instability and to propose a solution to this problem, a study concerning the discrete orthogonal Hahn polynomials (HPs) was achieved in this paper. The choice of HPs is justified by the fact that the latter generalize the Tchebichef and Krawtchouk polynomials. Indeed, by adjusting the parameters of HPs, we obtain the Tchebichef and Krawtchouk polynomials.

The calculation of the DOMs passes the calculation of the discrete orthogonal polynomials, the latter are defined from hypergeometric functions. This type of calculation is complicated and requires a very high execution time and leads to the propagation of numerical errors. In order to solve these problems, the researchers use the recursive calculation of DOPs with respect to the order n and with respect to the variable x. This method considerably reduces the complexity of the computation and the propagation of numerical errors. The problem of computing time is solved more or less by the use of matrix formulations and the symmetry properties of certain types of DOPs.

The study carried out in this paper shows that the instability of HPs comes from two sources: (i) the existence of gamma and factorial functions in the expressions of weight and square norm functions. (ii) the occurrence and propagation of numerical errors for high orders. To defeat the problem (i), we developed a recursive calculation of the functions of weight and square norm in order to eliminate the gamma and factorial functions. To solve the problem (ii), we used the Gram –Schmidt ortho-normalization method (GSOP) and the symmetry property of HPs [7].

After the computational stabilization of the HPs, we apply them for the reconstruction and compression of large 2D / 3D biomedical signals and images. For these applications, it is interesting to evaluate the quality of the reconstructed images and signals using evaluation criteria such as the Mean-Square Error (MSE) and the Signal-to-Noise Ratio (PSNR). The calculation of the values of the HPs strongly depends on the local parameters (a and b), which greatly influence the quality of reconstruction of signals and images. Consequently, the optimal selection of values of these parameters is essential to have a better quality of reconstruction of signals and images. In the literature on the analysis of images and signals by the method of moments, it is generally found that the selection of local parameters of polynomials occurs empirically if the number of local parameters is small (only one parameter). This choice becomes more complicated when the number of local parameters becomes high (2 or more parameters). Therefore, using a reliable method is very demanding; for that, we propose in this work a reliable method for the selection of the local parameters of the HPs. This method is based on the optimization algorithm called Artificial Bee Colony (ABC). The latter is used to select the values of the local parameters of HPs in order to obtain a better quality of the signal / images reconstructed through the minimization of MSE (or maximization of PSNR).

Motivated by the efficiency of ABC algorithm for the optimization of HPs parameters, we will present in this paper an optimal method for the compression of 2D / 3D signals and images of large sizes based on HMs and ABC. However, the rest of this article is organized as follows: in the second section, we present generalities on the calculation of HPs. In the third section, we present the recursive calculation of the HPs following the order n and following the variable x as well as the proposed stability improvement. In the fourth section, we present the Hahn discrete orthogonal moments (HMs) in the 1D, 2D and 3D domains. The fifth section presents the reconstruction / compression methods proposed based on HMs and the ABC algorithm. In the last section, the simulation results are presented in order to validate the efficiency and superiority of the algorithms proposed for the reconstruction and compression of large signals and images.

2 Generalities on discrete orthogonal Hahn polynomials

In this section, we briefly present the theoretical background of Hahn’s discrete orthogonal polynomials (HPs) and their computational methods, namely direct computation and recursive computation. The Hahn polynomials of order n and a discrete variable x are defined from the hypergeometric function 3F2(.) as follows [15]:

$$ {h}_n^{\left(a,b\right)}\left(x,N\right)=\frac{{\left(-1\right)}^n{\left(b+1\right)}_n{\left(N-n\right)}_n}{n!}{{}_3F}_2\left(-n,-x,n+1+a+b,b+1,1-N,1\right) $$
(1)

with n, x = 0, 1, …, N et a and b two real numbers such that a >  − 1andb >  − 1.

The generalized hypergeometric function 3F2() is defined by (Eq.2):

$$ {{}_3F}_2\left({a}_1,{a}_2,{a}_3,{b}_1,{b}_2,z\right)=\sum \limits_{k=0}^{\infty}\frac{{\left({a}_1\right)}_{\mathrm{k}}{\left({a}_2\right)}_{\mathrm{k}}{\left({a}_3\right)}_{\mathrm{k}}{z}^k}{{\left({b}_1\right)}_{\mathrm{k}}{\left({b}_2\right)}_{\mathrm{k}}k!} $$
(2)

with (a)k is the Pochhamer symbol defined by: (a)k = a(a + 1)(a + 2). …(a + k − 1).

The HPs satisfy the following orthogonality relation (Eq.3):

$$ \sum \limits_{x=0}^{N-1}{h}_n^{\left(a,b\right)}\left(x;N\right){h}_m^{\left(a,b\right)}\left(x;N\right)\omega (x)=\rho (n){\delta}_{nm} $$
(3)

with δnm is the symbol of Kronecker and ρ(n) is the square norm function defined by the following relation (Eq.4):

$$ \rho (n)=\frac{{\left(-1\right)}^nn!{\left(n+a+b+1\right)}_{N+1}{\left(b+1\right)}_n}{N!\left(2n+a+b+1\right){\left(a+1\right)}_n{\left(-N\right)}_n} $$
(4)

The function ω(x) is the weight function given by (Eq.5):

$$ \omega (x)=\left(\begin{array}{c}a+x\\ {}x\end{array}\right)\left(\begin{array}{c}b+N-x\\ {}N-x\end{array}\right) $$
(5)

Using the functions ω(x)andρ(n), we obtain the orthonormalized form of the HPs as follows (Eq.6):

$$ {\tilde{h}}_n^{\left(a,b\right)}\left(x;N\right)={h}_n^{\left(a,b\right)}\left(x;N\right)\sqrt{\frac{\omega (x)}{\rho (n)}} $$
(6)

The direct computation of HPs from Eq. (6) is very expensive in terms of computation time because of the gamma Γ(.) and factorial (.)! functions that define them. This problem is overcome by using the recurrence relations of the HPs with respect to the order n and with respect to the variable x.

2.1 Recurrence relation with respect to order n

The HPs satisfy the three-term recurrence relation with respect to order n defined as follows [39]:

$$ {\tilde{h}}_n^{\left(a,b\right)}\left(x;N\right)=\frac{B\times D}{A}{\tilde{h}}_{n-1}^{\left(a,b\right)}\left(x;N\right)-\frac{C\times E}{A}{\tilde{h}}_{n-2}^{\left(a,b\right)}\left(x;N\right) $$
(7)

with A, B, C, D and E are coefficients given by the following equations Table 1:

Table 1 the values of A, B, C, D and E
Full size table

The initial values of the HPs are calculated using the following two relations (Eq.8):

$$ {\displaystyle \begin{array}{c}{\tilde{h}}_0^{\left(a,b\right)}\left(x;N\right)=\sqrt{\frac{\omega (x)}{\rho (0)}}\\ {}{\tilde{h}}_1^{\left(a,b\right)}\left(x;N\right)=\left[-\left(b+1\right)\left(N-1\right)+\left(a+b+2\right)x\right]\sqrt{\frac{\omega (x)}{\rho (1)}}\end{array}} $$
(8)

2.2 Recurrence relation with respect to the variable x

The calculation of the HPs is carried out recursively with respect to the variable x using the defined three-term recurrence relation, for n = 0, 1, 2, …, N − 1andx = 2, 3, …, N − 1, by the following relation (Eq.9):

$$ {\displaystyle \begin{array}{c}{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right)=\frac{\sqrt{\omega (x)}}{\sigma \left(x-1\right)+\tau \left(x-1\right)}\times \left[\frac{2\sigma \left(x-1\right)+\tau \left(x-1\right)-{\lambda}_n}{\sqrt{\omega \left(x-1\right)}}{\tilde{h}}_n^{\left(a,b\right)}\left(x-1,N\right)-\frac{\sigma \left(x-1\right)\Big)}{\sqrt{\omega \left(x-2\right)}}{\tilde{h}}_n^{\left(a,b\right)}\left(x-2,N\right)\right]\\ {}\mathrm{with}\kern1.25em \\ {}\sigma (x)=x\left(N+a-x\right),\tau (x)=\left(b+1\right)\left(N-1\right)-\left(a+b+2\right)x\kern0.5em \mathrm{and}\kern0.75em {\lambda}_n=n\left(a+b+n+1\right)\end{array}} $$
(9)

The initial values of the HPs with respect to the variable x are given as follows (Eq.10):

$$ {\displaystyle \begin{array}{c}{\tilde{h}}_n^{\left(a,b\right)}\left(0,N\right)={\left(1-N\right)}_n\left(\begin{array}{c}n+b\\ {}n\end{array}\right)\sqrt{\frac{\omega (0)}{\rho (n)}}\\ {}{\tilde{h}}_n^{\left(a,b\right)}\left(1,N\right)=\frac{\left(n+b+1\right)\left(N-n-1\right)-n\left(N+a-1\right)}{\left(b+1\right)\left(N-1\right)}\times \sqrt{\frac{\omega (1)}{\omega (0)}}{\tilde{h}}_n^{\left(a,b\right)}\left(0,N\right)\end{array}} $$
(10)

The recursive calculation of the HPs with respect to the order n and with respect to the variable x considerably reduces the complexity and the time of implementation of these polynomials. However, this calculation is limited by two major problems, especially for high orders: (1) the problem of fluctuation of polynomial values (the appearance of NaN and Inf) due to the functions ρ(n)andω(x) which diverge from the argument 172 (Γ(172) = Inf), and (2) the problem of the propagation of numerical errors which destroy the orthogonality property of these polynomials. In order to solve the first problem, we will develop a recursive calculation of the functions ω(x) andρ(n) in order to eliminate the terms that cause the numerical fluctuations and for the second problem, we will proceed in a similar way to that followed in [7] to solve the problem of propagation of the numerical errors of the polynomials of Charlier. In this context, we propose to use the Gram-Schmidt Ortho normalization (GSOP) method for re-orthonormalization of Hahn polynomials in order to avoid the propagation of numerical errors. The two proposed solutions will be detailed in the following section.

3 Stable and fast computation of high order Hahn polynomials

In this section, we will develop a recursive computation of the functions that cause numerical fluctuations during the computation of high-order Hahn polynomials and we will also present the Gram-Schmidt ortho-normalization (GSOP) method to stabilize the values. Polynomials in the orthogonality domain.

3.1 Recursive calculation of weight and square norm functions

The recursive calculation of the weight function ω(x) is performed using the following relation (Eq.11):

$$ \omega \left(x+1\right)=\left\{\begin{array}{c}\frac{\left(N-x\right)\times \left(b+x\right)}{x\left(N+a-x\right)}\times \omega (x)x>0,\\ {}\frac{\Gamma \left(N+a\right)\times \Gamma \left(b+1\right)}{\Gamma (N)}x=0\end{array}\right. $$
(11)

We only see the term ω(0) that we denote ωN(0) still depends on the function Γ(N), which limits the calculation of ω(x) when the value of N becomes high. To solve this problem, we propose to compute this term recursively with respect to N by the following relation (Eq.12):

$$ {\omega}_N(0)=\left\{\begin{array}{c}\Gamma \left(1+a\right)\Gamma \left(b+1\right)N=1,\\ {}\left(N+a-1\right){\omega}_i(0)\mathrm{i}=2,3,\dots, N\end{array}\right. $$
(12)

The recursive calculation of the square norm function ρ(n) is performed using the following relation (Eq.13):

$$ \rho \left(n+1\right)=\left\{\begin{array}{c}\frac{\left(a+n\right)\times \left(b+n\right)\times \left(a+b+n+N\right)\times \left(N-n\right)\times \left(a+b+2\times n-1\right)}{\left(a+b+2\times n+1\right)\times n\times \left(a+b+n\right)}\times \rho (n)\mathrm{n}>0\\ {}\frac{a!\times b!\times \left(a+b+N\right)!}{\left(a+b+1\right)\times \left(a+b\right)!\times \left(N-1\right)!}\mathrm{n}=0\end{array}\right. $$
(13)

We observe that the term ρ(0) that we denote ρN(0) depends on N, which limits the calculation of ρ(n) when the value of N gets high. To solve this problem, we propose to compute this term recursively with respect to N as follows (Eq. 14):

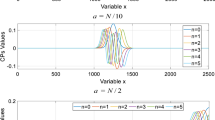
$$ {\rho}_N(0)=\left\{\begin{array}{c}\frac{\left(a+b+N\right)}{\left(N-1\right)}\times {\rho}_i(N)\mathrm{i}=2,3\dots, N\\ {}\frac{a!\times b!\times \left(a+b+1\right)}{\left(a+b+1\right)\times \left(a+b\right)!}\mathrm{N}=1\end{array}\right. $$
(14)

We can clearly see that the recursive calculation of the functions ω(x)and ρ(n) thus proposed is independent of the gamma and factorial functions which causes the fluctuations of the numerical values of the HPs which makes it possible to calculate the values of HPs without numerical fluctuations for any order and any values of a, b, x andn. Fig. 1 shows the plots of the values of the HPs up to order 4 for different values of the parameters a and bfor x = 0: 2000.

Fig. 1
figure 1

the plots of the first five terms of the HPs for different values of a and b for x = 0: 2000

Full size image

We observe from Fig. 1 hat the polynomial parameters (a, b) influence the accentuation region of these polynomials. When b < a, the HPs curves are shifted to the left. Likewise, the curves of HPs move to the right when b > a, and when a= b, we note that the HPs curves are symmetrically distributed on the index axis (x).

3.2 Gram-Schmidt orthonormalization method (GSOP)

In this subsection, we recall the basic steps of the Gram-Schmidt Orthonormalization (GSOP) process to stabilize polynomial values in the orthogonality domain. This process is based on three steps: the first is the calculation of the HPs for n = 0andn = 1, the second is the calculation of HPs from order 2 via one of the two recurrence relations defined in Eq. (7) and Eq. (9) and the third is the orthonormalization of HPs via the orthogonalization formula of Gram-Schmidt detailed in [7]. All of these steps are illustrated in Algorithm 1.

3.3 Quick calculation of HPs

If the problems of stability and fluctuations of the values of the HPs are solved by recursive calculation and by GSOP, the problem of calculation time still persists especially for the high orders of the HPs. To solve this problem, we will use an important property of HPs, which is the defined symmetry property, for a = b, by the following relation (Eq. 15):

$$ {\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right)={\left(-1\right)}^n{\tilde{h}}_n^{\left(a,b\right)}\left(\mathrm{N}-1-x,N\right) $$
(15)

By using this relation, we can calculate only half of the values of the HPs and the others are deduced via the symmetry relation which allows to considerably reduce the calculation time of the values of the HPs.

Algorithm 1 presents all the steps followed for the stable calculation of HPs.

Algorithm 1: the steps for the stable calculation of HPs.

figure a

The figures Fig. 2(a) and (b) show that the use of the GSOP algorithm made it possible to calculate all the Hahn polynomial values up to the last polynomial order without error. The Hahn polynomials thus calculated via the GSOP algorithm satisfy the orthogonality condition in Eq. (3).

Fig. 2
figure 2

Matrix of Hahn Polynomials values (a = b = 20) using GSOP algorithm for a: N = 2000, b: N = 4000 and the curves of Hahn’s polynomials to orders up to c: 2000, and d:4000

Full size image

4 Hahn’s discrete orthogonal moments

In this section, we will present the mathematical context of Hahn’s discrete orthogonal moment theory, including the computation of one-dimensional, two-dimensional and three-dimensional moments. Hahn’s discrete orthogonal moments (HMs) are defined as the orthogonal projection of information space (signal / image) on a basis formed by HPs.

4.1 Hahn’s one-dimensional moments (1D)

In this subsection, we will present the mathematical context of one-dimensional Hahn moments. The one-dimensional Hahn moments are defined as the projections of a signal on Hahn orthogonal polynomials. Therefore, for a 1D function signal f(x), the 1D HMs of order n are defined as (Eq. 16):

$$ {HM}_n=\sum \limits_{x=0}^{N-1}{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right)f(x)={P}_n^T\times f $$
(16)

The reconstruction of the signal is carried out from the HMs using the following formula (Eq. 17):

$$ \hat{f}(x)=\sum \limits_{x=0}^{N-1}{H}_n{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right)={P}_n\times {HM}_n $$
(17)

With Pn is the Hahn polynomial matrix defined by (Eq. 18):

$$ {P}_n={\left[{\tilde{h}}_0^{\left(a,b\right)}(x),{\tilde{h}}_1^{\left(a,b\right)}(x),\dots, {\tilde{h}}_{N-1}^{\left(a,b\right)}(x)\right]}^T $$
(18)

In order to measure the similarity between the original signal f(x) and the reconstructed signal \( \hat{f}(x) \), we use the mean squared error (MSE) which is defined as follows (Eq. 19):

$$ MSE=\frac{1}{N}\times \sum \limits_{x=0}^{N-1}{\left(f(x)-\hat{f}(x)\right)}^2 $$
(19)

The Percent Root Difference (PRD%) criterion can also be used to measure the difference between f(x) et \( \hat{f}(x) \). The PRD is defined by (Eq. 20):

$$ PRD=\sqrt{\frac{\sum \limits_{x=0}^{N-1}{\left(f(x)-\hat{f}(x)\right)}^2}{\sum \limits_{x=0}^{N-1}{\left(f(x)\right)}^2}} $$
(20)

4.2 Hahn’s two-dimensional moments (2D)

In this subsection, we will present the mathematical context of two-dimensional Hahn moments, the two-dimensional (2D) HMs of order (n, m) of an image f (x, y) of size M × N are defined as:

$$ {\displaystyle \begin{array}{c}{HM}_{nm}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}f\left(x,y\right){\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right){\tilde{h}}_m^{\left(a,b\right)}\left(y,N\right)\\ {}={P_n}^T\times f\times {P}_m\end{array}} $$
(21)

with n, m = 0, 1, 2, …, N − 1, x ∈ [0…N − 1], y ∈ [0…N − 1] \( {P}_n={\left[{\tilde{h}}_0^{\left(a,b\right)}(x),{\tilde{h}}_1^{\left(a,b\right)}(x),\dots, {\tilde{h}}_{N-1}^{\left(a,b\right)}(x)\right]}^T \)and \( {P}_m={\left[{\tilde{h}}_0^{\left(a,b\right)}(y),{\tilde{h}}_1^{\left(a,b\right)}(y),\dots, {\tilde{h}}_{N-1}^{\left(a,b\right)}(y)\right]}^T \).

The image reconstructed from 2D HMs is given by the following inverse transformation:

$$ {\displaystyle \begin{array}{c}\hat{f}\left(x,y\right)=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right){\tilde{h}}_m^{\left(a,b\right)}\left(y,N\right){HM}_{mn}\\ {}={P}_m\times {HM}_{nm}\times {P}_n^T\end{array}} $$
(22)

To measure the reconstruction error of 2D images, we can use the MSE criterion defined by (Eq. 23):

$$ MSE=\frac{1}{N\times M}\times \sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}{\left(f\left(x,y\right)-\hat{f}\Big(x,y\Big)\right)}^2 $$
(23)

4.3 Hahn’s three-dimensional (3D) moments

The 3D HMs of order (n, m, k) of a 3D image of size N × M × K voxels and intensity function f (x, y, z), are defined as follows (Eq. 24):

$$ {HM}_{mnk}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}\sum \limits_{z=0}^{K-1}{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right){\tilde{h}}_m^{\left(a,b\right)}\left(y,M\right){\tilde{h}}_k^{\left(a,b\right)}\left(z,K\right)f\left(x,y,z\right) $$
(24)

The inverse transformation of 3D HMs is given by (Eq. 25):

$$ \hat{f}\left(x,y,z\right)=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}\sum \limits_{z=0}^{K-1}{\tilde{h}}_n^{\left(a,b\right)}\left(x,N\right){\tilde{h}}_m^{\left(a,b\right)}\left(y,M\right){\tilde{h}}_k^{\left(a,b\right)}\left(z,K\right){HM}_{mnk} $$
(25)

The use of Eq. 23 for the calculation of 3D HMs is very expensive in terms of calculation time. In order to solve this problem, we use the matrix formula as follows: in the first step, we compute K temporary matrices in the z direction using the 2D matrix form of the HMs given by Eq. 21. In the second step, these matrices will be rearranged and multiplied by the polynomial matrix \( {\left\{{\tilde{h}}_k^{\left(a,b\right)}\left(z,K\right)\right\}}_{0\le z\le K-1}^{0\le k\le n} \) to get the HMs in 3D. The same steps are followed for the reconstruction of 3D images by the matrix method.

For a 3D image of size N × M × K, the MSE is defined as (Eq. 26):

$$ MSE=\frac{1}{N\times M\times K}\times \sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}\sum \limits_{z=0}^{K-1}{\left(f\left(x,y,z\right)-\hat{f}\Big(x,y,z\Big)\right)}^2 $$
(26)

The peak signal-to-noise ratio (PSNR) in decibels (dB) is also widely used to quantify the reconstruction error, this criterion is defined from MSE as follows (Eq. 27):

$$ \boldsymbol{PSNR}=10{\mathit{\log}}_{10}\frac{k^2}{MSE} $$
(27)

Where k is the maximum value of the image function.

Image / signal reconstruction is optimal if reconstruction errors are minimal (tend to zero). Therefore, MSE minimization (PSNR maximization) is paramount during signal / image reconstruction by HMs.

The image / signal reconstruction errors depend on the order of moments and the values of the local parameters a and b of the HPs. Therefore, an optimal selection of the order and the local parameters allows to have a good quality of reconstruction and vice versa. In order to optimize the values of a and b during the reconstruction, we propose to use the Artificial Bee Colony (ABC) algorithm [20]. This optimization algorithm simulates the intelligent behavior of bees when searching for food sources. It has shown high efficiency in solving optimization problems in various engineering fields [1, 2]. In the next section, we present the optimal reconstruction method using the HMs optimized by the ABC algorithm.

5 Optimal reconstruction of signals / images by HMs and the ABC algorithm

The functional diagram of the ABC algorithm given in Fig. 3 is suitable for optimal reconstruction of signals / images by HMs according to the steps below:

  • Step 1: initialize the parameters of the ABC algorithm as follows:

  • D = 2 (dimension of problem because one seeks the values of a and b).

  • CS = 20 (Colony size (CS) or swarm size).

  • SN=CS/2 (Number of solutions in the population).

  • Xmin = 0,Xmax = 50(the minimum and maximum value of the parameters a and b).

  • SA = 1, (number of scout bees).

  • Cmax =100, (Number of objective function evaluations MSE is the stop criterion).

  • Limit = (CS*D) /2), (the limit of a solution to be abandoned).

  • Step 2: Random generation of an initial population of solutions and evaluate the objective function (MSE) for each solution using the following equation (Eq. 23):

  • $$ {X}_i={X}_{\mathrm{min}}+\mathit{\operatorname{rand}}\left(0,1\right)\times \left({X}_{\mathrm{max}}-{X}_{\mathrm{min}}\right) $$
    (28)
Fig. 3
figure 3

Bee Colony (ABC) Algorithm Flowchart

Full size image

Where Xi is the new solution, Xmin and Xmax are the lower and upper limits of the search space (the range of parameters a and b) and rand(0, 1) is a random number of continuous uniform distribution over the interval [0, 1].

  • Step 3: Generate new solutions, then evaluate the objective function (MSE) for each solution. This step consists of three phases:

  1. (a)

    Employed Bee phase: Generate a new solution using the following equation (Eq. 29):

  2. (b)
    $$ {V}_{ij}={X}_{ij}+{\varphi}_{ik}\left({X}_{ij}-{X}_{kj}\right) $$
    (29)

With Xi is the ième solution, Vi is the new solution, Xk is an arbitrarily chosen solution, the index k is chosen arbitrarily between 1 and D and φik =  rand (0, 1).

Then, the bee employed applies a gourmet selection between the solutions Xi and Vi to decide which solution will be used in the following cycles of the algorithm ABC.

For each solution, calculate the probability value by the following equation (Eq. 30):

$$ {P}_i=\frac{f(i)}{\sum_1^{SN}f(j)} $$
(30)

Where f(i) is the adaptation value of the ième solution.

  1. (c)

    Spectator phase: select a solution according to the probability of each spectator, generate a new solution by Eq. (28) and apply a gourmet selection between the solutions.

  2. (d)

    Scout bee phase: When a solution is exhausted, replace it with an arbitrarily generated solution by a scout memorize the best solution.

  • Step 4: Repeat steps 1 to 3 until Limit is reached.

  • Step 5: Record the image / signal reconstructed in order n and the values of the parameters a and b corresponding to the best solution obtained by the ABC algorithm.

6 Compression of signals / images by HMs optimized by the ABC algorithm

In this section, we present the proposed compression technique based on HMs and the Artificial Bee Colony (ABC) algorithm.

The term data compression refers to the process of reducing the amount of data needed to represent information. In the literature, there are generally two types of compression: Lossless compression when data reconstruction is identical to the original but the compression rate is very low, and lossy compression where the compression rate is very high but with loss of data. In order to achieve high compression ratios, we focus our attention in particular on lossy compression. The lossy compression technique proposed using the ABC algorithm is summarized in Fig. 4. The main steps of this method are detailed below:

  • Step 1: initialize the parameters of the ABC algorithm (see step 1 section 5)

  • Step 2: calculate the HMs and minimize the objective MSE function using the ABC algorithm.

  • Step 3: determine the maximum (Max) and minimum (Min) value of the compressed file (HMs) and quantify the data class of these as a function of Min and Max (int8, int16, int32…).

  • Step 4: decompress the signal / image from the reverse operation of the HMs using the optimal parameters determined by the ABC algorithm.

  • Step 5: Evaluate the compression ratio.

Fig. 4
figure 4

The diagram of the proposed algorithm for signal / image compression

Full size image

An original signal or image of dimension Ndim with dim = 1 for a signal, dim = 2 for an image and dim = 3 for a volume (3D image), each of their values is represented by 2i bits. For HMs (the compressed file) of order ndim are represented by values each is represented by 2j bits.

The compression ratio (CR) of a compressed signal or image is defined by [31]:

$$ CR=\frac{\#\boldsymbol{bits}\ \boldsymbol{to}\ \boldsymbol{represent}f}{\#\boldsymbol{bits}\ \boldsymbol{to}\ \boldsymbol{represent}\hat{f}} $$
(31)

with f is the original signal or image and \( \hat{f} \) represents the compressed signal or image.

Using the definition of CR given by Eq. (32), we calculate CR of compressed signal or image by the following relation (Eq.32):

$$ CR={\left(\frac{N}{n}\times \frac{2^i}{2^j}\right)}^{\mathrm{dim}} $$
(32)

With N is the signal or image dimension, n is the polynomial order, i is j are values depend on the class of the signal data and HMs.

The polynomial order n which makes it possible to obtain the desired CR is calculated from Eq. (33) by the following relation (Eq. 33):

$$ n=\boldsymbol{round}\left(\frac{N}{\sqrt[\mathit{\dim}]{CR}}\times \frac{2^i}{2^j}\right) $$
(33)

The values of the compressed file are of real type with double precision, in this case each value is represented on 26 bits (8 octets). This requires a high storage space to save it. For this, we need the step of quantifying the values of the compressed file. In fact, the maximum (Max) and minimum (Min) value of the compressed file is determined in order to quantify all the values of the latter to an optimum data class according to the range of Max and Min values. Quantization is an important step in the proposed compression method, as it optimizes memory space to save the compressed signal or image.

7 Simulation results

In this section, we present the results of simulations performed to show the efficiency of the proposed optimization technique for the reconstruction and compression of bio-signals and 2D and 3D medical images. This section is subdivided into five subsections: first, we evaluate the efficiency of the proposed reconstruction method using bio-signals. The first test is devoted to prove the performance of the proposed method for different orders of reconstruction (50,100, 500 and 1000), while the second test presents a comparison of the proposed method with the conventional method which uses fixed values of the polynomial parameters (a, b) (a = 90, b = 10; a = 10, b = 90; a = 80, b = 20). In another test, we evaluate the performance of the proposed method with other methods based on discrete orthogonal moments. The robustness of the proposed method against noise is also tested. In the second sub-section, we present the results of simulations concerning the proposed compression method which will be applied to bio-signals. In the third subsection, we demonstrate the efficiency of the ABC algorithm with HMs in the reconstruction of color images. The fourth subsection illustrates the use of the proposed compression method in compressing 2D color images. In the last subsection, we use the proposed reconstruction method based on the ABC algorithm for the optimal reconstruction of 3D images.

7.1 Optimal reconstruction of signals by HMs and the ABC algorithm

To test the efficiency of the proposed algorithm for the reconstruction of large signals, several bio-signals are selected from the database MIT-BIH [23]. This database contains different types of bio-signals such as electrocardiogram (ECG), electroencephalogram (EEG) and electromyogram (EMG). In the first test, we reconstructed an ECG signal of size N = 1000 using HMs optimized by the ABC algorithm for orders ranging from 50 up to 1000 order. Figure 5 presents the original signal “MIT-BIH record 203” and a set of signals reconstructed by the HMs optimized by the ABC algorithm for orders n = 50, n = 100, n = 500 et n = 1000 . This figure also shows the values of the local parameters a and b of the HPs calculated using the ABC algorithm for each order. From the reconstruction results obtained in Fig. 5, we observe that for each order, the ABC algorithm determines the optimal values of the parameters a and b which allow the ECG signal to be reconstructed with minimal error. Indeed, we clearly see that the resemblance between the reconstructed signals and the original test signal increases with the growth of the orders of the HMs (for the order 50 we have the MSE = 0.45103, and for the order 1000 MSE = 0.000000606) which justifies the effectiveness of the proposed method based on the ABC algorithm for the efficient reconstruction of bio-signals.

Fig. 5
figure 5

Set of signals reconstructed by HMs of orders up to 1024 using the ABC algorithm

Full size image

To further illustrate the effectiveness of the proposed method for reconstructing bio-signals, we compare, in the second test, the MSE and PNSR reconstruction errors obtained on the basis of the conventional reconstruction, that is to say when the values HP parameters (a, b) are set by the user, and based on the proposed reconstruction method which is based on the ABC optimization algorithm where the values of the parameters are selected by this algorithm. Figure 6 shows the reconstruction of test results carried out using a signal called “MIT-BIH record 112” of size 1000 as a 7 shows the PSNR obtained for the signal “ECG” using both reconstruction methods. From the results of this test, it is clear that the proposed method based on the ABC algorithm is better compared to the conventional method since the MSE values obtained via the proposed method are lower compared to those obtained by the method. Conventional or local parameter values (a, b) are chosen by the user. In addition, we find that MSE values PSNR increase with increasing order of HMs up to order 1000, which means that the reconstructed signal becomes very similar to the original signal Fig. 7.

Fig. 6
figure 6

Set of signals reconstructed by HMs using: a proposed method based on the ABC algorithma = 32.269andb = 20.004, b the conventional method with a = 90, b = 10, c the conventional method with a = 10, b = 90, d the conventional method with a = 80, b = 20

Full size image
Fig. 7
figure 7

PSNR of the “ECG” signal reconstructed by HMs using the conventional method and the proposed method based on the ABC algorithm

Full size image

In the third test, we compare the performance of the proposed reconstruction method compared to other reconstruction methods based on the discrete orthogonal moments of Tchebichef (TMs) [6], Krawtchouk (KMs) [35], Meixner (MMs) [9] and Charlier (CMs) [8]. Figure 8 shows the PSNRs of the signals reconstructed by the different reconstruction methods. We observe from this figure that PSNR increases as the order of moments used increases. In addition, we notice that the HMs optimized by the ABC algorithm improve the quality of reconstruction of the bio-signals compared to the other types of moments used in this test, which clearly shows the efficiency of the proposed method compared to others. Reconstruction method.

Fig. 8
figure 8

PSNR of the ECG signals obtained by the moments used in the test

Full size image

In the following experiment, we test the robustness of HMs against noise. To do this, we are going to contaminate a “MIT-BIH record 110” signal of size N = 1000 by a random noise, then we reconstruct this signal by the HMs optimized by the ABC algorithm up to the order of 1000. results of this test are shown in Fig. 9.

Fig. 9
figure 9

a Original noisy signal, b The signal reconstructed by the HMs at order 1000 optimized via ABC

Full size image

The MSE and PSNR curves (Fig. 10) of the noisy signal “ECG” which is reconstructed up to the order of 1000 clearly show that the reconstruction error of the noisy signal decreases and tends towards zero with the increase in the orders of the signals. HMs and that the MSE of the noise-free signal is slightly lower than that of the noisy signal, indicating that HMs calculated by the ABC algorithm are very robust under noisy conditions.

Fig. 10
figure 10

MSE and PSNR of the “ECG” signal reconstructed without noise and in the presence of random noise

Full size image

In the following test, we validate the robustness of HMs for small signals. To do this, we reconstructed an ECG signal of size 10 × 10 by the HMs optimized by the ABC algorithm up to the maximum order 10. the results of this test are illustrated in Fig. 11, we observe that at each order of reconstruction there are optimal values of a and b with minimal error, and 10 is the optimal order (MSE = 0.000206, PSNR = 84.9843), which shows the efficiency of the proposed algorithm for small signals.

Fig. 11
figure 11

Set of signals size 10 × 10 reconstructed by HMs using proposed method

Full size image

7.2 Optimal signal compression by HMs and ABC algorithm

In this subsection, we use the HMs calculated by the ABC algorithm for the compression of bio-signals. To do this, we used in the first test a bio-signal “MIT-BIH record 111” selected from the database [23].

Figure 12 shows a set of test signals decompressed by the proposed method. This figure also represents the CR and MSE which corresponds to each decompressed signal. From the results obtained, it is observed that for each order the ABC algorithm makes it possible to have optimal values (a, b) of the HPs to compress the bio-signals. We also note that the MSE decreases with the decrease in CR. These results indicate that the proposed method based on the HMs and the ABC algorithm makes it possible to achieve a high CR while keeping a good quality of the decompressed signal since MSE remains low thanks to the use of the ABC algorithm which optimizes the values of the local parameters when compressing.

Fig. 12
figure 12

a decompressed signal using ABC-optimized HMs up to the order of 50, b decompressed signal using ABC-optimized HMs up to the order of 100, c decompressed signal using ABC-optimized HMs up to the order of 500 and d decompressed signal using ABC-optimized HMs up to the order of 1000.

Full size image

There are several signal compression techniques in the literature [19, 22, 26, 33]. In order to show the efficiency of the proposed algorithm, a comparison with these techniques is made in terms of PRD% and CR%. The comparison result is displayed in Fig. 13.

Fig. 13
figure 13

Comparison between the proposed compression algorithm with existing compression algorithms

Full size image

The results of the comparison shown in Fig. 13. shows that the proposed method is better compared to the other methods used in the test because for the same CR we can obtain a minimum PRD%. This is justified by the use of the ABC algorithm which minimizes errors during compression.

7.3 Optimal reconstruction of medical images by HMs and the ABC algorithm

To test the efficiency of the proposed method for image reconstruction, two real color images are used: “Brain” and “Brain1” of sizes 1024 × 1024. These are selected from the base [27]. Images are reconstructed using HMs optimized by the ABC algorithm for orders ranging from 10 up to the last 1024.

Figure 14 presents the original “Brain” images with a set of images reconstructed by the HMs optimized by the ABC algorithm for different orders. This figure also represents the values of the local parameters (a, b) of the HPs calculated by the ABC algorithm for each order. From the results obtained, it can be seen that the proposed method is reliable for the optimal reconstruction of color images since the reconstruction quality of these images increases with the increase in the order of HMs, and that the variation in the values of the polynomial parameters (a, b) does not follow any deterministic law which shows the efficiency of the ABC algorithm for the optimal selection of these parameters.

Fig. 14
figure 14

Set of images reconstructed from “Brain” and “Brain1” images by HMs optimized by ABC up to the order of: a 10, b 50, c 100, d 500 and e 1024

Full size image

The following test is performed to demonstrate the superiority of the proposed reconstruction method based on HMs optimized via ABC compared to other methods based on the discrete orthogonal moments of Krawtchok (KMs), Tchebichef (TMs), Charlier (CMs), and Meixner (MMs). To do this, we reconstruct a real heart ‘size image. This image is reconstructed by the various methods mentioned above.

Figure 15 shows the “Heart” image reconstructed by the different reconstruction methods as well as the corresponding reconstruction errors (MSE and PSNR). The results of this figure show that HMs optimized by ABC offers better quality of the reconstructed image compared to the other methods for all reconstruction orders since the values of MSE of the image reconstructed by the proposed method are always lower (PSNR higher) compared to those obtained by the other methods used in the test.

Fig. 15
figure 15

The “Heart” image reconstructed using, HMs with ABC, Tchebichef, Krawtchok, Charlier and Meixner

Full size image

To confirm the robustness of the HMs for the small images, we reconstructed the image “MARIO” of size 10 × 10 by the HMs using the ABC algorithm up to the maximum order 10. the results of this test are shown in Fig. 16, we observe that for each order of reconstruction there are optimal values of a and b with minimal error, and 10 is the optimal order (MSE = 5.7719 × 10−6, PSNR = 100.517), which shows the efficiency of the proposed algorithm for small images.

Fig. 16
figure 16

Set of images size 10 × 10 reconstructed by HMs using proposed method

Full size image

The structural similarity index (SSIM) measure is frequently used in many comparisons. SSIM emphasizes structural details and can provide higher structural similarity. Figure 17 shows the measurement of the structural similarity index (SSIM) for the 2D “Heart” image by the proposed method and the conventional method (a = 10 & b = 90,a = 90 & b = 10a = 80 & b = 20). The SSIM decreases as the reconstruction order gets larger until it reaches a stable value, where the reconstructed image will be maximally close to the original image.

Fig. 17
figure 17

Structural similarity «SSIM» for the 2D image “Heart” by the proposed method and the conventional method

Full size image

7.4 Optimal compression of images by HMs optimized by the ABC algorithm

In this compression test, we use a real color image of size 1024 × 1024: chosen from the base [27]. The image is compressed using the proposed method based on HMs optimized by ABC until the order (1024,1024).

Figure 18 shows a set of images compressed by the proposed method as well as the compression rates (CR) and the MSE and PSNR reconstruction errors of the decompressed images. Note that for each order there exists an optimal parameter of (a, b) which guarantees a better quality of the decompressed image. These results clearly justify the effectiveness of the proposed method applied to medical gluing images, in terms of high color CR and in terms of fewer errors of the reconstructed (decompressed) image.

Fig. 18
figure 18

The “Brain” image Compressed using HMs and ABC, a up to order 10, b up to order 50, c up to order 100, d up to order 500 and e up to order 1024

Full size image

7.5 Optimal reconstruction and compression of 3D images by HMs and the ABC algorithm

In this subsection, we test the ability of the proposed reconstruction method based on HMs and the ABC algorithm for 3D image reconstruction. To do this, we use 3D images of size 256 × 256 × 256voxels downloaded from the basis [5]. Fig. 19 shows the 3D image “Verterba” with a set of images reconstructed from this image by the method proposed for HMs of orders ranging from 50 to 256. This figure also shows the values of the parameters (a, b) optimized by each order of moments and the values of the errors MSE and PNSR. The results illustrated in this figure show that for each order of HMs, we have an optimal value of polynomial parameters (a, b) which allows to reconstruct the image “ Verterba “ 3D with fewer errors thanks to the use of the ABC algorithm.

Fig. 19
figure 19

The 3D image “Verterba” reconstructed using HMs with the ABC algorithm, for orders of moments 50, 100 and 256

Full size image

In the second test (Fig. 20), we compare the capacity of the reconstruction of 3D images by the proposed method based on the ABC algorithm and the conventional method where the choice of the values of the polynomial parameters a and b are chosen empirically (fixed by user) for all orders (a = b = 10, a = 10, b = 50 and a = 50, b = 10). The reconstruction test is carried out on the 3D “Corona virus” image of size 256 × 256 × 256 by HMs to order 100. The results of this test clearly show that the values (a, b)of HMs optimized by ABC offers a better quality of reconstruction (very low MSE and high PSNR) compared to the conventional method, which shows the efficiency of the proposed method for the selection of polynomial parameters and for the reconstruction of 3D images.

Fig. 20
figure 20

3D images reconstructed by HMs using ABC algorithm and several values of parameters a and b

Full size image

Figure 21 shows PSNR curves corresponding to the 3D reconstructed image “Corona virus” using the proposed method and the conventional method for the different polynomial values. (a, b)of HPs, a = b = 10, α = 10, b = 50 and a = 50, b = 10. We observe that PSNR increases as the order of 3D HMs increases. Furthermore, we can see that the proposed method is better in terms of good reconstruction quality since the values of PSNR via our method are always best compared to the conventional method.

Fig. 21
figure 21

PSNR of the ‘Corona virus’ image reconstructed by HMs using the ABC algorithm and several values of the parameters a and b

Full size image

8 Conclusion

In this paper, we have effectively solved the problem of choosing optimal values of the parameters of Hahn polynomials (HPs) through the use of the ABC algorithm. HPs are used to define Hahn moments (HMs) which are used for optimal reconstruction and compression of large 2D / 3D signals and images. The optimization is carried out via the ABC algorithm which guarantees a good choice of the parameters (a, b) during the reconstruction and the compression of the signals and the images. The results of the simulations clearly showed the effectiveness of the proposed methods compared to the conventional methods in terms of the choice of parameters (a, b) and in terms of the quality of reconstruction / compression of signals and images, so now we know the optimal parameters (a, b) in each order about signals and images. In a future work, we will use this approach in the classification of large signals and images.