Abstract
Multi-Target Multi-Camera (MTMC) vehicle tracking is an essential task of visual traffic monitoring, one of the main research fields of Intelligent Transportation Systems. Several offline approaches have been proposed to address this task; however, they are not compatible with real-world applications due to their high latency and post-processing requirements. This lack of suitable approaches motivates our proposal: A new low-latency online approach for MTMC tracking in scenarios with partially overlapping fields of view (FOVs), such as road intersections. Firstly, the proposed approach detects vehicles at each camera. Then, the detections are merged between cameras by applying cross-camera clustering based on appearance and location. Lastly, the clusters containing different detections of the same vehicle are temporally associated to compute the tracks on a frame-by-frame basis. The experiments show promising low-latency results while addressing real-world challenges such as the a priori unknown and time-varying number of targets and the continuous state estimation of them without performing any post-processing of the trajectories. Our code is available at http://www-vpu.eps.uam.es/publications/Online-MTMC-Tracking.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Intelligent Transportation Systems (ITS) are considered a key part of smart cities. Consistent with the accelerated development of modern sensors,
new computing capabilities and communication, ITS technology engages the attention of both academia and industry. ITS point to offer smarter transportation facilities and vehicles, along with safer transport services.
One of the main research fields on ITS is visual traffic monitoring using video analytics with data captured by visual sensors. This data can be used to provide information, such as traffic flow estimation, or to detect traffic patterns or anomalies. In recent years it has become an active field within the computer vision community [11, 44, 46], however it is still remains a challenging task [30], mainly if we consider the case of multiple cameras.
In contrast to mono-camera traffic monitoring, multi-camera setups requires of a more complex infrastructure, the capability of dealing with more simultaneously data, as well as a higher processing capability. Multi-Target Multi-Camera (MTMC) tracking algorithms are fundamental for many ITS technologies.
Different from Multi-Target Single-Camera (MTSC) tracking [3, 5, 22], MTMC tracking entails the analysis of visual signals captured by multiple cameras, considering setups with overlapping fields of view (FOVs), but also scenarios for wide-area monitoring, where cameras may be separated by large distances. Road intersections are well-known targets for monitoring due to the high number of reported accidents and collisions [37]. These intersections are known for their intrinsic and complex nature due to a variety of the vehicles’ behaviors. This kind of scenarios are usually monitored with multiple partially overlapping cameras, which introduces new challenges, but also powerful opportunities for video analysis (e.g. traffic flow optimization and pedestrian behaviour analysis).
The key issue to solve for the multi-camera tracking problem is an efficient data association across cameras, and, also, across frames. This is not a simple task since appearance from different views may vary significantly. A considerable amount of existing MTMC vehicle tracking algorithms perform an offline batch processing scheme to carry out the association [1, 4, 15,16,17, 23, 41, 45]. They consider previous and future frames, and often the whole video sequences at once, to merge vehicles trajectories across cameras and time. They also rely on post-processing techniques to refine the resulting trajectories. This offline scheme provides more robustness, compared to online designs, albeit it is not compatible with online applications; hence, limiting its applicability in real-time traffic monitoring scenarios.
In this paper, we describe the first, to the best of our knowledge, low-latency online MTMC vehicle tracking approach for cameras with partially overlapping FOVs capturing intersection scenarios. The proposed approach follows an online and frame-by-frame processing scheme.
Furthermore, compared to other state-of-the-art systems (see Table 1), our approach does not perform any post-processing track refinement, it is agnostic to potential motion patterns (i.e., it works without prior knowledge of vehicles paths within cameras’ FOV) and it does not require additional manual ad-hoc annotations (e.g. definition of regions and boundaries on the roads). These two last characteristics avoid the need of configuring each real set-up where the system is deployed, improving flexibility and generalising its use.
The proposed MTMC tracking approach builds upon detection of multiple vehicles on every single camera. Afterwards, a combined cross-camera agglomerative clustering, combining spatial locations (using GPS coordinates) and appearance features, is used to merge vehicles from different cameras. This clustering is evaluated using validation indexes and, finally, a temporal linkage of the obtained clusters is performed to obtain the trajectories of each moving vehicle in the scene along time.
This paper is an extended version of our related conference publication [28], with additional contributions as follows. First, we include and evaluate the impact of additional object detectors. Second, we remove any offline dependency in order to become a genuine online approach. Third, we design and train a completely new appearance feature extraction, and also investigate the impact of an additional dataset for training. Fourth, we improve the cross-camera clustering and temporal association reasoning. Fifth, we design and implement a new occlusion handling strategy. Last, we perform a wide ablation study to measure the impact of different parameters and strategies at different stages of the proposal, and we show results in a detailed comparison with the state-of-the-art.
The paper is organized as follows. Section 2 reviews the state-of-the-art in MTMC vehicle tracking. Section 3 describes the proposed approach. Section 4 presents the evaluation framework, the implementation details, the ablation study and, finally, a comparison with the state-of-the-art. Lastly, conclusion remarks are described in Section 5.
2 Related work
For the last recent years, several approaches devoted to track pedestrians in multi-camera environments have been published [2, 14, 24, 38, 47, 50]. The releases of public benchmarks such as MARS [49] and DukeMTMC [34] powered the research community to put efforts into Multi-Target Multi-Camera tracking oriented to people tracking.
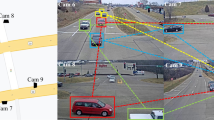
Due to the lack of appropriate publicly available datasets, MTMC tracking focused on vehicles was a nearly unexplored field. To encourage research and development in ITS problems, the AI City Challenge WorkshopFootnote 1 launched three distinct but closely related tasks: 1) City-Scale Multi-Camera Vehicle Tracking, 2) City-Scale Multi-Camera Vehicle Re-Identification and 3) Traffic Anomaly Detection. Focusing on MTMC tracking, the CityFlow benchmark was presented [42]. At the time of publication, it is the only dataset and benchmark for MTMC vehicle tracking. Figure 1 depicts four sample views from an intersection in the City-Flowbenchmark.
The major challenge of tracking vehicles is the viewpoint variation problem. As can be seen in Fig. 2, different vehicles may appear quite similar from the same viewpoint, however the same vehicle captured from different viewpoints may be difficult to recognise. It can be extremely hard, even for humans, to determine if two vehicles from different points of view depict the same car (e.g., as shown in Fig. 2, pairs [(a), (d)], [(b), (e)] and [(c), (f)]).
According to the processing scheme, MTMC tracking methods can be categorized in two groups: 1) offline methods, and 2) online methods. Offline tracking methods perform a global optimization to find the optimal association using the entire video sequence. The vehicles’ detections are temporally grouped into tracklets (short trajectories of detections) using MTSC tracking techniques, and, afterwards, tracklet-to-tracklet association is performed, mainly by using re-identification techniques: considering the whole video sequences at once [15, 17, 23, 41, 45], considering windows of frames [4], or even combining both approaches [16].
On the other side, online approaches need to perform cross-camera association of target detections on a frame-by-frame basis, using detectors’ outputs (usually, bounding boxes) as the smallest unit for matching, instead of tracklets.
As can be seen in Table 1, to the best of our knowledge, all existing approaches chose to work in an offline way. In order to remove false positive trajectories or ID switches [34], the offline approaches sometimes may apply post-processing filtering at the end of some intermediate stages [4, 23, 41], or at the end of the whole process [17]. Being aware of the motion patterns that the vehicles can adopt in every camera view, can also help to remove undesired trajectories and, therefore, increase the Recall evaluation metric [1, 4, 17, 41, 45]. Offline working also allows to apply additional temporal constraints to increase the performance [4, 17, 41]. Another strategy to improve overall performance consists in incorporating some additional manually annotated, scenario specific, information; for example, additional vehicle’s attributes (colour, type, etc.) for getting a better appearance model [41] or road boundaries [4].
It is common in the literature of MTMC tracking to treat the tracklet-to-tracklet cross-camera association task as a clustering problem, grouping them by appearance features [15, 35, 41], or by combining appearance and other constraints (e.g., time and location) [4, 17, 43, 48]. Clustering algorithms are often categorized into two broad categories: 1) partitioning algorithms (center-based, e.g. K-means [29], or density-based, e.g. DBSCAN [9]); and 2) hierarchical clustering [18] (being agglomerative or divisive). While hierarchical algorithms build clusters gradually (as a tree of clusters) and they do not require pre-specification of the number of clusters, partitioning algorithms learn clusters at once and they require pre-specification of the number of clusters (K-means) or the minimum number of points defining a cluster (DBSCAN). Therefore, hierarchical clustering is advantageous when there is no prior knowledge about the number of clusters, but on the contrary, it outputs a tree of clusters, commonly represented as a dendrogram. Such structure does not provide the number of clusters, but gives information about the relations between the data. For this reason, cluster validation techniques, such as Davies-Bouldin index [6], the Dunn index [8] or the Silhouette coefficient [20], are used to determine the number of clusters, which may differ for each technique. In the proposed apprach, as there is no prior knowledge about the number of vehicles in the scene, we apply agglomerative hierarchical clustering combining location and appearance information.
Existing MTMC vehicle tracking approaches firstly compute tracklets by temporally merging detections on every single camera, and then performing cross-camera tracklet-to-tracklet association. In contrast, we firstly compute clusters by cross-camera association of vehicle detections and, afterwards, on a frame-by-frame basis, we temporally associate the clusters to compute the tracks.
3 Proposed approach
In the proposed online Multi Target Multi Camera tracking approach, all cameras’ videos are processed simultaneously frame by frame, without any post-processing of the trajectories. The approach is composed of five processing blocks, as shown in Fig. 3. As input, we consider a network of calibrated and synchronized cameras with partially overlapping FOVs providing independent video sequences. Given a network of N cameras, the pipeline includes the following stages: (1) vehicle detection; (2) feature extraction; (3) homography projection, which projects single camera vehicles from each camera view to the world coordinates system (GPS) for providing location information; (4) cross-camera clustering, that is fed on the output of (2) and (3) blocks; and (5) temporal association of vehicles trajectories over time to compute the tracks. As result, the system generates tracks consisting on the identity and location of every vehicle along time. The design of the processing blocks is detailed in the following subsections, whilst the implementation details are given in Section 4.2.
Block diagram of the proposed approach. The inputs are frames from N cameras. The trajectories are computed for each frame. First, the vehicle detection block computes \({\mathscr{B}}\), the set of vehicle detections. \({\mathscr{B}}\) feeds both feature extraction and homography projection blocks. \(\mathcal {F}\) is the set of appearance feature descriptors and \(\mathcal {W}\) the set of GPS world coordinates of every vehicle. The cross-camera clustering block uses \(\mathcal {F}\) and \(\mathcal {W}\) to aggregate different views of the same vehicle and to compute the set of clusters \({\mathscr{L}}\) at each temporal instant. Lastly, the temporal association block associates clusters in \({\mathscr{L}}\) in a temporal way to compute the set of tracks \(\mathcal {T}\)
Table 2 summarizes the notation used in this section. The scope of each variable is also defined: Scenario refers to the set of cameras; Frames stand for all the simultaneous images coming from the cameras at each temporal instant; Sequence is comprised of all the aggregated frames coming simultaneously from the cameras. N, and Hn are intrinsic to the scenario, while r is a design parameter. D, \({\mathscr{B}}\), \(\mathcal {W}\), \(\mathcal {F}\), and \({\mathscr{L}}\) are computed at each temporal instant, needing the simultaneous frames. Last, \(\mathcal {T}\) is updated frame-by-frame for the whole sequence.
3.1 Vehicle detection
As most of the state-of-the-art MTMC tracking methods, we follow the tracking-by-detection paradigm. Therefore, the first stage of the pipeline is vehicle detection at each frame. Let b = [x, y, w, h] be a bounding box with [x, y] being the upper-left corner pixel coordinates, and [w, h] the width and height. Let define \({\mathscr{B}}=\left \{\textbf {b}_{d}, d \in [1, D]\right \}\) as the set of bounding boxes at each frame for all the cameras, with D the total number of detections.
Note that the proposal can incorporate any single-camera vehicle detection algorithm whose output is in a bounding box form.
3.2 Feature extraction
In order to describe the appearance of the dth bounding box detection, let fd be its k-dimensional deep feature descriptor. Let \(\mathcal {F}=\left \{\textbf {f}_{d},d \in [1, D]\right \}\) be the set of appearance feature descriptors for each frame and for all the detected vehicles.
Due to the intrinsic geometry of vehicles, their appearance may suffer strong variations across different camera views. This variance is such that it could be, even for a human being, very hard to determine if they are the same vehicle. Thus, in order to have highly discriminating features, we trained a model to improve vehicle classification ability in the faced scenario. More details on this vehicle specific model will be given in Section 4.2.2.
Class imbalance is a form of the imbalance problem [32], that occurs when there is an important inequality regarding the number of examples pertaining to each class in the data. When not addressed, it may have negative effects on the final performance. It is known that classes with a higher number of observations tend to dominate the learning process, hindering the learning and generalization of low-represented classes. In order to minimize the imbalance effects, instead of classical Cross-Entropy (CE) loss [10], we employ the focal loss (FL) proposed in [25].
3.3 Homography-based projection
This processing block computes the location of each detected vehicle on the common ground-plane employing GPS coordinates. Let Hn be the homography matrix that transforms coordinates from the image plane of the nth camera to the GPS coordinates of the common ground plane. Let the inverse matrix \(\textbf {H}_{n}^{-1}\) be the inverse transformation. We leverage the GPS coordinates to achieve a high-precision clustering based on the location information by applying camera projection. Given a bounding box b, one can obtain its associated GPS coordinates, i.e. [ϕ, λ] (latitude and longitude), by projecting the middle point of its base with the Hn transformation. \(\mathcal {W}=\left \{[\phi , \lambda ]_{d}, d \in [1, D]\right \}\), the set of GPS coordinates, is obtained after applying the transformation to the set \({\mathscr{B}}\). Figure 4 illustrates an example of the projected detections coming from different cameras.
Note that this block relies on the output of the object detection stage, and, along with the feature extraction module, it feeds the cross-camera clustering.
3.4 Cross-camera clustering
Given the sets \({\mathscr{B}}\), \(\mathcal {W}\) and \(\mathcal {F}\), the cross-camera clustering block associates different camera views of the same vehicle at each frame to compute \({\mathscr{L}}=\left \{l_{i}, i \in [1, L]\right \}\), the set of clusters at a given frame, being L be the number of created clusters. Clusters’ content ranges from a single detection, if the vehicle is only visible by one camera, to the maximum number of detections, defined by the maximum number of cameras capturing the scene. To create the clusters, we compute a frame-by-frame linkage by performing an agglomerative hierarchical clustering combining location and appearance features.
Hierarchical clustering [18] requires a square connectivity matrix of distances (dissimilarities) or similarities of the input data to merge. We compute the connectivity matrix Θ as a constrained pairwise features distance between all the vehicles coming from every camera at each frame. At each frame, we compute the pairwise Euclidean distance between the appearance feature vectors of all the vehicles under consideration, as follows:
Also at each frame, we compute the Euclidean pairwise distance between all the GPS coordinates of vehicles:
The spatial distance and the camera ID are used to apply some constraints. Since two vehicles’ detections widely separated in GPS coordinates are highly unlikely to come from the same vehicle, it is reasonable to assume a maximum association distance. This constraint narrows down the list of vehicles to be matched and improves the ability to distinguish different identities by focusing on comparing only nearby targets. Hence, the connectivity matrix Θ is computed as follows:
being r the maximum association radius. A second condition is applied for preventing vehicles’ detections from the same camera view to be merged together. It is done by constraining the association matrix as follows:
Let cd be the camera yielding the dth detection.
As stated above, hierarchical clustering methods departs from a connectivity matrix Θ to compute a tree of clusters and this cluster structure does not provide the number of clusters, but gives information on the relations between the data. These relationships can be represented by a tree diagram called dendrogram. In order to identify the optimal number of clusters, we use the Dunn index [8] for cluster validation. The aim of this index is to find clusters that are compact, with a small variance between members of the cluster, and well separated by comparing the minimal cluster distance to the maximal cluster diameter. The cluster diameter is defined as the distance between the two farthest elements in the cluster. This process provides the number of vehicles at every frame in the scene, in the form of clusters, as well as its location, in the form of the cluster’s centroid (outlined as the mean point at each coordinate axis of all the components). To sum, at every frame, each cluster designates an existing vehicle viewed by one or multiple cameras.
3.5 Temporal association
The last stage of the proposed approach links clusters over time to estimate the vehicle tracks. Let \(\textbf {t}_{j} = [\textbf {x}^{s_{start}}_{j},...,\textbf {x}^{s_{end}}_{j}]\) be the jth track defining the trajectory of a moving vehicle by a succession of states. Each state is described by \(\textbf {x}^{s}_{j}=[\phi ,\lambda ,v_{\phi },v_{\lambda }],\) where [ϕ, λ] is the target location and [vϕ, vλ] is the target velocity, both represented using GPS coordinates. Let us define \(\mathcal {T}=\left \{\textbf {t}_{j}, j \in [1, J]\right \}\) as the set of tracks along the video sequence. In contrast to previous sets \({\mathscr{B}}\), \(\mathcal {W}\) and \(\mathcal {F}\), that are initialized at each frame, \(\mathcal {T}\) is built incrementally, i.e. it is computed at the first frame and updated along time. In other words, tracks depict the location of clusters along time. As in the whole system, the temporal association is performed on-line, that is, frame-by-frame.
Vehicles’ motion is estimated using a constant-velocity Kalman filter [19]. The Kalman filter makes a prediction of the state of the target as a combination of the target’s previous state (at the previous frame) and the new measurement (at the current frame) using a weighted average. It results in a new state estimation lying in between the previous target state and the measurement. Thus, at each frame, on the one hand, we employ Kalman filter to get the estimated location of the tracks of the previous frame, and, on the other hand, we get the current vehicle measurements as the clusters resulting from the cross-camera association.
In order to associate both, we apply the Hungarian Algorithm [21] to solve the assignment problem, using an association matrix to enumerate all possible assignments. The association matrix is computed using the pairwise L2-norm, i.e. the euclidean distance, between the location of the estimated tracks and the clusters’ centroid location (see Section 3.4).
To provide robustness against occlusions, we designed two strategies: a blind occlusion handling and a reprojection-based occlusion handling. The first maintains the tracks alive during a short time when the detections associated to them are lost. Keeping on predicting the position of the track during that period allows to recover it in case the detections are recovered. This is helpful if the vehicle detector loses a detection, either due to a bad detection performance or a hard occlusion. The second strategy detects if a track has lost one or more of its associated detections and looks for the same track in the previous frame to get the information about the size of its previously associated bounding boxes. The new location in the current frame is inferred by applying the corresponding inverse homography matrix (e.g., \(\textbf {H}_{n}^{-1}\) assuming a detection is missing for the nth camera) to the estimated track position. Therefore, when this strategy reveals a track whose detection or detections are lost, mostly due to an occlusion the detector cannot deal with, we can generate an artificial detection with accurate estimates on the correct position and with the previous detected size of the occluded vehicle.
4 Experiments
4.1 Evaluation framework
4.1.1 Datasets
We considered the CityFlow benchmark [42], since there is no other publicly available dataset devoted to MTMC vehicle tracking with partially overlapping FOVs. The dataset comprises videos of 40 cameras, 195 total minutes recorded for all cameras, and manually annotated ground-truth consisting of 229,690 bounding boxes for 666 vehicles. The dataset is divided into 5 scenarios (S01, S02, S03, S04 and S05) covering intersections and stretches of roadways. S01 and S02 have overlapping FOVs, while S03, S04 and S05 are wide-area scenarios. The CityFlow benchmark also provides the camera homography matrices between the 2D image plane and the ground plane defined by GPS coordinates based on the flat-earth approximation.
We have also used VeRi-776 dataset for improving the feature extraction model by using it as additional training data. VeRi-776 [36] is one of the largest and most common datasets for vehicle re-identification in multi-camera scenarios. It comprises about 50,000 bounding boxes of 776 vehicles captured by 20 cameras.
4.1.2 Evaluation metrics
The MTMC tracking ground-truth provided by the CityFlow benchmark consists of the bounding boxes of multi-camera vehicles labeled with consistent IDs.
Following the CityFlow benchmark evaluation methodology, Identification Precision (IDP), Identification Recall (IDR) and F1 Score (IDF1) measures [34] are adopted:
where IDTP, IDFP and IDFN stand for True Positive ID, False Positive ID and False Negative ID, respectively. IDP (IDR) is the fraction of computed (ground-truth) tracks that are correctly identified. IDF1 is the ratio of correctly identified tracks over the average number of ground-truth and computed tracks.
Automatically obtained tracks by the proposed approach are pairwise compared with the ground-truth tracks. We declare a match, i.e., an IDTP, when two tracks temporarily coexist and the area of the intersection of the bounding boxes is higher than τIoU (with 0 < τIoU < 1) times the area of the union of the two boxes. Hence, τIoU is the Intersection Over Union (IoU) threshold. A high IDF1 score is obtained when the correct multi-camera vehicles are detected, accurately tracked within each camera view, and labeled with a consistent ID across all the views in the dataset.
4.1.3 Hardware and software
The algorithm and model training have been implemented using PyTorch 1.0.1 Deep Learning framework running on a computer using a 6 Cores CPU and a NVIDIA GeForce GTX 1080 12GB Graphics Processing Unit.
4.2 Implementation details
4.2.1 Vehicle detection
Regarding single-camera vehicle detection we have experimented with public detections, i.e. vehicle detections provided by the CityFlow Benchmark, and private detections, computed using a state-of-the-art algorithm. The public detections were obtained by using three popular detectors: Yolo v3 [33], SSD512 [27], and Mask R-CNN [12]. Yolo v3 is a one-stage object detector that solves detection as a regression problem. SSD512 is also a single-shot detector which directly predicts category scores and box offsets for a fixed set of default bounding boxes of different scales at each location. Mask R-CNN, on the contrary, is a two-stage detector consisting of a region proposal network that feeds region proposals into a classifier and a regressor.
Moreover, we have complemented the provided detections with those obtained by the EfficientDet [40] algorithm, a top-performing state-of-the-art object detector. EfficientDet is also a one-stage detector that uses EfficientNet [39] as the backbone network and a bi-directional feature pyramid feature network (BiFPN).
All these approaches make use of pre-trained models on the COCO benchmark [26]. For our purpose, we considered only detections classified as instances of the car, truck and bus classes.
4.2.2 Feature extraction
For the feature extraction network, we employ ResNet-50 [13] as backbone, but the original classification layer (fc_1 layer), shaped for image classification on the ImageNet dataset [7], is replaced by a new classification layer whose size is tailored to the total number of identities in the training data. In order to leverage the pretained weigths on Imagenet, we fine-tune the network but freeze it until the conv_5 layer.
To fine-tune the network, we used the CityFlow benchmark training data (S01, S03 and S04) and we also included the VeRi-776 dataset, bringing a total of 905 vehicle IDs for training (129 IDs from CityFlow, plus 776 IDs from VeRi-776). Since only training identities are known, the network learns features to correctly classify the 905 different training vehicle identities. We perform a validation methodology on pairs of unseen vehicles and comparing whether predictions are the same or not. Therefore, we check the network ability to discern different views of the same target. To create these pairs, we randomly select half of the data from S05 scenario to create a 169 IDs validation set. We forced the validation batch to contain approximately 50% of positive and 50% of negatives pairs. The pair selection is randomly done over the set of IDs, instead of the set of images, thus, IDs containing few samples are not paired. At inference, we adopt, as a 2048-dimensional descriptor, the output of the average pooling layer, just before the classifier.
Each input image containing a bounding box of a vehicle is adapted to the network by resizing it to 224x224x3 and pixels’ values are normalized by the mean and standard deviation of the ImageNet dataset. In order to reduce model overfitting and to improve generalization, we perform several random data augmentation techniques such as horizontal flip, dropout, Gaussian blur and contrast perturbation.
To minimize the loss function and optimize the network parameters, we adopt the Stochastic Gradient Descend (SGD) solver. Experimentally, the initial learning rate was set to 0.1 and we follow a step decay schedule dropping it by 0.1 every 25 epochs. Momentum was set to 0.9 and weight decay to 1e− 4.
4.3 Ablation study
This section measures the impact of the strategies defined for the different stages of the proposed approach. Firstly, the effect of using different vehicle detectors is evaluated. Secondly, the influence of the association radius parameter is analysed. Subsequently, we gauge the influence of the appearance model training method as well as the size of the feature embedding. And, finally, some additional strategies (e.g. occlusions handling) are assesed. All the experiments are evaluated on the testing scenario of the CityFlow benchmark dataset with partially overlapping FOVs, i.e. the S02 scenario. It is composed of 4 cameras pointing to an intersection roadway (see Fig. 1), aggregating, in total, 129 annotated vehicles whose trajectories are distributed along 8440 frames (2110 per camera) that have been captured at 10 fps.
Influence of the vehicle detector algorithm
Table 3 comprises the impact of different vehicle detectors on the overall performance of the proposed approach. As stated before, we consider three provided object detections coming from Yolo v3, SSD512 and Mask R-CNN, i.e. public detections. We also evaluate the performance of EfficientDet, a top-performing algorithm.
We experimented with three different score thresholds to get the output detections (0.1, 0.2 and 0.3). As stated before, public detections stand for the detections provided by the CityFlow benchmark, and private detections are obtained with state-of-the-art detectors. Regarding the public detections, one can observe that the compared detectors achieve the peak performance when a low threshold is applied. The results suggest that filtering the output detections by scores higher than 0.2 leads to a lower IDR in the MTMC tracking performance. This finding indicates that detections with low confidence (mostly generated by remote and partially visible vehicles) are still useful.
On the contrary, EfficientDet, since it is a better performing objecter detector, results in a higher IDR and IDP being filtered with 0.3 instead of 0.2. It enhances IDR by 3.37, compared with the best results of Mask-RCNN; however, IDP is degraded by 2.01. The reason for this decline is that EfficientDet is providing more False Positive trajectories arising from the detection of partially occluded vehicles that Mask-RCNN is not able to detect.
In the light of these results, we opted for adopting Mask R-CNN output detections filtered by 0.2 score as public detections, and EfficientDet output filtered out by 0.3, as private detections for the remainder of the experiments.
Influence of the association radius
Table 4 shows how the association radius r, used in the cross-camera clustering (see Section 3.4), affects the MTMC tracking performance of the proposed approach in the evaluated scenario. Due to the length of the cars, 5 meters is a reasonable association radius to consider. We sweep radius values of 5, 6.5, 8 and 9.5 meters. The results on the table indicate that the choice of the radius is quite relevant, having a significant impact in the performance, and also it is highly-dependant on the detection algorithm. The Mask-RCNN detector gets performance peak for r = 8, however, when using the EfficientDet detector a smaller radius, r = 5, is the optimal choice. The reason of this difference is related with bounding box accuracy (i.e. how the output bounding boxes fit the vehicles). Since the middle points of the bases of the bounding boxes from different camera views are projected to the ground-plane, the tighter the boxes are, the closer are the projections (see Fig. 5).
a and b depict the bounding boxes detections of the same vehicle under two different views at the same instant, as well as the middle point of their bases. Green color stands for an object detector providing a properly adjusted box, while the red one produce a wider box. c shows the projected points and the corresponding distances between them. Note that the tighter the bounding box is to the vehicle shape, the closer are the projections in the ground plane
Due to the common vehicles dimensions, it may be natural to think that a smaller radius should be enough to successfully associate several detections of the same vehicle. However, due to errors in the video transmission while capturing the data, some frames are skipped within some videos, so some cameras suffer from a subtle temporal misalignment (i.e. they are unsynchronized with respect to the others). Therefore, the optimal r values for the CityFlow benchmark using the proposed approach are 5 and 8 meters, given the two evaluated detectors.
Influence of the appearance feature model
Table 5 summarizes the effect of the training schemes on the model used to describe the appearance features of vehicles for the proposed MTMC tracking approach. The table lists the data that has been used for training the network (described in Section 4.2.2) and how the weights of the network were obtained. As the baseline, we use the model pretrained on the Imagenet dataset. As training data, we considered the training set of the CityFlow benchmark (S01, S03 and S04 scenarios) and also the training set of the CityFlow benchmark jointly with the VeRi-776 dataset. We tried two classification loss functions: Cross-Entropy loss (CE loss) and Focal Loss (FL).
Table 5 indicates that the tracking performance behaviours in a coordinated manner using both Mask R-CNN and EfficientDet detectors. In both cases, fine-tuning the network to the CityFlow benchmark has a slightly, but positive, influence. Including more training data, the VeRi-776 dataset, appears to improve the quality of the feature embeddings, resulting in a even better tracking performance.
Figure 6 depicts in red the distribution of the number of images per vehicle ID of the training set of the CityFlow dataset, illustrating that it is a quite unbalanced set with a very scattered distribution. The average of the distribution is μcity = 232.90, while the standard deviation is σcity = 201.19. From Table 5, we observe that training the CityFlow benchmark with the Focal loss, instead of the Cross-Entropy loss, has a positive influence in our MTMC tracking approach.
Figure 6 also depicts in blue the distribution of the number of images per vehicle ID of the VeRi-776 dataset; as one may observe, it is more balanced than the CityFlow set. Considering both datasets together, the join distribution is now described by μjoin = 89.35 and σcity = 102.25; as σjoin << σcity, one could say that the join dataset is less disperse than the single CityFlow, which can be an indicator for the subtle increase in performance obtained when the combined dataset is used. According to these results, we opt for using the combined dataset and the CE loss for the rest of the experiments.
Influence of size of the feature embedding
Table 6 comprises the experiments carried out to explore the effect of the size of the feature embeddings. As stated in Section 4.2.2, the output of the last average pooling layer of ResNet-50 provides a 2048-dimensional embedding. We set this embedding size as the baseline. In order to modify the length of the embedding, an additional fully connected layer of size 512, 1024 or 4096 is added at the end of the network. The additional fully connected layer is preceded by batch normalization and ReLU layers, and the training procedure is the same as described in Section 4.2.2. The results suggests that adding an additional layer, and, therefore, more complexity to the model, either to reduce or increase the embedding size, may decrease the performance, leading the model to overfitting.
Influence of additional strategies
The additional strategies we have designed are divided in two branches: removing small detected objects that are not considered in the ground-truth, and occlusion handling. The blind occlusion handling and the reprojection-based occlusion handling strategies are detailed in Section 3.5.
To avoid the existing bias in the ground-truth towards distant cars that are not annotated, we performed a size filtering strategy by removing detections whose area is under 0.10% of the total frame area.
Table 7 shows the ablation results of these strategies. As expected, we can observe that the procedure of removing small detections increases the IDP measure, using both object detectors, by 2.47 (1.87), while maintaining almost the same IDR. Since IDP reacts to false positives, this seems to indicate that the size filtering removes those small detections we track, but are not annotated in the ground-truth.
Both occlusion handling strategies improve the baseline tracking IDR significantly, 3.81 (7.02) and 4.21 (5.64) respectively, and also the IDP is being improved by 2.90 (4.85) and 2.43 (3.20). Contrary to expectations, the reprojection-based strategy is not overcoming the blind one. Another bias existing in the ground-truth could be the reason for explaining this, since occluded vehicles are not annotated.
When combining both occlusion handling strategies with size filtering, we achieve a higher precision than applying them separately, while recall is slightly narrowed. As in the previous comparison, these results suggest that the reprojection-based strategy does not provide improvements over the blind strategy due to the nature of the ground-truth. We consider using the baseline approach together with the blind occlusion handling and the size filtering strategies, a good trade-of between the IDP and IDR.
4.4 Comparison with the state-of-the-art
This section compares the proposed algorithm is compared with state-of-the-art approaches. Comparison is performed in the S02 scenario of the CityFlow benchmark, which is the only validation scenario with partially overlapping FOVs, as our method targets this type of scenarios.
The proposed approaches in the literature devoted to vehicles MTMC tracking, listed in Table 1, have been already compared in the The 2019 AI City Challenge [31] jointly over the testing scenarios S02 and S05. However, as S05 consists of non-overlapping cameras, to ensure a fair comparison, we perform the evaluation only over S02. For this purpose, we ran the public available codes and we evaluated them following the CityFlow benchmark evaluation methodology, detailed in Section 4.1.2.
Table 8 shows the evaluated performances in terms of IDP, IDR, IDF1, latency and total computational time. The listed approaches can be divided by the processing mode in two groups: offline and online processing. As described in Section 2, to the best of our knowledge there is no previous proposal dealing with online MTMC vehicle tracking. For this reason, all the state-of-the-art methods that we evaluated are offline approaches. It is important to remark that, in Table 8, the star symbol denotes a partial and downward estimation, only . The codes for the complete systems are not publicly available, and only solutions based on precomputed intermediate results are accessible; hence, we can only compute the running time of the available modules. Therefore, the overall latency of the compared offline approaches is expected to be much higher than the results reported in Table 8. Note that the duration of the sequence under evaluation is also included in the latency since these offline approaches require access to results for the whole video to compute tracklets at each camera and then compute multi-camera tracks in a global way. As our proposal yields tracking results incrementally, from the beginning of the sequence, it can achieve a really low latency, in comparison with the others methods.
Regarding the quantitative measures of the tracking performance: IDP, IDR and IDF1, offline methods using constraining priors tailored to the target scenario clearly benefit from this extra information (see Table 1). In contrast to the related work, the proposed approach: is agnostic to the motion patterns of the vehicles (allowing to filter erroneous tracks), does not perform any track post-processing (permitting to refine and unify tracks and by this way reducing ID switches) and, finally, does not make use of manual annotations. On this basis, with an online approximation we perform really close to offline state-of-the-art approaches, outperforming two of them in terms of Identification Recall.
Overall, our approach does not quite reach top performance in MTMC vehicle tracking, but its latency is three orders of magnitude smaller and the final computational cost is one order of magnitude faster, enabling a high performance operation on online mode with low-latency, that is a common requirement for many video-related applications, and also, in the generalization of the algorithms, avoiding hand-crafted strategies.
5 Conclusion
Not relying on manual ad-hoc annotations, having no prior knowledge about the number of targets, and providing the best result in the shortest possible time are crucial requirements for a convenient and versatile algorithm. This paper presents, to the best of our knowledge, the first online MTMC vehicle tracking solution. Unlike previous approaches, the proposed approach continuously computes and updates the targets’ state. We calculate clusters of detections of the same vehicle from different camera views applying a cross-camera clustering based on appearance and location. We train an appearance model to identify different views of the same vehicle leveraging homography matrices’ information. Using information from the previous frame and a temporal estimation, we developed an occlusion handling strategy able to extrapolate accurate detections even if the target is occluded. Since the state estimation is continually updated, this strategy is useful even if the target is long-term occluded.
This approach results in a low-latency MTMC vehicle tracking solution with quite promising results. Although performance is below its offline counterparts, the proposed one is a suitable solution for a real-world ITS technology.
The proposed approach is restricted to overlapping scenarios, due to the dependency on the spatial location of the association stage. Moreover, the proposed approach requires information of the cameras’ calibration (e.g., homographies), which is not always available in already deployed systems. Future research may focus on overcoming these constraints by maintaining the online and low-latency operation.
References
Chang MC, Wei J, Zhu ZA, Chen Y, Hu CS, Jiang M, Chiang CK (2019) Ai city challenge 2019 – city-scale video analytics for smart transportation. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Chen L, Ai H, Chen R, Zhuang Z, Liu S (2020) Cross-view tracking for multi-human 3d pose estimation at over 100 fps. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 3279–3288
Chen L, Lou J, Xu F, Ren M (2020) Grid-based multi-object tracking with siamese cnn based appearance edge and access region mechanism. Multimed Tools Applic 79(47):35333–35351
Chen Y, Jing L, Vahdani E, Zhang L, He M, Tian Y (2019) Multi-camera vehicle tracking and re-identification on ai city challenge 2019. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Ciaparrone G, Sánchez FL, Tabik S, Troiano L, Tagliaferri R, Herrera F (2020) Deep learning in video multi-object tracking: A survey. Neurocomputing 381:61–88
Davies DL, Bouldin DW (1979) A cluster separation measure. IEEE Trans Pattern Anal Mach Intell 2:224–227
Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L (2009) Imagenet: a large-scale hierarchical image database. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. IEEE, pp 248–255
Dunn JC (1973) A fuzzy relative of the isodata process and its use in detecting compact well-separated clusters. J Cybern 3(3):32–57
Ester M, Kriegel HP, Sander J, Xu X, et al. (1996) A density-based algorithm for discovering clusters in large spatial databases with noise. In: Kdd, vol 96, pp 226–231
Goodfellow I, Bengio Y, Courville A, Bengio Y (2016) Deep learning, vol 1. MIT Press, Cambridge
Guerrero-Ibáñez J, Zeadally S, Contreras-Castillo J (2018) Sensor technologies for intelligent transportation systems. Sensors 18(4):1212
He K, Gkioxari G, Dollár P, Girshick R (2017) Mask r-cnn. In: Proceedings of the IEEE international conference on computer vision, pp 2961–2969
He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 770–778
He Y, Wei X, Hong X, Shi W, Gong Y (2020) Multi-target multi-camera tracking by tracklet-to-target assignment. IEEE Trans Image Process 29:5191–5205
He Z, Lei Y, Bai S, Wu W (2019) Multi-camera vehicle tracking with powerful visual features and spatial-temporal cue. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Hou Y, Du H, Zheng L (2019) A locality aware city-scale multi-camera vehicle tracking system. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Hsu HM, Huang T, Wang G, Cai J, Lei Z, Hwang JN (2019) Multi-camera tracking of vehicles based on deep features re-id and trajectory-based camera link models. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Johnson SC (1967) Hierarchical clustering schemes. Psychometrika 32(3):241–254
Kalman RE (1960) A new approach to linear filtering and prediction problems. J Basic Eng 82(1):35–45
Kaufman L, Rousseeuw PJ (2009) Finding groups in data: an introduction to cluster analysis, vol 344. Wiley
Kuhn HW (1955) The hungarian method for the assignment problem. Naval Res Log Quart 2(1-2):83–97
Leal-Taixé L., Milan A, Schindler K, Cremers D, Reid I, Roth S (2017) Tracking the trackers: an analysis of the state of the art in multiple object tracking. arXiv:1704.02781
Li P, Li G, Yan Z, Li Y, Lu M, Xu P, Gu Y, Bai B, Zhang Y (2019) Spatio-temporal consistency and hierarchical matching for multi-target multi-camera vehicle tracking. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) Workshops
Liem MC, Gavrila DM (2014) Joint multi-person detection and tracking from overlapping cameras. Comput Vis Image Underst 128:36–50
Lin TY, Goyal P, Girshick R, He K, Dollár P (2017) Focal loss for dense object detection. In: Proceedings of the IEEE international conference on computer vision, pp 2980–2988
Lin TY, Maire M, Belongie S, Hays J, Perona P, Ramanan D, Dollár P, Zitnick CL (2014) Microsoft coco: common objects in context. In: European conference on computer vision. Springer, pp 740–755
Liu W, Anguelov D, Erhan D, Szegedy C, Reed S, Fu CY, Berg AC (2016) Ssd: single shot multibox detector. In: European conference on computer vision. Springer, pp 21–37
Luna E, Moral P, SanMiguel JC, Garcia-Martin A, Martinez JM (2019) Vpulab participation at ai city challenge 2019. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
MacQueen J, et al. (1967) Some methods for classification and analysis of multivariate observations. In: Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, vol 1, Oakland, pp 281–297
Menouar H, Guvenc I, Akkaya K, Uluagac AS, Kadri A, Tuncer A (2017) Uav-enabled intelligent transportation systems for the smart city: applications and challenges. IEEE Commun Mag 55(3):22–28
Naphade M, Tang Z, Chang MC, Anastasiu D, Sharma A, Chellappa R, Wang S, Chakraborty P, Huang T, Hwang JN, Lyu S (2019) The 2019 AI city challenge. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Oksuz K, Cam BC, Kalkan S, Akbas E (2020) Imbalance problems in object detection: a review. IEEE Transactions on Pattern Analysis and Machine Intelligence
Redmon J, Farhadi A (2018) Yolov3: an incremental improvement. arXiv:1804.02767
Ristani E, Solera F, Zou R, Cucchiara R, Tomasi C (2016) Performance measures and a data set for multi-target, multi-camera tracking. In: European conference on computer vision. Springer, pp 17–35
Ristani E, Tomasi C (2018) Features for multi-target multi-camera tracking and re-identification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 6036–6046
Shen Y, Xiao T, Li H, Yi S, Wang X (2017) Learning deep neural networks for vehicle re-id with visual-spatio-temporal path proposals. In: Proceedings of the IEEE international conference on computer vision, pp 1900–1909
Shirazi MS, Morris BT (2016) Looking at intersections: a survey of intersection monitoring, behavior and safety analysis of recent studies. IEEE Trans Intell Transp Syst 18(1):4–24
Sio CH, Shuai HH, Cheng WH (2019) Multiple fisheye camera tracking via real-time feature clustering. In: Proceedings of the ACM multimedia asia, pp 1–6
Tan M, Le Q (2019) Efficientnet: rethinking model scaling for convolutional neural networks. In: International conference on machine learning, pp 6105–6114
Tan M, Pang R, Le QV (2020) Efficientdet: scalable and efficient object detection. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 10781–10790
Tan X, Wang Z, Jiang M, Yang X, Wang J, Gao Y, Su X, Ye X, Yuan Y, He D, Wen S, Ding E (2019) Multi-camera vehicle tracking and re-identification based on visual and spatial-temporal features. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) workshops
Tang Z, Naphade M, Liu MY, Yang X, Birchfield S, Wang S, Kumar R, Anastasiu D, Hwang JN (2019) Cityflow: a city-scale benchmark for multi-target multi-camera vehicle tracking and re-identification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 8797–8806
Tang Z, Wang G, Xiao H, Zheng A, Hwang JN (2018) Single-camera and inter-camera vehicle tracking and 3d speed estimation based on fusion of visual and semantic features. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp 108–115
Veres M, Moussa M (2019) Deep learning for intelligent transportation systems: a survey of emerging trends. IEEE Transactions on Intelligent Transportation Systems
Wu M, Zhang G, Bi N, Xie L, Hu Y, Shi Z (2019) Multiview vehicle tracking by graph matching model. In: Proceedings of the IEEE/CVF Conference on computer vision and pattern recognition (CVPR) workshops
Yang Z, Pun-Cheng LS (2018) Vehicle detection in intelligent transportation systems and its applications under varying environments: a review. Image Vis Comput 69:143–154
Zhang X, Izquierdo E (2019) Real-time multi-target multi-camera tracking with spatial-temporal information. In: 2019 IEEE Visual communications and image processing (VCIP). IEEE, pp 1–4
Zhang Z, Wu J, Zhang X, Zhang C (2017) Multi-target, multi-camera tracking by hierarchical clustering: recent progress on dukemtmc project. arXiv:1712.09531
Zheng L, Bie Z, Sun Y, Wang J, Su C, Wang S, Tian Q (2016) Mars: a video benchmark for large-scale person re-identification. In: European conference on computer vision. Springer, pp 868–884
Zhipeng Z (2020) Collaborative tracking method in multi-camera system. Journal of Shanghai Jiaotong University (Science), 2
Acknowledgements
This work was partially supported by the Spanish Government (TEC2017-88169-R MobiNetVideo). We gratefully acknowledge the support of NVIDIA Corporation with the donation of the GPU used for the research of our group.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interests
Elena Luna, Juan C. SanMiguel, José M. Martínez and Marcos Escudero-Viñolo declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luna, E., SanMiguel, J.C., Martínez, J.M. et al. Online clustering-based multi-camera vehicle tracking in scenarios with overlapping FOVs. Multimed Tools Appl 81, 7063–7083 (2022). https://doi.org/10.1007/s11042-022-11923-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-022-11923-2