Abstract
Despite all its irrefutable benefits, the development of steganography methods has sparked ever-increasing concerns over steganography abuse in recent decades. To prevent the inimical usage of steganography, steganalysis approaches have been introduced. Since motion vector manipulation leads to random and indirect changes in the statistics of videos, MV-based video steganography has been the center of attention in recent years. In this paper, we propose a 54-dimentional feature set exploiting spatio-temporal features of motion vectors to blindly detect MV-based stego videos. The idea behind the proposed features originates from two facts. First, there are strong dependencies among neighboring MVs due to utilizing rate-distortion optimization techniques and belonging to the same rigid object or static background. Accordingly, MV manipulation can leave important clues on the differences between each MV and the MVs belonging to the neighboring blocks. Second, a majority of MVs in original videos are locally optimal after decoding concerning the Lagrangian multiplier, notwithstanding the information loss during compression. Motion vector alteration during information embedding can affect these statistics that can be utilized for steganalysis. Experimental results have shown that our features’ performance far exceeds that of state-of-the-art steganalysis methods. This outstanding performance lies in the utilization of complementary spatio-temporal statistics affected by MV manipulation as well as feature dimensionality reduction applied to prevent overfitting. Moreover, unlike other existing MV-based steganalysis methods, our proposed features can be adjusted to various settings of the state-of-the-art video codec standards such as sub-pixel motion estimation and variable-block-size motion estimation.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Development of wireless communications has brought countless advantages to our daily lives, albeit sometimes disadvantageous. The issue that lies at the heart of modern communications is the absence of high-level security. Hence, cryptography schemes have been applied to secure information from unauthorized access or modification; although it can not fulfill all expectations of security. Transmitting meaningless content through communication channels leaves a clue about secret communication; whereas we sometimes aim to hide the existence of confidential information. In these cases, steganography approaches are employed to cover communication with guiltless-looking media.Footnote 1
On the other hand, steganalysis approaches have been developed to detect the existence of confidential information in a suspicious media. These algorithms receive the suspicious media as input and classify it under the subject of clear media (without secret message) or dirty media (containing confidential information). The steganalyzer is sometimes assumed to know the exact steganography algorithm which might be applied for hiding information, or have some partial information about the steganography algorithm, or even is completely ignorant of the steganography method. Based on this available information, steganalysis approaches lie in two main categories: specific (targeted) and blind (universal) steganalysis. Specific steganalysis approaches have been designed to detect a particular steganography method, while blind steganalysis approaches have been developed to detect a group of steganography algorithms without having any detailed knowledge of the embedding strategy. Besides, quantitative steganalysis refers to the eavesdropper’s efforts to estimate the embedding rate or equivalently the length of the confidential message embedded in a host media [25, 35]. For that to be possible, full information about the steganography algorithm is required. Since obtaining detailed information about the steganography scheme is somewhat optimistical, blind steganalysis approaches are of great importance.
Among all steganography hosts including image, audio, video, network protocol packets, etc., because of its high capacity and information redundancy, videos are regarded as a suitable steganography host for embedding high volume secret messages. Nowadays, in order to decrease the cost of transmission and required storage space, all types of digital media are compressed. Lossy compression algorithms lead to some indeterministic components in the output media. These components are ideal covers for confidential information. Thus steganography is often performed during compression. Using more appropriate motion vectors for manipulation, better altering methods, and more proper video compression standards, MV-based steganography approaches have seemingly dominated MV steganalysis methods.
Video coding entails particular statistics in the motion vectors:
-
a)
The MVs belonging to the neighboring blocks in a coded frame are highly correlated. This correlation exists because (i) neighboring blocks are likely to belong to the same rigid object or static background (for more explanation, please refer to Fig. 2 in [20]), and (ii) the cost function employed during motion estimation encourages the MVs to be close together.
-
b)
The lossy coding stage during motion compensation can modify the statistics of video and shift the MVs from locally optimal to non-optimal. A majority of MVs, nevertheless, remain locally optimal from the receiver’s point of view.
Exploiting the aforementioned facts, we propose a spatio-temporal steganalysis feature extraction method to take full advantage of the clues that MV-based video steganography leaves on the statistics of a video. The rest of this paper is organized as follows. In Section 2, we position our work in literature by reviewing the related work on video steganography and steganalysis. Section 3 reviews the basic concepts of motion estimation algorithm. We then detail motion estimation and compensation during video encoding in Section 3. The proposed method is then described in Section 4 which includes the following contributions:
-
1)
We propose a novel MV-based steganalysis approach taking advantage of the complementary spatio-temporal features to capture the clues that MV-based steganography leaves on video statistics.
-
2)
The comparisons using four targeted MV-based steganography approaches reveal that the proposed approach outperforms its four MV-based steganalysis rivals. Indeed, our method indicates a dramatic improvement in the reliability of MV-based steganalysis methods.
-
3)
We have evaluated the effect of different compression settings, namely motion estimation algorithm and quantization parameter on detection reliability. The experimental results confirm the stability of our features under various settings. Moreover, experiments prove that our features’ performance is even robust against very low embedding rates.
-
4)
The proposed approach can detect the state-of-the-art MV-based steganography methods to a great extent blindly, i.e., without requiring any side information about the steganography approach, embedding rate, and motion estimation algorithm. The proposed method exploits the joint spatial-temporal features of MVs to reach better performance.
-
5)
Unlike the competitor steganalysis approaches, our features can even be extracted in the case of variable-block-size motion estimation. Besides, the proposed feature extraction approach is compatible with all existing video compression standards.
In Section 5, the experimental settings are explained and the experimental results are illustrated to confirm the superiority of our proposed method in both laboratory and real-world conditions. Since the H.264/AVC algorithm is still one of the most efficient compression algorithms concerning compression efficiency, coding speed, and prevalence, without loss of generality, the H.264/AVC baseline compression standard is applied in experiments. Finally, the conclusion is presented in Section 6.
2 Related work on video steganography and steganalysis
Video steganography methods can be divided into two main categories: inter-frame and intra-frame steganography methods. Intra-frame methods manipulate each video frame individually, and regardless of dependencies among frames [12, 22, 23, 31, 36, 56]. Except for capacity, intra-frame methods have no better performance than image steganography methods in the case of steganography criteria. These methods can also be revealed by image steganalysis attacks. On the contrary, inter-frame video steganography methods aim to take advantage of the temporal correlations among frames. These schemes include manipulating DCT coeficients [24, 28, 33, 62], embedding on quantization parameters [41, 50] or variable length codes [30], changing inter-prediction modes [26, 60] or motion vectores [1, 4, 5, 7, 13, 34, 55, 57, 58, 61].
A steganography algorithm is reliable, as long as it can remain undetectable against all existing steganalysis attacks. Accordingly, security is the main criterion of steganography. Since steganalysis attacks are accessible by the transmitter, steganography algorithms can be tested against them to determine whether they are trustworthy to employ for embedding or not. There exist a lot of measurements to demonstrate to what extent a steganography algorithm is secure, such as detection accuracy, ROC (Receiver Operation Characteristics) curve, and AUC (Area Under the Curve).
Motion vectors seem to be the best element of video coding to be employed to hide information for several reasons: First, MV-based video steganography leads to indirect and complicated changes in inter-frame and intra-frame statistics of the video. Besides, experiments have shown that much lower similarities exist among neighboring MVs in comparison with neighboring pixels (for more information, the reader is requested to refer to Fig. 1 and Fig. 2 in [43]). As a result, the detection complexity of MV-based steganography is higher than that of other methods, and MV alteration is the most robust strategy against steganalysis attacks [2]. Besides, due to the motion compensation step, MV manipulations do not cause perceptible degradation in the visual quality of the output video. Moreover, video steganalysis methods that model the embedding procedure as an additive noise cannot detect the presence of the message in MVs [7]. Hence, MV altering has been the most preferred video steganography strategy.
MV-based video steganography methods deal with two fundamental problems: (i) choosing MVs that after modification are as undetectable as possible, and (ii) designing a modification algorithm that leads to least changes in the statistics of the output video. Accordingly, MV-based steganography approaches have experienced three phases of progression [58]. In the first stage, MVs with large prediction error or magnitude were supposed to be the best cloak for confidential information, and the message was embedded in the magnitude or the phase of MVs [1, 13, 55, 61]. Because of selecting non-suitable MVs for modification and applying improper embedding algorithms, the aforementioned methods failed to preserve the statistical characteristics of the original video. In other words, embedded information by these methods is easily detectable by early generations of MV-based steganalysis approaches [6, 42].
It is obvious that more modifications with a particular embedding algorithm raise the detection probability. Hence in the second stage, Syndrome-Trellis Codes (STC) [4, 5, 15], Wet Paper Codes (WPC) [4, 7, 18, 19], and BCH codes [32] were introduced and applied to improve the embedding efficiency (number of embedded bits per modification [11]); this results not only in higher security, but also in improved imperceptibility. Based on the idea that MVs manipulations result in shifting the MVs from locally optimal to non-optimal, “Reversion Based features” [6] and “AoSo features” [48] have been introduced. Besides, the authors of [51] have proposed a high-dimensional feature set considering the correlations between each macro-block and its neighbors. In order to provide a higher level of security against steganalysis attacks, Cao et al. [5] proposed to select the most uncertain MVs for embedding. To provide robust steganalysis features against the second-generation steganography methods, Yao et al. [57] suggested a cost function based on the relationships between the MV of each macroblock and its neighbors.
Due to information loss in the motion compensation phase, some altered MVs are locally optimal after reconstruction at the receiver’s side. The methods which take advantage of this fact have formed the third stage of development in MV-based steganography [4, 20, 58]. To detect more subtle changes in the statistics of MVs after embedding, Zhang et al. [59] have proposed “Near-Perfect Estimation for Locally Optimality features” which exploits local optimality of motion vectors according to the Lagrangian multiplier applied during compression.
Taking all MV-based steganalysis methods into consideration, [6, 48, 59] have proved to provide the strongest MV-based steganalysis features ([39] has recently suggested an entropy-based feature set, the results of which are fairly similar to that of [59]). However, even these approaches cannot detect the currently best steganography methods (e.g., [4, 7, 20, 58]). In the following, the two state-of-the-art methods that inspired the proposed method will be described in details.
2.1 Near-perfect steganalytic features
Based on the assumption that an overwhelming majority of motion vectors are locally optimal w.r.t the Lagrangian multiplier from the receiver’s perspective, Zhang et al. [59] have proposed a 36-D steganalysis feature-set. This feature set called NP estimation features is exploited using each decompressed MV, its eight neighbors, and their corresponding SAD (Sum of Absolute Differences) based and SATD (Sum of Absolute Transposed Differences) based Lagrangian costs. NP estimation features consist of four types of features, each type containing nine dimensions as follows:
-
Feature Set 1: The jth feature of type 1 is defined as the probability that the SAD-based Lagrangian cost of jth MV position is minimum.
$$ \begin{array}{@{}rcl@{}} f_{1}^{SAD}({j})&=&\frac{1}{N}\sum\limits_{{k}=1}^{N}{\mu({k},{j})}\\ {j}&=&(1,2,...,9) \end{array} $$(1)$$ \mu({k,j}) = \delta(\operatornamewithlimits{arg\ min}_{mv}[J_{{b_{k}}, MV}^{SAD}],{mv_{j}(b_{k})}) $$(2)In (1), N is the number of blocks in a GOP (Group Of Pictures) including M P-frames. In (2), \(J_{{b_{k}}, MV}^{SAD}=\{J_{{b_{k}}, mv_{0}}^{SAD},J_{{b_{k}}, mv_{1}}^{SAD}, ..., J_{{b_{k}}, mv_{8}}^{SAD}\}\). Besides, δ(a, b) (for any arbitrary value of a and b) is equal to 1 if a = b, and equal to 0 if a ≠ b. As shown in Fig. 5, mv0(bk) refers to the decdeded motion vector for the block bk, and mv1 − 8(bk) are the eight closest neighboring MVs to the decoded MV. In this method, the closest distance (r in the Fig. 5) is set to one.
-
Feature Set 2: The jth feature of type 2 is defined as the exponentially magnified SAD between the cost of jth position and the minimum Lagrangian cost.
$$ f_{2}^{SAD}({j})=\frac{1}{Z}\sum\limits_{{k}=1}^{N}{exp\left\{\left|\frac{J_{{b_{k}}, MV}^{SAD}(i)-min(J_{{b_{k}}, MV}^{SAD})}{J_{{b_{k}}, MV}^{SAD}(j)}\right|\right\}}.\mu{(k,j)} {j}=(1,2,...,9) $$(3)$$ Z=\sum\limits_{{j}=1}^{9}\sum\limits_{{k}=1}^{N}{exp\left\{\left|\frac{J_{{b_{k}}, MV}^{SAD}(i)-min(J_{{b_{k}}, MV}^{SAD})}{J_{{b_{k}}, MV}^{SAD}(j)}\right|\right\}}.\mu{(k,j)} $$(4)
Feature sets 3 (\(f_{1}^{SATD}\)) and 4 (\(f_{2}^{SATD}\)) are similar to feature sets 1 and 2 respectively, with the only difference that these features are obtained by applying SATD instead of SAD.
There are three major drawbacks to this approach. First and foremost, as indicated in Table 1, local optimality of MVs according to the Lagrangian multiplier on the transmitter’s side does not guarantee that they are locally optimal from the receiver’s point of view; although in most of the video frames the number of locally optimal MVs on the receiver’s side is greater than the number of non-locally-optimal MVs. Secondly, in this approach, the MV’s nearest neighbor differs one unit to the original one; whereas the nearest MV should be adapted to the motion estimation resolution. It should not be left unmentioned that correlations of MVs in each frame are not considered in this feature set; while there are significant correlations between nearby MVs.
2.2 Improved steganalysis features
As depicted in Fig. 1, in [51], a feature set is defined by taking 20 possible combinations of the MVs of each macro-block and its two neighbors into account. Therefore, 9 × 9 = 81 features are introduced for each distribution as follows. First, the difference between the central MV and each of its two neighbors is calculated. The difference value can be one of the members of the set {− 4,− 3,− 2,− 1,0,1,2,3,4}. Any value larger than 4 and smaller than − 4 is rounded to 4 and − 4, respectively. Next, an 81-dimensional feature set is formed using joint differences of each MV and its two neighbors. Finally, 81 × 20 features are computed combining 20 possible distributions. If we want to consider temporal correlations of MVs, we can use two reference frames to add 4 × 20 × 81 more features.
Various distributions of one central macro-block and its two neighbors [51]. MVC is the current block, and MV1 and MV2 are its two neighbors
The major drawback of the aforesaid method is its relatively high dimensions, which may lead to the curse of dimensionality. There are also two other weaknesses in this method. First, it does not support video compression standards with sub-pixel accuracy; so it needs refinement to be proportionate to the common compression standards. Second, the features are exploited based on this assumption that MVs are computed using fixed-size macro-blocks; while in recent standards, MVs are computed based on variable-sized blocks to obtain a better compression ratio. Therefore, this algorithm is not implementable in standards with recent motion estimation algorithms.
3 General theory: motion estimation and compensation
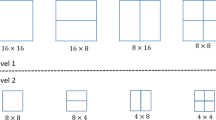
Compression algorithms have been developed to reach faster and cheaper transmission as well as reducing the required storage space. These days, the H.264/AVC algorithm is still one of the most common compression standards. In this algorithm, each P-frame is compressed using one reference frame. The P-frame is partitioned into non-overlapping macro-blocks containing 16 × 16 pixels. There are four decision modes for each macro-block: full (16 × 16), vertical (the macro-block is divided into two partitions of size 8 × 16), horizontal (the macro-block is divided into two partitions of size 16 × 8), and quadruple (the macro-block is divided into four partitions of size 8 × 8). For each decision mode, the optimal MV per partition is obtained based on a cost function (8) using a predetermined Lagrangian multiplier (5). Supposing an exemplary partitioned block (bk), the corresponding optimal MV (\(MV_{b_{K}}\)) is obtained using (9).
In (8), \(R_{b_{k},mv}\) is the number of required bits to transmit the candidate MV, and QP in (6) is quantization parameter. Besides, \(SAD_{b_{k},mv}\) in (7) is the sum of absolute differences between the pixels of the current block in the original P-frame (FOrg) and the corresponding block of mv in the reconstructed reference frame (FRec). Afterward, the optimal partitioning mode (ModeOpt) is chosen using (10). If the chosen mode is quadruple, the mode decision algorithm is implemented again on each 8 × 8 pixels partition (full (8 × 8), vertical (4 × 8 ), horizontal (8 × 4), and quadruple (4 × 4)) to select a mode with minimum cost (Fig. 2).
Left: Partitioning mode evaluation during P-frame encoding. Right: Tree structured motion compensation for H.264/AVC [37]
In (10), cfrmode is the final output bitrate of the macro-block based on the candidate partitioning mode, and SSDbk, MV, mode is the sum of squared differences between the original and the reconstructed (16 × 16) or (8 × 8) block [37].
4 Proposed steganalysis method
Overview
Figure 3 illustrates the block diagram of the proposed steganalysis feature extraction method based on the MVs’ spatio-temporal features termed as MVST.

The proposed features are designed to address the shortcomings of the predecessors mentioned in Section 2. We aim to extract a 54 − D steganalysis feature vector per every M consecutive P-frames (each GOP) containing N motion vectors (variable partition size which is allowed by the baseline profile of the H.264/AVC is considered in this study). The steganalysis feature vector consists of a 36 − D spatial feature set and an 18 − D temporal feature set. Using the following scheme, we extract spatial and temporal features and finally concatenate them together. Spatial features for each motion vector will be updated based on its differences with the MVs of eight neighboring partitions of its corresponding block. Temporal features will be updated based on the local optimality conditions of each MV by taking its reconstructed reference frame into account as described in [59].
4.1 Frame decoding
As the first step, the current frame and its reference frame are decoded and reconstructed using the input bitstream.
4.2 Partitioning mode extraction
For each motion vector, the partitioning mode is obtained during the process of decoding. The bitstream of partitioning mode is the first part of each MV’s bitstream, which can be extracted by Golomb − decoding (more details on the bitstream of H.264/AVC can be found in [40]). If the extracted number (Mode1) is smaller than three, we set s = 16 and Mode = Mode1. If the extracted number is equal to three, we set s = 8 and apply Golomb − decoding on the remaining bitstream to find Mode = Mode2. Subsequently, the partitioning mode is obtained based on (11) in which BSx and BSy are equivalent to the width and the height of the existing block, respectively (Fig. 2 illustrates the partitioning mode evaluation during P-frame encoding.).
4.3 Steganalysis feature updating
4.3.1 Spatial features extraction
Extracting the MVs of neighboring pixels
After decoding a P-frame completely, the MV of each pixel in the frame is determined. Since variable-sized blocks are allowed in recent video compression standards, it is possible that the corresponding pixels of each neighboring sub-block have different MV values (Fig. 4, left). Hence, in the proposed method, one position in each neighboring block is selected as the reference pixel. As illustrated in Fig. 4, supposing the situation of the pixel in the top-left corner of the central block is (i0, j0), the neighboring MVs are evaluated as follows (Fig. 4, right):
Calculating the spatial features
The rough idea behind this feature set is inspired by [51]. The difference between each of eight aforementioned MVs and the MV of the central block (MV0) is calculated. Afterwards, as indicated in (13), the features related to the horizontal differences between MVs (fh(K, D)) and vertical differences between MVs (fv(K, D)) are computed (ρ ∈{h, v}). In the mentioned equations, K ∈ [1,8] and T is the truncation threshold. The mentioned features are designed to capture the correlations between motion vectors corresponding to a static background or a same rigid object. The greater the difference between the MV corresponding to the current block and a neighboring pixel is, the less probable the two MVs are correlated together. Accordingly, we have considered the absolute difference of one (T = 1) as the upper bound of correlation (least correlation value). Therefore, each difference value greater than 1 and smaller than − 1 is rounded to 1 and − 1, respectively. Also Scale = 1/R (R is motion vector resolution and equivalent to 0.25 in experiments), and δ{a, b} = 1 if a = b; otherwise, δ{a, b} = 1. Finally, we will have a 9-D feature set per each horizontal or vertical neighbor. Combining features of all eight neighbors, we will have a vector containing 8 × 2 × 9 features.
4.3.2 Temporal features extraction
The MVs belonging to all blocks are extracted during the process of decoding the current P-frame. Supposing an exemplary block (bk) in the current P-frame, the decoded MV belonging to this block (MV0(bk)) determines its corresponding reference block in the reference frame (Fig. 5, right). In case any confidential information is embedded in this MV (for instance, one bit of a secret message), the decoded MV might differ from the original MV. The transmitter tries to apply the slightest possible changes to the MVs during embedding to leave as smallest clues as possible. Hence, the confidential information should have been embedded by replacing the original MV with one of its nearest MVs (Fig. 5, left). Notwithstanding the loss of information during motion compensation, the original MV that should be one of the closest MVs to the decoded MV is more likely to be the optimal MV compared to the other MVs on the receiver’s side. Accordingly, we compute and compare the optimality of these MVs using the feature set introduced in [59]. However, we have modified this feature set to be compatible with various video compression standards including H.264/AVC. Indeed, instead of using MVs with one unit difference, we use MVs demonstrated in Fig. 5 in which h and v are horizontal and vertical components of the decoded MV, and r is equivalent to the smallest possible changes in MVs during motion estimation (“ME-Resolution”).
4.4 Features’ dimensionality reduction
Regarding the fact that high dimensions of features lead to (i) requirement to a very big training set, (ii) increasing the probability of classifier overfitting, and (iii) curse of dimensionality, we suggest a dimensionality reduction stage. We reduce the dimensions of spatial features from 180-D to 36-D, and reduce the dimensions of temporal features from 36-D to 18-D by combining the correlated features.
We compute the horizontal (\(f_{H}^{{\rho }}\)), vertical (\(f_{V}^{{\rho }}\)), right diagonal (\(f_{RD}^{{\rho }}\)), and left diagonal (\(f_{LD}^{{\rho }}\)) spatial features as the average of features corresponding to two neighboring pixels as follows:
In order to further reduce the spatial feature’s dimensions, we sum up the features corresponding to the horizontal and vertical components of MVs, and obtain the 36-D spatial features (fs) as (15).
To reduce the dimensionality of temporal features, we sum up the SAD and SATD based features to obtain the 18-D temporal features as follows:
4.5 Spatio-temporal feature concatenation
Finally as shown in Fig. 6, combining 36-D spatial (fs) and 18-D temporal (ft) features, we obtain a 54-dimensional feature set using (17).
5 Experiments
5.1 Experimental Settings
5.1.1 Database
Figure 7 shows the first frame of 22 PAL QCIf video sequences (192 × 144 pixels) without prior compressionFootnote 2 being used to construct the database. These sequences are downloaded from [54]. The selected sequences consist of a wide range of videos concerning diversity in the texture of video, objects’ motion, camera movement, and the type of background. Because of containing different numbers of frames, all of the video sequences are divided into non-overlapping 60-frame sub-sequences, and utmost five 60-frame sub-sequences of each sequence are utilized for experiments. Totally, 84 video sub-sequences are used for training.
5.1.2 Video compression method
Because of its wide use and effectiveness, the H.264/AVC baseline profile is employed for video compression. Two different motion estimation algorithms are applied in this test: Exhaustive Search (FULL) and Hexagon-based Search (HEX) [63]. The search range is set to 8 pixels, and the motion estimation resolution is quarter-pixel. Also, three different quantization parameters (QP ∈{17,27,32}) are considered.
5.1.3 Competitor Steganalysis methods
To demonstrate the effectiveness of our proposed method, we compare its results with the results of steganalyzers MVRBF [6], AoSO [48], NPELO [59], which are the best video steganalysis methods against MV-based video steganography up to now. Meanwhile, in [6] features are extracted using macro-blocks; whereas, in the H.264/AVC algorithm, each macro-block may contain some sub-blocks. To adapt this method to the H.264/AVC algorithm, the features are extracted using sub-blocks. Also, these algorithms are not adjusted to video compression standards that support motion estimation with sub-pixel accuracy. As a result, they are not capable of detecting MV-based steganography methods which are applied to such compression standards. We had to refine them to compare their efficiency with our proposed method. Hence, the above schemes are revisited and all features are extracted with sub-pixel accuracy.
5.1.4 Steganography targets
To the best of our knowledge, TAR1 [5] and TAR4 [7] from the second generation, and TAR2 [58] and TAR3 [4] from the third generation are the best MV-based steganography methods until now. Thus these schemes are used in the experiment. Meanwhile, in [5] the set of Lagrangian multipliers used to evaluate MVs’ embedding cost function is λ = [0,2,4,6,8] and we set b = − 2 and α = 0.5 for the distortion function. Also, we set h = 8 for the syndrome-trellis coder used in all methods (Syndrome-trellis codes are downloaded from [16]).
5.1.5 Embedding
For each steganography method and each sequence, a random message with uniform distributionFootnote 3 and rates ER ∈{0.1,0.2,0.3} per MV is produced and embedded.
5.1.6 Training and classification
We split all embedded and compressed videos into 12-frame sub-sequencesFootnote 4, and a feature vector is obtained using each of these sub-sequences. The MATLAB’s SVM toolbox is used to train each steganalyzer applying Gaussian and polynomial kernels, and the best figures are listed.
5.1.7 Evaluation criteria for steganalysis performance
There are three major metrics to evaluate the security level of a steganography scheme against steganalysis attacks: Detection Accuracy, Receiver Operation Characteristics (ROC), and Area Under the Curve (AUC) which is also called Detector Reliability.Footnote 5 Since detector reliability provides better comparative information than others, we use this metric in experiments [2, 11, 14, 29]. Furthermore, in order to compare the discrimination capability of each steganalyzer, the detector reliability (AUC) is evaluated under different settings.
5.1.8 Performance evaluation setups
Steganalysis algorithms are mostly evaluated assuming some side information is available on the warden’s side. These pieces of information include steganography scheme, details about the compression algorithm which is not retrievable on the receiver’s side, the embedding rate, and the original cover. These are conditions that can be provided in the laboratory, while in the real world such information is inaccessible [27, 49]. To prove the effectiveness and detection capability of the proposed method in various conditions, we apply steganalysis approaches on four following setups:
-
Setup 1) Complete laboratory conditions: In this scenario, we suppose that side information about the type of motion estimation algorithm (e.g., FULL or HEX), embedding rate per MV, and the steganography scheme is available. Accordingly, different steganography schemes with different motion estimation algorithms and embedding rates are separately trained and classified.
-
Setup 2) Unknown ME algorithm: This scenario is according to the assumption that the warden is unaware of the ME algorithm, but has knowledge about the steganography algorithm and embedding rate. Therefore, experiments are carried out on a combination of video sequences compressed and embedded by employing full search (FULL) or fast search (HEX) algorithm.
-
Setup 3) Unknown ME algorithm and embedding rate: In this scenario, it is assumed that the steganalyzer has just side information about the steganography algorithm. Therefore, video sequences are grouped based on the type of steganography algorithm and each group contains sequences with different ME methods and embedding rates.
-
Setup 4) Real-world conditions: This scenario aims to address the reliability of the proposed manner under realistic conditions (worst conditions). We assume that the warden is completely ignorant of the ME method, embedding rate, and even steganography scheme. So steganalysis tests are performed exploiting a mixture of video sequences with various settings.
In the last two setups, embedded sequences with various settings are randomly selected and fed into the classifier to obtain detector reliability.Footnote 6 This stage is repeated 30 times and detector reliability is the average value of them.
5.2 Experimental results
-
(i)
Setup 1: In this setup, granting detailed information about the steganography algorithm, quantization parameter, ME algorithm, and embedding rate to the wardens, we aim to measure the reliability of detectors under various settings. Therefore, sequences grouped based on their properties are subjected to the proposed and rival detectors. The corresponding results are compared in Table 2.
Table 2 Detector reliability of the proposed blind steganalyzer (MVST), NPELO, AoSO, and MVRB against TAR1-4, using Setup1 with different motion estimation algorithms (ME), embedding rates (ER), and quantization parameters (QP) As it can be seen, all of the detectors have shown an acceptable performance against TAR1, especially the proposed algorithm and MVRB. These considerable results of the MVRB originate from the weakness of TAR1, which is the selection of embedded MVs based on SAD and without taking the Lagrangian cost into account. consequently, the number of MVs that are optimal concerning SAD is increased after embedding. This increase is sharper when it comes to higher embedding rates and larger quantization parameters (raising the Lagrangian multiplier results in decreasing the influence of SAD on the Lagrangian cost). Since its features are exactly exploited based on SAD, MVRB is successful in tracing TAR1. The performance of two other rivals is negatively influenced when video compression is conducted using a fast search algorithm, while the proposed method has shown a steady level of detection. Indeed, proposed features have proved to reach almost distinctive classes and perfect detection against TAR1.
In sharp contrast to TAR1, TAR2 has demonstrated acceptable resistance against competitors. The stego sequences produced by this method are, however, overwhelmingly perceptible by our proposed features. The majority of results of AoSO and MVRB are fairly close to random-guessing. Using HEX motion estimation algorithm has resulted in weakening the competitors.
Table 2 indicates near-complete resistance of TAR3 and TAR4 against AoSO and MVRB in the HEX search conditions. Indeed, these detectors indicate better performance in the FULL search setting. The reason is that both MVRB and AoSO features are exploited based on SAD, and there are more optimal MVs with respect to SAD after motion estimation with the exhaustive search. It can be perceived from the figures that the performance of competitors degrades when a fast motion estimation algorithm is applied. This degradation is far sharper in NPELO, the results of which are as worse as other rivals in the HEX setting. By contrast, the proposed features have maintained a high level of detection against TAR3 and TAR4 in various settings.
In summation, the results have confirmed that the proposed features are far more reliable than rivals’ features. Furthermore, our detector’s reliability remains relatively stable even at low embedding rates.
-
(ii)
Setup 2: In order to specify how far our proposed features are robust against different ME algorithms, training and classification are carried out on a combination of sequences compressed by FULL and HEX search. The results are listed in Table 3.
Table 3 Detector reliability of the proposed blind steganalyzer (MVST), NPELO, AoSO, and MVRB against TAR1-4, using Setup2 with different embedding rates (ER) and quantization parameters (QP) The figures show that the proposed and rival features can detect TAR1 to a high extent, notwithstanding the lack of knowledge about the motion estimation algorithm. Conversely, rivals have no better performance than random-guessing in detecting TAR2 when the payload rate is low (0.1 and less). These schemes have demonstrated better results in tracing TAR3 and TAR4 with the aforesaid setup. Additionally, figures signify that AoSO is slightly inferior to MVRB.
-
(iii)
Setup 3: Having knowledge about the embedding rate on eavesdropper’s side seems unrealistic. Hence, the classifier should be trained by a combination of sequences altered with different embedding rates.
As illustrated in Table 4, the shortage of information about the embedding rate has not affected the reliability of detectors. Surprisingly, TAR1 is blindly detectable by the proposed features. In other words, our detector can distinguish the clean media from the media manipulated using TAR1 to a high extent, without requiring partial information. Likewise, it has achieved dramatic detection rates against TAR2-4. Compared to our approach, AoSO and MVRB have shown to be too weak to trace TAR2-3, with their reliability hovering around 0.53.
Table 4 Detector reliability of the proposed blind steganalyzer (MVST), NPELO, AoSO, and MVRB against TAR1-4, using Setup3 with different quantization parameters (QP) Overall, a noticeable superiority in the results of our method in comparison to rivals can be observed.
-
(iv)
Setup 4: In preceding setups, we supposed all detectors as targeted steganalysis methods. In this setup, we attempt to figure out whether the proposed method and opponents can be regarded as universal steganalysis methods or not.
Table 5 suggests that the performances of rivals are considerably degraded when prior knowledge about the embedding algorithm is not accessible, whereas all of the steganography methods are vulnerable to our proposed features. The figures of all targets imply that these outstanding methods can be easily trapped by the proposed method.
6 Conclusion
In this paper, using Spatio-temporal statistics of motion vectors, we have proposed, implemented, and evaluated a blind steganalysis method for detecting MV-based steganography algorithms. The proposed approach is designed to boost the performance in MV-based video steganalysis by addressing the shortcomings of the previous approaches. Indeed in contrast to the previous method, the proposed method is (i) capable of jointly utilizing the spatio-temporal statistics of the MVs to improve the detection accuracy, (ii) capable of capturing the subtle statistical clues about MV-based steganography by considering the video codec configuration in the feature extraction stage, (iii) generalized to the different video codec configurations namely variable-block-size and sub-pixel motion estimation, (iv) and less vulnerable to overfitting compared to some rival methods due to low dimension of features thanks to the dimensionality-reduction stage.
Experimental results have shown that the proposed features’ performance has surpassed the prior outstanding MV-based steganalysis schemes. What sets our proposed steganalysis feature extraction method apart from previously proposed ones is its adaptability to various video compression settings and algorithms. On top of that, the proposed features perform relatively stable in different conditions including different steganography methods, ME algorithms, quantization parameters, and even low embedding rates.
In recent video compression standards, Lagrangian based cost functions are applied to increase the compression efficiency. These functions decide based on the number of bits needed for transmitting the MV, and the SAD between the existing and reference block. The effect of MV’s length of the code in the Lagrangian cost is in direct relationship with the Lagrangian multiplier. Therefore, a greater Lagrangian multiplier leads to approaching each MV to its reference MVs, and consequently more correlations among MVs; So it can be inferred that applying smaller quantization parameters causes more resistance against the spatial features. Due to exploiting joint spatio-temporal features, the proposed method has reached the best detection reliability compared to rivals. In real-world conditions where no information about the steganography algorithm, motion estimation method, and embedding rate is available, the proposed features have shown very promising detection results (more than 95% compared to only 65% in case of the best rival). Our approach has shown a remarkable improvement in blind MV-based steganalysis so that the prominent MV-based steganography methods are no longer reliable.
For future work, we aim to consider the scenarios where the confidential information is just embedded in the MVs belonging to deformable objects using object detection and tracking approaches [8,9,10]. Tracking these objects is specifically important since embedding confidential information in their corresponding MVs leads to less evidence of steganography.
Notes
Prior compression may have an impact on the performance of steganalyzers [17].
Distribution of the embedded message can affect the steganalyzers’ performance [21].
The more the number of P-frames of the trained sub-sequences is, the more stable the obtained features are, but the resolution of the detector may be negatively affected [48].
Steganalysis methods do not directly classify the suspicious media as innocent or guilty. In fact, they first present the characteristics of each sample. The class of each sample is then estimated using a threshold. The performance of steganalyzer under different decision thresholds can be illustrated by AUC [3].
It should be noted that the number of compressed samples and stego samples subjected to the classifier must agree; otherwise, the classification results would be unsatisfactory. Indeed, Machine learning algorithms are incapable of producing precise classifiers if they are provided with an imbalanced dataset [38].
References
Aly HA (2011) Data hiding in motion vectors of compressed video based on their associated prediction error. IEEE Transactions on Information Forensics and Security 6(1):14–18
Böhme R (2010) Principles of modern steganography and steganalysis. Springer, Berlin, pp 11–77. https://doi.org/10.1007/978-3-642-14313-7_2
Böhme R (2010) Advanced statistical steganalysis, ser. Information security and cryptography, vol 0. Springer, Berlin. Online. Available: http://link.springer.com/10.1007/978-3-642-14313-7
Cao Y, Zhang H, Zhao X, Yu H (2015) Video steganography based on optimized motion estimation perturbation. In: Proceedings of the 3rd ACM Workshop on Information Hiding and Multimedia Security. ACM, New York, pp 25–31, DOI https://doi.org/10.1145/2756601.2756609
Cao Y, Zhang H, Zhao X, Yu H (2015) Covert Communication by Compressed Videos Exploiting the Uncertainty of Motion Estimation. IEEE Commun Lett 19(2):203–206
Cao Y, Zhao X, Feng D, Features R-B (2012) Video steganalysis exploiting motion vector reversion-based features. IEEE Signal Processing Letters 19(1):35–38
Cao Y, Zhao X, Feng D, Sheng R (2011) Video steganography with perturbed motion estimation. In: Proceedings of the 13th International Conference on Information Hiding, ser. IH’11. Online. Available: http://dl.acm.org/citation.cfm?id=2042445.2042463. Springer, Berlin, pp 193–207
Chen Y, Tao J, Liu L, Xiong J, Xia R, Xie J, Zhang Q, Yang K (2020) Research of improving semantic image segmentation based on a feature fusion model. J Amb Intell Human Comput. https://doi.org/10.1007/s12652-020-02066-z
Chen Y, Tao J, Zhang Q, Yang K, Chen X, Xiong J, Xia R, Xie J (2020) Saliency detection via the improved hierarchical principal component analysis method. Wirel Commun Mobil Comput 2020:8822777. https://doi.org/10.1155/2020/8822777
Chen Y, Wang J, Xia R, Zhang Q, Cao Z, Yang K (2019) The visual object tracking algorithm research based on adaptive combination kernel. J Amb Intell Human Comput 10(12):4855–4867. https://doi.org/10.1007/s12652-018-01171-4
Cox I, Miller M, Bloom J, Fridrich J, Kalker T (2008) Digital watermarking and steganography, 2nd edn. Morgan Kaufmann Publishers Inc., San Francisco
Dalal M, Juneja M (2018) Video steganography techniques in spatial domain—a survey. In: Mandal J. K., Saha G., Kandar D., Maji A. K. (eds) Proceedings of the international conference on computing and communication systems. Springer, Singapore, pp 705–711
Fang DY, Chang LW (2006) Data hiding for digital video with phase of motion vector
Fawcett T (2006) An Introduction to ROC analysis. Pattern Recogn Lett 27 (8):861–874. https://doi.org/10.1016/j.patrec.2005.10.010
Filler T, Judas J, Fridrich J (2011) Minimizing additive distortion in steganography using syndrome-trellis codes. IEEE Transactions on Information Forensics and Security 6(3 Part 2):920–935
Fridrich J (1999) Online. Available: http://dde.binghamton.edu/download/syndrome/
Fridrich J, Goljan M, Du R (2001) Steganalysis based on jpeg compatibility, vol 4518, p 11
Fridrich J, Goljan M, Lisonek P, Soukal D (2005) Writing on wet paper. IEEE Trans Signal Process 53(10):3923–3935
Fridrich J, Goljan M, Soukal D (2004) Perturbed quantization steganography with wet paper codes. In: Proceedings of the 2004 Workshop on Multimedia and Security, ser. MM&Sec ’04. ACM, New York, pp 4–15, DOI https://doi.org/10.1145/1022431.1022435
Ghamsarian N, Khademi M (2020) Undetectable video steganography by considering spatio-temporal steganalytic features in the embedding cost function. Multimedia Tools and Applications https://doi.org/10.1007/s11042-020-08617-y
Ghasemzadeh H (2017) Multi-layer architecture for efficient steganalysis of undermp3cover in multi-encoder scenario, arXiv:1710.01230
Hu SD, Kin Tak U (2011) Novel video steganography based on non-uniform rectangular partition. In: 2011 14th IEEE International Conference on Computational Science and Engineering, pp 57–61
Hu Y, Zhang C, Su Y (2007) Information hiding based on intra prediction modes for h.264/avc. In: 2007 IEEE International Conference on Multimedia and Expo, pp 1231–1234
Idbeaa TF, Samad SA, Husain H (2015) An adaptive compressed video steganography based on pixel-value differencing schemes. In: 2015 International Conference on Advanced Technologies for Communications (ATC), pp 50–55
Jan Kodovský JF (2013) Quantitative steganalysis using rich models, pp. 8665–8665 – 11. https://doi.org/10.1117/12.2001563
Kapotas SK, Skodras AN (2008) A new data hiding scheme for scene change detection in h.264 encoded video sequences. In 2008 IEEE International Conference on Multimedia and Expo, pp 277–280
Ker AD, Bas P, Böhme R, Cogranne R, Craver S, Filler T, Fridrich J, Pevný T (2013) Moving steganography and steganalysis from the laboratory into the real world. In: Proceedings of the first ACM workshop on information hiding and multimedia security. https://doi.org/10.1145/2482513.2482965. ACM, New York, pp 45–58
Li Y, Chen HX, Zhao Y (2010) A new method of data hiding based on H.264 encoded video sequences. In: International Conference on Signal Processing Proceedings ICSP, 1833–1836
Li B, He J, Huang J, Qing Shi Y (2011) A survey on image steganography and steganalysis. Journal of Information Hiding and Multimedia Signal Processing 2 (4):142–172
Liao K, Lian S, Guo Z, Wang J (2012) Efficient information hiding in h.264/avc video coding. Telecommun Syst 49(2):261–269. https://doi.org/10.1007/s11235-010-9372-5
Liu B, Liu F, Yang C, Sun Y (2008) Secure steganography in compressed video bitstreams. In: 2008 Third International Conference on Availability, Reliability and Security. Online. Available: http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=4529506. IEEE, pp 1382–1387
Mstafa RJ, Elleithy KM (2015) A novel video steganography algorithm in the wavelet domain based on the klt tracking algorithm and bch codes. In: 2015 Long Island Systems, Applications and Technology, pp 1–7
Neufeld A, Ker AD (2013) A study of embedding operations and locations for steganography in h.264 video, pp. 8665–8665 – 14. Online. Available: https://doi.org/10.1117/12.2003680
Pan F, Xiang L, Yang XY, Guo Y (2010) Video steganography using motion vector and linear block codes. In: 2010 IEEE international conference on software engineering and service sciences, pp 592–595
Pevny T, Fridrich J, Ker AD (2012) From blind to quantitative steganalysis. In: IEEE Transactions on Information Forensics and Security, vol 7, no 2, pp 445–454
Rana S, Bhogal RK (2018) A highly secure video steganography inside dwt domain hinged on bcd codes. In: Singh R., Choudhury S., Gehlot A. (eds) Intelligent Communication, Control and Devices. Springer, Singapore, pp 719–729
Richardson IE (2003) H.264 and MPEG-4 video compression: Video Coding for Next-generation Multimedia. WILEY, (1)
Rout N, Mishra D, Mallick MK (2018) Handling imbalanced data: A survey. In: Reddy MS, Viswanath K, Shiva Prasad KM (eds) International Proceedings on advances in soft computing, intelligent systems and applications. Springer, Singapore, pp 431–443
Sadat ES, Faez K, Saffari Pour M (2018) Entropy-based video steganalysis of motion vectors. Entropy 20(4). Online. Available: http://www.mdpi.com/1099-4300/20/4/244
Schöffmann K, Fauster M, Lampl O, Böszörmenyi L, Kermarrec A-M, Bougé L (2007) An evaluation of parallelization concepts for baseline-profile compliant h.264/avc decoders. In: Priol T (ed) Euro-Par 2007 Parallel Processing. Springer, Berlin, pp 782–791
Shanableh T (2012) Data hiding in MPEG video files using multivariate regression and flexible macroblock ordering. IEEE Trans Info Forensics Secur 7(2):455–464
Su Y, Zhang C, Zhang C (2011) A video steganalytic algorithm against motion-vector-based steganography. Signal Process 91(8):1901–1909. https://doi.org/10.1016/j.sigpro.2011.02.012
Tasdemir K, Kurugollu F, Sezer S (2016) Spatio-temporal rich model-based video steganalysis on cross sections of motion vector planes. IEEE Trans Image Process 25:3316–3328
Wang C-P, Wang X-Y, Chen X-J, Zhang C (2017) Robust zero-watermarking algorithm based on polar complex exponential transform and logistic mapping. Multimedia Tools and Applications 76(24):26355–26376. https://doi.org/10.1007/s11042-016-4130-7
Wang C, Wang X, Xia Z, Zhang C (2019) Ternary radial harmonic fourier moments based robust stereo image zero-watermarking algorithm. Info Sci 470:109–120. Online. Available: http://www.sciencedirect.com/science/article/pii/S0020025517301238
Wang C, Wang X, Xia Z, Zhang C, Chen XJ (2016) Geometrically resilient color image zero-watermarking algorithm based on quaternion exponent moments. J Vis Commun Image Representation 41:247–259. Online. Available: http://www.sciencedirect.com/science/article/pii/S1047320316302103
Wang C, Wang X, Zhang C, Xia Z (2017) Geometric correction based color image watermarking using fuzzy least squares support vector machine and bessel k form distribution. Signal Process 134:197–208. Online. Available: http://www.sciencedirect.com/science/article/pii/S0165168416303528
Wang K, Zhao H, Wang H (2014) Video steganalysis against motion vector-based steganography by adding or subtracting one motion vector value. IEEE Transactions on Information Forensics and Security 9(5):741–751
Wilcox R (2012) Introduction to robust estimation and hypothesis testing (Third Edition), ser. Statistical Modeling and Decision Science. Academic Press, [Online]. Available: http://www.sciencedirect.com/science/article/pii/B9780123869838000159
Wong K, Tanaka K, Takagi K, Nakajima Y (2009) Complete video quality-preserving data hiding. IEEE Trans Circuits Sys Vid Technol 19(10):1499–1512
Wu HT, Liu Y, Huang J, Yang XY (2014) Improved steganalysis algorithm against motion vector based video steganography. In: 2014 IEEE International Conference on Image Processing (ICIP), pp 5512–5516
Xia Z, Wang X, Li X, Wang C, Unar S, Wang M, Zhao T (2019) Efficient copyright protection for three ct images based on quaternion polar harmonic fourier moments. Signal Process 164:368–379. Online. Available: http://www.sciencedirect.com/science/article/pii/S0165168419302336
Xia Z, Wang X, Zhou W, Li R, Wang C, Zhang C (2019) Color medical image lossless watermarking using chaotic system and accurate quaternion polar harmonic transforms. Signal Process 157:108–118. Online. Available: http://www.sciencedirect.com/science/article/pii/S0165168418303712
Xiph.org. (1999) https://media.xiph.org/video/derf/
Xu C, Ping X, Zhang T (2006) Steganography in compressed video stream. In: Proceedings of the first international conference on innovative computing, information and control - volume 1, ser. ICICIC ’06. IEEE Computer Society, Washington, pp 0–3, DOI https://doi.org/10.1109/ICICIC.2006.158
Yang G, Li J, He Y, Kang Z (2011) AEU - International journal of electronics and communications. In: An information hiding algorithm based on intra-prediction modes and matrix coding for H.264/AVC video stream, vol 65, pp 331–337. http://www.sciencedirect.com/science/article/pii/S1434841110001056
Yao Y, Zhang W, Yu N, Zhao X (2015) Defining embedding distortion for motion vector-based video steganography. Multimedia Tools and Applications 74 (24):11163–11186. https://doi.org/10.1007/s11042-014-2223-8
Zhang H, Cao Y, Zhao X (2016) Motion vector-based video steganography with preserved local optimality. Multimedia Tools and Applications 75(21):13503–13519. https://doi.org/10.1007/s11042-015-2743-x
Zhang H, Cao Y, Zhao X (2017) A steganalytic approach to detect motion vector modification using near-perfect estimation for local optimality. IEEE Transactions on Information Forensics and Security 12(2):465–478
Zhang H, Cao Y, Zhao X, Zhang W, Yu N (2014) Video steganography with perturbed macroblock partition. In: Proceedings of the 2Nd ACM workshop on information hiding and multimedia security. ACM, New York, pp 115–122, DOI https://doi.org/10.1145/2600918.2600936
Zhang M, Guo Y (2014) Video steganography algorithm with motion search cost minimized. In: 2014 9th IEEE Conference on Industrial Electronics and Applications, pp 940–943
Zhang Y, Zhang M, Yang X, Guo D, Liu L (2017) Novel video steganography algorithm based on secret sharing and error-correcting code for h.264/avc. Tsinghua Sci Technol 22(2):198–209
Zhu C, Lin X, Chau L-P (2002) Hexagon-based search pattern for fast block motion estimation. IEEE Trans Circuits Sys Vid Technol 12(5):349–355
Funding
Open access funding provided by University of Klagenfurt.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghamsarian, N., Schoeffmann, K. & Khademi, M. Blind MV-based video steganalysis based on joint inter-frame and intra-frame statistics. Multimed Tools Appl 80, 9137–9159 (2021). https://doi.org/10.1007/s11042-020-10001-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-020-10001-9